浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(3): 462-471 doi: 10.3785/j.issn.1008-973X.2021.03.006

土木与交通工程

基于反步法的列车制动缸压力精确控制

雷驰,, 吴萌岭

同济大学 铁道与城市轨道交通研究院，上海 201804

Backstepping based precise control of brake cylinder pressure for train

LEI Chi,, WU Meng-ling

Institute of Rail Transit, Tongji University, Shanghai 201804, China

收稿日期: 2020-02-26  

Received: 2020-02-26  

作者简介 About authors

雷驰（1991—），男，博士生，从事轨道车辆制动与安全技术研究.orcid.org/0000-0002-9072-8198.E-mail：wnleichi2009@sina.com , E-mail：wnleichi2009@sina.com

摘要

针对重载列车电控空气（ECP）制动系统，提出基于反步法的制动缸压力精确控制方法. 通过等效连续化处理和线性化处理，建立具有严格反馈方式的ECP制动系统控制模型；引入已知上界的不确定项，采用指数趋近律的滑模变结构，实现系统局部鲁棒性；基于反步法设计控制律，构造误差变量以及 Lyapunov函数；引入一阶滤波器，解决控制律中存在的“微分项数爆炸”问题. 硬件在环试验结果表明：与传统控制器相比，基于反步法的制动缸压力控制器具有更高的控制精度，其稳态控制误差在±8 kPa内，且调压过程无明显超调；在控制器中引入控制死区，可以大幅降低AV/RV阀的动作次数，提高系统使用寿命.

关键词： 电控空气制动系统 ; 等效连续化 ; 反步控制器 ; 精确控制 ; 压力

Abstract

A precise control method of brake cylinder pressure based on backstepping was proposed for the heavy-haul train equipped with electronically controlled pneumatic (ECP) brake system. A control model of ECP brake system with strict feedback form was established through equivalent continuous processing and linearization. By introducing the uncertainties with known upper bound, and adopting the sliding mode variable structure with exponential approach law, the local robustness of the system was achieved. A control law based on backstepping was designed by constructing error variables and Lyapunov function. A first-order filter was introduced to solve the problem of counting the derivative repeatedly in the control law. The performance of the controller was analyzed through hardware-in-loop test. Test results showed that, comparing with the traditional controller, the controller of brake cylinder pressure based on backstepping had a higher control accuracy, and its steady state control error was within the range of ±8 kPa without obviously overshoot in the pressure regulation process. In addition, the introduction of dead zone in the controller can significantly reduce the operation times of the AV/RV valve and improve the service life of the system.

Keywords： electronically controlled pneumatic brake system ; equivalent continuous processing ; backstepping controller ; precise control ; pressure

PDF (1546KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

雷驰, 吴萌岭. 基于反步法的列车制动缸压力精确控制. 浙江大学学报(工学版)[J], 2021, 55(3): 462-471 doi:10.3785/j.issn.1008-973X.2021.03.006

LEI Chi, WU Meng-ling. Backstepping based precise control of brake cylinder pressure for train. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(3): 462-471 doi:10.3785/j.issn.1008-973X.2021.03.006

我国重载单元列车技术研究始于20世纪80年代，至今列车编组质量已经由5000 t级提高到20000 t以上[1]. 随着列车长度的增加、牵引质量的提升，传统的空气制动技术难以保证列车制动和缓解的同步性. 因此，电控空气（electronically controlled pneumatic, ECP）制动系统的应用成为一种发展趋势. 在ECP制动系统中，各车辆通过控制2个on/off开关电磁阀（EP阀）动作，实现制动缸充排气，以实现制动缸的压力调节作用. 由于on/off电磁阀非开即关的非连续特性，传统的基于连续系统模型的控制方法不再适用. 此外，制动系统内压力空气的强非线性也增加了压力控制的难度.

Situm等[2]为了实现气动伺服系统的精确位置控制，设计PID控制器，并在考虑气源压力波动问题时引入模糊逻辑对控制器参数进行调节. 针对气动系统数学模型中存在的建模误差大、模型参数不确定以及系统外部干扰等因素， Karpenko等[3-6]采用定量反馈理论，设计固定增益的PI控制器，还分别利用速度误差触发式积分重置和减小加速度超调控制策略，缓解了控制阀死区和气缸摩擦力对控制精度的不利影响. Pandian等[7]通过用气缸两侧气腔的空气压力差作为其中一个状态量实现系统的降阶，并基于此降阶模型设计滑模控制器. 罗卓军[8]利用制动缸非线性设计的滑模控制器实现了制动缸压力的精准控制.

本研究对制动系统模型进行等效连续化处理和线性化处理，运用反步法技术设计制动缸压力控制器，通过硬件在环试验，分析并验证控制器的控制效果.

1. 电控空气制动系统简化模型

ECP制动系统简化模型如图1所示. 简化模型不计管路泄露，且视副风缸为恒压源. 制动时，AV阀打开，RV阀关闭，副风缸向制动缸充气；缓解时，AV阀关闭，RV阀打开，制动缸内压缩空气排入大气. EP阀与制动缸之间的管路连接简化为EP阀输出腔和节流孔.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   ECP制动系统简化模型

Fig.1   Simplified model of ECP brake system


不考虑腔体内气体的热传递过程，简化模型可表示为

$\left. \begin{array}{l} {{\dot p}_1} = \dfrac{{\kappa RT}}{{{V_1}}}{Q_1}, \\ {{\dot p}_2} = \dfrac{{\kappa RT}}{{{V_2}}}\left( {{Q_2} - {Q_1}} \right). \\ \end{array} \right\}$
(1)

式中： ${\dot p_1}$和 ${\dot p_2}$分别为制动缸和EP阀输出腔的气体压强变化率，V1和V2分别为制动缸和EP阀输出腔的等效体积，Q1和Q2分别为流入制动缸和EP阀输出腔的气体质量流量，T为腔体内气体温度，R为空气的气体常数，κ为空气的比热比.

1.1. 制动缸简化模型

1）充气（Q1为正）：p2≥p1

${Q_1} = {C_{q1}}{A_1}{p_2}\sqrt {\frac{2}{{RT}}} {g_{{\rm{in}}}}\left( {\frac{{{p_1}}}{{{p_2}}}} \right).$
(2)

其中，

$\;{g_{{\rm{in}}}}\left( {\frac{{{p_1}}}{{{p_2}}}} \right)\! =\! \left\{ {\begin{array}{*{20}{l}} \!\! \!\!\!\!{\sqrt {\dfrac{\kappa }{{\kappa - 1}}\left[ {{{\left( {\dfrac{{{p_1}}}{{{p_2}}}} \right)}^{\frac{2}{\kappa }}} \! -\! {{\left( {\dfrac{{{p_1}}}{{{p_2}}}} \right)}^{\frac{{\kappa + 1}}{\kappa }}}} \right]} }{,\;0.528\;3\! \leqslant\! \dfrac{{{p_1}}}{{{p_2}}} \!\leqslant 1.0;} \\ \!\!\!\!\!\! {\sqrt {\dfrac{\kappa }{{\kappa + 1}}{{\left( {\dfrac{2}{{\kappa + 1}}} \right)}^{\frac{2}{{\kappa - 1}}}}} }{,\;0 < \dfrac{{{p_1}}}{{{p_2}}} < 0.528\;3.} \end{array}} \right.$
(3)

2）排气（Q1为负）：p2<p1

${Q_1} = {C_{q1}}{A_1}{p_1}\sqrt {\frac{2}{{RT}}} {g_{{\rm{out}}}}\left( {\frac{{{p_2}}}{{{p_1}}}} \right).$
(4)

其中，

$\;{g_{{\rm{out}}}}\left( {\frac{{{p_2}}}{{{p_1}}}} \right) =\! \left\{ {\begin{array}{*{20}{l}} \!\! \!\!\!{ \!-\! \!\sqrt {\dfrac{\kappa }{{\kappa \! -\! 1}}\left[ \!{{{\left(\! {\dfrac{{{p_2}}}{{{p_1}}}}\! \right)}^{\frac{2}{\kappa }}}\! \!-\!\! {{\left( {\dfrac{{{p_2}}}{{{p_1}}}} \right)}^{\frac{{\kappa + 1}}{\kappa }}}}\! \right]} }{,\;0.528\;3 \!\leqslant \!\dfrac{{{p_2}}}{{{p_1}}} \!\leqslant\! 1.0;} \\ \!\! \! \!\!{ \!-\! \sqrt {\dfrac{\kappa }{{\kappa + 1}}{{\left( {\dfrac{2}{{\kappa + 1}}} \right)}^{\frac{2}{{\kappa - 1}}}}} }{,\;0 < \dfrac{{{p_2}}}{{{p_1}}} < 0.528\;3.} \end{array}} \right.$
(5)

A1为制动管路的有效横截面积；Cq1为气体流经制动管的气流系数.

1.2. EP阀输出腔模型

1）制动时，流入EP阀输出腔的质量流量Q2记为Q2.c，则

${Q_{2.{{\rm{c}}}}} = {C_{q2.{{\rm{c}}}}}{A_{2.{{\rm{c}}}}}{p_{\rm{s}}}\sqrt {\frac{2}{{RT}}} {g_{{\rm{in}}}}\left( {\frac{{{p_2}}}{{{p_{\rm{s}}}}}} \right).$
(6)

2）缓解时，流入EP阀输出腔的质量流量Q2记为Q2.d，则

${Q_{2.{\rm{d}}}} = {C_{q2.{\rm{d}}}}{A_{{\rm{2}}{\rm{.d}}}}{p_2}\sqrt {\frac{2}{{RT}}} {g_{{\rm{out}}}}\left( {\frac{{{p_{{\rm{atm}}}}}}{{{p_2}}}} \right).$
(7)

式中：ps为副风缸气体压强，patm为大气压强，Cq2.c、Cq2.d分别为气体流经AV阀和RV阀的气流系数，A2.c、A2.d分别为AV阀和RV阀的阀孔有效横截面积.

用A2表示任意阀孔有效横截面积，其计算公式为

${A_2} = {\rm{{\text{π}} }}d{x_{\rm{v}}}(t).$
(8)

式中：d为任意阀芯有效直径，xv(t)为阀芯位移.

制动时，流经AV阀的气体质量流量为正；缓解时，流经RV阀的气体质量流量为负. 因此，Q2可表示为

${Q_2} = {Q_{2.{{\rm{c}}}}}+{Q_{2.{\rm{d}}}}.$
(9)

2. 具有严格反馈方式的制动缸压力控制模型

2.1. 等效连续化处理

电磁阀的不连续特性导致Q2具有不连续性特性，因此，在气动系统的压力控制以及位置控制中，一般用一个PWM周期内的平均质量流量代替实际的不连续质量流量[9-10]，即

$\left. \begin{array}{l} {Q_{{\rm{2}}{{\rm{.c}}}}} = {\rm{{\text{π}}}}{C_{q2.{{\rm{c}}}}}{d_{2.{{\rm{c}}}}}{{\bar x}_{2.{{\rm{c}}}}}{p_{\rm{s}}}\sqrt {\dfrac{2}{{RT}}} {g_{{\rm{in}}}}\left( {\dfrac{{{p_2}}}{{{p_{\rm{s}}}}}} \right), \\ {Q_{{\rm{2}}{\rm{.d}}}} = {\rm{{\text{π}} }}{C_{q2.{\rm{d}}}}{d_{{\rm{2}}{\rm{.d}}}}{{\bar x}_{2.{\rm{d}}}}{p_2}\sqrt {\dfrac{2}{{RT}}} {g_{{\rm{out}}}}\left( {\dfrac{{{p_{{\rm{atm}}}}}}{{{p_2}}}} \right). \\ \end{array} \right\}$
(10)

式中：d2.c和d2.d分别为AV阀和RV阀的阀芯有效直径， $ \bar{x} $2.c和 $ \bar{x} $2.d分别为AV阀和RV阀在一个PWM周期内的阀芯平均运动位移.

$ \bar{x} _2 $是与PWM控制信号占空比τ有关的函数[11-12]：

$ {\bar x_2} = \left\{ {\begin{array}{*{20}{l}} {0,\;\;\tau \in [0,{\tau _1});}\\ {\dfrac{{{\tau _2} + {\tau _4}}}{2}{{\left[ {\dfrac{{\tau - {\tau _1}}}{{{\tau _2}}}\left( {1\! +\! \dfrac{{{\tau _3}}}{{{\tau _2}}}} \right)} \right]}^2}{x_{\rm{m}}},\;\tau \in [{\tau _1},{\tau _{12}});}\\ {\left[ {\left( {\dfrac{{{\tau _2} \!+\! {\tau _3}}}{{{\tau _2}}}} \right)\tau \!-\! {\tau _1} \!-\! \dfrac{{{\tau _2}}}{2} \!+\! \dfrac{{{\tau _4}}}{2} - \dfrac{{{\tau _1}{\tau _3}}}{{{\tau _2}}}} \right]{x_{\rm{m}}},\;\tau \in [{\tau _{12}},{\tau _{{\rm{on}}}});}\\ {\left( {\tau + {\tau _3} - {\tau _1} + \dfrac{{{\tau _4} - {\tau _2}}}{2}} \right){x_{\rm{m}}},\;\tau \in [{\tau _{{\rm{on}}}},1 - {\tau _{{\rm{off}}}});}\\ {\left( {\tau + {\tau _3} - {\tau _{\rm{c}}} + \dfrac{{{\tau _4} - {\tau _2}}}{2}} \right){x_{\rm{m}}},\;\tau \in [1 - {\tau _{{\rm{off}}}},{\tau _{34}});}\\ \left[ {1 - \dfrac{{{{(\tau + {\tau _3} - {\tau _{\rm{c}}} - 1)}^2}}}{{2{\tau _4}}} - \dfrac{{{\tau _2}{{(\tau + {\tau _3} - {\tau _{\rm{c}}} - 1)}^2}}}{{2\tau _4^2}}} \right]{x_{\rm{m}}}, \\\tau \in [{\tau _{34}},1 - {\tau _3});\\ {{x_{\rm{m}}},\;\tau \in [1 - {\tau _3},1).} \end{array}} \right. $
(11)

式中：τ1=tdo/TPWM，τ2=tmo/TPWM，τ3=tdc/TPWM，τ4=tmc/TPWM，τc=(1−τ−τ3)τ1/τ4，τ12=τ1+τ22/(τ2+τ3)，τ34=1−τ3+τ42/(τ1+τ4)，τon=τ1+τ2，τoff=τ3+τ4；TPWM为PWM信号周期，xm为阀芯最大运动位移；tdo为电磁阀开启滞后延时，tmo为电磁阀开启运动延时，tdc为电磁阀关闭滞后延时，tmc为电磁阀关闭运动延时.

如图2所示为3种控制方法下的电磁阀阀芯平均位移特性. 由式（11）可知，采用固定频率、占空比可控的PWM信号对电磁阀进行控制时存在控制死区、饱和区和非线性区. 为了有效补偿因质量流量死区造成的控制滞后和因质量流量饱和区造成的控制超前，高钦和等[13]提出将死区和饱和区线性转换补偿的方法，即将PWM控制信号的占空比从[0,1.0]映射到[τ1，1−τ3]中，转换公式为

图 2

新窗口打开| 下载原图ZIP| 生成PPT

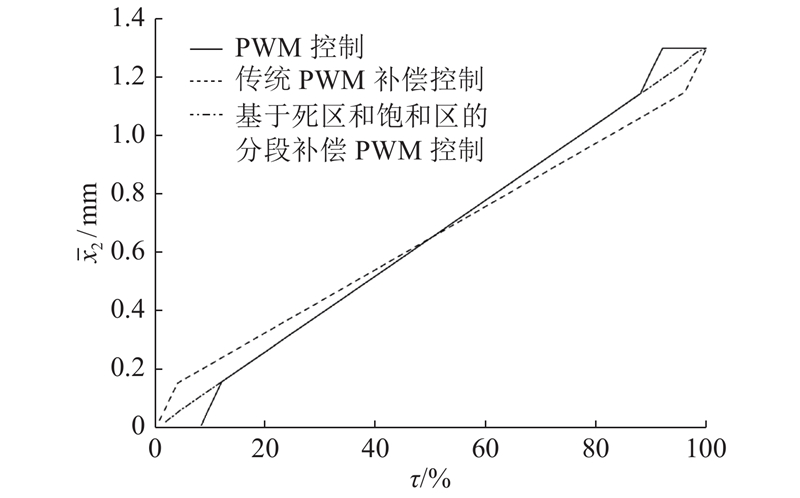
图 2   3种控制方法下的电磁阀平均位移特性

Fig.2   Average displacement characteristics of solenoid valve spool under three control methods


$\tau ' = (1 - {\tau _1} - {\tau _3})\tau + {\tau _1}.$
(12)

式中： $\tau '$为转换后的PWM控制信号占空比.

该控制方法虽然能有效补偿电磁阀的死区和饱和区，但是改变了通过流量变化率. 因此，本研究采用基于死区和饱和区分段补偿的PWM控制：1）将包含死区和非线性区段的[0，τ1+τ2）转变为[τ1，τ1+τ2），转换公式为

${\tau _{\rm{d}}} = \frac{{{t_{\rm{mo}}}}}{{{t_{\rm{do}}} + {t_{\rm{mo}}}}}\tau + {\tau _1}.$
(13)

2）将包含饱和区和非线性区段的（1−τ3−τ4,1]线性转换为（1−τ3−τ4,1−τ3]，其转换公式为

${\tau _{\rm{d}}} = \frac{{{t_{\rm{mc}}}}}{{{t_{\rm{dc}}} + {t_{\rm{mc}}}}}\tau + \frac{{{t_{\rm{dc}}}}}{{{t_{\rm{dc}}} + {t_{\rm{mc}}}}} - {\tau _3}.$
(14)

基于分段补偿的PWM控制信号的占空比可将[0,1]映射到[τ1,1−τ3]：

${\tau _d} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{t_{\rm{mo}}}}}{{{t_{\rm{do}}} + {t_{\rm{mo}}}}}\tau + {\tau _1},\;\tau \in [0,{\tau _1} + {\tau _2});}\\ {\tau ,\;\tau \in [{\tau _1} + {\tau _2},1 - {\tau _3} - {\tau _4}];}\\ {\dfrac{{{t_{\rm{mc}}}}}{{{t_{\rm{dc}}} + {t_{\rm{mc}}}}}\tau + \dfrac{{{t_{\rm{dc}}}}}{{{t_{\rm{dc}}} + {t_{\rm{mc}}}}} - {\tau _3},\;\tau \in (1 - {\tau _3} - {\tau _4},1].} \end{array}} \right.$
(15)

采用分段补偿的PWM控制信号既可以有效补偿电磁阀的死区和饱和区，同时不改变阀芯平均通过流量变化率.

综上所述，ECP制动系统的不连续系统模型可等效转化为连续系统模型，且EP阀输出腔的气体质量流量的精确控制可通过控制PWM周期的占空比参数实现.

2.2. 线性化处理

反步控制方法能较好地处理非线性系统控制问题，且设计结构简单、具有严格的理论推导依据，但是该方法要求被控系统必须满足严格反馈方式. 因此，在运用反步控制法之前，需要对制动缸压力控制模型进行转换处理.

具有严格反馈方式的系统，采用如下模型进行描述：

$\left. \begin{array}{l} {{\dot x}_1} = f{}_1({x_1}) + {l_1}({x_1}){x_2}, \\ {{\dot x}_2} = f{}_2({x_1},{x_2}) + {l_2}({x_1},{x_2}){x_3}, \\ \vdots \\ {{\dot x}_i} = f{}_i({x_1},{x_2}, \cdots ,{x_i}) + {l_i}({x_1},{x_2}, \cdots ,{x_i}){x_{i + 1}}, \\ \vdots \\ {{\dot x}_{n - 1}} = f{}_{n - 1}({x_1},{x_2}, \cdots ,{x_{n - 1}}) + {l_{n - 1}}({x_1},{x_2}, \cdots ,{x_{n - 1}}){x_n}, \\ {{\dot x}_n} = f{}_n({x_1},{x_2}, \cdots ,{x_n}) + {l_n}({x_1},{x_2}, \cdots ,{x_n})\mu . \\ \end{array} \right\}$
(16)

式中：x=（x1, x2,···, xn）T为系统状态变量，μ为系统的控制输入. 为了将制动系统的数学模型转换为具有严格反馈方式的系统结构，须将制动缸气体质量流量转换为Q1=f(p1)+l(p1)p2形式. 由于式（2）中的gin(p1/p2)与式（4）中gout(p1/p2)为非线性函数，须进行线性化处理.

当p2≥p1时，对于函数gin(p1/p2)进行五段式分段函数处理：

$\begin{array}{l} {g_{{\rm{in}}}}\left( {\dfrac{{{p_1}}}{{{p_2}}}} \right) = \\ \left\{\!\!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}}\\ \begin{array}{l} \dfrac{{0.000\;1}}{{0.528\;3}}\dfrac{{{p_1}}}{{{p_2}}} + 0.484\;1,\; \dfrac{{{p_1}}}{{{p_2}}} \in \left[0,\; {0.528\;3} \right); \\ \dfrac{{0.484\;2 \!-\! 0.451\;4}}{{0.528\;3\! - \!0.7}}\left(\! {\dfrac{{{p_1}}}{{{p_2}}}\! - \!0.7} \right) \!+ \!0.451\;4 ,\; \dfrac{{{p_1}}}{{{p_2}}} \in \left[0.528\;3,\; {0.7} \right); \\ \dfrac{{0.451\;4\! - \!0.354\;8}}{{0.7\! -\! 0.85}}\left( \!{\dfrac{{{p_1}}}{{{p_2}}} \!-\! 0.85} \right) \!+\! 0.354\;8,\; \dfrac{{{p_1}}}{{{p_2}}} \in \left[0.7,\; {0.85} \right); \\ \dfrac{{0.354\;8 \!-\! 0.217\;5}}{{0.85 \!- \!0.95}}\left( \!{\dfrac{{{p_1}}}{{{p_2}}}\! - \!0.95} \right) \!+\! 0.217\;5,\; \dfrac{{{p_1}}}{{{p_2}}} \in \left[0.85,\; {0.95} \right); \\ \dfrac{{0.217\;5}}{{0.95 - 1}}\left( {\dfrac{{{p_1}}}{{{p_2}}} - 1} \right) ,\; \dfrac{{{p_1}}}{{{p_2}}} \in [0.95,\; 1] . \\ \end{array} \end{array}} \right.\end{array} $
(17)

经过分段处理的制动缸气体质量流量可表示为

$\begin{array}{l} {Q_1}^{\prime } = {W_1}{p_2}{g_{{\rm{in}}}}\left( {\dfrac{{{p_1}}}{{{p_2}}}} \right). \end{array} $
(18)

式中：W1=Cq1+A1. ECP制动系统的数学模型转换为具有严格反馈方式的结构：

$ \left. {\begin{array}{l}{\dot{p}}_{1}=\dfrac{\kappa RT}{{V}_{1}}\left( {\alpha {p}_{1}+\beta {p}_{2}} \right),\\ {\dot{p}}_{2}=-\dfrac{\kappa RT}{{V}_{2}}\left( {\alpha {p}_{1}+\beta {p}_{2}} \right)+\dfrac{\kappa RT}{{V}_{2}}{Q}_{2}.\end{array}} \right\}$
(19)

$\alpha = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \dfrac{{0.000\;1}}{{0.528\;3}}{W_1} ,\;\qquad\qquad\!\!\dfrac{{{p_1}}}{{{p_2}}} \in \left[0,\; {0.528\;3} \right); \\ \dfrac{{0.484\;2 - 0.451\;4}}{{0.528\;3 - 0.7}}{W_1} ,\;\dfrac{{{p_1}}}{{{p_2}}} \in \left[0.528\;3,\; {0.7} \right) ; \\ \dfrac{{0.451\;4 - 0.354\;8}}{{0.7 - 0.85}}{W_1} ,\;\dfrac{{{p_1}}}{{{p_2}}} \in \left[0.7,\; {0.85} \right) ;\\ \dfrac{{0.354\;8 - 0.217\;5}}{{0.85 - 0.95}}{W_1} ,\;\dfrac{{{p_1}}}{{{p_2}}} \in \left[0.85,\; {0.95} \right); \\ \dfrac{{0.217\;5}}{{0.95 - 1}}{W_1} ,\;\qquad\qquad\!\!\!\dfrac{{{p_1}}}{{{p_2}}} \in [0.95,\; 1] . \\ \end{array} \end{array}} \right.$
(20)

$\beta = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} \begin{array}{l} 0.484\;1{W_1} ,\;{{{p_1}}}/{{{p_2}}} \in \left[0, {0.528\;3} \right) ; \\ {\rm{0}}{\rm{.585\;1}}{W_1} ,\;{{{p_1}}}/{{{p_2}}} \in \left[0.528\;3, {0.7} \right) ; \\ 0.902\;2{W_1} ,\;{{{p_1}}}/{{{p_2}}} \in \left[0.7, {0.85} \right) ; \\ 1.521\;9{W_1} ,\;{{{p_1}}}/{{{p_2}}} \in \left[0.85, {0.95} \right); \\ 4.35{W_1}{\rm{ }} ,\;\quad{{{p_1}}}/{{{p_2}}} \in [0.95, 1] . \\ \end{array} \end{array}} \end{array}} \right.$
(21)

当p2<p1时，可采用同样的方法，对非线性函数gout(p1/p2)进行分段函数处理，以得到对应的具有严格反馈方式的结构模型.

3. 反步控制器设计

基于反步法理论进行制动缸压力控制器设计，流程图如图3所示. 具体步骤如下：1）通过比较EP阀输出腔压强p2和制动缸实际压强p1的大小，确定气体质量流量转换系数α和β；2）计算实际制动缸压强p1与目标值p1d之差，确定EP阀输出腔压力的理论参考值p2d；3）计算实际EP阀输出腔压力p2与理论参考值p2d之差，确定流经EP阀的气体质量流量Q2. 当Q2>0时，AV阀开启，副风缸向制动缸充气；当Q2<0时，RV阀开启，制动缸向大气排气. 结合阀芯结构参数以及反步法计算得到的理论气体质量流量Q2计算阀芯平均运动位移，根据基于死区和饱和区分段补偿的PWM控制策略中平均位移与占空比的映射关系，推导出AV/RV阀的PWM周期的占空比.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   制动缸压力控制器设计流程图

Fig.3   Flow chart of brake cylinder pressure controller design


在搭建满足反步法控制的ECP制动系统的数学模型时，式(1)忽略了缸内气体热传递过程；对气体质量流量式（2）、（4）进行线性化处理时引入了模型误差；此外，系统还存在气体泄漏等误差因素. 因此，在设计制动缸压力控制器之前，应在式（19）的基础上引入已知上界的不确定项，以消除建模误差.基于反步法控制器的ECP制动系统数学模型可表示为

$ \left. {\begin{array}{l}{\dot{p}}_{1}=\dfrac{\kappa RT}{{V}_{1}}\left( {\alpha {p}_{1}+\beta {p}_{2}} \right)+\Delta {p}_{1},\\ {\dot{p}}_{2}=-\dfrac{\kappa RT}{{V}_{2}}\left( {\alpha {p}_{1}+\beta {p}_{2}} \right)+\dfrac{\kappa RT}{{V}_{2}}{Q}_{2}+\Delta {p}_{2}.\end{array}} \right\}$
(22)

式中：Δp1与Δp2为不确定项，且|Δp1|≤B1，|Δp2|≤B2，B1与B2分别为不确定项Δp1与Δp2的上界.

定义误差变量

$\left. \begin{array}{l} {s_1} = {p_1} - {p_{1{\rm{d}}}}, \\ {s_2} = {p_2} - {p_{2{\rm{d}}}}. \\ \end{array} \right\}$
(23)

3.1. EP阀输出腔理论压力虚拟控制律设计

对s1求导，求出EP阀输出腔理论压力p2d：

$ {\dot{s}}_{1}={\dot{p}}_{1}-{\dot{p}}_{1{\rm{d}}}=\frac{\kappa RT}{{V}_{1}}(\alpha {p}_{1}+\beta {p}_{2})+\Delta {p}_{1}-{\dot{p}}_{1{\rm{d}}}.$
(24)

取滑模趋近律为指数趋近：

${\dot s_1} = - {B_1}{\rm{sgn}} \;({s_1}) - {\sigma _1}{s_1}.$
(25)

式中：B1、σ1均为正常数，且σ1为s1的自适应参数. 设计p2d的虚拟控制律

${p_{2{\rm{d}}}} = \frac{1}{{\dfrac{{\kappa RT}}{{{V_1}}}\beta }}\left[ { - \dfrac{{\kappa RT}}{{{V_1}}}\alpha {p_1} + {{\dot p}_{1{\rm{d}}}} - {B_1}{\rm{sgn}} \;({s_1}) \hat \sigma {}_1{s_1}} \right].$
(26)

式中： $\hat{\sigma }$1为σ1的估计值，估计误差为 $ {\tilde \sigma _1} $=σ1− $ {\hat \sigma _1} $，σ1的自适应律为 $\dot{\tilde{\sigma }}_1$=ρ1$s^2_1 $，ρ1为自适应调节速率的正常数.

构造Lyapunov函数为

${Y_1} = \frac{1}{2}s_1^2 + \frac{1}{{2{\rho _1}}}\tilde \sigma _1^2.$
(27)

则

$ \begin{split}&{\dot{Y}}_{1}=s{}_{1}\dot{s}{}_{1}+\frac{1}{{\rho }_{1}}{\tilde{\sigma }}_{1}{\dot{\tilde{\sigma }}}_{1}=\\& {s}_{1}\left[\dfrac{\kappa RT}{{V}_{1}}(\alpha {p}_{1}+\beta {p}_{2})+\Delta {p}_{1}-{\dot{p}}_{1{\rm{d}}}\right]-{s}_{1}^{2}\left({\sigma }_{1}-{\hat{\sigma }}_{1}\right).\\[-12pt]\end{split}$
(28)

式中：令s2=p2−p2d，则p2=s2+ p2d，带入式（28）可得

$\begin{split} {{\dot Y}_1} =& {s_1}\left[ {\frac{{\kappa RT}}{{{V_1}}}\alpha {p_1} + \dfrac{{\kappa RT}}{{{V_1}}}\beta \left( {{s_2} + {p_{2{\rm{d}}}}} \right)+\Delta {p_1} - {{\dot p}_{1{\rm{d}}}}} \right]- \\ & s_1^2\left( {{\sigma _1} - {{\hat \sigma }_1}} \right)= \\ &\dfrac{{\kappa RT}}{{{V_1}}}\beta {s_1}{s_2} - s_1^2{{\hat \sigma }_1} - {B_1}\left| {{s_1}} \right| + \Delta {p_1}{s_1} - s_1^2\left( {{\sigma _1} - {{\hat \sigma }_1}} \right) \leqslant \\ &\dfrac{{\kappa RT}}{{{V_1}}}\beta {s_1}{s_2} - s_1^2{\sigma _1} - {B_1}\left| {{s_1}} \right| + \left| {\Delta {p_1}} \right|\left| {{s_1}} \right|. \\[-12pt] \end{split} $
(29)

因为|Δp1|≤B1，所以

${\dot Y_1} \leqslant \dfrac{{\kappa RT}}{{{V_1}}}\beta {s_1}{s_2} - s_1^2{\sigma _1}.$
(30)

此时若s2→0，则 $ \dot{Y} $1≤0，则s1可逐渐收敛至0.

3.2. EP阀输出腔的气体质量流量控制律设计

对s2求导，求出流入EP阀输出腔的气体质量流量Q2:

$ \begin{split} {{\dot s}_2} = &{{\dot p}_2} - {{\dot p}_{2{\rm{d}}}} = \\ & - \dfrac{{\kappa RT}}{{{V_2}}}(\alpha {p_1} + \beta {p_2}) + \dfrac{{\kappa RT}}{{{V_2}}}{Q_2} + \Delta {p_2} - {{\dot p}_{2{\rm{d}}}}. \\[-12pt] \end{split} $
(31)

取滑模趋近律为指数趋近：

${\dot s_2} = - {B_2}{\rm{sgn}} ({s_2}) - {\sigma _2}{s_2}.$
(32)

式中：B2、σ2均为正常数，且σ2为s2的自适应参数. 设计流入EP阀输出腔的气体质量流量Q2的控制律：

$\begin{split} {Q_2} = \dfrac{1}{{\dfrac{{\kappa RT}}{{{V_2}}}}}\left[ \dfrac{\kappa RT}{{{V}_{2}}}(\alpha {{p}_{1}}+\beta {{p}_{2}})+{{{\dot{p}}}_{2{\rm{d}}}}- \right.\\ \qquad\left. {{B}_{2}}\text{sgn}\ ({{s}_{2}})-{{{\hat{\sigma }}}_{2}}{{s}_{2}}-\dfrac{\kappa RT}{{{V}_{1}}}\beta {{s}_{1}} \right]. \end{split}$
(33)

式中： $\hat{\sigma }_2$为σ2的估计值，估计误差为 $ \tilde \sigma _2$=σ2− $ {\hat \sigma _2}$，σ2的自适应律为 $\dot{\tilde{\sigma }}_2$=ρ2$ s^2_2 $，ρ2为自适应调节速率的正常数.

构造Lyapunov函数为

${Y_2} = \frac{1}{2}s_1^2 + \frac{1}{2}s_2^2+\frac{1}{{2{\rho _1}}}\tilde \sigma _1^2+\frac{1}{{2{\rho _2}}}\tilde \sigma _2^2.$
(34)

对式（34）进行求导，并将式（33）带入

$\begin{split} {{\dot Y}_2} \leqslant & \dfrac{{\kappa RT}}{{{V_1}}}\beta {s_1}{s_2} - s_1^2{\sigma _1}+s{}_2{{\dot s}_2} + \dfrac{1}{{{\rho _2}}}{{\tilde \sigma }_2}{{\dot {\tilde \sigma }}_2} = \\ &- s_1^2{\sigma _1} - s_2^2{\sigma _2} - {B_2}\left| {{s_2}} \right| + \Delta {p_2}{s_2}. \\ \end{split} $
(35)

因为|ΔP2|≤B2，所以

${\dot Y_2} \leqslant - s_1^2{\sigma _1} - s_2^2{\sigma _2} \leqslant 0.$
(36)

由于 $ \dot{Y} $2≤0，s2可逐渐收敛至0，使 $ \dot{Y} $1≤0，s1可逐渐收敛至0，即全部状态变量误差均可收敛至0，实现了整个系统的渐进稳定.

3.3. AV/RV阀的PWM周期的占空比计算

求出AV/RV电磁阀的PWM信号占空比τd.c，τd.d.

当Q2≥0时，AV电磁阀开启，RV电磁阀关闭，此时制动系统处于充气状态，

$ {\overline{x}}_{2.{\rm{c}}}({\tau }_{d{\rm{.c}}})=\frac{{Q}_{2}}{{\rm{{\text{π}} }}{C}_{q.{\rm{c}}}{d}_{2.{\rm{c}}}{p}_{{\rm{s}}}\sqrt{2/(RT)}{g}_{\rm{in}}({p}_{2}/{p}_{{\rm{s}}})}.$
(37)

当Q2<0时，RV电磁阀开启，AV电磁阀关闭，此时制动系统处于排气状态，

$ {\overline{x}}_{2.\rm{d}}({\tau }_{d\rm{.d}})=\frac{{Q}_{2}}{{\rm{{\text{π}} }}{C}_{q.\rm{d}}{d}_{2.\rm{d}}{p}_{2}\sqrt{2/(RT)}{g}_{\rm{out}}({p}_{\rm{atm}}/{p}_{2})}.$
(38)

由式（11）计算得到阀芯平均运动位移 $\overline{x}_2$对应的τ：

$\tau = {f^{ - 1}}({\bar x_2}).$
(39)

再由式（15）计算出基于分段补偿的PWM控制信号的τd：

${\tau _d} = f(\tau ).$
(40)

3.4. “微分项数爆炸”问题分析

由式（26）、（33）可知，虚拟控制量p2d的控制律中包含制动缸目标函数的导数项 $ \dot{p}_{\rm{1d}} $，Q2控制律包含虚拟控制变量的导数项 $ \dot{p} $2d. 因此存在着对制动缸压力控制目标函数的两次求导，增加了控制器的计算量，易造成“计算爆炸”问题.

在反步法设计中引入一阶滤波器估计虚拟控制输入的导数，避免“计算爆炸”问题，同时对可能包含传感器噪声的输入信号进行滤波，改善了系统的动态特性.令

${\hat p_{2{\rm{d}}}} = \dfrac{1}{{\dfrac{{\kappa RT}}{{{V_1}}}\beta }}\left[ { - \frac{{\kappa RT}}{{{V_1}}}\alpha {p_1} + {{\dot p}_{1{\rm{d}}}} - \frac{{B_1^2{s_1}}}{{2\varepsilon }} - \hat \sigma {}_1{s_1}} \right].$
(41)

式中：ε为任意小的正常数. 若p2d能渐进跟踪 $\hat{p}$2d，则s1同样能够收敛到ε的某个邻域内，即s2→0. 此时让 $\hat{p}$2d通过一阶滤波器来代替p2d，即

${p_{2{\rm{d}}}} = \frac{1}{{\lambda s + 1}}{\hat p_{2{\rm{d}}}}.$
(42)

式中：λ为滤波常数，是极小的正常数. 虚拟控制的导数为

${\dot p_{2{\rm{d}}}} = \frac{{{{\hat p}_{2{\rm{d}}}} - {p_{2{\rm{d}}}}}}{\lambda }.$
(43)

相应地，流经EP阀的气体质量流量可表示为

$\begin{split} {Q_2} =& \dfrac{1}{{\dfrac{{\kappa RT}}{{{V_2}}}}}\left[ \dfrac{\kappa RT}{{{V}_{2}}}(\alpha {{p}_{1}}+\beta {{p}_{2}})+{{{\dot{p}}}_{2\text{d}}}- \right.\\ & \left. \dfrac{B_{2}^{2}{{s}_{2}}}{2\varepsilon }-{{{\hat{\sigma }}}_{2}}{{s}_{2}}-\dfrac{\kappa RT}{{{V}_{1}}}\beta {{s}_{1}} \right]. \end{split}$
(44)

令目标制动缸压力为 $\hat{p}_{\rm{1d}}$，经过一阶滤波器后得到p1d，则

${p_{1{\rm{d}}}} = \frac{1}{{\lambda s + 1}}{\hat p_{1{\rm{d}}}}.$
(45)

p1d为输入制动缸压力控制器的制动缸目标压力，此时，

${\dot p_{1{\rm{d}}}} = \frac{{{{\hat p}_{1{\rm{d}}}} - {p_{1{\rm{d}}}}}}{\lambda }.$
(46)

4. 硬件在环试验与分析

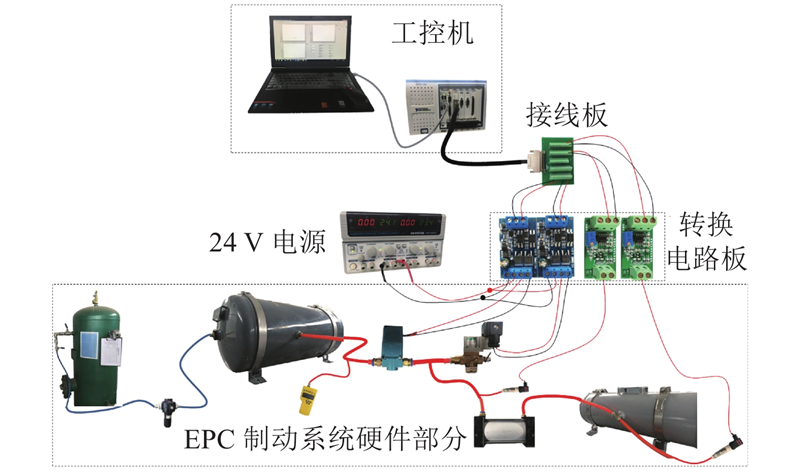
搭建硬件在环试验台，如图4所示. 该试验台主要由工控机、ECP制动系统硬件、信号转换电路、DC24 V电源、接线板等组成. 工控机基于NI-PXI系统，搭载有反步控制算法，用以实时控制ECP制动系统的制动缸压力；ECP制动系统硬件包括1 MPa风源、100 L副风缸、30 L制动缸、1.5 L小风缸（模拟EP输出腔）、2个on/off开关电磁阀、压力传感器、管路等；信号转换电路用于处理工控机与传感器之间信号采集的匹配问题；电源给各个电器元件供电.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   ECP制动系统硬件在环（HIL）试验台示意图

Fig.4   Schematic diagram of ECP brake system (HIL) test bench


4.1. 参数设置

如表1所示为AV电磁阀和RV电磁阀选用参数，PWM频率为10 Hz.

结合式（11）可得AV阀与RV阀的阀芯动作位移与占空比的关系：

表 1   AV/RV电磁阀特性参数

Tab.1  AV/RV solenoid valve characteristic parameters

类别 tdo/ms tmo/ms tdc/ms tmc/ms d/ms xm/ms Cq2
AV阀 8 7 1 2 6 0.3 0.68
RV阀 5 6 2 4 10 0.25 0.6

新窗口打开| 下载CSV


${\bar x_{2.{{\rm{c}}}}} = \left\{ {\begin{array}{*{20}{c}} \!\!\!\!\!\!\!\! \begin{array}{l} 0 , \\ 12{\left[ {{\tau _{{\rm d}{{\rm{.c}}}}} - 0.08} \right]^2}{x_{{\rm{m}}.{{\rm{c}}}}} ,\\ \left( {1.14{\tau _{{\rm{d}}{{\rm{.c}}}}} - 0.116} \right){x_{{\rm{m}}.{{\rm{c}}}}} ,\\ \left( {{\tau _{{\rm{d}}{{\rm{.c}}}}} - 0.095} \right){x_{{\rm{m}}.{{\rm{c}}}}} ,\\ \left( {5{\tau _{{\rm{d}}{{\rm{.c}}}}} - 3.975} \right){x_{{\rm{m}}.{{\rm{c}}}}} ,\\ \left[ {1 - 112.5{{\left( {5{\tau _{{\rm{d}}{{\rm{.c}}}}} - 4.95} \right)}^2}} \right]{x_{{\rm{m}}.{{\rm{c}}}}}, \\ {x_{{\rm{m}}.{{\rm{c}}}}}, \\ \end{array} \!\!\!\!\!\!\!\!\begin{array}{l} {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0,0.08} \right)} \right.; \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0.08,0.141} \right);} \right. \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0.141,0.15} \right)} \right.; \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0.15,0.97} \right)} \right.; \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0.97,0.986} \right)} \right.; \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0.986,0.99} \right)} \right.; \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {\left. {0.99,1} \right)} \right.. \\ \end{array} \end{array}} \right.$
(47)

$\begin{array}{l} {{\bar x}_{2.{\rm{d}}}} = \\ \left\{ {\begin{array}{*{20}{c}} \!\!\!\!\!\!\! \!\begin{array}{l} 0, \\ 0.2{\left[ {{{\left( {{\tau _{{\rm{d}}{\rm{.d}}}} - 0.05} \right)} / {0.09}}} \right]^2}{x_{{\rm{m}}.{\rm{d}}}}, \\ \left[ {{{\left( {4{\tau _{{\rm{d}}{\rm{.d}}}} - 0.05} \right)} / 3} - 0.06} \right]{x_{{\rm{m}}.{\rm{d}}}}, \\ \left( {{\tau _{{\rm{d}}{\rm{.d}}}} - 0.04} \right){x_{{\rm{m}}.{\rm{d}}}}, \\ \left( {2.25{\tau _{{\rm{d}}{\rm{.d}}}} - 1.215} \right){x_{{\rm{m}}.{\rm{d}}}} , \\ \left[ {1 - 31.25{{\left( {2.25{\tau _{{\rm{d}}{\rm{.d}}}} - 2.205} \right)}^2}} \right]{x_{{\rm{m}}.{\rm{d}}}}, \\ {x_{{\rm{m}}.{\rm{d}}}}, \\ \end{array} \!\!\!\!\!\!\!\!\begin{array}{l} {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0,0.05} \right)} \right.; \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0.05,0.095} \right);} \right. \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0.095,0.11} \right)} \right.; \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0.11,0.94} \right)} \right.; \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0.94,0.962} \right)} \right.; \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0.962,0.98} \right)} \right.; \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {\left. {0.98,1} \right)} \right.. \\ \end{array} \end{array}} \right.\end{array}$
(48)

式中： $ \bar{x} $2.c/ $ \bar{x} $2.d， $ \bar{x} $m.c/ $ \bar{x} $m.d以及τd.c、τd.d分别为AV/RV电磁阀阀芯的平均位移、阀芯最大位移量以及制动缸压力控制器计算得到的PWM占空比. 结合式（15）可得

${\tau _{{\rm{d}}\_{{\rm{c}}}}} = \left\{ {\begin{array}{*{20}{l}} \!\!\!\!\!\!\!\!\begin{array}{l} {{7{\tau _{{\rm{d}}{{\rm{.c}}}}}} / {15}}+0.08 ,\\ {\tau _{{\rm{d}}{{\rm{.c}}}}}, \\ {{\left( {2{\tau _{{\rm{d}}{{\rm{.c}}}}}+1} \right)} / 3} - 0.01, \\ \end{array} &\begin{array}{l} {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {0,0.15} \right); \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {0.15,0.97} \right); \\ {\tau _{{\rm{d}}{{\rm{.c}}}}} \in \left[ {0.97,1} \right]. \\ \end{array} \end{array}} \right.$
(49)

${\tau _{{\rm{d}}\_{\rm{d}}}} = \left\{ {\begin{array}{*{20}{l}} \!\!\!\!\!\!\!\! \begin{array}{l} {{6{\tau _{{\rm{d}}{\rm{.d}}}}} / {11}}+0.05, \\ {\tau _{{\rm{d}}{\rm{.d}}}}, \\ {{\left( {2{\tau _{{\rm{d}}{\rm{.d}}}} + 1} \right)} / 3} - 0.02, \\ \end{array} &\begin{array}{l} {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {0,0.11} \right); \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {0.11,0.94} \right); \\ {\tau _{{\rm{d}}{\rm{.d}}}} \in \left[ {0.94,1} \right]. \\ \end{array} \end{array}} \right.$
(50)

式中：τd_c、τd_d分别为AV/RV电磁阀实际接收到的PWM信号占空比. 因此，制动缸压力控制器的实际输出为τd_c、τd_d.

基于反步法的制动缸压力控制器其他参数如表2所示.

表 2   基于反步法的制动缸压力控制器参数

Tab.2  AV/RV solenoid valve characteristic parameters

参数 符号 数值
不确定项上界 B1，B2 0.5
误差变量自适应参数初值 σ10，σ20 1×10−8，1×10−9
自适应变化率 ρ1，ρ2 1×10−11
边界层厚度 ε 0.02
一阶滤波器 λ 0.005

新窗口打开| 下载CSV


4.2. 试验结果与分析

分别在阶跃和正弦输入信号下，对比分析基于反步法的制动缸压力控制器与传统制动缸压力控制器的稳态控制误差、充排气时间、超调等参数，评价控制器的稳态和瞬态控制性能.

4.2.1. 阶跃制动与缓解作用分析

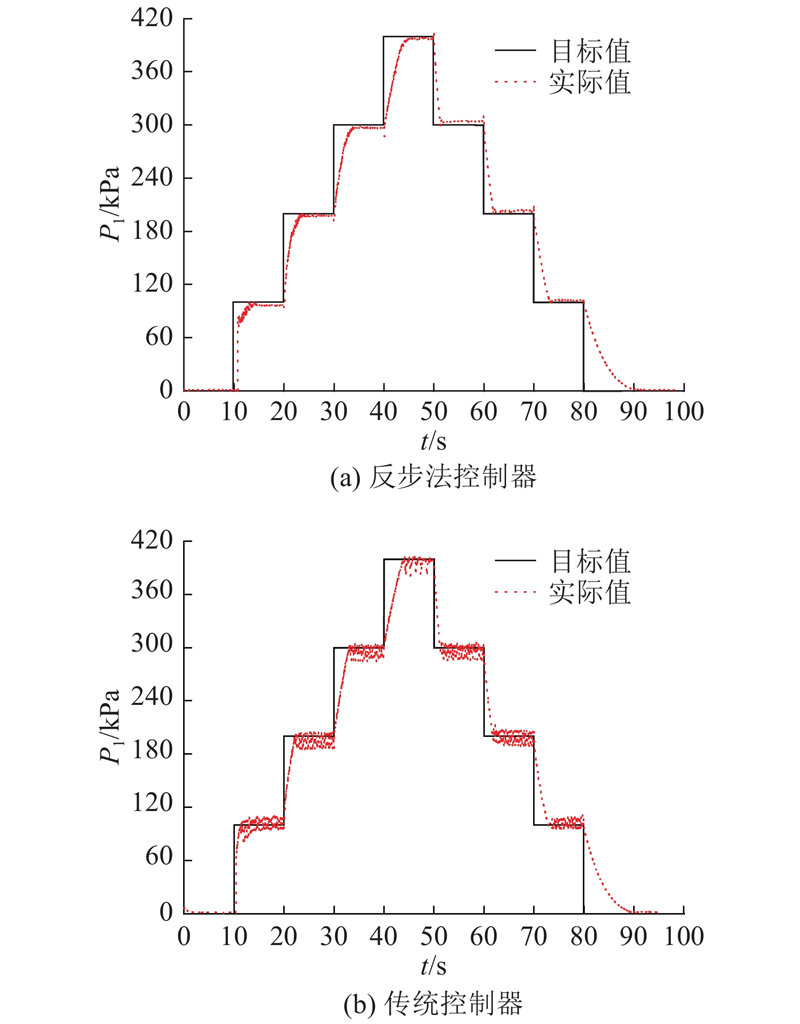
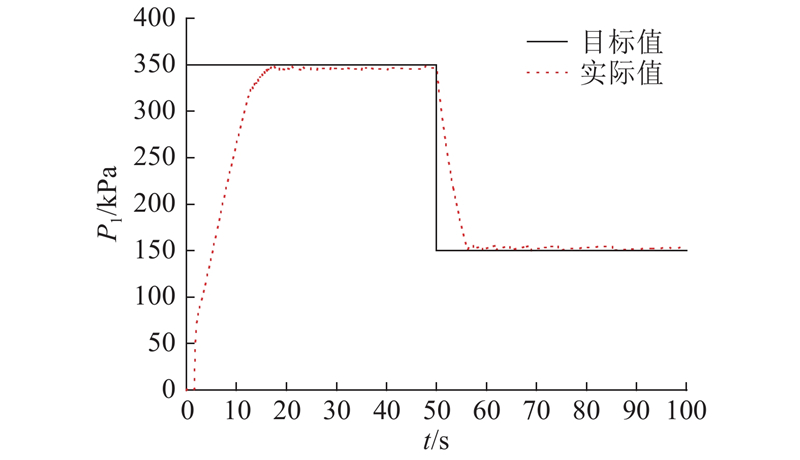
设置目标制动缸压力为阶段上升/下降，试验结果如图5所示. 虽然2种控制器在响应时间上差异不大，但是在稳态控制误差方面有着较大的差异. 传统制动缸压力控制器的稳态控制误差在−15~20 kPa，而基于反步法的制动缸压力控制器可使得制动缸压力误差保持在±5 kPa以内. 此外，由图5（a）可知：充气时，制动缸压力目标值均比实际值大；排气时，目标值则比实际值小. 这是因为在制动缸实际压力逐渐接近目标值时，误差变量s逐渐变小，使得自适应参数变化率 $ \dot{\sigma } $以及误差变量的变化率 $\dot s$逐渐减小. 因此在逐渐接近目标值阶段，控制器输出占空比较小的PWM信号，用以连续调整制动缸的实际压力，这样就可以有效避免过充/超排现象发生.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   制动系统阶跃响应

Fig.5   Step response of brake system


为进一步说明控制器输出的控制信号占空比，绘制阶跃响应下占空比信号如图6所示. 由图5（a）和图6可知，当目标制动缸压力逐步增大时，AV电磁阀接收到的占空比为99%的控制信号的持续时间变长. 这是由于目标制动缸压力的上升使得制动缸与副风缸压差变小，流经AV电磁阀的气体质量流量减小，为达到目标值，AV电磁阀开启时间更长. 同样地，当目标制动缸压力逐步减小时，RV电磁阀接收到的占空比为98%的控制信号的持续时间也在增加. 在充气过程中，随着实际值无限逼近目标值，由于未设置控制死区，此时AV电磁阀仍然不断工作，并且占空比基本维持在15%左右；而RV电磁阀在真实值接近于目标值后占空比稳定在10%附近.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

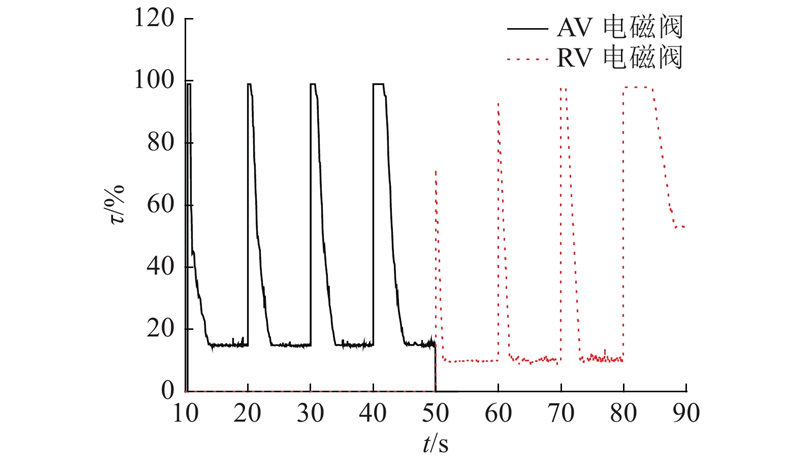
图 6   阶跃响应下反步控制器输出的占空比信号

Fig.6   Duty cycle output signal of backstepping controller in step response


4.2.2. 正弦输入信号分析

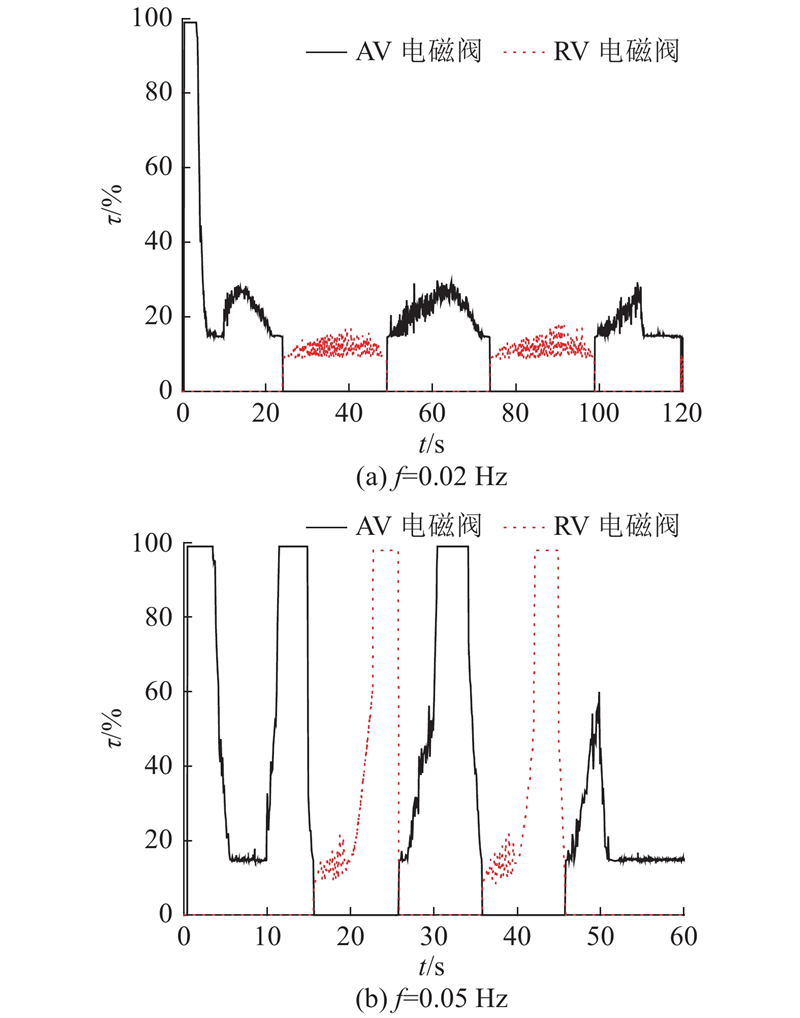
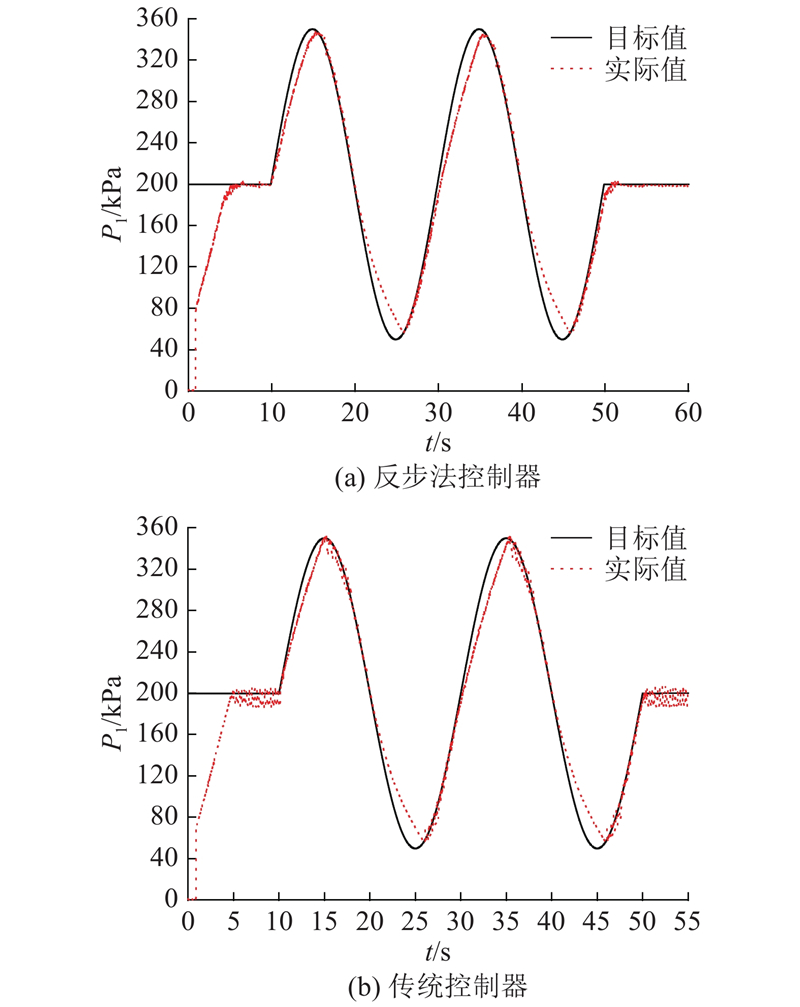
以不同频率f的正弦输入信号作为目标压力，考察2种制动缸压力控制器的响应特性. 当目标压力的频率为0.02 Hz时，如图7所示，2种控制方法均能够较好地跟踪目标压力.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   制动系统频率响应（f=0.02 Hz）

Fig.7   Frequency response of brake system（f=0.02 Hz）


对基于反步法的制动缸压力控制器而言，当输入信号频率为0.02 Hz时，系统控制误差在±8 kPa以内，其输出控制信号如图9（a）所示，在控制过程中AV电磁阀的占空比主要在15%~35%变化，而RV电磁阀占空比在10%~18%波动. AV/RV电磁阀的占空比范围除了受AV/RV电磁阀本身的延时特性参数约束外，还受电磁阀的结构参数影响. 由于RV电磁阀的孔径比AV电磁阀的大，RV电磁阀的占空比波动范围比AV电磁阀的小.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   频率响应下反步控制器输出的占空比信号

Fig.9   Duty cycle output signal of backstepping controller in frequency response


对于传统制动缸压力控制器而言，当输入信号频率为0.02 Hz时，其控制误差为−10~20 kPa. 其中，在前1/4周期内制动缸实际压力比目标值小，这是由于在前1/4周期时，随着制动缸压力的逐步上升，制动缸与外界大气压的压差逐渐变大，制动缸与副风缸的压差则逐渐变小，由于RV电磁阀孔径较大，使得气体的排气速率更快，导致制动缸实际压力比目标压力小.

当输入频率为0.05 Hz时，如图8所示，2种控制器在0~1/4周期和1/2~3/4周期内，制动缸实际压力均跟不上目标压力的变化. 在此期间，控制器的控制误差是由系统本身的响应速率主导的，因此两者的控制误差基本相同. 由图9（b）可知，在0~1/4周期和1/2~3/4周期内，AV电磁阀或RV电磁阀的占空比已达到最大值. 在1/4~1/2周期和3/4~1周期内，系统本身的响应速率能够满足控制要求，此时的控制误差主要由控制策略引起，AV电磁阀的占空比主要在15%~99%波动，RV电磁阀的占空比在10%~98%变化.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   制动系统频率响应（f=0.05 Hz）

Fig.8   Frequency response of brake system（f=0.05 Hz）


综上所述，在稳态控制误差方面，基于反步法的制动缸压力控制器，具有绝对的优势；在响应速度方面，2个控制器基本相同.

4.3. 控制死区分析

为了减少制动系统AV/RV电磁阀的动作次数以延长其使用寿命，引入控制死区，即当制动缸压力与目标压力的差值在±5 kPa内时，控制系统认为制动缸压力已达到目标值，制动缸进入保压状态. 在基于反步法的制动缸压力控制器中引入控制死区后，制动缸压力响应如图10所示，AV/RV电磁阀的PWM信号占空比如图11所示.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   带控制死区的制动缸压力响应特性

Fig.10   Brake cylinder pressure response characteristics with dead-time control


图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   带有控制死区的PWM信号占空比

Fig.11   Duty cycle of PWM signal with dead-time control


与阶跃输入信号的制动系统响应特性相比，引入控制死区后AV/RV电磁阀的动作次数明显减少. 同时，由图11可知，在制动保压阶段AV电磁阀多次开启，且开启的时间间隔越来越长，这是由于充气使得制动缸内的气体温度升高，并高于缸壁温度，在保压过程中缸壁与缸体内的气体之间存在热传递过程，使缸内气体温度下降，导致制动缸压力下降；当压力下降到控制死区以外时，AV阀动作，使得气压重新回到控制死区内；随着时间推移，在多次传热过程中缸内气体温度逐渐接近缸壁温度，温差的减小使得制动缸压力上升速度逐步减慢，因此AV阀的动作间隔越来越长. 在缓解保压阶段RV电磁阀也具有上述特性. 该特征为流动压缩空气的固有特性，由充/排气、压力波动、热传导与温度场局部变化引起.

此外，在制动保压阶段AV电磁阀的PWM控制信号占空比均为25%，而RV电磁阀的占空比均为10%，这是由于只有在|s1|>5 kPa的瞬间电磁阀才能动作，根据反步法控制策略计算得到开启瞬间的占空比是固定值.

5. 结　论

（1）应用基于反步法的制动缸压力控制器控制制动缸压力，当目标制动缸压力为阶跃输入信号时，最大稳态控制误差不超过5 kPa，当目标制动缸压力为0.02 Hz正弦输入信号时，最大稳态控制误差不超过8 kPa. 与传统制动缸压力控制器相比，基于反步法的制动缸压力控制器能有效提高制动缸压力控制精度，且调压过程无明显超调.

（2）当目标制动缸压力为0.05 Hz正弦输入信号时，制动缸压力控制精度受系统硬件响应速度限制，控制算法的改进基本无法提升控制精度.

（3）在制动缸压力控制器中引入控制死区，可以大幅降低AV/RV阀的动作次数，提高系统硬件使用寿命.

（4）本研究基于搭建的硬件在环试验环境初步验证了基于反步法的制动缸压力控制器的可行性，在后续的研究中应通过实车试验进一步验证控制器的有效性.

参考文献

马大炜, 王成国, 张波

我国重载列车制动技术的研究

[J]. 铁道车辆, 2009, 47 (5): 8- 11

DOI:10.3969/j.issn.1002-7602.2009.05.002      [本文引用: 1]

MA Da-wei, WANG Cheng-guo, ZHANG Bo

Research on braking technology for heavy haul trains in our country

[J]. Rolling Stock, 2009, 47 (5): 8- 11

DOI:10.3969/j.issn.1002-7602.2009.05.002      [本文引用: 1]

SITUM Z, NOVAKOVIC B

Servo pneumatic position control using fuzzy logic PID gain scheduling

[J]. Journal of Dynamic Systems, Measurement and Control, 2004, 127 (2): 376- 387

DOI:10.1115/1.1767857      [本文引用: 1]

KARPENKO M, SEPEHRI N

Development and experimental evaluation of a fixed-gain nonlinear control for a low-cost pneumatic actuator

[J]. IEEE Proceedings of Control Theory and Applications, 2006, 153 (6): 629- 640

DOI:10.1049/ip-cta:20045084      [本文引用: 1]

KARPENKO M, SEPEHRI N. QFT synthesis of a position controller for a pneumatic actuator in the presence of worst-case persistent disturbances [C]// 2006 American Control Conference. Minneapolis: [s. n.], 2006: 3158-3163.

KARPENKO M, SEPEHRI N. Design and experimental evaluation of a nonlinear position controller for a pneumatic actuator with friction [C]// 2004 American Control Conference. Boston: [s. n.], 2004: 5078-5083.

KARPENKO M, SEPEHRI N. QFT design of a PI controller with dynamic pressure feedback for positioning a pneumatic actuator [C]// 2004 American Control Conference. Boston: [s. n.], 2004: 5084-5089.

[本文引用: 1]

PANDIAN S R, HAYAKAWA Y, KANAZAWA Y, et al

Practical design of a sliding mode controller for pneumatic actuators

[J]. Journal of Dynamic Systems, Measurement, and Control, 1997, 119 (4): 666- 674

DOI:10.1115/1.2802376      [本文引用: 1]

罗卓军. 基于数理模型的列车直通式电空制动系统闭环鲁棒控制[D]. 上海: 同济大学, 2016: 46-60.

[本文引用: 1]

LUO Zhuo-jun. Robust control study on a direct-acting electro-pneumatic train brake system based on mathe matical models [D]. Shanghai: Tongji University, 2016: 46-60.

[本文引用: 1]

HEJRATI B, NAJAFI F

Accurate pressure control of a pneumatic actuator with a novel pulse width modulation-sliding mode controller using a fast switching on/off valve

[J]. Proceedings of the Institution of Mechanical Engineers. Part I: Journal of Systems and Control Engineering, 2013, 227 (2): 230- 242

[本文引用: 1]

LAI J Y, MENQ C H, SIGNH R

Accurate position control of a pneumatic actuator

[J]. Journal of Dynamic Systems, Measurement and Control, 1990, 112 (4): 734- 739

DOI:10.1115/1.2896202      [本文引用: 1]

BARTH E J, ZHANG J L, GOLDFARB M. Sliding mode approach to PWM-controlled pneumatic systems [C]// 20th Annual American Control Conference. Anchorage: [s.n.], 2002: 2362-2367.

[本文引用: 1]

SHEN X R, ZHANG J L, BARTH E J, et al

Nonlinear model-based control of pulse width modulated pneumatic servo systems

[J]. Journal of Dynamic Systems, Measurement, and Control, 2005, 128 (3): 663- 669

[本文引用: 1]

高钦和, 刘志浩, 宋海洲

基于高速开关阀的液压缸速度控制系统设计

[J]. 流体传动与控制, 2013, 57 (2): 5- 9

DOI:10.3969/j.issn.1672-8904.2013.02.004      [本文引用: 1]

GAO Qin-he, LIU Zhi-hao, SONG Hai-zhou

Design of hydraulic cylinder speed control system based on high speed switch valve

[J]. Fluid Power Transmission and Control, 2013, 57 (2): 5- 9

DOI:10.3969/j.issn.1672-8904.2013.02.004      [本文引用: 1]

/

〈 〉