压电精密运动平台被广泛应用于精密制造、光学对准、生物显微观察和微纳操作等领域^[1-4]。传统的二维压电精密运动平台多采用电机驱动、滚珠丝杠驱动和电磁驱动等方式，其精度受机械摩擦的影响较大，响应速度较慢，系统复杂度高。此外，电机、滚珠丝杠等传统机械结构易受装配误差和回程间隙的影响，难以满足高精度应用需求。压电驱动具有纳米级分辨率、高频响应、无摩擦等优点，逐渐成为高精度运动平台的主流驱动方式之一。但是，压电陶瓷的输出位移往往较小，难以满足毫米级、微米级行程的需求^[5]。柔性结构虽然能够提供无摩擦、无回程间隙的运动方式，但其行程受限，难以兼顾高精度和大行程的要求^[6]。近年来，学者们广泛采用柔性放大机构来提升二维精密运动平台的性能。Jin等^[7]设计了一种二维串联压电精密运动平台，该平台沿X、Y向的工作行程分别为3.89 μm和3.99 μm，具有较小的轴间耦合误差，但因串联结构的质量较大，其固有频率仅为113.65 Hz。Yuan等^[8]设计了一种基于三角放大机构的二维并联压电精密运动平台，该平台沿X、Y向的工作行程分别为31.8 μm和41.0 μm，但其固有频率仅为90.5 Hz。Zhang等^[9]提出了一种基于桥式放大机构的二维并联压电精密运动平台，其沿X、Y向的工作行程分别可达346.1 μm和357.2 μm，但桥式放大机构极大地降低了平台的刚度，导致其固有频率仅为44 Hz，难以应用于实际。

综上所述，在二维压电精密运动平台的优化设计中，实现大行程与快速响应的协同设计一直是最具挑战性的难题之一。一方面，压电陶瓷驱动的精密运动平台虽能实现较大的输出行程，但其位移放大机构在提升行程的同时会导致结构尺寸增大、固有频率下降及输出刚度衰减；另一方面，实现多自由度协同工作会引发运动耦合问题，这种多自由度间的耦合干扰不仅会影响定位精度，还会增加控制复杂度，制约了精密运动平台的整体性能^[10]。因此，想要设计大行程-高带宽的二维压电精密运动平台，必须合理选用压电堆栈与柔性放大机构，兼顾刚度与位移放大性能，以突破快速响应与大行程难以同时实现的技术瓶颈。

针对上述问题，本文从柔性放大机构的作用机理出发，设计了一种新型的二维压电精密运动平台。首先，基于矩阵位移法建立精密运动平台的静/动力学一体化理论模型，并利用ANSYS Workbench软件开展静/动力学有限元仿真；随后，搭建实验测试系统，对精密运动平台的静态和动态性能进行测试，以验证理论分析与仿真结果的准确性。

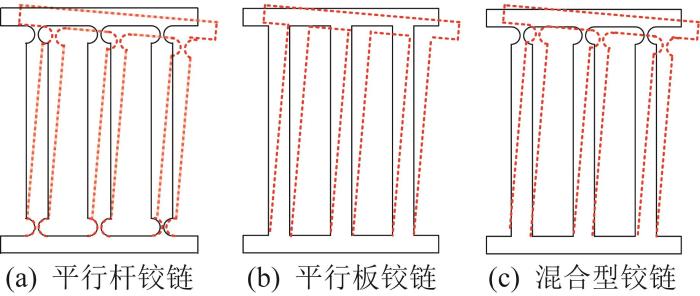
在柔性放大机构的运动过程中，柔性铰链为主要变形载体，通过其弹性变形来实现位移的传递与放大。常见的柔性铰链分为平行杆铰链、平行板铰链及混合型铰链三种类型，如图1所示。平行杆铰链的两端通过转动副连接，在工作时变形主要集中在铰链部位，而杆件自身的变形可忽略不计。平行板铰链由2片或多片薄板平行排列组成，依靠薄板的弯曲变形实现位移输出，其具备较小的耦合效应和较强的变形能力，适用于大位移运动平台。混合型铰链的性能介于上述两者之间。在这3种铰链中，平行板铰链具有最小的等效质量和最高的刚度^[11]。因此，本文选择平行板铰链作为变形机构。

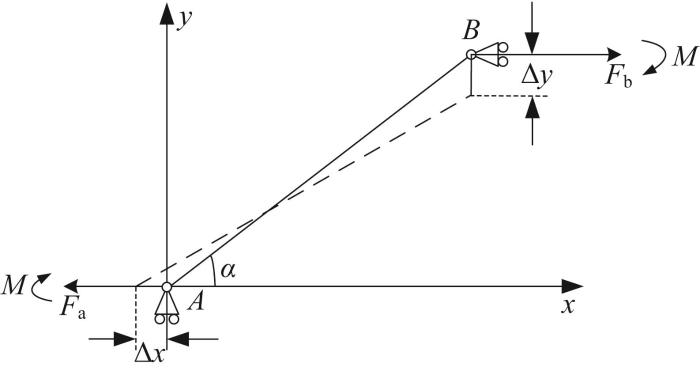
根据柔性放大机构的放大原理，可将其分为基于三角形放大原理的桥式构型、Scott-Russell（S-R）构型以及基于杠杆放大原理的杆式构型。其中，S-R构型的结构复杂、对称性差且整体臃肿，其在实际工程中的应用较少^[12]。相比之下，桥式和杆式构型具备对称性良好、结构紧凑以及加工便利等优势，在实际工程中得到了广泛应用。图2所示为桥式构型的放大原理。

根据图2，桥式构型的输入—输出关系可由以下数学模型描述：

式中：F为作用在两对称端点上的等效力，F_a为端点A处所施加的力，F_b为端点B处受到的约束反力，M为施加力产生的约束力矩，l_b为柔性臂长度，α为因形变而产生的角位移。

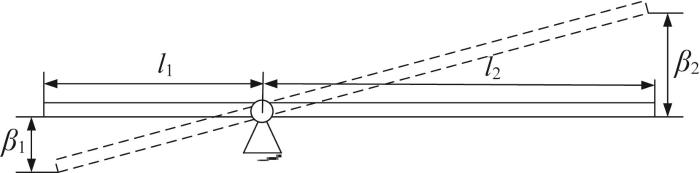
图3所示为杆式构型的放大原理，其可视作一个费力杠杆。

根据图3，可得出杆式构型的放大倍数：

式中：A_m为杆式构型的整体放大倍数，l₁为输入侧柔性臂的长度，l₂为输出侧柔性臂的长度。

当采用多级串联杆式构型时，其整体放大倍数可表示为：

式中：A_mn 为第n级杆式构型的放大倍数。

桥式构型虽然结构稳定，但在实现纵向位移放大的过程中易产生横向偏移，削弱了其在精密应用场景中的适用性。杆式构型能够实现较高的位移放大倍数，且其结构设计具有更高的灵活性和可调节性。因此，本文最终选择杆式构型作为二维压电精密运动平台的位移放大机构。

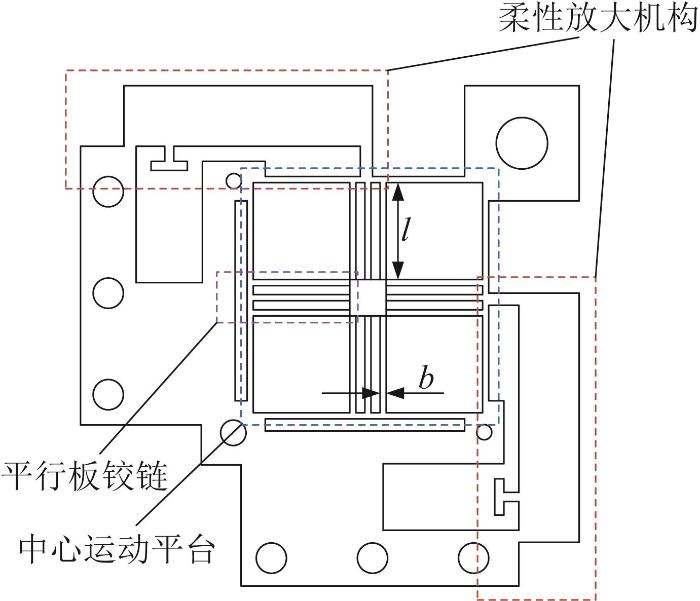
二维压电精密运动平台整体构型的初步设计如图4所示，分为柔性放大机构以及中心运动平台两部分，柔性放大机构依靠压电陶瓷驱动。

针对压电陶瓷输出位移小且测量困难的问题，本文在中心运动平台中设计了凸台结构。该结构具有双重功能：1）作为位移测量基准点，便于运动轨迹检测；2）约束精密运动平台在非工作方向上的自由度，以改善其动态响应特性。

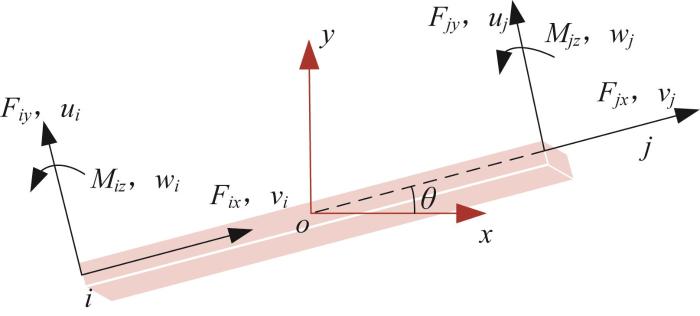
在构建二维压电精密运动平台的静/动力学一体化模型时，柔性铰链可视作柔性单元。如图5所示，柔性单元的结构特性如下：每个柔性单元由i和j两个节点构成，且每个节点具有3个独立的自由度。图中：u_i 和u_j 表示各节点的轴向位移、v_i 和v_j 表示各节点的横向位移，w_i 和w_j 表示各节点的转角，F_ix 和F_jx 表示轴向节点力，F_iy 和F_jy 表示径向节点力，M_iz 和M_jz 表示绕z轴产生的弯矩。

在静/动力学一体化建模中，各柔性单元的动力刚度矩阵需从预先建立的矩阵库中选取。第q个柔性单元的刚度矩阵 K_q 可表示为：

式中：E为材料的弹性模量，A_q 为柔性单元的横截面积，I_q 为柔性单元的截面惯性矩，l_q 为柔性单元长度。

在柔性机构中，不发生变形且尺寸效应可忽略的刚性体可等效为集中质量节点^[13]。由惯性力产生的集中质量节点的动力刚度矩阵 K_m (ω)可表示为：

式中：m为集中质量节点的质量，J为集中质量节点的转动惯量，ω为动态频率。

为实现全局分析，需将柔性单元的相关参数从局部坐标系o-xyz转换至参考坐标系o'-x'y'z'，通过坐标变换统一转换至参考坐标系。假设第q个柔性单元相对于所设参考坐标系的转角为θ_q，则第q个柔性单元的坐标变换矩阵 R_q 可表示为：

第q个柔性单元在参考坐标系下的动力刚度矩阵 D_q (ω)可表示为：

在参考坐标系中，第q个柔性单元的节点力和节点位移的关系如下：

式中： F_{q, i} 和 F_{q, j} 分别为第q个柔性单元i端和j端的节点力， F_{q, i} =[F_{q, ix} F_{q, iy} M_{q, iz} ]， F_{q, j} =[F_{q, jx}F_{q, jy}M_{q, jz} ]； x_{q, i} 和 x_{q, j} 分别为第q个柔性单元i端和j端的节点位移， x_{q, i} =[u_qiv_qi w_qi ]， x_{q, j} =[u_qj v_qj w_qj ]； k_{q, 1}、 k_{q, 2}、 k_{q, 3}和 k_{q, 4}分别为第q个柔性单元在参考坐标系下的刚度矩阵的分块阵。

在二维压电精密运动平台的位移放大过程中，柔性铰链的数量对其性能具有重要影响。因整个精密运动平台结构对称，仅分析单个平行板铰链中的柔性铰链数量即可。为确定最佳的柔性铰链数量，在铰链长度l=16 mm、高度h=10 mm及宽度b=1 mm的前提下，对精密运动平台输入1 μm的位移进行分析。选取柔性铰链数量为2、3、4这3种情况，分别进行有限元静态仿真分析，获取不同铰链数量下精密运动平台的位移放大倍数及侧向误差，同时进行模态分析，结果如表1所示。

由表1可以看出，随着柔性铰链数量的增加，精密运动平台的一阶固有频率整体呈增大趋势，但变化幅度较小，而位移放大倍数则逐渐降低。此外，当柔性铰链数量为3时，精密运动平台的侧向误差最小。综合考虑一阶固有频率、位移放大倍数及侧向误差等因素，最终确定的柔性铰链数量为3。

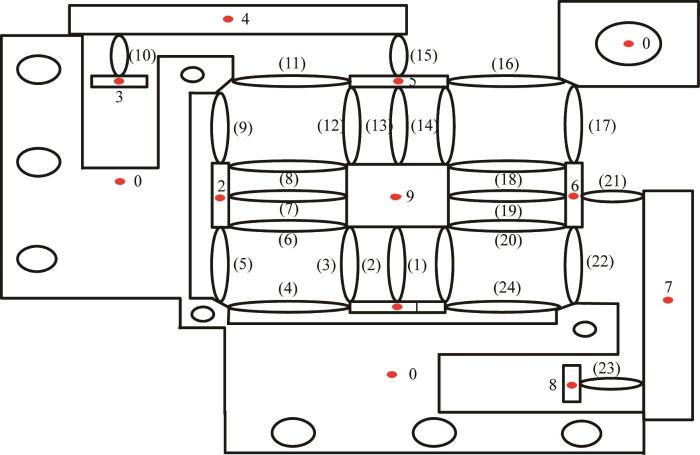
通过离散化，连续结构可被划分为有限数量的节点和单元^[14]。本文所设计的精密运动平台可以被离散化为由多个柔性单元和集中质量节点构成的结构，如图6所示。将各柔性单元和集中质量节点依次进行编号，各柔性单元编号为q（q=1, 2, …, 24），集中质量节点编号为p（p=1, 2, …, 9）；所有固定边界条件均标记为0。该精密运动平台的输入力分别作用于节点3或节点8，其输出端对应节点9。

对于图6所示的离散化精密运动平台，依次取每个柔性单元的节点为研究对象。根据力平衡方程，可得：

式中： x_p 为集中质量节点的位移。

随后，依次对所有力平衡方程进行分析，整合得到精密运动平台的静力学模型，具体如下：

式中： F_{in, 1}、 F_{in, 2}为输入力， F_out为输出力。

将式(11)代入式(10)，可得基于所有节点建立的弹性静力学模型，可表示为：

根据式(12)与胡克定律，可得整个精密运动平台的通用动力刚度模型：

其中：

式中： K_eω为精密运动平台的动力刚度矩阵。

上述通用动力刚度模型能够完整地表征精密运动平台在静态和动态条件下的力学行为。当激励频率ω=0 Hz时，该刚度模型为静力学模型，此时可根据外部载荷条件求解平台的静态特性参数。通过求解动力刚度矩阵 K_e ω的特征方程^[15]来确定精密运动平台的固有频率，式(15)的所有正根即为各阶固有频率。

为提升二维压电精密运动平台的动态响应速度、定位精度及稳定性，对其进行结构尺寸优化。本文提出了一种两阶段优化策略：先基于梯度分析实现设计变量的敏感度排序，再根据敏感度排序结果，采用约束优化方法对关键设计变量进行分层优化，从而协同提升精密运动平台的静/动态性能。

根据式(14)所示的动力刚度模型，可将精密运动平台的位移放大倍数A_m和固有频率f表示为设计变量（柔性铰链的宽度b和高度h）的显式函数：

其中：

式中：K_x 为轴向刚度，K_y 为弯曲刚度，m_s为精密运动平台的等效质量，A为柔性铰链的横截面积，I为柔性铰链的截面惯性矩。

为分析设计变量b和h对刚度K_x 和K_y 的敏感度，通过计算位移放大倍数A_m和固有频率f的偏导数来分析其敏感度，可得：

由式(16)至(18)可知，铰链宽度b主要影响轴向刚度K_x，铰链高度h主要影响弯曲刚度K_y；铰链宽度b是影响位移放大倍数A_m的主要参数，铰链高度h是影响固有频率f的关键因素。

本文所建立的动力刚度模型通过参数b和h实现了对精密运动平台静/动态力学特性的数学表征。联立式(14)和式(15)，可得：

式中：Ω_N 为精密运动平台通用动力刚度矩阵 K_eω行列式为0时对应的N组固有频率解的集合；f_{1, N} 为N组最小固有频率的集合，即最佳一阶固有频率的集合。

目前，类似精密运动平台的一阶固有频率为2 000~2 400 Hz ^[16]，位移放大倍数为2.7~3.1^[17]，具备一定的工作性能，但在高速精密运动控制等应用场景中，仍需进一步优化以提高其带宽和运动增益。为避免输入信号高频分量引起的机械振动，同时解决由刚度约束导致的运动行程不足的问题^[18]，本文设定精密运动平台的一阶固有频率高于2 150 Hz，位移放大倍数大于3.0，以综合提升其抗振性能和运动性能。

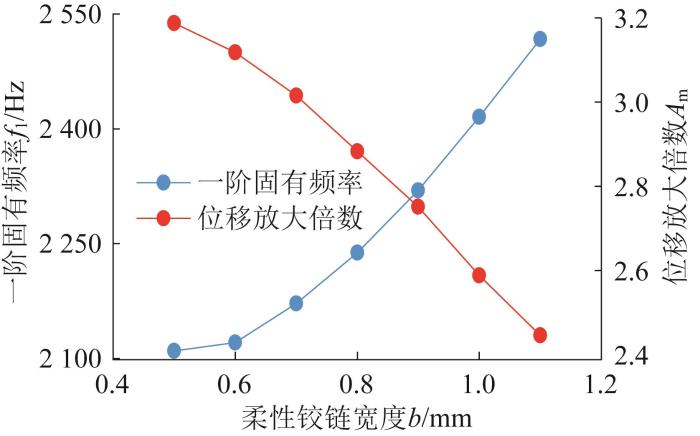
首先，分析柔性铰链宽度b对精密运动平台性能的影响。在保持单个平行板铰链中柔性铰链数量为3、长度l=16 mm、高度h=10 mm的情况下，设定铰链宽度b=0.5~1.1 mm，并对精密运动平台输入端施加1 μm位移。基于上述约束条件，利用MATLAB软件对不同柔性铰链宽度下精密运动平台的一阶固有频率和位移放大倍数进行分析，结果如图7所示。

由图7可知，柔性铰链宽度b的增大会显著提升精密运动平台的整体刚度。随着铰链宽度的增大，精密运动平台的位移放大倍数呈减小趋势，而一阶固有频率逐渐增大。

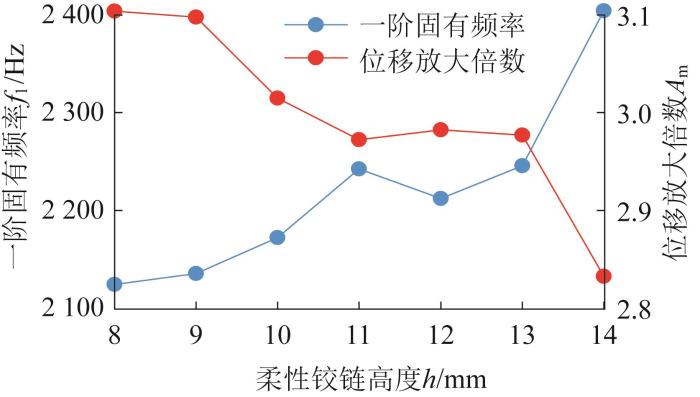
进一步分析柔性铰链高度h对精密运动平台性能的影响。在保持单个平行板铰链中柔性铰链数量为3、长度l=16 mm、宽度b=0.7 mm的情况下，设定铰链高度h=8~14 mm，并在精密定位平台输入端施加1 μm位移。基于上述约束条件，利用MATLAB软件分析不同柔性铰链高度下精密运动平台的一阶固有频率和位移放大倍数，结果如图8所示。

由图8可知，柔性铰链高度h的增大会显著提升精密运动平台的整体刚度。随着铰链高度的增大，尽管在h=12 mm处出现局部转折，但整体上位移放大倍数呈下降趋势，而一阶固有频率则持续增大。

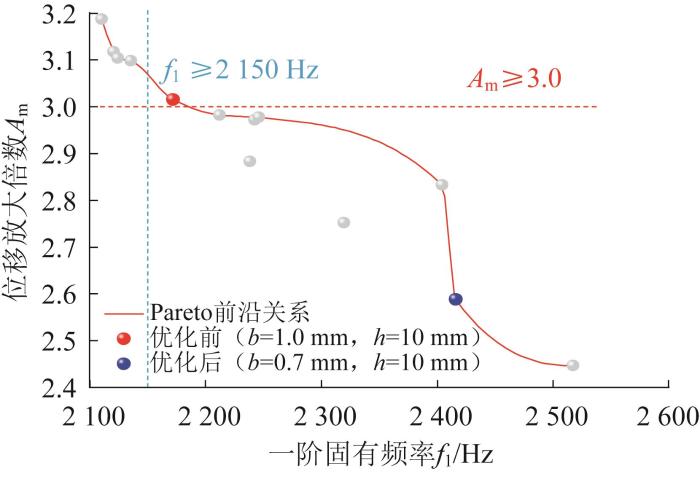
为获得最优的柔性铰链尺寸参数，基于上述分析结果绘制对应的Pareto前沿关系曲线，如图9所示。由图9可知，当柔性铰链的宽度b=0.7 mm、高度h=10 mm时，精密运动平台的位移放大倍数A_m=3.012，一阶固有频率f₁=2 172 Hz，相较于优化前（b=1.0 mm，h=10 mm，A_m=2.588，f₁=2 416 Hz），一阶固有频率降低了10.1%，但输出位移提升了16.4%，满足大行程与快速响应的工作要求。因此，本文最终选用的柔性铰链尺寸参数如下：b=0.7 mm，h=10 mm。

二维压电精密运动平台基于柔性铰链的弹性变形实现多自由度位移输出，其在周期性压电陶瓷激励下需要保持纳米级定位精度并承受持续冲击载荷。因此，精密运动平台的输出性能与其材料选取有着密切联系。如表2所示，钛合金材料强度高且耐腐蚀，但质量大，加工难度较高。不锈钢材料可加工性高，易获取，但抗疲劳性差，长期使用可能会产生局部变形^[19]。硅橡胶虽柔软且耐高低温，但生产效率较低。聚氨酯材料抗撕裂强度高，耐使用，但制造工艺复杂，其性能在长期高温的工作环境中会下降^[20]。铝合金材料密度较低，大约是钢铁的1/3，但其强度相对较高；此外，采用铝合金材料加工的精密运动平台往往具有较大的行程，且易加工，可在有效减小质量的同时提高动态响应速度和定位精度。因此，本文选用铝合金材料来设计精密运动平台。

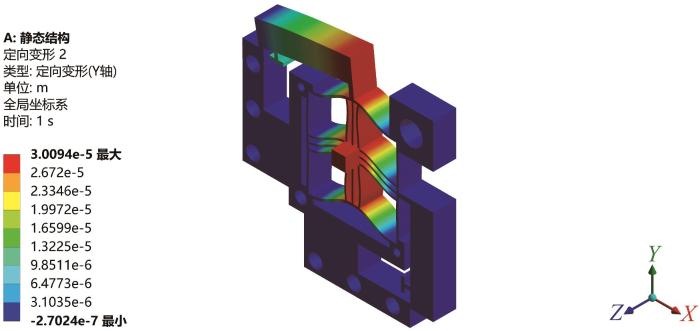
为验证优化设计后二维压电精密运动平台的性能，使用ANSYS Workbench软件对其进行有限元仿真分析。在精密运动平台输入端施加10.0 μm的输入位移，对其进行静态分析，结果如图10所示。结果表明，该精密运动平台中心凸台处的输出位移为30.094 μm，位移放大倍数为3.009。

在精密运动平台通孔处边界条件固定的条件下，对其进行模态分析，前3阶模态分析结果如图11至图13所示。由图11至图13可知，前2阶模态为精密运动平台需要实现的主运动，对应的模态振型分别以沿X方向的平动和沿Y方向的平动为主，一阶、二阶固有频率分别为2 172.0 Hz和2 219.3 Hz；三阶模态为沿Z方向的偏转，对应的固有频率为 5 650.2 Hz。精密运动平台的前2阶固有频率与三阶及以上的高阶模态的固有频率相差较大，说明其在位移放大过程中不易受到干扰。

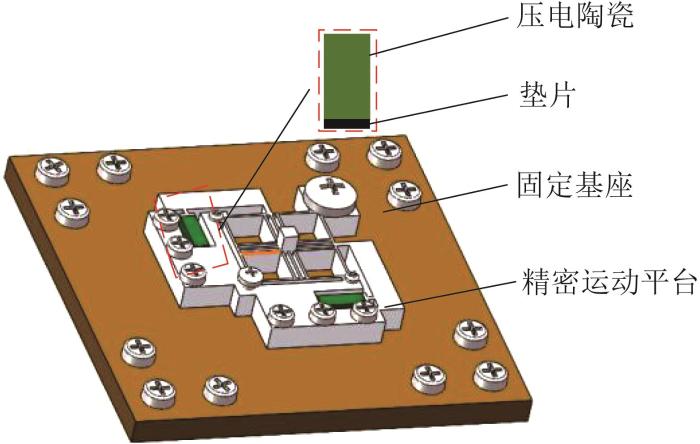
为了对所设计的二维压电精密运动平台进行性能测试，构建专用的压电驱动系统。基于上文分析，建立压电驱动系统装配模型，如图14所示。

根据图14，搭建图15所示的压电驱动系统性能测试平台。采用普源DG4102信号发生器提供输入电压信号，该信号经压电陶瓷驱动器放大后驱动压电陶瓷（哈尔滨芯明天公司生产的PSt150/5×5/20H低压叠堆式压电陶瓷），实现位移输出。利用LK-H050激光位移传感器采集精密运动平台的位移信号。所采集的数据经位移传感器控制器处理后，传输至上位机以获得输出波形。

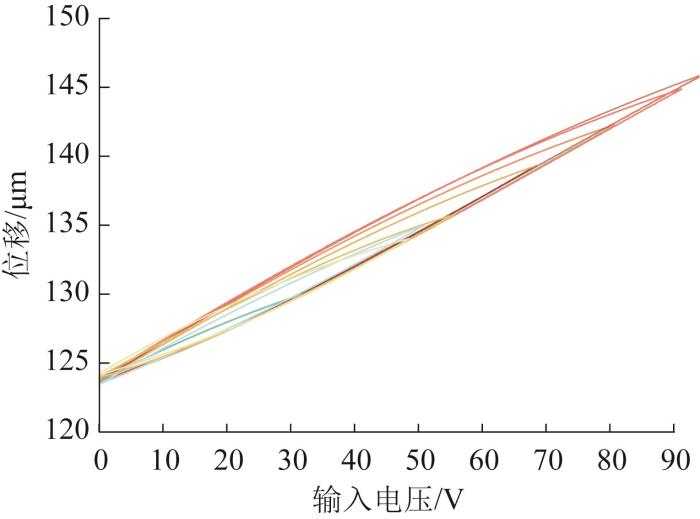
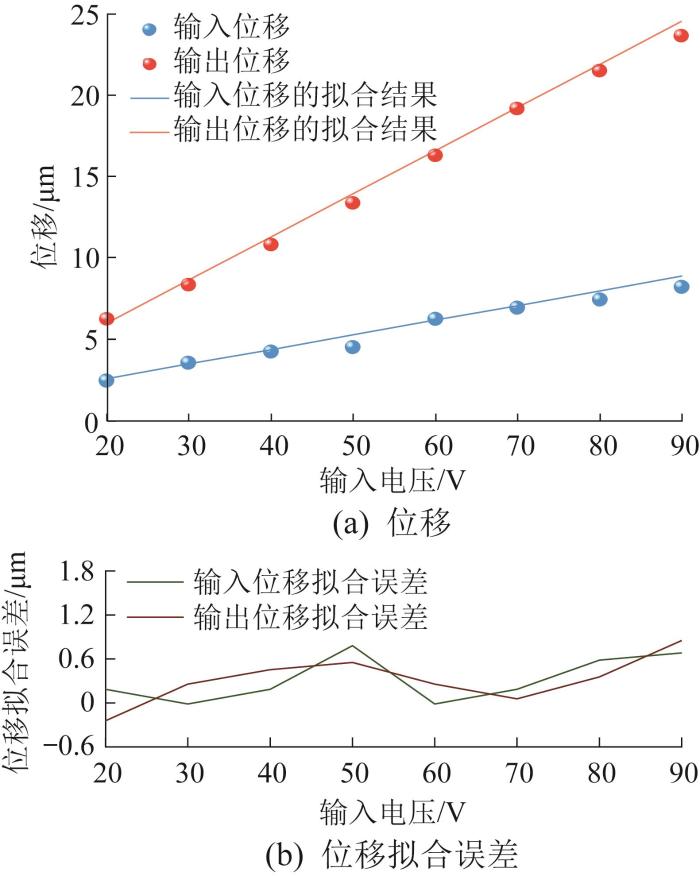
基于图15所示的压电驱动系统性能测试平台，利用上位机对精密运动平台的位移信号进行采集与处理。在驱动频率固定为10 Hz的条件下，通过实验测得精密运动平台在不同输入电压下的位移响应曲线（三角波信号），如图16所示。从图16中可以观测到，精密运动平台存在明显的迟滞现象，这主要是由压电陶瓷材料固有的迟滞特性导致的^[21]。实验测得的精密运动平台的输入位移、输出位移及其线性拟合结果和对应的位移放大倍数分别如图17和表3所示。

由表3可知，本文所设计的精密运动平台在不同电压条件下工作时，其位移放大倍数基本在2.5~3.0范围内，平均位移放大倍数为2.771。综合实际加工误差、材料致密度以及实验测量误差等的影响，精密运动平台位移放大倍数的实测值与仿真值3.009之间的相对误差为7.910%，在允许范围内。

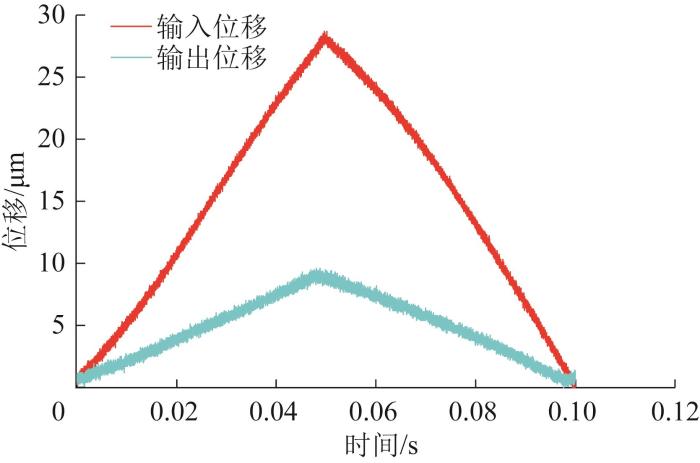
为了进一步验证输入位移为10.0 μm条件下精密运动平台的位移放大倍数仿真结果的准确性，对压电陶瓷输入120 V电压，通过实验测量该条件下的输入、输出位移，结果如图18所示。由图18可知，当输入电压为120 V时，精密运动平台的输入位移为9.620 μm，输出位移为28.805 μm，位移放大倍数为2.994，与仿真值3.009之间的相对误差为0.499%。

输入信号的高频分量接近系统的一阶固有频率时会引发共振，从而影响系统精度。为避免共振现象，输入信号的频率需控制在系统一阶固有频率的1%~10%范围内^[22]。因此，对精密运动平台的一阶固有频率进行测试至关重要。

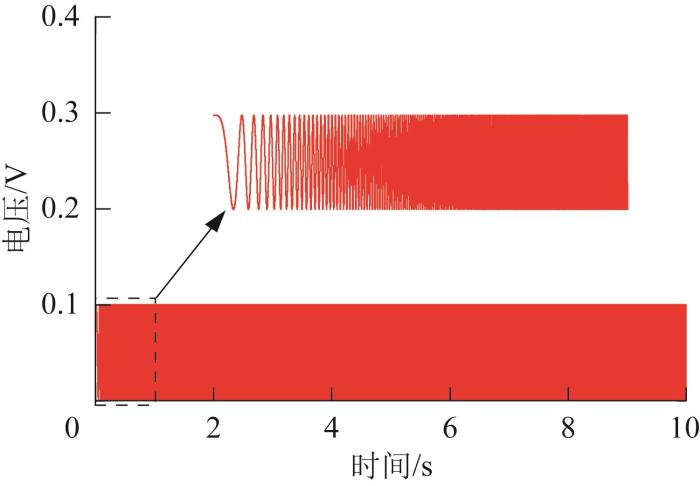
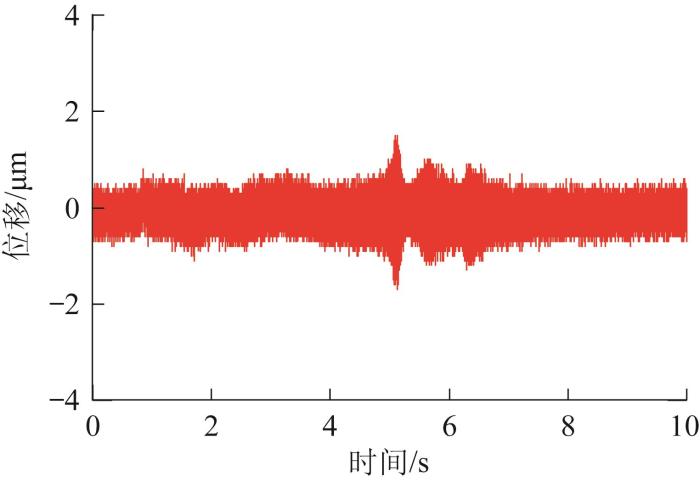
在实验中，信号发生器产生频率连续线性递增的正弦扫描信号，如图19所示，频率范围设为0.1~4 000 Hz。为保护压电陶瓷，设置电压幅值为0.1 V。在该条件下，压电驱动系统的频率响应曲线如图20所示。结果显示，压电驱动系统在t≈5.118 s时发生共振，振幅约为1.5 µm，该共振点对应的频率即为精密运动平台的一阶固有频率。利用频率公式ft=f_s+ft-fst/T（f_s为扫描起始频率，f_t为扫描终止频率，T为扫描时间）进行求解，可得精密运动平台的一阶固有频率约为2 123 Hz。

本文针对传统二维压电精密运动平台行程受限、难以满足大行程与快速响应需求的问题，基于杆式放大原理设计了一种新型的二维压电精密运动平台。首先，基于矩阵位移法建立了精密运动平台的静/动力学一体化模型，并在此基础上，通过敏感度分析和约束优化方法系统地优化了柔性铰链的尺寸参数及空间布局，实现了位移输出与动态响应性能的协同优化。然后，通过有限元仿真分析了精密运动平台的静/动态性能，并搭建压电驱动系统性能测试平台，对精密运动平台的静/动态性能进行了实验验证。实验结果表明，该精密运动平台的一阶固有频率为2 123 Hz；在不同输入位移下，平均位移放大倍数为2.771，与仿真结果的相对误差为 7.910%；当输入电压为120 V时，输出位移可达28.805 μm，位移放大倍数为2.994，与仿真结果的相对误差约为0.499%。所设计的精密运动平台表现出良好的静/动态性能，且结构相对紧凑，具有一定的实际应用价值。本文研究为柔性精密运动平台的性能优化提供了一定参考。

本文链接：https：//www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.05.151