随着科学技术的迅猛发展，对微机电技术、微加工与制造技术、微操作技术和微装配技术等领域的探索日益深入。如今，这些技术已迈入微米级乃至纳米级的高精度时代。压电陶瓷凭借高分辨率、强大输出力、高刚度以及快速频率响应等诸多优点，在众多技术领域，尤其是光学、生物医疗、机器人和航空航天等前沿领域，展现出了卓越的精密驱动与定位能力^[1]，这使得压电陶瓷成为工程领域应用最广泛的智能材料之一。然而，压电陶瓷存在明显的局限性，即其输出位移相对较小。即使是堆叠型压电陶瓷，其输出位移也通常仅为自身尺寸的0.1%~0.2%^[2]。为了克服这一技术挑战，学者们普遍采用了一种创新的解决方案：设计以柔性铰链为核心的位移放大机构^[3]。这种机构能够有效地将压电陶瓷产生的微小位移放大至亚毫米甚至毫米级，极大地扩展了压电陶瓷在精密工程领域的应用潜力和应用范围。现阶段，国内外很多高校和学者针对利用位移放大机构和运动导向机构设计精密定位平台展开了广泛研究。李天翼^[4]设计了一种二自由度解耦大行程微纳定位平台，该定位平台的一阶固有频率为337.2 Hz，在x、y方向上的运动耦合率分别为1.31%和1.62%，运动行程分别为89.2 μm和85.9 μm。Tang等^[5]设计了一种基于杠杆放大机构的二维精密定位平台，实验结果显示，该定位平台的一阶固有频率为831 Hz，位移放大倍数为4.2，在x、y方向上的运动行程分别为119.7 μm和121.4 μm，交叉耦合位移误差小于2%，具有良好的原子力显微镜扫描性能。Li等^[6]设计了一种二自由度柔性并联微定位平台，其由压电陶瓷驱动，利用双平行四边形复合铰链进行导向解耦，可实现输入与输出的完全解耦，实验结果表明，该定位平台在x、y方向上的运动行程均为117 μm，位移放大倍数为5.85。

研究表明，基于压电陶瓷驱动的精密定位平台是一种具备微米级或纳米级定位分辨率和精度的先进装置，它构成了精密定位技术的核心组成部分^[7]。该类精密定位平台凭借卓越的性能，如高精度定位、高分辨率位移、优良的频响特性、无需润滑以及抗磁场干扰等，在多个领域得到了广泛应用^[8]。当前，众多公司成功研发的各类精密定位平台已在实际应用中展现出成熟且广泛的适用性。这些精密定位平台在光学工程、生物医疗、机器人和航空航天等领域发挥着重要作用，持续推动着相关技术的进步与创新。

基于压电陶瓷驱动的精密定位平台虽具有诸多优点，但仍存在一些缺陷：需设计位移放大机构来解决压电陶瓷驱动器输出位移较小的问题。然而，这种设计往往会导致定位平台的结构尺寸增大、固有频率减小及输出刚度降低等问题，从而影响其整体性能。此外，一些定位平台的耦合运动较大，这会降低其定位精度。耦合运动是指不同方向上的运动相互干扰，导致定位平台难以精确控制各个方向的位移。这种耦合运动不仅会影响定位平台的定位精度，还可能会增加定位平台的复杂性和控制难度。

基于此，笔者利用双桥臂桥式放大机构、双级平行四边形机构和复合平行四边形机构，将三者对称分布，巧妙融合，实现了对基于压电陶瓷驱动的精密定位平台结构的创新设计。相较于其他精密定位平台，所设计的精密定位平台基本实现了完全解耦，且具有更大的位移放大倍数、更大的运动行程及更高的输出刚度。通过对所设计的精密定位平台进行静力学建模和动力学建模，来计算其位移放大倍数、输出刚度和一阶固有频率。同时，对精密定位平台进行有限元仿真并搭建相应的实验装置，以对其性能进行进一步分析与验证。

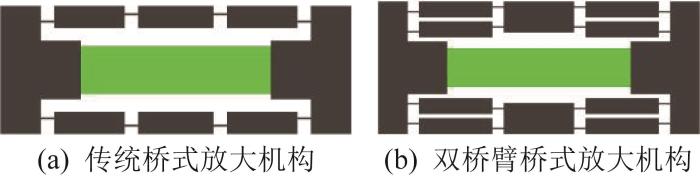
常见的位移放大机构有桥式放大机构^[9-10]、杠杆放大机构^[11]和Scoot-Russell放大机构^[12-13]。传统的桥式放大机构如图1(a)所示，其具有稳定、高效、放大倍数大、灵活性好及结构坚固紧凑等优点^[14]。由于桥式放大机构的连接臂中带有刚性单元，在被压电陶瓷驱动时，其连接臂在非工作方向上产生形变，使得位移损失较小，因此桥式放大机构具有较大的放大倍数。双桥臂桥式放大机构如图1(b)所示。相较于传统的桥式放大机构，其输出端在非工作方向上的刚度更大，使得压电陶瓷内部不易受扭转力和剪切力的影响。这一特性使得双桥臂桥式放大机构能够更好地抵抗精密定位平台不同自由度之间的寄生运动、载荷及其他因素所产生的不利影响，实现了对压电陶瓷的有效保护。此外，双桥臂桥式放大机构能够在几乎不影响位移放大倍数的同时提高输出刚度。基于此，本文选择双桥臂桥式放大机构来设计精密定位平台。

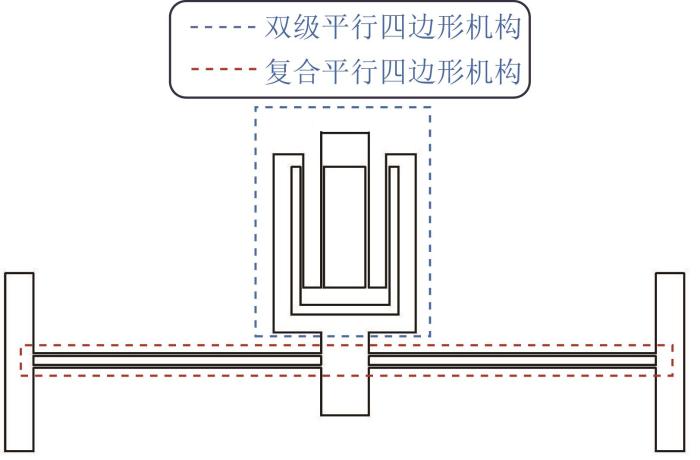
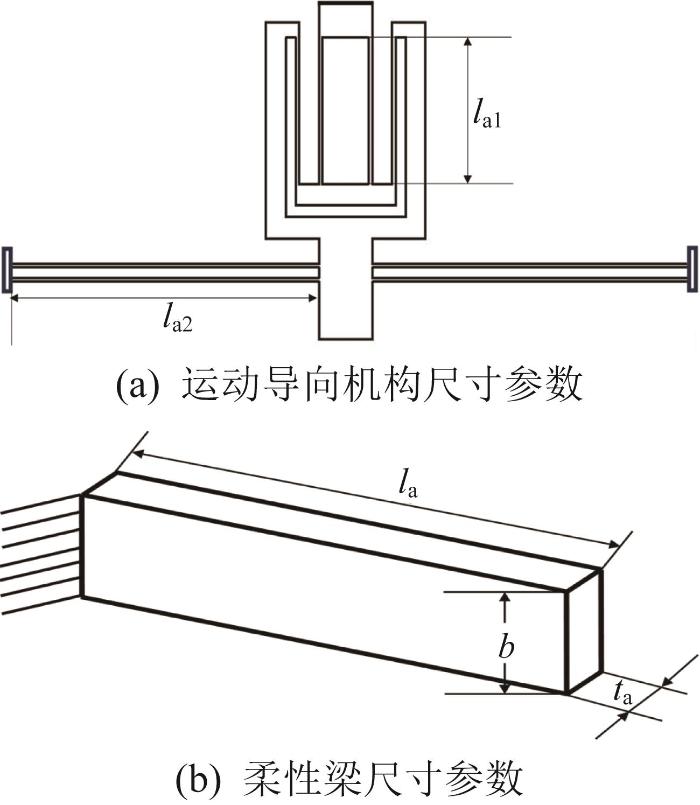
为实现多自由度精密定位平台的高精度定位和精确控制，通常利用具有解耦功能的运动导向机构来减小其各运动方向之间的干涉。本文选择图2所示的双级平行四边形机构和复合平行四边形机构作为精密定位平台的运动导向机构。其中：双级平行四边形机构在非工作方向上产生的耦合位移能够相互抵消；复合平行四边形机构的结构完全对称，其在非工作方向上的刚度较大，但在运动导向方向上的刚度较小，故可在不影响运动导向的基础上实现解耦。

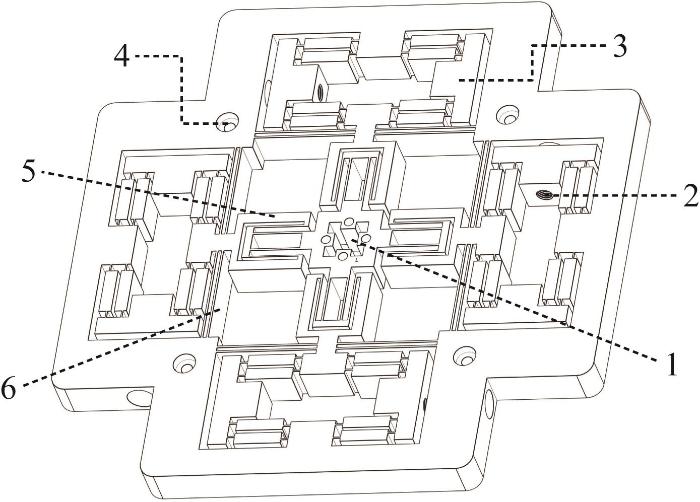
本文所设计的二维精密定位平台的整体结构如图3所示，其外形尺寸（长×宽×高）为290 mm×290 mm×20 mm。该精密定位平台包含4组双桥臂桥式放大机构、4组复合平行四边形机构和4个双级平行四边形机构（对称分布），在实现运动导向的同时可有效防止寄生耦合运动。

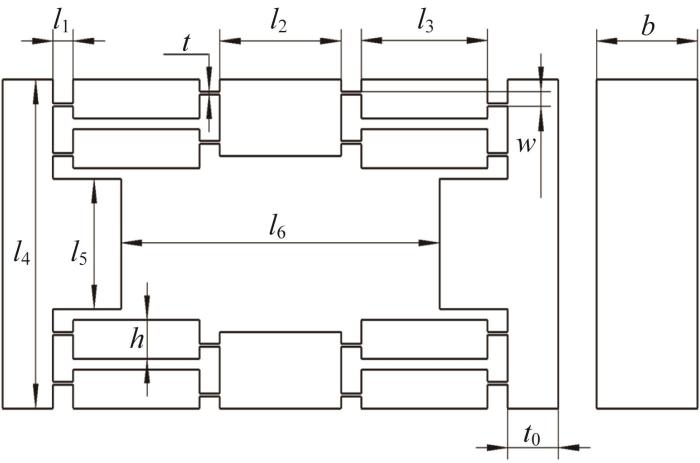
本文所设计的精密定位平台中双桥臂桥式放大机构的尺寸参数如图4所示。

根据弹性梁理论，柔性铰链的静力学特性可由柔度矩阵来表征。双桥臂桥式放大机构中的柔性铰链类型为直角型柔性铰链，其柔度矩阵 C_k可表示为^[15]：

式中：E为材料的弹性模量，G为材料的切变模量，l1、b、t分别为柔性铰链的长度、宽度和厚度。

由于双桥臂桥式放大机构为完全对称结构，为方便分析，选择其1/4结构进行柔度分析。利用坐标变换理论，可得1/4双桥臂桥式放大机构的平面柔度矩阵 C_f，表示为：

其中：

A= l1t2+6l1w2Ebt3

B= -3l1w(l1+2l3)Ebt3

C= -3l1w(l1+2l3)Ebt3

D= l1Gbt+2l1(16l12+27l1l3+9l32)3Eb3t

式中：l₃为桥臂的长度，w为柔性铰链的间距。

双桥臂桥式放大机构中柔性铰链的输出位移 X 与输入力 F 的关系可表示为：

其中：

式中：δx、δy、θz分别为柔性铰链在相应方向上产生的线位移和角位移；Fx、Fy、Mz分别为柔性铰链在相应方向上受到的力和转矩，其中Mz=Fxw/2。

联立式(2)与式(3)，可得双桥臂桥式放大机构的输出位移δy与输入力Fx之间的关系：

则双桥臂桥式放大机构的位移放大倍数R可表示为：

双桥臂桥式放大机构的输入刚度K_in可表示为：

令Fx=0 N，可得双桥臂桥式放大机构的输出刚度K_out：

本文所设计的精密定位平台中的2种运动导向机构均可视作由多根柔性梁串联和并联而成，且整体结构完全对称以及每根柔性梁的变形形态相同。运动导向机构与单根柔性梁的尺寸参数如图5所示。

根据欧拉-伯努利梁的变形理论和力学分析，可得单根柔性梁的刚度K_a：

式中：Ia为惯性矩，Ia=bta3/12； la、ta为单根柔性梁的长度和厚度。

单级平行四边形机构由2根柔性梁并联而成，由刚度并联计算法可知，其刚度K_s可表示为：

双级平行四边形机构由2个单级平行四边形机构串联而成，由刚度串联计算法可知，其刚度K_d可表示为：

式中：la1为双级平行四边形机构中柔性梁的长度。

复合平行四边形机构由2个单级平行四边形机构并联而成，由刚度并联计算法可知，其刚度K_c可表示为：

式中：la2为复合平行四边形机构中柔性梁的长度。

由此可得，整个精密定位平台的运动导向机构在单自由度方向上的负载刚度K_g可表示为：

将Ia=bta3/12代入式(12)，则负载刚度K_g可表示为：

模块法是一种独特的研究方法，其核心思想是先将位移放大机构和运动导向机构分割为2个独立的组成部分并分别进行理论建模，再利用两者接触面上作用力与反作用力相等的力学关系将2个模型巧妙地融合在一起，以构建整个精密定位平台的静力学模型^[16]。模块法的优势在于灵活性和精确性，通过分步建模，可针对位移放大机构和运动导向机构的不同特性分别选用最合适的方法进行处理，从而避免对简单机构进行复杂运算^[17]。

根据上文基于弹性梁理论与柔度矩阵法求得的双桥臂桥式放大机构的输出刚度和运动导向机构的负载刚度，利用模块法构建整个精密定位平台的静力学模型。经静力学分析可知，在单个自由度方向上，2个双桥臂桥式放大机构与运动导向机构为并联分布，将两者的刚度相加即可得精密定位平台在单个自由度方向上的输出刚度K_t：

则精密定位平台的位移放大倍数R_t为：

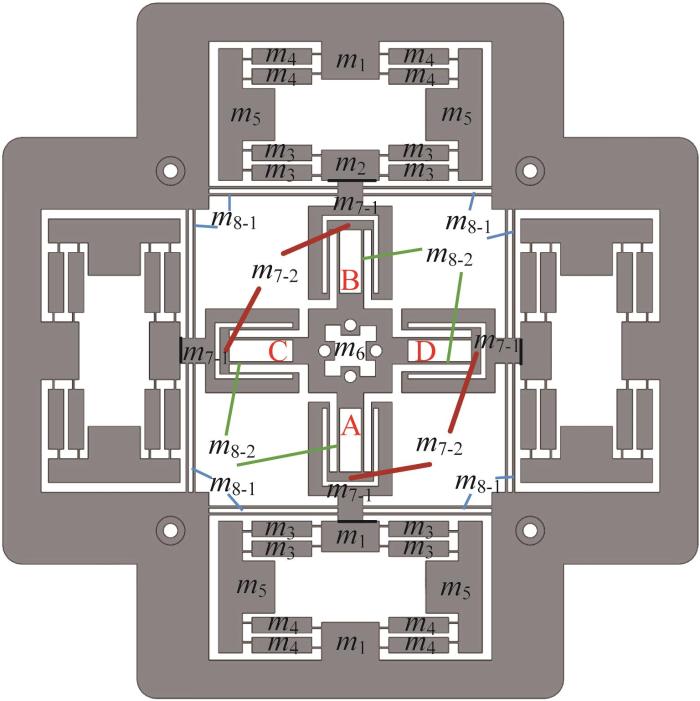
利用拉格朗日定理对精密定位平台进行动力学建模，其质量分布如图6所示。图中：m₁~m₅为双桥臂桥式放大机构各构件的质量，m₆为工作平台的质量，m_8-1、m_8-2分别为复合平行四边形机构和双级平行四边形机构中单根柔性梁的质量，m_7-1、m_7-2分别为双级平行四边形机构中除柔性梁外的其余构件的质量。

根据图6，对精密定位平台进行动能分析，可得其等效质量M_e：

基于拉格朗日方程可得该精密定位平台沿输出方向的动力学方程：

式中：q_i （i=1, 2）为广义坐标，K_e为精密定位平台的等效刚度。

精密定位平台的等效刚度即为其输出刚度K_t，即：

因此，根据频率计算公式，可得精密定位平台的一阶固有频率f：

为了验证理论计算结果的准确性，将在SolidWorks软件中建立的二维精密定位平台模型导入ANSYS Workbench软件，对其位移放大倍数、解耦性能、输出刚度以及固有频率进行有限元仿真分析。精密定位平台所用材料为7075铝合金，其密度为2 810 kg/m³，杨氏模量为71.7 GPa，泊松比为0.33。与其他材料相比，7075铝合金具有较高的杨氏模量和屈服强度。因此，在材料的可承受范围内，精密定位平台能够输出更大的位移。设网格划分单元尺寸为1 mm，以保证有限元仿真分析的精度。所设计的二维精密定位平台的尺寸参数如表1所示。

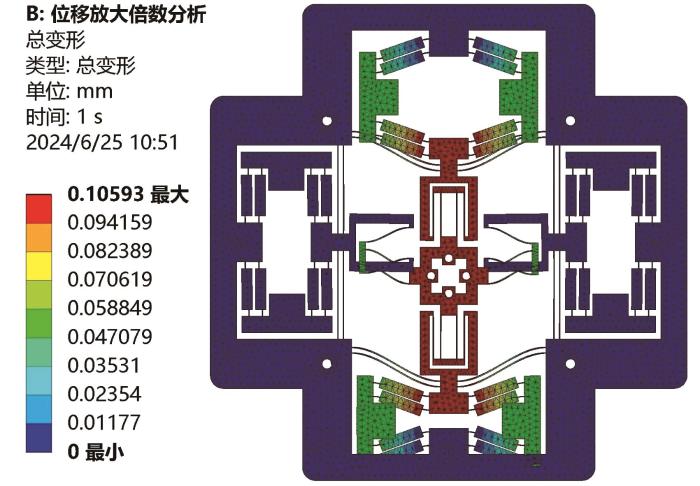
二维精密定位平台的结构完全对称，其在x和y两个运动方向上的静力学性能完全相同，因此本文仅以沿y方向的运动为例进行分析。通过有限元仿真分析得到精密定位平台沿y方向的运动位移，如图7所示。在仿真时，共向双桥臂桥式放大机构两边施加10 μm的位移。图7结果显示，该精密定位平台沿y方向移动了105.93 μm，耦合位移为0.05 μm，通过计算可得其位移放大倍数约为10.59，而理论计算得到的位移放大倍数为11.27，两者的相对误差为6.42%。进一步分析可知，该精密定位平台可实现完全解耦。产生耦合位移的主要原因是当工作平台沿y方向运动时，复合平行四边形机构和双级平行四边形机构会带动x方向上的2个双桥臂桥式放大机构运动，从而产生极其微小的偏转；此外，有限元仿真分析时所设置的网格并不完全对称，导致精密定位平台左右两端的偏转程度不同，从而产生沿x方向的耦合位移。

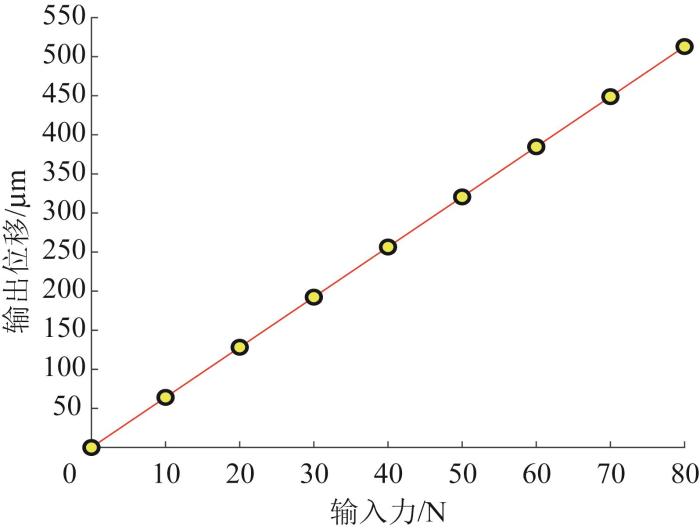
为了验证刚度理论模型的准确性，在二维精密定位平台输出端施加递增的输入力，通过有限元仿真分析得到相应的输出位移，不同输入力与输出位移的关系如图8所示。由图8可知，输入力与输出位移呈线性正相关；有限元仿真分析得到的精密定位平台的输出刚度为157 N/mm，而理论计算得到的输出刚度为172 N/mm，两者的相对误差为9.55%。由此可知，所构建的刚度理论模型具有较高的准确性。

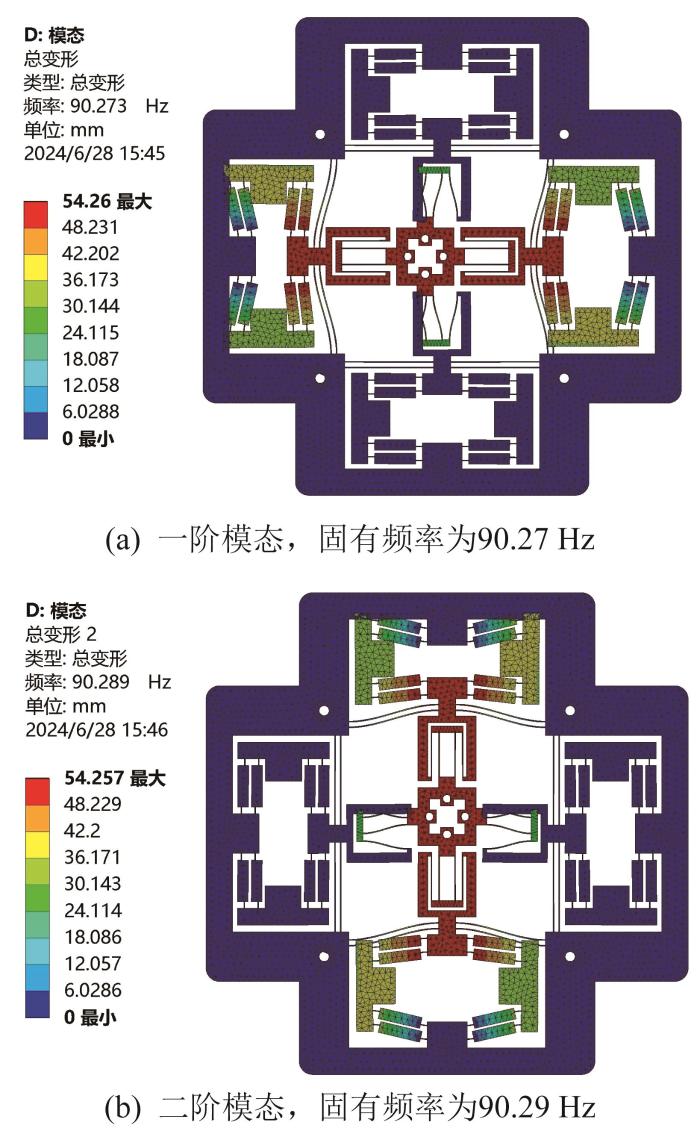
为了验证二维精密定位平台的动力学性能，对其固有频率进行有限元仿真分析。该精密定位平台前两阶固有频率的仿真结果如图9所示。其中，一阶模态为沿y方向的运动，二阶模态为沿x方向的运动。在实际应用中，机构的前两阶模态为主要运动方向，由于精密定位平台结构完全对称，其一阶模态和二阶模态基本相同。通过有限元仿真分析得到的精密定位平台的一阶固有频率为90.27 Hz，而理论计算得到的一阶固有频率为83.28 Hz，两者的相对误差为7.74%，由此验证了动力学理论模型的准确性。

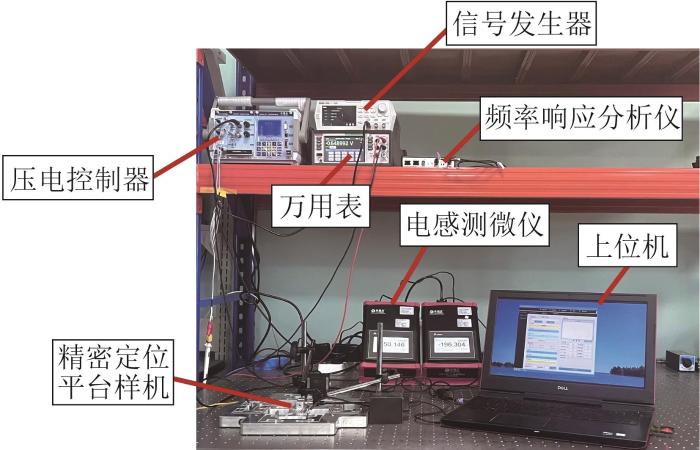
为了进一步验证二维精密定位平台的性能以及所建立的理论模型的准确性，通过慢走丝线切割的方式加工图10所示的精密定位平台样机，并搭建相应的实验装置，如图11所示。其中，压电陶瓷驱动器的型号为PSt150/14/40 VS20（哈尔滨芯明天科技有限公司），其行程为38 μm，刚度为120 kN/mm；压电控制器的型号为E01.D3（哈尔滨芯明天科技有限公司），可与压电陶瓷驱动器配合，以实现闭环线性输出；信号发生器的型号为DG822（RIGOL公司），其具备广泛的频率覆盖范围，最高可达到25 MHz；位移传感器的型号为E75LVDT（哈尔滨芯明天科技有限公司），其测量范围为0~1 mm，分辨率为0.05 μm；万用表的型号为DMM6500（Keithley公司），用于测量压电陶瓷驱动器的电感电压，以计算输出位移；频率响应分析仪（哈尔滨芯明天科技有限公司）用于测量精密定位平台的固有频率。

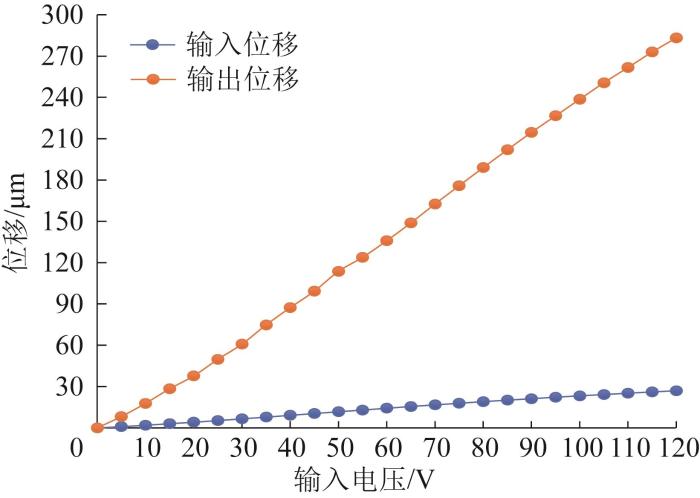
首先，给压电陶瓷驱动器输入0~120 V的驱动电压，步进为5 V，利用电感测微仪来测量精密定位平台的输入位移及输出位移，结果如图12所示。由图12可知，通过实验测得的精密定位平台的平均位移放大倍数约为9.78，而有限元仿真分析得到的位移放大倍数约为10.59，两者的相对误差为8.28%，出现上述现象的原因可能是精密定位平台样机存在加工误差。

然后，给压电陶瓷驱动器施加150 V的驱动电压并进行测试，测得精密定位平台在x、y方向上的运动行程均为310 μm。

最后，当精密定位平台沿y方向运动时，利用位移传感器测得其沿x方向的最大耦合位移为0.82 μm；同理，当精密定位平台沿x方向运动时，利用位移传感器测得其沿y方向的最大耦合位移为0.58 μm。结果表明，该精密定位平台具有较好的解耦性能，但存在耦合位移且沿x、y方向不同，这可能是因为加工误差使得精密定位平台的结构不完全对称，且2个方向上的位移传感器灵敏度有所差异。

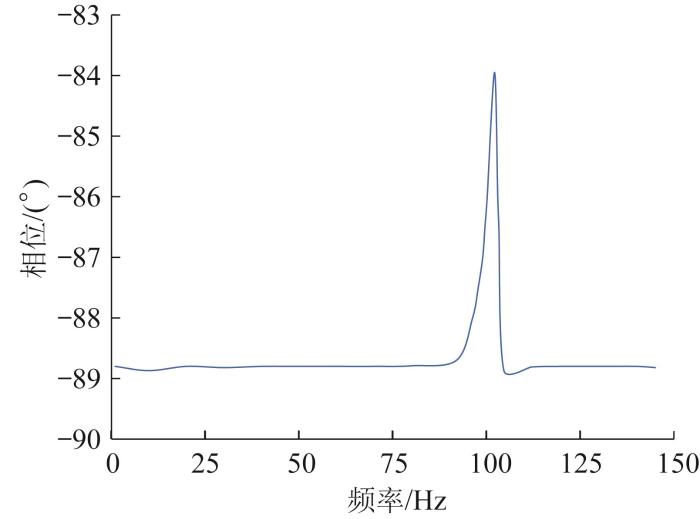
为了测试精密定位平台的频响特性，利用信号发生器输入电压幅值为1 V、频率为1~500 Hz的正弦波扫频信号。该扫频信号被压电控制器放大至12 V，用于驱动压电陶瓷驱动器；随后，压电陶瓷驱动器内部的电阻应变片捕捉相应的电信号，并将其传输回频率响应分析仪，从而获得精密定位平台的一阶固有频率，结果如图13所示。从图13中可以看出，该精密定位平台的一阶固有频率为102.10 Hz，实测值大于仿真值，这是因为在有限元仿真分析过程中未考虑压电陶瓷驱动器的刚度以及精密定位平台样机的加工误差。

精密定位平台的位移放大倍数、输出刚度和一阶固有频率的理论计算值、仿真值以及实测值的对比如表2所示。对比结果验证了理论计算的准确性以及精密定位平台的优异性能。

本文设计了一种基于压电陶瓷驱动的二维精密定位平台。首先，基于弹性梁理论和柔度矩阵法，对双桥臂桥式放大机构和运动导向机构分别进行了静力学建模，进而利用模块法推导得到整个精密定位平台的位移放大倍数和输出刚度，并利用拉格朗日方程推导了其一阶固有频率的表达式。随后，通过ANSYS Workbench软件对精密定位平台进行静力学及动力学有限元仿真分析。结果显示，对于精密定位平台的位移放大倍数、输出刚度和一阶固有频率，理论计算结果与有限元仿真结果的相对误差分别为6.42%、9.55%、7.74%，验证了所建立的各理论模型的准确性。最后，搭建了精密定位平台实验装置，通过实验测得所加工的精密定位平台样机的位移放大倍数约为9.78，在x、y方向上的运动行程均为310 μm，输出刚度为167 N/mm，一阶固有频率为102.10 Hz。结果表明，所设计的二维精密定位平台具有位移放大倍数大、输出刚度高和解耦性能优异等优点，具有较高的实用价值。