基于行为树的单舵轮AGV路径规划

doi:10.3785/j.issn.1008-973X.2026.03.020

基于行为树的单舵轮AGV路径规划

林桂娟^,, 李子涵, 陈潇晨, 王宇

1. 厦门理工学院机械与汽车工程学院，福建厦门 361024

2. 厦门理工学院精密驱动与传动福建省高等学校重点实验室，福建厦门 361024

Single-steering-driven AGV path planning based on behavior tree

LIN Guijuan^,, LI Zihan, CHEN Xiaochen, WANG Yu

1. School of Mechanical and Automotive Engineering, Xiamen University of Technology, Xiamen 361024, China

2. Fujian Provincial Key Laboratory of Precision Drive and Transmission, Xiamen University of Technology, Xiamen 361024, China

收稿日期: 2025-03-1

基金资助:

福建省自然科学基金资助项目(2025J011285).

Received: 2025-03-1

Fund supported:

福建省自然科学基金资助项目(2025J011285).

作者简介 About authors

林桂娟（1978—），女，教授，从事智能制造及机电工程的研究.orcid.org/0009-0002-6551-7222.E-mail：linguijuan@xmut.edu.cn , E-mail：linguijuan@xmut.edu.cn

摘要

针对传统算法不适用于单舵轮自动导引运输车（AGV）的问题以及仓储物流作业的高秩序性需求，提出基于Nav2行为树的整体导航系统. 构建整体运行有向图，提出基于站点与航向约束的改进Dijkstra全局路径规划算法. 基于多目标组合优化的梯度引导改进DWA算法，采用分离轴与三邻域扩展方式改进A*规划避障路径，二者共同工作进行局部路径规划. 基于Nav2的行为树，构建避障策略. 仿真显示，与传统算法相比，采用改进Dijkstra算法的节点遍历数最高降低81.6%，寻路时间最高降低42.1%. 与传统DWA相比，改进DWA在无障碍物路径跟随中，误差均方根最高可以降低73.78%，控制精度小于50 mm. 实车验证可知，与传统DWA相比，采用改进DWA算法的跟踪误差最高降低50.26%，应对动静障碍物时均能准确地判断，具有较高的灵活性和精确性.

关键词： 单舵轮自动导引运输车 ; Nav2 ; 仓储物流 ; 路径规划 ; 行为树

Abstract

A navigation system based on the Nav2 behavior tree was proposed to address the inapplicability of traditional algorithm for single-steering-wheel automated guided vehicle (AGV) and the high-orderliness requirement of warehouse logistics operation. An overall operational directed graph was constructed, and an improved global path planning algorithm based on site and heading constraints was developed using a modified Dijkstra approach. A gradient-guided dynamic window approach (DWA) enhanced through multi-objective optimization was introduced, while an improved A* algorithm with a separated-axis and tri-neighborhood expansion strategy was employed to plan obstacle avoidance paths. These two methods operated cooperatively to achieve local path planning, and an obstacle avoidance strategy was constructed within the Nav2 behavior tree framework. The simulation results showed that the proposed Dijkstra algorithm reduced the number of traversed nodes by up to 81.6% and the pathfinding time by up to 42.1% compared with traditional algorithms. The improved DWA achieved a maximum reduction of 73.78% in the root mean square error (RMSE) during obstacle-free path following compared with the traditional DWA, maintaining control accuracy within 50 mm. Real-vehicle experiments demonstrated that the improved DWA algorithm reduced the tracking error by up to 50.26% compared with the traditional DWA. The improved DWA algorithm can accurately identify and respond to both static and dynamic obstacles, exhibiting high flexibility and precision.

Keywords： single-steering-wheel automated guided vehicle ; Nav2 ; warehouse logistics ; path planning ; behavior tree

PDF (2866KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

林桂娟, 李子涵, 陈潇晨, 王宇. 基于行为树的单舵轮AGV路径规划. 浙江大学学报(工学版)[J], 2026, 60(3): 643-650 doi:10.3785/j.issn.1008-973X.2026.03.020

LIN Guijuan, LI Zihan, CHEN Xiaochen, WANG Yu. Single-steering-driven AGV path planning based on behavior tree. Journal of Zhejiang University(Engineering Science)[J], 2026, 60(3): 643-650 doi:10.3785/j.issn.1008-973X.2026.03.020

自动导引运输车（automated guided vehicle，AGV）是通过多传感器信息与控制器系统交互实现自动运行的设备，在现代工业生产行业中广泛应用^[1-3]. 单舵轮AGV是仓储物流搬运中不可或缺的装备，对叉车的数量与功能需求持续增加^[4-6]. 为了提升叉车的智能化水平，以满足客户日益增长的个性化需求，开发高自动化的叉车已成为必然趋势^[7-9]. 研究适用于单舵轮AGV且同时兼顾全局路径规划和局部路径规划的导航算法对提升仓储物流效率具有重要的意义.

Wu等^[10]提出融合改进A*与改进DWA的混合动态路径规划算法，优化A*算法路径转折点冗余问题,引入路径点距离和速度作为评价指标改进DWA. 王倩等^[11]融合蚁群算法和动态窗口法，提出多指标寻优的启发式函数和信息素更新策略，提升蚁群的寻优能力和未知环境下机器人的避障能力. 郭建等^[12]改进Dijkstra算法并采用MPC优化，提出融合改进Dijkstra算法和MPC的路径规划算法. 刘宇庭等^[13]融合改进A*算法与ROA-DWA，调整启发式函数权重与自适应速度因子，提高动态避障效率. 段震等^[14]提出融合IGJO与TEB的路径规划方法，提升寻优精度，并引入TEB动态规划避开移动障碍. Wu等^[10,13-14]研究双轮差速模型和履带式底盘模型，不适用于单舵轮AGV. 王倩等^[11]的研究表明，整体路径的全局随机性过大，不利于在有秩序的环境中运行.

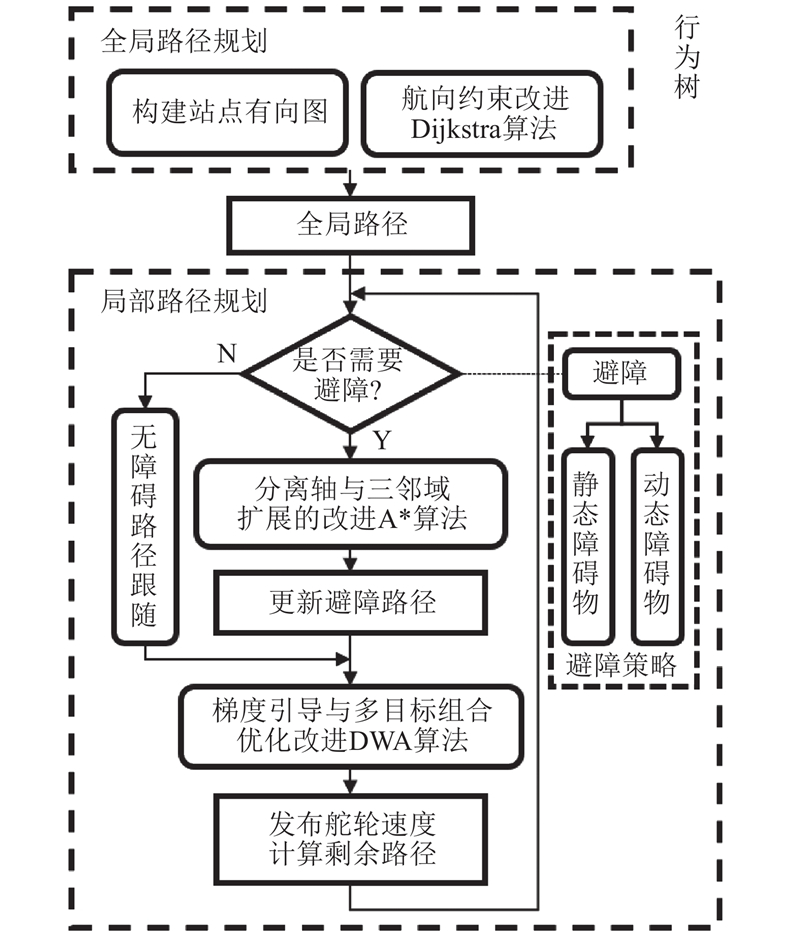
基于图搜索的Dijkstra算法更适用于仓储环境中的路径规划，Dijkstra算法在计算最短路径时，通常假设移动能力均匀且自由^[15]. 单舵轮AGV在转向和运动方式上具有独特的限制，在路径选择上必须考虑到转向半径和操作灵活性，Dijkstra算法的线性路径规划可能导致路径不够灵活且效率较低，因此需要结合单舵轮AGV的运动特性进一步优化. 传统的DWA算法注重枚举模拟轨迹群并且只判断每个轨迹群的终点位置与参考点的契合度，忽略了整条轨迹与前向路径的契合程度^[16-17]，当开展局部路径规划时，极易出现模拟轨迹与期望轨迹偏差较大的情况. 为了解决传统算法不适用于单舵轮AGV的问题，针对仓储环境中物流作业的高秩序性需求，提出基于Nav2行为树融合路径规划与避障策略的整体导航系统. 具体创新点如下. 1）构建整体物流环境的单舵轮AGV运行有向图，提出基于站点与航向约束的改进Dijkstra全局路径规划算法. 2）提出基于多目标组合优化的梯度引导改进DWA算法，提出分离轴与三邻域的改进A*算法规划避障路径，二者共同工作进行局部路径规划. 3）提出基于Nav2行为树的避障策略构建方式，使得单舵轮AGV在仓储物流环境中可以应对不同属性的障碍物，灵活性更高. 通过仿真与实车验证，保证算法的可实现性与高效性.

1. 全局路径规划

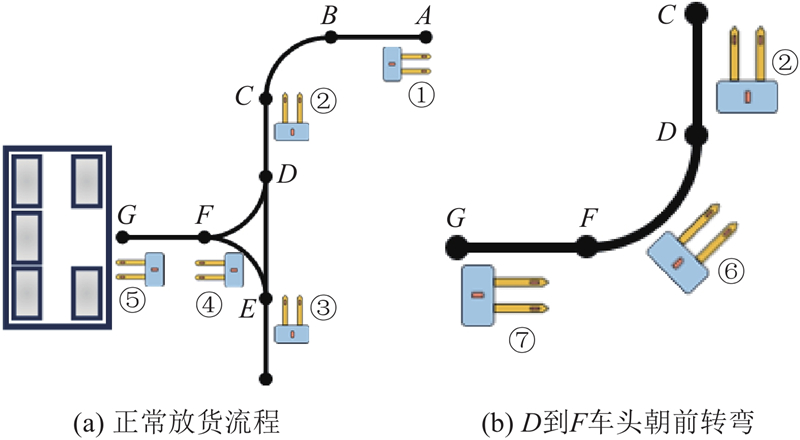
1.1. 单舵轮AGV库位交互

单舵轮AGV无法原地旋转，仓储物流中单舵轮AGV与库位交互时，期望以叉齿方向进入库位，须按照圆弧轨迹过弯，图1所示. 图1中，AGV从A点前往G点的库位，满足图中的位姿⑤. 图1(a)中，AGV从起始位姿①，当经过BC段圆弧时变为位姿②，经过CD段. 从D点经过E点，再以叉齿方向转弯到达F点，即图1(a)中的位姿③和④，最后按照期望位姿⑤到达库位点G. 假设AGV从D点直接通过圆弧前往F，到达G点后的小车位姿与期望位姿⑤不符，如图1(b)中的位姿⑦.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 单舵轮AGV入库位的流程

Fig.1 Flow of single-steering AGV inbound positioning

1.2. 航向约束改进Dijkstra算法

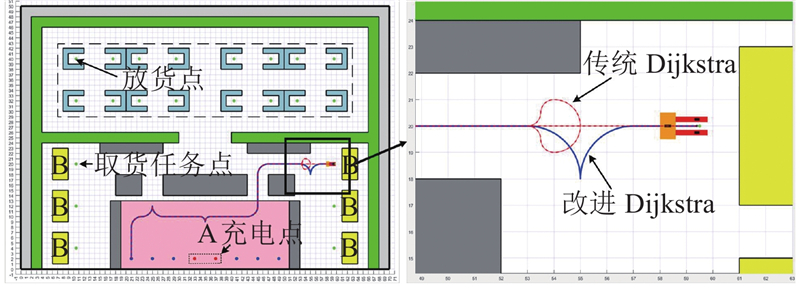
针对仓储物流整体环境须保持秩序性、单舵轮AGV转弯需要一定的转弯半径以及传统Dijkstra算法面对大型网图时搜寻效率低的问题，提出基于站点与航向约束的改进Dijkstra算法，流程如图2所示. 思路如下. 1）在整体静态环境地图中规划出整体仓储物流中的各点位，部署期望路径站点，除非必要的倒车入库路径，其余均以车头朝前的运行方式. 2）在全局地图中设置站点位置和与相邻节点的期望运行方向后，构建全图信息. 提出采用构建子图的方式，根据起点和终点的状态信息构建不同的子图，极大地减少了路径搜索时间. 3）构建航向约束扩展子图，防止出现传统Dijkstra算法中不考虑运行方向，即图1(b)的实际与期望位姿不符的情况.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 改进Dijkstra算法的流程

Fig.2 Process of improved Dijkstra algorithm

2. 局部路径规划

2.1. 梯度引导与多目标组合优化改进DWA算法

针对传统的DWA算法忽略整条轨迹与前向路径的契合程度，提出基于多目标组合优化的梯度引导改进DWA算法，如图3所示. 构建舵轮速度与侧向跟踪误差的数学模型、舵轮速度与角度偏差的数学模型. 结合梯度下降分配权重及组合优化，获取动态窗口域的最优解. 根据前向模拟时间模拟出连续的多组速度，将最优速度发布到控制底盘.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 改进DWA算法的流程

Fig.3 Process of improved DWA algorithm

结合单舵轮AGV的运动学模型，得到舵轮速度、侧向跟踪误差和角度偏差的数学模型，如下所示.

(1)$ \left.\begin{array}{l}e_{\mathrm{d}}(\theta)=\left|A(\theta)\cos\gamma_{\mathrm{p}}-B(\theta)\sin\gamma_{\mathrm{p}}\right|, \\ A(\theta)=y_0-y_{\mathrm{p}}+v\cdot\cos\theta\cdot\mathrm{d}t\cdot\sin\left(\gamma_0+\dfrac{v\cdot\sin\theta\cdot\mathrm{d}t}{2l}\right) ,\\ B(\theta)=x_0-x_{\mathrm{p}}+v\cdot\cos\theta\cdot\mathrm{d}t\cdot\cos\left(\gamma_0+\dfrac{v\cdot\sin\theta\cdot\mathrm{d}t}{2l}\right).\end{array}\right\} $

(2)$ e_{\mathrm{h}}(\theta)=\left|\gamma_0-\gamma_{\mathrm{p}}+\dfrac{v \cdot \sin (\theta) \cdot {\mathrm{d}} t}{l}\right|. $

式中：v为舵轮的线速度，θ为舵轮的偏转角度，(x₀, y₀)、$ \gamma _0 $分别为全局坐标系下的当前位姿和偏航角，(x_p, y_p)、$ \gamma_{\rm{p}} $分别为全局坐标系下的预瞄点位姿和偏航角，e_d(θ)为侧向跟踪误差，e_h(θ) 为角度偏差，A(θ)、B(θ)分别为横向误差分量和纵向误差分量. 梯度引导计算如下所示：

(3)$ \left.\begin{array}{l}\theta_{e_{\mathrm{d}},i+1}=\theta_i-\boldsymbol{m}\cdot\nabla e_{\mathrm{d}}\left(\theta_i\right) ,\\ \theta_{e_{\mathrm{h}},i+1}=\theta_i-\boldsymbol{m}\cdot\nabla e_{\mathrm{h}}\left(\theta_i\right).\end{array}\right\} $

式中：m为梯度因子. 权重分配后的θ结果如下：

(4)$ \theta_{i+1}=a \theta_{e_{\mathrm{d}},i+1}+\beta \theta_{e_{\mathrm{h}},i+1}. $

式中：a为侧向跟踪误差的计算权重，β为角度偏差的计算权重. 收敛条件如下：

(5)$ \left|\left[a e_{\mathrm{d}}\left(\theta_{i+1}\right)+\beta e_{\mathrm{h}}\left(\theta_{i+1}\right)\right]-\left[a e_{\mathrm{d}}\left(\theta_i\right)+\beta e_{\mathrm{h}}\left(\theta_i\right)\right]\right|\lt \varepsilon . $

式中：ε为较小的值.

当AGV进行货物搬运作业时，在任务过程中将着重优化侧向跟踪误差，须提高权重a. 在接近任务点前着重优化角度偏差，须提高权重β. 在经由多次实验研究后，当AGV在任务过程中时，a与β分别设置为0.72和0.28；当AGV接近任务点时，a与β分别设置为0.34和0.66.

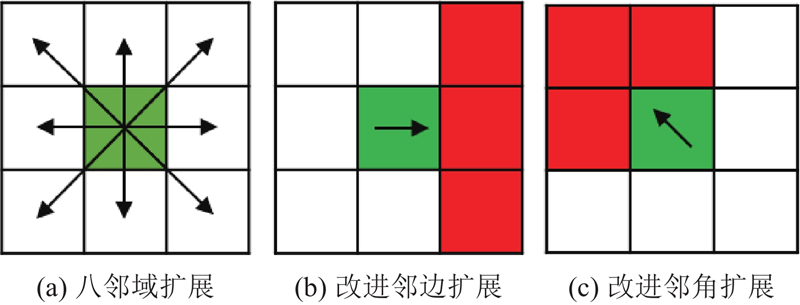
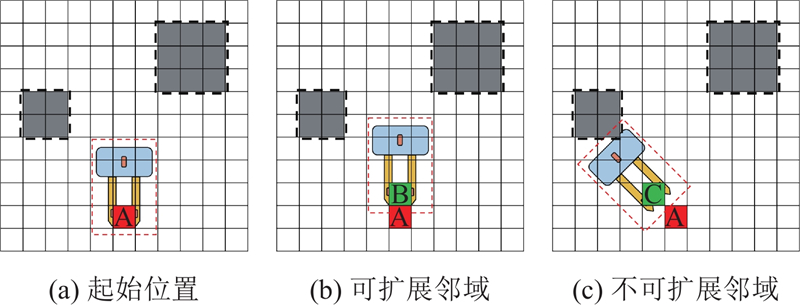
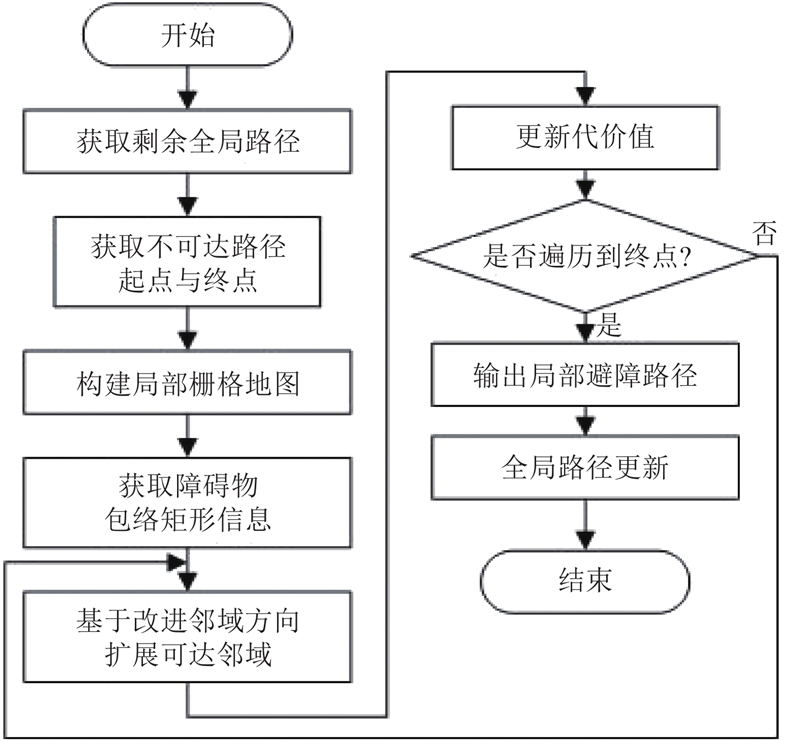
2.2. 避障路径规划

AGV路径跟随时可能会存在未知的障碍物，需要等到AGV接近时才可感知到^[18-19]. 本研究在AGV上配置相机传感器，实时获取周围环境的点云数据，经过处理后获取障碍物信息，进一步判断出前向全局路径中不可达路径点的索引. 结合单舵轮AGV运动学模型，提出基于分离轴与三邻域扩展的改进A*算法，获取车体轮廓和障碍物包络矩形，判定局部可达点，以规划避障路径，如图4所示. 传统的A*算法基于八邻域的方式，不断扩展邻居节点.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 改进A*邻域扩展方式

Fig.4 Improved A* neighborhood expansion approach

结合父节点的矢量方向，获取其方向正前方与斜前方左右45°的三邻域节点作为扩展节点，如图4(b)箭头右列的三邻域格、4(c)箭头所示的左上角3个域格所示，防止AGV规划出锯齿型路径，以降低路径跟随精度.

分离轴定理（separating axis theorem，SAT）是用于检测2个凸形状是否相交的几何方法^[20]. 判定局部可达点的方式如图5所示. 避障路径规划算法的流程如图6所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 局部可达点的搜索方法

Fig.5 Search method for local reachable point

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 避障路径规划算法的流程

Fig.6 Process of obstacle avoidance path planning algorithm

图5中，AGV在栅格地图中的起始位置如栅格A所示，车体轮廓如虚线矩形所示，障碍物轮廓如黑色虚线矩形所示. 当利用A*算法向邻域扩展时，结合运行方向获得邻域栅格中的车体轮廓，如图5(b)所示. 其中栅格B为扩展邻域，利用分离轴定理判定其与任意障碍物轮廓均未相交，则判定栅格B为栅格A的可扩展领域，即为局部可达点. 反之，如图5(c)所示，当扩展栅格C时与障碍物相交，则此点不可达.

3. 行为树导航算法融合

Navigation2（Nav2）集成了行为树引擎Behavior Tree Engine，用于管理机器人执行任务时的逻辑流，确保机器人行为的顺序和条件判断合理^[21-22]. 行为树是树形结构的决策模型，允许开发者设计复杂的任务序列，并通过条件判断动态选择执行的路径^[23].

3.1. 避障策略

在仓储物流环境中，制定一系列的运行策略,能够保证员工和AGV安全的同时提高运行效率. 当AGV进行运输作业，遇到障碍物时，合理的逻辑处理可以有效地避免主干通道堵塞，保证整体物流的连续性^[24]. 针对可能遇到不同运动属性的障碍物，构建针对动静障碍物的避障策略，见图7.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 避障策略的流程

Fig.7 Process of obstacle avoidance strategy

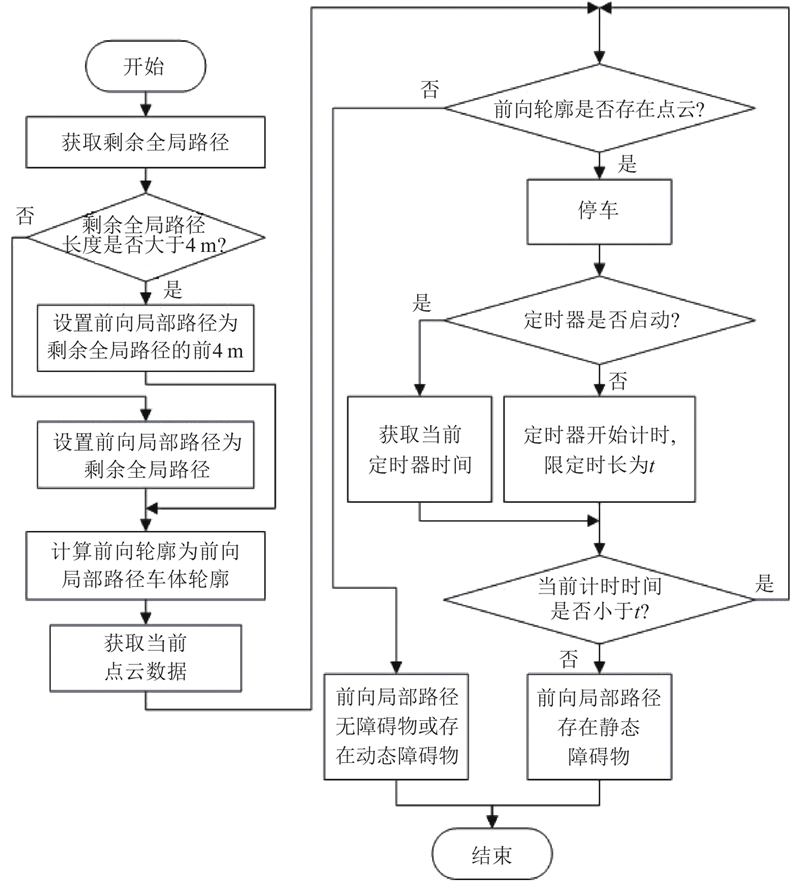
1）在剩余全局路径中获取前向4 m的所有路径点，若剩余路径不足4 m，则取全部，称作前向局部路径.

2）计算前向局部路径的车体运行轮廓，称作前向轮廓，获取相机传感器获取的点云数据，判断前向轮廓内是否存在点云，即是否存在障碍物.

3）前向轮廓存在点云后停车，设定计时时间t. 在t时间内障碍物离开前向轮廓，判定为动态障碍物，则恢复运行，无须避障. 若在t时间后前向轮廓存在障碍物，则判定前向局部路径存在静态障碍物，更新避障路径，恢复运行.

3.2. 行为树构建导航算法

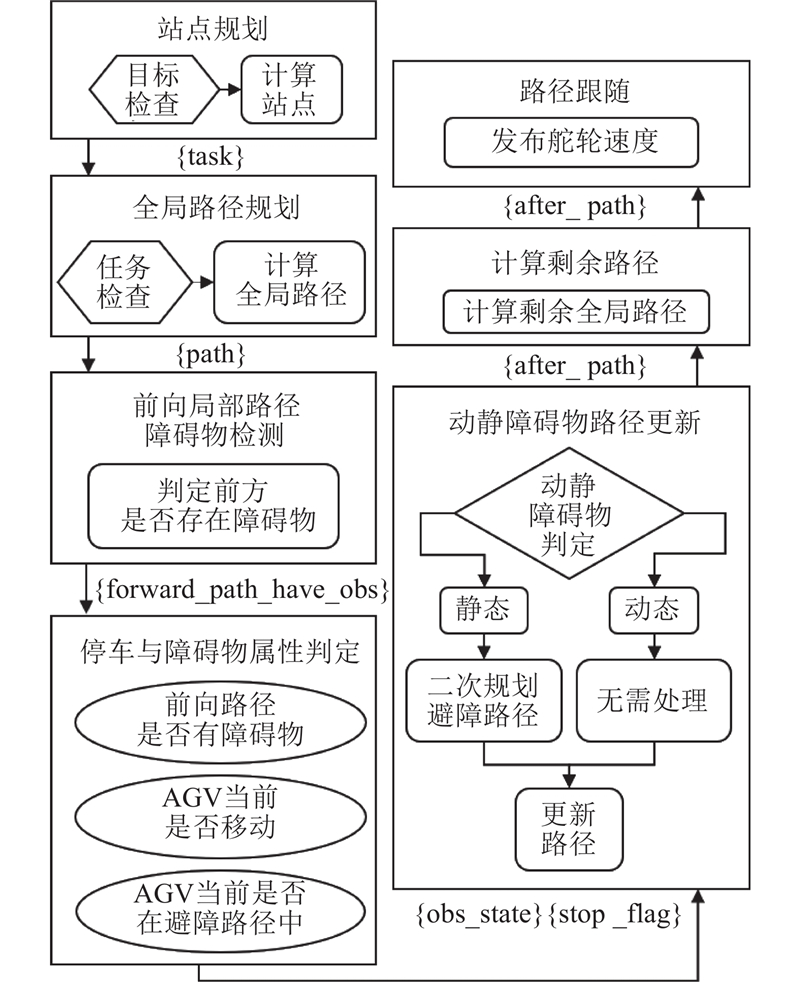
对导航功能的各个模块展开深入研究，还须统筹全局的节点，将每一子块串联成整体导航系统，行为树导航系统的架构如图8所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 行为树导航系统的架构

Fig.8 Architecture of behavior tree navigation system

构建整体导航系统的Navigator节点，将站点规划、路径规划、前向局部路径障碍物检测、停车与障碍物属性判定、动静障碍物路径更新、计算剩余路径和路径跟随这7个模块串联结合，形成完整的导航与避障系统. 完整的行为树Navigator节点如图9所示.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 行为树Navigator节点

Fig.9 Behaviour tree Navigator node

4. 仿真与应用

4.1. 算法仿真

4.1.1. 全局路径规划

在仿真平台MATLAB R2021b中搭建模拟仓储仿真环境，搭建70 mx50 m整体仓储环境，具体信息如下.

A区域为AGV停车与充电区域，中间虚线框的两点为AGV充电点，其余6点为AGV停车点，以叉齿方向进入站点. 6个B区域为取货区域，对应的站点为AGV取货任务点. C区域包含16个U型放货区域，对应的站点为AGV放货点. 在Gazebo中进行模拟导航仿真实验，环境建模和限制信息与此处相同. 采用传统Dijkstra算法与改进Dijkstra算法得到的结果如图10所示. 其中，虚线为传统Dijkstra规划路径，实线为改进Dijkstra规划路径，对比数据如表1所示. 其中，N为遍历节点数，L为路径长度，T为寻路时间，ΔN为节点遍历优化率，ΔT为寻路效率的提升率.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 停车点到取货点的仿真对比

Fig.10 Simulation comparison of parking point to pick-up point

表 1 全局路径规划的仿真对比数据

Tab.1 Simulation comparison data of global path planning

任务信息	传统Dijkstra			改进Dijkstra			优化效率
任务信息	N	L/m	T/s	N	L/m	T/s	∆N/%	∆T/%
停车点→取货点	174	63.53	0.31	111	59.53	0.26	36.2	16.1
取货点→放货点	174	69.17	0.31	162	68.60	0.30	6.9	3.2
放货点→充电点	174	80.62	0.35	166	80.05	0.28	4.6	20.0
充电点→停车点	174	32.13	0.38	32	32.13	0.22	81.6	42.1

新窗口打开| 下载CSV

图10中，传统的Dijkstra算法只寻求长度最短而未考虑到入库位姿，在进入任务点前以“小圆弧旋转矫正位姿”的方式二次修正路径，延长路径长度且无法满足仓储环境的任务秩序性，利用基于航向约束改进的Dijkstra算法可以避免此类问题. 如表1所示，改进Dijkstra算法的节点遍历数较传统Dijkstra算法大大降低，最高可以降低81.6%，且面对复杂图时，寻路时间最高可以降低42.1%.

4.1.2. 无障碍物路径跟随仿真

为了防止直线与标准圆弧衔接处产生曲率跳变而影响AGV路径跟随性能，利用同半径贝塞尔曲线优化标准圆弧部分^[25]. 按照MATLAB仿真搭建的全局仓储物流环境平面图，以1꞉1的比例构建三维模拟仓储物流环境，AGV舵轮的最大线速度为1.5 m/s，最大线加速度为3.0 m/s²，最大摆动角速度为1.0 rad/s，舵轮摆动中心至运动中心的距离为1.261 m.

选取“停车点到取货点”与“取货点到放货点” 2组实验进行对比. 结果如图11、12所示.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

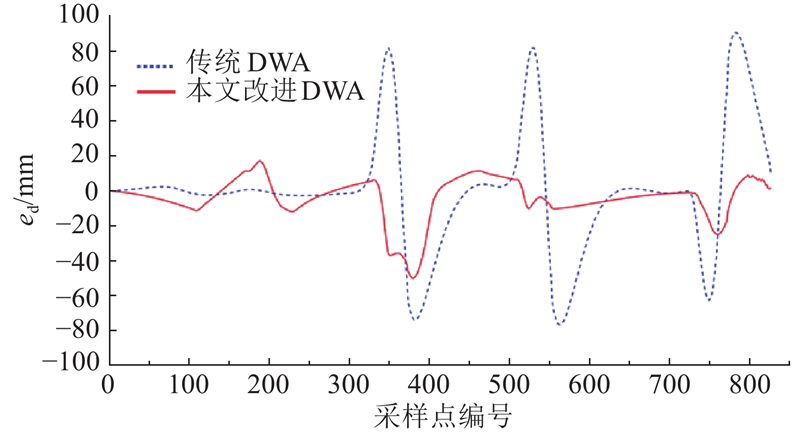
图 11 “停车点到取货点” 路径跟随

Fig.11 ‘Parking point to pick-up point’ path-following map

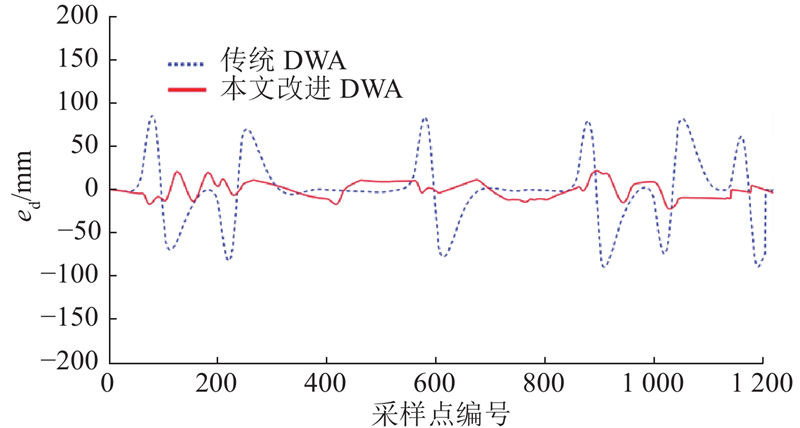
图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12 “取货点到放货点” 路径跟随

Fig.12 ‘Pick-up point to drop-off point’ path-following map

在“停车点到取货点”任务中，改进算法的侧向跟踪误差均方根为12.611 mm，较传统DWA算法降低了44.88%. 在“取货点到放货点”任务中，改进算法的侧向跟踪误差均方根为9.209 mm，较传统DWA算法降低了73.78%. 提出的改进DWA控制算法的整体误差控制在0~50 mm，表示控制精度可达50 mm，符合仓储物流的运行需求.

4.1.3. 动静障碍物的避障仿真

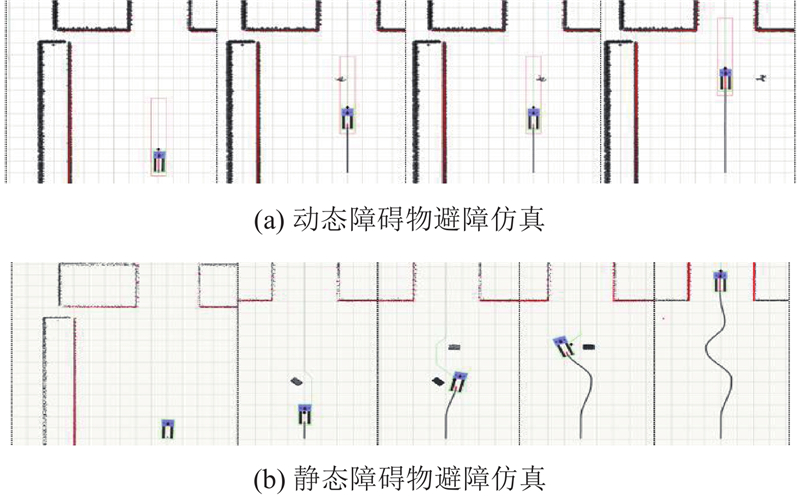
基于构建的避障策略，模拟场景“AGV在运行过程中检测到一个匀速移动的人经过前向路径并在短时间内离开前向路径范围”，对动态障碍物检测场景进行仿真. 模拟场景“AGV在运行过程中检测到2个储物柜静止在前向路径中”，对静态障碍物检测场景进行仿真. 避障仿真的实验结果如图13所示.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13 避障仿真的实验结果

Fig.13 Experimental result of obstacle avoidance simulation

从实验结果可知，行为树使各部分节点独立工作，解耦程度较高，提高运行稳定性. 面对各类型障碍物，AGV可以准确识别并判断属性，做出相应的动作，进一步验证该导航算法的可实现性.

4.2. 应用测试

结合仓储物流环境与实际的项目经验，路径跟随精度是衡量导航算法在实时执行过程中，AGV跟随预定路径的准确度. 以“整体路径跟随误差极值”判断精度的高低，结合诸多学者关于单舵轮AGV路径跟随精度的研究和实际生产需求的标准，将整体路径的跟随误差极值精度指标设定为0~15 mm^[26].

4.2.1. 无障碍物路径跟随实验

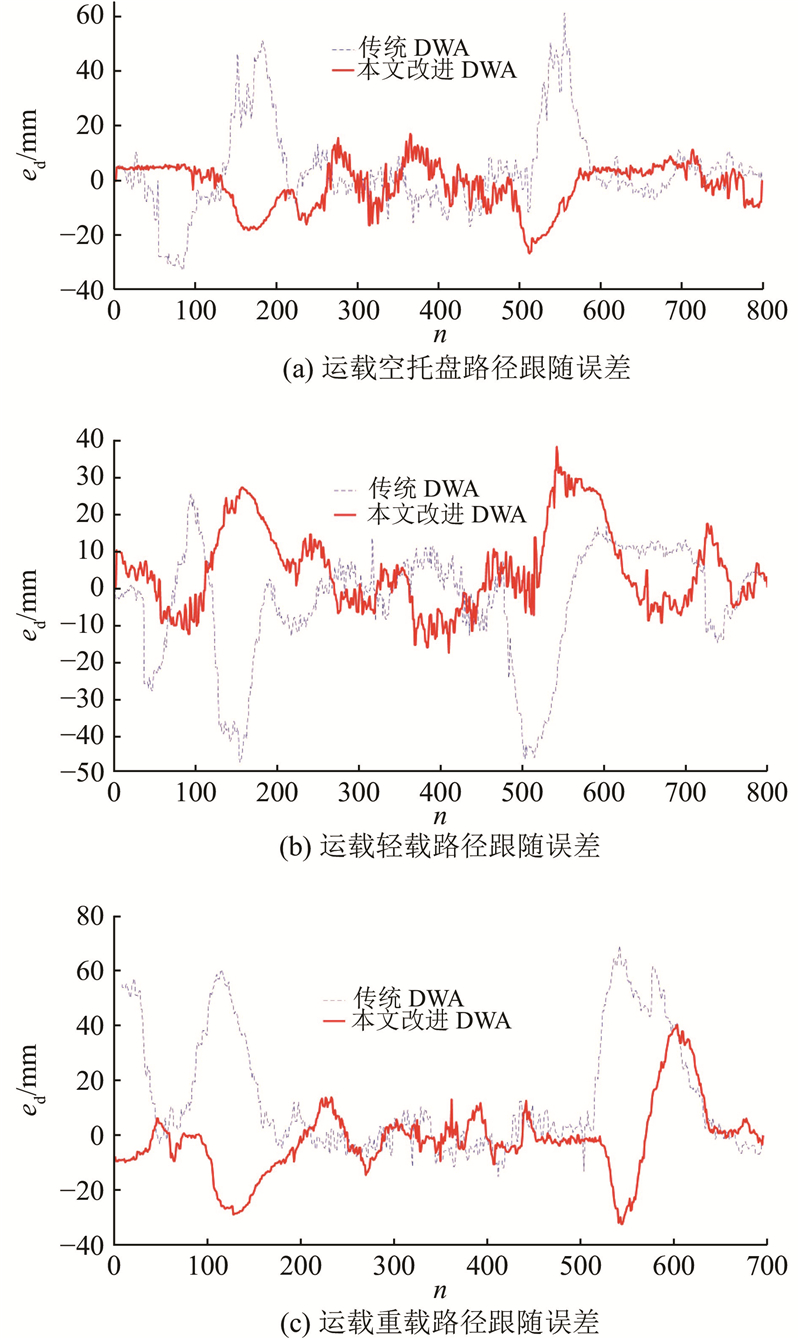
搭建整体仓储导航环境进行实验. 选取空托盘、轻载和重载3种货物作为取货对象，分别部署传统DWA算法和改进的DWA算法. 通过多次实验，分析无障碍物路径跟随时与期望路径的侧向跟踪误差，如图14所示.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14 实车路径跟随误差结果

Fig.14 Real-vehicle path following error result

从图14可知，AGV运载空托盘时，改进DWA算法的均方根为8.499 mm，传统DWA算法的均方根为16.085 mm，整体误差降低了47.15%. 同理，AGV分别运载轻载货物与重载货物时，改进DWA算法的整体误差较传统DWA降低了24.03%和50.26%，路径跟随能力更强.

4.2.2. 动静障碍物避障实验

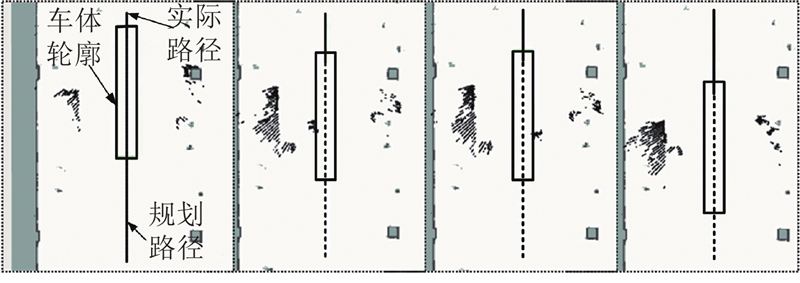
以行走的人作为动态障碍物经过AGV前向路径，AGV检测到障碍物信息后经由行为树判断，障碍物在设定时间内离开前向路径后AGV恢复运行，避让动态障碍物，AGV运行路径如图15的粗实线所示. 其中，粗实线曲线为实际运行路径，虚实线曲线为规划路径，粗实线包络多边形为前向局部路径车体轮廓.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15 动态障碍物避障运行路径图

Fig.15 Operation path diagram of dynamic obstacle avoidance

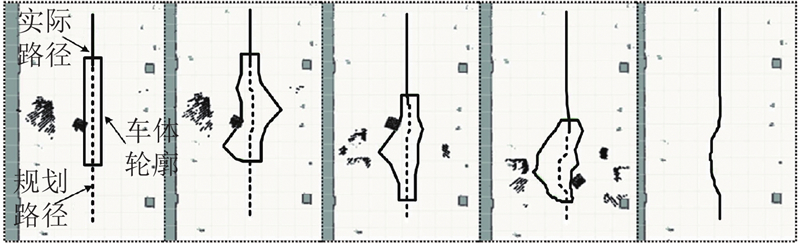
在前向路径放置2个静态障碍物，AGV运行时检测到障碍物停车，超过设定时间后障碍物依旧存在于前向路径，进入静态障碍物的避障逻辑判断，更新避障路径后恢复运行，跟随更新后的轨迹. AGV运行路径如图16的粗实线所示. 其中，粗实线为已实际运行路径，虚实线为规划路径，粗实线包络多边形为前向局部路径车体轮廓.

图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16 静态障碍物避障运行路径图

Fig.16 Static obstacle avoidance operation path diagram

从图15、16可知，基于行为树构建的避障策略运行时检测到不同属性的障碍物，均具有良好的避障效果，保证了整体运行的稳定性.

5. 结　论

（1）在全局路径规划方面，提出基于站点与航向约束的改进Dijkstra算法. 从仿真对比可知，改进Dijkstra算法的节点遍历数较传统Dijkstra算法最高可以降低81.6%，且面对复杂图时，寻路时间最高可以降低42.1%.

（2）在局部路径规划方面，提出基于多目标组合优化的梯度引导改进DWA算法，并提出基于分离轴与三邻域的改进A*算法规划避障路径，二者共同工作进行局部路径规划. 从仿真验证可知，改进DWA控制算法的无障碍物路径跟随误差均方根较传统算法最高可以降低73.78%,控制精度可达0~50 mm.

（3）在避障策略方面，提出基于Nav2行为树的避障策略，使单舵轮AGV在仓储物流环境中能够应对不同属性的障碍物，灵活性更高. 从仿真验证可知，在应对静态和动态障碍物时均准确识别并判断，进一步验证了该导航算法的可实现性.

（4）在某公司的单舵轮AGV运行平台上进行实验. 结果表明，当搬运不同质量的货物时，改进DWA算法的无障碍物路径跟随误差较传统DWA低，最高可以降低50.26%.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

YIN X, CAI P, ZHAO K, et al

Dynamic path planning of AGV based on kinematical constraint A* algorithm and following DWA fusion algorithms

[J]. Sensors, 2023, 23 (8): 4102

DOI:10.3390/s23084102 [本文引用: 1]

[2]

孙孝飞, 郭捷, 魏灿名, 等

3C智能制造工厂的AGV智慧物料传输与调度综述

[J]. 中南大学学报: 自然科学版, 2025, 56 (2): 514- 535

SUN Xiaofei, GUO Jie, WEI Canming, et al

Review of AGV smart material transmission and dispatching in 3C smart manufacturing factories

[J]. Journal of Central South University: Science and Technology, 2025, 56 (2): 514- 535

[3]

文生平, 苏毅龙, 瞿弘毅

Mecanum轮全向AGV轨迹跟踪级联控制器设计

[J]. 华南理工大学学报: 自然科学版, 2025, 53 (1): 49- 61