六轴喷涂机器人本体作业范围有限制,为了满足大型部件的自动喷涂要求,通常会配置外部轴与机器人本体进行联动以拓展作业范围. 在当前工业机器人主流构型中,具有中空非球形手腕的7R 6-DOF(六自由度)喷涂机器人因运动范围广、灵活性高,被广泛应用于喷涂作业[4]. 当机器人配置外部轴后,系统总自由度将超过6个,导致机器人运动冗余. 在这种状态下的机器人具有无穷多个逆运动学解,使得机器人系统的灵活性更高,若不采用合理的机器人轨迹规划策略,极可能产生机器人本体与外部轴运行不匹配导致轨迹不平滑,引发系统的抖动现象,影响喷涂质量和缩短系统使用寿命. 因此,在设计和应用冗余机器人系统时,应特别关注轨迹规划策略的合理性,确保系统稳定且可靠.
冗余机器人轨迹规划方法主要有3种,分别是几何法[5-7]、代数解法[8]和数值迭代法[9-11]. 几何法是将机器人各关节与末端执行器建立数学关系,通过对应的数学关系,在已知机器人末端执行器在笛卡尔空间中的位置和姿态的情况下,求解机器人各时刻关节角度或位置. 几何法适用于结构相对简单,关节数较少的机器人. 代数解法常采用雅可比矩阵及其变形求解关节速度与末端执行器线速度和角速度之间的微分关系,常用求解方法有闭环伪逆法和梯度下降法. 代数解法在机器人多解或无解的情况下无法求解. 数值迭代解法将机器人轨迹规划问题转换为在一定约束条件下求目标函数最优解问题,通常采用群优化算法进行优化计算. 数值迭代解法通过全局优化目标函数,能够在多解或无明确解析解的情况下获得更优解,且对奇异性问题具有更强的鲁棒性. 如孔令竹[12]提出基于灰狼优化算法的机械臂避障轨迹规划方法,实现机械臂各连杆全局避障且轨迹平滑,但收敛速度较慢. 李甚霖等[13]结合萤火虫算法与遗传算法优化机械臂轨迹时间,使搜索精度和效率得到提升,但在复杂环境下算法对高维冗余变量和多约束条件的适应性不足,容易陷入局部最优. 徐强等[14]提出改进模拟退火遗传算法,通过多种策略优化机械臂轨迹,提升了算法求解质量和效率,但算法对参数(如退火衰减系数、遗传操作概率)调优依赖性强. Bai等[15]提出基于Cauchy折射的人工蜂群算法并进行冗余机械臂逆运动学问题求解,提升了收敛精度和速度,但算法复杂度较高. 冗余机器人进行大型部件喷涂时的运动幅度大、运行时间长,为了提升机器人喷涂效率和喷涂质量,减小外部轴磨损,延长机器人系统整体使用寿命,本研究基于改进粒子群算法,对具有外部轴的冗余机器人喷涂轨迹进行优化.
1. 冗余机器人运动学建模
1.1. 冗余机器人运动学模型
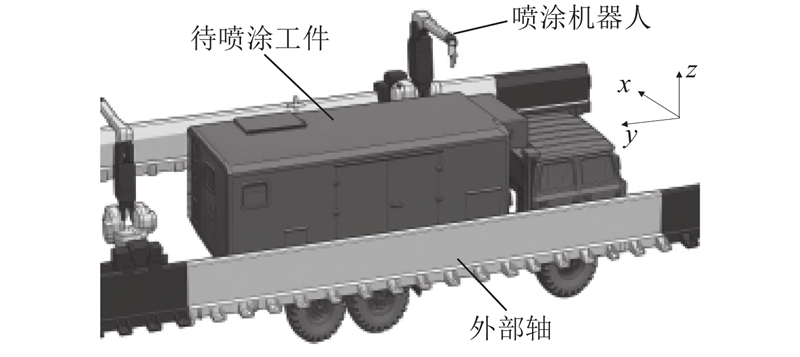
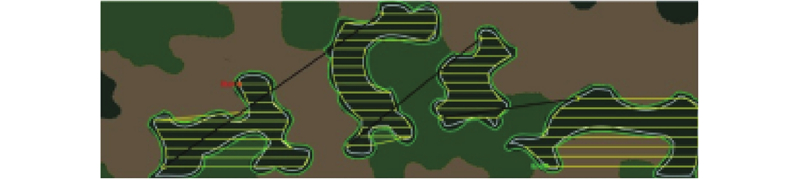
大尺寸工件喷涂所需的作业空间大,喷涂系统通常为6轴喷涂机器人附加外部轴的形式. 冗余喷涂机器人系统由2台7R 6-DOF喷涂机器人和2条7轴导轨组成,待喷涂工件摆放其中,如图1所示. 根据实际机器人喷涂应用需求,以ABB IRB 5500型7R 6-DOF喷涂机器人为研究对象,机器人本体的Y轴方向上配置外部轴以进行移动喷涂. 如表1机器人系统采用改进Denavit-Hartenberg(D-H)参数法[16-18]确定机器人的D-H参数,其中Ai为关节轴,
图 1
表 1 冗余机器人的Denavit-Hartenberg参数
Tab.1
| A1 | 0 | 0 | ||
| A2 | 0 | 0 | ||
| A3 | 0 | 0 | ||
| A4 | 0 | |||
| A5 | 0 | |||
| A6 | 0 | |||
| A7 | 0 | |||
| A8 | 0 |
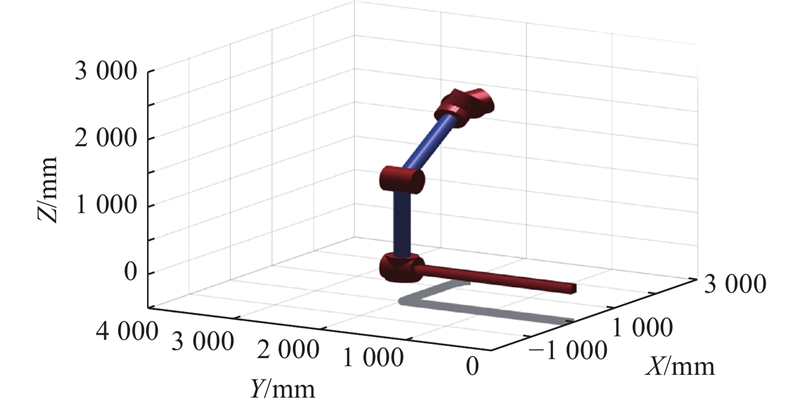
图 2
1.2. 冗余机器人逆运动学求解
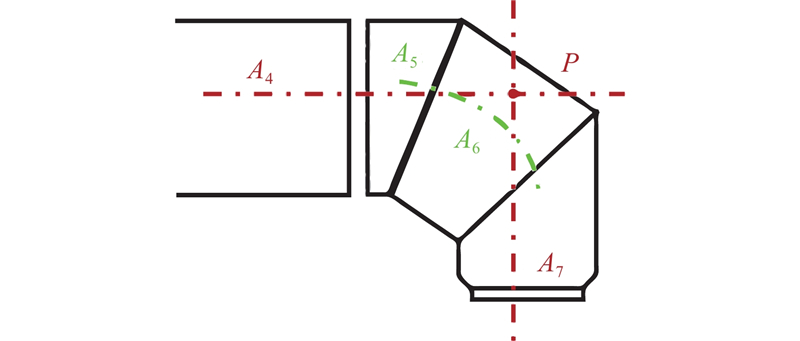
机器人在配置移动外部轴之后处于冗余状态. 在机器人运动范围内,已知末端执行器在笛卡尔空间的位置和姿态,可解出无穷多组逆运动学解,赋予系统的冗余关节合适的变量值,是求冗余机器人逆运动学解相对简单的方法. 田威等[19]针对附加外部轴的工业机器人提出分站式定位逆解方法,为冗余机器人的逆运动学求解提供了思路. 已知末端执行器位姿矩阵:
对应的指定外部轴位置y,有
图 3
1.3. 冗余机器人轨迹优化问题描述
由于外部轴的引入,机器人系统的喷涂轨迹规划须进行整体优化,以提高机器人外部轴与机器人本体之间的耦合度,保证机器人在喷涂过程中的动作柔顺性,减小机器人外部轴的磨损,延长机器人系统使用寿命. 已知机器人在笛卡尔空间下以梯形加减速的方式进行速度规划,以恒定速度执行喷涂任务,且机器人末端与机器人关节轴空间有如下关系:
式中:
为了实现机器人各关节运动幅度和机器人喷涂能量损耗综合最优,定义包含机器人各关节运动幅度适应度和喷涂过程中机器人能量损耗适应度的目标函数,并为机器人关节引入不同的权重. 适应度目标函数为
式中:
式中:
2. 改进粒子群算法
2.1. 传统粒子群算法原理
粒子群优化(particle swarm optimization, PSO)源于对鸟群捕食行为的研究,基本思想是通过群体成员之间的协作和信息共享来寻求最优解空间. 在初始化个体时,个体均带有位置和速度属性,个体寻优过程会随机生成速度矢量,并更新对应位置. 个体均记录自己的最优位置,即局部最优解,群体中所有个体的最优位置可以看作是群体的全局最优解. 通过不断更新粒子速度和位置,群体逐渐向全局最优解靠拢. 算法基本原理:在
式中:
2.2. 改进粒子群算法
PSO中的惯性权重表示当前速度受前一刻速度影响的程度. 在每个粒子通过调整自己的速度和位置来寻找最优解的过程中,惯性权重决定了粒子速度变化的惯性大小. 当惯性权重较大时,粒子更多地继承前一时刻的速度,优点是有利于粒子在更大的空间范围内搜索,从而增强算法的全局搜索能力,缺点是算法收敛速度慢,不能进行精确搜索. 当惯性权重较小时,粒子对前一时刻速度的继承减少,这有利于粒子在小范围内进行精确搜索,增强算法局部搜索能力,但容易导致算法收敛速度过慢或陷入局部最优. 因此将惯性权重改为动态自适应函数,使算法在搜索前期侧重于全局搜索能力,搜索后期侧重于局部搜索能力,达到最佳搜索效果. 改进后的惯性权重为
式中:
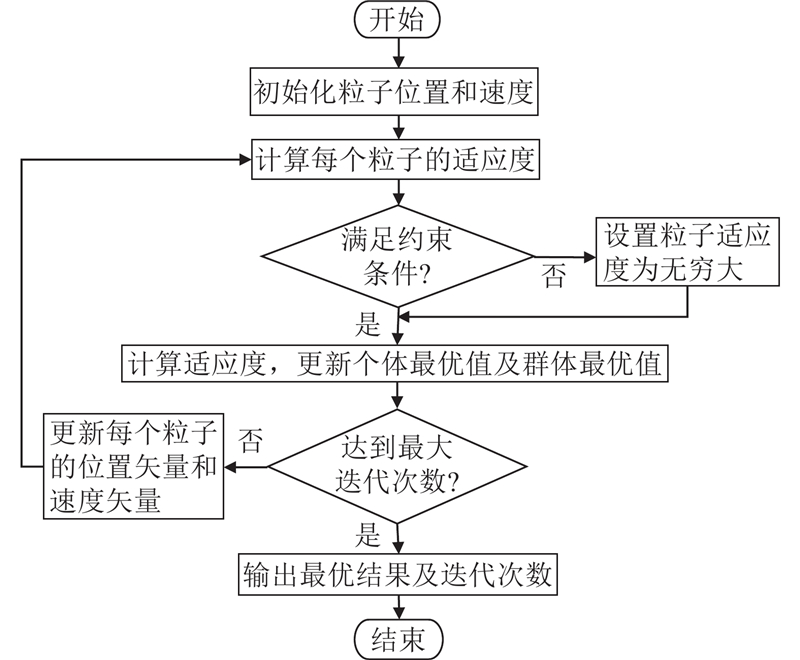
图 4
2.3. 冗余机器人轨迹优化问题求解
针对冗余机器人轨迹优化问题,构建改进粒子群算法求解器,求解器初始化步骤如下. 1)初始化求解器相关参数,设置各个粒子初始位置和速度分别为
式中:
3. 喷涂仿真实验与分析
图 5
图 6
3.1. 实验准备及参数设置
3.1.1. 喷涂沉积模型构建
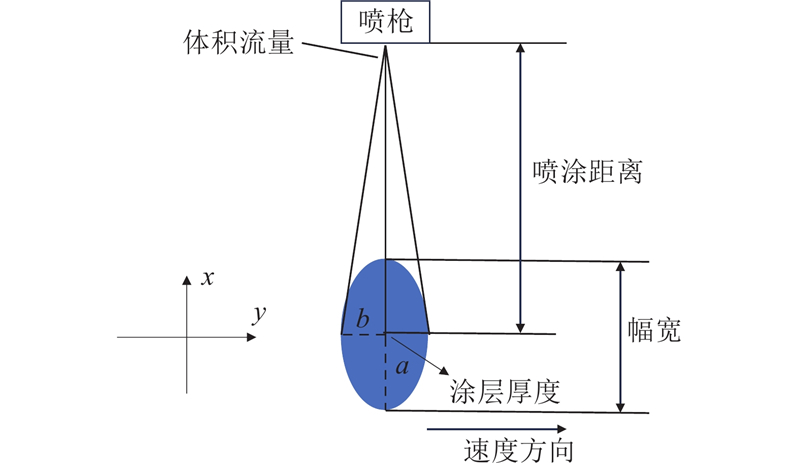
为了保证喷涂质量,在实验轨迹规划之前,针对涂料特性构建机器人喷涂沉积模型,以确定机器人喷涂时的路径宽幅、喷涂距离和喷涂速率等参数. 根据如图7所示的机器人迷彩喷涂设备及喷嘴特点,采用椭圆双
图 7
式中:
3.1.2. 实验流程及参数设置
在RobotStudio中规划喷涂路径,设置喷涂仿真相关参数;通过Matlab构建机器人运动学模型,代入优化求解器,求解最优外部轴位置. 将优化前后对应的外部轴位置代入RobotStudio中,进行喷涂仿真,监测仿真过程中的机器人各关节位置变化情况以及系统整体能量损耗情况. 在使用求解器求解外部轴最优位置时,须对求解器相关参数初始化. 为了使算法性能达到最优,设置
3.2. 直线喷涂实验
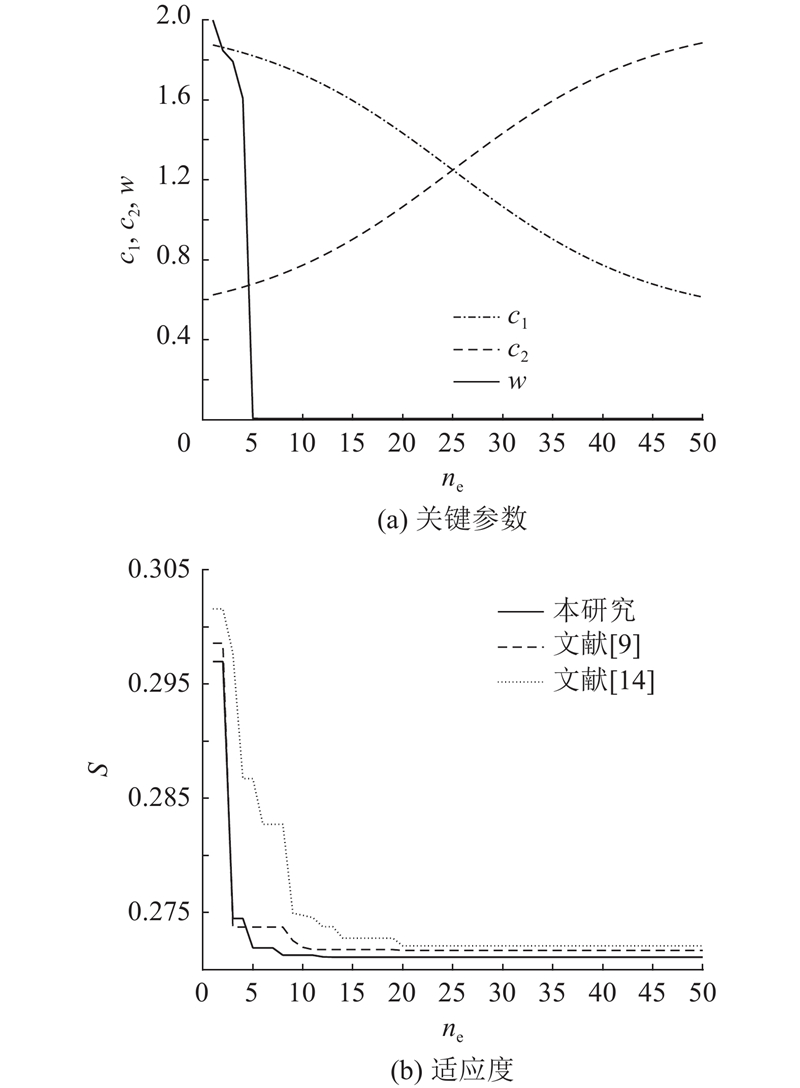
直线喷涂实验主要验证机器人模拟喷涂斑点迷彩填充路径时的轨迹优化效果. 在RobotStudio中规划长度为2 300 mm的喷涂路径,喷涂速度为800 mm/s,喷涂加速度为10 000 mm/s2,喷涂距离为50 mm,设定的直线喷涂起点和终点位置如表2所示. 分别采用GA-PSO算法[9]、改进模拟退火遗传算法[14]和所提算法迭代求解冗余机器人各关节轴位置,算出迭代过程中算法参数和适应度S的变化情况,结果如图8所示,其中ne为迭代次数. 随着迭代次数增加,
表 2 直线喷涂路径点
Tab.2
| 路径点序号 | x/mm | y/mm | z/mm |
| 1 | −300 | ||
| 2 |
图 8
图 8 算法关键参数和适应度变化曲线
Fig.8 Variation curves of key parameters and fitness for algorithm
考虑到群优化算法存在随机性,对直线最优外部轴轨迹重复求解30次,记录各个算法的平均收敛次数
表 3 不同算法的综合优化性能指标对比
Tab.3
图 9
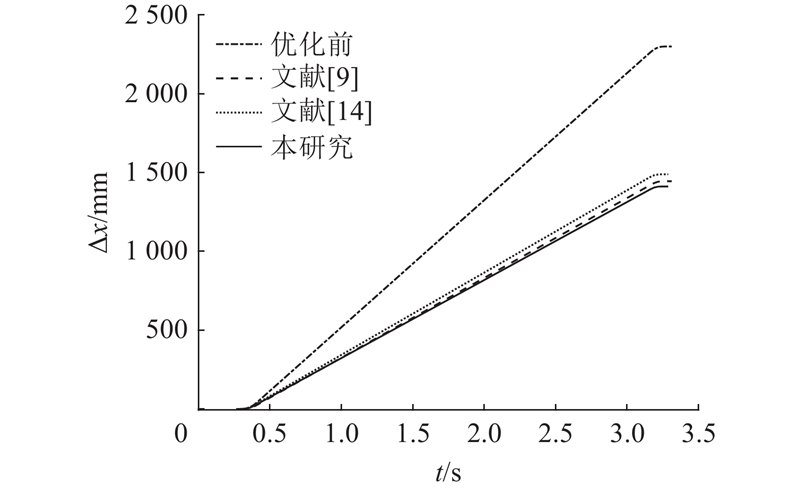
图 9 算法优化前后冗余机器人外部轴位移对比(直线喷涂)
Fig.9 Displacement comparison of redundant robot’s external axis before and after algorithm optimization (linear spraying task)
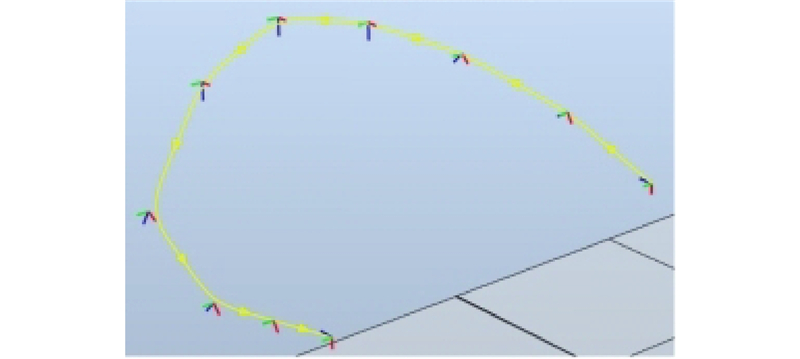
3.3. 曲线喷涂实验
表 4 曲线喷涂路径点
Tab.4
| 路径点 | x/mm | y/mm | z/mm | |
| 1 | 1 700 | 0 | 1 000 | 90 |
| 2 | 1 800 | 400 | 1 400 | 60 |
| 3 | 2 000 | 800 | 1 700 | 45 |
| 4 | 2 100 | 1 200 | 1 900 | 0 |
| 5 | 2 150 | 1 600 | 2 000 | 0 |
| 6 | 2 100 | 2 000 | 1 850 | 0 |
| 7 | 1 900 | 2 400 | 1 500 | 30 |
| 8 | 1 800 | 2 200 | 1 100 | 45 |
| 9 | 1 700 | 2 000 | 1 000 | 60 |
| 10 | 1 600 | 1 800 | 900 | 90 |
表 5 算法优化前后各路径点对应的冗余机器人外部轴位移
Tab.5
图 10
图 10 算法优化前后冗余机器人本体轴位移对比 (直线喷涂)
Fig.10 Base-axis displacement comparison of redundant robot before and after algorithm optimization (linear spraying task)
图 11
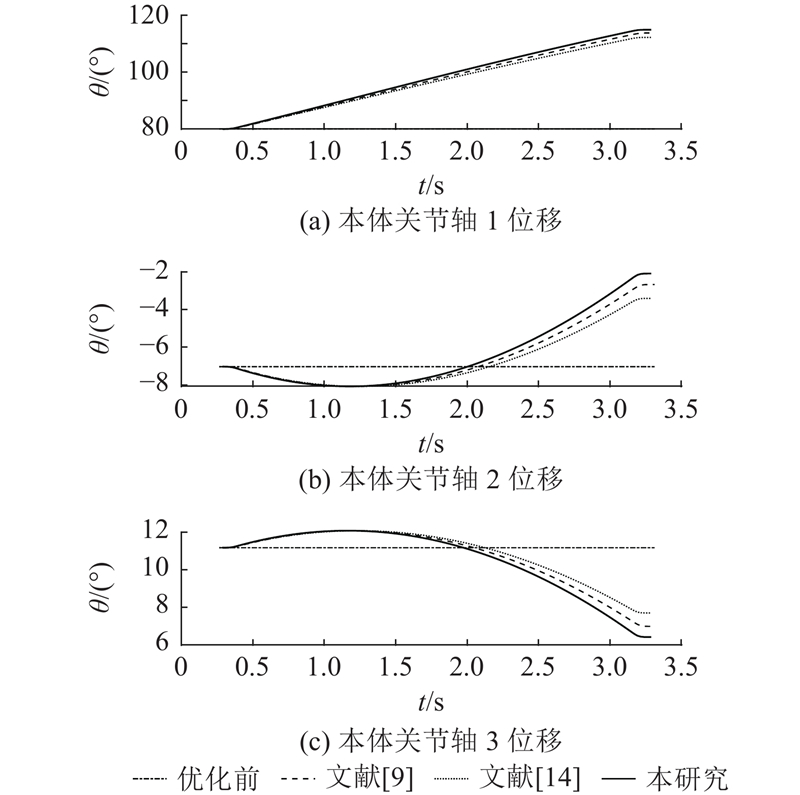
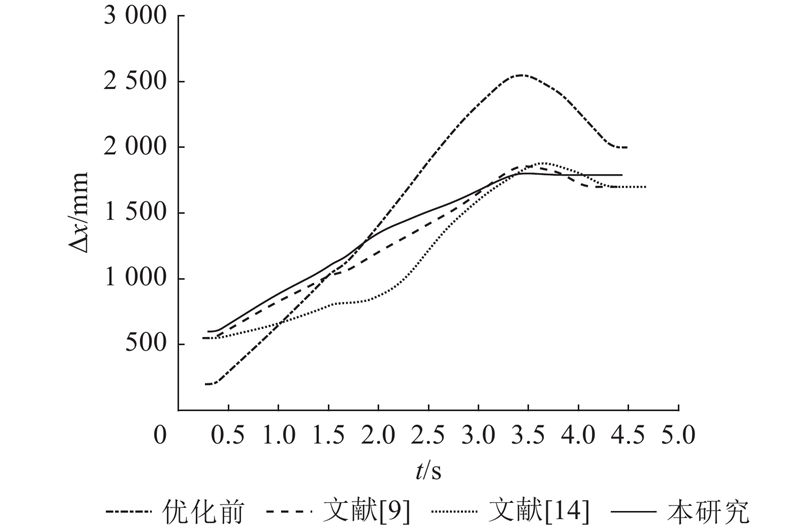
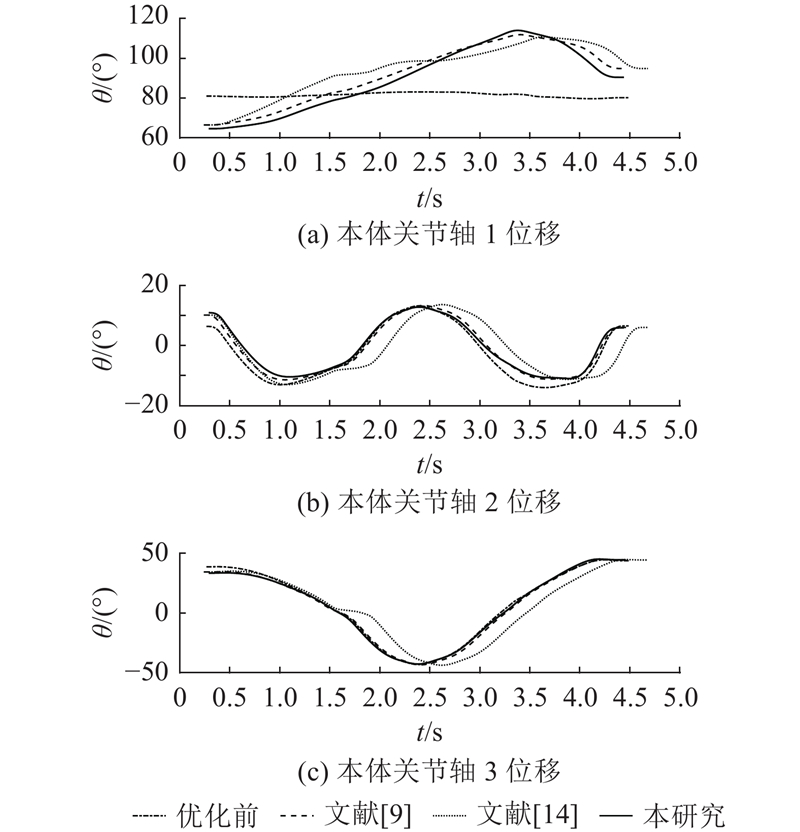
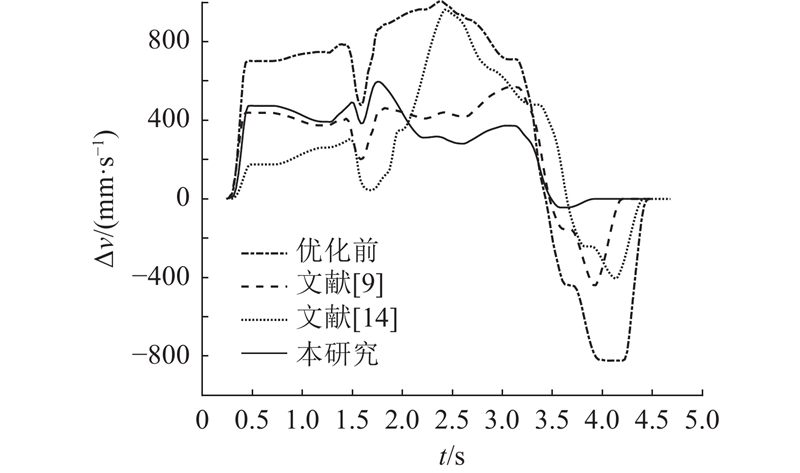
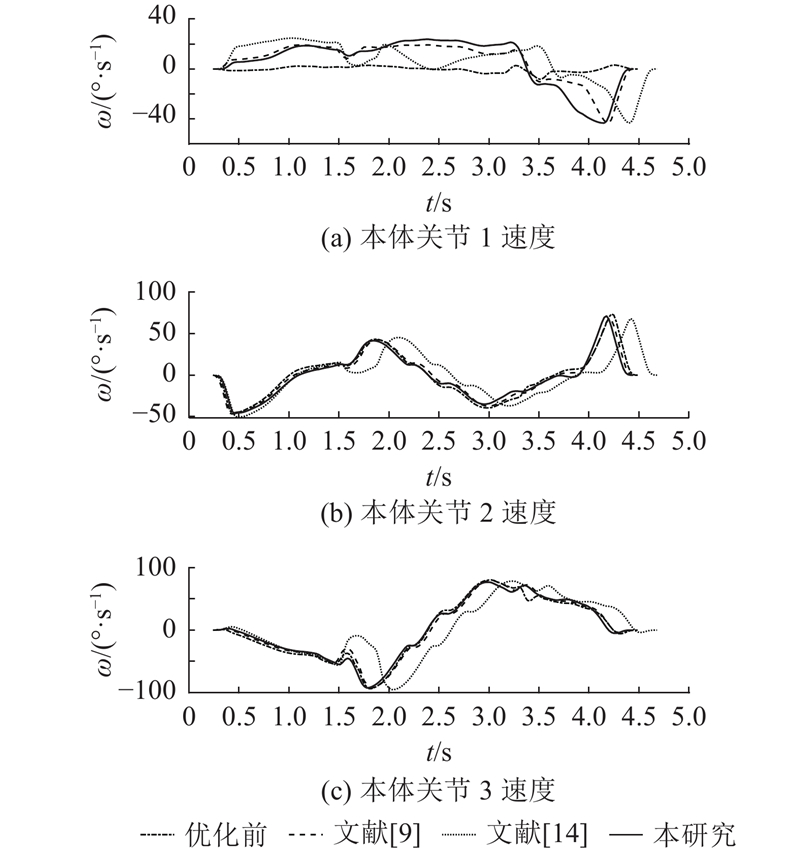
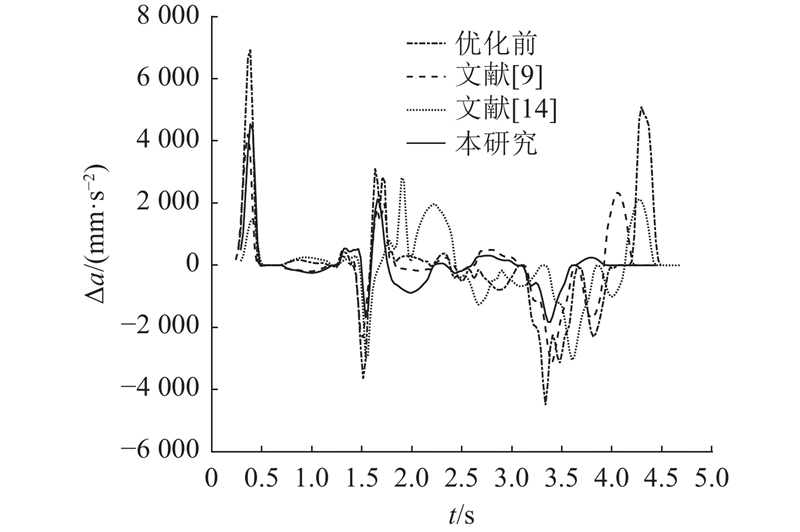
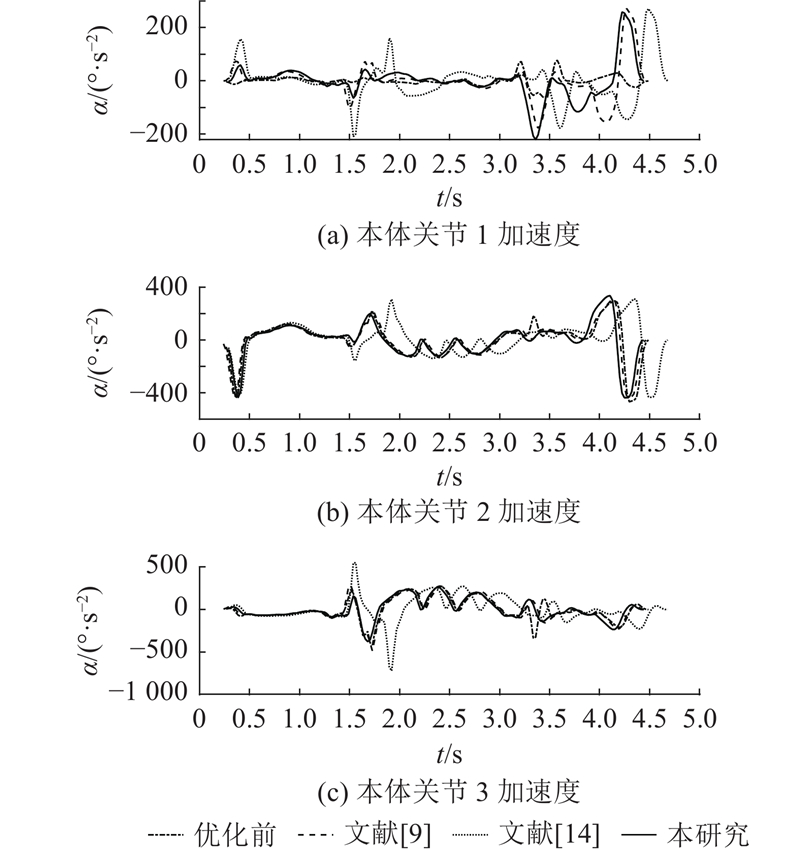
分析优化前和采用不同算法优化后外部轴和本体1、2、3轴在喷涂过程的轨迹、速度和加速度变化情况,如图12~17所示. 由图12可以看出,算法优化后机器人的外部轴移动幅度明显降低,采用所提算法优化后的外部轴轨迹较对比算法优化的效果更佳. 结合数据可知,采用所提算法优化后,机器人的外部轴运动幅度较优化前的降低了58.7%,较GA-PSO算法的降低了17.8%,较改进模型退火遗传算法的降低了21.0%. 由图16可以看出,采用所提算法优化后的外部轴最大加速度较优化前的大幅减小,相较于对比算法均有所减小,说明外部轴关节冲击得到明显改善. 结合图13、15、17分析可知,算法优化前的机器人末端执行器线速度主要由外部轴提供,算法优化后,机器人通过外部轴与本体轴之间配合使末端达到指定线速度,即优化后冗余机器人外部轴与本体轴之间耦合度提高. 由喷涂仿真可知,在执行曲线喷涂任务中,算法优化前的机器人系统能量损耗为4 367.1 J,经GA-PSO算法优化后为3 289.3 J,经改进模型退火遗传算法优化后为3 448 J,经所提算法优化后为3 196.2 J. 所提算法优化的机器人系统能量损耗相较于优化前的降低了26.8%,相较GA-PSO算法优化的降低了2.8%,相较改进模型退火遗传算法优化的降低了7.3%. 该结果验证了所提算法的有效性.
图 12
图 12 算法优化前后冗余机器人外部轴位移对比 (曲线喷涂)
Fig.12 Displacement comparison of redundant robot’s external axis before and after algorithm optimization (curved spraying task)
图 13
图 13 算法优化前后冗余机器人本体轴位移对比 (曲线喷涂)
Fig.13 Base-axis displacement comparison of redundant robot before and after algorithm optimization (curved spraying task)
图 14
图 14 算法优化前后冗余机器人外部轴速度对比 (曲线喷涂)
Fig.14 Velocity comparison of redundant robot’s external axis before and after algorithm optimization (curved spraying task)
图 15
图 15 算法优化前后冗余机器人本体轴速度对比 (曲线喷涂)
Fig.15 Base-axis velocity comparison of redundant robot before and after algorithm optimization (curved spraying task)
图 16
图 16 算法优化前后冗余机器人外部轴加速度对比 (曲线喷涂)
Fig.16 Acceleration comparison of redundant robot’s external axis before and after algorithm optimization (curved spraying task)
图 17
图 17 算法优化前后冗余机器人本体轴加速度对比 (曲线喷涂)
Fig.17 Base-axis acceleration comparison of redundant robot before and after algorithm optimization (curved spraying task)
4. 结 语
针对大型部件喷涂过程中冗余机器人的轨迹优化问题,以冗余机器人运动幅度和能量损耗为优化目标,提出基于粒子群的机器人运动轨迹优化方法. 对冗余机器人建立运动学模型,利用改进粒子群算法构建轨迹优化求解器,通过设计自适应惯性权重和非线性学习因子,加速算法的收敛速度和寻优精度,求解得到喷涂路径各目标点对应的最优外部轴位置. 通过喷涂仿真验证所提算法的有效性,分析算法优化前后机器人各关节的运动幅度变化和系统能量损耗情况. 实验结果表明,在直线路径和曲线路径喷涂实验中,所提算法的收敛速度较现有算法更快,寻优效果更好,所提算法能够有效优化冗余机器人的喷涂轨迹. 尽管本研究提出的喷涂机器人轨迹优化方法在能量损耗与运动平滑性方面取得了显著效果,但算法的大规模路径求解计算效率仍有提升空间. 下一步工作将结合凸优化理论与高性能求解器,通过将轨迹优化问题转化为可快速求解的凸优化模型,以实现方法的实时性求解与工程应用推广.
参考文献
喷涂机器人风机叶片分片喷涂轨迹优化
[J].
Spraying robot trajectory optimization for fan blade fragment
[J].
Generating optimized trajectories for robotic spray painting
[J].DOI:10.1109/TASE.2022.3156803 [本文引用: 1]
串联六轴机械臂逆运动学几何解法
[J].
Inverse kinematics of geometric algorithm of series six-axis manipulator
[J].
关节角参数化结合接近矢量可行方向的五自由度机械臂逆运动学求解
[J].
Inverse kinematics solution of 5-DOF manipulator via joint angle parameterization and feasible direction of approach vector
[J].
A novel closed-form solution for the inverse kinematics of redundant manipulators through workspace analysis
[J].DOI:10.1016/j.mechmachtheory.2017.12.005 [本文引用: 1]
基于A*算法与组合函数的分拣机械臂轨迹规划
[J].
Sorting robotic arm trajectory planning based on A* algorithm and combination function
[J].
Trajectory planning algorithm and simulation of 6-DOF manipulator
[J].
基于改进萤火虫算法的冗余机器人轨迹规划
[J].
Trajectory planning for redundant robot based on improved glowworm swarm optimization algorithm
[J].
基于灰狼优化算法的机械臂避障轨迹规划
[J].
Obstacle-avoidance trajectory planning of manipulator based on grey wolf optimization algorithm
[J].
基于萤火虫-遗传算法的机械臂轨迹时间优化
[J].
Time optimization of manipulator trajectory based on firefly-genetic algorithm
[J].
基于改进模拟退火遗传算法的机械臂轨迹优化
[J].
Trajectory optimization of robotic arm based on improved simulated annealing genetic algorithm
[J].
串联机器人运动学分析与研究
[J].
Kinematic analysis and research of serial robot
[J].
附加外部轴的工业机器人自动钻铆系统分站式任务规划与控制技术
[J].
Process planning and control technology on multi-station working mode of robot drilling and riveting system with auxiliary axis
[J].
Inverse kinematics of a 7R 6-DOF robot with nonspherical wrist based on transformation into the 6R robot
[J].DOI:10.1155/2017/2074137 [本文引用: 1]
Review of the damped least-squares inverse kinematics with experiments on an industrial robot manipulator
[J].DOI:10.1109/87.294335 [本文引用: 1]
基于改进的粒子群算法求解供应链网络均衡问题
[J].
Research on supply chain network equilibrium model based on improved particle swarm optimization
[J].
基于改进粒子群优化算法的六自由度机器人轨迹优化算法
[J].
Trajectory of 6-DOF robot based on improved particle swarm optimization algorithm
[J].