道路交通运输的能源消耗和温室气体排放会对环境产生负面影响[1]. 车辆编队的各成员车辆以队列形式在较短的车间距下稳定行驶,能够通过减少成员间空气阻力来降低能源消耗和碳排放. 乘客舒适度是评估队列控制性能的指标,它是指乘客(包括驾驶员)在车辆行驶过程中的舒适程度. 车辆剧烈变速可能对驾驶安全和乘客健康产生不良影响,因此乘客舒适度分析的重要性日益突出[2]. 乘客舒适度、能耗以及跟踪性能在控制方案中存在耦合关系,这给队列控制带来了新的难点[3]. 随着网联自动驾驶车辆(connected autonomous vehicle, CAV)市场渗透率的持续增长以及车路协同基础设施的推广部署,道路交通即将长期处于人工驾驶车辆(human-driven vehicle, HDV)和CAV共存的局面[4],不同驾驶模式的跟驰特性差异将加剧队列控制的复杂性. 如何在考虑乘客舒适度的前提下,设计面向CAV与HDV混合队列的协作控制方法以优化队列能耗是待解决的重要问题.
按照混合车辆队列控制目标是否促使各成员合作将已有研究工作一分为二[5],其中合作控制目标包括队列稳定性与跟踪性能,非合作目标主要包括能耗与乘客舒适度. 1)在研究混合车辆队列稳定性方面,边有钢等[6]提出适用于双向多车跟随式拓扑的混合队列控制器,将前后车信息引入CAV的控制设计,分析前后车信息对混合队列稳定性的影响. 李淑庆等[7]针对由协作式巡航控制(cooperative adaptive cruise control,CACC)车辆、自适应巡航控制(adaptive cruise control,ACC)车辆以及HDV组成的混合车队,考虑车辆之间的退化机制,应用传递函数理论,推导队列稳定性判别准则,分析不同队列规模下的稳定性. Zhan等[8]将数据驱动方法与模型预测控制(model predictive control,MPC)相结合,分别设计集中式MPC和分布式MPC控制器,以消除停起波动. 2)为了优化混合车辆队列的能耗,Hu等[9]提出灵活的间距策略,确保所有CAV编队成员都保持节能驾驶模式. Yao等[10]通过引入燃料消耗和交通排放模型,研究CAV渗透率对混合交通流的燃油消耗和排放的影响. Zhao等[11]提出递进视野的模型预测控制方法以降低能耗,还将该方法扩展到动态编队分割和合并规则. 3)车辆行驶平稳性将直接影响乘客舒适度,车辆的加速度过大会严重影响编队的乘客舒适度[12]. 秦严严等[13]分析CACC车辆、ACC车辆与HDV混合交通流的驾驶舒适性. Li等[14]提出考虑乘客舒适度的CACC系统,在保证混合交通稳定性的前提下,提高驾驶员的身心舒适度. Tian等[15]使用智能驾驶员模型(intelligent driver model,IDM)作为HDV的跟驰模型,将加速度导数作为控制变量,采用加速度描述车辆能耗,将加速度导数和加速度分别作为加权项,设计MPC控制律,在降低能耗的同时提高驾驶舒适性. 文献[13]、[14]未涉及能耗优化;文献[15]涉及的车辆能耗建模参量单一,描述混合队列车辆实时能耗的准确性欠佳.
本研究在队列稳定控制的基础上,以乘客舒适度为约束,以降低能耗为优化目标,提出混合车辆队列协作控制新算法. 1)针对队列中的CAV,建立乘客舒适度约束,采用实时优化(real-time optimization,RTO)的分布式模型预测控制(distributed model predictive control,DMPC)方法(RTODMPC)在确保车辆稳定协作的基础上降低实时能耗. 2)针对队列中的HDV,采用乘客舒适度和能耗性能良好的智能驾驶员跟驰模型,考虑前车扰动推理得到稳定跟驰条件. 3)引入贴合实际的基于动力的综合油耗模型(Virginia tech comprehensive power based fuel consumption model, VT-CPFM),通过对瞬时油耗的计算提升能耗优化性能. 4)对所提算法进行仿真分析,验证算法的跟踪性能,将从初始状态到稳态的平均发动机功率作为能耗性能指标,对比不同控制方案的能耗优化性能.
1. 问题描述
由
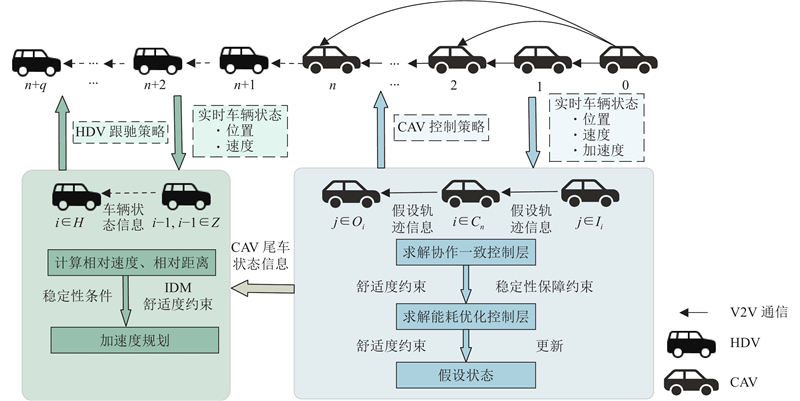
图 1
图 1 网联自动驾驶车辆和人工驾驶车辆协作控制框架
Fig.1 Collaborative control framework of connected autonomous vehicle and human-driven vehicle
1.1. 车辆非线性纵向动力学模型
混合车辆队列中的第
式中:
令车辆
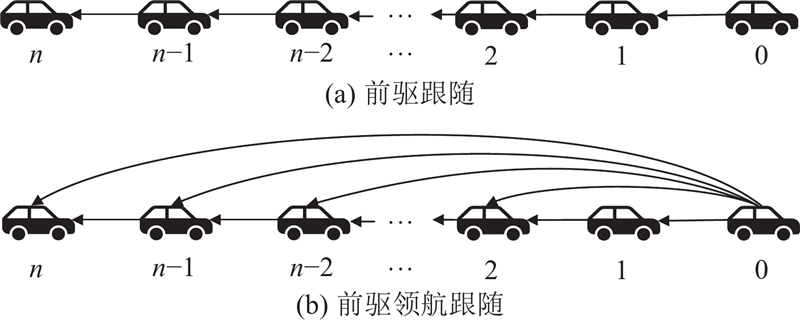
1.2. 网联自动驾驶车辆通信拓扑
采用图论模型,将混合车辆队列跟随序列中的CAV间的通信拓扑记为有向图
1.3. 车辆能耗模型
VT-CPFM将油耗表征为车辆功率的二阶多项式函数,能够精确计算车辆的实时油耗[18]. 采用VT-CPFM表示车辆的综合油耗. 车辆
式中:
其中
1.4. 混合车辆队列跟踪性能控制目标
跟踪性能控制目标要求队列中车辆与前车保持相同的车速,队列车辆之间还须保持期望的车间距. 对于CAV和HDV,车辆与前车的跟踪性能控制目标为
式中:
其中
2. 基于能耗优化的混合车辆队列协作控制算法
为了在实现混合队列CAV与HDV协作的基础上降低能耗,同时保障乘客舒适度,本研究提出实时优化的分布式模型预测控制与智能驾驶员模型结合的协作控制方法(RTODMPC-IDM). 1)针对CAV队列控制,DMPC能够在最优控制的框架下有效处理多约束和多目标优化问题,RTO能够平衡多目标间的冲突. RTODMPC为分层架构,由协作一致控制层(上层)和能耗优化控制层(下层)构成;上层保证车辆跟踪性能,下层降低车辆能耗. 在RTODMPC中,所有CAV通过V2V传输共享自身在预测范围内的假设轨迹信息,每辆 CAV 结合自车状态按序求解上层与下层优化问题. 通过引入控制输入和加速度约束保障乘客舒适度,采用VT-CPFM构建下层目标函数,以更充分降低能耗. 2)针对HDV,选择IDM. 原因是IDM跟驰模型具有良好的乘客舒适性,同时保持低能耗[19]. 在IDM减速操作中,HDV在达到稳定的跟驰状态前或者到达停止线前,减速度逐渐增大至舒适值,然后平滑减小到0;加速操作被最大加速度约束. 推导前车扰动下跟驰行为的线性稳定性条件,在此基础上,每辆HDV通过IDM根据自车与前车的相对距离、相对速度及自车速度,确定自车加速度并保障乘客舒适度.
2.1. 网联自动驾驶车辆实时优化的分布式模型预测控制算法
RTODMPC的上下层具有相同的时间尺度,能够实现双层实时求解. 考虑当前时刻
2.1.1. 协作一致性控制层
考虑式(4)描述的CAV动力学系统,车辆
式(10)为协作一致控制层最优控制问题的目标函数,其中
式(12)为初始条件,式(13)为系统约束,式(14)保证预测状态和假设状态终端相等,式(15)为假设状态终端的迭代. 为了保证乘客舒适度,分别对加速度及其变化率进行约束:设置加速度约束为
式(17)中
式中:
本层最优状态通过车辆状态方程式(4)和最优控制输入式(19)完成更新迭代:
根据式(19)、(20),得到目标函数的最优值:
2.1.2. 能耗优化控制层
上层的最优成本构建下层稳定性的上限约束,在保证跟踪性能和稳定性的基础上降低能耗. 引入VT-CPFM构建能耗优化控制层的目标函数,设计最优化问题式为
式(23)为能耗优化控制层最优控制问题的目标函数,式(24)为车辆
为了保证上层优化的可行解对下层优化,对于优化问题式(22),其约束包括协作一致控制层的所有约束,即式(12)~(15)和乘客舒适度约束;优化问题式(22)还须满足迭代可行性及系统稳定性保证约束,即式(25). 结合目标函数及约束条件,求得下层的最优控制输入:
通过车辆状态方程式(4)及
将最优控制输入
其中
其中
在下层最优控制输入序列中,
2.2. 人工驾驶车辆跟驰模型及跟驰稳定性分析
根据IDM跟驰模型,将HDVi,
式中:
2.2.1. 跟驰模型
采用IDM车辆跟驰模型来描述HDV的加速度. HDVi,
式中:
2.2.2. 跟驰稳定性分析
在CAV满足控制系统稳定性的基础上,考虑混合车辆队列中CAV尾车对HDV跟驰稳定性的影响,分析得到跟驰稳定性条件. 假设CAV尾车
式中:
结合式(32),将式(38)线性化,得到
式中:
由式(39)得到差分方程:
假设扰动
将
如果
依次类推,跟随序列中HDV的IDM参数须遵循式(47)对应的稳定性条件,以保持跟驰稳定.
3. 数值仿真验证
图 2
图 2 网联自动驾驶车辆的通信拓扑
Fig.2 Communication topology for connected autonomous vehicle
表 1 所提能耗控制方法的参数设置
Tab.1
| 参数 | 数值 |
3.1. 协作性能仿真
设置2个典型仿真场景:恒速领航车辆场景和变速领航车辆场景,验证混合车辆队列协作中的跟踪性能以及加速度和控制输入是否满足乘客舒适度约束. 恒速领航车辆场景中领航车辆以恒定的速度行驶,是比较温和的条件;变速领航车辆场景中领航车辆速度存在调整.
3.1.1. 恒速领航车辆场景
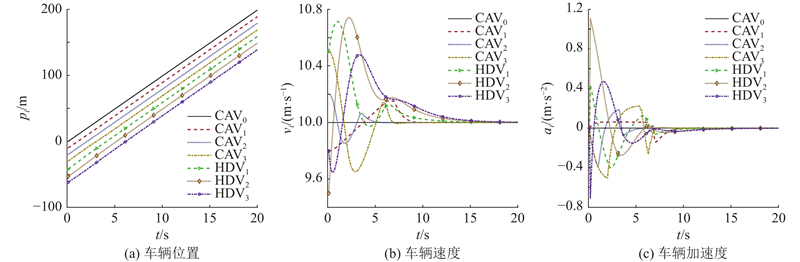
设跟随车辆序列n = 3,q = 3. 仿真开始时,领航车辆的初始状态为
图 3
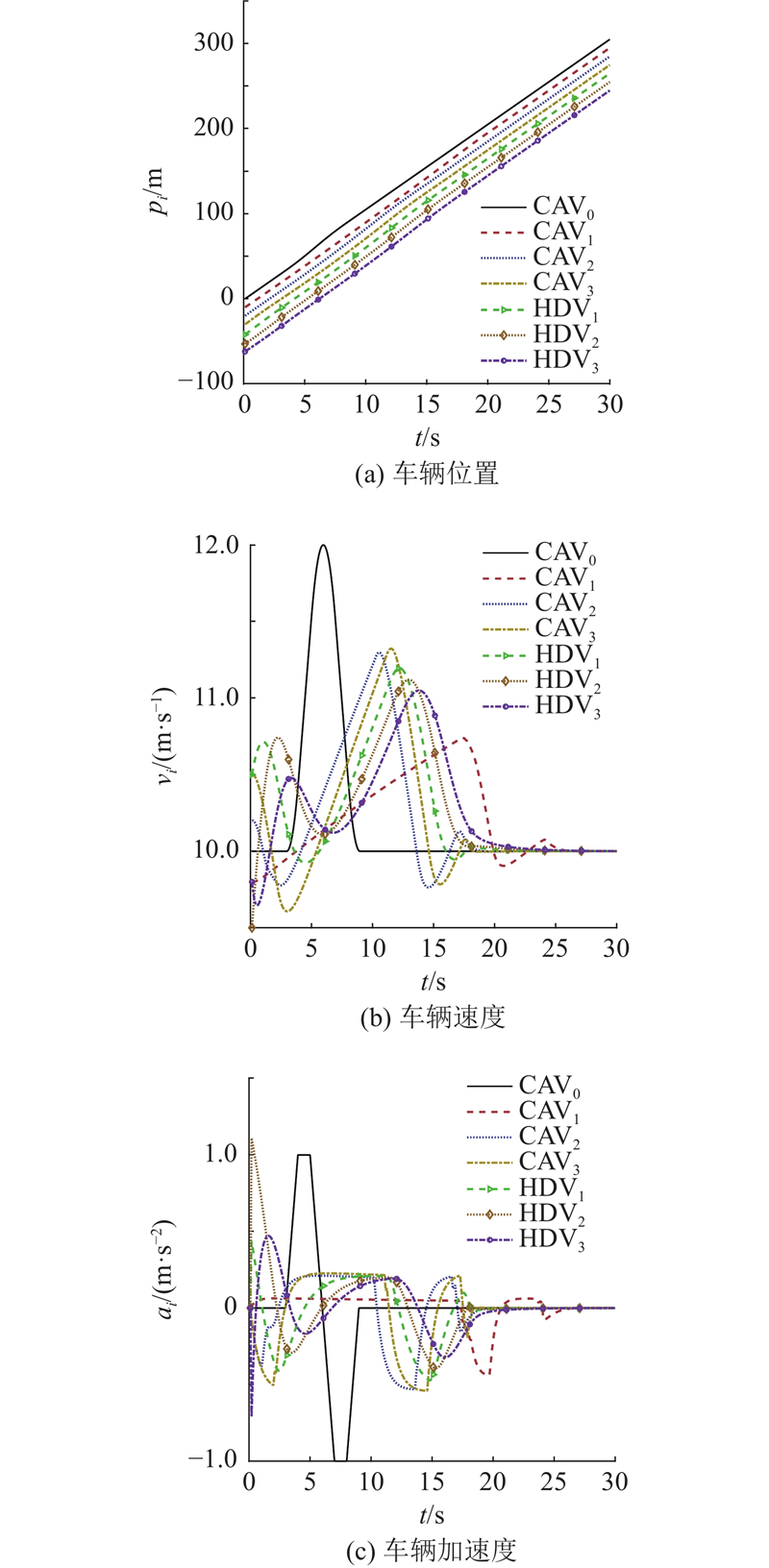
图 3 恒速领航车辆场景的车辆状态
Fig.3 Vehicle states in constant speed leader vehicle scenario
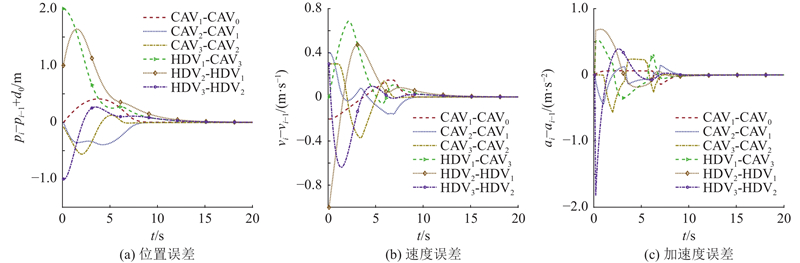
图 4
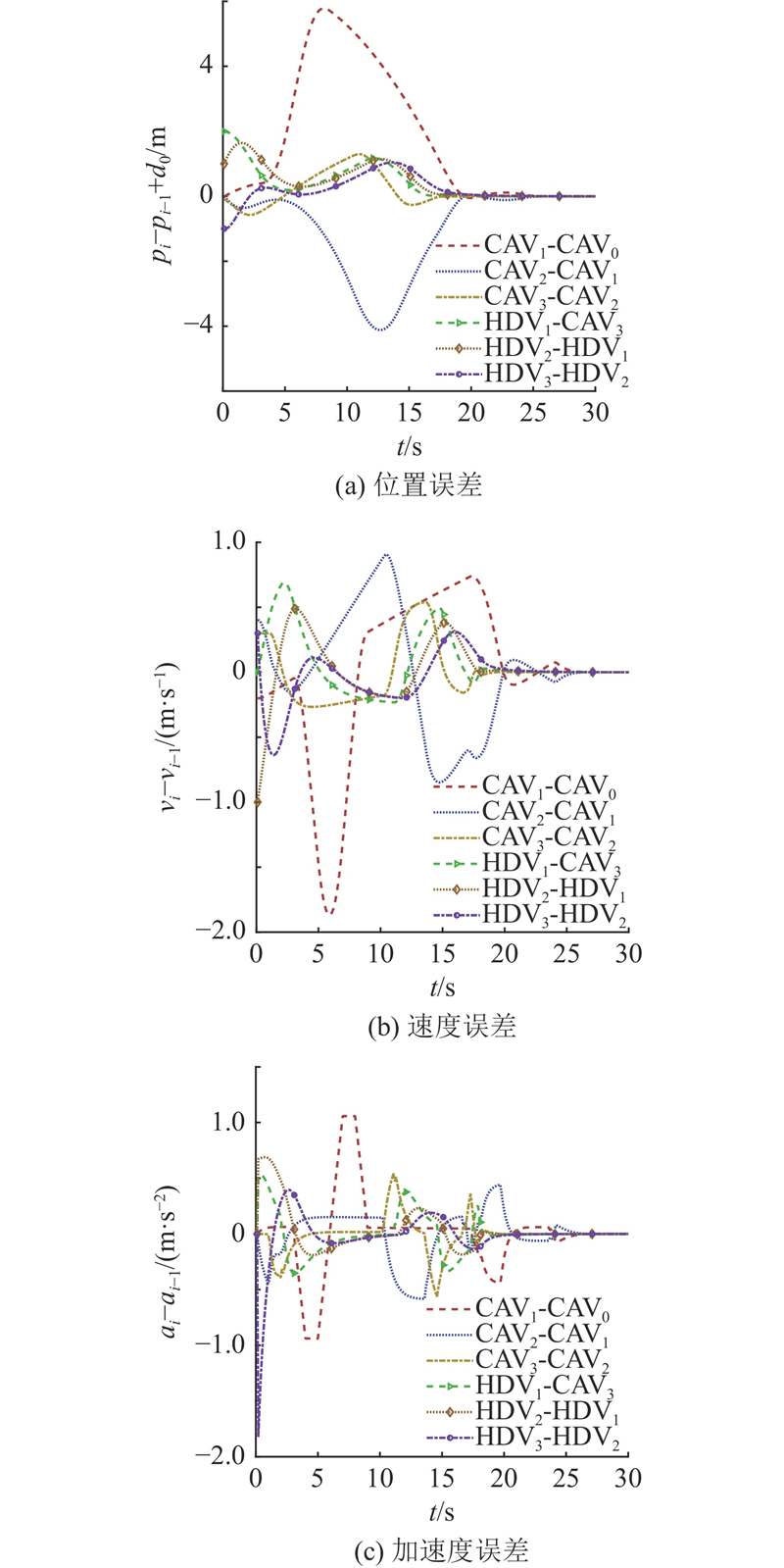
图 4 恒速领航车辆场景的车辆状态误差
Fig.4 Vehicle state error in constant speed leader vehicle scenario
图 5
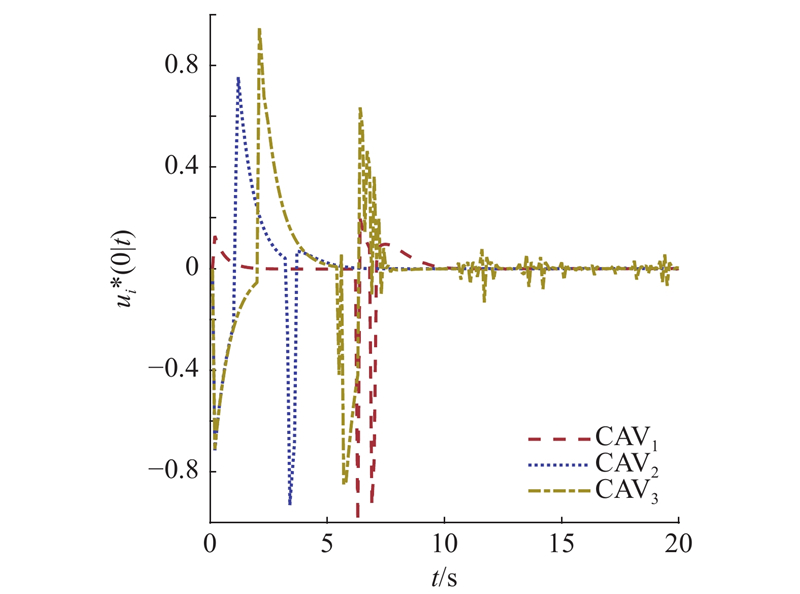
图 5 恒速领航车辆场景的网联自动驾驶车辆控制输入
Fig.5 Control input of connected autonomous vehicle in constant speed leader vehicle scenario
3.1.2. 变速领航车辆场景
变速领航车辆场景的车辆个数和跟随车辆初始状态与恒速领航车辆场景设置相同,CAV间选取PLF通信拓扑. 本场景中领航车辆速度存在变化,加速度设置为
图 6
图 6 变速领航车辆场景的车辆状态
Fig.6 Vehicle states in variable speed leader vehicle scenario
图 7
图 7 变速领航车辆场景的车辆状态误差
Fig.7 Vehicle state error in variable speed leader vehicle scenario
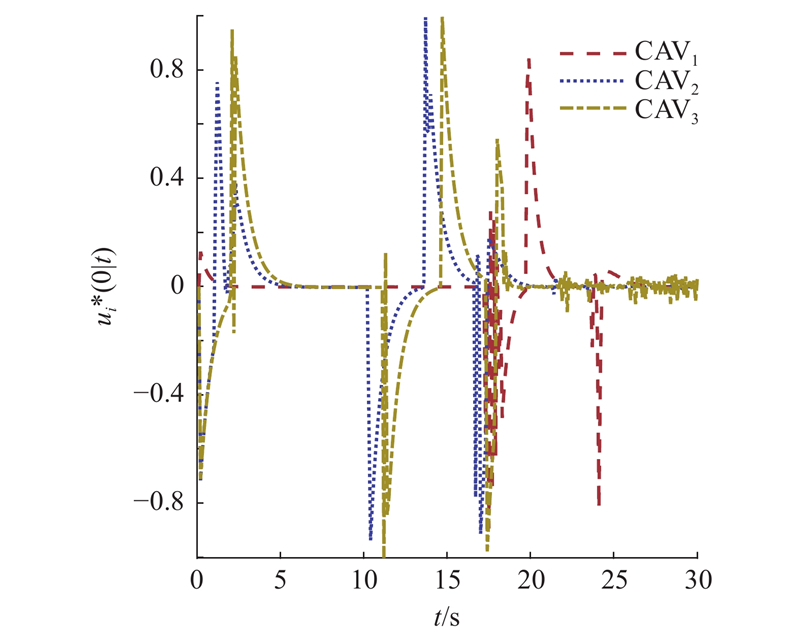
图 8
图 8 变速领航车辆场景的网联自动驾驶车辆控制输入
Fig.8 Control input of connected autonomous vehicle in variable speed leader vehicle scenario
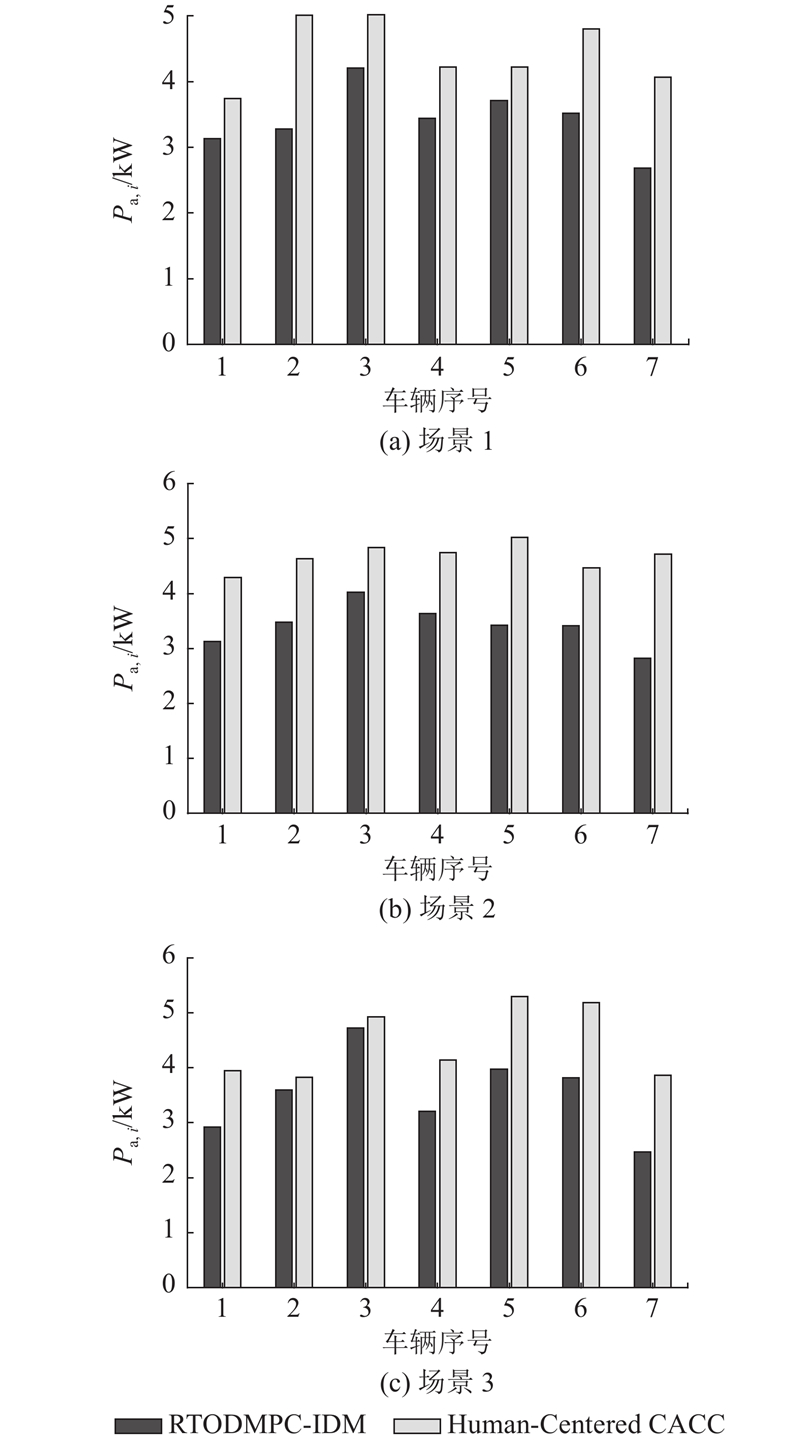
3.2. 能耗对比仿真
表 2 能耗控制方法仿真对比实验的车辆状态分布
Tab.2
| 场景编号 | |||
| 1 | |||
| 2 | |||
| 3 |
式中:
图 9
图 9 不同控制方法在3种场景中的能耗对比
Fig.9 Energy consumption comparison of different control methods in three scenarios
4. 结 语
本研究针对混合车辆队列最优能耗控制问题,以保障乘客舒适度为约束条件,提出结合实时优化分布式模型预测控制与智能驾驶员模型的协作控制方法. 对于CAV,设置分层控制架构,建立协作一致控制层(上层)和能耗优化控制层(下层),将精确的VT-CPFM引入能耗模型下层,从而在保证稳定协作的同时优化瞬时能耗. 对于HDV,采用IDM跟驰模型,分析得出跟驰模型的稳定性条件. 仿真结果表明:在所提方法控制下,车辆成员可以稳定实现协作,该方法能够满足乘客舒适度且跟踪性能良好. 3组不同车辆初始状态分布情况下的对比仿真结果表明,相较Human- Centered CACC,所提方法能够有效降低能耗. 未来研究将针对更普适的由CAV领航的CAV与HDV随机混合分布的队列,计划视本研究中的队列为子队列,以便将原混合队列从各领航CAV处拆分形成多个CAV+HDV子队列,在保障子队列间安全的前提下,通过控制每个子队列领航CAV完成整体队列控制.
参考文献
Future directions of intelligent vehicles: potentials, possibilities, and perspectives
[J].DOI:10.1109/TIV.2022.3157049 [本文引用: 1]
Ride comfort analysis and multivariable co-optimization of the commercial vehicle based on an improved nonlinear model
[J].
A switched control strategy of heterogeneous vehicle platoon for multiple objectives with state constraints
[J].
Expression of concern for: toward sustainable intelligent transportation systems in 2050: fairness and eco-responsibility
[J].DOI:10.1109/TIV.2023.3286873 [本文引用: 1]
Multiobjective platooning of connected and automated vehicles using distributed economic model predictive control
[J].DOI:10.1109/TITS.2022.3170977 [本文引用: 1]
基于双向多车跟随式拓扑的混合车辆队列稳定性研究
[J].DOI:10.3969/j.issn.1001-7372.2022.03.007 [本文引用: 1]
Study on the stability of mixed vehicular platoon based on bidirectional multiple-vehicle following topologies
[J].DOI:10.3969/j.issn.1001-7372.2022.03.007 [本文引用: 1]
协作式巡航控制下混合车队队列稳定性
[J].
String stability of mixed platoon under cooperative adaptive cruise control
[J].
Data-driven modeling and distributed predictive control of mixed vehicle platoons
[J].DOI:10.1109/TIV.2022.3168591 [本文引用: 1]
Eco-platooning for cooperative automated vehicles under mixed traffic flow
[J].DOI:10.1109/TITS.2021.3056122 [本文引用: 1]
Fuel consumption and transportation emissions evaluation of mixed traffic flow with connected automated vehicles and human-driven vehicles on expressway
[J].DOI:10.1016/j.energy.2021.120766 [本文引用: 1]
A platoon based cooperative eco-driving model for mixed automated and human-driven vehicles at a signalised intersection
[J].DOI:10.1016/j.trc.2018.05.025 [本文引用: 1]
混有CACC车辆和ACC车辆的混合交通流驾驶舒适性
[J].
Driving comfort of traffic flow mixed with cooperative adaptive cruise control vehicles and adaptive cruise control vehicles
[J].
Cooperative adaptive cruise control for string stable mixed traffic: benchmark and human-centered design
[J].DOI:10.1109/TITS.2017.2760805 [本文引用: 4]
Stability and scalability of homogeneous vehicular platoon: study on the influence of information flow topologies
[J].DOI:10.1109/TITS.2015.2402153 [本文引用: 1]
Practical string stability of platoon of adaptive cruise control vehicles
[J].DOI:10.1109/TITS.2011.2143407 [本文引用: 1]
Virginia tech comprehensive power-based fuel consumption model: model development and testing
[J].DOI:10.1016/j.trd.2011.05.008 [本文引用: 1]
Fuel economy optimization for platooning vehicle swarms via distributed economic model predictive control
[J].
Stability analysis of an extended intelligent driver model and its simulations under open boundary condition
[J].DOI:10.1016/j.physa.2014.10.063 [本文引用: 2]
Cooperative energy management of automated vehicles
[J].DOI:10.1016/j.conengprac.2016.08.018 [本文引用: 1]