为了破解含平衡阀阀控缸的“稳定性-精度”矛盾,本文提出非线性MPC轨迹平稳跟踪方法. 建立含平衡阀阀控缸DAE模型并简化为仿射非线性状态空间形式. 通过部分反馈线性化分离零动态、剖析失稳机理,构造控制Lyapunov函数(CLF),证明局部可镇定. 以 CLF 水平集设置终端代价与约束,设计闭环渐近稳定的 NMPC. 通过不同的负载实验,与传统的前馈-反馈(FF-PI)控制进行对比,验证利用该方法,可以在保证稳定性的前提下显著提升跟踪精度.
1. 系统的非线性建模
1.1. 系统的非线性DAEs模型
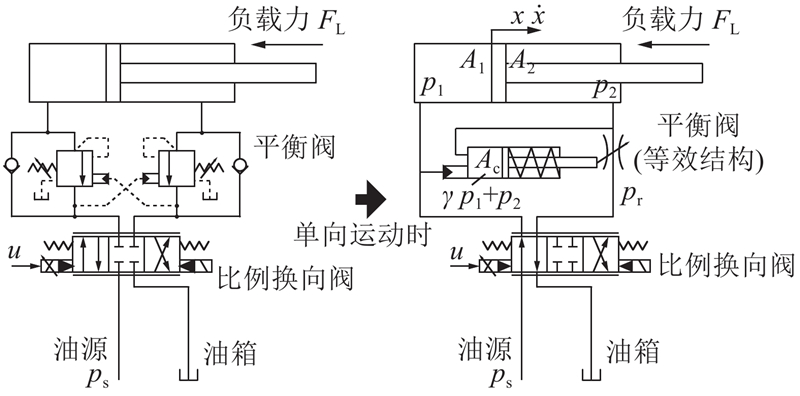
所研究系统的液压原理图如图1所示.
图 1
图 1 含平衡阀阀控液压缸的原理图
Fig.1 Schematic diagram of valve-controlled hydraulic cylinder with counterbalance valve
式中:
假设比例阀阀芯的动态特性可忽略,记
式中:ps为供油压力,pr为回油路平衡阀与比例阀之间的压力.
记平衡阀阀芯位移为
联立式(3)、(4),可得
平衡阀阀芯为含摩擦的弹簧-质量二阶系统,
式中:
当液压缸正向运动时,忽略内、外泄漏,进油腔、出油腔的流量分别为
式中:
式(8)、(9)是一组微分-代数方程(DAEs).
1.2. 模型处理及简化
1.2.1. DAEs到仿射状态空间模型的简化
根据式(9),引入回油压力增益函数
使得
平衡阀阀芯开度-通流面积关系
根据隐函数定理可知,式(8)、(9)表示的DAE可以通过式(11)化为唯一等价的ODE,
从式(13)可知,所研究的系统并非仿射非线性系统. 对式(13)进行合理简化,记
式中:
1.2.2. 平衡阀阀芯摩擦力的简化
式(6)中包含非线性摩擦力
式中:
1.2.3. 缓变参数的简化
液压缸两腔体积
通过变换与简化,式(8)、(9)改写为
记
2. 系统分析
2.1. 系统的部分反馈线性化
记系统的输出函数为
系统相对阶
式中:
系统
式中:
式中:
记
将
2.2. 系统的可镇定性分析
由
式中:
系统零动态在平衡点的稳定性决定了系统能否实现输出轨迹的精确跟踪[20]. 系统零动态
假设1:
假设2:平衡阀阀芯位置快速收敛于平衡点处,即
假设2通过控制器设计来保证,将在3章详细阐述. 在假设2下,平衡阀动态退化为式(28)表示的几何约束,系统退化为降阶系统
用
系统的
结合假设1,由
式(33)等号右边第1项为二次型,恒小于等于零,因此
整理得到
将
同理可得,当
综上可知,当控制器镇定进油腔压力
从式(37)可知,
系统
3. NMPC抑振轨迹跟踪控制
NMPC须实现以下功能. 1)通过控制器的设计,保证假设2成立. 2)当系统处于
3.1. NMPC抑振轨迹跟踪控制器的结构
记降阶系统
系统
当NMPC的采样时间
记阶段代价函数(stage cost)为
式中:
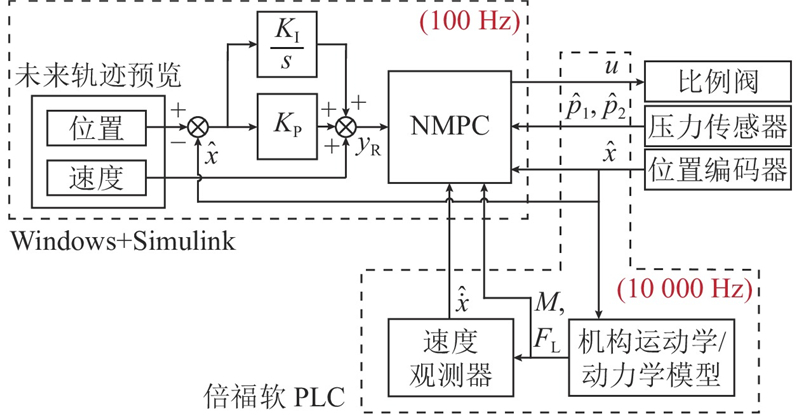
式(41)表示的NMPC用于速度内环跟踪速度轨迹,位置环利用PI控制在既有速度轨迹上叠加修正,提出的控制器如图2所示.
图 2
3.2. NMPC速度轨迹跟踪
3.2.1. 阶段代价函数设计
设计阶段代价函数保证假设2成立. 根据式(16)可知,
利用假设2,将式(28)代入式(25),通过部分反馈线性化得到前馈输入:
NMPC的阶段代价函数为
3.2.2. 终端代价及终端约束设计
根据2.2节可知,系统
终端状态应在某一满足式(35)的邻域内,记满足式(36)的终端状态集合为
终端状态应取值于CLF的水平集,
CLF水平集作为终端不等约束,可以保证NMPC在收敛域内的渐近稳定性[21]. 将终端状态集合设计为
3.3. 控制器的实现
3.3.1. 速度观测器
在降阶系统(29)中,
式中:惯量
3.3.2. 控制器及其参数设置
图 3
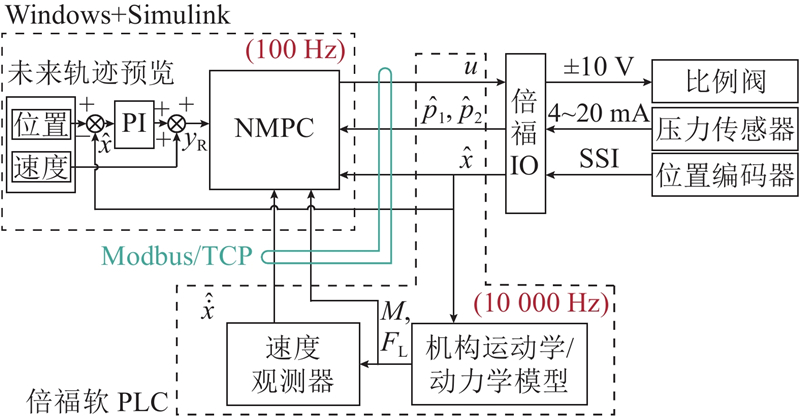
图 3 控制器的实现和信号细节图示
Fig.3 Diagram of controller implementation and signal details
为了提升NMPC的运行效率,当求解最优化问题时,使用上一控制周期的解作为初值,即热启动(warm start)策略,对求解器的迭代次数设定上限. 控制器的具体参数和配置详见表1.
表 1 NMPC的参数和配置
Tab.1
| 控制器参数 | 设置值 | 代价函数系数 | 设置值 | |
| 预测/控制时域N | 12步 | 轨迹误差项系数 | 2.0 | |
| 控制周期 | 0.01 | 输入项系数 | 0.1 | |
| 速度观测器周期/ms | 0.1 | 阀芯镇定项系数 | 10.0 | |
| 迭代次数限制 | 60 | 终端CLF系数 | 1.0 |
此外,模型参数通过实验进行精确标定,平衡阀开口与通流面积的函数
4. 实验验证
4.1. 实验装置
为了模拟含平衡阀阀控缸的变负载运动控制场景,实验在可调末端配重的单关节实验台上进行,如图4所示.
图 4
图 4 用于验证的可变负载运动控制实验台
Fig.4 Variable load motion control test bench used for validation
实验台在不同位置处,负载重力折算到液压缸的负载力不同,可以模拟实机变负载力工况. 试验台可以实现不同负载力方向的工况,如图5所示.
图 5
实验台的各参数及元件信息见表2.
表 2 实验台的各参数与元件信息
Tab.2
| 实验台配置 | 参数/型号 | 实验台配置 | 参数/型号 | |
| 液压缸型号 | ATOS CKN | 平衡阀 | SUN MWEG | |
| 液压缸行程/mm | 500 | 平衡阀先导比 | 4.5 | |
| 比例伺服阀 | Parker D1FP | 平衡阀设定压力/MPa | 14 | |
| 压力传感器 | Trafag 8252 | 角度编码器 | 禹衡JKW-6E |
4.2. 用于对比的控制器
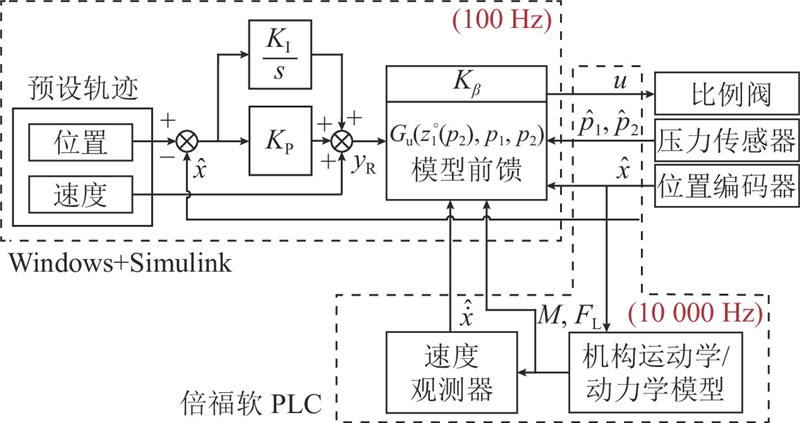
选用传统的模型前馈-反馈控制器(下称FF-PI控制器)作为对比基准,所用的模型与NMPC控制器一致. FF-PI控制器与提出控制器的主要区别在于将NMPC部分替换为式(42)所述的模型前馈. FF-PI控制器如图6所示.
图 6
选用2种不同的参数控制器用于对比,控制器的增益参数未进行寻优调试,选取原则是跟踪快速、精度可接受(平均误差小于1 mm),且静差迅速消除. 所设的增益参数如表3所示. 表中,
表 3 用于对比的控制器配置
Tab.3
| 控制器 | ||
| 所提出方法 | 8.0 | 1.5 |
| 同增益FF-PI | 8.0 | 1.5 |
| 小增益FF-PI | 4.0 | 1.5 |
4.3. 实验设计
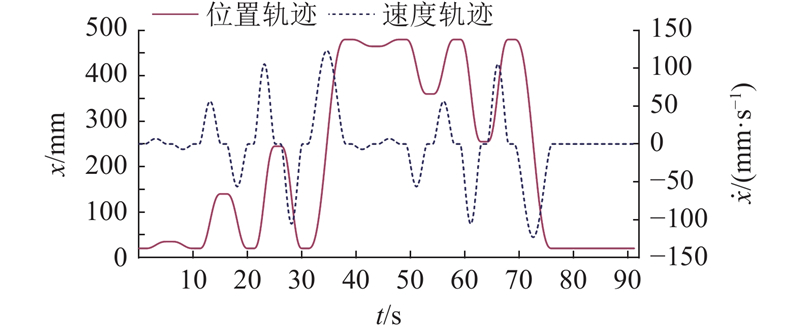
实验分别在无配重和240 kg配重2种工况下开展. 运动控制实验所跟踪的预规划轨迹如图7所示,在不同的负载力方向下,包含低、中、高3种速度水平的正、反向运动. 其中,t为时间.
图 7
4.4. 实验结果与分析
4.4.1. 抑振效果的对比
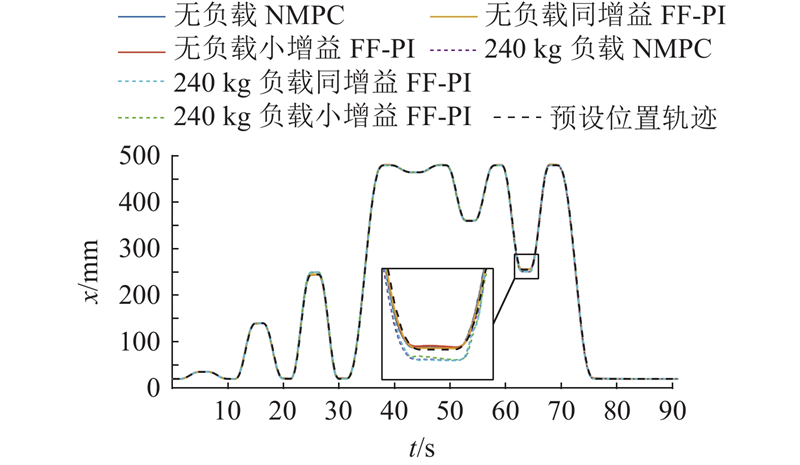
系统位置轨迹的跟踪情况如图8所示. 可以看出,位置轨迹与预设轨迹基本吻合,跟踪控制精度高.
图 8
图 8 不同工况下的位置轨迹跟踪
Fig.8 Position trajectory tracking under different operating conditions
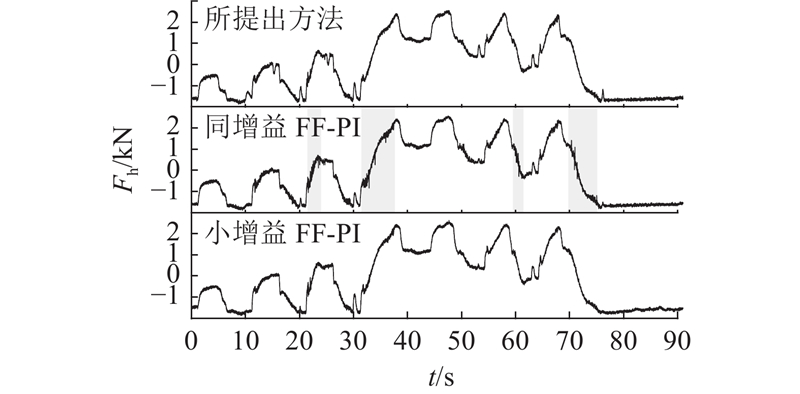
图 9
图 9 无末端负载下不同控制器的液压驱动力曲线
Fig.9 Hydraulic drive force under different controllers without terminal load
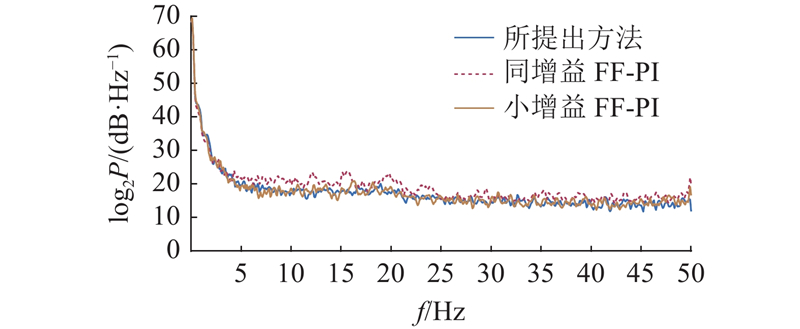
图 10
图 10 无末端负载下不同控制器的液压驱动力功率谱密度
Fig.10 Power spectral density of hydraulic drive force under different controllers without terminal load
当无末端负载时,同增益FF-PI控制器出现小范围失稳振动,主要集中在负载力与速度同向时(即负负载工况). 在该工况下,利用所提出方法以及小增益FF-PI,均未出现失稳振动.
图 11
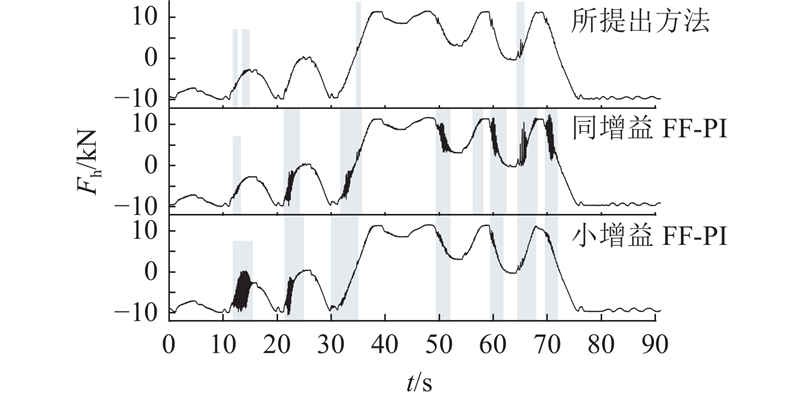
图 11 240 kg负载下所提出不同控制器的液压驱动力曲线
Fig.11 Hydraulic drive force under different controllers with 240 kg terminal load
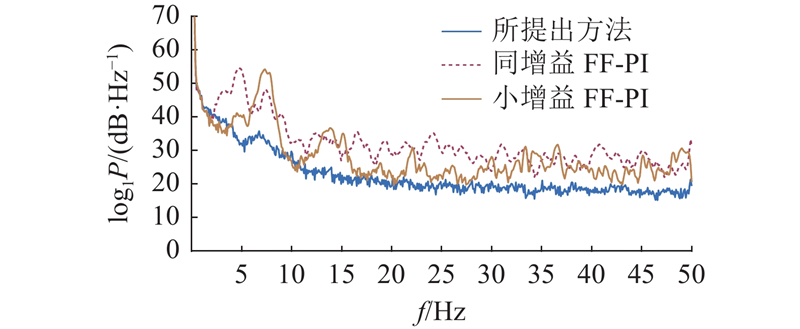
图 12
图 12 240 kg负载下不同控制器的液压驱动力功率谱密度
Fig.12 Power spectral density of hydraulic drive force under different controllers with 240 kg terminal load
在240 kg末端负载下,不同增益的FF-PI均出现了频繁、严重的失稳振动,特别是系统在负负载工况下出现了100%的失稳率;利用提出方法,有效抑制了振动,与2种FF-PI控制器相比,在不同工况下的平均振幅显著降低. 记所提出方法对应的功率谱密度为
式中:
表 4 提出方法与FF-PI控制器的平均液压力振幅对比
Tab.4
| 控制器 | 负载工况/kg | ||
| 同增益FF-PI | 无 | 35.52 | |
| 小增益FF-PI | 无 | 0.06 | 1.36 |
| 同增益FF-PI | 240 | 9.28 | 88.19 |
| 小增益FF-PI | 240 | 5.71 | 73.18 |
与传统的FF-PI控制相比,提出方法在抑振方面均有不同程度的提升:与小增益FF-PI相比,无末端负载时降幅不明显,240 kg负载时振幅平均降低了73.18%. 与相同增益的FF-PI相比,无负载下振幅平均降低了35.52%,240 kg负载下振幅平均降低了88.19%,抑振性能具有显著的提升,证明了提出控制器在抑振方面的优越性.
4.4.2. 跟踪精度对比
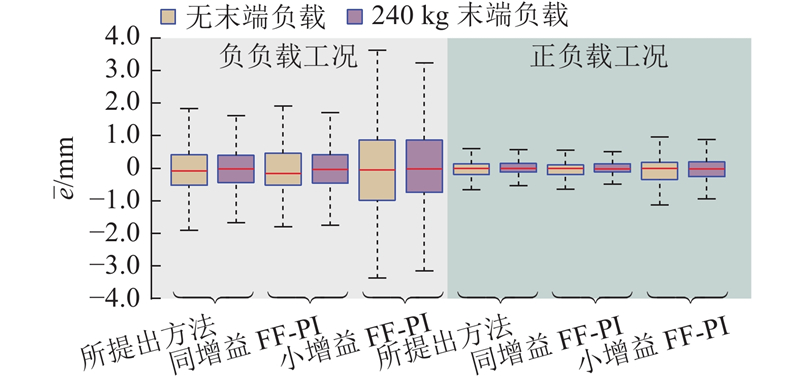
图 13
图 13 不同控制器轨迹跟踪的误差箱线图
Fig.13 Box plot of trajectory-tracking error for different controllers
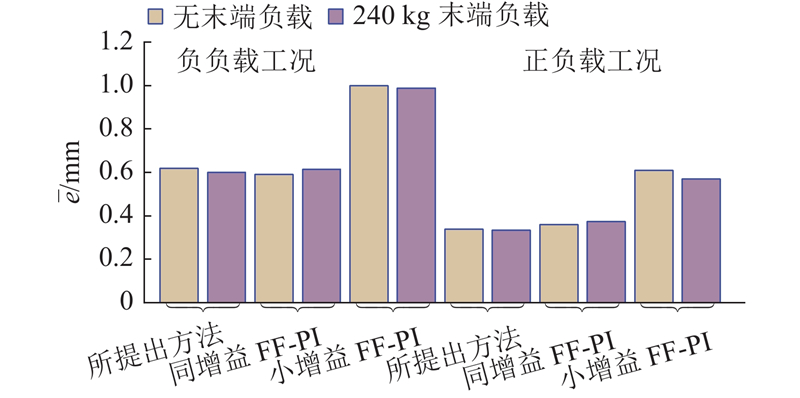
图 14
图 14 不同控制器轨迹跟踪的均方误差
Fig.14 Mean-squared trajectory-tracking error for different controllers
综上可知,含平衡阀阀控缸系统在负负载工况下更容易出现失稳、精度降低的问题. 与相同增益的FF-PI相比,提出方法具有显著的抑振能力,带载情况下的振幅平均降低88.19%,且轨迹精度相近,平均轨迹误差相差不超过5%. 与小增益FF-PI相比,提出方法具有更优的带载抑振能力和更高的轨迹精度. 所提控制器在不失稳的前提下保证了控制精度,突破了传统控制方法中稳定性与精度的矛盾.
5. 结 论
(1) 通过部分反馈线性化发现,含平衡阀阀控缸系统存在零动态. 这一点导致传统FF-PI控制无法通过参数调整兼顾精度和稳定性.
(2) 本研究揭示了含平衡阀系统易失稳、难以设计全局镇定控制器的主要原因如下:系统零动态稳定性条件及收敛域不易解析获得.
(3) 通过构造局部CLF,证明了含平衡阀阀控缸系统具有局部可镇定性,提出可保证局部渐近稳定的NMPC轨迹跟踪控制方法. 理论上的渐近稳定性是含平衡阀系统抑振的关键.
(4) 实验表明,所提出的控制方法实现了稳定的高精度轨迹跟踪控制,在不同负载工况下较传统方法均具有优越性,有较大的工程应用价值. 所提方法所需的算力较高,将在未来的工作中进行研究和改进.
参考文献
Adaptive feedforward control of a pressure compensated differential cylinder
[J].DOI:10.3390/app10217847 [本文引用: 2]
Experimental research characteristics of counterbalance valve for hydraulic drive control system of mobile machine
[J].DOI:10.15199/48.2019.04.18 [本文引用: 1]
Towards digital twin development of counterbalance valves: modelling and experimental investigation
[J].DOI:10.1016/j.ymssp.2022.110049 [本文引用: 3]
Optimal energy consumption and response capability assessment for hydraulic servo systems containing counterbalance valves
[J].DOI:10.1115/1.4056497 [本文引用: 1]
Energetic and dynamic impact of counterbalance valves in fluid power machines
[J].DOI:10.1016/j.enconman.2013.08.021 [本文引用: 1]
Novel concept for stabilising a hydraulic circuit containing counterbalance valve and pressure compensated flow supply
[J].DOI:10.1080/14399776.2016.1172446 [本文引用: 1]
Dynamics modeling and bifurcation analysis for valve-controlled hydraulic cylinder system containing counterbalance valves
[J].DOI:10.1007/s42417-021-00342-6 [本文引用: 1]
Preliminary experimental research on the influence of counterbalance valves on the operation of a heavy hydraulic manipulator during long-range straight-line movement
[J].DOI:10.3390/en15155596 [本文引用: 1]
A novel pressure-feedback based adaptive control method to damp instabilities in hydraulic machines
[J].DOI:10.4271/2012-01-2035 [本文引用: 1]
Using input shaping and pressure feedback to suppress oscillations in slewing motion of lightweight flexible hydraulic crane
[J].DOI:10.1080/14399776.2015.1089071 [本文引用: 1]
Dynamic improvement of hydraulic excavator using pressure feedback and gain scheduled model predictive control
[J].DOI:10.1109/JSEN.2021.3083677 [本文引用: 1]
Active damping control of the large-scale flexible hydraulic manipulators with independent metering system
[J].
The zero dynamics of a nonlinear system: from the origin to the latest progresses of a long successful story
[J].DOI:10.1016/j.ejcon.2013.05.014 [本文引用: 1]
Constrained model predictive control: stability and optimality
[J].DOI:10.1016/S0005-1098(99)00214-9 [本文引用: 1]
SNOPT: an SQP algorithm for large-scale constrained optimization
[J].DOI:10.1137/S1052623499350013 [本文引用: 1]