中国正在快速步入深度老龄化社会，据2021年的人口数据统计可知，我国60岁以上人口占总人口的18.9%，老年人群脑卒中病高发. 研究表明，75%以上的卒中患者出院后存在后遗症^[1-2]，包括下肢运动功能障碍^[3]. 重度卒中患者下肢的平均力量仅为健康成人的30%~50%^[4-5]，严重影响患者运动与平衡功能，患者的日常活动明显受限，跌倒风险随之增加. 康复训练是降低卒中致残率的有效方法之一，目前卒中患者的康复训练主要采用康复师人工训练，康复师供不应求.

近年来，国内外学者和临床针对卒中患者下肢的功能训练，提出下肢外骨骼机器人辅助步态训练的新型康复方法^[6-7]，与传统步态训练联合实施，能够有效改善卒中患者的步态特征，提高躯体的平衡性，增加下肢的稳定性，解决康复师的供需问题. 下肢外骨骼机器人的康复训练步态关节轨迹主要采用基于模型的方法、自适应方法和智能寻优方法等生成^[8-20]. 下肢外骨骼机器人辅助步态训练与患者有主观适配性，匹配合适的康复训练步态能够充分调动患者的积极性. 对于康复训练步态的评价，主要从步行功能分级、运动指数、功能性步行能力等方面对功能性水平、对称性水平、平衡功能等步态观察性评估指标进行主观定性评价，主要形式包括Holden步行功能分级量表^[21]、Rivermead运动指数量表^[22]、Functional Ambulation Category Scale （FAC）功能性步行能力量表^[23]、Tinetti Gait Analysis （TGA）量表^[24]、Rancho Los Amigos （RLA）步态观察分析表^[25]、Wisconsin 步态量表^[26]、Fugl-Meyer 平衡功能量表^[27]等.

康复训练步态的匹配依赖于康复师的经验和观察，强调医从性，易忽略患者产生的恐惧感、不适感和受挫感等直观体验和认知感受. 何灿群等^[28]提出认知过程不是大脑内部事件，而是与身体及其环境密切相关的. 刘佳蕾等^[29]从具身认知的视角出发，探讨膝关节康复机的情感化设计策略，提升使用膝关节康复机的体验. 刘宏宇^[30]引入具身认知及其相关理论，分析可穿戴产品的多模态交互过程对满足潜在心理需求的影响，提供了以多模态交互可穿戴产品为对象的具身交互可视化设计方法.

综上所述，目前的下肢外骨骼机器人辅助步态训练应用处于起步阶段，康复训练步态匹配过程存在调试周期长、依赖人工经验的问题；不匹配的康复训练步态影响患者的康复体验感，可能使患者产生排斥心理. 为了提高康复训练步态的适配程度，本文提出考虑具身认知的下肢外骨骼康复训练步态匹配方法，将身体体验和感官感受作为反馈引入下肢外骨骼步态评价中，构建考虑具身认知的康复训练步态适配评价指标体系，建立下肢外骨骼康复训练步态的效用度量方法. 利用Z-number对康复训练步态进行模糊语言评价，通过模糊不确定性下的证据推理方法融合康复训练步态评价置信度，在康复训练过程中迭代匹配合适的康复训练步态. 通过实验，验证本文所提方法的正确性.

在下肢外骨骼机器人辅助步态的训练过程中，穿戴者对康复训练步态的理解是具有身体性的，即身体是感知康复训练步态的主体，穿戴者关于康复训练步态的认知是身体在体验环境的过程中建立的，身体带来的直观体验和认知经验都会影响人对不同步态的感受. 将身体体验和感官感受作为反馈引入下肢外骨骼康复训练的步态评价中，有助于分析康复训练步态对康复心理情绪形成的机制和特点、探索与认知经验间的关系，实现康复训练步态的适配，充分调动患者的积极性.

在时空参数、关节角度、具体任务、主观量表等传统康复训练步态评价指标的基础上，结合穿戴者的感知、认知和行为活动所具有的身体性，提出考虑具身认知的康复训练步态适配评价指标. 在步态评价指标中融合穿戴者模糊的直观体验和认知经验，精确量化评价康复训练步态的效用度，帮助穿戴者适配康复训练步态. 考虑具身认知的康复训练步态适配评价指标如表1所示.

在康复训练步态的C_Ⅰ直观感受评价指标方面，在穿戴者体验康复训练步态的过程中，身体触觉系统可以感知压力、冷感、热感、痛感、肌肉运动感. 基本方位系统为穿戴者对地球的永恒导向，包括对指向地心垂直方向和水平面方向的方位知觉. 听觉系统感知康复训练步态使用过程中外骨骼的振动. 视觉系统可以分辨环境总体特征和物体特征，洞察环境变化，分辨不同运动和不同事件. 穿戴者通过身体触觉系统感知外骨骼与地面的接触情况，使他们能够直接感受到脚部与地面的接触压力和分布均匀性. 基于基本方位系统的方向感知，穿戴者可以通过自己的身体姿态与水平方向和地心垂直方向关系的感知，准确判断是否处于平衡状态. 这种身体姿态的感知与外骨骼步态的稳定性直接相关. 通过触觉、听觉和视觉系统，可以使穿戴者获得关于步态时空参数、关节角度、肌肉力矩、对称性等量化参数的直观体验. 从具身认知的角度出发，身体体验直接影响穿戴者对步态稳定性和安全性的认知，结合认知经验形成穿戴者对于运动突变情况、平衡性情况、跌倒风险的个人理解.

在康复训练步态的C_Ⅱ认知经验评价指标方面，穿戴者的身体触觉系统对于人机接触面压力分布是否均匀、大小是否可以接受的知觉，加上基本方位系统对于人机系统位移的判断，会影响穿戴者对步态帮助程度、同步性的认知. 通过听觉系统感知外骨骼运动时产生的声音，比如摩擦声或机械声，不同频率和音调的声音也会帮助穿戴者形成是否存在人机活动对抗性的认知. 知觉系统的感知结合穿戴者的认知经验，形成穿戴者对于康复训练步态在舒适度和交互性方面的认知.

在康复训练步态的C_Ⅲ治疗师观察评价指标方面，为了减少穿戴者由于运动能力较差产生的对关节活动范围较小步态的偏好或由于对康复的迫切需求产生的对于难度较大步态的偏好，引入康复师在下肢外骨骼机器人的辅助步态训练过程中对于穿戴者关节活动范围的观察评价.

在步态康复初期，穿戴者对康复训练步态的认知存在较大的模糊和不确定性，难以用精确的数值描述下肢康复外骨骼步态评价指标的属性. 采用Z-number自然语言术语定性描述下肢康复外骨骼步态评价指标的属性值，在对康复训练步态评价指标的属性进行模糊约束的同时，加入康复训练步态自然语言术语评价的可靠性度量，同时处理认知过程和决策结果的不确定性，实现对于步态的准确理解和精确评价.

在康复训练步态训练前期的康复训练步态匹配过程中，假设有M个已知关节参考轨迹的步态组成的方案集$G = \{ {G_1},{G_2},\cdots ,{G_M}\} $，$C = \{ {c_1},{c_2},\cdots, {c_J}\} $为由J个评价指标组成的属性集，对应的权重向量为$w = [{w_1},{w_2},\cdots, {w_J}],$$0 \leqslant {w_j} \leqslant 1.0,$$\displaystyle \sum\nolimits_{j = 1}^L {{w_j} \leqslant 1.0} $. 设第m个康复训练步态G_m的第j个评价指标的语言Z-number的属性值为${Z_{mj}} = (A,B)$^[31]，模糊数A是康复训练步态的评价等级语言术语集S_A的语言型变量，是关于评价等级的模糊约束，隶属度函数为${\mu _A}(x)(x \in {x_A},{x_A} \in R)$，评价等级语言变量x_A及对应的三角模糊数如表2所示. 模糊数B是确定度语言术语集S_B的语言型变量，是关于A的可靠性判断，隶属度函数为${\mu _B}(x)(x \in {x_B},{x_B} \in R)$，确定度语言变量x_B及对应的三角模糊数如表3所示. 例如，穿戴者训练使用第1个康复训练步态G₁后，对“c₁:运动突变情况”评价为“一般，较确定”和“较好，较不确定”，则对应的语言Z-number的值记为$ {Z_{11}} = \{ ({R_3},{U_4}), ({R_4},{U_2})\} $. 将语言型变量通过统一的标准转化为模糊数，对于评价等级语言术语集S_A和确定度语言术语集S_B，隶属度函数为

(1)$ \mu (x) = \left\{ {\begin{array}{*{20}{c}} 0, & x \in ( - \infty ,{a_1}); \\ \dfrac{{x - {a_1}}}{{{a_2} - {a_1}}}, & x \in [{a_1},{a_2}]; \\ \dfrac{{{a_3} - x}}{{{a_3} - {a_2}}}, & x \in [{a_2},{a_3}]; \\ 0, & x \in ({a_3},+\infty ). \end{array}} \right. $

式中：a₁、a₂、a₃分别为左边界、中值和右边界，a₂表示最可能的情况，a₁和a₃表示最不可能的情况.

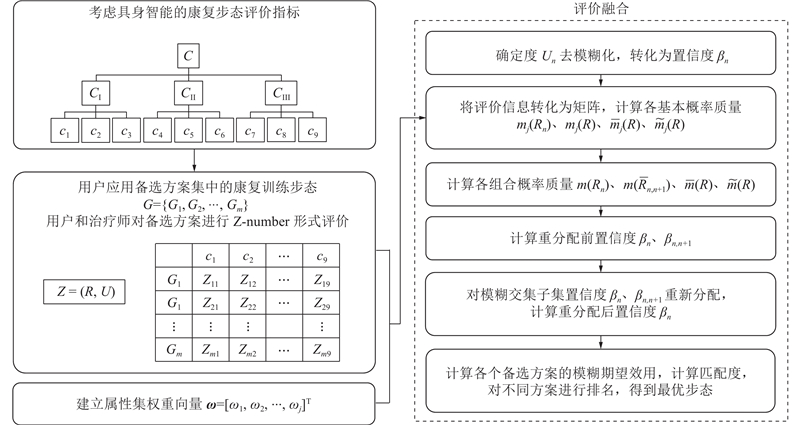
在康复训练步态评价的过程中，使用模糊的自然语言术语来定义评估等级，各等级自然术语的含义会有所重叠，因此很难将评估等级定义为独立的清晰集. 例如，评估等级为“较好”和“很好”被定义为2个相关的模糊集，其交集不为空. 针对康复训练步态评价的自然语言术语非相互独立特性和传统的模糊方法无法处理置信结构中的未知部分等概率不确定性问题，采用非模糊递归证据推理方法通过区间效用来描述不完备评估的特征，将模糊信息转化为模糊置信结构，形成模糊置信决策矩阵，对每个备选方案进行匹配度的度量. 康复训练步态评价置信度融合与步态匹配度度量过程如图1所示.

1）将确定度语言变量去模糊化，映射为精确数形式的置信度.

由于三角模糊数形式的康复训练步态评价的确定度U_n不能参与模糊效用推理过程，将U_n去模糊化，作为置信度β_n参与康复训练步态的模糊效用推理过程. U_n采用的去模糊化方法^[32]为

(2)$ {\text{Crisp}}(\widetilde U) = \frac{{\displaystyle \int {x\mu (x){\text{d}}x} }}{{\displaystyle \int {\mu (x){\text{d}}x} }}. $

式中：$ \mu (x) $为U_n的隶属度函数；$ {\text{Crisp}}(\widetilde U) $为U_n去模糊化后的精确数，即置信度β_n.

2）将康复训练步态的语言Z-number评价信息转化为置信决策矩阵，计算各康复训练步态的基本概率质量.

假设有M个已知关节参考轨迹的康复训练步态集、N个等级的评价等级集R、J个评价指标，则步态G_m在评价指标c_j上被评估为评价等级R_n的置信度为β_n,j(G_m)，则用置信结构$S({c_j}({G_m})) = \{ {R_n},{\beta _{n,j}}({G_m});n = 1,2,\cdots ,N\} $表示该评估. 其中${\beta _{n,j}}({G_m}) \geqslant 0$且$\displaystyle \sum\nolimits_{n = 1}^N {{\beta _{n,j}}({G_m})} \leqslant 1$. 若$\displaystyle \sum\nolimits_{n = 1}^N {{\beta _{n,j}} ({G_m})} = 1$，则说明评估是完整的；反之，说明评估存在“未知”. 所有备选步态的评估由M×J的置信决策矩阵表示.

将康复训练步态评价指标c_j的评价等级R_n及其置信度β_n,j(G_m)转换为康复训练步态的基本概率质量，康复训练步态的基本概率质量计算公式如下.

(3)$ {m_{n,j}} = {m_j}({R_n}) = {w_j}({\beta _{n,j}}({G_m})). $

(4)$ {m_{R,j}} = {m_j}(R) = 1 - \sum\nolimits_{n = 1}^N {{m_{n,j}} = 1 - {w_j}} \sum\nolimits_{n = 1}^N {({\beta _{n,j}}({G_m}))} . $

(5)$ {\overline m _{R,j}} = {\overline m _j}(R) = 1 - {w_j}. $

(6)$ {\widetilde m_{R,j}} = {\widetilde m_j}(R) = {w_j}\left(1 - \sum\nolimits_{n = 1}^N {{\beta _{n,j}}({G_m})} \right). $

(7)$ {m_{R,j}} = {\overline m _{R,j}}+{\widetilde m_{R,j}}. $

式中：m_n,j为基本概率质量；β_R,j为剩余概率质量，分配给整个集合R，当前未分配给任何单独的评价等级；${\overline m _{R,j}}$为由于相对权重而未被分派的概率质量；${\widetilde m_{R,i}}$为由于“无知”而未被分派的概率质量；w_j为第j个评价指标c_j的相对权重.

3）计算康复训练步态的组合概率质量.

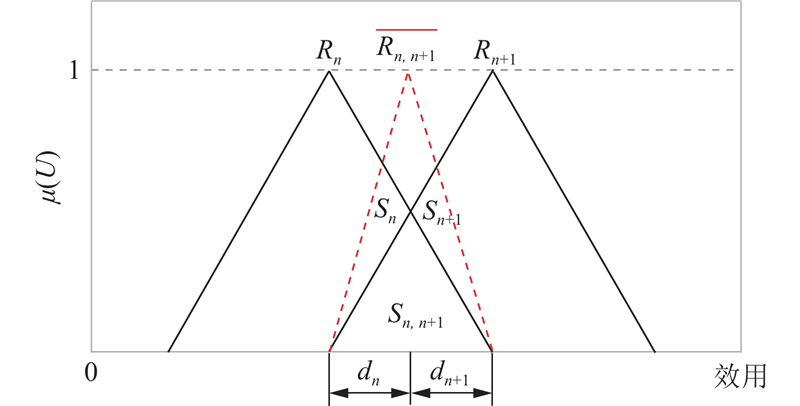
由于康复训练步态的评价等级集R的相邻2个模糊等级相互依赖，采用非递归模糊ER算法聚合评价信息^[33]. 设R_n,n+1为2个相邻模糊评价等级R_n和R_n+1的模糊交集子集，则组合概率质量的计算公式如下.

(8)$ m({R_n}) = k\left\{ \prod\nolimits_{j = 1}^L {[{m_j}({R_n})+{m_j}(R)]} - \prod\nolimits_{j = 1}^L {{m_j}(R)} \right\} . $

(9)$ \begin{split} &m({\overline R _{n,n+1}}) = k\mu _{{R_{n,n+1}}}^{\max }\bigg\{ \prod\nolimits_{j = 1}^L {[{m_j}({R_n})} +{m_j}({R_{n+1}})+{m_j}(R)] -\bigg.\\ & \prod\nolimits_{j = 1}^L {[{m_j}({R_n})+{m_j}(R)]} - \prod\nolimits_{j = 1}^L {[{m_j}({R_{n+1}})+{m_j}(R)]} +\\ &\bigg.\prod\nolimits_{j = 1}^L {{m_j}(R)} \bigg\} . \\[-1pt]\end{split}$

(10)$ \widetilde m(R) = k\left\{ \prod\nolimits_{j = 1}^L {{m_j}(R) - \prod\nolimits_{j = 1}^L {{{\overline m }_j}(R)} } \right\} . $

(11)$ \overline m (R) = k\prod\nolimits_{j = 1}^L {{{\overline m }_j}(R)} . $

(12)$ \begin{split} k =& \left\{ \sum\nolimits_{n = 1}^{N - 1} {(1 - \mu _{{R_{n,n+1}}}^{\max })} \left[\prod\nolimits_{j = 1}^L {({m_j}({R_n})+{m_j}(R))} - \right. \right.\\ &\left. \prod\nolimits_{j = 1}^L {{m_j}(R)} \right]+\sum\nolimits_{n = 1}^{N - 1} \mu _{{R_{n,n+1}}}^{\max }\left[\prod\nolimits_{j = 1}^L{({m_j}({R_n}} ) +\right. \\&{m_j}({R_{n+1}})) -\left. \prod\nolimits_{j = 1}^L {({m_j}({R_{n+1}})+{m_j}(R))} \right]+\\&\left. \prod\nolimits_{j = 1}^L ({{m_j}({R_N})+{m_j}(R)} )\right\} ^{ - 1}. \\[-1pt]\end{split} $

式中：模糊交集子集R_n+1最大隶属度$\mu _{{R_{n,n+1}}}^{\max }$通常小于$1$；${\overline R _{n,n+1}}$为模糊交集子集R_n+1归一化的结果，归一化使得${\overline R _{n,n+1}}$可以作为最大隶属度$\mu _{{{\overline R }_{n,n+1}}}^{\max } = 1$的模糊评价等级，与其他定义的模糊评价等级以相同尺度进行评估.

4）计算重新分配前置信度及模糊交集子集置信度.

根据组合概率质量m(R_n)、$m({\overline R _{n,n+1}})$、$\overline m (R)$，计算得到重新分配前置信度和模糊交集子集置信度. 置信度的计算公式如下：

(13)$ \{ {R_n}\} :{\beta _n} = \frac{{m({R_n})}}{{1 - \overline m (R)}}. $

(14)$ \{ {\overline R _{n,n+1}}\} :{\beta _{n,n+1}} = \frac{{m({{\overline R }_{n,n+1}})}}{{1 - \overline m (R)}}. $

(15)$ \{ R\} :{\beta _R} = \frac{{\overline m (R)}}{{1 - \overline m (R)}}. $

5）对模糊交集子集置信度β_n+1重新分配.

在康复训练步态评价的过程中，将模糊评价等级的效用定义为模糊等级效用. 模糊效用等级应该与其相应的模糊评价等级有相同的形式，即三角模糊数的模糊效用等级也是三角模糊数. 由于${\overline R _{n,n+1}}$不是最初定义的模糊评价等级，置信度β_n,n+1应该重新分配. 如图2所示，${\overline R _{n,n+1}}$仅与R_n和R_n+1相交，则β_n,n+1只须分配给β_n和β_n+1. 模糊交集子集置信度分配系数的计算公式如下.

(16)$ {\mathrm{A}}{{\mathrm{F}}_n} = \frac{1}{2}\left[\left(1 - \frac{{{d_n}}}{{{d_n}+{d_{n+1}}}}\right)+\frac{{{S_n}}}{{{S_n}+{S_{n+1}}}}\right]. $

(17)$ {\mathrm{A}}{{\mathrm{F}}_{n+1}} = \frac{1}{2}\left[\left(1 - \frac{{{d_{n+1}}}}{{{d_n}+{d_{n+1}}}}\right)+\frac{{{S_{n+1}}}}{{{S_n}+{S_{n+1}}}}\right]. $

(18)$ {\mathrm{Bel}}({\overline R _{n,n+1}} \subset {R_n}) = \frac{{{S_n}+{\mathrm{A}}{{\mathrm{F}}_n} \cdot {S_{n,n+1}}}}{{{S_n}+{S_{n,n+1}}+{S_{n+1}}}}. $

(19)$ {\mathrm{Bel}}({\overline R _{n,n+1}} \subset {R_{n+1}}) = \frac{{{S_{n+1}}+{\mathrm{A}}{{\mathrm{F}}_n} \cdot {S_{n,n+1}}}}{{{S_n}+{S_{n,n+1}}+{S_{n+1}}}}. $

模糊评价等级R_n的最终置信度为${\beta _n}+{\beta _{n,n+1}} \times {\mathrm{ Bel}} ({\overline R _{n,n+1}} \subset {R_n})+{\beta _{n - 1,n}}{\mathrm{Bel}}({\overline R _{n - 1,n}} \subset {R_n})$，模糊评价等级R₁和R_N的置信度分别为${\beta _{1,2}}{\mathrm{Bel}} ({\overline R _{1,2}} \subset {R_1})$和${\beta _N}+ {\beta _{N - 1,N}}{\mathrm{Bel}}({\overline R _{N - 1,N}} \subset {R_N})$. 整个集合$R = \{ {R_1},{R_2},\cdots , {R_N}\} $的置信度是β_n. 设上述的最终置信度为β_1F, β_2F,···,β_NF和β_n，则最终评价等级可以表示为$S(y({G_m})) = \{ {R_n},{\beta _{N{\mathrm{F}}}}({G_m}); n = 1,2,\cdots ,N\} $，实现多项评价指标的聚合.

6）计算康复训练步态的模糊期望效用，即该康复训练步态的效用度. 依据匹配度进行康复训练步态的排名，计算匹配度最高的康复训练步态.

康复训练步态的效用反映了穿戴者和理疗师的偏好和相对期望程度，用期望函数度量. 对不同的康复训练步态方案进行排名，需要计算各个备选方案的模糊期望效用. 康复训练步态G_m的聚合评价S(y(G_m))的期望效用u(S(y(G_m)))、最大效用u_max(G_m)、最小效用u_min(G_m)的计算公式如下.

(20)$ u(S(y({G_{{m}}}))) = \sum\nolimits_{n = 1}^N {{\beta _{n{\mathrm{F}}}}({G_{m}})} u({R_n}). $

(21)$ \begin{split} {u_{\max }}({G_{{m}}}) = &\sum\nolimits_{n = 1}^{N - 1} {{\beta _{n{\mathrm{F}}}}({G_{m}})} u({R_n}) +\\ &({\beta _{N{\mathrm{F}}}}({G_m})+{\beta _R}({G_m}))u({R_n}).\end{split} $

(22)$\begin{split} {u_{\min }}({G_{{m}}}) =& ({\beta _{1{\mathrm{F}}}}({G_m})+{\beta _R}({G_m}))u({R_1})+ \\ &\sum\nolimits_{n = 2}^N {{\beta _{n{\mathrm{F}}}}({G_m})} u({R_n}). \end{split} $

式中：u(R_n)为评价等级R_n的模糊效用. 若S(y(G_m))存在不完整的评价，则${u_{\max }}({G_{{m}}}) \ne {u_{\min }}({G_{{m}}})$；若S(y(G_m))是完整的，则${\beta _R}({G_{{m}}}) = 0$，$u(S(y({G_{{m}}}))) = {u_{\max }}({G_{{m}}}) = {u_{\min }}({G_{{m}}})$.

针对康复训练步态期望效用u(S(y(G_m)))，采用形心法对康复训练步态G_m排名以进行匹配选择. 将期望效用u(S(y(G_m)))隶属度函数图形形心与坐标原点的距离D作为匹配度，D越大表示康复训练步态G_m表现越好，则匹配度$D$的计算公式如下：

(23)$ D = \sqrt {{{\left( {\frac{{{a_1}+{a_2}+{a_3}}}{3}} \right)}^2}+{{\left( {\frac{{{\mu _{\max }}}}{3}} \right)}^2}} . $

将提出方法应用于课题组研发的下肢外骨骼机器人中，针对多名实验者进行康复训练步态匹配方法的实验验证. 选择其中一名具有代表性的健康成员作为实验者对其实验过程进行论述. 该名实验者为25岁男性，身高为171.8 cm，体重为56.6 kg. 实验者使用课题组研发的6自由度下肢康复外骨骼装置，拄拐杖行走模拟下肢外骨骼步态康复训练，其中双侧髋关节、双侧膝关节为主动控制. 使用盘式电机（Maxon，EC90flat），安装有限位开关，以防止损坏设备，确保穿戴者安全. 下肢外骨骼机器人通过控制各个关节节点单元的角度信息对整个系统进行控制，利用扰动观测器和比例积分微分控制器来实现控制. 驱动器采用循环同步位置模式，保证移动的平滑性和连续性. 康复训练步态库中的步态由IMU（IM948）设备采集，进行光顺、连续性处理后得到^[13].

为了使所用的康复训练步态具有代表性，根据实验者的身高、体重、下肢参数，在康复训练步态库中初步筛选出3组备选康复训练步态$G = \{ {G_1},{G_2}, {G_3}\} $，关节参考轨迹包括双侧髋关节、双侧膝关节轨迹. 实验者在进行了适应性训练后，和治疗师对9个康复训练步态指标进行评价，指标的权重为${w_j} = {0.1(j = 1,2,\cdots ,9)}$. 3组康复训练步态的模糊评价信息如表4所示.

1）将确定度语言变量去模糊化，以得到精确数形式的置信度. 根据式(2)对确定度语言变量去模糊化，得到$ {\beta _1}=0.167,\;{\beta _2}=0.250, \;{\beta _3}= 0.500,\;{\beta _4}=0.750, {\beta _5}=0.833 $.

2）将评价信息转化为矩阵，计算各基本概率质量. 根据表4与β_n建立评价矩阵，得到3组备选康复训练步态的置信度矩阵. 根据式(3)~(5)，结合指标权重${{{w}}_j} $，计算得到基本概率质量.

3）计算各组合概率质量. 根据式(12)，结合m_j(R_n)、m_j(R)、${\overline m _j}(R)$、${\widetilde m_j}(R)$，计算得到${k_1} = 1.050\;1$，${k_2} = 1.069\;6$，${k_3} = 1.225\;6$. 根据式(8)~(11)，结合m_j(R_n)、m_j(R)、${\overline m _j}(R)$、${\widetilde m_j}(R)$及k，计算得到组合概率质量.

4）根据式(13)~(15)，结合组合概率质量m(R_n)、$m({\overline R _{n,n+1}})$、$\overline m (R)$，计算得到置信度.

5）对模糊交集子集置信度β_n,n+1重新分配. 根据式(16)、(17)计算得到${\mathrm{A}}{{\mathrm{F}}_n} = 0.5$，${\mathrm{A}}{{\mathrm{F}}_{n+1}} = 0.5$. 根据式(18)、(19)计算得到分配系数：${\mathrm{Bel }}({\overline R _{n,n+1}} \subset {R_n}) = 0.5$，${\mathrm{Bel}}({\overline R _{n,n+1}} \subset {R_{n+1}}) = 0.5$.

各步态评价等级的最终置信度如下.

$ \begin{gathered} {\beta _{1{\rm{F}}}} = \begin{array}{*{20}{c}} 0,\; {0.018\;9},\; {0.617\;1},\; {0.238\;9},\; 0 .\end{array} \\ {\beta _{2{\rm{F}}}} = \begin{array}{*{20}{c}} 0,\; 0,\; {0.267\;4},\; {0.425\;7},\; {0.127\;7} .\end{array} \\ {\beta _{3{\rm{F}}}} = \begin{array}{*{20}{c}} {0.972},\; {0.210\;1},\; {0.411\;5},\; {0.190\;1},\; 0 .\end{array} \\ \end{gathered} $

6）计算各个备选康复训练步态的模糊期望效用，对不同方案进行排名，得到最优康复训练步态. 根据式(20)~(23)，计算得到u(S(y(G_m)))、u_max(G_m)、u_min(G_m)的三角模糊数及匹配度D，如表5所示. 按照匹配度的大小顺序排列，康复训练步态的优先级排序为${G_2} > {G_1} > {G_3}$，即康复训练步态G₂为最优匹配方案.

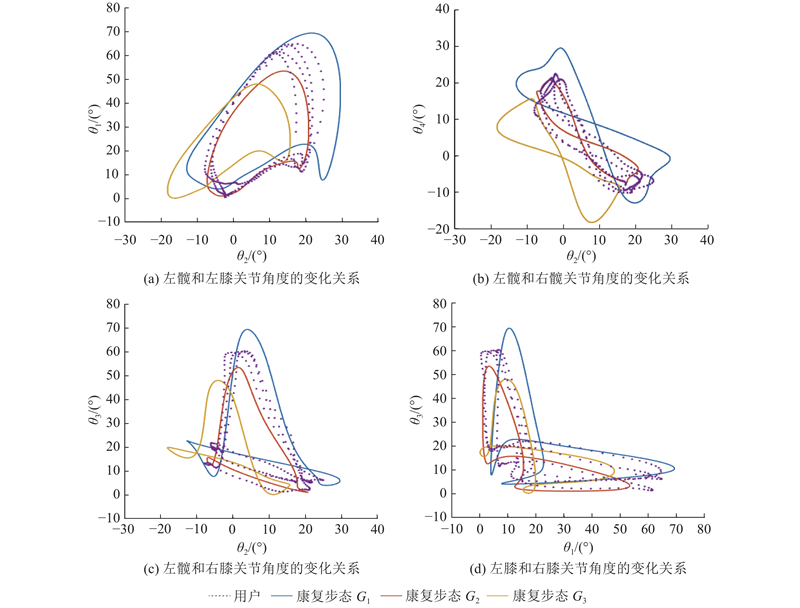
下肢外骨骼康复训练步态在使用过程中，单关节角度随时间的变化规律和各关节运动的协同变化规律共同影响实验者的康复训练步态体验，会影响实验者的评价. 实验者自身多个步态周期和3组实验康复训练步态下的关节轨迹协同变化，如图3所示分别为左髋与左膝关节协同关系、左髋与右髋关节协同关系、左髋与右膝关节协同关系以及左膝与右膝关节协同关系. 图中，θ₁、θ₂分别为左膝、左髋关节角度，θ₃、θ₄分别为右膝、右髋关节角度. 从几何形状上看，协同变化曲线的基本轮廓相似但存在差异，说明在正常行走过程中，下肢各关节之间的协同关系遵循一定的规律，且对于不同的个体存在差异. 为了分析关节协同变化的规律，采用主成分分析（principal components analysis，PCA）法进行数据降维. 分别对实验者自身多个步态周期平均值和3组康复步态进行PCA分解，用余弦相似度度量实验者自身步态与3组康复步态的关节协同变化规律图形的相似度：

(24)$ {\varphi _i}(S,G) = \frac{{{{\boldsymbol{\lambda}} _i}\cdot {{\boldsymbol{\delta}} _i}}}{{||{{\boldsymbol{\lambda}} _i}||\; ||{{\boldsymbol{\delta}} _i}||}} . $

式中：S为实验者数据；G为康复训练步态数据；λ_i、δ_i为受试者和康复训练步态的第i个协同变化关系数据的PCA特征向量；φ_i为0~1.0，越接近1.0，则图形趋势的相似度越高.

φ_i的计算结果如表6所示，${\varphi _1}(S,{G_2}) > {\varphi _1}(S,{G_3}) > {\varphi _1}(S,{G_1})$，说明G₂与实验者自身的相似度最高，与图3(a)的结论一致. 从表6可知，${\varphi _2}(S,{G_1}) > {\varphi _2}(S,{G_2})$，说明G₁与实验者自身步态图形趋势更相似. 如图3(b)所示，实验者自身步态与康复训练步态G₂的左右髋关节运动范围幅度的相似度明显大于实验者自身步态与康复训练步态G₁的相似度. 综上所述，运动范围幅度对相似度的影响更显著，G₂更接近实验者自身步态. 表6与图3(b)~(d)一致表明，在左髋与右膝关节协同关系、左膝与右膝关节协同关系中，康复训练步态G₂与实验者更接近，其次是G₁，最次是G₃. 如图3(d)所示，康复步态G₃的膝关节轨迹在最值附近变化较复杂，而实验者自身曲线的变化较平稳，这与φ₃(S,G₃)和φ₄(S,G₃)计算结果较小的结论一致，表明G₃与实验者步态的关节协同变化规律的相似性较差. 综上，康复训练步态G₂的关节协同运动规律最接近实验者的自身步态，在使用过程中可能给实验者带来更加适合自己、更加舒适的身体体验，且更加符合实验者对于适合步态的认知经验. 协同变化曲线的相似度φ_i为康复步态G₁和G₂获得较高的评价提供了理论支持，验证了具身认知的下肢康复外骨骼步态评价指标体系的可行性.

在下肢外骨骼辅助的步态康复初期步态选择过程中，存在康复训练步态匹配调试周期长、依赖人工经验的问题. 本文提出基于具身认知的下肢外骨骼康复训练步态匹配方法，建立基于具身认知的下肢外骨骼康复训练步态评价指标. 引入基于Z-number的模糊语言评价形式，运用模糊不确定性下的证据推理方法，进行下肢外骨骼康复训练步态评价置信度融合与步态匹配度求解，排序得到最优的康复训练步态方案. 该方法充分考虑具身性在康复训练步态选择过程中的重要作用，克服了传统方法无法处理模糊决策信息的局限性，实例结果验证了提出方法的可行性.