海洋环境的复杂性和未知性给人类的海洋活动带来巨大挑战，海洋资源的高效探索和利用成为当前亟待解决的问题^[1]. 自主水下航行器(autonomous underwater vehicle, AUV)能够在水下环境中自主执行任务，具有活动范围大、机动性好、安全、智能化等优点，成为完成各种水下任务的重要工具. 在未知的水下环境中，AUV难以自主规划出安全可靠的高质量路径，因此路径规划是AUV应用中的关键问题^[2]. AUV路径规划是指为AUV确定其在水下环境中的运动路径的过程^[3]. 随着人工智能的快速发展，机器学习技术为解决AUV的路径规划问题提供了更多可能. 强化学习作为新兴的机器学习范式，具有高度的智能性、灵活性和适应性. 强化学习模仿人类从零开始掌握一项技能的过程，被广泛应用于机器人控制、推荐系统、自动驾驶等多个领域^[4]. 在进行AUV路径规划研究中，强化学习算法在每个时间步骤根据当前环境状态和预测的未来状态选择最优的行动，例如前进、后退或者转向等，通过环境反馈的奖励信号不断修正和调整策略，帮助AUV逐步找到最优的路径^[5].

虽然强化学习能够在路径规划中适应复杂动态环境，避免局部最优解问题，但是实际应用面临多重挑战. 强化学习算法不但需要大量的数据和计算资源，还需要实时调整各种参数来实现最佳效果^[6]. 在实际海洋环境中，洋流会对AUV的位置、时间成本和能量消耗等产生潜在影响，由于传感器的探测范围有限，AUV只能获取附近海流和障碍物的信息，可能出现先验环境知识不完整的情况. 本研究引入人工势场法(artificial potential field, APF)与强化学习相结合的路径规划策略. 人工势场法为AUV设置吸引力和斥力场，能够有效地引导AUV避开障碍物，优化行进方向. 传统的势场法容易导致局部最优解问题，且难以应对复杂的三维水下环境，本研究进一步提出融合自适应势场法和深度强化学习的三维水下AUV路径规划方法(3D underwater AUV path planning method integrating adaptive potential field method and deep Q-network, IADQN). IADQN利用自适应势场法优化AUV的行进方向，确保AUV在寻优过程中有效躲避障碍物，提高任务执行的安全性和可靠性；采用优先经验回放策略，改善数据提取时重要经验利用不足的问题，提高训练效率和样本利用率；动态调整奖励函数确保AUV快速生成最优路径. 在此基础上，基于真实的海底环境数据对IADQN进行仿真验证.

有多种算法被用于AUV的路径规划研究，如A*^[7]、人工势场^[8]、快速探索随机树(rapidly-exploring random tree，RRT)等. Zhang等^[9]将AUV动力学纳入A*算法中，在充分考虑AUV动态约束以及位置和姿态信息的同时，规划出安全的路径. Chen等^[10]提出改进人工势场蚁群算法的优化方案，通过将人工势场的高效求解与蚁群算法的最优求解能力相结合，平衡了路径平滑性、最优解和迭代效率. Yu等^[11]提出基于圆柱体的启发式快速探索随机树算法，通过主要从圆柱子集定义的空间中采样的方式来提高路径质量.

水下环境比较复杂，传统的算法在处理高维度或不确定的环境中往往表现不佳（如陷入局部最优解，计算复杂度高），强化学习算法能够更好地处理这些情况，被越来越多地应用于解决路径规划问题. 基于强化学习的路径规划方法不依赖先验信息，它通过AUV与环境的不断交互和试错来获取信息，并利用奖赏机制进行策略优化. 经典的Q-learning算法在处理高维状态空间时容易出现“维数灾难”问题，难以满足复杂水下环境中的路径规划需求. 近端策略优化^[12](proximal policy optimization, PPO)和深度Q网络(deep Q-network, DQN)^[13]因其在处理高维状态空间和策略优化方面的独特优势，逐渐成为路径规划领域的研究热点. PPO是在线学习算法，通过与环境的持续交互不断更新和优化策略，在强化学习领域中应用广泛. Wen等^[14]提出结合协方差矩阵适应进化策略和元学习的动态近端策略优化算法，通过引入迁移学习，在复杂环境下提高多机器人系统的障碍规避能力和适应性. 祁璇等^[15]改进近端策略优化算法，采用多步长动作选择策略和动态奖励值函数，显著提高了自动引导车路径规划和任务调度的效率. PPO依赖于与环境的持续交互，在信号不稳定或环境无法持续交互的情况下难以应用. DQN是离线学习算法，通过神经网络逼近最优动作值函数，能够结合经验回放机制在大状态空间下进行学习. Yang等^[16]提出基于N步优先级双DQN算法的AUV路径规划方案，利用经验筛选机制提高了算法在动态三维海洋环境中的避障性能和稳定性. Xing等^[17]提出基于改进DQN的算法，通过优化数据选择和动态奖励机制，并将网络分为价值函数和优势函数，在复杂环境下高效地完成了完全覆盖路径规划任务. 相较于PPO，DQN更适合处理信号不稳定或环境无法持续交互的情况，在水下环境中更具优势. 但是，传统的DQN算法依赖于固定的数据集进行训练，对环境变化敏感度较低，无法及时响应动态环境的变化. 本研究融合自适应势场法和DQN算法，使AUV能够在高维状态空间下有效进行动作选择和避障，提高动态海洋环境中AUV任务的执行效率.

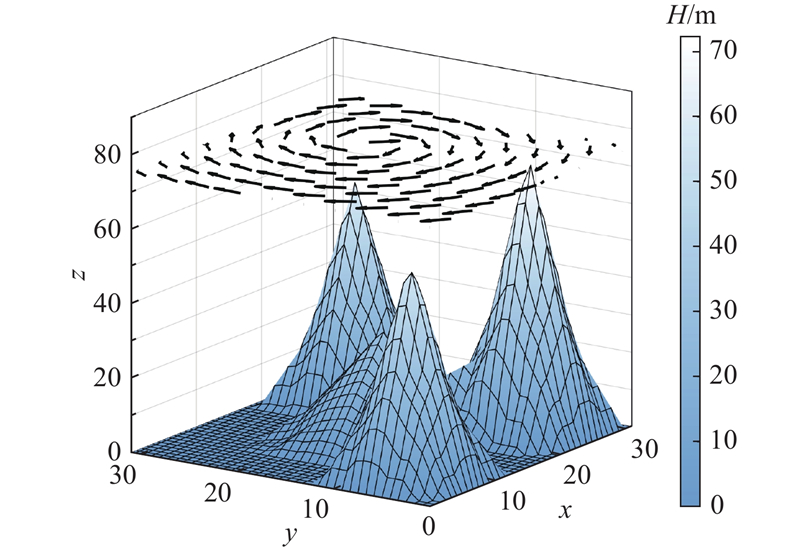
考虑真实的水下环境（包括海底地形特征、洋流等因素），海底地形取自136.75° E~136.80° E，22.55° N~22.60° N. 由于洋流在短时间和小范围内相对稳定，在三维网格图上采用矢量箭头指示洋流的大小和方向. 洋流随空间和时间变化的数学模型^[18]如下：

(1)$ \psi (x,y,t) = A\sin\; ({\text{π}}f(x,{{t}}))\sin\; ({\text{π}}y), $

(2)$ f(x,t) = a(t){x^2}+b(t)x, $

(3)$ a(t) = \mu \sin\; (\omega t), $

(4)$ b(t) = 1 - 2\mu \sin \;(\omega t). $

其中ψ(x,y,t)描述洋流中流体运动的函数，控制流体运动的方式和速度；A为模拟洋流的强度；f(x,t)表示洋流的形状变化；μ调整洋流的振幅，ω为频率参数，决定洋流变化的速度，调整μ和ω可以控制漩涡洋流的形态、大小和运动方式，从而更好地模拟真实环境中的洋流现象. 位置越深的洋流强度越小，垂直方向洋流的分量远远小于水平方向的，因此不考虑垂直方向的洋流影响. 三维水下地形洋流仿真如图1所示，其中β为纬度，λ为经度，D为深度.

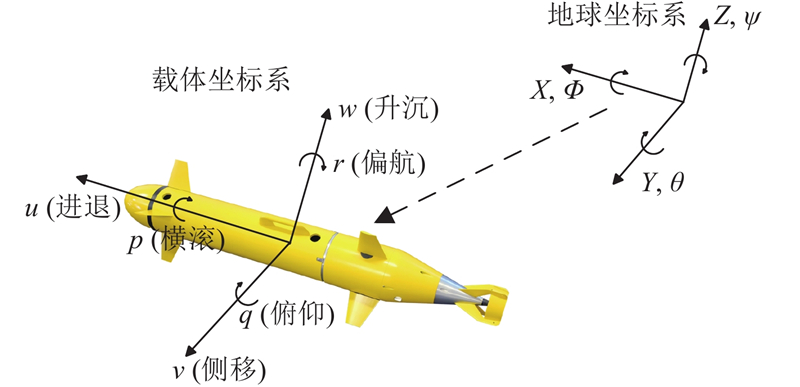
在三维环境中，AUV的六自由度模型如图2所示. AUV的位置向量$ \boldsymbol{p}=[x,y,z] $，姿态向量$ \boldsymbol{\theta }=[\phi ,\theta ,\psi ] $. 线速度矢量$ \boldsymbol{v}=[u,v,w] $，角速度矢量$ \boldsymbol{\omega }=[p,q,r] $. 假设AUV的重量和浮力相等，其中心垂直位于z轴上，忽略非线性流体动力阻尼项和横摇运动，角速度恒定，AUV动力学模型如下：

(5)$ x = u\cos\; (\theta )\cos\; (\psi ) - v\cos\; (\phi )\sin\; (\psi ) +w\sin \;(\phi )\cos\; (\psi ), $

(6)$ y = u\cos\; (\theta )\sin\; (\psi )+v\cos\; (\phi )\cos \;(\psi )+w\sin\; (\phi )\sin \;(\psi ), $

(7)$ z = - u\sin \;(\theta )+v\sin \;(\phi )\cos\; (\theta )+w\cos\; (\phi )\cos \;(\theta ), $

(8)$ \phi = p+q\sin \;(\phi )\tan \;(\theta )+r\cos \;(\phi )\tan \;(\theta ), $

(9)$ \theta = q\cos \;(\phi ) - r\sin \;(\phi ), $

(10)$ \psi = \frac{{q\sin \;( \phi )}}{{\cos \;(\theta )}}+\frac{{r\cos \;(\phi )}}{{\cos \;(\theta )}}. $

式中：x、y、z为AUV在惯性坐标系中的位置坐标；u、v、w为AUV在惯性坐标系中的速度分量；θ、ϕ、ψ为AUV的欧拉角，描述了航行姿态；p、q、r为AUV的角速度分量，详细如表1所示. 式(5)~(7)为位置方程，式(8)~(10)为姿态方程.

在路径规划中，控制AUV速度的大小和运动方向，使AUV以较小的转弯角度进行运动，实现路径更加平滑并且运行时间更短. 本研究不仅考虑AUV的速度和方向，还进行加速度控制，以进一步优化路径. 假设在同一平面上洋流速度大小固定，$ {\boldsymbol{v}}_{\mathrm{A}\mathrm{U}\mathrm{V}} $、$ {\boldsymbol{a}}_{\mathrm{A}\mathrm{U}\mathrm{V}} $分别为AUV的速度和加速度，$ {\boldsymbol{v}}_{\mathrm{o}\mathrm{c}\mathrm{e}} $为洋流的速度. 限定$ {\boldsymbol{v}}_{{\mathrm{max}}} $为AUV在直线上速度最大值，$ {\boldsymbol{v}}_{{\mathrm{tur}}} $为拐弯时速度最大值. 根据矢量合成定律，设定AUV初始速度为2 m/s，AUV的实际速度$ {{\boldsymbol{v}}} $计算式为

(11)$ {\boldsymbol{v}} = {{\boldsymbol{v}}_{{\text{AUV}}}}+{{\boldsymbol{v}}_{{\text{oce}}}} , $

(12)$ ||{\boldsymbol{v}}|| = \min\; (||{{\boldsymbol{v}}_{{\text{AUV}}}}||,{{\boldsymbol{v}}_{\max }}) . $

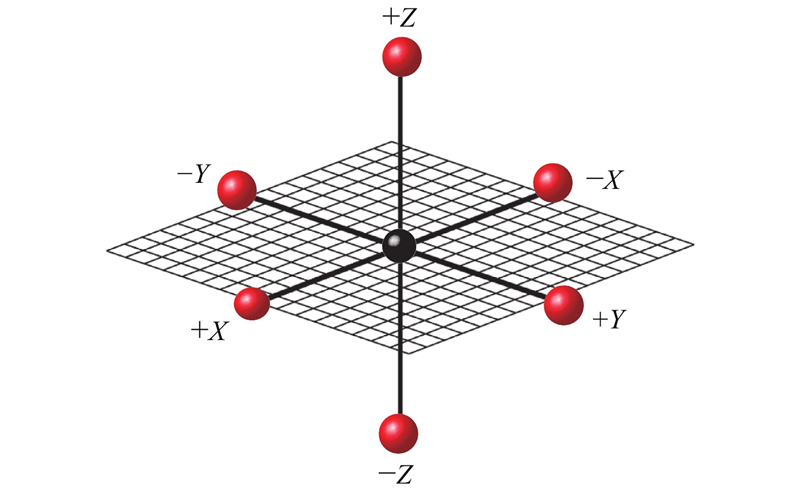
若AUV在加速中速度超过最大速度，则实际速度将被限制. 如图3所示为AUV在三维网格环境中的6个动作方向. AUV在运行过程中感知障碍物，并将障碍物信息作为输入状态的一部分，以便根据策略做出动作选择. 障碍物信息通常由部署在AUV上的传感器收集.

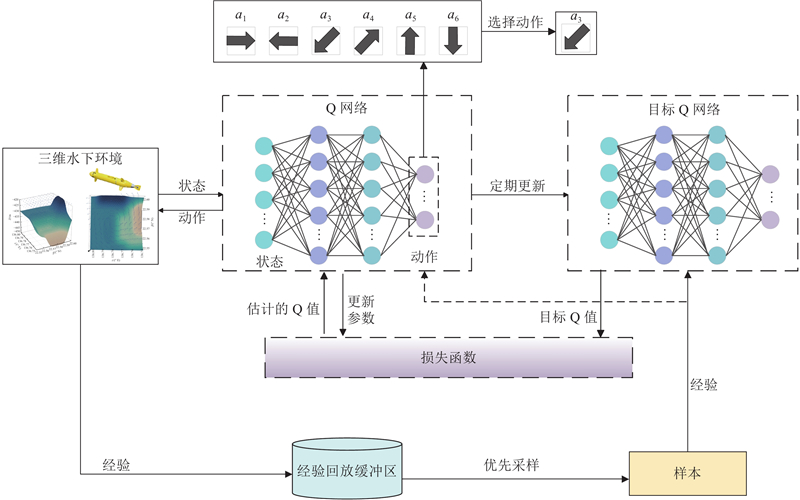
在复杂的水下环境中，深度强化学习在前期训练时须耗费大量时间和资源来收集数据进行模型训练和优化. 本研究提出自适应势场法辅助AUV的动作选择，确保在寻优过程中AUV能够有效躲避障碍物，从而提高任务执行的安全性和可靠性. 采用优先经验回放策略，以优化经验缓冲区中重要经验利用不足的问题，提高训练效率和样本利用率. 通过调整动态奖励函数，保证AUV快速生成最优路径. 其中IADQN将AUV附近的环境信息以及本身信息作为强化学习中神经网络的状态输入，准确总结海洋环境特征并指导网络更新. IADQN框架如图4所示.

人工势场法具有计算量小，模型构建容易，动态避障效果显著等突出优点^[19]. 将人工势场法直接用于AUV的动作选择会导致AUV陷入局部最小值，无法到达目标点的情况；此外当目标点的势场不是整个势场中的最小值时，可能会产生目标点不可达的情况. 本研究提出自适应势场法来优化AUV的动作选择，通过引入距离修正函数解决不可达目标点问题，并根据AUV附近障碍物的数量自适应地采用不同的方法解决局部最小值问题.

决定障碍物斥力势场的因素是AUV与障碍物间的距离，当AUV未进入障碍物的影响范围时，受到的势能值为零. 在AUV进入障碍物的影响范围后，两者的间距越大，AUV受到的斥力越小；反之，间距越小，受到的斥力越大，传统的斥力场势能函数为

(13)$ {U_{{\mathrm{rep}}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{k_{{\mathrm{rep}}}}{{\left(\dfrac{1}{{d({\boldsymbol{X}},{{\boldsymbol{X}}_0})}} - \dfrac{1}{{{d_0}}}\right)}^2},}&{0 \leqslant d({\boldsymbol{X}},{{\boldsymbol{X}}_0}) \leqslant {d_0};} \\ {0,}&{d({\boldsymbol{X}},{{\boldsymbol{X}}_0}) \geqslant {d_0}.} \end{array}} \right. $

式中：$ \boldsymbol{X}=(x,y,z) $为AUV当前位置的坐标向量，$ {\boldsymbol{X}}_{0}=(x,y,z) $为障碍坐标向量，$ {k}_{{\mathrm{rep}}} $为斥力势场系数，$ {d}_{0} $为障碍最大影响距离，$ d(\boldsymbol{X},{\boldsymbol{X}}_{0})=\left|\right|\boldsymbol{X}-{\boldsymbol{X}}_{0}\left|\right| $. 目标点处的势场值不是总势场的最小值，这是不可达目标点问题的本质. 为了克服传统APF中目标点不可达的问题，在斥力场势能函数中加入距离修正函数，引力势场保持不变. 距离修正函数平衡斥力和引力的变化，特别是在斥力势场快速增加的情况下，当AUV接近目标点时，添加修正函数确保目标点处于总势场中的最小值. 改进的斥力场势能函数为

(14)$ {U_{{\mathrm{rep}}}} = \left\{ {\begin{array}{*{20}{l}} {{k_{{\mathrm{rep}}}}f(d({\boldsymbol{X}},{{\boldsymbol{X}}_0})){{\left(\dfrac{1}{{d({\boldsymbol{X}},{{\boldsymbol{X}}_0})}} - \dfrac{1}{{{d_0}}}\right)}^2}{d^e}({\boldsymbol{X}},{{\boldsymbol{X}}_g}),}\quad\\\qquad {0 \leqslant d({\boldsymbol{X}},{{\boldsymbol{X}}_0}) \leqslant {d_0};} \\ {0,}\quad\;{d({\boldsymbol{X}},{{\boldsymbol{X}}_0}) \geqslant {d_0}.} \end{array}} \right. $

式中：$ {\boldsymbol{X}}_{g}=(x,y,z) $为目标点坐标向量；e为常数，加入e是为了平衡距离的变化，使分子变化比分母更快；$ d(\boldsymbol{X},{\boldsymbol{X}}_{g})=\left|\right|\boldsymbol{X}-{\boldsymbol{X}}_{g}\left|\right| $，引入连续的、渐进减弱的函数$ f\left(x\right) $：

(15)$ f(d({\boldsymbol{X}},{{\boldsymbol{X}}_0})) = {{\mathrm{exp}}\;{( - a_{\mathrm{S}}{{(d({\boldsymbol{X}},{{\boldsymbol{X}}_0}))}^2})}}. $

式中：a_S为控制函数陡峭程度的参数. 式（15）能够使斥力在安全距离附近的变化更加平滑.

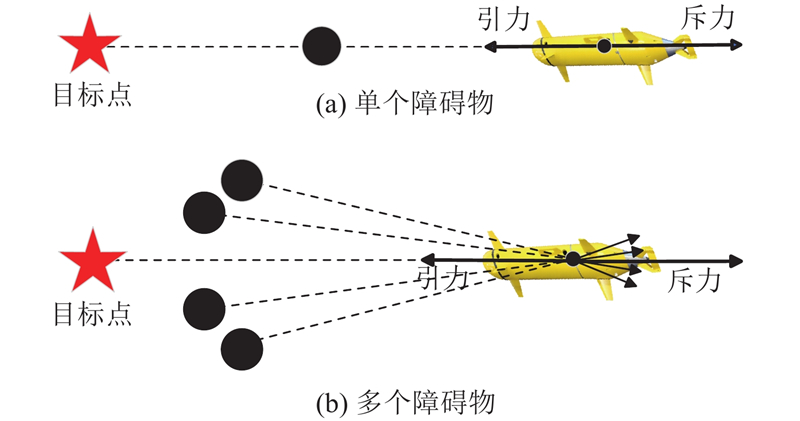
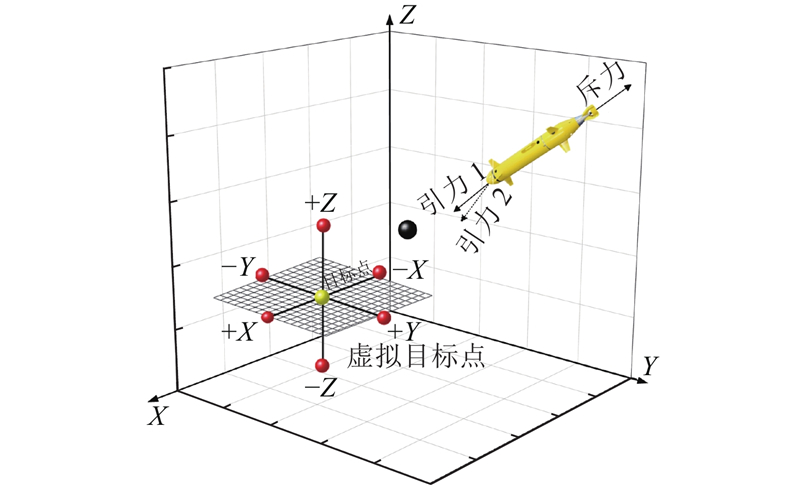
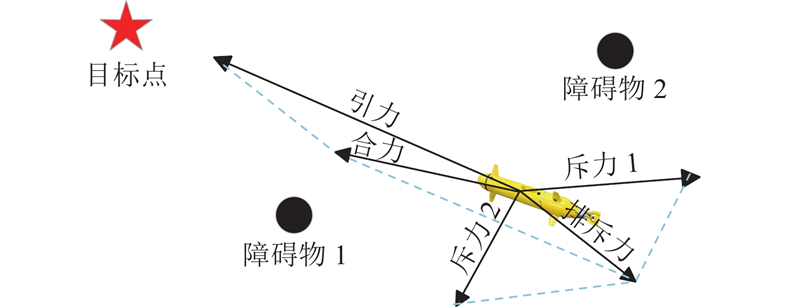
如图5所示，局部最小值的产生可能存在多种情况：AUV、障碍物和目标点共线，AUV在某点处受到的引力和斥力大小相等，方向相反；多个障碍物产生的斥力和目标点产生的引力共线，所受合力为0，这种情况下AUV停滞或在此处徘徊. 为了解决局部最小值问题，假设AUV装配声呐发射装置以确认其前进方向上有无障碍物并能识别障碍物的位置. 当障碍物较少时，引入虚拟子目标点概念；当前进方向障碍物较多时，引入“无障碍前进”规则.

虚拟子目标点以目标点为圆心，周围6个位置上（上、下、左、右、前、后）的随机一点被认为是虚拟子目标点. 如图6所示，浅色圆圈（小）代表实际目标点，深色圆圈（小）代表虚拟子目标点，深色圆圈（大）代表障碍物. 在局部最小值的情况下，目标点设置为虚拟子目标点，因此原始目标点施加的引力（表示为引力1）被虚拟子目标点（表示为引力2）施加的引力取代. 当AUV所在位置的势场合力不为0时，虚拟子目标点将被删除，并恢复原始目标点，以确保AUV路径的连续性.

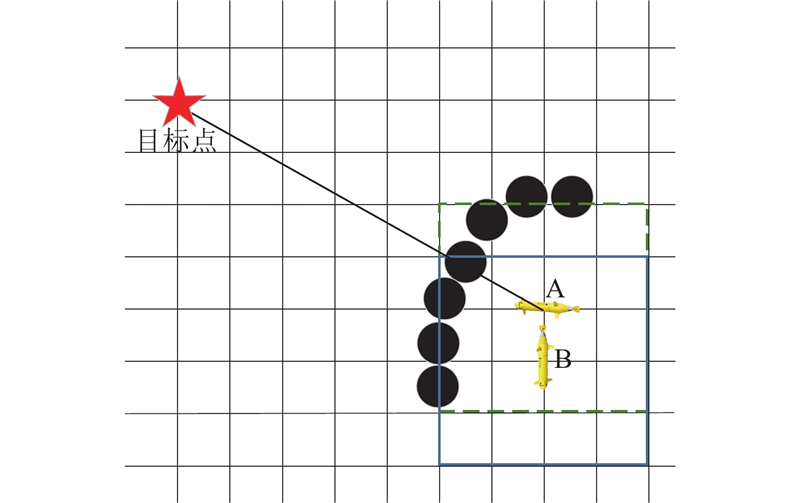
若障碍物较多，并且处于局部最小值位置，采用“无障碍前进”规则，即向没有探测到障碍物的方向前进. 如图7所示，点A为局部最小值位置，虚线为点A的位置探测范围，因此AUV选择向下的动作到达点B，实线为点B的位置探测范围.

将自适应势场法应用于DQN的动作选择过程中. 通过结合APF与DQN，充分利用势场信息来引导AUV的决策过程，使其在动态环境中不仅能够避开障碍物，还能够有效地探索和利用路径信息，从而提升整体路径规划的效果. 如图8所示，AUV在行驶过程中受到人工势场的影响，合力决定了其下一步的行驶方向. 传统DQN方法在进行动作选择时，一般使用经典ε-贪婪算法在动作空间中随机选择动作，当概率$ n < \varepsilon $时，从动作空间中随机选择动作；当概率为$ n\geqslant \varepsilon $时，选择最大状态动作值函数arg max Q(s,a)对应的动作：

(16)$ a = \left\{ {\begin{array}{*{20}{l}} {{\mathrm{rac}},}&{n < \varepsilon ;} \\ {\arg \max Q(s,a),}&{n \geqslant \varepsilon .} \end{array}} \right. $

加入人工势场法后，动作选择为

(17)$ a = \left\{ {\begin{array}{*{20}{l}} {{\mathrm{rac}}}\;\;\;{或}\;\;\;{{\mathrm{apf}},} &{n < \varepsilon ;} \\ {\arg \max Q(s,a),}&{n \geqslant \varepsilon .} \end{array}} \right. $

式中：s为状态，rac为随机选择的动作，apf为势场作用下选择的动作，当$ n < \varepsilon $时，通过生成随机数，并根据该随机数落在由人工势场下的动作与随机动作的平分占比划定的范围内来选择相应的动作. 为了使AUV在充分利用现有知识的同时保持一定程度的探索，解决探索利用问题，使用衰减$ \varepsilon $算法进行调整：

(18)$ \varepsilon = \left\{ {\begin{array}{*{20}{l}} {\varepsilon \times {\varepsilon _{{\mathrm{dec}}}},}&{\varepsilon > {\varepsilon _{\min }};} \\ {{\varepsilon _{\min }},}&{\varepsilon = {\varepsilon _{\min }}.} \end{array}} \right. $

式中：$ {\varepsilon }_{{\mathrm{dec}}} $为$ \varepsilon $衰减值，$ {\varepsilon }_{{\mathrm{min}}} $为最小$ \varepsilon $值. 经典的$ \varepsilon $-贪婪算法以固定的$ \varepsilon $概率对环境进行随机搜索，若这个固定值设置较大，将导致AUV在充分了解环境后仍进行大量不必要的随机搜索；若这个值设置较小，则AUV将很难建立对环境的全面了解. 本研究的衰减$ \varepsilon $算法将$ \varepsilon $设置为随模型参数更新而减少的参数. 衰减$ \varepsilon $算法使智能体能够根据搜索调整探索概率，以减少不必要的探索行为.

模型训练时抽样的经验数据质量不均匀将导致学习效率低下的问题，为此在算法中使用优先经验回放机制. 该方法根据每个经验数据的重要性来确定其优先级，能够在采样时更多地选择更重要的经验，从而提高学习效率. TD-error为动作价值估计与实际回报之差，常被用来更新网络，作为估计值的修正，TD-error反映算法对经验真实价值的评估程度. TD-error值较大的样本被赋予更高的优先级，TD-error值较小的样本被赋予较低的优先级. 优先级计算式为

(19)$ {P_i} = |{\delta _i}|+\xi , $

(20)$ P\left( i \right) = \frac{{p_i^\partial }}{{\displaystyle\sum\nolimits_k {p_k^\partial } }}. $

式中：$ {P}_{i} $为第i个样本的优先级；$ {\delta }_{i} $为TD-error值；$ \xi $为大于0的常数；P(i)为第i个样本被选中的概率；∂为从0到1的超参数，影响优先级，当∂=0时为随机抽样；k为经验缓冲区的样本数. 频繁使用具有较高TD-error值的经验会导致偏差，为了避免偏差导致训练过程出现振荡甚至分散的问题，利用重要性抽样方法来适当降低高优先级的权重，使得在训练时候每个样本训练对于梯度下降的影响相同，从而确保结果的收敛性，样本i的采样权重：

(21)$ {w_i} = {\left(\frac{1}{k}.\frac{1}{{P(i)}}\right)^\eta }. $

其中$ \eta $为超参数，$\eta\in (0,1.0) $，作用是提高优先经验回放对收敛结果的影响. $ \eta $越大，低优先级样本的采样权重越大.

奖励函数也称为即时奖励或增强信号. AUV执行动作后，环境会根据该动作做出反馈信息，用于评估该动作的表现. 奖励函数通常是标量，正值表示奖励，负值表示惩罚. 在AUV路径规划模型的训练和测试过程中，奖励函数的设计决定了神经网络训练的效果和效率. 奖励函数作为AUV行为决策有效性和安全性的评价指标，具有结果导向作用. 在传统的DQN算法中，只有当智能体碰到障碍物或者到达终点时才会有奖励，其他动作没有任何有效的反馈. 为了解决传统奖励函数收敛速度慢、训练周期长的问题，本研究对奖励函数进行优化，提出改进的奖励函数设计方法. 奖励函数rew被分解为2个部分：位置奖励函数（包括目标奖励函数r_dis和避障奖励函数r_obs）、方向奖励函数（包括洋流方向奖励函数r_dir和平滑度奖励函数r_smo）. 目标奖励函数引导AUV快速到达目标点，表示AUV和目标的距离；避障奖励函数使AUV与障碍物保持一定距离；洋流方向奖励函数定义为AUV当前的方向和当前位置洋流方向的夹角；平滑度奖励函数表示AUV在路径规划中转弯的频率.

(22)$ {\mathrm{rew}} = r_{{\mathrm{dis}}}+r_{{\mathrm{obs}}}+r_{{\mathrm{dir}}}+r_{{\mathrm{smo}}}. $

每次动作后，根据AUV当前状态和环境设置动态奖励函数. $ {d}_{t}^{k-1} $为第k−1时刻AUV到目标点的距离，$ {d}_{t}^{k} $为k时刻AUV到目标点的距离，c为常数. 当$ {d}_{t}^{k-1} $>$ {d}_{t}^{k} $时，表示AUV执行当前动作后距离目标点更近，此时$ {r}_{{\mathrm{dis}}} $为正，说明环境给予AUV正的奖励. 正奖励值随着AUV到目标点距离的缩短呈指数变化，加速AUV接近目标点，起势能的作用. 当AUV在k时刻距离目标点更远时，将获得负奖励值.

(23)$ r_{{\mathrm{dis}}} = \frac{{d_{\mathrm{t}}^{k - 1} - d_{\mathrm{t}}^k}}{{|d_{\mathrm{t}}^{k - 1} - d_{\mathrm{t}}^k|}}{c^{|d_{\mathrm{t}}^{k - 1} - d_{\mathrm{t}}^k|}}. $

为了帮助AUV快速脱离危险区域（AUV靠近障碍物，但尚未与障碍物发生碰撞），加大障碍物附近的惩罚力度. 为了避免AUV陷入局部情况，危险区域的惩罚不宜过于密集. 危险区域的惩罚与障碍物位置的惩罚应有一定差距，避障奖励函数为

(24)$ r_{{\mathrm{obs}}} = \left\{ {\begin{array}{*{20}{l}} {{r_1}},&{0 < d({X_{\text{g}}},X) \leqslant {d_{{\mathrm{mid}}}}}; \\ {{r_2}},&{{d_{{\mathrm{mid}}}} < d({X_{\text{g}}},X) \leqslant {d_0}} .\end{array}} \right. $

其中$ {d}_{{\mathrm{mid}}} $，$ {d}_{0} $为定值，用来判定AUV到障碍物的距离；r₁、r₂为奖励值，r₁绝对值大于r₂绝对值，并且，r₁、r₂都为负常数.

考虑洋流方向与AUV行驶方向的夹角，通过余弦相似度，确保AUV在洋流中行驶时以较大概率顺着洋流的方向运动，洋流方向奖励函数为

(25)$ \cos (\theta ) = \frac{{{{ {\boldsymbol{v}} }_{{\mathrm{auv}}}} \cdot {{{\boldsymbol{v}} }_{{\mathrm{oce}}}}}}{{||{{{\boldsymbol{v}} }_{{\mathrm{auv}}}}||\cdot ||{{{\boldsymbol{v}} }_{{\mathrm{oce}}}}||}}, $

(26)$ r_{{\mathrm{dir}}} = \tau \cos (\theta ). $

其中$ \theta $为洋流方向与AUV行驶方向的夹角，$ \tau $为常数.

为了减少AUV拐弯次数，提高路径平滑度，每当AUV运动方向发生变化时，给予固定的负奖励. 平滑度奖励函数为

(27)$ r_{{\text{smo}}} = - \gamma . $

其中$ \gamma $为正常量，对路径中的运动方向变化进行惩罚，促进路径的平滑性. IADQN的伪代码如算法1所示.

算法1　　融合自适应势场法和深度强化学习的三维水下AUV路径规划方法

1. 输入：神经网络权重θ、小批量k、执行步数s、步长h、重放周期K和大小N、指数α

2. 初始化重放内存 ℌ = $ \varnothing $, $ \Delta $ = 0, p1=1

3. for s = 1 to T do

4. while s_t !=终点 do

5. 随机生成在(0, 1)之间的一个数prob

6. if prob < ε then

7. $ {A}_{t} $ = 随机动作或apf

8. else

9. $ {A}_{t} $ = $ {{\mathrm{max}}}_{a}Q({s}_{t},a) $

10. end if

11. 观察 $ {s}_{t},{R}_{t},{\gamma }_{t} $

12. 存储 $ ({s}_{t-1},{A}_{t-1},{R}_{t},{\gamma }_{t},{s}_{t}) $ 到 ℌ 并且具有最高的优先级 $ {p}_{t}={{\mathrm{max}}}_{i < t}{p}_{i} $

13. if t $ \equiv $0 mod K then

14. for j= 1 to k do

15. $ j\sim P\left(j\right)={p}_{j}^{\alpha }/{\displaystyle\sum }_{i}{p}_{j}^{\alpha } $

16. 计算重要性采样权重$ {w}_{j}={(N\cdot P(j\left)\right)}^{-\eta }/{{\mathrm{max}}}_{i}{\omega }_{i} $

17. 计算 TD-error $ {\delta }_{j}={R}_{j} $$ +{\gamma }_{j}{{\mathrm{max}}}_{a}Q({s}_{j},a))- Q({s}_{j-1}, {A}_{j-1}) $

18. 更新优先级 $ {p}_{j}\leftarrow \left|{\delta }_{j}\right| $

19. 累计权重变化 $ \Delta \leftarrow \Delta +{\omega }_{j}\cdot{\delta }_{j}\cdot{\nabla }_{\theta }Q({s}_{j-1},{A}_{j-1}) $

20. end for

21. 更新权重 $ \theta \leftarrow \theta +h \cdot\Delta $,reset $ \Delta =0 $

22. 复制到目标网络 $ {Q}_{{\mathrm{target}}}\leftarrow \theta $

23. end if

24. 选择动作 $ {A}_{t}\sim {\pi }_{\theta }\left({s}_{t}\right) $

25. end for

海底数据来自国家海洋数据中心西太平洋海域^[20]，使用Python语言开发，通过Anaconda管理实验环境，使用PyTorch框架构建和训练模型，实现IADQN. 为了客观评估不同路径规划方法在多种环境下的性能，在三维水下、海底局部、动态障碍物环境下，对IADQN、APF、A*、RRT、DQN、PPO等方法的路径平滑度、路径长度、AUV与洋流的最大夹角和AUV的运行时间等性能指标进行评价. 实验部分参数取值如表2所示.

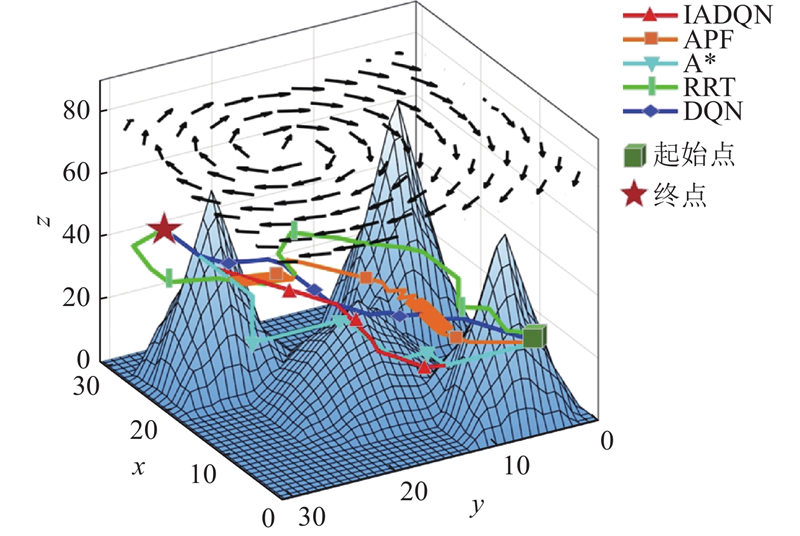
在30 m×30 m×90 m的三维环境下对5种路径规划方法进行对比分析，三维水下环境如图9所示. 如图10所示，IADQN生成的路径平滑度最高，其路径转弯较少，路线更为流畅. 主要原因是IADQN奖励函数中的平滑度奖励机制通过惩罚转弯促使路径更加流畅. 相比之下，DQN方案的路径平滑度较低，原因是该方法侧重于找到可行路径，缺乏对平滑度的优化. A*、RRT和APF生成的路径中存在较多急转弯和不规则曲线，主要原因是这些方法对路径的平滑性关注较少. 如表3所示为不同方法的性能指标对比，其中l为路径长度，S_o为路径平滑度，γ_max为AUV与洋流最大夹角，t_r为运行时间. IADQN在多个关键指标上表现优异. 虽然IADQN的路径略长于DQN，但IADQN保证了AUV与洋流的最大夹角更小，降低了洋流对AUV行进的影响，使AUV能够更加快速地完成任务. 与其他经典方案相比，IADQN在路径长度和时间效率之间表现出更好的协调性. APF由于其自身特点，容易陷入局部最优，导致路径徘徊，生成路径和运行时间均过长；A*在路径长度上接近IADQN，但其运行时间稍长，且在应对洋流时表现不如IADQN；RRT在路径长度上表现良好，但在洋流环境中表现较差. 综上所述，IADQN在复杂三维环境中能够更好地平衡多个指标，提供更优的路径规划方案.

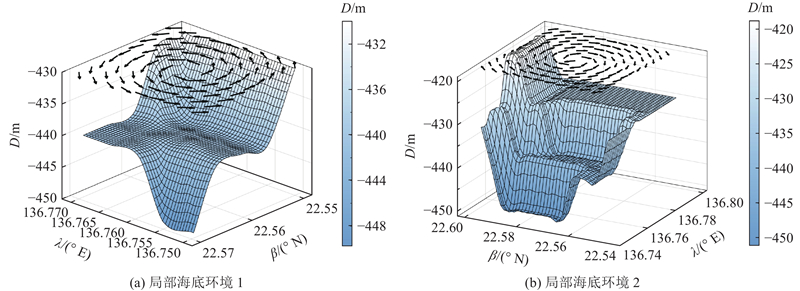
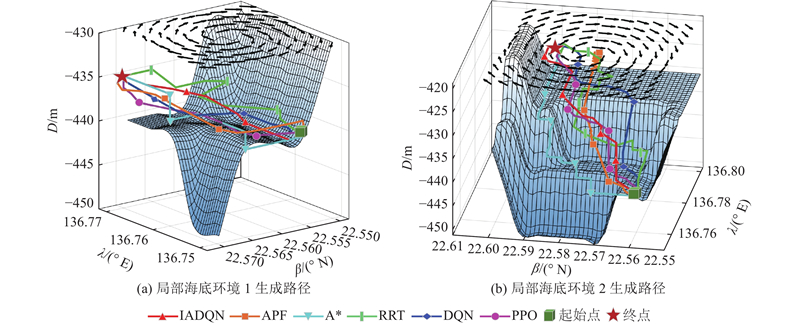
数据采自西太平洋海域136.75° E~136.77° E，22.55° N~22.57° N（局部海底环境1）和136.75° E~136.80° E，22.55° N~22.60° N（局部海底环境2）. 如图11所示，2个区域的三维环境包含如山峰侧面、洋流的复杂特征. 如图12所示，6种路径规划方案都可以在2种不同的未知环境中成功生成无碰撞路径. IADQN引入平滑度奖励机制，有效地避免了路径中的急转弯和不规则曲线，平滑度最高. 如表4所示，DQN在路径长度方面表现较好，由于与洋流的最大夹角较大，导致AUV的运行时间稍长. 在传统路径规划方法（APF、A*、RRT）中，APF虽然能够实时生成运动轨迹，但容易陷入局部最小值，导致未能顺利到达终点，并且路径中存在局部振荡和较长的路径长度；RRT生成的路径较长，且与洋流的夹角较大；A*在路径长度上表现良好，但运行时间较长. 相比之下，PPO在洋流环境下和运行时间上不如IADQN，并且需要与环境进行实时交互. 综合来看，IADQN在路径长度、洋流环境适应性和运行时间上表现出明显优势.

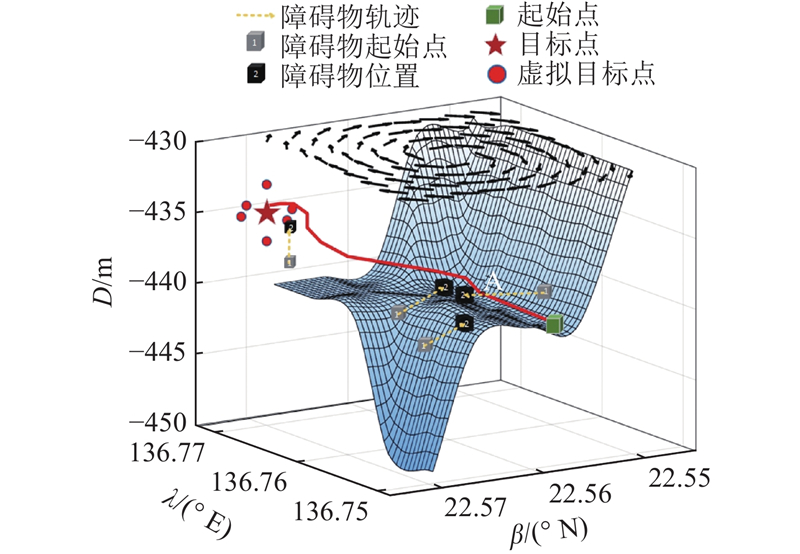
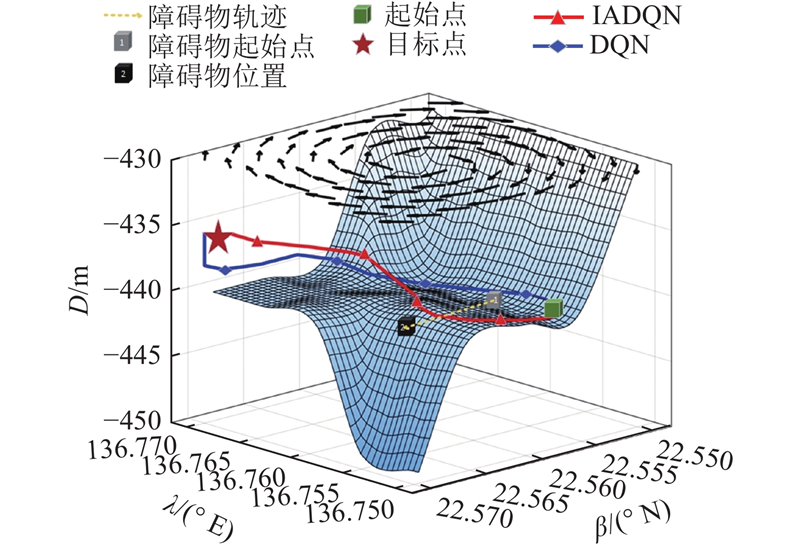
在环境中添加动态障碍物，深色和浅色方块表示动态障碍物不同时刻的位置，虚线箭头表示动态障碍物轨迹. 在IADQN作用下，AUV可以根据附近环境躲避障碍物，AUV的运行轨迹如图13所示. AUV从起点出发，运行到点A时，检测到附近障碍物较多，前进方向改变，随机选择动作前进. 在快到达目标点时，AUV检测到附近有少量障碍物，并且处于局部最小值点，因此选择虚拟子目标点法进行优化.

IADQN和DQN在动态海域环境下生成的路径如图14所示，虚线箭头是动态障碍物运动轨迹. 可以看出，IADQN路径较为平滑，AUV能够顺利避开动态障碍物，路径相对较短. 在接近终点时，IADQN能够很好地调整运动方向，避免与障碍物碰撞，并在洋流的影响下优化最终路径，使AUV快速到达目标.

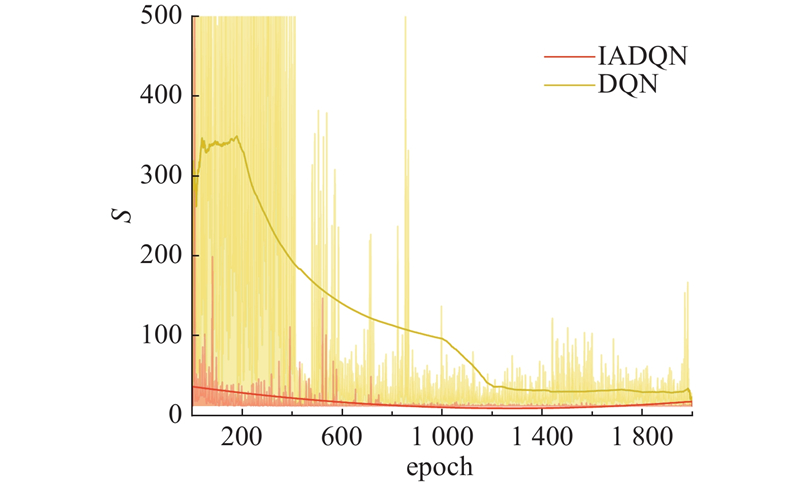
在动态障碍物环境下，IADQN和DQN的收敛情况如图15所示，其中epoch为训练的轮数，S为在每轮中完成任务所需的步数. 由图可知，DQN在训练初期步数多，且波动较大，随着训练的进行，步数逐渐减少，但仍有明显的波动，说明DQN在动态环境中的收敛过程不稳定. 大约在500轮之后，DQN逐渐趋于稳定，但在某些情况下仍有较大的步数波动. 相比之下，IADQN从训练初期开始就表现出较少的步数，且波动幅度显著小于DQN方案，说明IADQN在动态障碍物环境下能够更快速、更稳定地收敛. 该分析结果表明IADQN在处理动态障碍物环境时，能够更有效地找到最优路径，其鲁棒性和适应性均优于传统DQN.

针对未知水下环境中的AUV路径规划问题，本研究提出融合自适应势场法和深度强化学习的三维水下AUV路径规划方法. 构建真实海洋环境模型，海底地形数据从真实数据中获取，为研究提供了环境基础. 将自适应势场法用于辅助深度强化学习，所提路径规划方法综合考虑当前位置的洋流信息和位置特征，有效避免了碰撞，减少了洋流对AUV运动的影响. 设计动态奖励函数，在洋流影响下进行局部避障路径规划. 仿真实验和对比分析结果表明，与其他路径规划方法相比，所提方法不仅在路径长度、路径平滑度和运行时间上优势明显，而且具有更快的收敛速度和更高的成功率，能够更有效地学习环境的动态特性并做出更快速的决策. 未来的工作将致力于利用元强化学习来解决复杂动态洋流环境下的AUV路径规划问题.