四足机器人因其出色的运动能力和较强的地形适应性成为应用前景非常广阔的特种机器人,常被用于探索、搜救和军事领域等,其在具有挑战性的障碍[1]和自然地形中具有巨大的应用潜力,如Minitaur[2]、MIT Cheetah[3]、HYQ[4]和ANYmal[5]等,这些四足机器人在复杂的地形中具有良好的运动稳定性. Raibert于20世纪80年代实现了机器人的步态控制,提出的“弹跳高度-前进速度-机体位姿”三体解耦控制理论[6]实现了腿足式机器人的平衡控制,此后高动态控制策略对四足机器人的发展和应用作出了巨大的贡献,如应用于Atlas[7]的质心动力学(centroidal dynamics, CD)[8]、线性倒立摆模型(linear inverted pendulum model , LIPM)和模型预测控制(model predictive control, MPC)[9-10]等.
动物表现出多模式的行为,而受到生物学启发的机器人可以在具有挑战性的地形中更有效地保持平衡和协调. 朱雅光等[11]的研究发现,基于响应外部信息并实现各种行为的神经架构的机器人[12]在复杂地形上的运动具有卓越的协调控制能力,如四足机器人的鲁棒感知运动[13]、多环境下机器人的自适应控制[14-15]. 作为人与环境交互的工具,具有神经控制器的四足机器人非常必要,该控制器能够响应外部感觉和自我感知信息,实现多步态平滑切换[16]和包括小跑在内的多种运动行为. 作为基本的神经组件,中央模式生成器(central pattern generator, CPG)主要负责为动物生成有节奏的运动,如爬行、跳跃、行走和跑步. 生物启发式的CPG控制已被证明在各种机器人[17-18]中是成功的,包括利用人工神经网络穿越不规则地形的机器人[19]、使用CPG实现滑行步态过渡控制的蛇形机器人[20]及通过CPG控制两足动物运动[21]等.
目前,大多数具有神经控制机制的机器人都将CPG信号与运动模块耦合,很难考虑腿部的独立控制,增大了模型的复杂性. 作为一类受生物启发的神经网络,能够自主、自我调节控制的CPG是四足机器人有节律运动必不可少的. 在复杂多变的环境中,具有简单模型和高调节能力的神经控制机制是必需的.
本文融合CPG和MPC,提出神经网络动力学控制策略,提高机器人运动的响应性和步态的多样性. CPG的作用体现在信号控制精度、行为模式多样性和平滑运动过渡方面,通过各种步态参数生成多种运动行为,使用MPC作为控制器,在不同步态参数下寻求保持机器人平衡的最佳反作用力,提高腿足式机器人的运动稳定性. 基于CPG-MPC控制架构的机器人可以实时实现多种行为,通过实验验证了基于CPG-MPC策略的不同步态模式的性能.
1. 全肘式四足机器人
1.1. 四足机器人样机结构设计
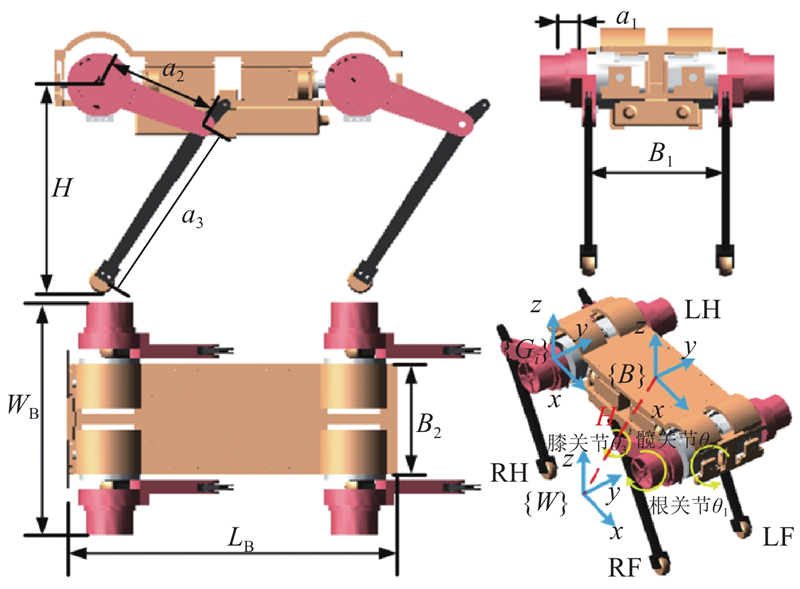
四足机器人的样机如图1所示,该机器人由机身龙骨和腿部结构组成,共有12个自由度. 简化腿部结构,将单腿设计为根关节、髋关节和膝关节,腿部关节配备直流无刷电机进行驱动,实现力矩及位置控制. 为了均衡腿部关节的质量,膝关节和髋关节的驱动电机放置在同轴侧大腿与机身的连接处,膝关节通过连杆完成运动传递. 为了获得关节的转动角度及角速度,关节驱动电机配备了14位编码器. 此外,在质心位置处搭载惯性测量单元,用来获取机身的加速度与姿态角信息. 为了缓解冲击带给机体结构的损坏,增大足端与地面接触的摩擦力,选用圆饼型橡胶作为足端,并且配备有六维力传感器. 四足机器人采用全肘式结构,平衡不均匀受力部位;材料选为铝合金,降低四足机器人在运动过程中产生的惯性力,结构的具体参数如表1所示.
图 1
表 1 四足机器人的结构参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 髋部长度α1/mm | 58 | 机身宽度WB/mm | 420 | |
| 大腿长度α2/mm | 190 | 髋部距离B1/mm | 245 | |
| 小腿长度α3/mm | 330 | 机身宽度B2/mm | 200 | |
| 机身高度H/mm | 350 | 机身质量m/kg | 30.32 | |
| 机身长度LB/mm | 590 | — | — |
1.2. 运动学模型
合理的运动学模型是实现上层控制策略的基础,如图2所示,四足机器人的左后、左前、右后与右前腿依次表示为LH、LF、RH与RF. 定义机身坐标{B}位于机器人质心(center of mass, CoM),设置x轴正方向为机器人的前进方向,z轴正方向垂直于机身平面竖直向上,y轴由右手定则确定. 世界坐标{W}位于机身坐标投影于地面的垂直方向,到机身坐标{B}的距离为H. 为了便于正逆运动学的求解,定义根关节坐标系{Gi}(i=1,2,3,4)位于髋关节与根关节轴线的相交处, 机身坐标系和根关节坐标系的x、y、z指向相同. 由于4条单腿结构的参数相同,建立任意条单腿的D-H模型,根据几何法求得4条腿的运动学方程. 通过计算确定足端相对根关节坐标系{Gi}下的位置为
图 2
式中:si = sin θi, ci = cos θi, sij = sin (θi+θj), cij = cos (θi +θj);λ为左、右腿的符号变量,右腿为λ = −1,左腿为λ = 1.
将机身形心在世界坐标系{W}的位置表示为WPc=[Wx, Wy, Wz]T ,则任意腿足端相对于世界坐标系{W}下的位置表示为
式中:BPfi为足端基于坐标系{B}中的位置描述,
2. 模型预测控制的方法
足式机器人作为欠驱系统,在某一运动方向成为欠驱方向前,为了保证机器人在该方向上具有稳定性,需要提前计算这个方向的足端作用力. 这需要控制器具有一定的预测性,可以提前调整各项状态参数,模型预测控制则成为足式机器人的主流控制策略.
2.1. 单刚体模型的建立
除了提出的世界坐标系{W}和机身坐标系{B},为了描述机器人的惯性张量、足端位置和足端反作用力等其他参数,引入定向机身坐标系{C},坐标系的原点与坐标系{B}的原点重合,方向与坐标系{W}相同,如图3所示为简化后的单刚体模型(SRBD). 图中,足端圆点表示足端与地面的接触点,足端竖直向上的直线是基于坐标系{W}描述的足端反作用力,记作Wfi(i = 1, 2, 3, 4),机器人本体的重力记作G(= mg),虚线描述基于坐标系{B}的足端位置,记作BPfi(i=1, 2, 3, 4),后面描述足端位置参数简写为Pfi,实线描述基于坐标系{W}的足端位置,记作WPfi(i=1, 2, 3, 4). WPc是机器人质心基于坐标系{W}的描述,后面质心位置参数简写为Pc.
图 3
在刚体动力学模型(SRBD)中,足端反馈力U作为输出直接施加于机器人,控制机器人的位置和姿态. 根据牛顿-欧拉运动定律,可以得到机身平动和转动的关系式,即
式中:I为基于坐标系{B}的惯性张量,ω为机器人的角速度,Pfi×定义为足端位置矢量的叉乘形式.将近似后的状态量之间的映射关系进行整合,可得机器人的状态空间表达式,即整理式(3),可得刚体动力学模型的连续状态空间表达式:
式中:
为了简化研究对象,将刚体动力学模型的状态空间表达式离散化,即用△t表示模型预测控制的周期,采用前向欧拉法对连续状态空间表达式离散化,则
式中:Ak=I+△t·Ac, Bk=△t·Bc, k = 0, 1, 2,···.
2.2. 足端力的优化求解
根据模型预测控制原理,将求解反作用力U视为求解k个预测时域最优控制量的模型预测控制问题,表达式如下:
式中:X(i+1)为前i+1个预测时域的状态量;U(i+1)为前i+1个预测时域的控制量,Ui,m为第i次预测的控制量的第m个元素;X0和Xref分别为初始状态量和参考状态量;Q(i+1)和R(i+1)分别为前i+1个预测时域的状态权重矩阵和能耗权重矩阵;
其中Ai和Bi分别为第i次预测的状态矩阵和控制矩阵;cmin和cmax为足端力的上、下限. 整理式(6),可得二次规划的标准形式:
优化问题(7)是二次规划问题,可以通过优化求解器来解决,如qpOASES. 在求解方程后,通过转矩映射将控制矢量U施加于机器人,即τ1=JTU. SRBD模型使用了忽略腿部惯性的假设,该假设适用于准静态运动. 若腿部与机身的质量比非常大,则施加于腿部的力矩在动力学中起着重要作用. 为了尽可能减少机器人腿部惯性的影响,增加了惯性补偿力矩,即
式中:Ml为腿的惯性矩阵,
3. 运动神经控制系统
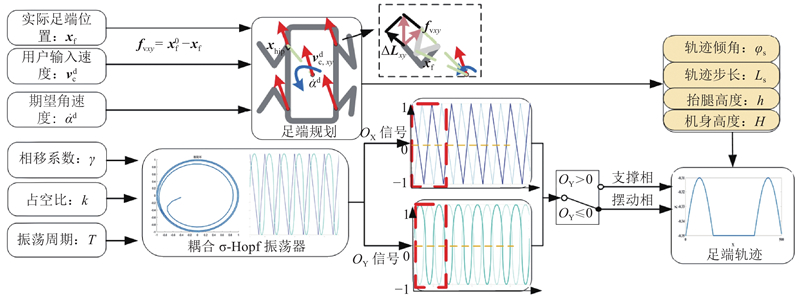
运动神经控制系统主要由中枢神经网络和落足点规划模块组成,是控制系统的规划层. 腿足式机器人的步态生成和步态模式的切换主要依赖可靠的节律信号,该信号由中枢神经网络产生. 落足点模块根据机器人的运动状态和环境信息求解适当的足端位置,使得机器人在复杂环境中不仅可以实现多种稳定行为,还能够及时调整位置和姿态,以躲避和跨越各种障碍物.
3.1. 中枢模式发生器
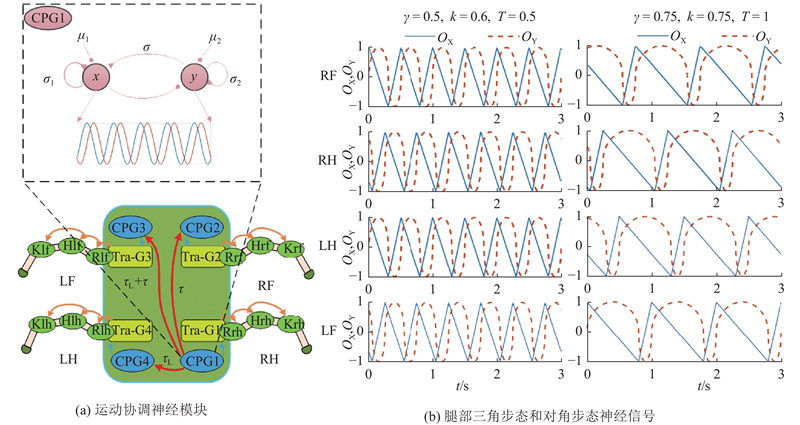
基于神经架构的机器人能够对外部信息作出响应并实现各种复杂的运动行为[22],因此CPG被广泛应用于机器人运动控制. 考虑到强耦合、控制复杂及传统CPG模型难以控制机器人足端轨迹的问题,通过改进的σ-Hopf谐振子来控制四足机器人运动时的占地系数、运动频率与相位差,其公式表示为
式中:OX和OY为步态信号,r为极限环半径,μ为振幅,μ1和μ2为外反馈,占地因子k用来控制单腿摆动相和支撑相之间的时间比率,相位调节因子γ实现机器人的步态切换,周期T控制机器人的运动周期.
图 4
3.2. 落足点规划
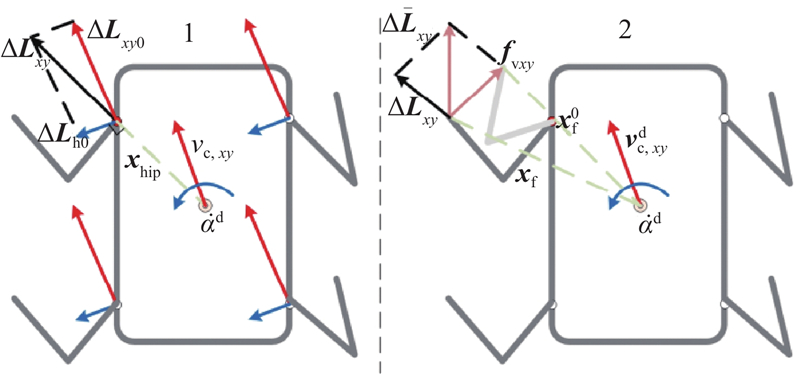
腿的摆动主要是为了足端达到期望的落足点位置,间接地控制机器人躯干的位姿和速度,保证机身的稳定性. 良好的足端轨迹可以减小足端落地时对地面的冲击力,提高腿部适应复杂地形的能力. 在设计足端的摆动轨迹时,需要重点考虑期望落足点、步长和抬腿高度等. 机器人期望的线速度和角速度参数由用户输入,其中横向速度
图 5
式中:fsw为摆动相的频率. 航向角速度
式中:xhip为坐标系{G}在坐标系{B}中的位置描述.
对“线速度-位移”向量ΔLxy0和“角速度-位移”向量ΔLh0矢量求和,可以得到“速度-位移”矢量ΔLxy,即
为了足端摆动相的起始点尽可能接近期望位置并减少位移误差累积,计算虚拟起始点与当前实际起始点的差值,即
式中:
通过
式中:
图 6
图 7
式中:Kp和Kd分别为摆动腿的刚度和阻尼系数,θ和
4. 基于MPC-CPG的神经控制系统
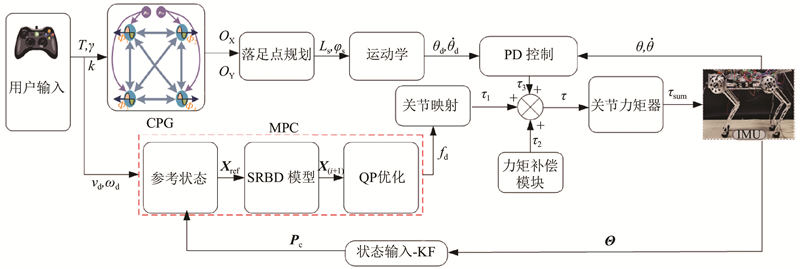
机器人的控制系统可以简化为运动规划和运动控制2部分. 完善控制系统使机器人拥有智能性和对复杂环境的适应性已成为四足机器人研究的重要组成部分,而融合神经网络的四足机器人逐渐拥有了感知地形和路线自主规划的能力. 设计的四足机器人的神经控制器如图8所示. 控制框架主要由4个部分组成:步态机(CPG)、状态估计器、模型预测控制器(MPC)和参考轨迹生成器. 步态机采用σ-Hopf振荡器,主要的控制参数是相移系数γ、振荡频率ε(=1/T)和占空比k,参考轨迹生成器用于生成预测时域的机身状态信息Xref. 落足点规划模块主要根据机器人当前的位置信息和期望信息生成步长Ls和轨迹平面倾角φs,结合CPG信号规划足端的期望位置Pf,d. 运动学模块将期望足端位置Pf,d转换成期望关节转角θd,与实际的关节转角一起组成基于关节空间的PD控制器. 模型预测控制器主要负责根据建立的单刚体模型完成控制量的优化,控制器根据约束目标、约束方程及对应的权重系数计算得到合理的足端反力U;除此之外,控制器内还包含腿惯性补偿模块,提高控制器的精度,使机器人更加精确地完成期望动作. 状态估计器是根据卡尔曼滤波原理并结合惯性测量单元向上位机反馈信息,估计机器人实际的位置和角度.
图 8
5. 仿真和实验
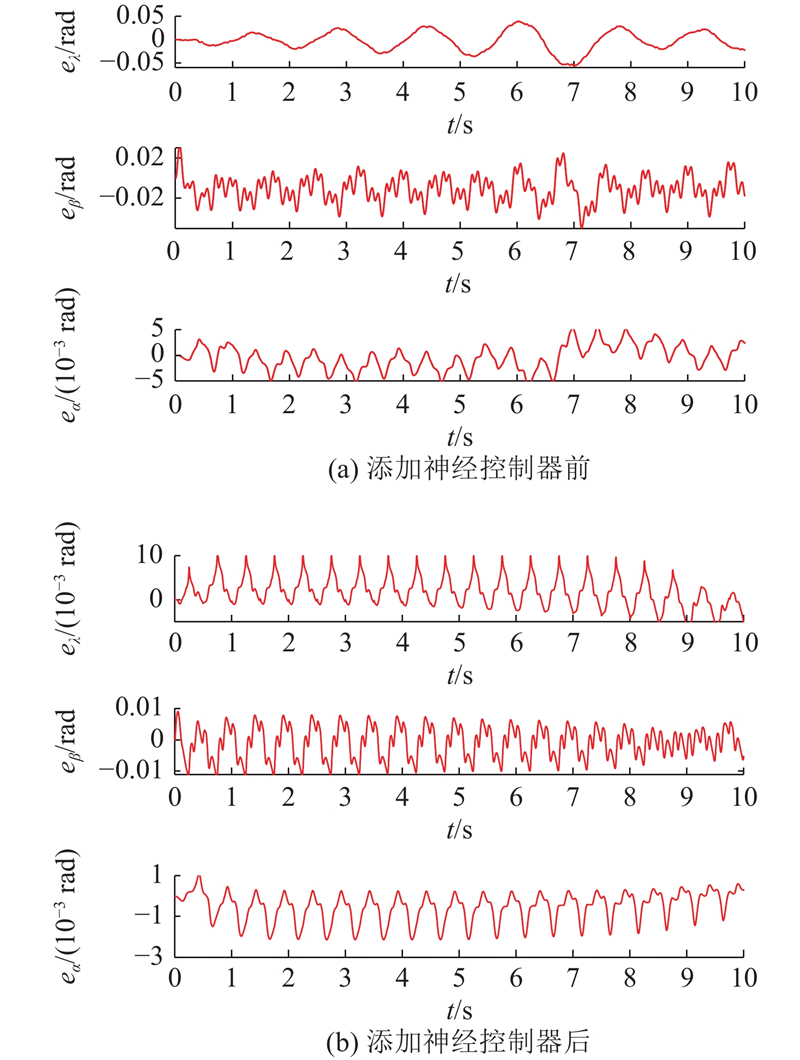
为了验证神经控制器的有效性,通过仿真和实验平台进行多种实验. 其中仿真平台完成神经控制器的对比实验,机器人位置跟踪、全向运动和多步态运动实验在实验平台上完成.
5.1. 仿真测试
图 9
图 10
图 11
图 12
图 13
5.2. 实验验证
图 14
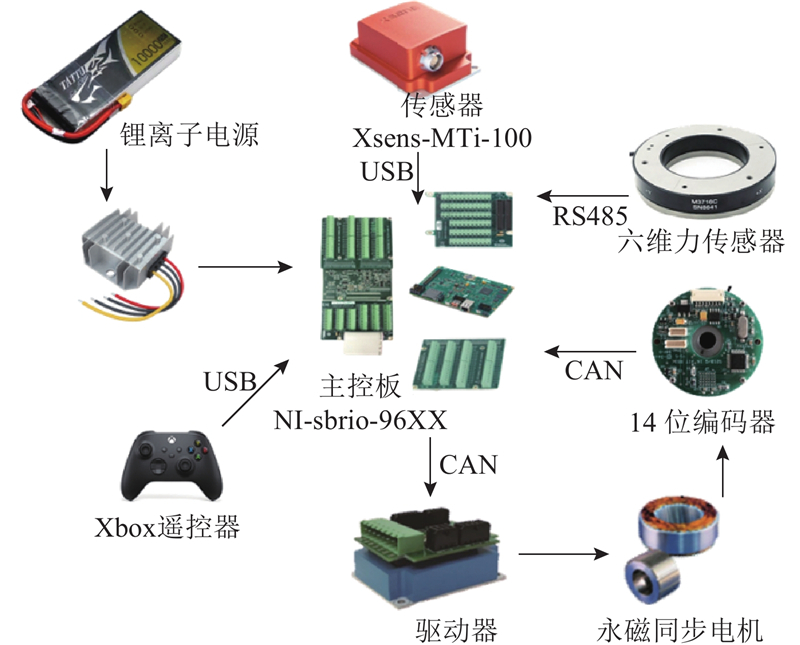
机器人的硬件控制模块包括电机、驱动器和传感器等. 位姿传感器负责获取机器人的位置和姿态信息,力传感器检测足端力,编码器检测关节电机转动的角度,用户通过遥控器向上位机NI-sbRIO发送命令,其板载有RS-232接口、RS-485接口、CAN接口、USB接口和以太网网口等,实现了上位机和位姿传感器、遥控器、驱动器和编码器之前的数据通信. NI-sbRIO主控制器处理器型号为Xilinx Zynq-7xxx,为双核异构处理器,其中ARM核为Cortex-A9架构,主频高达667 MHz,用于准确、高效地运行CPG-MPC控制算法.
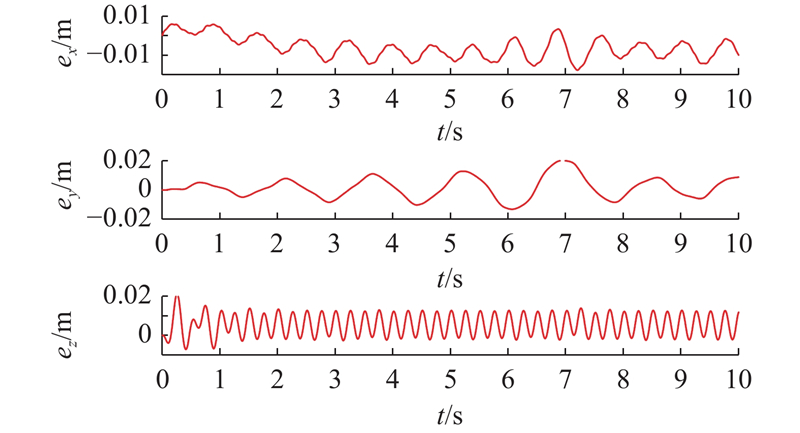
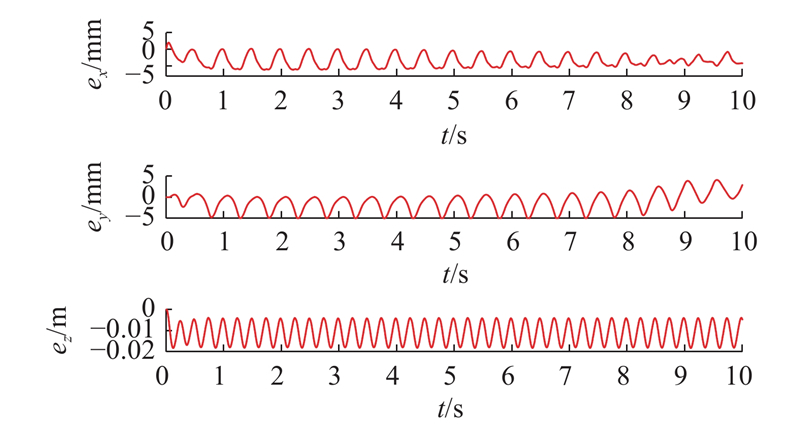
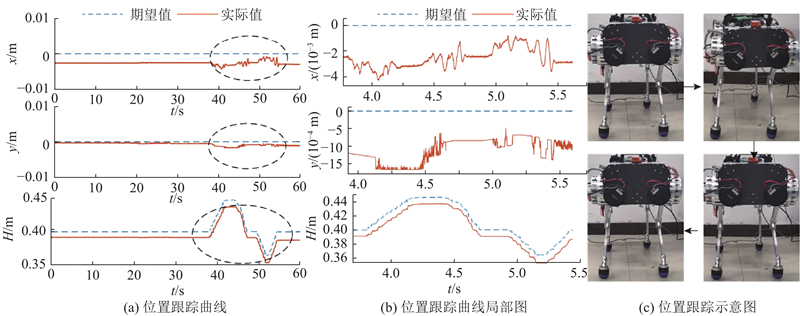
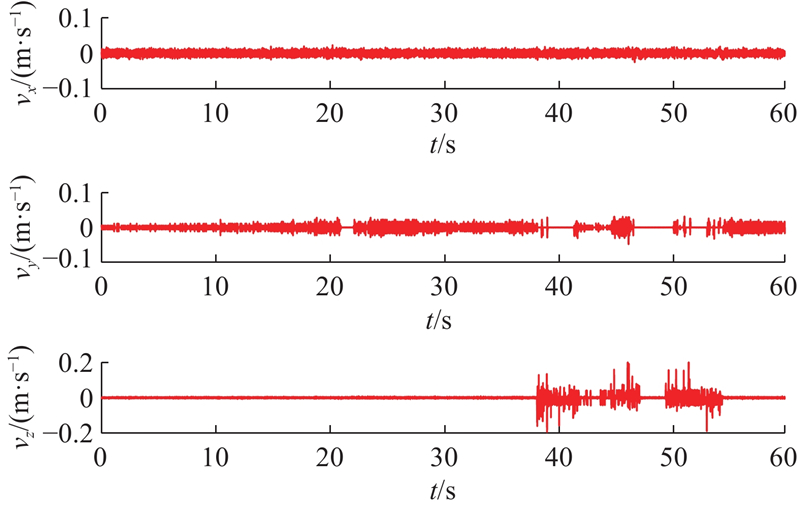
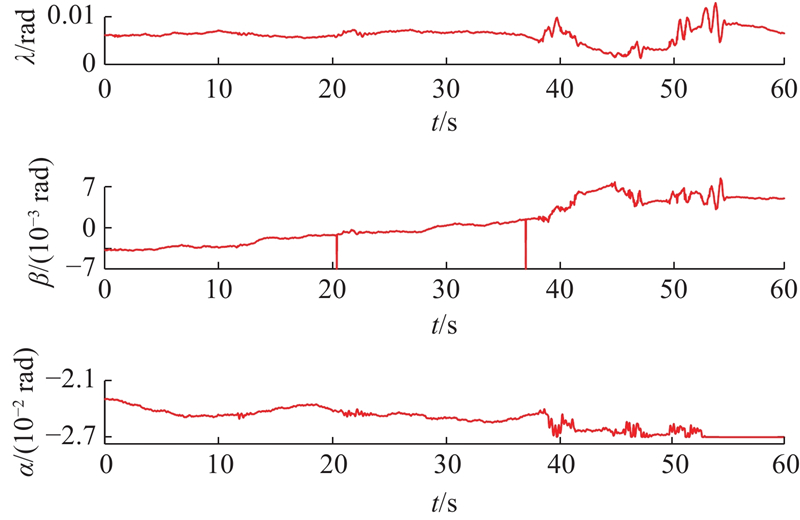
5.2.1. 位置跟踪实验
图 15
图 16
图 17
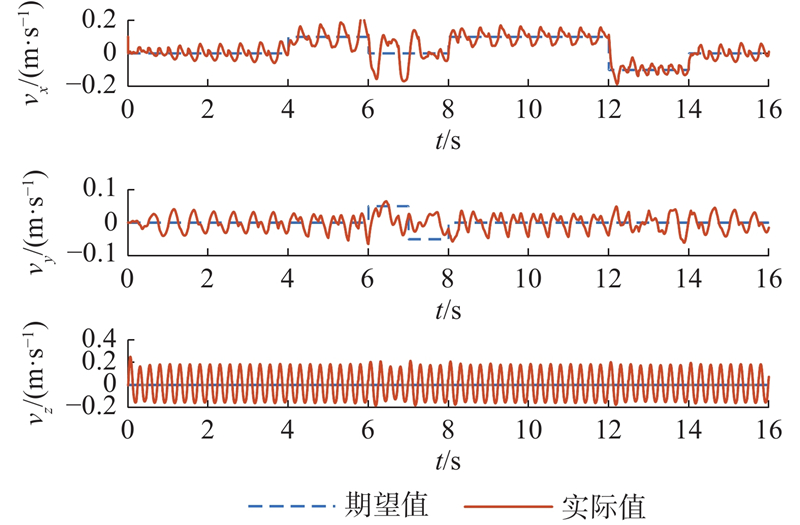
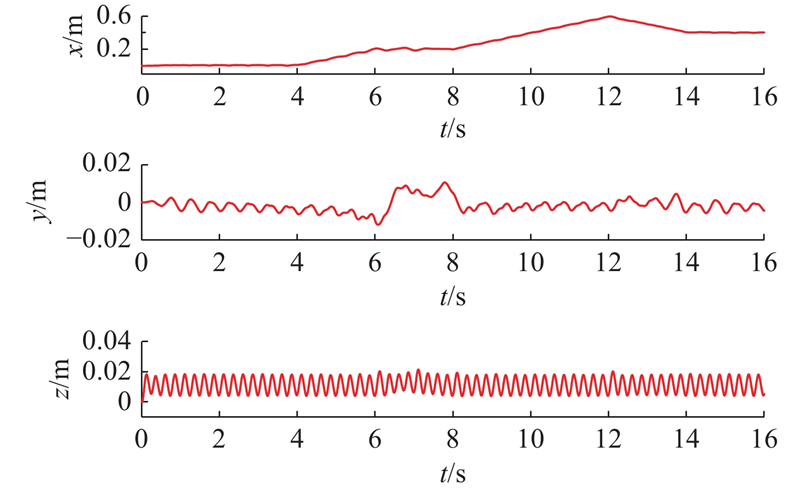
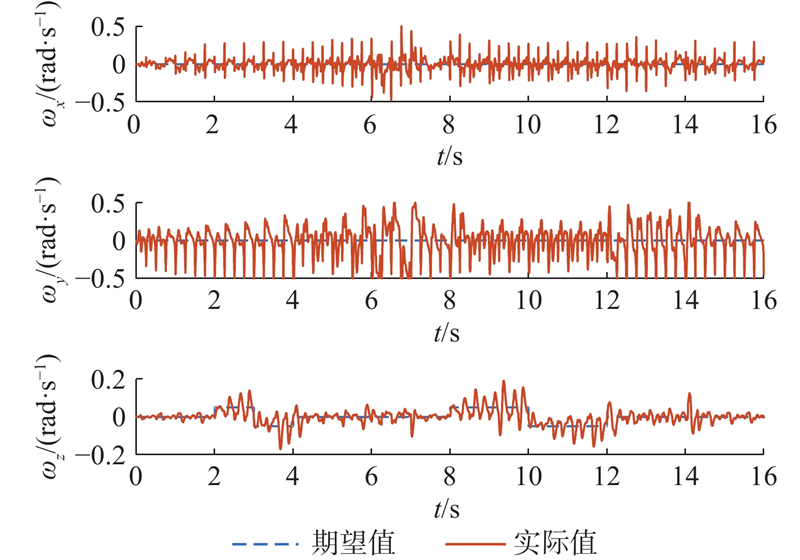
5.2.2. 全向运动实验
图 18
图 19
图 20
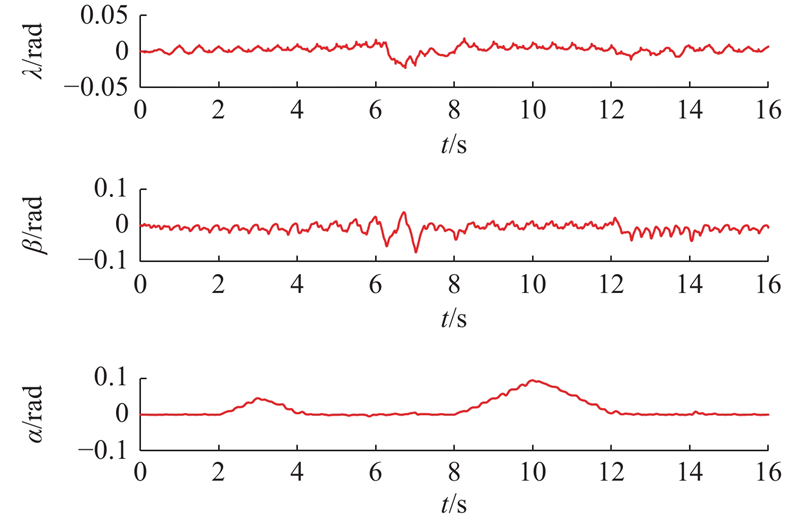
图 20 全向运动的姿态角速度曲线
Fig.20 Attitude angular velocity curve of omnidirectional motion
图 21
图 22
5.2.3. 多步态稳定性实验
为了测试和总结基于模型预测原理的神经控制器对多种常规和特殊步态的响应性以及运动参数对机器人稳定性的影响,开展30组实验,其中γ取0.50、0.55、0.60、0.65、0.70、0.75,k取0.75、0.76、0.78、0.80、0.82.
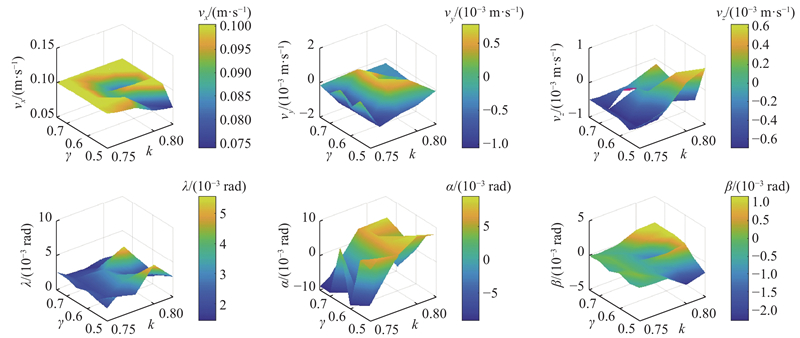
如图23所示为不同γ和k所对应的机器人质心速度和姿态角示意图. 图中,不同的颜色区域表示不同的数值,在图23的区域颜色变浅的过程中,区域代表的数值在递增. 机身高度方向速度vz相对于vx和vy比较稳定,最大值出现在k =0.80~0.82和0.76~0.78处,约为±0.000 6 m/s. 翻滚角为0.001~0.006 rad,最大值出现在k = 0.8附近. 偏航角的最大值出现在右下角,约为−0.002 rad,当k = 0.75~0.78时,机器人的实际偏航角接近0. 从图23可以看出,随着γ的增加和k的减小,vx接近期望速度0.1 m/s,vy和vz接近0,姿态角的实际值也接近0,即当足端下落时,对地面的冲击减小,同时有更多足端接触地面,机器人的速度和角度参数更接近期望值,这意味着机器人平地前行时的状态更稳定.
图 23
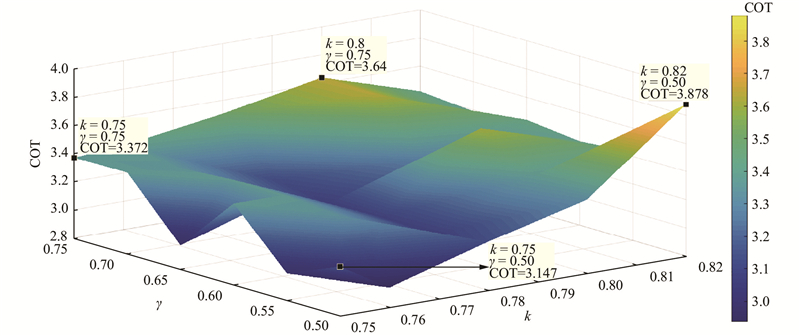
为了更加直观地探究机器人的运动状态对稳定性的影响,引入能耗参数(cost of transport,COT)评价指标,如图24所示为k和γ的COT. 可以看出,COT值在3.0~4.0的范围内波动,随着k的增加,足端触地时加剧了对地面的冲击,导致机器人的COT参数增大. 当k = 0.82,γ = 0.5时,COT最大,约为3.878. 当k = 0.8且γ = 0.75时,结合图23可知,此时质心沿z方向的速度和偏航角偏离期望值较大,所以COT增长至3.64. 总体分析可知,当机器人的k从0.5变化到0.75且γ从0.82下降到0.75,机器人以接近0.1 m/s的速度前进时,COT从3.878逐渐下降到3.372,机器人以更低的能耗率完成工作,这意味着机器人的状态更加稳定.
图 24
6. 结 语
为了提高四足机器人的环境自适应性和行为多样性,本文设计融合CPG和MPC的神经控制器. 通过实验验证了利用提出方法可以实现机器人位置的跟踪调整,完成全向复合运动,同时可以根据工况及时调整机器人运动步态,达到降低机器人的COT,实现稳定运动的目的. 在所提方法的基础上,可以针对融合机器人复杂时变非线性动力学模型与中枢模式发生器开展进一步的研究,提高控制精度和强扰动情况下的机器人自适应调整能力.
参考文献
Jumping over obstacles with MIT Cheetah 2
[J].DOI:10.1016/j.robot.2020.103703 [本文引用: 1]
Vertical hopper compositions for preflexive and feedback-stabilized quadrupedal bounding, pacing, pronking, and trotting
[J].DOI:10.1177/0278364918779874 [本文引用: 1]
Design of HyQ: a hydraulically and electrically actuated quadruped robot
[J].DOI:10.1177/0959651811402275 [本文引用: 1]
Pronto: a multi-sensor state estimator for legged robots in real-world scenarios
[J].DOI:10.3389/frobt.2020.00068 [本文引用: 1]
Efficient multicontact pattern generation with sequential convex approximations of the centroidal dynamics
[J].DOI:10.1109/TRO.2020.3048125 [本文引用: 1]
基于虚拟运动神经网络的六足机器人行为控制
[J].
Behavior control of hexapod robot based on virtual motoneuron network
[J].
Neural control of robot manipulators with trajectory tracking constraints and input saturation
[J].
Learning robust perceptive locomotion for quadrupedal robots in the wild
[J].DOI:10.1126/scirobotics.abk2822 [本文引用: 1]
Unknown payload adaptive control for quadruped locomotion with proprioceptive linear legs
[J].DOI:10.1109/TMECH.2022.3170548 [本文引用: 1]
Multi-environment robotic transitions through adaptive morphogenesis
[J].DOI:10.1038/s41586-022-05188-w [本文引用: 1]
Sprawling quadruped robot driven by decentralized control with cross-coupled sensory feedback between legs and trunk
[J].
Combining reflexes and external sensory information in a neuromusculoskeletal model to control a quadruped robot
[J].
Goal-directed CPG-based control for tensegrity spines with many degrees of freedom traversing irregular terrain
[J].DOI:10.1089/soro.2015.0012 [本文引用: 1]
Towards autonomous locomotion: CPG-based control of smooth 3D slithering gait transition of a snake-like robot
[J].DOI:10.1088/1748-3190/aa644c [本文引用: 1]
Biped locomotion control through a biomimetic CPG-based controller
[J].DOI:10.1007/s10846-016-0407-3 [本文引用: 1]
Trajectory optimization for wheeled-legged quadrupedal robots driving in challenging terrain
[J].DOI:10.1109/LRA.2020.2990720 [本文引用: 1]
A simple yet effective whole-body locomotion framework for quadruped robots
[J].DOI:10.3389/frobt.2020.528473 [本文引用: 1]