移动机器人技术的应用已从制造业和仓储物流拓展到医疗保健、环境监测和家庭服务等领域^[1]. 移动机器人可以适应人类不能胜任的危险多变的动态作业环境^[2-3]. 国际机器人联合会（International Federation of Robotics，IFR）报告显示，到2021年，用于运输、医疗或酒店等各种应用的移动机器人市场已增长37%^[4].

作为移动机器人自主导航的一个关键模块，速度规划负责生成给定路径的最优速度分布^[5]. 其中，最优性体现在车辆运动学、初始及终止条件和贴近运动限制极限方面^[6]. 目前，常用的速度规划方法可以分为基于传统方法改进的速度规划方法和基于优化的速度规划方法两大类. 对传统方法的改进包括对时间弹性带方法^[7]、滑动窗口法^[8]、启发式方法^[9]、插值法^[10]及微分方程法^[11]等的改进. 基于传统方法改进的速度规划方法大多只提供可行的控制运动，难以贴近运动限制极限达到最优速度，无法处理恶劣的场景. 这种限制导致了基于优化的速度规划方法的发展. 这些方法将速度规划表述为优化问题^[12-16]，通过优化器进行求解.

基于优化的速度规划方法虽然在解决贴近运动限制极限的问题上取得显著进展，但大多数现有方法仍存在一些不足. 一方面，大部分基于优化的速度规划方法通常忽略了加加速度约束，这在实际机器人应用中可能引发问题. 加加速度约束是车辆动力学的关键性质之一，它限制了机器人在短时间内改变速度的能力，对于确保稳定和安全的运动至关重要. 另一方面，部分基于优化的速度规划方法未充分考虑车轮物理约束对机器人运动的影响. 车轮电机对下发速度指令的跟踪能力会影响机器人跟踪路径的精度.

基于上述考虑以及移动机器人在实际运动中受到非完整约束的影响，本文提出兼顾运动效率与执行器跟踪性能的移动机器人通用速度规划方案. 该方案将原始速度规划任务视为具有精确表述的机器人运动学和严格描述的多阶状态约束条件的最小时间最优控制问题. 其中没有特别处理速度切换点，一旦运动学约束和多阶状态约束得到充分满足，何时加速/减速或如何避免状态超限的策略将由优化过程自动确定. 在根据可达性分析通过线性规划递推出初始解的基础上，采用约束松弛方法与内点法相结合的同步迭代优化算法，求解最优控制问题. 通过仿真实验，验证该算法的适用性和有效性.

当研究最优速度规划问题时，假定移动机器人的几何路径由上层路径规划器生成，几何路径以笛卡尔空间中带有路径参数$s$的曲线${\boldsymbol{p}}\left( s \right)$表示. 将原本的速度规划任务转化为最小时间最优控制问题.

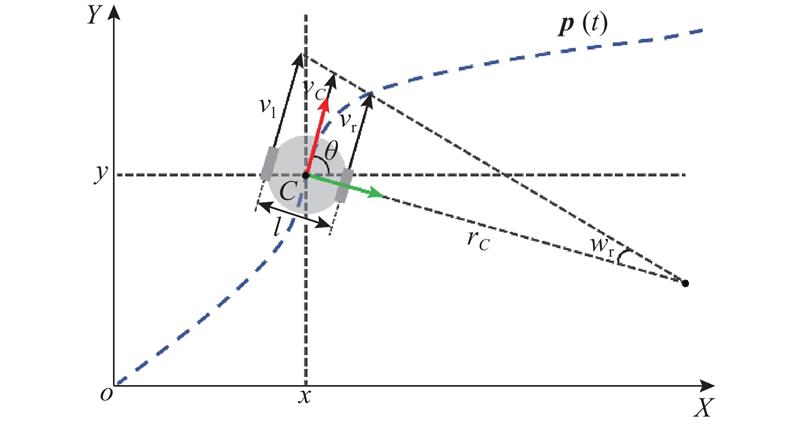
双轮差分驱动机器人是典型的具有非完整约束的欠驱动系统，运动模型如图1所示.

图1中，$ {\boldsymbol{p}}(t) = {\left[ {x(t),y(t)} \right]^{\mathrm{T}}} $为笛卡尔空间中给定的几何路径，$\left( {x,\;y} \right)$为机器人质心$C$在二维空间中的位置信息，$\theta $为速度方向即当前运动方向与$X$轴正方向的夹角，$l$为两轮的轴距，${r_C}$ 为机器人质心的转弯半径，$\left( {{v_C},{\omega_C}} \right)$分别为机器人质心的线速度和角速度，$\left( {{v_{\text{l}}},{v_{\text{r}}}} \right)$分别为左、右驱动轮的线速度. 车轮线速度与机器人质心的速度关系为

(1)$ \left[ \begin{gathered} {v_C} \\ {\omega_C} \\ \end{gathered} \right] = {\boldsymbol{J}}\left[ \begin{gathered} {v_{\text{r}}} \\ {v_{\text{l}}} \\ \end{gathered} \right] = \left[ \begin{gathered} \begin{array}{*{20}{c}} 0.5&0.5\end{array} \\ \begin{array}{*{20}{c}} {{l^{-1}}}&{ - {l^{-1}}} \end{array} \\ \end{gathered} \right]\left[ \begin{gathered} {v_{\text{r}}} \\ {v_{\text{l}}} \\ \end{gathered} \right]. $

式中：

$ \left[ \begin{gathered} {v_C} \\ {\omega_C} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\sqrt {{{\dot x}^2}+{{\dot y}^2}} } \\ {{{(\ddot x\dot y - \dot x\ddot y)}}{{{{\left( {{{\dot x}^2}+{{\dot y}^2}} \right)}^{-{3}/{2}}}}}} \end{array}} \right]. $

其中，${\dot{\square }} $定义为$\square $相对于时间$t$的导数. 通过引入关于时间单调递增的路径参数$s:\left[ {0,T} \right] \to \left[ {0,} \right.$$\left. {{s_{\rm{end}}}} \right]$，给定路径${\boldsymbol{p}}$在时域和$s$域的变换关系为${\boldsymbol{p}}{\left( t \right)_{t \in \left[ {0,\;T} \right]}} \to {\boldsymbol{p}}{(s)_{s \in \left[ {0,\;{s_{{\mathrm{end}}}}} \right]}}$，其中$T$为移动机器人运动至给定路径终点的终止时刻^[5]. 将$ \dot x = x'\dot s $、$ \dot y = y'\dot s $代入式(1)，可以得到关于路径参数$s$的车轮速度：

(2)$ {{\boldsymbol{J}}\left[ \begin{gathered} {v_{\text{r}}} \\ {v_{\text{l}}} \\ \end{gathered} \right] = {\boldsymbol{a}}\left( s \right) \dot s,} \quad {{\boldsymbol{a}}\left( s \right) = \left[ \begin{gathered} \sqrt {{{ {x'} }^2}+{{{y'}}^2}} \\ {{\left(x''y' - x'y''\right)}{\left({{{ {x'} }^2}+{{ {y'} }^2}}\right)^{-1}}} \end{gathered} \right].} $

式中：$ \square^{\prime } $定义为$ \square $相对于路径参数$s$的导数. 通过对式(2)的连续求导，分别得到车轮关于路径参数$s$的加速度和加加速度：

(3)$\left.\begin{aligned} &{\boldsymbol{J}}\left[ {\begin{array}{*{20}{l}}{{{\dot v}_{\rm{r}}}}\\{{{\dot v}_1}}\end{array}} \right] = {\boldsymbol{b}}(s){{\dot s}^2} + {\boldsymbol{a}}(s)\ddot s,\\& {\boldsymbol{b}}(s) = \left[\begin{aligned} & {{({x^\prime }{x^{\prime \prime }} + {y^\prime }{y^{\prime \prime }})}}{{ {({{ {{x'^2 }} }} + {{ {{y'^2}}}})^{-1/2}} }}\\&{{\left[ {\left( {{x^{\prime \prime \prime }}{y^\prime } - {x^\prime }{y^{\prime \prime \prime }}} \right)\left( {{{x'}^2} + {{y'}^2}} \right) - 2\left( {{x^\prime }{x^{\prime \prime }} + {y^\prime }{y^{\prime \prime }}} \right)\left( {{x^{\prime \prime }}{y^\prime } - {x^\prime }{y^{\prime \prime }}} \right)} \right]}}{{{{\left( {{{x'}^2} + {{y'}^2}} \right)}^{ - 2}}}}\end{aligned} \right].\end{aligned}\right\} $

(4)$\left. \begin{aligned} & {{\boldsymbol{J}}\left[ \begin{gathered} {{\ddot v}_{\text{r}}} \\ {{\ddot v}_{\text{l}}} \\ \end{gathered} \right] = {\boldsymbol{c}}\left( s \right) {{\dot s}^3}+3 {\boldsymbol{b}}\left( s \right) \dot s \ddot s+{\boldsymbol{a}}\left( s \right) \dddot s,} \\ & {{\boldsymbol{c}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{{\left[\left( {{{{x''} }^2}+x'x'''+{{{y''} }^2}+y'y'''} \right) \left( {{{{x'} }^2}+{{{y'} }^2}} \right) - {{\left( {x'x''+y'y''} \right)}^2}\right]}}{{{{\left( {{{{x'} }^2}+{{{y'} }^2}} \right)}^{-{3}/{2}}}}}} \\ \left\{{{\left[ {\left( {{x^{\left( 4 \right)}}y'+x'''y'' - x''y''' - x'{y^{\left( 4 \right)}}} \right) \left( {{{{x'} }^2}+{{{y'} }^2}} \right){{ - 2}} \left( {{{{x''} }^2}+x'x'''+{{{y''} }^2}+y'y'''} \right) \left( {x''y' - x'y''} \right)} \right] }}\right. \times \\ \left.{{\left( {{{{x'} }^2} + {{{y'} }^2}} \right) - {\text{4}} \left[ {\left( {x'''y' - x'y'''} \right) \left( {{{{x'} }^2} + {{{y'} }^2}} \right) - 2 \left( {x'x'' + y'y''} \right) \left( {x''y' - x'y''} \right)} \right] \left( {x'x'' + y'y''} \right)}}\right\} \times {{{{\left( {{{{x'} }^2} + {{{y'} }^2}} \right)}^{{-3}/{2}}}}} \end{array}} \right]} .\end{aligned} \right\}$

移动机器人的运动规划主要包含3种约束条件：每一时刻的状态边界约束、相邻时刻的状态转移约束及起止时刻的状态点约束. 将这3种约束统一纳入约束生成器中，并在优化过程中输出到求解器中.

移动机器人的状态边界约束表现为车轮上运动学性能的物理极限及车体上运动学性能的规则极限. 车轮速度约束为

(5a)$ \left[ {\begin{array}{*{20}{c}} {{v_{{\text{r}},\min }}} \\ {{v_{{\text{l}},\min }}} \end{array}} \right] \leqslant {{\boldsymbol{J}}^{ - 1}} {\boldsymbol{a}}\left( s \right) \dot s \leqslant \left[ {\begin{array}{*{20}{c}} {{v_{{\text{r}},\max}}} \\ {{v_{{\text{l}},\max }}} \end{array}} \right]. $

式中：$ \left( {{v_{{\text{l}},\min }},{v_{{\text{r}},\min }},{v_{{\text{l}},\max }},{v_{{\text{r}},\max}}} \right) $分别为左、右车轮的速度边界约束.

车轮加速度约束为

(5b)$ \left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{\text{r}},\min }}} \\ {{{\dot v}_{{\text{l}},\min }}} \end{array}} \right] \leqslant {{\boldsymbol{J}}^{ - 1}} \left( {{\boldsymbol{b}}\left( s \right) {{\dot s}^2}+{\boldsymbol{a}}\left( s \right) \ddot s} \right) \leqslant \left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{\text{r}},\max}}} \\ {{{\dot v}_{{\text{l}},\max }}} \end{array}} \right]. $

式中：$ \left( {{{\dot v}_{{\text{l}},\min }},{{\dot v}_{{\text{r}},\min }},{{\dot v}_{{\text{l}},\max }},{{\dot v}_{{\text{r}},\max}}} \right) $分别为左、右车轮的加速度边界约束.

车轮加加速度约束为

(5c)$\begin{split} \left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{\text{r}},\min }}} \\ {{{\ddot v}_{{\mathrm{l}},\min }}} \end{array}} \right] & \leqslant {{\boldsymbol{J}}^{ - 1}} \left( {{\boldsymbol{c}}\left( s \right) {{\dot s}^3}+3 {\boldsymbol{b}}\left( s \right) \dot s\ddot s+{\boldsymbol{a}}\left( s \right) \dddot s} \right)\leqslant \\& \left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{\text{r}},\max}}} \\ {{{\ddot v}_{{\text{l}},\max }}} \end{array}} \right]. \end{split} $

式中：$ \left( {{{\ddot v}_{{\text{l}},\min }},{{\ddot v}_{{\text{r}},\min }},{{\ddot v}_{{\text{l}},\max }},{{\ddot v}_{{\text{r}},\max}}} \right) $分别为左、右车轮的加加速度边界约束.

车体速度约束为

(5d)$ \left[ {\begin{array}{*{20}{c}} {{v_{{C},\min }}} \\ {{\omega_{{C},\min }}} \end{array}} \right] \leqslant {\boldsymbol{a}}\left( s \right) \dot s \leqslant \left[ {\begin{array}{*{20}{c}} {{v_{{C},\max}}} \\ {{\omega_{{C},\max }}} \end{array}} \right]. $

式中：$\left( {{v_{{C},\min }},{\omega_{{C},\min }},{v_{{C},\max}},{\omega_{{C},\max }}} \right)$分别为车体速度的边界约束.

车体加速度约束为

(5e)$ \left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{C},\min }}} \\ {{{\dot \omega}_{{C},\min }}} \end{array}} \right] \leqslant {\boldsymbol{b}}\left( s \right) {\dot s^2}+{\boldsymbol{a}}\left( s \right) \ddot s \leqslant \left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{C},\max}}} \\ {{{\dot \omega}_{{C},\max }}} \end{array}} \right]. $

式中：$ \left( {{{\dot v}_{{C},\min }},{{\dot \omega}_{{C},\min }},{{\dot v}_{{C},\max}},{{\dot \omega}_{{C},\max }}} \right) $分别为车体加速度的边界约束.

车体加加速度约束为

(5f)$ \left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{C},\min }}} \\ {{{\ddot \omega}_{{C},\min }}} \end{array}} \right] \leqslant {\boldsymbol{c}}\left( s \right) {\dot s^3}+3 {\boldsymbol{b}}\left( s \right) \dot s\ddot s+{\boldsymbol{a}}\left( s \right) \dddot s \leqslant \left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{C},\max}}} \\ {{{\ddot \omega}_{{C},\max }}} \end{array}} \right]. $

式中：$ \left( {{{\ddot v}_{{C},\min }},{{\ddot \omega}_{{C},\min }},{{\ddot v}_{{C},\max}},{{\ddot \omega}_{{C},\max }}} \right) $分别为车体加加速度的边界约束.

式(5a)~(5f)表明，机器人运动受限于能量资源与物理机构. 车轮上的加加速度约束用来削弱电机的残余振动，车体上的加加速度约束用来保证机器人运动过程平稳光滑.

由于驱动轮与地面接触运动为纯滚动无滑动，差分移动机器人的运动学模型为

(6)$ \frac{{\mathrm{d}}}{{{\mathrm{d}}t}}\left[ {\begin{array}{*{20}{c}} {x\left( t \right)} \\ {y\left( t \right)} \\ {\theta \left( t \right)} \\ {{v_{C}}\left( t \right)} \\ {{\omega_{C}}\left( t \right)} \\ {{a_{C}}\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{v_{C}}\left( t \right)\cos \;\theta \left( t \right)} \\ {{v_{C}}\left( t \right)\sin \;\theta \left( t \right)} \\ {{\omega_{C}}\left( t \right)} \\ {{a_{{v_{C}}}}\left( t \right)} \\ {{a_{{\omega_{C}}}}\left( t \right)} \\ {{j_{C}}\left( t \right)} \end{array}} \right]. $

式中：${a_{C}}$为机器人质心的总加速度，$ {j_{C}} $为机器人质心的总加加速度，${a_{{v_{C}}}}、{a_{{\omega_{C}}}}$分别为质心的线加速度和角加速度. 通过路径参数$s:\left[ {0,T} \right] \to \left[ {0,} \right.$$\left. {{s_{{\mathrm{end}}}}} \right]$，式(6)被转移到$\left( {s,\dot s,\ddot s,\dddot s} \right)$相平面，机器人的状态更新被映射为相平面上路径参数的更新，如下所示：

(7)$ \frac{{\mathrm{d}}}{{{\mathrm{d}}s}}\left[ {\begin{array}{*{20}{c}} {\dot s} \\ {\ddot s} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\ddot s}}{{\dot s}}} \\ {\dfrac{{\dddot s}}{{\dot s}}} \end{array}} \right]. $

在${s_i}$位置对式（7）进行2阶泰勒展开并舍去关于$O\left( {{\varDelta ^2}\left( s \right)} \right)$的余项，有

(8)$ \left.\begin{split} & {\dot s = {{\dot s}_i}+\frac{{{{\ddot s}_i}}}{{{{\dot s}_i}}}\varDelta \left( s \right),} \\ & {\ddot s = {{\ddot s}_i}+\frac{{{{\dddot s}_i}}}{{{{\dot s}_i}}}\varDelta \left( s \right).} \end{split}\right\} $

式中：$s \in \left[ {{s_i},{s_{i+1}}} \right] \subset \left[ {0,{s_{{\mathrm{end}}}}} \right]$且$\varDelta \left( s \right) = s - {s_i}$.

为了保证在起止时刻状态量和控制量剖面满足给定条件，可以约束相平面上路径参数的起止状态：

(9)$ \left.\begin{split} & \left[ {\dot s\left( 0 \right),\ddot s\left( 0 \right),\dddot s\left( 0 \right)} \right] = \left[ {{{\dot s}_0},{{\ddot s}_0},{{\dddot s}_0}} \right], \\ & \left[ {\dot s\left( {{s_{\rm{end}}}} \right),\ddot s\left( {{s_{\rm{end}}}} \right),\dddot s\left( {{s_{\rm{end}}}} \right)} \right] = \left[ {{{\dot s}_{{s_{\rm{end}}}}},{{\ddot s}_{{s_{\rm{end}}}}},{{\dddot s}_{{s_{\rm{end}}}}}} \right]. \end{split}\right\} $

为了最小化移动机器人的运动时间，优化的目标函数定义为

(10)$ f\left( t \right) = \int_{\tau = 0}^T {1{\mathrm{d}}\tau } = \int_{\tau = 0}^T {\frac{{{\rm{ds}}}}{{{\rm{ds}}}}{\mathrm{d}}\tau } = \int_{s = 0}^{{s_{\rm{end}}}} {\frac{1}{{\dot s}}{\rm{d}}s} . $

将目标函数映射到$\left( {s,\dot s} \right)$相平面上，机器人的时间最优性体现在对$s - \dot s$曲线上界的逼近程度. 对于给定的相平面上界曲线$s - {\dot s_{\rm{ref}}}$，优化目标函数为

(11)$ f\left( s \right) = \int_{s = 0}^{{s_{\rm{end}}}} {{{\left( {\dot s - {{\dot s}_{\rm{ref}}}} \right)}^2}{\rm{d}}s} . $

将原移动机器人的速度规划任务转化为如下Bolza最优控制问题.

(12)$ \left. {\begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\min }&目标函数\text{(11);}\\{{\rm{s}}.{\rm{t}}{\rm{.}}}&状态边界约束\text{ }({\mathrm{5a}})\sim ({\mathrm{5f}}),\\{}&状态转移约束\text{ (7) }或\text{ (8)},\\{}&状态点约束\text{ (9)}.\end{array}}\end{array}} \right\}$

由于在相平面上路径参数$s$与各阶导数$\left( {\dot s,\ddot s,\dddot s} \right)$间存在复杂的非线性关系及优化目标函数需要在初始解的基础上进行迭代优化，优化问题(12)被解耦为2个部分进行求解.

式(12)旨在解决机器人从初始状态移动到终止状态的过程中车轮的物理极限和环境对车体的规则要求与给定路径$ {\boldsymbol{p}}(s) $之间的潜在冲突. 采用数值方法，求解提出的最优控制问题(12). 时间连续状态和控制曲线被近似为分段多项式函数，最优控制问题被完全离散化，从而转化为非线性规划问题. 由于状态和控制剖面是“同时”离散化的，这种离散化过程称为“同步”方法. 在同一层次上，离散状态和控制剖面在动态优化的实践和分析中具有许多优势^[17].

基于内点法的非线性规划求解器对于具有大量不等式约束的大规模非线性规划问题是有效的. 基于内点法的同步方法的详细原理见文献[18,19].

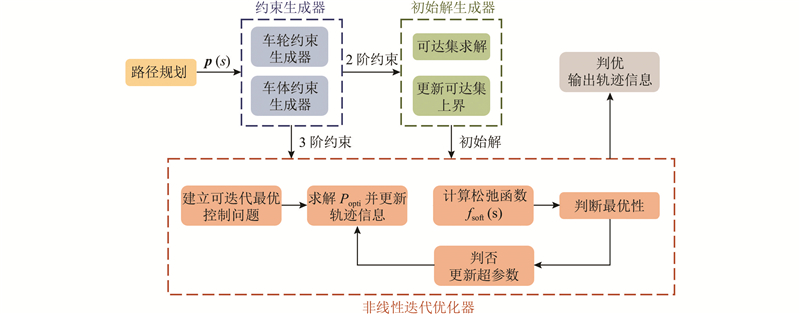
所提移动机器人最优速度规划算法的流程框图如图2所示，算法整体上由约束生成器、初始解生成器及非线性优化器3部分构成. 在上层路径规划得到含参曲线$ {\boldsymbol{p}}(s) $后，经约束生成器将车轮与车体约束解耦，分别发送到初始解生成器和非线性优化器中. 非线性优化器根据初始解生成器中得到的初始解优化求解，输出轨迹信息. 主要的计算步骤如下.

1) 对由上层路径规划得到的含参曲线$ {\boldsymbol{p}}(s) $进行约束生成，使用参数$s$将车轮约束与车体约束映射到相平面上，并将这些约束分解为关于$\left( {s,\dot s,\ddot s} \right)$的线性约束（1、2阶约束）与非线性约束（3阶约束）.

2) 忽略非线性因素，纳入约束生成器中的1、2阶约束，对于离散化后的路径$ {\boldsymbol{p}}(s) $，自后而前递归求解每个位置的可达集. 考虑起始时刻的状态，自前而后根据贪婪算法递归更新每个可达集的上界，输出初始解.

3) 考虑非线性因素，纳入约束生成器中的3阶约束，建立可迭代最优控制问题${{{P}}_{\rm{opti}}}$. 在每轮迭代中，求解${{{P}}_{\rm{opti}}}$并计算松弛函数${f_{\rm{soft}}}\left( s \right)$进行最优性判断. 当${f_{\rm{soft}}}\left( s \right)$小于给定阈值时，说明运动学可行性得到了保证，则输出轨迹信息；反之更新松弛函数中的迭代优化参数，继续迭代求解${{{P}}_{\rm{opti}}}$.

在非线性优化中，初始解对优化速度与优化结果的影响极大. 通过拆分约束，建立2阶约束下的时间最优轨迹规划问题，得到该约束下的最优解与相关变量的取值范围. 该问题的伪代码见算法1.

对于给定路径$ {\boldsymbol{p}}(s) $，算法1通过$N+1$个采样点将路径分为$N$段. 结合式(5a)、(5b)、(5d)、(5e)，算法1在每个采样点上均满足如下2阶约束：

(13)$ {\boldsymbol{B}}\left( s \right){\dot s^2}+{\boldsymbol{A}}\left( s \right)\ddot s \leqslant {\boldsymbol{L}}. $

式中：

$ {{\boldsymbol{B}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {\left[\kern-0.15em\left[ {{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{a}}\left( s \right)} \right]\kern-0.15em\right]} \\ {\left[\kern-0.15em\left[ { - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{a}}\left( s \right)} \right]\kern-0.15em\right]} \\ {{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{b}}\left( s \right)} \\ { - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{b}}\left( s \right)} \\ {\left[\kern-0.15em\left[ {{\boldsymbol{a}}\left( s \right)} \right]\kern-0.15em\right]} \\ {\left[\kern-0.15em\left[ { - {\boldsymbol{a}}\left( s \right)} \right]\kern-0.15em\right]} \\ {{\boldsymbol{b}}\left( s \right)} \\ { - {\boldsymbol{b}}\left( s \right)} \end{array}} \right],} \;\;{{\boldsymbol{A}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}} \\ {\boldsymbol{0}} \\ {{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{a}}\left( s \right)} \\ { - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{a}}\left( s \right)} \\ {\boldsymbol{0}} \\ {\boldsymbol{0}} \\ {{\boldsymbol{a}}\left( s \right)} \\ { - {\boldsymbol{a}}\left( s \right)} \end{array}} \right],}$

${{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {v_{{\text{r}},\max }^2},&{v_{{\text{l}},\max }^2} \end{array}} \right]}^{\rm{T}}}} \\ { {{\left[ {\begin{array}{*{20}{c}} {v_{{\text{r}},\min }^2},&{v_{{\text{l}},\min }^2} \end{array}} \right]}^{\rm{T}}}} \\ {{{\left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{\text{r}},\max }}},&{{{\dot v}_{{\text{l}},\max }}} \end{array}} \right]}^{\rm{T}}}} \\ { - {{\left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{\text{r}},\min }}},&{{{\dot v}_{{\text{l}},\min }}} \end{array}} \right]}^{\rm{T}}}} \\ {{{\left[ {\begin{array}{*{20}{c}} {v_{{C},\max }^2},&{\omega_{{C},\max }^2} \end{array}} \right]}^{\rm{T}}}} \\ { {{\left[ {\begin{array}{*{20}{c}} {v_{{C},\min }^2},&{\omega_{{C},\min }^2} \end{array}} \right]}^{\rm{T}}}} \\ {{{\left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{C},\max }}},&{{{\dot \omega}_{{C},\max }}} \end{array}} \right]}^{\rm{T}}}} \\ { - {{\left[ {\begin{array}{*{20}{c}} {{{\dot v}_{{C},\min}}},&{{{\dot \omega}_{{C},\min }}} \end{array}} \right]}^{\rm{T}}}} \end{array}} \right]}. $

$\left[\kern-0.15em\left[ {\boldsymbol{\alpha}} \right]\kern-0.15em\right]$表示对向量${\boldsymbol{\alpha}} $的每个元素对应乘方. 在每个采样段$ \left[ {{s_i},{s_{i+1}}} \right] $上，均有如下的匀加速度状态更新方程：

(14)$ \dot s_{i+1}^2 = \dot s_i^2+2{\varDelta _i}{\ddot s_i},{\text{ }}\varDelta_i = {s_{i+1}} - {s_i}. $

算法1的第3~5行给出了递归迭代的状态集（可达集）求解过程. 在$\left[ {{s_i},{s_{i+1}}} \right]$区间上假设采样点${s_{i+1}}$的速度区间${H_{i+1}}$（即可达集）已知，则采样点${s_i}$的速度区间${H_i} = [\underline {\dot s_i^2} ,\bar {\dot s}_i^2]$可以通过以下线性规划问题得到：

(15)$ \left.\begin{split}& \bar {\dot s}_i^2 = \max \dot s_i^2, \\ & \underline {\dot s_i^2} = \min \dot s_i^2; \\ {\text{s}}{\text{.t}}{\text{. }}&\dot s_i^2+2{\varDelta _i}{{\ddot s}_i} \in {H_{i+1}}, \\ & {\boldsymbol{B}}\dot s_i^2+{\boldsymbol{A}}{{\ddot s}_i} \leqslant {\boldsymbol{L}}. \end{split}\right\} $

式（15）表明，对于任意的${\dot s_{i+1}}$，都可以找到对应的${\dot s_i}$. 换言之，${H_i}$状态集总是可以转移到${H_{i+1}}$状态集（可达集的性质）. 若算法1没有从第6行退出，则所有的可达集均被得到且线性规划问题可解. 考虑到起始时刻的状态$\dot s_0^2$，算法1的第7~10行给出了初始解的求解过程. 在$\left[ {{s_i},{s_{i+1}}} \right]$区间上假设采样点${s_i}$的最优速度${\tilde {\dot s}_i}$已知，则采样点${s_{i+1}}$的最优速度${\tilde {\dot s}_{i+1}}$可以通过以下线性规划问题得到：

(16)$ \left.\begin{split} & \tilde {\dot s}_i^2 = \max \;(\tilde {\dot s}_i^2+2{\varDelta _i}{{\ddot s}_i}); \\ {\text{s}}{\text{.t}}{\text{. }}& \tilde {\dot s}_i^2+2{\varDelta _i}{{\ddot s}_i} \in {H_{i+1}}, \\ & {\boldsymbol{B}}\tilde {\dot s}_i^2+{\boldsymbol{A}}{{\ddot s}_i} \leqslant {\boldsymbol{L}}. \end{split}\right\} $

每个可达集的上界被该点的最优速度更新，进一步作为初始条件，在非线性优化中使用.

在得到初始解与可达集后，确定状态量$\left( {s,\dot s,\ddot s} \right)$构成的凸空间. 轨迹规划问题的非线性主要体现在${s_i}$位置上$\left( {{{\dot s}_i},{{\ddot s}_i}} \right)$与${\dddot s_i}$的非线性关系及$\left[ {{s_i},{s_{i+1}}} \right]$区间上$\left( {{{\dot s}_{i+1}},{{\ddot s}_{i+1}}} \right)$与$\left( {{{\dot s}_i},{{\ddot s}_i},{{\dddot s}_i}} \right)$的非线性关系. 通过纳入加加速度约束，建立3阶约束下的迭代优化算法，得到最优轨迹规划问题(12)的解，伪代码如下所示.

其中，${\lambda _{\rm{soft}}}$为对状态转移约束的软化程度进行加权的参数，${\lambda _{\rm{soft}}}$越大表明对状态转移约束越严格，在迭代过程中${\lambda _{\rm{soft}}}$被不断放大，直至松弛函数小于阈值；$ {\lambda _{{\mathrm{soft0}}}} $为$ {\lambda _{\rm{soft}}} $的初始值；${\varepsilon _{{\mathrm{epoch}}}}$为迭代求解最优控制问题的轮数；${\varepsilon _{\max}}$为可迭代求解最优控制问题的最大轮数；${{\rm{TLV}}_{\rm{soft}}}$为松弛函数可接受阈值；$\delta $为软化参数${\lambda _{\rm{soft}}}$更新的步长.

算法2建立可迭代的最优控制问题，在每次迭代过程中，求解该问题并得到最优轨迹信息. 利用算法2计算松弛函数，与给定阈值进行比较. 若小于阈值，则退出迭代输出信息；反之，则更新超参数继续迭代. 具体而言，利用该迭代算法解决了以下优化问题：

(17)$ \left.\begin{split} \min & \sum\limits_{i = 0}^N {{{\left( {{{\dot s}_i} - {{\tilde {\dot s}}_i}} \right)}^2}} +{\lambda _{\rm{soft}}}{f_{\rm{soft}}}\left( s \right); \\ {\text{s}}{\text{.t}}{\text{. }}& {{\dot s}_i} \in {H_i}, \\& {\boldsymbol{B}}\dot s_i^2+{\boldsymbol{A}}{{\ddot s}_i} \leqslant {\boldsymbol{L}}, \\& {\boldsymbol{C}}\dot s_i^3+{\boldsymbol{D}}{{\dot s}_i}{{\ddot s}_i}+{\boldsymbol{E}}{{\dddot s}_i} \leqslant {\boldsymbol{\varGamma}} .\end{split}\right\} $

松弛函数及式(17)的相关系数定义如下：

$ {f_{\rm{soft}}} = \sum\limits_{i = 0}^N {\left[ {{{\left( {{{\dot s}_{i+1}} - {{\dot s}_i} - \frac{{{{\ddot s}_i}}}{{{{\dot s}_i}}}\varDelta \left( s \right)} \right)}^2} + {{\left( {{{\ddot s}_{i+1}} - {{\ddot s}_i} - \frac{{{{\dddot s}_i}}}{{{{\dot s}_i}}}\varDelta \left( s \right)} \right)}^2}} \right]} , $

$ \begin{split} & {{\boldsymbol{C}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{c}}\left( s \right)} \\ { - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{c}}\left( s \right)} \\ {{\boldsymbol{c}}\left( s \right)} \\ { - {\boldsymbol{c}}\left( s \right)} \end{array}} \right],}\;\; {{\boldsymbol{D}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {3{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{b}}\left( s \right)} \\ { - 3{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{b}}\left( s \right)} \\ {3{\boldsymbol{b}}\left( s \right)} \\ { - 3{\boldsymbol{b}}\left( s \right)} \end{array}} \right],} \\ & {{\boldsymbol{E}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{J}}^{ - 1}}{\boldsymbol{a}}\left( s \right)} \\ { - {{\boldsymbol{J}}^{ - 1}}{\boldsymbol{a}}\left( s \right)} \\ {{\boldsymbol{a}}\left( s \right)} \\ { - {\boldsymbol{a}}\left( s \right)} \end{array}} \right],}\;\; {{\boldsymbol{\varGamma}} = \left[ {\begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{\text{r}},\max }}},\;{{{\ddot v}_{{\text{l}},\max }}} \end{array}} \right]}^{\rm{T}}}} \\ { - {{\left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{\text{r}},\min }}},\;{{{\ddot v}_{{\text{l}},\min }}} \end{array}} \right]}^{\rm{T}}}} \\ {{{\left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{C},\max }}},\;{{{\ddot \omega}_{{C},\max }}} \end{array}} \right]}^{\rm{T}}}} \\ { - {{\left[ {\begin{array}{*{20}{c}} {{{\ddot v}_{{C},\min }}},\;{{{\ddot \omega}_{{C},\min }}} \end{array}} \right]}^{\rm{T}}}} \end{array}} \right].} \end{split} $

为了解决约束优化问题(12)，将其解耦成基于可达性分析的初始解生成算法与考虑3阶约束的迭代优化算法. 利用算法1生成相平面$\left( {s,\dot s,\ddot s} \right)$的初始解，为算法2的部分优化变量生成凸空间. 算法2中的${{ P}_{\rm{opti}}}$随着迭代而更新，因为$\dddot s$的约束总是根据相平面上$\left( {\dot s,\ddot s} \right)$的轨迹更新. 假设不考虑$\left( {\dot s,\ddot s} \right)$的更新，$\dddot s$的自由空间将被削减，使得问题的最优性甚至可行性丧失. 迭代更新$\left( {\dot s,\ddot s} \right)$减少了由于遗漏$\dddot s$的自由空间而造成的可行性/最优性损失.

在迭代过程中，不断提高相平面上轨迹的可行性/最优性. 假设在${\varepsilon _{{\mathrm{epoch}}}} = 0$处初始参考轨迹没有运动学上可行的解存在. 在这种情况下，恢复运动可行性成为最小化目标函数的主要方案，因此得到的优化结果与初始参考轨迹的不同主要在于减少了运动学不可行性. 虽然没有完全消除运动学上的不可行性，但所得到的轨迹在形状上更接近于可行，为后续迭代提供了进一步改进的机会.

当算法2从第7行退出时实现最优. 随着迭代的继续，运动学不可行性接近${0^+}$，且${\lambda _{\rm{soft}}}$的增大可以加速该过程. 当运动不可行性较小时，目标函数中的第1项占主导地位，因此最小化目标函数接近于最小化式(11). 最终推导出的有效最优值相当于在${{\rm{TLV}}_{\rm{soft}}}$精度水平下最小化式(11).

通过仿真实验，验证所提方法的可行性、最优性和通用性. 数值算法在Ubuntu上使用C++进行实现，所有优化问题都使用CasADi （CasADi是用于非线性优化和最优控制的开源软件框架）来解决，为构建和求解各种优化问题提供了灵活、高效的接口^[20]. 开展MATLAB联合仿真，使用先锋P3-DX机器人进行实验，如图3所示.

同步动态优化算法的基本参数和机器人的仿真参数设置如表1所示.

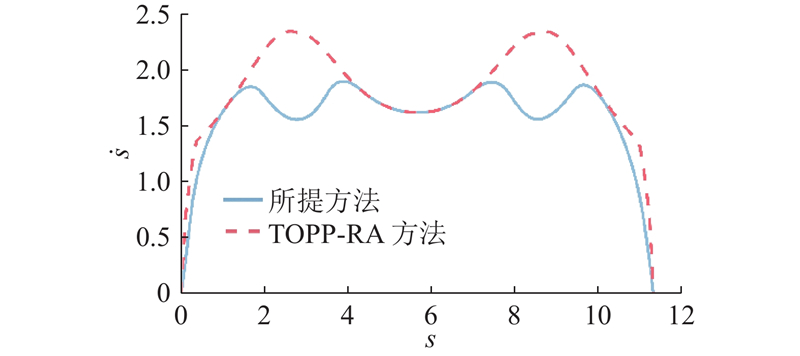
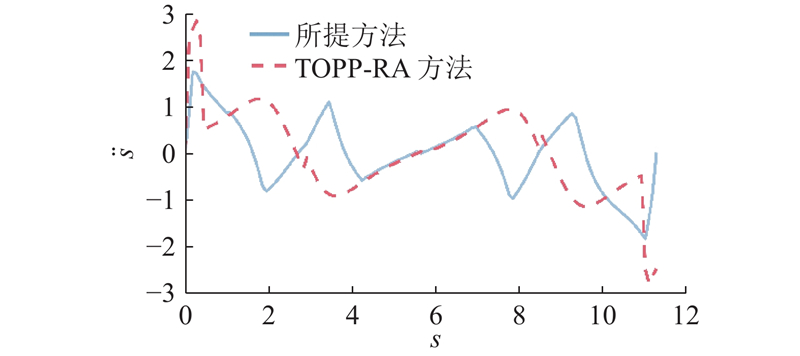
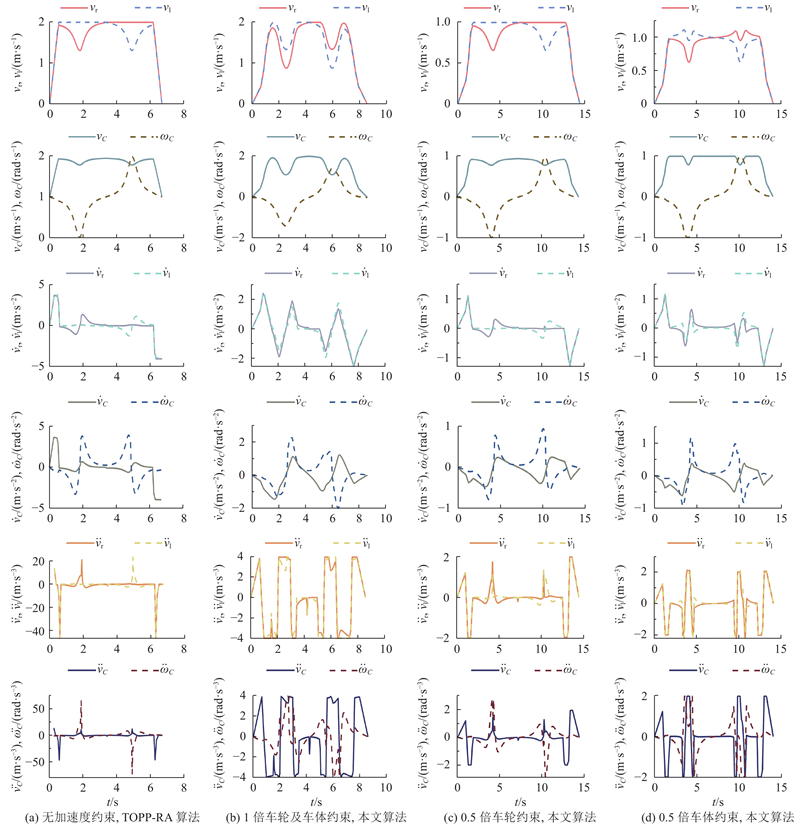
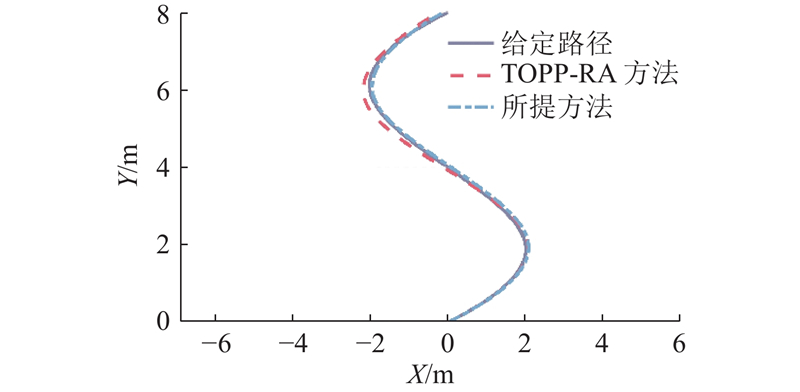
为了验证所提算法在控制由忽略加加速度约束引起的加速度突变方面的有效性以及构造的速度规划方案的最优性，以具体的几何路线为例，将速度规划仿真结果与基于凸优化的速度规划算法（TOPP-RA）^[5]的仿真结果进行比较. 利用TOPP-RA和所提方法得到的在$\left( {s,\dot s} \right)$和$\left( {s,\ddot s} \right)$相平面上的结果分别如图4、5所示. 如图4所示，所提方法的速度曲线完全被包含在凸空间内. 图5中，由于TOPP-RA缺乏对加加速度的限制，引起相邻路径点之间的加速度突变. 这种突然的加速度变化在图4的速度曲线中表现得十分明显，在加速和减速部分之间没有平滑的过渡. 这种突然的加速度变化会导致突然和不稳定的运动，这在许多实际应用中是不可接受的. 为了解决该问题，所提算法施加了明确的加加速度约束限制，使得相邻路径点之间的加速度曲线更平滑. 如图5所示，利用所提方法，限制了加速度突变. 此外，所提方法在图4的速度曲线上呈现出更平滑的过渡，特别是在表示加速和减速的部分，保证了附近部分不会违反各阶约束.

如表2所示，与TOPP-RA算法及Ruckig算法^[21]相比，所提算法在兼顾关节空间（车轮）约束与笛卡尔空间（车体或路径）约束的同时，实现了对加加速度的有效约束.

在实验中，为了评估所提算法的鲁棒性和通用性，开展具有不同约束的实验. 具体而言，评估了所提算法在3种不同约束限制下的性能，如图6所示. 图中，第1~6列分别为车轮速度曲线、车体速度曲线、车轮加速度曲线、车体加速度曲线、车轮加加速度曲线、车体加加速度曲线. 从图6可以看出，由于TOPP-RA方法没有对加加速度进行约束，加速度发生骤变. 所提方法在满足加速度约束（1倍车轮及车体约束）的情况下，得到最小化的执行时间，并且加速度剖面均匀变化，在表示加速和减速的部分之间实现更平滑的转换. 随着约束的严格化（0.5倍车轮约束和0.5倍车体约束），执行时间相应增加. 当添加了加加速度约束后，相应的速度、加速度、加加速度曲线至少有一条在运动过程的某个时刻达到约束的极值. 换言之，对于运动极限的贴近反映在各曲线对于约束边界的逼近. 不同的约束条件决定路径参数的优化范围，从而得到不同的路径最优配速. 除此之外，车轮约束和车体约束对控制加速度突变具有相似但存在差异的效果，在需要严格遵守约束的情况下，不能仅使用其中一种约束进行替代.

在联合仿真中，对该方法的性能进行定量和定性分析. 具体来说，如图7所示为给定几何路径、TOPP-RA联合仿真的输出路径和所提算法联合仿真的输出路径. 如表3所示为所提方法与TOPP-RA方法的性能. 结果表明，在运行过程中，所提算法的横向（X方向）位置误差和纵向（Y方向）位置误差均有不同程度的减小. 与TOPP-RA方法相比，平均路径误差和最大路径位置误差在X方向分别减小了约21%和47%，在Y方向分别减小了约53%和45%. 所提算法对加加速度的有效约束保证了执行器能够在自身能力范围内跟踪输入速度，因此所提方法的位置误差较小.

对于路径规划与速度规划解耦的导航系统来说，移动机器人在兼顾运动效率与执行器跟踪性能的条件下进行运动是一个关键的挑战. 若无法达到给定约束下的最优速度从而产生振荡，则控制器开始跟踪次优速度或不可行速度，这对机器人来说十分不利（危险）. 本文开发了全面有效的同步动态优化框架，将原始速度规划任务视为具有精确表述的机器人运动学和严格描述的多阶状态约束条件的最小时间最优控制问题. 根据可达性分析，在采用线性规划过程得到的初始解基础上，结合约束松弛方法与内点法，通过同步迭代优化求解最优控制问题. 通过仿真实验，验证了以上算法的有效性. 下一步将在移动服务机器人物理样机上进行相关的验证实验，探索约束放松方法，实现实时性能.