如今,电液伺服系统正向高性能方向发展,多种控制方法被开发出来,如:PI控制器[6]、基于反馈线性化的控制器[7]、自适应控制器[8]、鲁棒控制器[9]、滑模控制器[10]等,这些控制器都可以使系统输出按照参考信号运动. 然而,由于系统中存在外部干扰力、摩擦力、参数变动、结构振动以及未建模特性等系统不确定性,系统难以达到高性能. 反步控制将系统模型分成多个子模型,针对每个子模型选取Lyapunov函数,推导得出虚拟控制律和实际控制律[11-12],进一步通过匹配特定的系统参数变动[8,13],加入参数自适应律来提高系统性能. 随后,障碍Lyapunov函数在反步中应用[11,14],用来限制系统的输出在一定范围内,提高了系统性能. Yang等[11]和Won等[14]将障碍Lyapunov函数应用在反步控制中,结合系统模型,得到相应的控制律,通过仿真和实验验证了方法的有效性. 董振乐等[13]构建带有匹配和不匹配干扰项的电液伺服系统模型,设计预设性能控制器,并进行了验证. Yao等[8]得出部分系统参数与系统状态之间的映射关系,并在反步控制中加以补偿,提高了系统性能.
滑模观测器也是重要的系统状态重构手段[20],用滑模观测器中的不连续函数
本研究利用扩张滑模观测器在线估计系统不确定性,并通过系统实时输出反馈设计参数自适应律,最终设计基于障碍Lyapunov函数的自适应反步控制器,补偿不匹配系统不确定性和匹配更新系统参数,实现电液伺服系统高精度控制.
1. 电液伺服系统模型
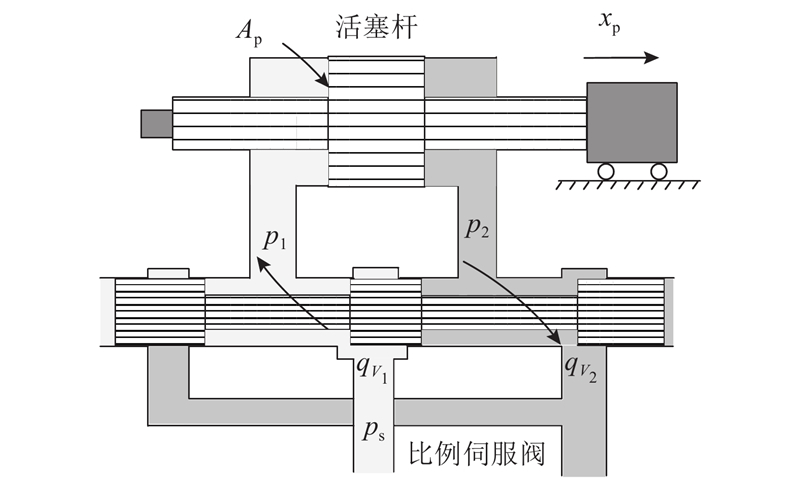
如图1所示为阀控液压缸原理图. 图中,
图 1
图 1 阀控液压缸原理图
Fig.1 Schematic diagram of servo valve controlled hydraulic cylinder
式中:
式中:FL为液压缸活塞杆的外部干扰力,FF为液压缸活塞杆与缸筒之间的摩擦力,m为负载的总质量,Bp为液压油的黏性阻尼系数. 液压缸的负载体积流量是由电液伺服阀的阀芯位移控制的,可以得到
式中:xv为伺服阀的阀芯位移,Cd为伺服阀的排放系数,
式中:Δpr为伺服阀的额定压降,
式中:θ1=Ap/m,θ2=Bp/m,θ3=4Apβe/Vt,θ4=4Ctlβe/Vt,θ5=4βe/Vt;由于液压缸的物理量参数的计量误差和其他参数的估计误差,系统状态方程中的参数与实际物理系统中的参数存在差异,因此,在系统的状态方程中考虑参数变动,Δθ1、Δθ2、Δθ3和Δθ4表示θ1、θ2、θ3和θ4的参数变动;Δ1为由外部干扰力、摩擦力、参数变动、结构振动和未建模特性带来的系统不确定性,表示由系统不确定性带来的液压缸活塞杆的负载波动,Δ1=−FL/m−FF/m+Δθ1x3−Δθ2x2+μ,μ表示活塞杆在运动过程中带动整个系统的机械结构运动产生的结构振动和一些油液非线性等未建模特性;Δ2表示由θ3和θ4的参数变动带来的系统不确定性,表示由系统不确定性带来的液压缸两腔的油压波动,Δ2=−Δθ3x2−Δθ4x3;Υj为集成系统不确定性Δj的变化速率,j=1,2; y=x1表示系统的位移输出.
假设1 电液伺服系统的期望位移
假设2 函数f1(x2,x3)和f2(x2,x3)相对于x2和x3是满足Lipschitz条件的. 存在4个Lipschitz常数γ1、γ2、γ3和γ4满足如下条件:
式中:
2. 控制器设计
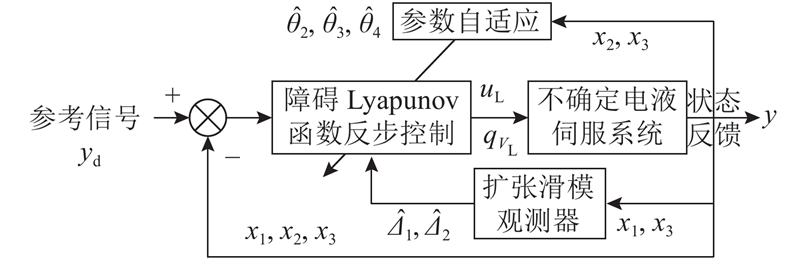
如图2所示为整体闭环控制系统结构图. 基于电液伺服系统的状态空间模型,利用扩张滑模观测器的观测值
图 2
2.1. 扩张滑模观测器设计
基于电液伺服系统的状态方程(式(5)),考虑如下5阶扩张滑模观测器:
式中:
理论1 存在足够大的控制增益
证明 考虑如下3个滑模面为
可以得到如下不等式:
因此,如果使
基于假设2,可以得到
若使
类似地,基于假设2,有
若使
可见
因此,只要
类似于式(17),式(18)也是一阶微分方程. 因此,只要
因此,
利用滑模观测器的等值注入原理及合适的饱和函数,针对电液伺服系统的扩张滑模观测器的最终形式[25]可以表示为
式中:δi为3个小的正实数.
2.2. 参数自适应映射
在实际物理系统中,液压油的黏性阻尼系数Bp、液压油的体积弹性模量βe和液压缸的总体泄漏系数Ctl都是估计值. 因此,考虑电液伺服系统模型中
则参数自适应律可以表示为
式中:
由扩张滑模观测器补偿的
2.3. 基于障碍Lyapunov函数的自适应反步控制器设计
定义电液伺服系统的状态跟踪误差向量如下:
式中:z1为系统输出位移跟踪误差,|z1|<kb,kb为系统跟踪误差限定;系统的输出满足kcl<y=x1<kcu,kcu=yd+kb,kcl=yd−kb;α1和α2为控制器设计的2个虚拟控制量.
理论2 结合电液伺服系统状态方程(式(5))和扩张滑模观测器的2个估计值
同时,参数自适应函数适当选择为
式中:ki为控制增益. 如果控制增益Lj+3适当选择为Lj+3>kj+1/4且ki>0,则|z1|<kb;z会在t>0后落入一个有界的超球面Hr内,并且在t>t0的情况下保持在Hr内.
式中:ξj=Lj+3−kj+1/4.
证明 考虑如下障碍Lyapunov函数为
基于虚拟控制量α1(式(24)),可以得到
基于
基于虚拟控制量
由于
基于
由于θi+1为固定值,
同时,参数自适应律可以选择为
进一步地,可以得到参数自适应函数,如式(25)所示. 将式(34)代入式(33),得到
因此,如果Lj+3>kj+1/4,z会在有限时间t1>0内落入Hr内且在t>t0的情况下保持在Hr内;进一步地,在t>t0情况下,系统的输出跟踪误差|z1|<kb, 证毕.
2.4. 闭环控制系统稳定性分析
定义Lyapunov函数为
可以得到其对时间的导数为
基于式(11)、(13)~(15)、(18)、(22)、(24) ~(25)、(32)的结果,式(37)可以重写为
如果
选择Lj+3>kj+1/4,使得ξj>0,加之ki>0,可以看出式(39)中只有
根据理论2,超球面Hr的大小取决于
显然,整体闭环控制系统稳定.
3. 仿真和实验验证
为了验证所提出的控制方法的有效性,选取参考信号为yd=0.01sin (2πt) ,在仿真中给定2个集成系统不确定性Δj,Δ1=6sin (2πωt), Δ2=2×1012×sin (2πωt),验证控制系统的性能. 在实验中,系统不确定性中的参数变动Δθ1、Δθ2、Δθ3和Δθ4是模型的参数与电液伺服系统实验台真实参数的差异,摩擦力FF在液压缸的活塞杆与缸筒之间产生,结构振动和未建模特性μ是液压缸活塞杆运动带动实验台的机械结构振动以及油液的非线性等导致的,外部干扰力FL是由控制系统在力加载液压缸上施加1 V的控制信号产生的. 如表1所示为电液伺服系统的关键参数. 采用如下3种不同控制方法分别进行仿真和实验来验证本研究所提出的控制器的性能.
表 1 电液伺服系统关键参数
Tab.1
| 参数 / 单位 | 数值 |
| Ap / m2 | 1.88×10−3 |
| βe / Pa | 6.9×108 |
| ΔPr / Pa | 6×106 |
| Ps / Pa | 8×106 |
| Bp/(N·m−1·s) | 7500 |
| m / kg | 500 |
| Vt / m3 | 0.38×10−3 |
| umax / V | 10 |
| 38 | |
| Ctl / (m3·s−1·Pa−1) | 4.6×10−16 |
1) 反步控制器:根据状态方程,反步控制器的控制律为
2) 基于障碍Lyapunov函数的反步控制器:使
3) 基于扩张滑模观测器的鲁棒控制器(本研究所提出的控制器):基于扩张滑模观测器的估计值
3.1. 仿真结果
均方根误差可以阐明3个控制器的性能:
式中:Rin,i为参考信号,Rout,i为系统反馈信号,n为信号的长度.
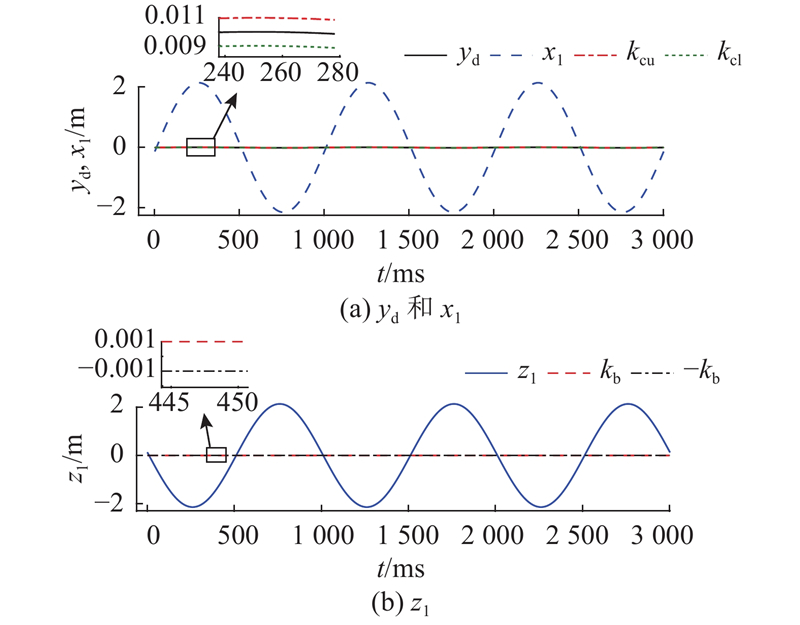
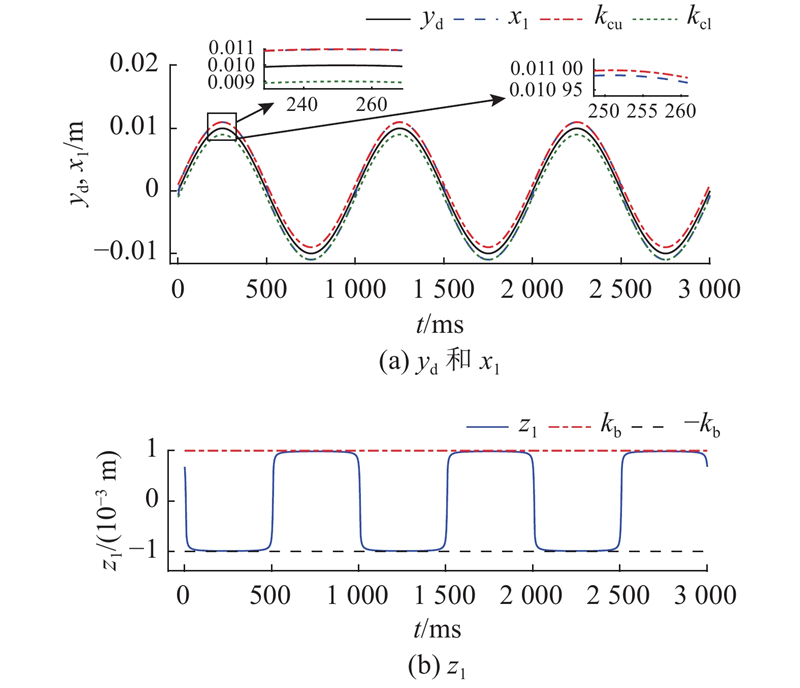
如图3~5所示,分别为反步控制器、基于障碍Lyapunov函数的反步控制器、基于扩张滑模观测器的控制器(本研究所提出的控制器)的仿真结果. 可以看出,在预定干扰Δ1和Δ2的作用下,传统的反步控制器已经发散,甚至不能保证系统输出按照参考轨迹运行;基于障碍Lyapunov函数的反步控制器具有较强鲁棒性,在预定干扰Δ1和Δ2的作用下,可以保证系统的跟踪误差在kb=0.001 m内,但误差较大;扩张滑模观测器不仅可以估计系统的全状态,而且还可以利用扩张的状态估计集成系统不确定性,加上参数自适应律实时更新系统参数,可见本研究所提出的控制器性能优于基于障碍Lyapunov函数的反步控制器和传统的反步控制器. 3种控制器的跟踪误差峰值分别为2.1325 、9.8732×10−4 、1.7009×10−4 m,均方根误差分别为1.5077 、9.5947×10−4 、1.2117×10−4 m. 可见3种控制器的性能如下:本研究所提出的控制器>基于障碍Lyapunov函数的反步控制器>传统的反步控制器.
图 3
图 3 仿真中反步控制器的性能
Fig.3 Performance of backstepping controller in simulation study
图 4
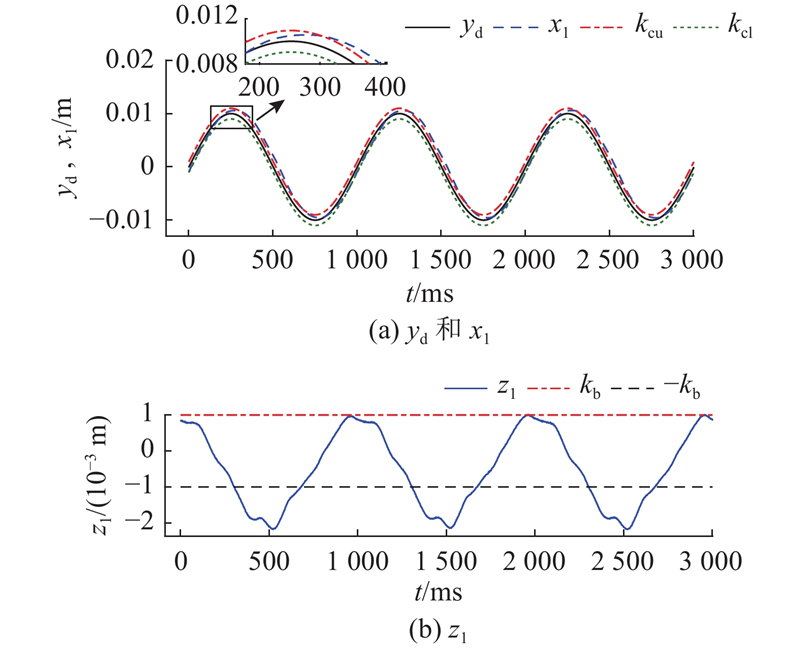
图 4 仿真中基于障碍Lyapunov函数的反步控制器的性能
Fig.4 Performance of barrier Lyapunov function-based backstepping controller in simulation study
图 5
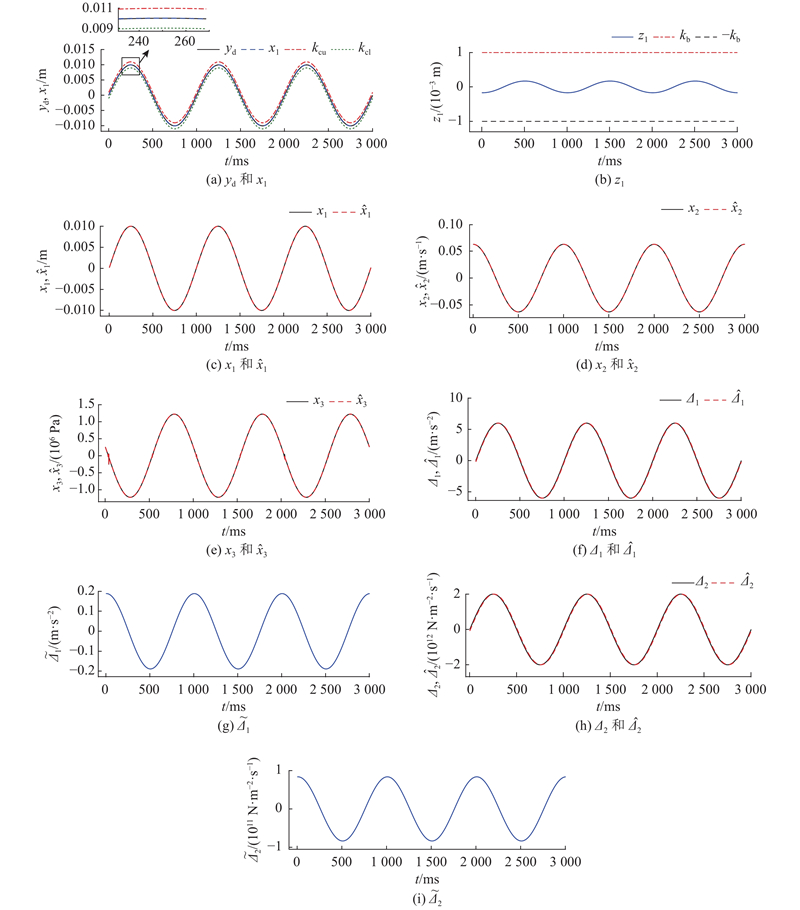
图 5 仿真中所提出的控制器的性能
Fig.5 Performance of proposed controller in simulation study
为了彰显所提出的控制方法的鲁棒性,在仿真中给定较大的集成系统不确定性值:Δ1=6×sin (2πωt)、Δ2=2×1012sin (2πωt),在此干扰值作用下,反步控制器甚至不能保持液压缸的活塞杆按照参考信号运行. 基于障碍Lyapunov函数的反步控制器具有较强的鲁棒性,能使系统稳定运行,但不能保证高性能. 如图5(c)~(e)所示,扩张滑模观测器完整重构了电液伺服系统状态变量xi;如图5(f)~(i)所示,观测器在重构状态变量xi之后,利用2个扩张状态重构了系统不确定性Δj,且重构误差良好;进一步,通过扩张滑模观测器估计系统不确定性Δj,并在控制器中补偿,加之参数自适应律,不仅使系统的跟踪误差小于kb,还提高了系统跟踪精度,从而进一步增强了控制器的鲁棒性.
3.2. 实验结果
如图6所示为电液伺服系统实验台. 如图7所示为电液伺服系统实验台的实际控制系统. 控制系统的硬件为上位机、工控机、PCI-1716板卡、ACL-6126板卡以及信号调理系统. 位移传感器和2个油压传感器的4~20 mA电流信号由信号调理系统转换为2~10 V电压信号,最后由PCI-1716采集. 控制电压(±10 V)由板卡ACL-6126输出,并由信号调理系统转换为±40 mA电流信号来控制伺服阀,从而控制电液伺服系统运作. 基于MATLAB xPC 快速原型技术,上位机和工控机(IPC-610)通过TCP/IP网络连接. 在MATLAB/Simulink中编写好的控制程序会被转换为C程序,并通过网络下载至工控机中,来控制实验台实时运转. 整个控制系统的采样频率为1 000 Hz.
图 6
图 7
图 8
图 8 实验中反步控制器的性能
Fig.8 Performance of backstepping controller in experimental study
图 9
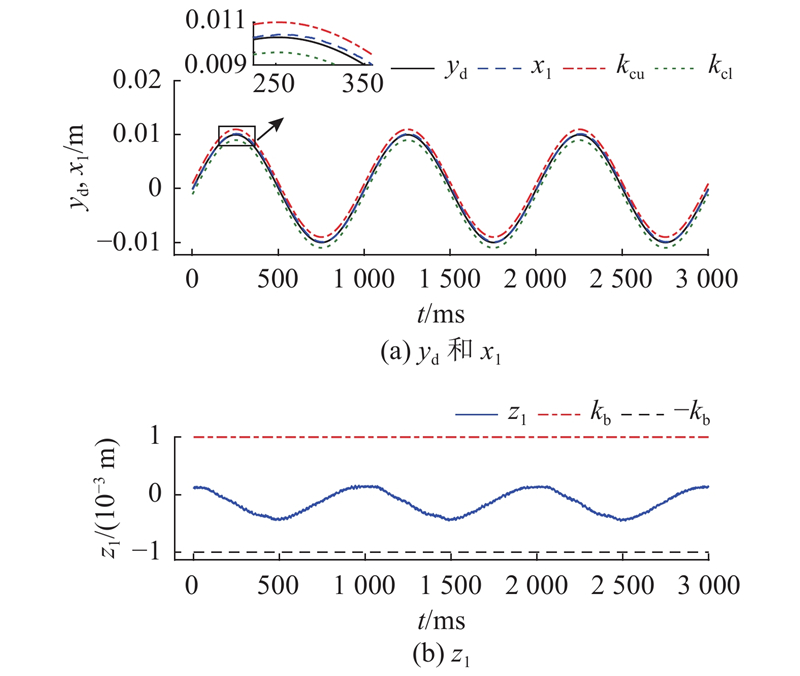
图 9 实验中基于障碍Lyapunov函数的反步控制器的性能
Fig.9 Performance of barrier Lyapunov function-based backstepping controller in experimental study
图 10
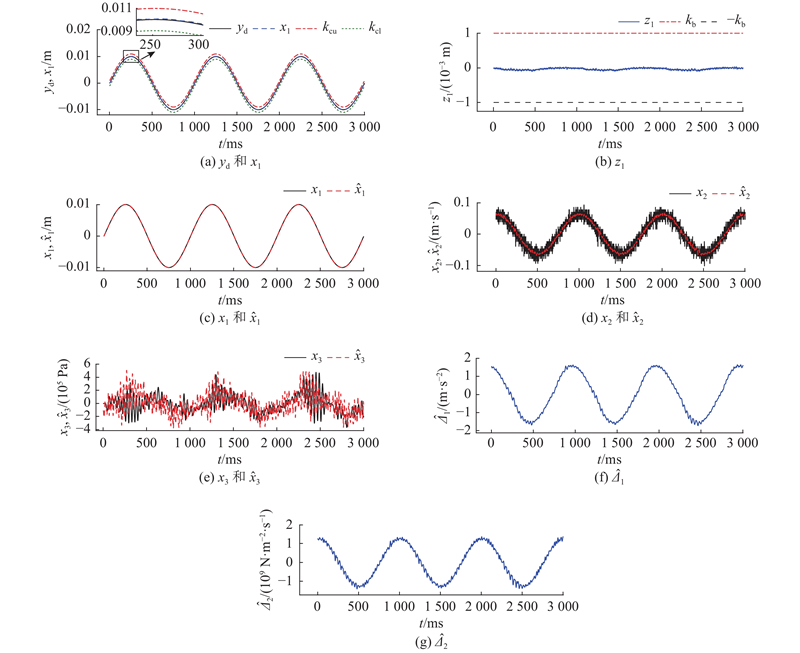
图 10 实验中所提出的控制器的性能
Fig.10 Performance of proposed controller in experimental study
3种控制器的跟踪误差峰值分别为0.0022 、4.6006×10−4 、1.0237×10−4 m,均方根误差分别为0.0012、2.3992×10−4、4.1999×10−5 m. 可见 3种控制器的性能如下:所提出的控制器>基于障碍Lyapunov函数的反步控制器>传统的反步控制器.
扩张滑模观测器在实验中实时重构出来的系统不确定性的值如下:Δ1的幅值约为[−1.5, 1.5] m/s2,Δ2的幅值约为[−1.5×109, 1.5×109] N/(m2·s),明显小于仿真中给定的干扰值Δ1=6sin (2πωt) , Δ2=2×1012sin (2πωt),因此,仿真中传统的反步控制器出现了发散的状况.
在系统不确定性的作用下,在仿真和实验过程中,传统的反步控制器不能保证系统跟踪误差|z1|≤kb;基于障碍Lyapunov函数的反步控制器具有较强的鲁棒性,虽然能够使系统的跟踪误差|z1|≤kb,但难以满足高性能. 扩张滑模观测器在仿真和实验中,都展现了优良的性能,通过重构的系统不确定性,加上补偿系统参数变动,整体提高了系统鲁棒性.
4. 结 论
为了适应高性能电液伺服系统的需求,提出基于扩张滑模观测器的控制方法,利用扩张滑模观测器在线估计和补偿系统不确定性,通过系统的输出反馈设计参数自适应律,从而实时更新系统参数,最后利用障碍Lyapunov函数使系统的输出误差小于kb,达到高精度控制.
(1)考虑电液伺服系统的外部干扰力、摩擦力、参数变动、结构振动及未建模特性等系统不确定性,构建电液伺服系统状态空间模型.
(2)基于状态空间描述模型,设计五阶扩张滑模观测器,通过定义合适的滑模面证明提出的扩张滑模观测器的稳定性;利用扩张滑模观测器的系统不确定性估计值,加之参数自适应律,设计基于障碍Lyapunov函数的自适应反步控制器,并证明闭环控制系统的稳定性.
(3)仿真和实验结果表明,扩张滑模观测器可以同时估计系统的全状态和系统不确定性,所提出的控制器性能优于基于障碍Lyapunov函数的反步控制器和传统的反步控制器.
(4)本研究仅针对双出杆液压缸构建了状态空间模型,并设计了相应的控制方法,未来将进一步根据单出杆液压缸的模型,应用本研究所提出的算法进行进一步验证.
参考文献
不确定受扰电液伺服系统智能自学习PID控制
[J].DOI:10.13195/j.kzyjc.2021.1001 [本文引用: 1]
Intelligent self-learning PID control of electro-hydraulic servo system with uncertain disturbances
[J].DOI:10.13195/j.kzyjc.2021.1001 [本文引用: 1]
An improved method combined SMC and MLESO for impedance control of legged robots’ electro-hydraulic servo system
[J].DOI:10.1016/j.isatra.2022.03.009 [本文引用: 1]
Robust force control with a feed-forward inverse model controller for electro-hydraulic control loading systems of flight simulators
[J].DOI:10.1016/j.mechatronics.2016.06.004 [本文引用: 1]
Real-time electro-hydraulic hybrid system for structural testing subjected to vibration and force loading
[J].DOI:10.1016/j.mechatronics.2015.10.009 [本文引用: 1]
Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller
[J].DOI:10.1016/j.autcon.2021.103722 [本文引用: 1]
基于干扰观测器的电液伺服系统反馈线性化滑模控制
[J].DOI:10.11832/j.issn.1000-4858.2018.07.002 [本文引用: 1]
Feedback linearization sliding mode control based on disturbance observer for electro-hydraulic servo system
[J].DOI:10.11832/j.issn.1000-4858.2018.07.002 [本文引用: 1]
Adaptive robust motion control of single-rod hydraulic actuators: theory and experiments
[J].DOI:10.1109/3516.828592 [本文引用: 4]
基于开环补偿与鲁棒控制的电液位置伺服加载系统研究
[J].DOI:10.3969/j.issn.1001-4551.2022.01.009 [本文引用: 1]
Electro-hydraulic position servo loading system based on open loop compensation and robust control
[J].DOI:10.3969/j.issn.1001-4551.2022.01.009 [本文引用: 1]
A new adaptive sliding mode controller based on the RBF neural network for an electro-hydraulic servo system
[J].DOI:10.1016/j.isatra.2021.12.044 [本文引用: 1]
Dual extended state observer-based backstepping control of electro-hydraulic servo systems with time-varying output constraints
[J].DOI:10.1177/0142331219883056 [本文引用: 3]
匹配和不匹配干扰共存时电液伺服系统预设性能渐近跟踪控制
[J].
Asymptotic prescribed performance tracking control of electro-hydraulic servo systems under matched and unmatched disturbances
[J].
High-gain disturbance observer-based backstepping control with output tracking error constraint for electro-hydraulic systems
[J].
Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems
[J].DOI:10.1016/j.cnsns.2015.02.008 [本文引用: 2]
基于双干扰观测器的非对称缸电液系统位置控制
[J].
Position control of asymmetric cylinder electro-hydraulic system based on dual disturbance observer
[J].
Extended-state-observer-based output feedback nonlinear robust control of hydraulic systems with backstepping
[J].DOI:10.1109/TIE.2014.2304912 [本文引用: 1]
Backstepping control of electro-hydraulic system based on extended-state-observer with plant dynamics largely unknown
[J].
Nonlinear control with high-gain extended state observer for position tracking of electro-hydraulic systems
[J].DOI:10.1109/TMECH.2020.2985619 [本文引用: 2]
New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor
[J].
Sliding-mode-observer-based adaptive control for servo actuator with friction
[J].DOI:10.1109/TIE.2007.894718 [本文引用: 1]
Extended sliding mode observer based control for Markovian jump linear systems with disturbances
[J].DOI:10.1016/j.automatica.2016.03.020 [本文引用: 1]
Sliding-mode observer-based mechanical parameter estimation for permanent magnet synchronous motor
[J].
Extended sliding mode observer based robust adaptive backstepping controller for electro-hydraulic servo system: theory and experiment
[J].DOI:10.1016/j.mechatronics.2022.102841 [本文引用: 3]
Extended sliding mode observer-based admittance control for hydraulic robots
[J].DOI:10.1109/LRA.2022.3147244 [本文引用: 1]
Extended sliding mode observer-based high-accuracy motion control for uncertain electro-hydraulic systems
[J].DOI:10.1002/rnc.6421 [本文引用: 1]