输入: ${x_{t - 1}} = \left( {{\text{mean}}\;(F_{\text{c}}^{t - 1}),{{\rm{var}}}\; (F_{\text{c}}^{t - 1})} \right)$ ${u_{t - 1}} = \left( {{D^{t - 1}},{K^{t - 1}}} \right) $ 输出 : ${u_t} = \left( {{D^t},{K^t}} \right)$ . 1. 随机生成u 0 ,执行u 0 生成x 0 ,合并两者,(x 0 , u 0 )构 成初始化数据集D 0 ; 2. for Trail k =1 to K do 3. 利用数据D 训练第k 个BNN模型; 4. for Time = t to t end do 5. for 6. $ {}^k{u_t} = {\text{CMA - ES}}\left( {\min P\left( {{x_{t - 1}},{}^k{u_{t - 1}}{\text{|}}{\boldsymbol{\theta}} } \right)} \right) $ k 7. do 8. 随机采用固定轨迹采样法和随机轨迹采样 法,推导每步轨迹状态x t $ {}^k{u_t} $ W 内的总成本R ,选择令R 最大的作为 $ u_t^{\text{o}} $ $u_t^{\text{o}}$ k 步产生的数据Dk D .
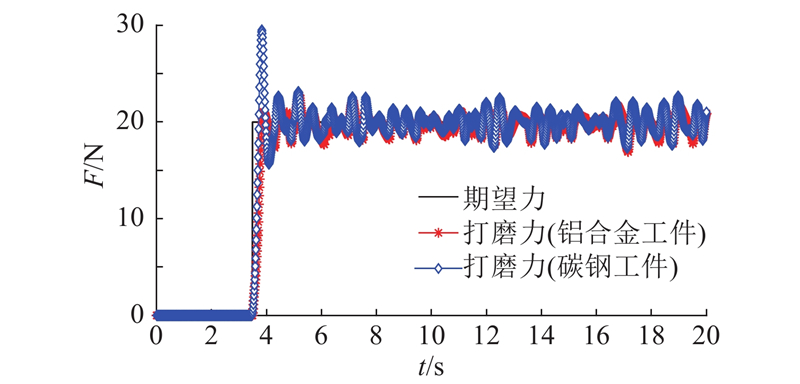
将所提机器人打磨力控制方法设计为机器人强化学习自适应打磨力控制器. 在控制器中设置集成概率模型的BNN数量为5,每个BNN均具有2层64个神经元的隐藏层,激活函数选用Swish函数,每次自助法采样数量为总体样本数量的50%,且对网络权重作L2正则化,采用小批量随机梯度下降法,利用Adam优化算法优化训练过程,单个BNN模型的训练迭代次数设置为3.0×104 次. 选取初始阻抗参数M (t 0 )=3 kg、D (t 0 )=30 N·m/s和K (t 0 )=2 N/m,并设阻抗参数的待训练参数取值范围分别为D (t )∈[10, 200]和K (t )∈[0, 20]. 分别设打磨期望力(即打磨作业目标状态量)为15、20、30 N,期望的打磨力方差 $F_{\text{e}}^{\text{s}}$ x tar 对应取为[15, 0]、[20, 0]和[30, 0],开展自适应打磨力控制对比仿真. 当取x tar =[20, 0]时,训练后的机器人强化学习自适应打磨力控制器,分别对铝合金工件和碳钢工件进行打磨仿真,其材料刚度分别为3.5×104 、1.0×105 N/m. 设置仿真时间为20 s,仿真步长为0.01 s;将仿真时间分为10个参数修正段,每段时间长为2 s(即对应为200步). 在每个参数修正段结束后,根据所提方法,主动自适应调节阻抗参数. 在Matlab/Simulink中,构建机器人强化学习自适应打磨力控制器,通过对机器人打磨系统虚拟样机联合仿真控制,按照子午线打磨路径,对叶片进行打磨作业仿真实验. 第一次训练时,1)在阻抗参数取值范围内随机取10组待训练参数D (t )、K (t ),t =1~10 s,获取初始的状态量数据集 ${x_t}$ ${u_t}$ . 2)对数据集进行自助法采样,获取5个子数据集. 3)分别利用5个数据集训练EPM中的5个BNN模型. 在第一次训练结束后,后续每次均采用所提方法更新阻抗参数.
[1]
ZHU D, FENG X, XU X, et al Robotic grinding of complex components: a step towards efficient and intelligent machining–challenges, solutions, and applications
[J]. Robotics and Computer-Integrated Manufacturing , 2020 , 65 : 101908
DOI:10.1016/j.rcim.2019.101908
[本文引用: 1]
[2]
黄云, 肖贵坚, 邹莱 航空发动机叶片机器人精密砂带磨削研究现状及发展趋势
[J]. 航空学报 , 2019 , 40 (3 ): 022508
[本文引用: 1]
HUANG Yun, XIAO Gui-jian, ZOU Lai Current situation and development trend of robot precise belt grinding for aero-engine blade
[J]. Acta Aeronautica et Astronautica Sinica , 2019 , 40 (3 ): 022508
[本文引用: 1]
[3]
LIU L, ULRICH B J, ELBESTAWI M A. Robotic grinding force regulation: design, implementation and benefits [C]// IEEE International Conference on Robotics and Automation . Cincinnati: IEEE, 1990: 258-265.
[4]
WANG Q, WANG W, ZHENG L, et al Force control-based vibration suppression in robotic grinding of large thin-wall shells
[J]. Robotics and Computer-Integrated Manufacturing , 2021 , 67 : 102031
DOI:10.1016/j.rcim.2020.102031
[5]
LI D, YANG J, ZHAO H, et al Contact force plan and control of robotic grinding towards ensuring contour accuracy of curved surfaces
[J]. International Journal of Mechanical Sciences , 2022 , 227 : 107449
DOI:10.1016/j.ijmecsci.2022.107449
[本文引用: 1]
[6]
ZHANG T, XIAO M, ZOU Y B, et al Robotic curved surface tracking with a neural network for angle identification and constant force control based on reinforcement learning
[J]. International Journal of Precision Engineering and Manufacturing , 2020 , 21 : 869 - 882
DOI:10.1007/s12541-020-00315-x
[本文引用: 1]
[7]
甘亚辉, 段晋军, 戴先中 非结构环境下的机器人自适应变阻抗力跟踪控制方法
[J]. 控制与决策 , 2019 , 34 (10 ): 2134 - 2142
[本文引用: 1]
GAN Ya-hui, DUAN Jin-jun, DAI Xian-zhong Adaptive variable impedance control for robot force tracking in unstructured environment
[J]. Control and Decision , 2019 , 34 (10 ): 2134 - 2142
[本文引用: 1]
[8]
李超, 张智, 夏桂华, 等 基于强化学习的学习变阻抗控制
[J]. 哈尔滨工程大学学报 , 2019 , 40 (2 ): 304 - 311
[本文引用: 2]
LI Chao, ZHANG Zhi, XIA Gui-hua, et al Learning variable impedance control based on reinforcement learning
[J]. Journal of Harbin Engineering University , 2019 , 40 (2 ): 304 - 311
[本文引用: 2]
[9]
ZHOU H, MA S, WANG G, et al A hybrid control strategy for grinding and polishing robot based on adaptive impedance control
[J]. Advances in Mechanical Engineering , 2021 , 13 (3 ): 1 - 21
[本文引用: 1]
[10]
SHEN Y, LU Y, ZHUANG C A fuzzy-based impedance control for force tracking in unknown environment
[J]. Journal of Mechanical Science and Technology , 2022 , 36 : 5231 - 5242
DOI:10.1007/s12206-022-0936-6
[本文引用: 2]
[11]
ZHONG Y, WANG T, PU Y, et al An adaptive bilateral impedance control based on nonlinear disturbance observer for different flexible targets grasping
[J]. Computers and Electrical Engineering , 2022 , 103 : 108388
DOI:10.1016/j.compeleceng.2022.108388
[本文引用: 2]
[12]
WU X, HUANG Z, WAN Y, et al A novel force-controlled spherical polishing tool combined with self-rotation and co-rotation motion
[J]. IEEE Access , 2020 , 8 : 108191 - 108200
DOI:10.1109/ACCESS.2020.2997968
[本文引用: 1]
[13]
MOHAMMAD A E K, HONG J, WANG D, et al Synergistic integrated design of an electrochemical mechanical polishing end-effector for robotic polishing applications
[J]. Robotics and Computer-Integrated Manufacturing , 2019 , 55 : 65 - 75
DOI:10.1016/j.rcim.2018.07.005
[本文引用: 1]
[14]
郭万金, 赵伍端, 于苏扬, 等 无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法
[J]. 浙江大学学报: 工学版 , 2023 , 57 (8 ): 1655 - 1666
[本文引用: 3]
GUO Wan-jin, ZHAO Wu-duan, YU Su-yang, et al Active adaptive online trajectory prediction for robotic grinding on surface without prior model
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (8 ): 1655 - 1666
[本文引用: 3]
[15]
HOGAN N. Impedance control: an approach to manipulation [C]// 1984 American Control Conference . San Diego: IEEE, 1984: 304-313.
[本文引用: 1]
[16]
OTT C, MUKHERJEE R, NAKAMURA Y. Unified impedance and admittance control [C]// 2010 IEEE International Conference on Robotics and Automation . Anchorage: IEEE, 2010: 554-561.
[本文引用: 1]
[17]
肖蒙. 机器人打磨加工过程中恒力控制方法研究[D]. 广州: 华南理工大学, 2020.
[本文引用: 1]
XIAO Meng. Research on constant force control methods in robot grinding process [D]. Guangzhou: South China University of Technology, 2020.
[本文引用: 1]
[18]
DEISENROTH M P, RASMUSSEN C E. PILCO: a model-based and data-efficient approach to policy search [C]// 28th International Conference on Machine Learning . Washington: Omnipress, 2011: 465-472.
[本文引用: 1]
[19]
张铁, 肖蒙, 邹焱飚, 等 基于强化学习的机器人曲面恒力跟踪研究
[J]. 浙江大学学报: 工学版 , 2019 , 53 (10 ): 1865 - 1873
[本文引用: 1]
ZHANG Tie, XIAO Meng, ZOU Yan-biao, et al Research on robot constant force control of surface tracking based on reinforcement learning
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (10 ): 1865 - 1873
[本文引用: 1]
[20]
KINGMA D P, SALIMANS T, WELLING M. Variational dropout and the local reparameterization trick [EB/OL]. (2015-12-20)[2023-03-12]. https://arxiv.org/pdf/1506.02557.pdf.
[本文引用: 1]
[21]
JOSPIN L V, LAGA H, BOUSSAID F, et al Hands-on bayesian neural networks: a tutorial for deep learning users
[J]. IEEE Computational Intelligence Magazine , 2022 , 17 (2 ): 29 - 48
DOI:10.1109/MCI.2022.3155327
[本文引用: 1]
[22]
KINGMA D P, WELLING M. Auto-encoding variational bayes [EB/OL]. (2022-12-11)[2023-03-12]. https://arxiv.org/pdf/1312.6114.pdf.
[本文引用: 1]
[23]
CHUA K, CALANDRA R, MCALLISTER R, et al. Deep reinforcement learning in a handful of trials using probabilistic dynamics models [EB/OL]. (2018-11-02)[2023-03-12]. https://arxiv.org/pdf/1805.12114.pdf.
[本文引用: 1]
[24]
QUIRYNEN R, VUKOV M, ZANON M, et al Autogenerating microsecond solvers for nonlinear MPC: a tutorial using ACADO integrators
[J]. Optimal Control Applications and Methods , 2015 , 36 (5 ): 685 - 704
DOI:10.1002/oca.2152
[本文引用: 1]
[25]
HANSEN N. The CMA evolution strategy: a comparing review [M]// LOZANO J A, LARRAÑAGA P, INZA I, et al. Towards a new evolutionary computation . Berlin: Springer, 2006, 192: 75-102.
[本文引用: 1]
[26]
普亚松, 史耀耀, 蔺小军, 等 基于对数四元数的工业机器人Hermite样条曲线姿态插值
[J]. 西北工业大学学报 , 2019 , 37 (6 ): 1165 - 1173
DOI:10.1051/jnwpu/20193761165
[本文引用: 1]
PU Ya-song, SHI Yao-yao, LIN Xiao-jun, et al Interpolating industrial robot orientation with Hermite spline curve based on logarithmic quaternion
[J]. Journal of Northwestern Polytechnical University , 2019 , 37 (6 ): 1165 - 1173
DOI:10.1051/jnwpu/20193761165
[本文引用: 1]
[27]
郭万金, 于苏扬, 赵伍端, 等 机器人主动柔顺恒力打磨控制方法
[J]. 东北大学学报: 自然科学版 , 2023 , 44 (1 ): 89 - 99
[本文引用: 1]
GUO Wan-jin, YU Su-yang, ZHAO Wu-duan, et al Grinding control method of robotic active compliance constant-force
[J]. Journal of Northeastern University: Natural Science , 2023 , 44 (1 ): 89 - 99
[本文引用: 1]
[28]
ZHANG T, YUAN C, ZOU Y Research on the algorithm of constant force grinding controller based on reinforcement learning PPO
[J]. The International Journal of Advanced Manufacturing Technology , 2023 , 126 : 2975 - 2988
DOI:10.1007/s00170-023-11129-2
[本文引用: 1]
Robotic grinding of complex components: a step towards efficient and intelligent machining–challenges, solutions, and applications
1
2020
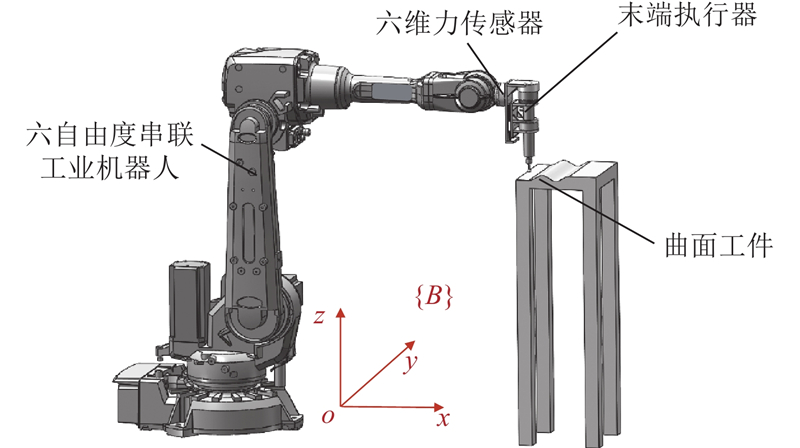
... 现代高端装备制造业对工件的尺寸精度和表面质量要求越来越高. 小批量、不同形状的工件多采用人工打磨方式进行精加工,存在一致性差、生产效率低的问题[1 ] . 机器人打磨以高灵巧性、低成本的特点正成为越来越重要的工件柔顺打磨作业实现途径. 基于工业机器人的打磨技术已成为高端制造业中连续接触式作业(如打磨和抛光)的有力抓手,是解决人工作业工作效率低、改善工作环境和提升工件加工质量的重要工具之一. 高性能打磨工业机器人作为新兴产业和技术的重要载体和现代产业的关键装备,不仅是持续促进生产水平提高的强力支撑,而且有力推动了智能制造的高质量发展[2 -5 ] . ...
航空发动机叶片机器人精密砂带磨削研究现状及发展趋势
1
2019
... 现代高端装备制造业对工件的尺寸精度和表面质量要求越来越高. 小批量、不同形状的工件多采用人工打磨方式进行精加工,存在一致性差、生产效率低的问题[1 ] . 机器人打磨以高灵巧性、低成本的特点正成为越来越重要的工件柔顺打磨作业实现途径. 基于工业机器人的打磨技术已成为高端制造业中连续接触式作业(如打磨和抛光)的有力抓手,是解决人工作业工作效率低、改善工作环境和提升工件加工质量的重要工具之一. 高性能打磨工业机器人作为新兴产业和技术的重要载体和现代产业的关键装备,不仅是持续促进生产水平提高的强力支撑,而且有力推动了智能制造的高质量发展[2 -5 ] . ...
航空发动机叶片机器人精密砂带磨削研究现状及发展趋势
1
2019
... 现代高端装备制造业对工件的尺寸精度和表面质量要求越来越高. 小批量、不同形状的工件多采用人工打磨方式进行精加工,存在一致性差、生产效率低的问题[1 ] . 机器人打磨以高灵巧性、低成本的特点正成为越来越重要的工件柔顺打磨作业实现途径. 基于工业机器人的打磨技术已成为高端制造业中连续接触式作业(如打磨和抛光)的有力抓手,是解决人工作业工作效率低、改善工作环境和提升工件加工质量的重要工具之一. 高性能打磨工业机器人作为新兴产业和技术的重要载体和现代产业的关键装备,不仅是持续促进生产水平提高的强力支撑,而且有力推动了智能制造的高质量发展[2 -5 ] . ...
Force control-based vibration suppression in robotic grinding of large thin-wall shells
0
2021
Contact force plan and control of robotic grinding towards ensuring contour accuracy of curved surfaces
1
2022
... 现代高端装备制造业对工件的尺寸精度和表面质量要求越来越高. 小批量、不同形状的工件多采用人工打磨方式进行精加工,存在一致性差、生产效率低的问题[1 ] . 机器人打磨以高灵巧性、低成本的特点正成为越来越重要的工件柔顺打磨作业实现途径. 基于工业机器人的打磨技术已成为高端制造业中连续接触式作业(如打磨和抛光)的有力抓手,是解决人工作业工作效率低、改善工作环境和提升工件加工质量的重要工具之一. 高性能打磨工业机器人作为新兴产业和技术的重要载体和现代产业的关键装备,不仅是持续促进生产水平提高的强力支撑,而且有力推动了智能制造的高质量发展[2 -5 ] . ...
Robotic curved surface tracking with a neural network for angle identification and constant force control based on reinforcement learning
1
2020
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
非结构环境下的机器人自适应变阻抗力跟踪控制方法
1
2019
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
非结构环境下的机器人自适应变阻抗力跟踪控制方法
1
2019
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
基于强化学习的学习变阻抗控制
2
2019
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
... [8 , 10 -11 ],存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
基于强化学习的学习变阻抗控制
2
2019
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
... [8 , 10 -11 ],存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
A hybrid control strategy for grinding and polishing robot based on adaptive impedance control
1
2021
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
A fuzzy-based impedance control for force tracking in unknown environment
2
2022
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
... , 10 -11 ],存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
An adaptive bilateral impedance control based on nonlinear disturbance observer for different flexible targets grasping
2
2022
... 针对主动柔顺控制打磨作业,机器人末端执行器的性能直接影响打磨作业的柔顺性,其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向. 阻抗控制是实现主动柔顺力控制的有效方式,其通过调节系统刚度实现输出力的柔顺调控. 为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题,Zhang等[6 ] 建立机器人末端执行器与工件表面的接触模型和力映射关系,提出基于强化学习算法的机器人力控制方法. 甘亚辉等[7 ] 针对未知刚度及位置多变工况,设计自适应变阻抗力跟踪控制方法,通过建立阻抗模型来适应多变工况刚度的不确定性,并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数. 李超等[8 ] 提出基于强化学习的学习变阻抗控制方法,将高斯过程模型作为系统的变换动力学模型,在成本函数中加入能量损失项,实现了误差和能量的权衡. Zhou等[9 ] 基于机器人系统与环境的接触模型,采用自适应阻抗实现了打磨力控制和位置跟踪控制. Shen等[10 ] 提出基于模糊理论的自适应阻抗控制,通过递归最小二乘迭代计算估计环境参数,使得控制系统在没有环境先验信息的情况下跟踪期望打磨力. Zhong等[11 ] 将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合,实现了对期望接触力和轨迹的跟踪. 上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8 , 10 -11 ] ,存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
... -11 ],存在数据更新过程慢与效率低的局限,对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业,在打磨力控制的实时性和稳定性方面存在一定的不足. 机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高,通常需要严格控制打磨力的精度和超调量. ...
A novel force-controlled spherical polishing tool combined with self-rotation and co-rotation motion
1
2020
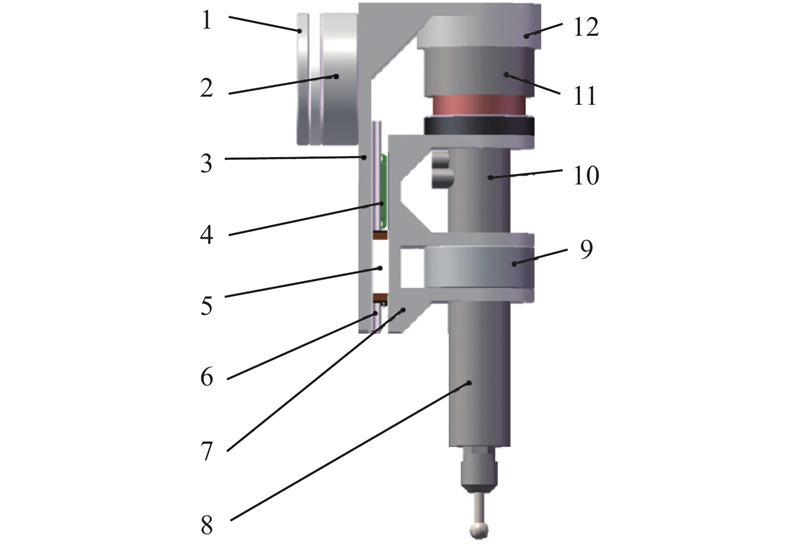
... 机器人打磨系统主要由工业机器人与末端执行器构成. 末端执行器的柔顺打磨作业由主动力控制技术实现,末端执行器的位置和姿态(简称位姿)由工业机器人控制. 工件的打磨质量与材料去除率有关,根据Preston材料去除理论,材料去除率与工具对工件的法向打磨力正相关[12 ] . 为了实现材料去除率可控,保证打磨质量,提高机器人打磨系统动态响应性能[13 ] ,设计柔顺浮动力控末端执行器[14 ] ,如图1 所示. 该末端执行器通过音圈电机驱动打磨主轴往复直线轴向平移运动,实现打磨工具平移浮动调节,主动柔顺控制实现法向打磨力稳定准确控制,打磨主轴带动打磨工具高速旋转运动,轴向平移和旋转运动互不干扰,两者的调节控制便捷. 应用主动力控制技术进行法向打磨力稳定准确控制,并通过机器人进行打磨位姿控制,降低对工业机器人本体的力控制要求,减小力控制和位姿控制的复杂性. ...
Synergistic integrated design of an electrochemical mechanical polishing end-effector for robotic polishing applications
1
2019
... 机器人打磨系统主要由工业机器人与末端执行器构成. 末端执行器的柔顺打磨作业由主动力控制技术实现,末端执行器的位置和姿态(简称位姿)由工业机器人控制. 工件的打磨质量与材料去除率有关,根据Preston材料去除理论,材料去除率与工具对工件的法向打磨力正相关[12 ] . 为了实现材料去除率可控,保证打磨质量,提高机器人打磨系统动态响应性能[13 ] ,设计柔顺浮动力控末端执行器[14 ] ,如图1 所示. 该末端执行器通过音圈电机驱动打磨主轴往复直线轴向平移运动,实现打磨工具平移浮动调节,主动柔顺控制实现法向打磨力稳定准确控制,打磨主轴带动打磨工具高速旋转运动,轴向平移和旋转运动互不干扰,两者的调节控制便捷. 应用主动力控制技术进行法向打磨力稳定准确控制,并通过机器人进行打磨位姿控制,降低对工业机器人本体的力控制要求,减小力控制和位姿控制的复杂性. ...
无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法
3
2023
... 机器人打磨系统主要由工业机器人与末端执行器构成. 末端执行器的柔顺打磨作业由主动力控制技术实现,末端执行器的位置和姿态(简称位姿)由工业机器人控制. 工件的打磨质量与材料去除率有关,根据Preston材料去除理论,材料去除率与工具对工件的法向打磨力正相关[12 ] . 为了实现材料去除率可控,保证打磨质量,提高机器人打磨系统动态响应性能[13 ] ,设计柔顺浮动力控末端执行器[14 ] ,如图1 所示. 该末端执行器通过音圈电机驱动打磨主轴往复直线轴向平移运动,实现打磨工具平移浮动调节,主动柔顺控制实现法向打磨力稳定准确控制,打磨主轴带动打磨工具高速旋转运动,轴向平移和旋转运动互不干扰,两者的调节控制便捷. 应用主动力控制技术进行法向打磨力稳定准确控制,并通过机器人进行打磨位姿控制,降低对工业机器人本体的力控制要求,减小力控制和位姿控制的复杂性. ...
... 柔顺浮动力控末端执行器[14 ] ...
... Compliant floating force-controlled end-effector [14 ] ...
无先验模型曲面的机器人打磨主动自适应在线轨迹预测方法
3
2023
... 机器人打磨系统主要由工业机器人与末端执行器构成. 末端执行器的柔顺打磨作业由主动力控制技术实现,末端执行器的位置和姿态(简称位姿)由工业机器人控制. 工件的打磨质量与材料去除率有关,根据Preston材料去除理论,材料去除率与工具对工件的法向打磨力正相关[12 ] . 为了实现材料去除率可控,保证打磨质量,提高机器人打磨系统动态响应性能[13 ] ,设计柔顺浮动力控末端执行器[14 ] ,如图1 所示. 该末端执行器通过音圈电机驱动打磨主轴往复直线轴向平移运动,实现打磨工具平移浮动调节,主动柔顺控制实现法向打磨力稳定准确控制,打磨主轴带动打磨工具高速旋转运动,轴向平移和旋转运动互不干扰,两者的调节控制便捷. 应用主动力控制技术进行法向打磨力稳定准确控制,并通过机器人进行打磨位姿控制,降低对工业机器人本体的力控制要求,减小力控制和位姿控制的复杂性. ...
... 柔顺浮动力控末端执行器[14 ] ...
... Compliant floating force-controlled end-effector [14 ] ...
1
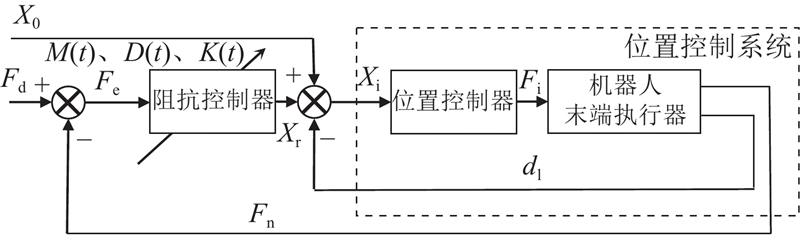
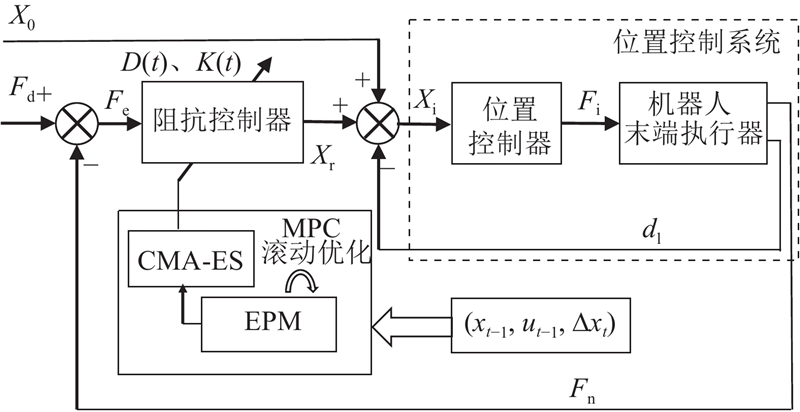
... Hogan[15 ] 针对接触作业的力控制问题,提出阻抗控制方法. 有学者将阻抗控制分为基于力的阻抗控制和基于位置的阻抗控制,后者可以实现较高的位置控制精度[16 ] . 基于位置的阻抗控制基本思想是将位置控制器作为控制系统的内环,将阻抗控制器作为控制系统的外环,外环产生位置修正量,内外环控制共同作用构成闭环控制回路. 通过反馈力计算阻抗控制器输出的位置补偿量,调节内环位置控制器的输入位置,实现对接触过程的力控制. 将基于位置的阻抗控制设计为变阻抗控制器作为控制外环,通过变阻抗控制实现对内环的位置控制系统的自适应补偿,从而实现对机器人打磨力的柔顺控制,提升机器人打磨作业的柔顺性和鲁棒性. 如图3 所示为该变阻抗控制的控制框图,数学模型为 ...
1
... Hogan[15 ] 针对接触作业的力控制问题,提出阻抗控制方法. 有学者将阻抗控制分为基于力的阻抗控制和基于位置的阻抗控制,后者可以实现较高的位置控制精度[16 ] . 基于位置的阻抗控制基本思想是将位置控制器作为控制系统的内环,将阻抗控制器作为控制系统的外环,外环产生位置修正量,内外环控制共同作用构成闭环控制回路. 通过反馈力计算阻抗控制器输出的位置补偿量,调节内环位置控制器的输入位置,实现对接触过程的力控制. 将基于位置的阻抗控制设计为变阻抗控制器作为控制外环,通过变阻抗控制实现对内环的位置控制系统的自适应补偿,从而实现对机器人打磨力的柔顺控制,提升机器人打磨作业的柔顺性和鲁棒性. 如图3 所示为该变阻抗控制的控制框图,数学模型为 ...
1
... 在打磨工具与工件的接触作业过程中,机器人打磨系统的控制量与工具及工件接触的状态量具有马尔科夫性[17 ] ,将机器人打磨系统的动力学传递函数描述为 ...
1
... 在打磨工具与工件的接触作业过程中,机器人打磨系统的控制量与工具及工件接触的状态量具有马尔科夫性[17 ] ,将机器人打磨系统的动力学传递函数描述为 ...
1
... 式中: $\left( {{x_t},{u_t}} \right)$ ${x_t}$ ${u_t}$ f 为系统的动力学传递函数,可以表示该马尔科夫过程的状态转移概率. 将状态的微分作为训练的输出量,可以近似学习动力学模型的梯度,与直接学习状态的值相比,学习状态的微分能够更清晰地描述系统的动态特性,因此更具优势[18 ] . ...
基于强化学习的机器人曲面恒力跟踪研究
1
2019
... 针对工具与工件接触状态和阻抗参数的非线性关系,以t 时间段工具与工件的打磨力的均值和标准差 $\left( {{\text{mean}}\;(F_{\text{c}}^t),{{\rm{var}}}\; (F_{\text{c}}^t)} \right)$ [19 ] ,以阻尼系数和刚度系数 $\left( {{D^t},{K^t}} \right)$ ${x_t} = \left( {{\text{mean}}\;(F_{\text{c}}^t),{{\rm{var}}} \;(F_{\text{c}}^t)} \right)$ ${u_t} = \left( {{D^t},{K^t}} \right)$ t 时间段与t −1时间段状态量的微分为 ...
基于强化学习的机器人曲面恒力跟踪研究
1
2019
... 针对工具与工件接触状态和阻抗参数的非线性关系,以t 时间段工具与工件的打磨力的均值和标准差 $\left( {{\text{mean}}\;(F_{\text{c}}^t),{{\rm{var}}}\; (F_{\text{c}}^t)} \right)$ [19 ] ,以阻尼系数和刚度系数 $\left( {{D^t},{K^t}} \right)$ ${x_t} = \left( {{\text{mean}}\;(F_{\text{c}}^t),{{\rm{var}}} \;(F_{\text{c}}^t)} \right)$ ${u_t} = \left( {{D^t},{K^t}} \right)$ t 时间段与t −1时间段状态量的微分为 ...
1
... 1) BNN模型构建. BNN模型将传统BP神经网络的权重以概率分布的形式描述,建立输入和输出之间的概率分布关系,利用贝叶斯定理和变分推断思想,以证据下界(evidence lower bound,ELBO)作为损失函数训练网络权重,使拟合的BNN在有先验数据的区域表现出较小的不确定性,在无先验数据的区域表现出较大的不确定性. 利用BNN模型拟合控制系统,描述控制系统控制量和状态量之间的分布关系,即可量化由于测量引起的认知不确定性. BNN模型对网络的可训练网络模型参数的权重进行重参数化[20 ] ,使网络参数以概率分布的形式呈现. 假设网络模型输出Y
Hands-on bayesian neural networks: a tutorial for deep learning users
1
2022
... 式中:D 为观测数据. 对于复杂的深度贝叶斯神经网络模型,后验分布的高维性与非凸性使得证据(边缘分布) $\displaystyle\int\nolimits_{\boldsymbol{\theta}} {P\left( {{\boldsymbol{Y}}|{\boldsymbol{x}},{\boldsymbol{\theta}} '} \right)P\left( {{\boldsymbol{\theta}} '} \right){\text{d}}{\boldsymbol{\theta}} '}$ [21 ] . 引入变分推断[22 ] ,通过参数化后验分布(变分后验分布)逼近真实后验. 变分推断的准确度可用变分后验分布与真实分布的近似度描述. KL散度(Kullback Leibler divergence)是描述2种分布近似度常用的方法,其通过Shannon信息熵理论描述概率分布之间的差异性. 假设样本真实后验概率为 $ P\left( {H|D} \right) $ ${q_{_{ \boldsymbol{\theta}}} }\left( H \right)$
1
... 式中:D 为观测数据. 对于复杂的深度贝叶斯神经网络模型,后验分布的高维性与非凸性使得证据(边缘分布) $\displaystyle\int\nolimits_{\boldsymbol{\theta}} {P\left( {{\boldsymbol{Y}}|{\boldsymbol{x}},{\boldsymbol{\theta}} '} \right)P\left( {{\boldsymbol{\theta}} '} \right){\text{d}}{\boldsymbol{\theta}} '}$ [21 ] . 引入变分推断[22 ] ,通过参数化后验分布(变分后验分布)逼近真实后验. 变分推断的准确度可用变分后验分布与真实分布的近似度描述. KL散度(Kullback Leibler divergence)是描述2种分布近似度常用的方法,其通过Shannon信息熵理论描述概率分布之间的差异性. 假设样本真实后验概率为 $ P\left( {H|D} \right) $ ${q_{_{ \boldsymbol{\theta}}} }\left( H \right)$
1
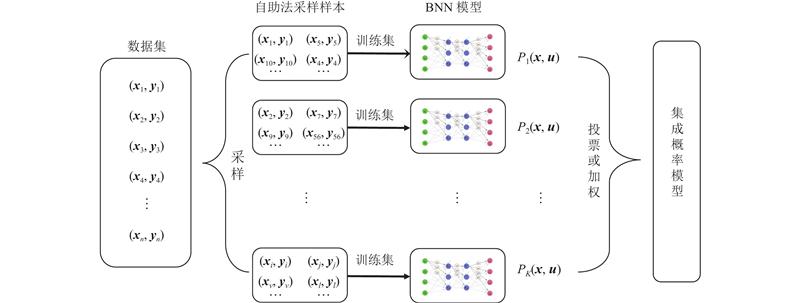
... 2) 集成概率模型构建. 机器人时变耦合非线性打磨作业接触环境引起的系统随机不确定性可以通过集成概率模型的方法来描述,即根据多次采样的数据集拟合多个BNN模型,构建集成概率模型,联合描述系统随机不确定性[23 ] ,表征机器人打磨系统的打磨工具与工件接触状态和阻抗参数之间的非线性关系. 采用自助法(Bootstrapping),从原始数据集中有放回地均匀抽样创建模拟数据集,将有限样本经由K 次重复抽样,建立足以代表母体样本分布的K 个子样本. 利用自助采样的K 个样本,训练出K 个BNN模型,利用模型预测采样轨迹法合成为集成概率模型. 动力学模型f (x ,u K 个BNN模型的输出分布P i x ,u 图4 所示. ...
Autogenerating microsecond solvers for nonlinear MPC: a tutorial using ACADO integrators
1
2015
... 在已知系统传递函数的基础上,根据初始状态量和控制量算出一系列预测域的状态量和控制量轨迹;采用反馈校正,对状态量和控制量进行优化;在控制过程中,采用滚动时域优化方法,在每个控制周期进行局部优化,提高控制系统的抗扰性和稳定性[24 ] . 通过非线性状态传递函数,求解h 步预测域的状态轨迹 ${{\boldsymbol{x}}_t},{{\boldsymbol{x}}_{t+1}},\cdots,{{\boldsymbol{x}}_{t+h}}$
1
... 2) 基于协方差矩阵自适应进化策略算法的参数优化. 由于不宜采用集成概率模型计算梯度,选择非梯度优化算法解算最优控制量. CMA-ES算法作为数值优化算法,在求解非梯度的优化问题时具有全局收敛和收敛快速的优点[25 ] ,主要实现步骤如下. a) 采样重组:采用多变量正态分布生成新的样本点. 在第z 代中,k 个子代样本点生成式为 ...
基于对数四元数的工业机器人Hermite样条曲线姿态插值
1
2019
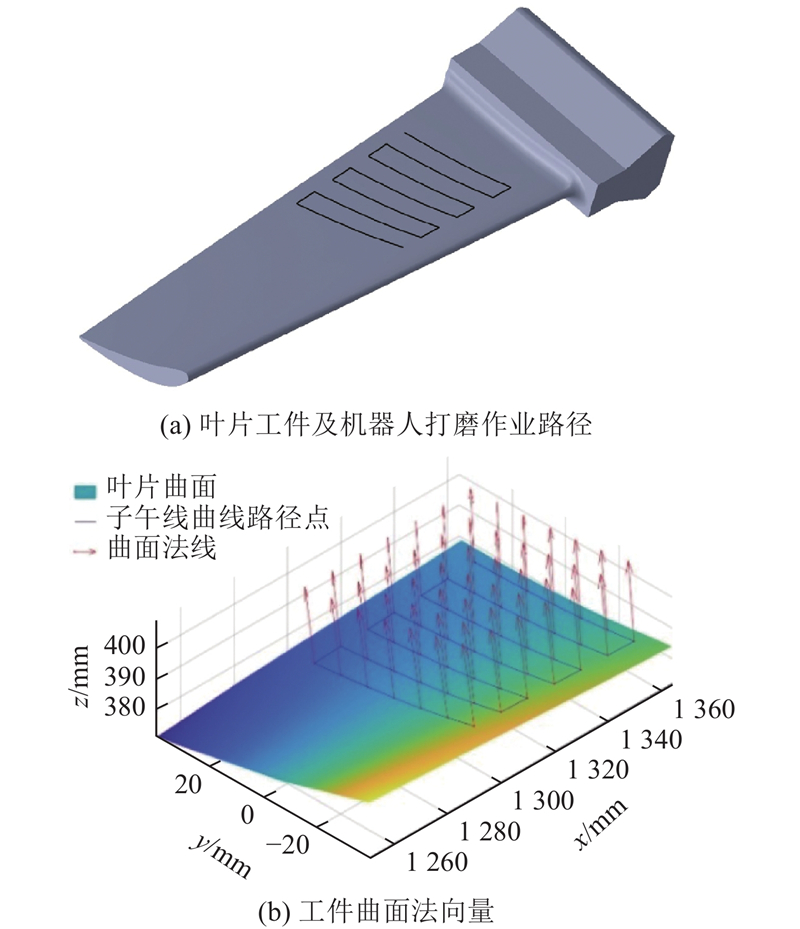
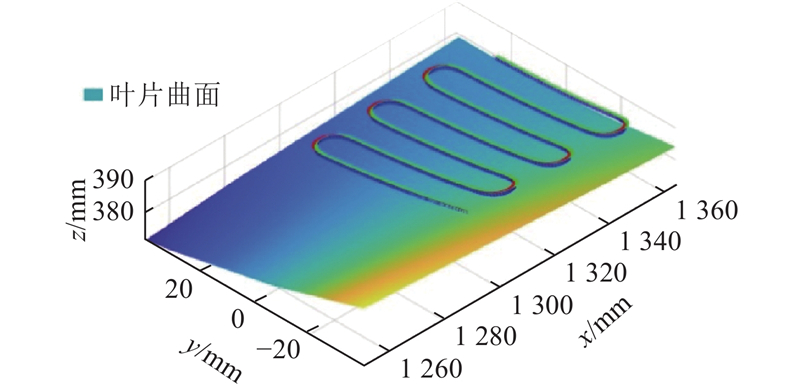
... 1) 作业空间打磨路径和打磨姿态规划. 如图6 (a)所示,采用子午线作为打磨作业路径,利用NURBS曲线插值对打磨作业笛卡尔空间位置进行轨迹规划. 在叶片上根据子午线的形状,采样48个路径点作为型值点,其空间位置和相对应的叶片曲面法向量如图6 (b)所示. 将型值点作为控制点,利用5次NURBS曲线插值,对打磨路径进行插值平滑处理,求得经过平滑后的机器人末端执行器的作业工具末端点空间位置. 为了实现机器人打磨姿态平滑过渡,将姿态矩阵转换为单位四元数,利用单位对数四元数法,将单位四元数转换为三维空间点[26 ] ,对转换后的三维空间点进行5次NURBS曲线插值. 根据打磨路径和打磨姿态规划结果,获得机器人打磨系统对应打磨工具轨迹如图7 所示. ...
基于对数四元数的工业机器人Hermite样条曲线姿态插值
1
2019
... 1) 作业空间打磨路径和打磨姿态规划. 如图6 (a)所示,采用子午线作为打磨作业路径,利用NURBS曲线插值对打磨作业笛卡尔空间位置进行轨迹规划. 在叶片上根据子午线的形状,采样48个路径点作为型值点,其空间位置和相对应的叶片曲面法向量如图6 (b)所示. 将型值点作为控制点,利用5次NURBS曲线插值,对打磨路径进行插值平滑处理,求得经过平滑后的机器人末端执行器的作业工具末端点空间位置. 为了实现机器人打磨姿态平滑过渡,将姿态矩阵转换为单位四元数,利用单位对数四元数法,将单位四元数转换为三维空间点[26 ] ,对转换后的三维空间点进行5次NURBS曲线插值. 根据打磨路径和打磨姿态规划结果,获得机器人打磨系统对应打磨工具轨迹如图7 所示. ...
机器人主动柔顺恒力打磨控制方法
1
2023
... 通过不同期望力的仿真实验可知,所提方法仅在十几次训练后,机器人打磨系统即可使打磨力绝对跟踪误差的最大值、方差和均值均减小至某一较小值,同时对于不同刚度工件也具有较好的打磨力跟踪性能,较好地实现了机器人打磨系统的主动自适应变阻抗打磨力控制,验证了所提方法的有效性. 对于恒定打磨力控制,模糊自适应变阻抗控制是常用方法,当其对某一种恒定打磨期望力调节好适宜模糊逻辑控制参数之后,对其他恒定打磨期望力的跟踪效果通常会变差,自适应性能不高[27 -28 ] . 因此,当模糊变阻抗控制器对不同的恒定打磨期望力进行跟踪时,均应人为调整模糊逻辑参数. 与之相比,本研究所提方法在自适应打磨力控制器经过离线训练后,对于跟踪不同的恒定打磨期望力不需要再次调整参数,仅通过少量训练即可实现变阻抗控制器的主动自适应参数调节,具有较强的自适应性. 所提方法为机器人打磨系统对不同工件以不同期望恒定打磨力开展柔顺打磨作业提供了主动自适应柔顺恒力控制方法. ...
机器人主动柔顺恒力打磨控制方法
1
2023
... 通过不同期望力的仿真实验可知,所提方法仅在十几次训练后,机器人打磨系统即可使打磨力绝对跟踪误差的最大值、方差和均值均减小至某一较小值,同时对于不同刚度工件也具有较好的打磨力跟踪性能,较好地实现了机器人打磨系统的主动自适应变阻抗打磨力控制,验证了所提方法的有效性. 对于恒定打磨力控制,模糊自适应变阻抗控制是常用方法,当其对某一种恒定打磨期望力调节好适宜模糊逻辑控制参数之后,对其他恒定打磨期望力的跟踪效果通常会变差,自适应性能不高[27 -28 ] . 因此,当模糊变阻抗控制器对不同的恒定打磨期望力进行跟踪时,均应人为调整模糊逻辑参数. 与之相比,本研究所提方法在自适应打磨力控制器经过离线训练后,对于跟踪不同的恒定打磨期望力不需要再次调整参数,仅通过少量训练即可实现变阻抗控制器的主动自适应参数调节,具有较强的自适应性. 所提方法为机器人打磨系统对不同工件以不同期望恒定打磨力开展柔顺打磨作业提供了主动自适应柔顺恒力控制方法. ...
Research on the algorithm of constant force grinding controller based on reinforcement learning PPO
1
2023
... 通过不同期望力的仿真实验可知,所提方法仅在十几次训练后,机器人打磨系统即可使打磨力绝对跟踪误差的最大值、方差和均值均减小至某一较小值,同时对于不同刚度工件也具有较好的打磨力跟踪性能,较好地实现了机器人打磨系统的主动自适应变阻抗打磨力控制,验证了所提方法的有效性. 对于恒定打磨力控制,模糊自适应变阻抗控制是常用方法,当其对某一种恒定打磨期望力调节好适宜模糊逻辑控制参数之后,对其他恒定打磨期望力的跟踪效果通常会变差,自适应性能不高[27 -28 ] . 因此,当模糊变阻抗控制器对不同的恒定打磨期望力进行跟踪时,均应人为调整模糊逻辑参数. 与之相比,本研究所提方法在自适应打磨力控制器经过离线训练后,对于跟踪不同的恒定打磨期望力不需要再次调整参数,仅通过少量训练即可实现变阻抗控制器的主动自适应参数调节,具有较强的自适应性. 所提方法为机器人打磨系统对不同工件以不同期望恒定打磨力开展柔顺打磨作业提供了主动自适应柔顺恒力控制方法. ...