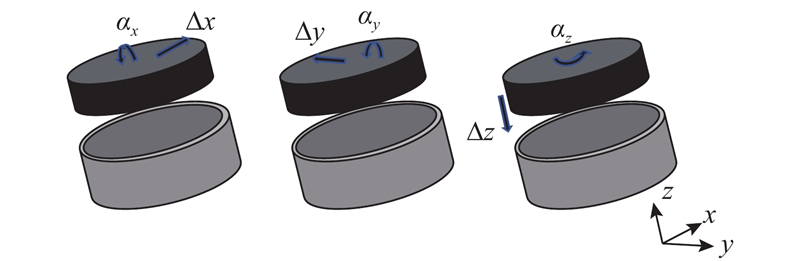
轴孔装配是装配作业中最基本的装配单元，占据装配作业的约40%,并且大口径部件装配在航空航天、武器装备、船舶制造等领域应用广泛^[1]. 目前，实现大口径部件的自动化装配仍然是个挑战^[2-3]. 一些主动的力控制策略已被应用于实际装配任务，并具有一定的实用性. Zhang等^[4]基于简化分析方法，针对轴孔装配任务提出更实用的模糊力控制策略. Pan等^[5]建立空间机械臂等效刚度模型，然后沿着装配方向建立柔性指数，提出考虑等效刚度优化的空间机械臂装配任务控制方法，有效减小了接触碰撞扰动的影响. 然而，当上述控制算法应用于复杂接触模型装配场景时，需要大量时间和精力来调整控制器参数以适应新的装配任务. 因此，需要不依赖于物理接触模型分析的高级算法来较好地执行大口径轴孔装配任务.

受人类工人通过学习经验^[6]完成轴孔装配任务启发，工业机器人可以通过学习装配技能来完成复杂的轴孔装配. 因此，可以应用标准强化学习（reinforcement learning， RL）使机器人通过试验学习装配技能，而不仅仅是将人类的技能传递给机器人程序^[7]. 单纯的RL方法是通过对动作空间进行离散化来输出离散动作， 因此在连续的、高维的^[8]机器人控制任务存在较大的局限性. 通过将深度学习引入强化学习中，得到深度强化学习(deep reinforcement learning， DRL)算法^[9]，该算法利用神经网络的强大知识表征能力，处理大量轴孔接触状态数据^[10-11]， 在装配动作规划这类典型的序贯决策问题上表现出显著性能. 特别是深度确定性决策梯度(deep deterministic policy gradients， DDPG)算法，在诸多应用场景中都能够稳定有效地完成连续的高维动作控制任务. 另外，为了解决DRL算法经验和样本数据不足、训练代价高^[12]、探测动作安全性低^[13]等问题，人们选择了与其他控制方法协同的深度强化学习算法.

Kumar等^[14]对强化学习控制器进行改进，相较于基于Lyapunov理论的马尔可夫博弈控制器，其所提出的模糊RL控制器具有卓越的跟踪性能和更低的计算复杂性. Zarandi 等^[15]提出柔性模糊强化学习算法，该算法用基于模糊规则的系统来逼近值函数. Ren 等^[16]将人类成功操纵任务的基本思想，即可变顺应性和学习应用于机器人组装. Xu等^[17]采用DDPG算法实现了多轴孔装配任务，采用模糊奖励机制来提高探索效率. Zhang等^[18]提出人机协同强化学习算法，以优化装配过程中的任务序列分配方案，实现复杂装配操作的人机协作. Ma等^[19]提出示教学习和强化学习相结合的方式，实现了PCB板上排针的插入任务. Hou等^[20]提出模糊逻辑驱动的基于可变时间尺度预测的强化学习(fuzzy logic-driven variable time-scale prediction-based reinforcement learning， FLDVTSP-RL)方法，相比传统深度Q网络，可以有效减少装配时间.

上述方法都是应用于小型轴孔装配任务的. 在大口径轴孔装配过程中零件具有较大的惯性，就会有较大的冲击力，可能会导致部件的损伤. 为了解决大口径轴孔装配任务中的上述问题，本研究提出基于模糊动作的深度确定性决策梯度(deep deterministic policy gradients with fuzzy actions， DDPGFA)算法，该算法以DDPG算法为基础，解决大部件轴孔接触状态建模困难问题，能获得较为准确的状态数据. 引入模糊动作策略，加快离线训练速度，得到更加精确和稳定的机器人动作输出. 进行大口径轴孔装配的实验，对比有无模糊策略的强化学习算法控制效果，验证DDPGFA算法的有效性.

在实际装配任务中，由于较难获取精确的接触环境参数，控制策略可能产生较大的接触力误差. 对于装配精度要求较高时的大口径轴孔装配任务，比如如图1所示，零件直径超过200 mm，且装配精度要求为0.05 mm的装配任务，须在装配过程中保持较小的装配力，以及较稳定的装配速度.

基于强化学习的装配机器人训练过程如图2所示. 图中， ${\boldsymbol{s}}$为传感器输出的状态量； ${F_X}、{F_Y}$分别为力传感器输出的X向和Y向力信息； $({{\boldsymbol{s}}_i}{\text{, }}{{\boldsymbol{a}}_i}{\text{, }} {r_i}{\text{, }} {{\boldsymbol{s}}_{i+1}})$为训练过程中的小批量采样数据，s_i为每次从经验池采样得到的一组状态量， ${\boldsymbol{a}}_i$表示DDPG算法的输出动作， $r_i$表示每一步得到的奖励，下标 $i$表示训练步数. 首先由机器人位置编码和力-力矩传感器获得装配系统的状态信息，然后输入DDPG网络和模糊动作策略. Actor网络和Critic网络通过从记忆库中抽取小批量样本（mini-batch）进行训练，并由Actor网络产生动作. 模糊动作策略根据状态信息得到动作系数，最后产生最终动作. 在动作执行完成后，装配环境根据设计好的回报函数返回对应的奖励，模型存储 $({{\boldsymbol{s}}_i}{\text{,}}{{\boldsymbol{a}}_i}{\text{,}}{r_i}{\text{,}}{{\boldsymbol{s}}_{i+1}})$并进行学习，整个过程重复循环.

在建立轴孔柔顺装配策略时，主要目的是在每一个轴孔接触状态下确定机械臂对轴的姿态的调整动作，以确保零部件的完好和顺利装配. 因此对DDPGFA算法应用于轴孔装配做了以下几方面的工作.

1）状态空间 $ {\boldsymbol{s}} $的设置. 为了满足强化学习所依据的马尔可夫性，在本研究所规划的轴孔柔顺装配策略中，将每一步的状态定义为X-Y-Z轴线方向受到的力和零件的空间位置，模型的输入表示为

(1) $ {\boldsymbol{s}} = [{F_X},{F_Y},{F_Z},{T_X},{T_Y},{T_Z},{\boldsymbol{P}}]. $

式中： $ {F_X}、{F_Y}、{F_Z}、{T_X}、{T_Y}、{T_Z} $为机器人上力传感器读取的力信息； $ {\boldsymbol{P}} $为大重部件的位姿信息，可以从机器人自带的位置感知器中获得.

在实际装配任务中，为了降低接触力模型的复杂度，减少计算量，可以将对算法决策没有影响的 $ {T_Z} $维度删去. 减少维度处理可以减少计算量、简化神经网络模型. 因此实际状态就变为

(2) $ {\boldsymbol{s}} = [{F_X},{F_Y},{F_Z},{T_X},{T_Y},{\boldsymbol{P}}]. $

2）输出动作空间 ${\boldsymbol{a}}_i$的设定. 模型的输出为每一步机器人执行的动作，如图3所示.

动作空间 ${{\boldsymbol{a}}_i}$表示为

(3) $ {{\boldsymbol{a}}_i} = [{\varDelta _X},{\varDelta _Y},{\varDelta _Z},{\alpha _X},{\alpha _Y},{\alpha _Z}]. $

式中： $\varDelta$表示零件在X-Y-Z轴线方向上的位移增量， $ \alpha $表示零件在绕X-Y-Z轴方向上的角度增量.

3）奖励函数r的设计. 在大口径部件装入的过程中，要求大口径部件的受力要尽可能保持在一个相对合理的范围内，奖励函数应该引导模型学会根据零件的受力情况来进行插入装配动作的调整. 从对装配过程影响较大的力和位移2个因素来设计奖励函数. 首先，依据在径向力安全阈值范围内的实际装配深度来获得主要奖励；其次，设计2种结束状态，分别为单个径向力或单个径向累积位移超过预定范围时的状态；最后设计装配成功的奖励，即轴向累积位移达到预定值. 模型中的奖励函数设计如下：

(4) $ r=\left\{\begin{array}{c}\begin{array}{cc}({P}_{{\rm{h}}}-{P}_{{\rm{a}}}) k,& {F}_{{\rm{t}}} >{F}_{{\rm{T}}}; \\0,& {\displaystyle \sum _{i=1}^{n}{\varDelta }_{Z} > {A}_{{\rm{sum}}z}}.\end{array}\end{array}\right. $

式中： $ {P_{\rm{h}}} $为预定的装配深度； $ {P_{\rm{a}}} $为实际装配深度； $ k $ 为装配深度的奖励系数； ${F_{\rm{T}}}$ 为零件受到的径向力的阈值；F_t为实际受到的径向力， $ {F_{\rm{t}}} = \sqrt {{F_X}^2+{F_Y}^2} $；A_sumz为z向累积运动量的阈值. 当 $ {F_{\rm{t}}} $＞ $ {F_{\rm{T}}} $时，会得到一个负向的奖励值，反之，得到一个正向的奖励. 另外，设 $ {A_{{\rm{sum}}z}} \approx 0.8{A_{\rm{h}}} $，A_h为轴孔设计时的插入深度. 如果Z向累积运动量大于阈值 $ {A_{{\rm{sum}}z}} $，则说明Z向已经运动到位，结束本次训练循环，设置奖励为0.

在模糊策略设计中，使用模糊规则来给出X向和Y向的动作调整系数. 大口径部件在装配时会因夹具的刚性不足而产生抖动，因此利用模糊控制对输入精确度要求不高的特点，设计模糊控制规则，以减小抖动误差对装配过程的影响.

模糊策略的设计，首先是模糊控制器的输入和输出. 考虑到强化学习输出有X、Y、Z 3个方向上的动作，其中Z向动作为插入动作，X和Y向为调整动作，因此模糊策略只对X和Y方向进行控制. 由此输入和输出量如图4所示. 图中， H_X、H_Y分别为方向X和Y上的动作调整系数.

在装配过程中，方向X和Y相对于孔轴心来说具有对称性，因此隶属度函数A(F_X)和A(F_Y)相同，A(H_X)和A(H_Y)相同，隶属度函数示意图如图5所示.

输入F_X和F_Y被分为3个范围，S、P、L分别表示偏小、合适、偏大，在装配训练中X和Y的径向力阈值为30 N，因此输入隶属度范围为[−30，30]. 输出 $ {H_X}，{H_Y} $也被分为3个范围，D、U、I分别表示减小、不变、增大，为了使输出力在较小范围内变动，输出隶属度范围设为[0.9，1.1]，这样能使算法具有较好的调整功能.

为了便于强化学习算法输出力的调节，依据前面建立的隶属度函数和已有的力控经验制定相应的模糊规则，如表1所示.

由确定性策略梯度（deterministic policy gradient， DPG）训练出来的行为评判法是DDPGFA算法的基础^[21]. DDPGFA是针对连续行为的策略学习方法，它基于策略-评估网络结构，直接使用动作值函数来学习动作策略. DDPGFA算法包含4个网络，分别为 Actor网络、策略Actor网络、Critic网络和策略Critic网络.

探索策略的目标是防止智能定位于局部最优. 为此，采用贪婪策略来执行探索行为. 在线学习阶段算法的步骤如算法1^[12]所示.

算法1.　　DDPGFA算法

输入阶段：初始化最大实验次数T₁ ;每次装配实验最大探索次数T₂；网络参数更新频率f ;延迟更新因子 $ \tau $；批量采样大小N

随机初始化Actor网络 $ \mu ({\boldsymbol{s}}|{\theta ^\mu }) $和critic网络 $ Q({\boldsymbol{s,a}}|{\theta ^Q}) $的参数 $ {\theta ^\mu } $和 $ {\theta ^Q} $;

初始化目标网络参数 $ \mu ' $和 $ Q' $并赋值， $ {\theta ^{\mu '}} \leftarrow {\theta ^\mu } $, $ {\theta ^{Q'}} \leftarrow {\theta ^Q} $;

初始化经验回放池 $ R $

将Actor和Critic的参数赋值给相应目标网络;

For episode =1 to T₁ do

初始化动作中的随机噪声 $ {{\boldsymbol{N}}_i} $，观测最初状态 $ {{\boldsymbol{s}}_1} $

For i=1 to T₂ do

根据当前策略和随机噪声采样获得动作： ${{\boldsymbol{a}}_{{i}}} \sim \mu ({{\boldsymbol{s}}}|{\theta ^\mu })+{\boldsymbol{\varepsilon}} \,,{\boldsymbol{\varepsilon}}\sim {{\boldsymbol{N}}_i}$.

将 $ {F_X}、{F_Y} $输入模糊控制器并计算 ${H_X}、{H_Y}$;

机器人执行动作：

$ \hat{{{\boldsymbol{a}}}_{i}}={\left[{\varDelta }_{X}{{ H}}_{X}\text{,}{\varDelta }_{Y}{{ H}}_{Y}\text{,}{\varDelta }_{Z}\text{,}{\alpha }_{X}\text{,}{\alpha }_{Y}\text{,}{\alpha }_{Z}\right]}_{i}. $

计算奖赏 $ {r_i} $， 观测执行后的状态 ${{\boldsymbol{s}}_{{{i}}+{{1}}}}$;

存储数据对 $ ({{\boldsymbol{s}}_{{i}}}{\text{,}}{{\boldsymbol{a}}_{{i}}}{\text{,}}{r_i}{\text{,}}{{\boldsymbol{s}}_{{{i}}+{{1}}}}) $于经验池 $ R $中

从 $ R $中随机采样N个 $ ({{\boldsymbol{s}}_{{i}}}{\text{,}}{{\boldsymbol{a}}_{{i}}}{\text{,}}{r_i}{\text{,}}{{\boldsymbol{s}}_{{{i}}+{{1}}}}) $数据对;

设 ${y_i} = {r_i}+\gamma Q'({{\boldsymbol{s}}_{{{i}}+{{1}}}},\mu '({{\boldsymbol{s}}_{{{i}}+{{1}}}}|{\theta ^{\mu '}})|{\theta ^{Q'}}).$

计算损失函数:

$ L = \frac{1}{N}\sum\nolimits_i {{{({y_i} - Q({{\boldsymbol{s}}_{{i}}},{{\boldsymbol{a}}_{{i}}}|{\theta ^Q}))}^2}} . $

采用Adam optimizer更新 $ {\theta ^Q} $;

计算策略网络的更新梯度 ${\nabla _{{\theta ^\mu }}}{J_\beta }(\mu ) \approx \frac{1}{N}\times \sum\limits_i {({\nabla _a}Q({\boldsymbol{s}},{\boldsymbol{a}}|{\theta ^Q}){|_{{\boldsymbol{s}} = {{\boldsymbol{s}}_i},{\boldsymbol{a}} = \mu ({{\boldsymbol{s}}_i})}} \cdot {\nabla _{{\theta ^\mu }}}\mu ({\boldsymbol{s}}|{\theta ^\mu }){|_{{\boldsymbol{s}} = {{\boldsymbol{s}}_i}}})}$.

更新策略Actor网络和策略Critic网络参数

$ {\theta ^{{\mu '}}} = \tau {\theta ^\mu }+(1 - \tau ){\theta ^{{\mu '}}} ,\;\; {\theta ^{{Q'}}} = \tau {\theta ^Q}+(1 - \tau ){\theta ^{{Q'}}} . $

End for

End for

建立的虚拟轴孔装配环境与实际装配环境基本相同，模拟大口径部件装配过程的部分环境参数值如表2所示.

状态设置：为了显示轴入孔阶段的详细过程，设置7个状态量，分别是X、Y、Z轴的力和力矩，还有轴和孔的相对位姿信息，其中Z向转矩 ${T_Z}$设置为0.

动作设置：动作集使用了较为灵活的6个基本动作，包含了X、Y、Z轴移动和转动.

回报设置：依据轴孔装配中主要参数变化情况，即径向力和径向累积位移来设计回报函数，以引导机器人快速高效地装轴入孔. 为了安全起见，在装配过程中指定了力的阈值并将其纳入奖励函数. 单一的径向力或单一的径向累积位移超过设定的范围是给定的2个结束状态. 奖励函数表示为

(5) $ r = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {({P_{\rm{h}}} - {P_{\rm{a}}})k,}&{{F_{\rm{t}}} - {F_{\rm{T}}} > \delta ;} \\ { - 1,}&{|{F_X}| > F_{{\rm{T}}X}{\text{或}}|{F_Y}| > F_{{\rm{T}}Y};} \\ { - 1,}&{\displaystyle \sum\limits_{i = 1}^n {\varDelta_X > {A_{{\rm{sum}}x}}{\text{或}}\displaystyle \sum\limits_{i = 1}^n {\varDelta_Y > {A_{{\rm{sum}}y}}}; } } \\ {0,}&{\displaystyle \sum\limits_{i = 1}^n {\varDelta_Z > {A_{{\rm{sum}}z}}}. } \end{array}} \end{array}} \right. $

式中：A_sumx、A_sumy分别为X、Y方向累积运动量的阈值，F_TX、F_TY分别为X、Y方向力的安全阈值. 如果 $ {F_X} $或者 $ {F_Y} $的绝对值大于安全阈值 $ F_{{\rm{T}}X} $和 $ F_{{\rm{T}}Y} $，则设置奖励为−1，且退出训练过程；如果X轴的累积运动量大于安全阈值 ${A_{{\rm{sum}}x}}$，或者Y轴方向的累积运动量大于安全阈值 ${A_{{\rm{sum}}y}}$，则设置奖励为−1，且退出训练过程.

网络结构设置：单独的DDPG算法和DDPGFA算法的参数如表3所示.

在训练过程中，在迭代过程中记录智能体获得的累积奖励，并在相同装配条件下测试DDPG装配策略的训练效果， 如图6所示为2种装配算法训练过程中的总奖励Rew随训练回合T的变化曲线.

从2种算法的奖励曲线可以看出，DDPGFA算法在训练快速性方面强于DDPG算法，相比之下，训练成功所用回合数减少了15%.仿真图表明，经过150轮训练，训练过程逐渐稳定下来，在每一次成功的训练过程中都能将各轴上的力维持在预定的阈值内.

装配任务由KUKA六自由度机器人执行，机器人重复定位精度为 ±50 $ {\text{μm}} $. 六维力传感器安装在夹具与机器人末端连接处. 位置和方向可以很容易地从机器人控制器上测量. 计算机通过利用python开发的TCP/IP协议与机器人控制器通信. 力控制器根据特定的快速指令从力传感器读取受力值. 这样，每个时间步采集状态数据的时间约为2 s.对于本次大口径轴孔装配任务，对有模糊策略和无模糊策略的算法分别设置4组初始位置不同的实验，如表4所示. 表中， $W_X、W_Y、W_Z $分别为X、Y、Z轴方向初始轴孔相对位置. 实验1~4的初始轴孔相对位置分别为轴孔装配间隙的5、10、20、25倍.

在实验过程中接触力F随装配步数t的变化如图7所示. 如表5所示，统计了不同算法下X和Z方向的装配力，因为这2个系列的力可以大致代表装配过程的力. 对比实验1和实验3，可以看出，在不同的位置偏差下，单纯的DDPG算法很难保持稳定的总装配步骤和装配时间，而DDPGFA算法在不同的位置偏差下可以保持稳定的装配过程，说明DDPGFA算法在优化过程中明显优于DDPG算法，其收敛过程更加稳定.

此外，在相同的位置误差下，DDPGFA算法的平均装配力明显小于DDPG算法的装配力变化，装配力降低了约30%.在实验3和实验4中，DDPG算法的力的波动较大；在实验4中，DDPG算法装配失败. 虽然有明显的位置偏差，但DDPGFA算法调整得较平稳，装配力也在可接受的范围内.

综上所述，基于DDPGFA算法的装配策略比基于单独的DDPG算法的具有更稳定的训练过程和更强的求解能力，更能够满足大直径轴孔零件的装配任务要求，验证了改进算法的有效性.

提出用于大口径轴孔装配任务的DDPGFA装配策略，该策略通过将模糊动作与传统的DDPG算法结合，完成轴入孔的装配训练阶段，然后应用于实际的装配过程.

装配训练过程表明，提出的DDPGFA策略可以实现更平滑的收敛状态，并具有更快的收敛速度，在仿真训练上比典型的DDPG算法快15%. 在实际装配过程中，DDPGFA策略在相同的初始位置偏差下有更稳定的装配步骤. 并且在装配过程中，装配接触力减少了约30%，可以更快、更精确地进行机器人装配动作调整. 实验结果证明所提控制策略的可行性和高效性.

在后续研究中，将考虑采用不同尺寸的轴孔来做对比实验，制定更加泛用的控制策略，实现多种轴孔的柔顺装配.