<img src="https://www.zjujournals.com/eng/images/1008-973X/images/logo.png" class="img-responsive">

图 1 遥控船

Fig.1 Drone ship

图 2

图 2 40F型螺旋桨

Fig.2 40F propeller

1.3. 船的自航数值模拟

假定船圆周运动的速度为V_a，保持V_a不变，左螺旋桨转速为0，通过调节右螺旋桨的转速n，得到右螺旋桨的推力T_n和船航行阻力R_n随n的变化曲线. 2条曲线相交的点即为自航点，得到V_a船速下所对应的螺旋桨的转速n_a和推力T_a. 由推力和两桨之间的距离，可以计算船的转船力矩M_a（已知螺旋桨转速的方法与上述方法类似，保持螺旋桨转速不变，通过调节船速获得自航点）.

通过船的自航数值模拟，可以得到船在稳定状态下某一船速所对应的螺旋桨转速和螺旋桨推力，计算出M_a，后续船舶的圆周运动数值模拟会基于M_a得到船的转弯角速度，从而计算出船的转弯半径.

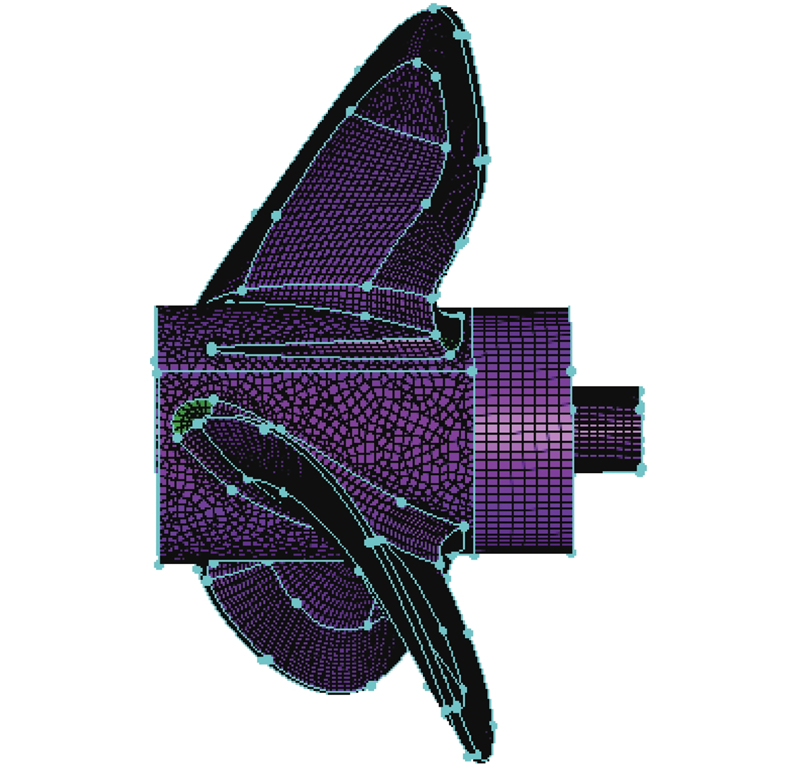
1.3.1. 网格处理

船体表面主要采用结构网格配有少量的非结构网格，如图3所示. 为了更好地捕捉自由液面，在吃水线附近设置密度较高的网格. 如图4所示为螺旋桨的表面网格，桨叶边缘位置和根部及桨毂的边界区域均采用高密度结构网格，其余部分采用非结构网格.

图 3

图 3 船体三维网格

Fig.3 Three-dimensional grids of hull

图 4

图 4 螺旋桨三维网格

Fig.4 Three-dimensional grids of propeller

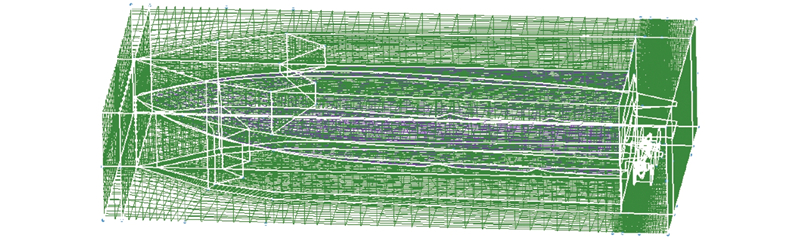
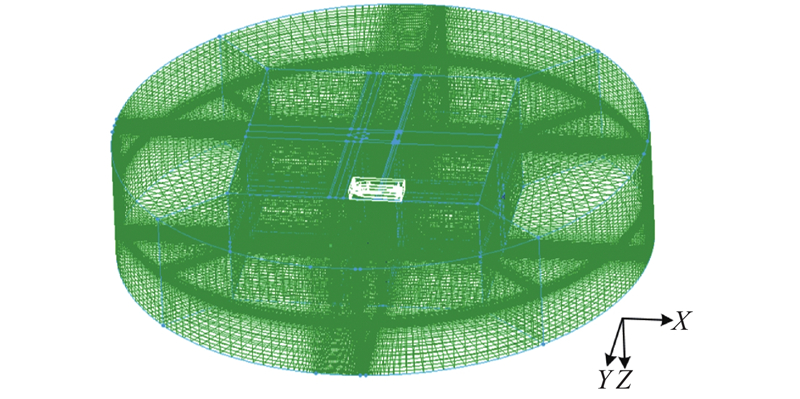
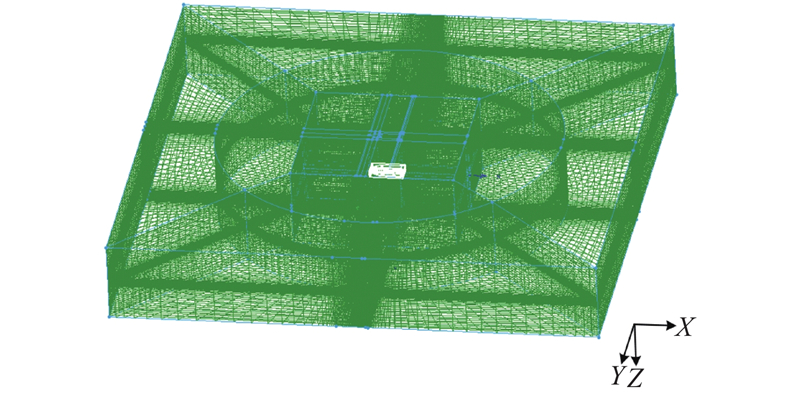
在计算过程中，采用滑移网格技术模拟螺旋桨的旋转运动. 整个流场划分成2个旋转域和1个静止域，共计470万个网格. 其中2个旋转域有230万网格，占网格总数的48.93%，静止域有240万网格. 2个旋转域为包含螺旋桨的圆柱体. 由于螺旋桨的桨叶部分在仿真计算中较重要，划分了部分边界层网格. 分别在左、右螺旋桨外侧生成一个圆柱体，用非结构网格填充圆柱体内部除螺旋桨外的剩余空间，得到2个旋转域网格.

利用网格分块技术对整个船身的网格进行划分，除船艉包含2个旋转域的长方体外，其余均为结构网格，如图5所示. 通过设置路径线对长方体6个表面的网格进行延伸，获得整个计算域，如图6所示，除2个旋转域外，其余均为静止域部分. 自航计算域的大小如下：船的前后间距分别为2倍、6倍船长，船的左右间距大约为2倍船长，船的上下间距大约为1倍船长.

图 5

图 5 船体周围的三维网格

Fig.5 Three-dimensional grids of hull around

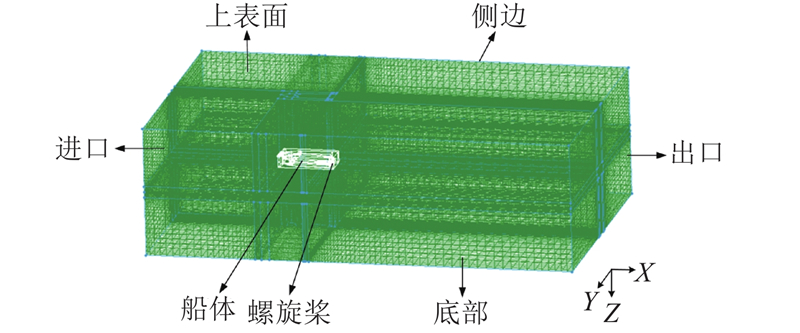
1.3.2. 边界条件

1）入口边界设定：本文的来流方向为指向X轴方向（从船前指向船尾），将图6的inflow边界设置为速度入口，大小为0.441 m/s.

2）出口边界设定：将图6的outflow边界设置为开放式出口.

3）壁面边界设定：将图6的hull、side、top、bottom边界设置为 Wall，其中的hull为无滑移壁面，其余3个为自由滑移壁面.

4）交界面设定：在2个旋转域和静止域相交的网格设置交界面，交界面模型为滑移网格模型（transient rotor-stator）^[15].

图 6

图 6 船体的自航计算域

Fig.6 Calculated parts of hull

1.3.3. 计算结果及分析

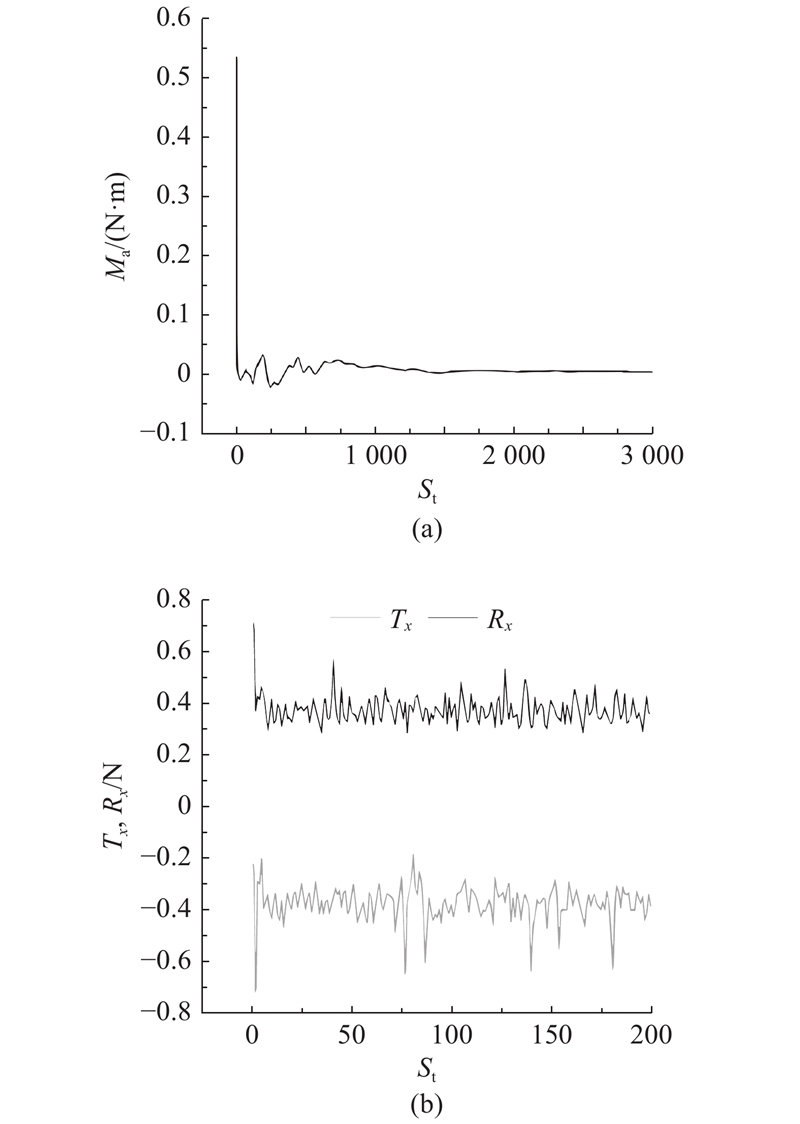
在求解器中依次将推力在x方向投影的面积分作为螺旋桨推力T_x，阻力在船体表面积的面积分R_x作为螺旋桨的推力. 将船舶阻力和螺旋桨推力数值模拟结果的稳定性作为判断收敛性的依据. 在每一步迭代过程中，均对上述2个值进行数值求解，如图7所示为当残差<10⁻⁶时，迭代200步的计算结果. 图中，S_t为迭代时间步长. 可知，船舶阻力和螺旋桨推力的波动范围定义为±0.1.

图 7

图 7 力矩、螺旋桨推力和船舶阻力随步长的波动

Fig.7 Moment of force, thrust of propeller and resistance of ship calculated in every time step

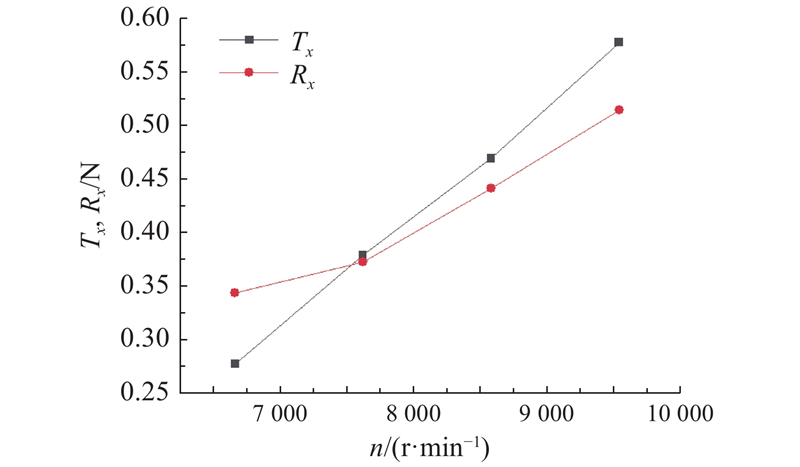
通过船舶的圆周运动模拟，得到当右螺旋桨转速为6 660、7 620、8 580、9 540 r/min时的螺旋桨推力和船阻力，如图8所示. 可知，当螺旋桨转速为7 560 r/min时，螺旋桨的推力和船航行的阻力相等，都为0.37 N. 已知两螺旋桨间的距离为0.038 m，则转动力矩 ${M_{\rm{a}}} = F l = 0.37 \times 0.038 \div 2 = 0.007\;03{\rm{N \cdot m}}$.

图 8

图 8 当转速为6 500~10 000 r/min时自航点的确定

Fig.8 Determination of self-navigation match points when rotation speed is between 6 500 and 10 000 r/min

从文献[16]可知，当螺旋桨的位置越接近自由液面、进速系数越小时，螺旋桨的吸气现象越严重，螺旋桨的推力越小. 本文中螺旋桨的安装位置离水面较近，且螺旋桨的进速系数较小，为了更准确地模拟螺旋桨推力，在仿真过程中考虑自由液面的存在. 如图9所示为螺旋桨周围的自由液面图. 图中，φ_w为水占总体积的比例. 螺旋桨的抽吸作用使得螺旋桨上方的部分空气通过空气腔被自由液面带入水下^[16]，影响螺旋桨的推力.

图 9

图 9 螺旋桨转速为7 560 r/min时右侧螺旋桨附近的自由液面分布图

Fig.9 Distribution of freedom surface around right propeller when rotation speed of propeller is 7 560 r/min

兴波阻力作为船舶阻力的一部分，通过设置自由液面可以解决波浪对船舶阻力的影响，获得较真实的船舶阻力^[17]. 如图10的波高图所示，本文的z轴是指向下方的，图10中颜色越深表示该处的波越高，螺旋桨的高速旋转使得后方产生较大的波浪，船身周围为燕尾状的波纹. 图中，h_w为波高.

图 10

图 10 螺旋桨转速为7 560 r/min时船行驶后形成的波高图

Fig.10 Distribution of wave height after ship passed when rotation speed of propeller is 7 560 r/min

1.4. 船的圆周运动数值模拟

整个流场由2个计算域组成：一个是旋转域，一个是静止域. 整个计算域表面给定x轴向的速度V_a（船的航行速度），通过调节旋转域的角速度 $\omega_{\rm{a}} $（船的转动角速度），得到船的转动力矩M_n随 $\omega $变化的曲线. 用M_n=M_a的一条直线插值上述曲线，得到M_n=M_a时的 $\omega $_a，由公式R=V/ $\omega $计算船的转弯半径R_a.

通过船的圆周运动数值模拟，得出船在某一转动角速度下的转动力矩与前面自航模拟得到的结果相等. 利用该角速度和船速，可以计算船的转动半径.

1.4.1. 网格处理

利用自航数值模拟的网格划分方法，得到长方体状的网格. 在长方体外侧生成一个圆柱体框架，并与内部的长方体框架相连，用结构网格填充两框架间的空间，构建圆柱状的旋转域网格，如图11所示.

图 11

图 11 旋转域

Fig.11 Rotation parts

利用类似的方法在旋转域网格外侧生成4个体网格，得到整个计算域. 如图12所示，除上述旋转域外的其余部分为静止域.

图 12

图 12 整个计算域

Fig.12 Whole calculated parts

1.4.2. 边界条件

1）远场边界设定：给定X轴方向（从船前指向船尾）的速度矢量，大小为0.441 m/s.

2）壁面边界设定：船身和螺旋桨的表面设为无滑移壁面.

3）交界面设定：旋转域和静止域相交的网格设置为交界面，交界面模型为多参考系模型（frozen rotor）^[15].

1.4.3. 计算结果及分析

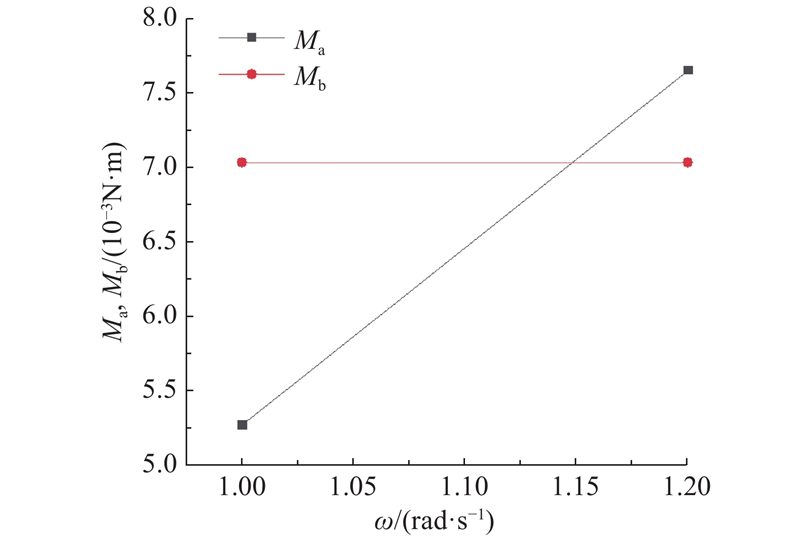
选用同样的收敛方法，选取角速度为−9.55、−11.46 r/min 2种工况作为研究对象，得出船身受到的转船阻力矩. 绘制如图13所示的转动力矩M_a，用自航结果计算的单个螺旋桨推力和螺旋桨偏心安装位置为力臂算出的转船推力矩M_b. 为了得到船的转弯角速度，利用2种方法计算船的转动力矩. 基于螺旋桨推力得到固定的转动力矩M_a；基于船舶阻力得到转动阻力矩随转弯角速度变化的曲线（即为图中的转动力矩M_b），2条线的交点即为船体的实际转弯角速度. 得到转船力矩为0.007 03 N·m时的角速度为−10.96 r/min.

图 13

图 13 角速度的判定

Fig.13 Determination of angular velocity

船的转动半径为

$ R_{\rm{a}} = {V_{\rm{a}}}/{\omega_{\rm{a}} } = 0.384\;{\rm{m}}. $

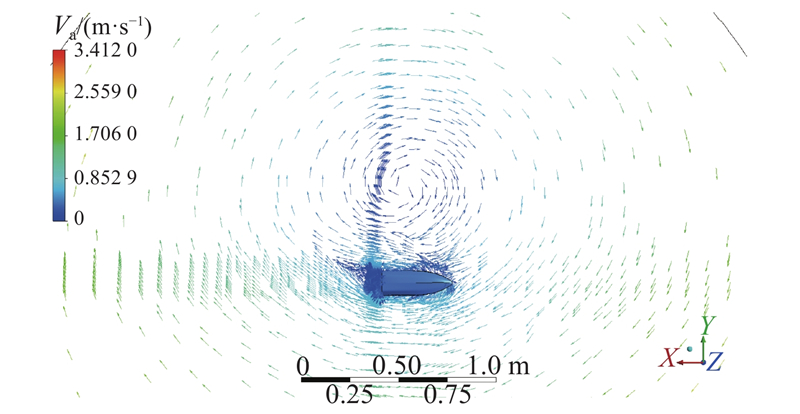
选取角速度为−9.55 r/min的计算结果，开展流场分析发现，船侧面形成一个涡，涡的中心和船的重心相距一个转弯半径.

数值模拟过程是船的逆时针圆周运动，因此在船的左侧形成顺时针旋转的涡，如图14所示. 如图15所示为流线图，在船的左侧进行旋转运动，水流的速度由中心向外侧逐渐变大，船身周围的水流速度基本和所求的船速相等.

图 14

图 14 当船以−10.96 r/min速度转弯时的速度矢量图

Fig.14 Distribution of velocity vector when rotation speed of ship is −10.96 r/min

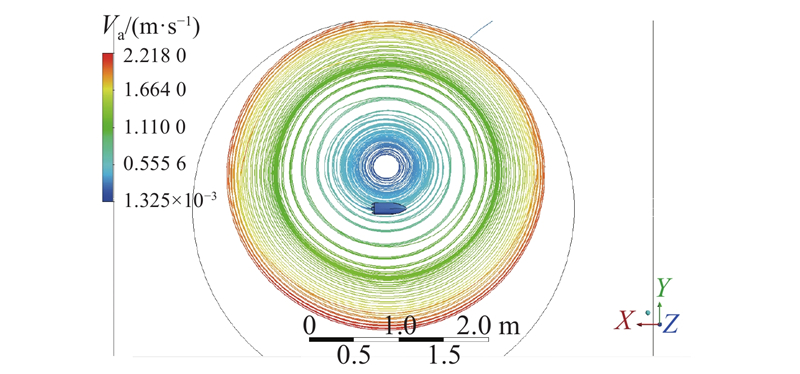
图 15

图 15 当船以−10.96 r/min速度转弯时的流线图

Fig.15 Streamlines of ship when rotation speed of ship is −10.96 r/min

2. 实验研究

2.1. 实验方法

参考Muske等^[17]的实验思路，设计的实验平台如图16所示. 该实验平台主要由以下5部分组成：水池、刻度尺、摄像机、支架、可调云台.

图 16

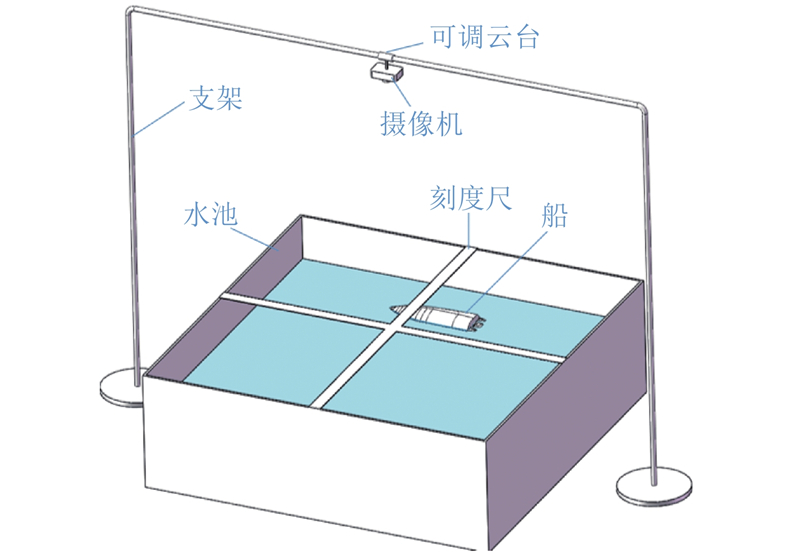
图 16 无人船转弯半径测试的实验平台设计图

Fig.16 Experimental system of unmanned ship turning radius

无人船在水池中进行匀速圆周运动，摄像机从水池上空往下拍摄，得到无人船匀速转1周的视频，通过剪辑软件把视频分割成独立的照片. 借助水池纵向和横向粘贴的刻度尺，确定任意时刻无人船的位置点. 在各个坐标点添加船转半周的时间，寻找新时间点所对应的照片，得到新时间点时船的位置点，由这2个位置点计算无人船的转弯半径.

2.2. 实验结果及分析

通过实验得到一段无人船圆周运动的视频，利用剪辑软件截取船匀速左转一圈的一段视频. 视频总长为5.8 s，即船转一圈的时间为5.8 s. 通过剪辑软件中的连续截图功能，视频播放过程中每隔0.1 s截一张图，如图17所示，总共得到59张图.

图 17

图 17 部分实验拍摄图

Fig.17 Some of experimental records

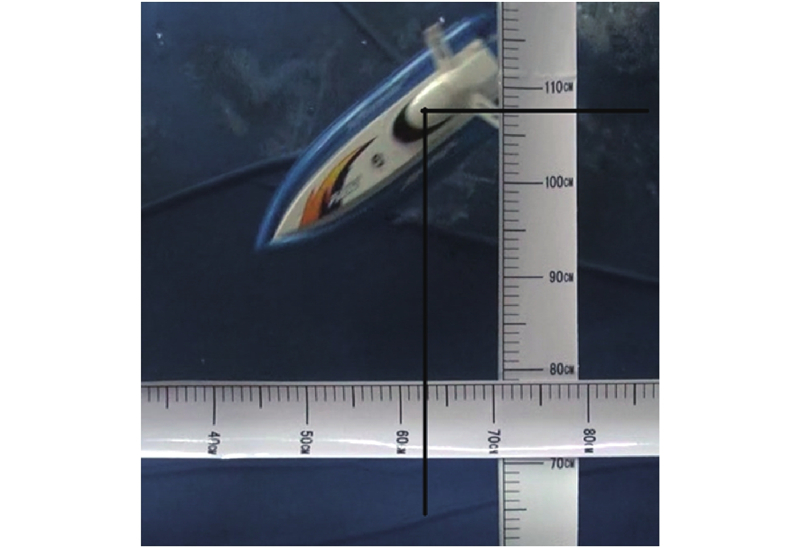
打开某张截取的图片，以0.6 s的截图为例，以船的重心为顶点，如图18所示，分别绘制横向和纵向2条垂线. 此时，纵向线与软尺相交于62.9，横向垂线与软尺相交于107.6，由此可得0.6 s时船的重心位置为（62.9,107.6）. 需要2.9 s，通过上述方法得到船转半圈（即3.5 s）时船的重心位置（94, 43），依据这2个点的坐标值计算出船匀速圆周运动时的转弯半径为35.85 cm.

图 18

图 18 无人船重心位置的确定

Fig.18 Location of gravity center of autonomous ship

为了降低实验的测量误差，随机选取6组数据进行转弯半径的求解. 求解这6组数据的平均值，作为船舶实际的转弯半径.

根据摄像机的成像原理可知，同一张照片中的2个物体，距离相对远的物体会被缩小. 通过上述实验所得的转弯半径不是实际的转弯半径，需要进行换算操作. 摄像机和船重心间的直线距离为126 cm，刻度尺所在平面和船重心所在平面之间的垂直距离为18 cm，则实际转弯半径为

$ r = \frac{{35.62 \times (126 + 18)}}{{126}}{\text{ = }}0.407\;{\rm{m}}. $

将仿真得到的转弯半径和实验结果作比较，误差为5.56%，基本能够满足工程实用的要求.

3. 结　论

（1）在滑移网格模型中，运用螺旋桨自身旋转产生推力的方法，可以较准确地模拟螺旋桨的推力和船的阻力.

（2）对包含船、桨在内的大区域网格旋转，可以较准确地模拟船的圆周运动.

（3）船在旋转运动时，水流的速度由中心向外侧逐渐变大，船身周围的水流速度和所求的船速基本相等.

（4）船转弯半径的数值模拟结果与试验测量值之间的相对误差为5.56%.

当螺旋桨转速或船速中任一项确定时，可以采用上述数值模拟方法，对船圆周运动的转弯半径进行有效预报，这有助于研究双桨的转速差和船的转弯角度之间的关系，推动无人船自主航行控制的发展.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

陈真义. 小型水面无人船航行状态感知系统研究[D]. 武汉: 武汉理工大学, 2014.

CHEN Zhen-yi. Research on small unmanned surface vehicle sailing state obtaining system [D]. Wuhan: Wuhan University of Technology, 2014.

DOI:10.1016/j.oceaneng.2020.107793 [本文引用: 1]

[2]

张树凯, 刘正江, 张显库, 等

无人船艇的发展及展望

[J]. 世界海运, 2015, 38 (9): 29- 36

URL

ZHANG Shu-kai, LIU Zheng-jiang, ZHANG Xian-ku, et al

The development and prospect of unmanned craft

[J]. Shipping Industry of the World, 2015, 38 (9): 29- 36

URL

[3]

CHEN P F, HUANG Y M, PAPADIMITRIOU E, et al

Global path planning for autonomous ship: a hybrid approach of fast marching square and velocity obstacles methods

[J]. Ocean Engineering, 2020, 214: 107793

[4]

赵英序, 朱景伟, 边涛, 等

基于PMSM的双螺旋桨USV推进系统建模与仿真

[J]. 大连海事大学学报:自然科学版, 2018, 44 (1): 17- 24

ZHAO Ying-xu, ZHU Jing-wei, BIAN Tao, et al

Modeling and simulation of twin-propeller unmanned surface vehicle propulsion system based on PMSM

[J]. Journal of Dalian Maritime University: Natural Science Edition, 2018, 44 (1): 17- 24

[5]

叶金铭, 熊鹰, 孙海涛, 等

空泡螺旋桨诱导的双桨船脉动压力数值预报

[J]. 哈尔滨工程大学学报, 2013, 34: 568- 574

YE Jin-ming, XIONG Ying, SUN Hai-tao, et al

Numerical prediction of pressure fluctuations induced by cavitating propeller on twin-screw ship

[J]. Journal of Harbin Engineering University, 2013, 34: 568- 574

[6]

郭海鹏. 基于CFD的双桨双舵船四自由度MMG模型建模及操纵性预报研究[D]. 上海: 上海交通大学, 2019.

GUO Hai-peng. Research on the CFD-based modeling of 4-DoF MMG model and maneuverability prediction for a twin-propeller twin-rudder ship [D]. Shanghai: Shanghai Jiao Tong University, 2019.

[7]

庄丽帆, 刘源, 凌杰, 等

基于船-桨-舵组合系统舵球节能效果数值预报

[J]. 中国水运, 2018, 18 (9): 79- 81

ZHUANG Li-fan, LIU Yuan, LING Jie, et al

Numerical prediction of rubber energy saving effects based on boat-propeller-rudder system

[J]. China Water Transport, 2018, 18 (9): 79- 81

DOI:10.3969/j.issn.2095-2783.2017.07.001

[8]

齐慧博, 刘业宝, 张克正, 等

基于CFD方法的桨舵干扰非定常水动力性能研究

[J]. 中国科技论文, 2017, 12 (7): 725- 728

QI Hui-bo, LIU Ye-bao, ZHANG Ke-zheng, et al

Unsteady hydrodynamic performance of propeller and rudder system studied by CFD

[J]. China Sciencepaper, 2017, 12 (7): 725- 728

DOI:10.3969/j.issn.2095-2783.2017.07.001

[9]

SAKAMOTO N, KUME K, KAWANAMI Y, et al

Evaluation of hydrodynamic performance of pre-swirl and post-swirl ESDs for merchant ships by numerical towing tank procedure

[J]. Ocean Engineering, 2019, 178: 104- 133

DOI:10.1016/j.oceaneng.2019.02.067 [本文引用: 1]

[10]

祝启波. 基于船-桨-舵全耦合求解的船舶自航性能数值预报方法研究[D]. 镇江: 江苏科技大学, 2016.

ZHU Qi-bo. Numerical prediction method research of ship self-propulsion performance based on hull-propeller-rudder system [D]. Zhenjiang: Jiangsu University of Science and Technology, 2016.

[11]

陈志明, 袁剑平, 严谨, 等

基于MRF方法和滑移网格的螺旋桨水动力性能研究

[J]. 船舶工程, 2020, 42 (Supple.1): 157- 162

CHEN Zhi-ming, YUAN Jian-ping, YAN Jin, et al

Study on hydrodynamic performance of propeller based on MRF model and sliding mesh

[J]. Ship Engineering, 2020, 42 (Supple.1): 157- 162

[12]

林焰, 何靖仪

基于RANS法的船舶动力及自由运动预报

[J]. 船舶工程, 2019, 41: 52- 57

LIN Yan, HE Jing-yi

Prediction of ship resistance and free motion based on RANS method

[J]. Ship Engineering, 2019, 41: 52- 57

[13]

陈如星, 周瑞平, 林晞晨

基于CFX的螺旋桨激振力数值预报研究

[J]. 武汉理工大学学报, 2014, 36 (7): 73- 79

CHEN Ru-xing, ZHOU Rui-ping, LIN Xi-chen

Numerical simulation of the propeller-induced force based on CFX

[J]. Journal of Wuhan University of Technology, 2014, 36 (7): 73- 79

[14]

周晓明. 螺旋桨功率与推力数据库的建立[D]. 杭州: 杭州电子科技大学, 2020.

ZHOU Xiao-ming. Establishment of propeller power and thrust database [D]. Hangzhou: Hangzhou Dianzi University, 2020.