多通道和多模射频通信系统往往包含多个射频收发器芯片,系统性能在很大程度上取决于时钟抖动和时钟相位的一致性,当不同接收机之间的时钟相位偏差过大时,系统的增益、信噪比以及通信质量都会下降[1-2]. 并且射频前端通道间须满足良好的相位一致性,因此为其提供的本振信号也须满足相位同步[3-5]. 在射频收发器中,基于小数分频锁相环(phase locked loop, PLL)的频率综合器既能够提供系统的时钟信号,又是产生本振信号的常用方式. 由于各个射频收发器的工作过程、电压、温度(PVT)条件通常难以完全一致,在对PLL输入相同参考时钟时,PLL间输出信号的相位仍然会产生差异[4]. 如何对PLL输出信号相位实行高精度控制,实现不同射频收发器芯片间的本振信号相位、时钟信号相位同步,变得越来越重要.
上海交通大学[4]在PLL内部的分频器后串接采样器,消除由于分频器延时不同造成的PLL间输出相位不一致的问题,但该方法只适用于分频器的分频比为整数的PLL,输出信号频率的分辨率较低. 瑞典爱立信有限公司[6]在多个RF前端电路中将参考信号与本振信号混频,作为输出信号,通过时间数字转换器(time-to-digital converter, TDC)测量本振信号与公共参考信号的时间差,以此确定输出信号的初始相位,并根据相位值调整PLL输出信号的相位,但这种方法需要采用高精度的TDC设计以保证同步后得到较低相位误差,电路实现成本较高. Markulic 等[7-11]采用数字时间转换器(digital-to-time converter, DTC)控制PLL输出信号的相位,但DTC对PVT条件的变化较为敏感,且难以满足高精度和线性相位控制的需求[1]. Huang 等[1]在小数分频PLL中的 delta-sigma 调制器(delta-sigma modulator, DSM)内部增加了相移模块,能够对输出信号相位进行一定的线性控制,但PLL相位同步后仍有0.936°的较大相位误差.
针对上述问题,设计适用于小数分频PLL的相位同步算法. 设计相位累加采样点数选取算法,实现快速且高精度的数字鉴相器,用于精确计算不同片PLL输出信号与参考信号的相位差,降低设计成本且相位差计算结果精度高. 通过实时控制DSM的小数分频比实现在0°~360°内线性调整PLL输出信号相位,且不受PVT条件变化的影响. 使用本设计实现PLL相位同步后的相位误差低于文献[1]中的结果,且能够快速实现多锁相环间的相位同步.
1. 小数分频PLL及多片PLL相位同步
图 1
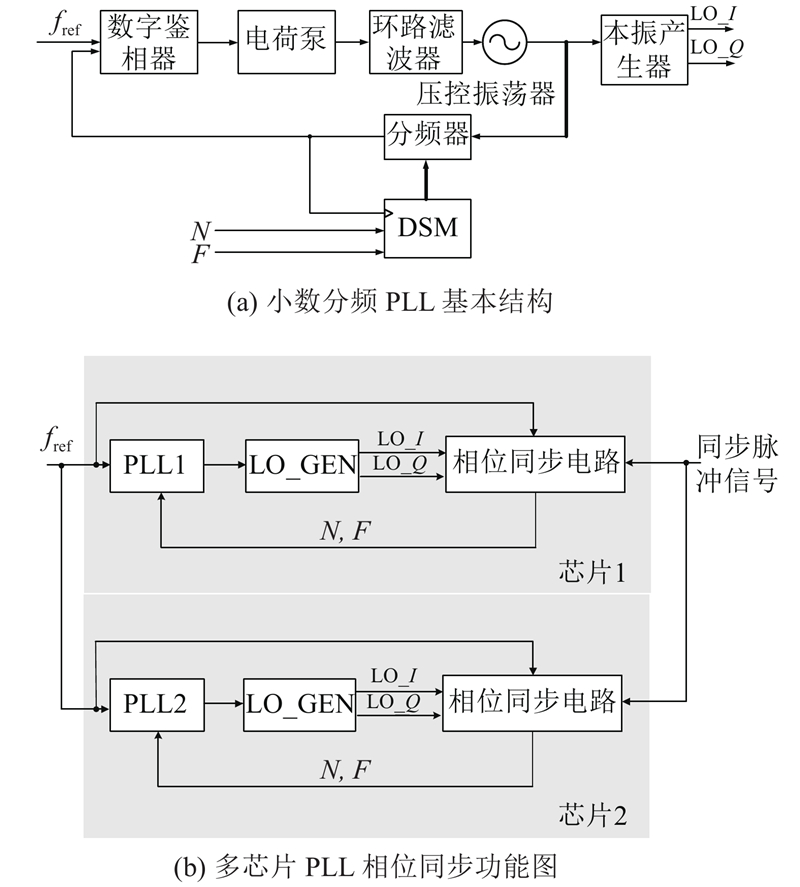
图 1 小数分频PLL基本结构以及多芯片PLL相位同步功能图
Fig.1 Basic structure of fractional frequency PLL and multi-chip PLL phase synchronization function diagram
在不同的收发器芯片内,PLL模块工作时的PVT条件不一致,导致同一时刻,不同芯片中PLL模块的DSM控制码字几乎是随机的,并且不同PLL内部各个模块间信号的延时也不一致. 因此,即使每个PLL模块采用相同的参考时钟,能够产生相同频率的输出信号,也会存在不确定的相位偏差. 多芯片同步需要提取该不确定结果,将所有芯片内的PLL输出信号都同步到相同的相位上.
多芯片PLL相位同步的功能图如图1(b)所示,每一个PLL都由同一个参考时钟输入,通过本振产生器(LO_GEN)产生相应I、Q正交的本振信号. 每个芯片内部都包含一个相位同步电路,用于控制PLL的分频比(N、F),实时调节PLL输出信号的相位,直到各芯片内的PLL输出信号相位同步.
2. 小数分频PLL相位同步电路
2.1. 小数分频PLL相位同步电路工作原理
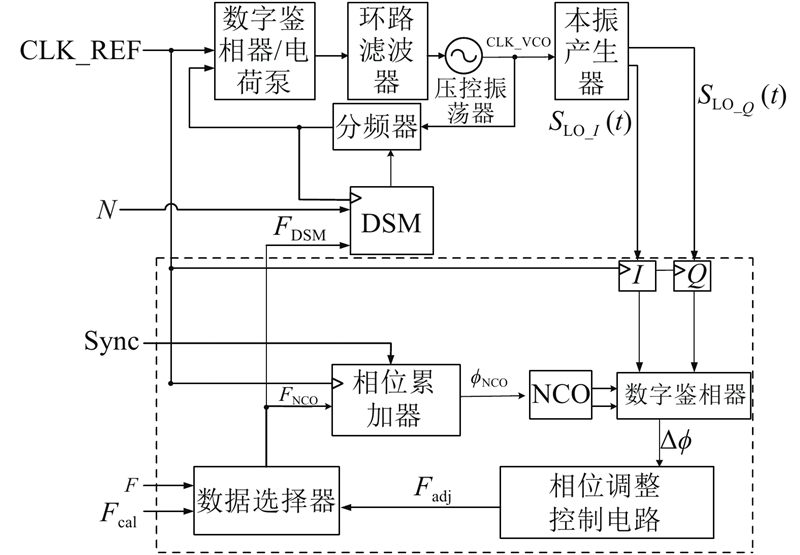
本文设计的小数分频PLL相位同步电路结构框图如图2所示。图中,CLK_VCO为压控振荡器输出信号,Fcal为小数分频比偏移量;虚线框内部分为实现相位同步算法电路的结构. 主要由相位累加器、数字振荡器(NC oscillator, NCO)、数字鉴相器、相位调整控制电路组成. 相位同步电路实质是能够修正DSM输入小数分频比的电路.
图 2
图 2 小数分频PLL相位同步电路结构框图
Fig.2 Block diagram of fractional frequency PLL phase synchronization circuit
当同步指示信号Sync拉高时,所有PLL相位同步电路内的相位累加器被复位,基于参考时钟CLK_REF产生相同的参考相位信号
不同PLL在锁定后,Δ
在计算出相位差Δ
在每一次相位调整后,再次计算Δ
2.2. 快速高精度数字鉴相器
2.2.1. 数字鉴相原理
PLL产生的信号频率较高,直接将其与NCO输出信号进行相位比较,实现较为困难. 由于该信号为正弦(余弦)波信号,只有1种频率成分,可以通过参考时钟CLK_REF进行欠采样后再计算其与NCO输出信号的相位差. 假设PLL输出2路正交的本振信号分别为
式中:
由采样定理可知,经参考时钟欠采样的信号在频域内被搬移到小于参考时钟频率一半的范围内. 假设当前小数分频比F满足F<0.5,则经参考时钟频率欠采样后的信号分别为
设定的I、Q正交NCO输出信号分别为
式中:
取
NCO查找表的位数本应为25 bits,为了节省资源,本文设计的NCO截取相位累加器的高16 bits作为NCO查找表的输入,使式(7)中的Δ
该相位误差大小对本文最终要实现小于0.35°的设计指标的影响极小,可以暂且忽略不计.
2.2.2. 相位累加采样点数选取算法
在数字鉴相器原理的基础上,设计相位累加采样点数的选取算法,消除相位差中的高次谐波分量的同时,降低相位差计算的误差,并缩短相位差计算所需的时间.
在实际电路中,由于PLL输出信号经过参考频率欠采样输出的信号为单比特信号(方波信号,除基频输出外,还包含2、3、4等高次谐波成分),取值只有0和1这2种可能,与NCO输出信号进行三角运算后,得到的
式中:
理论上当累加采样点数刚好等于1个NCO输出信号周期时,累加时长可以达到最小. 以F = 0.1为例,10个采样点可将所有的高频分量滤除. 但在实际应用中,小数分频比F不一定能被1除尽,即NCO输出信号的单个周期所需的采样点数不一定为整数,若单取1个NCO周期的采样点累加,必将引入计算误差,只能通过多个NCO周期的累加降低误差大小. 而累加采样点数的选取如果不合适,对相位差计算结果会造成较大影响. 比如在较为极端的情况下,如果采样点数包含的周期数恰好比整数个周期再多出半个周期,而这半个周期又恰好都为正或负,则计算结果将引入很大的计算误差.
本文采用如下方法进行累加采样点数计算和缩短鉴相时间. 设NCO输出信号单个周期的采样点数为K(K不一定为整数),
由式(10)可知K与小数分频比呈反比关系,当PLL工作在极小的小数分频比时,K很大. 为了缩短相位差计算总时间,提高鉴相速度,累加采样点数不能过大,因此在计算相位差时,在初始设定的小数分频比上加1个偏移量Fcal,使单个周期的采样点数K减少,即
加上Fcal后不能影响实际的相位差计算结果,即Fcal必须满足
式中:M为大于0的自然数,Ncal为最大累加采样点数. 设Ncal个采样点里包含NCO信号周期的个数为P,则
式中:floor为向上取整函数. 将该周期数乘以每个周期所需的采样点数K,数值四舍五入后即得到算法最终的累加采样点数Nadd.
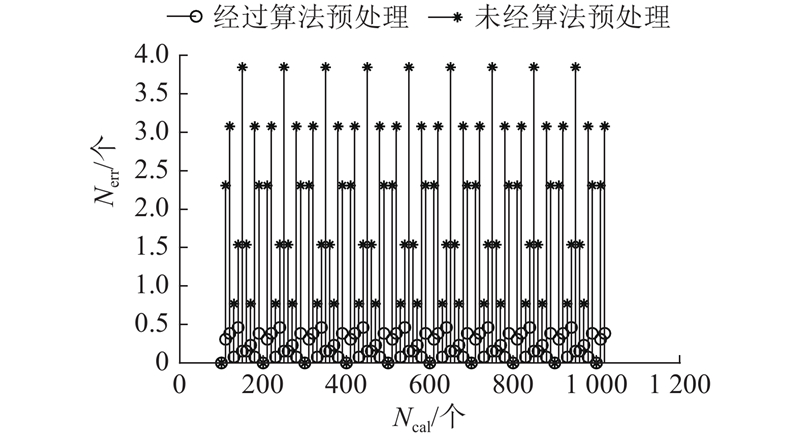
式中:round为四舍五入函数. 由此得到的Nadd最多误差0.5个采样点. 以F=0.03,Fcal=0.1为例,经算法预处理和未经算法预处理的误差采样点数随Ncal变化曲线如图3所示. 由图可以看出,经过算法预处理得到的Nadd中所包含的误差采样点数Nerr始终小于0.5,比未经算法预处理的Ncal中所包含的最大误差采样点数减少了约87%.
图 3
2.3. 相位调整控制电路
2.3.1. 相位调整实现方法
在实际电路中,PLL进行相位调整时的受限因素很多。比如当调整的相位差过大时,会导致压控振荡器(VCO)输出信号频率改变量过大,VCO子带覆盖的频率范围较窄,大的频率切换容易跳出当前子带的频率范围,最终导致PLL失锁. 因此对PLL进行相位调整时,不能一次直接将所需的相位偏移量调整完,而是要分多个参考时钟周期进行相位调整.
相位调整控制电路的功能是计算每个参考时钟周期内,PLL模块进行相位调整时小数分频比的调整量Fadj,并实时控制相位累加器的频率控制字FNCO以及DSM输入的小数分频比FDSM的大小. 相位同步电路设置3种状态:1)相位差计算状态
2)PLL相位调整状态
3)相位跟踪状态
2.3.2. 相位调整量Fadj的计算方法
假设PLL进行相位调整所需的时间包含参考时钟的周期数为Nadj,则
化简式(18)得到
数字鉴相器模块输出的相位差Δ
由式(20)、(21)可得
将式(22)代入式(16)可得PLL相位调整时FNCO、FDSM的值,从而根据相位差Δ
3. 仿真验证
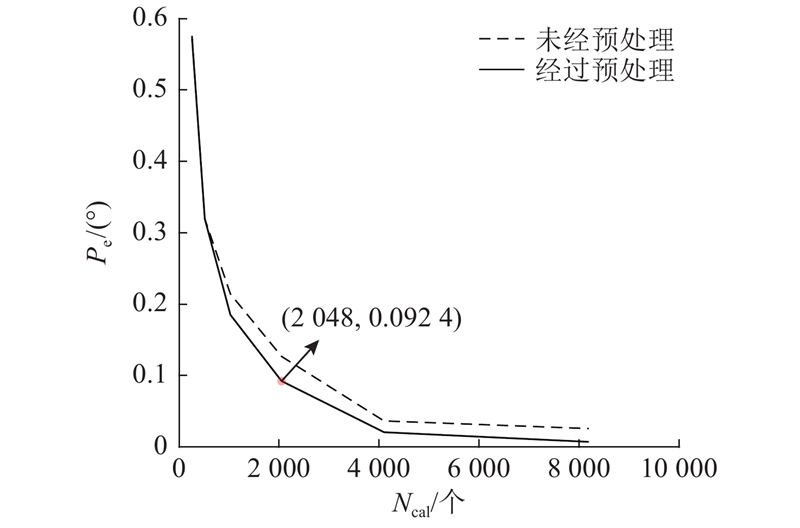
以F = 0.14为例,对数字鉴相器进行Simulink仿真,得到相位差计算结果的误差Pe随累加采样点数Ncal变化的曲线如图4所示. 由图可以看出,累加采样点数越大,计算结果的误差越小. 将采样点数进行预处理,由式(14)计算得到最终累加采样点数Nadd后,计算结果的误差比未经预处理的误差低. 由于累加采样点数过大会增加电路的计算量和同步总时长,本文最终选取的累加采样点数Ncal=2 048,此时的计算误差Pe=0.092 4°,已满足高精度鉴相的需求.
图 4
图 4 相位差计算结果的误差随累加采样点数变化曲线
Fig.4 Error curve of phase difference calculation results with accumulated sampling points
使用Verilog HDL(硬件描述语言)设计小数分频PLL相位同步的数字电路,并使用Simulink、cadence仿真工具搭建小数分频PLL模型、相位同步电路的联合仿真电路. 输入参考时钟频率
如图5所示为PLL1与PLL2模块在相位同步电路未工作前,输出信号的波形. 图中,LO_I1与LO_Q1分别为PLL1输出的2路经参考频率欠采样得到的正交信号,LO_I2与LO_Q2分别为PLL2输出的2路经参考频率欠采样得到的正交信号. 从图中可知在2个PLL锁定后,输出信号存在较大的相位差.
图 5
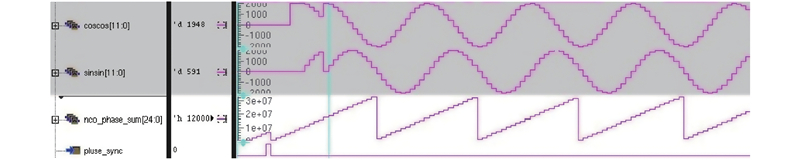
如图6所示为NCO产生信号及其相位信号波形. 图中,sinsin、coscos为NCO生成的2路正交信号. nco_phase_sum为相位累加器的输出值,即为公共参考信号相位值,其位宽为25 bits,表示范围0°~360°,溢出后再从0开始增加. pluse_sync为相位同步指示信号,当电路检测到该信号的上升沿时,复位所有PLL内的相位累加器,同步电路开始工作.
图 6
图 7
图 8
图 9
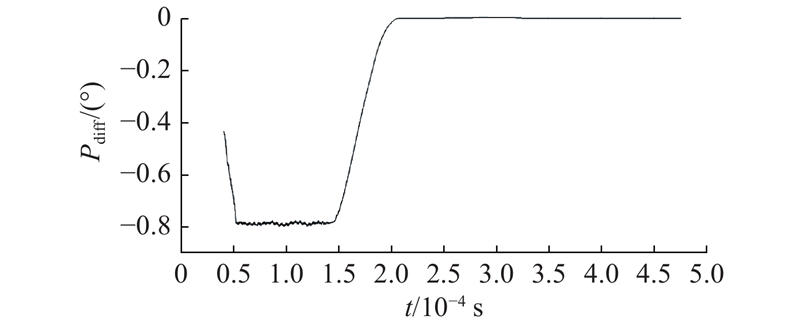
图 9 2个PLL输出信号之间相位差随时间变化曲线
Fig.9 Curve of phase difference with time between two PLL output signals
4. 结 语
本文设计能够线性调整相位的PLL相位同步电路,其中的相位累加采样点数选取算法有效降低相位差计算结果的误差,并且给出多个PLL输出信号相位与参考相位同步的电路设计过程. 在系统响应耗时方面,整个相位同步电路从开始工作到实现相位同步所需的时间仅为210 ms(系统时钟为25 MHz),收敛速度快,实现同步后的相位误差仅有0.35°,本设计适用于对时钟相位一致性要求高的多通道射频通信系统中. 本设计对NCO相位精度的要求较高,如何进一步提高NCO设计的精度,同时节省硬件资源开销须深入研究.
参考文献
Low-noise fractional-N PLL with a high-precision phase control in the phase synchronization of multichips
[J].DOI:10.1109/LMWC.2018.2842680 [本文引用: 4]
Clock synchronization in wireless sensor networks based on Bayesian estimation
[J].DOI:10.1109/ACCESS.2020.2984785 [本文引用: 1]
A high-linearity digital-to-time converter technique: constant-slope charging
[J].
A 2.25~2.7 GHz area-efficient subharmonically injection-locked fractional-N frequency synthesizer with a fast-converging correlation loop
[J].
A 1.7 GHz fractional-N frequency synthesizer based on a multiplying delay-locked loop
[J].
A 65 nm 19.1-to-20.4 GHz sigma-delta fractional-N frequency synthesizer with two-point modulation for FMCW radar applications
[J].DOI:10.1587/transele.E102.C.64 [本文引用: 1]
应用于K波段分数分频频率综合器的多模分频器设计与优化
[J].
Design and optimization of multi-modulus-divider for K-band fractional-N frequency synthesizer
[J].
基于小数分频锁相环的低杂散频率源设计
[J].DOI:10.3969/j.issn.1003-0107.2019.04.017 [本文引用: 1]
Design of frequency source with low spurious based on fractional-N PLL
[J].DOI:10.3969/j.issn.1003-0107.2019.04.017 [本文引用: 1]
小数分频锁相环杂散抑制技术研究和应用
[J].
Research and application of spurious suppression technology of fractional frequency PLL
[J].
一种低相位噪声的UHF频段小数分频频率综合器
[J].
A low-phase-noise UHF-band fractional-N frequency synthesizer
[J].
锁相环小数N分频频率综合器中的Sigma-delta调制器设计
[J].DOI:10.3969/j.issn.1002-8692.2011.17.018 [本文引用: 1]
Design of sigma-delta modulator in fractional-N PLL frequency synthesizer
[J].DOI:10.3969/j.issn.1002-8692.2011.17.018 [本文引用: 1]