基于发动机与电动机动态响应的差异[4-5],为了降低输出轴转矩的波动,Yoshiok等[6-7]提出采用电动机转矩对发动机转矩补偿的方式,弥补发动机响应滞后的问题. Zhu等[8]根据控制阶段的不同,提出分阶段的基于速度跟踪的动力源补偿控制律. Ma等[9]表明基于转动惯量补偿的电动机控制策略可以有效地抑制66%的输出轴转矩波动,且车速未出现显著的降低现象. Lin等[10]研究电动机转矩补偿控制策略在降低多种驱动模式与制动模式间切换冲击的有效性. 上述研究大多只考虑发动机实际转矩输出的滞后性,但转矩输出极易产生波动振荡的问题. HEV在大范围道路行驶条件下会受到道路坡度变化、路面附着系数变化和传感器测量噪声等外部干扰的影响,严重时甚至会恶化HEV模式切换过程的动力学性能.
本文从抗干扰协调控制器设计的角度出发,构造多变量线性扩张状态观测器,用于实时估计外界干扰. 通过干扰补偿再分配算法二次更新各阶段电机转矩命令,降低干扰带来的冲击影响,提升模式切换品质.
1. 双行星排式功率分流动力系统建模
1.1. 双行星排式功率分流动力系统
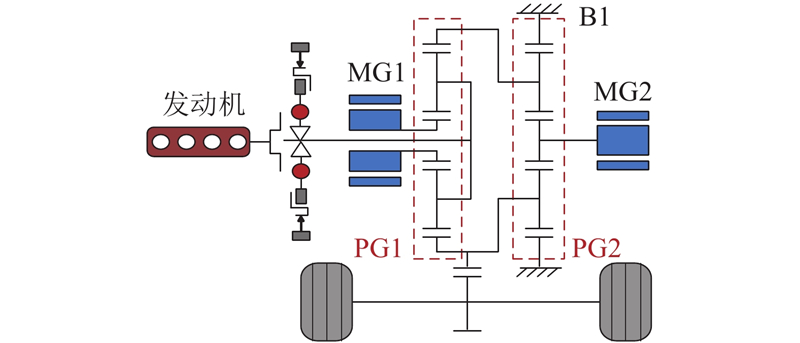
研究的双行星排式功率分流系统如图1所示. 其中,发动机与前排行星架相连,电机MG1与前排太阳轮相连,电机MG2与后排太阳轮相连,后行星排的齿圈固定,前排齿圈和后排行星架相连传递动力并由后排行星架输出. 通过控制电机MG1和MG2可以实现对发动机转速和转矩的解耦,调节MG1的转矩可以实现发动机调速,从而改善发动机的工作区间,降低燃油消耗.
图 1
根据动力源和制动器的工作状态,可以实现混合动力汽车的8种工作模式:MG2单独驱动、MG1和MG2联合驱动、发动机单独驱动、混合驱动、停车充电、复合制动、机械制动及停车. 其中,比较典型的工作模式如表1所示. 由于纯电动模式(electric driving mode)至混合驱动模式(hybrid driving mode)的切换过程(简称为E-H切换过程)涉及发动机的拖转、启动及调速过程等多种中间状态,与其他驱动模式切换相比较复杂. 重点研究E-H切换过程中该系统的动态特性.
表 1 典型的工作模式
Tab.1
| 工作模式 | 发动机 | MG1 | MG2 | B1 | 说明 |
| 纯电动 | 关 | 开 | 开 | 锁止 | 车速较低,负荷较低,且SOC较大 |
| 混合驱动 | 开 | 开 | 开 | 锁止 | 整车负荷持续增加或SOC低 |
1.2. 瞬态模型搭建
1.2.1. 发动机模型
一般来说,发动机的建模方法主要包括理论建模法和试验建模法. 理论建模法需要对发动机工作过程进行详细的热力学、燃烧学、动力学分析,建立可准确描述发动机动态特性的非线性数学模型,但这种模型过于复杂,计算相对耗时. 参考文献[14],以“发动机稳态查表模型”和“一阶惯性延迟环节”相结合的方式来表征发动机的动态特性:
式中:TE和ωE分别为发动机的输出转矩和角速度;τE为发动机转矩响应的时间常数;f为发动机稳态转矩与节气门开度α、发动机角速度之间的映射函数,通常由发动机台架试验数据构建而成.
1.2.2. 电机模型
与发动机相似,电机MG1和MG2的动态模型采用试验建模与理论建模相结合的方法,建立电机工作效率与转矩、转速相关的准稳态查表模型. 电机的机械部分采用时间常数较小的一阶惯性延迟环节来近似模拟动态特性,以MG2为例,
式中:TMG2为电机MG2的输出转矩,τm为电机转矩响应的时间常数,TMG2-0为电机初始目标转矩.
1.2.3. 动力耦合机构模型
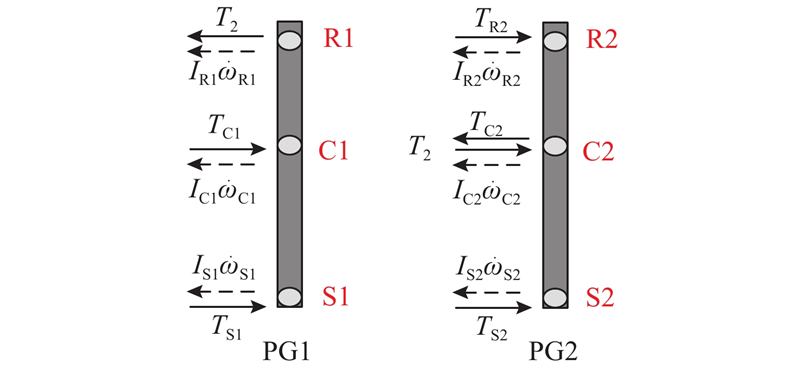
为了模拟功率分流式混合动力汽车的动态性能,需要搭建瞬态模型. 忽略行星架上行星齿轮的转动惯量、系统的弹性和阻尼,根据杠杆原理可得如图2所示的双行星排杠杆模型. 图中,IR1、IC1和IS1分别为前行星排PG1中齿圈、行星架和太阳轮的集中转动惯量,ωR1、ωC1和ωS1分别为上述构件的角速度,后行星排同理;T2为前排齿圈和后排行星架之间的作用内力矩;TR2为作用在齿圈R2上的外力矩;TC2为耦合装置输出轴端受到的来自整车的外力矩;TC1、TS1和TS2分别为发动机、MG1和MG2作用在相应构件上的外力矩.
图 2
由图2可知,对于前行星排PG1,有
PG2的力矩平衡方程为
式中:k1和k2分别为前、后行星排的特征参数,
其中TMG1、IMG1和ωMG1分别为电机MG1的输出转矩、惯量和角速度;TMG2、IMG2和ωMG2分别为电机MG2的输出转矩、惯量和角速度;TE、IE和ωE分别为发动机的输出转矩、惯量和角速度; Iout为整车质量等效到输出轴端的转动惯量;ωout为行星架C2的输出角速度;Tout为输出端负载,包括整车行驶阻力等效到行星架C2输出轴端的阻力矩Treq和制动力矩等效到输出轴的阻力矩Tbrk,
根据构件连接方式和行星排结构特有的转速关系,可知
综合式(3)~(16),可得
式中:
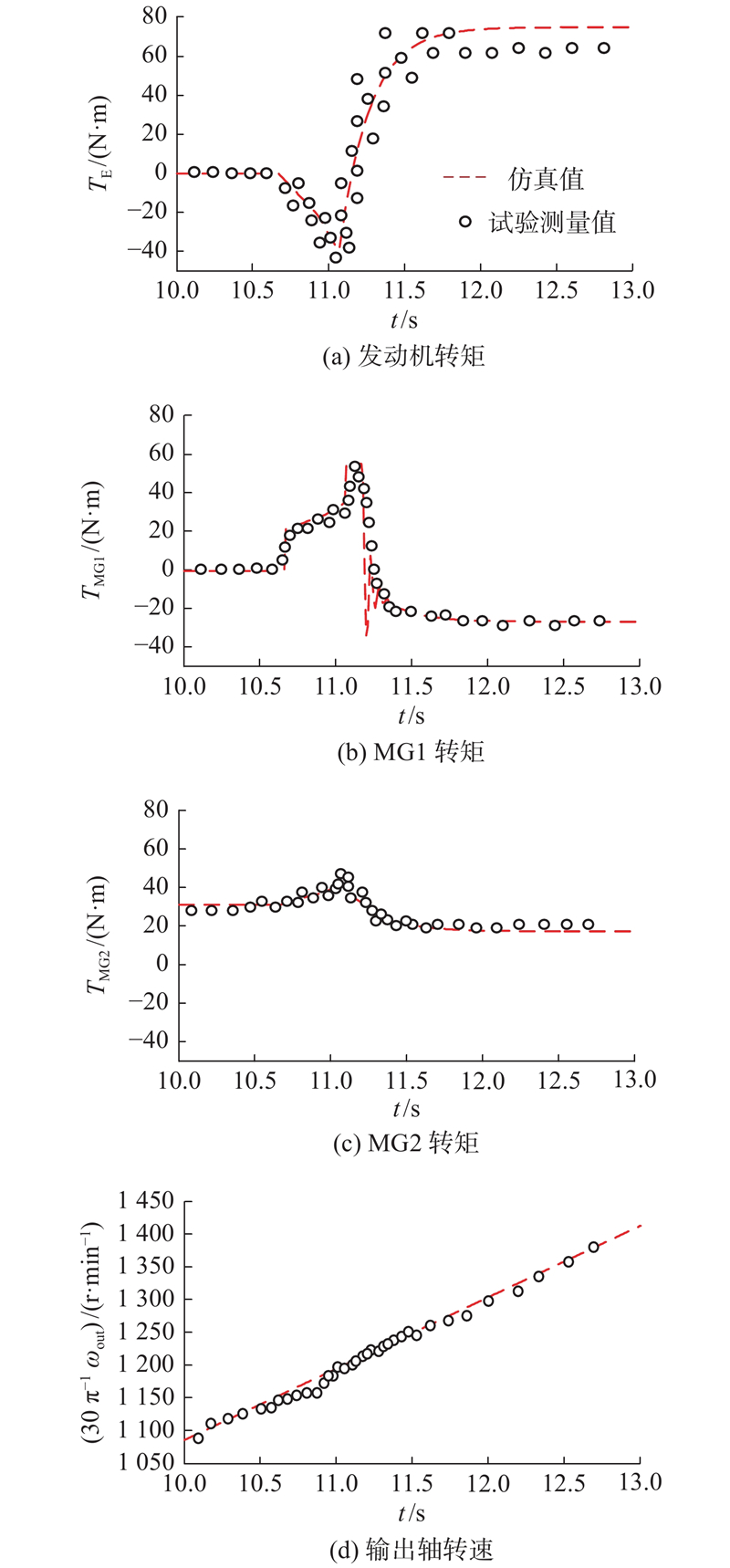
图 3
图 3 整车模式切换响应仿真与试验对比图
Fig.3 Comparison between simulation and test of vehicle mode switching response
表 2 整车关键部件参数
Tab.2
| 参数 | 数值 | |
| 发动机 | 最大功率(转速) | 54 kW(4 700 r/min) |
| 发动机 | 最大扭矩 | 115 N·m |
| 电机MG1 | 最大功率(转速) | 15 kW(8 000 r/min) |
| 电机MG1 | 最大扭矩 | 55 N·m |
| 电机MG2 | 最大功率(转速) | 30 kW(12 000 r/min) |
| 电机MG2 | 最大扭矩 | 305 N·m |
| 动力电池 | 容量 | 6.5 A·h |
| 动力电池 | 额定电压 | 288 V |
| 行星轮系特征参数 | 前排PG1 | 1.842 |
| 行星轮系特征参数 | 后排PG2 | 2.48 |
| 整车 | 满载质量 | 1 398 kg |
| 整车 | 迎风面积 | 1.746 m2 |
| 整车 | 空气阻力系数 | 0.3 |
| 整车 | 滚动阻力系数 | 0.008 |
| 整车 | 滚动半径Rt | 0.287 m |
| 整车 | 主减速器速比io | 3.93 |
| 整车 | kp1/ki1 | 0.025/0.015 |
| 整车 | kp2/ki2 | 0.5/0.000 1 |
2. 多变量线性扩张状态观测器设计及收敛性分析
2.1. 扩张状态观测器设计
混合动力汽车在实际行驶过程中,容易受到道路坡度变化、路面附着系数、执行器噪声、传感器测量噪声等外部干扰的作用[15]. 模式切换过程具有明显的瞬态性,使得整车切换平顺性对微小的外部干扰相对“敏感”,严重时甚至导致整个切换系统失稳,因此设计考虑外部干扰的混合动力汽车动态协调控制策略对实车应用方面具有重要的现实意义.
Chen等[18]的研究表明,HEV模式切换过程中影响模式切换响应的主要干扰因素不仅包括发动机转矩执行干扰,还有负载转矩干扰. 由于路面工况的多变性,导致HEV直接受到路面干扰的作用,继而引起负载转矩的连锁变化. 这种路面干扰直接作用于车辆,容易引起明显的纵向冲击. 将路面坡度变化、滚动阻力系数变化干扰统一综合为输出端负载Tout干扰为d2. 综上所述,主要针对这2种干扰展开研究.
令发动机转矩输出TE干扰为d1,输出端负载Tout干扰为d2,则由式(17)可得包含干扰的耦合机构模型:
将式(22)、(23)转换为下述状态空间模型:
系统的多变量线性扩张观测器为
式中:Z1为状态向量X的实时估计值,Z2为扩展状态向量
为了提高多变量线性扩张观测器的灵活性和准确性,将观测器的增益变量由传统的标量改为矩阵形式[21]:
式中:β01、β02、β11、β12均为正数.
2.2. 收敛性分析
由式(24)~(31)可知
设定新的状态变量为Xn=[e,Z2],控制向量Un=[−
式中:
对系统(35)进行拉氏变换,可得
式中:Xn(s)、Un(s)分别为Xn、Un对应的拉氏变换向量.
设
传递函数关系如下:
将s = jw代入式(41)、(42),并将其转换为下述标量形式:
从式(43)、(44)可知,令误差系统(35)中第i通道的最大频率为wi,当满足βΔi >> wi时,可以使得下述关系式成立,验证了该扩张状态观测器的收敛性.
3. 基于扩张状态观测器估计补偿的协调控制策略
通过设计式(29)、(31)所示的扩张状态观测器,可以获得综合干扰的估计值Z2,推算得到发动机转矩干扰d1和输出端负载干扰d2的估计值分别为
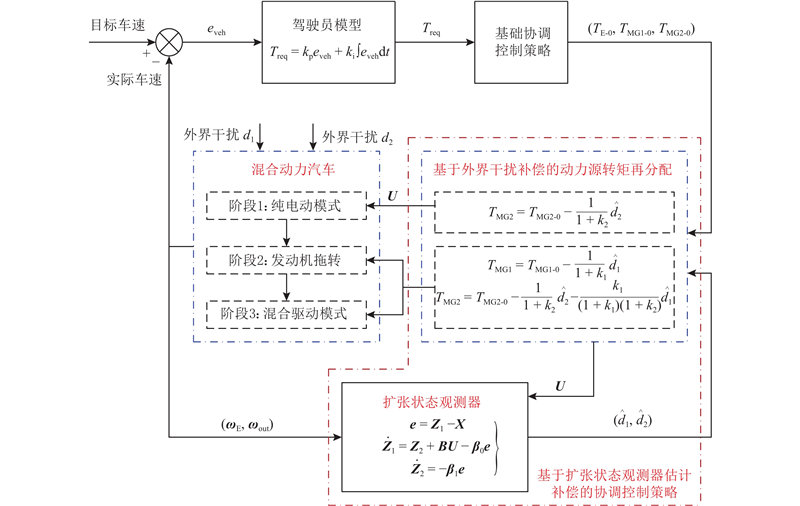
提出如图4所示的混合动力汽车模式切换控制框图. 其中驾驶员模型采用PI控制模拟,以目标车速和实际车速差为输入,通过调节比例系数和积分系数计算输出保证车速跟踪的整车需求驱动扭矩Treq. 利用基础协调控制策略,将Treq分解为发动机初始目标转矩TE-0、MG1初始目标转矩TMG1-0和MG2初始目标转矩TMG2-0. 根据E-H模式切换过程的3个阶段(纯电动、发动机拖转和混合驱动),可以推导出各动力源初始目标转矩的显示表达式. 当混合动力汽车工作于纯电动模式时,发动机的转矩为0,电机MG1控制发动机在零转速点,输出端转速和转矩保持不变,相应两电机的目标转矩为
图 4
图 4 混合动力汽车模式切换控制框图
Fig.4 Block diagram of mode switching control for hybrid electric vehicle
式中:kp1和ki1分别为电机MG1控制器中的比例参数和积分参数.
当车辆纵向车速超过一定阈值Vthr(本文设定为32 km/h)时,纯电动模式满足不了行驶需求,需要在0.5 s内起动发动机至怠速ωE-target(94.2 rad/s)[22]. 为了消除电机MG1拖转发动机对输出端的影响,在发动机拖转阶段设计补偿转矩ΔTMG2,此时电机MG1和MG2的目标转矩为
图 5
一旦发动机转速超过怠速,HEV迅速切换至混合驱动模式,此时发动机和电机MG2共同驱动车辆行驶,电机MG1调速发动机工作于经济角速度ωE-e(157 rad/s),得到MG1和MG2综合补偿控制律:
由于该模式切换过程易受到发动机转矩和行驶路况的干扰,设计扩张状态观测器实时估计. 通过如下所示的各阶段电机转矩补偿再分配策略,减小外界干扰带来的冲击影响.
1)纯电动阶段.
2)发动机拖转阶段及混合驱动阶段.
为了验证该协调控制策略的有效性,以带宽为20 Hz、方差分别为20、100 N·m的高斯白噪声来模拟发动机转矩输出干扰d1和输出端负载Tout干扰d2. 为了分析2种干扰对模式切换响应的影响规律,采取分别加入噪声的仿真形式. 本文的线性扩张状态观测器中,观测增益矩阵为βΔ = diag [50, 200],相应的β0 = diag [100, 400],β1 = diag [2500, 40000].
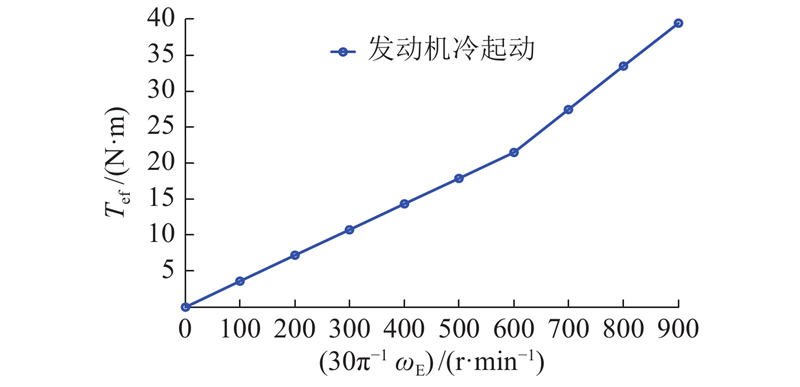
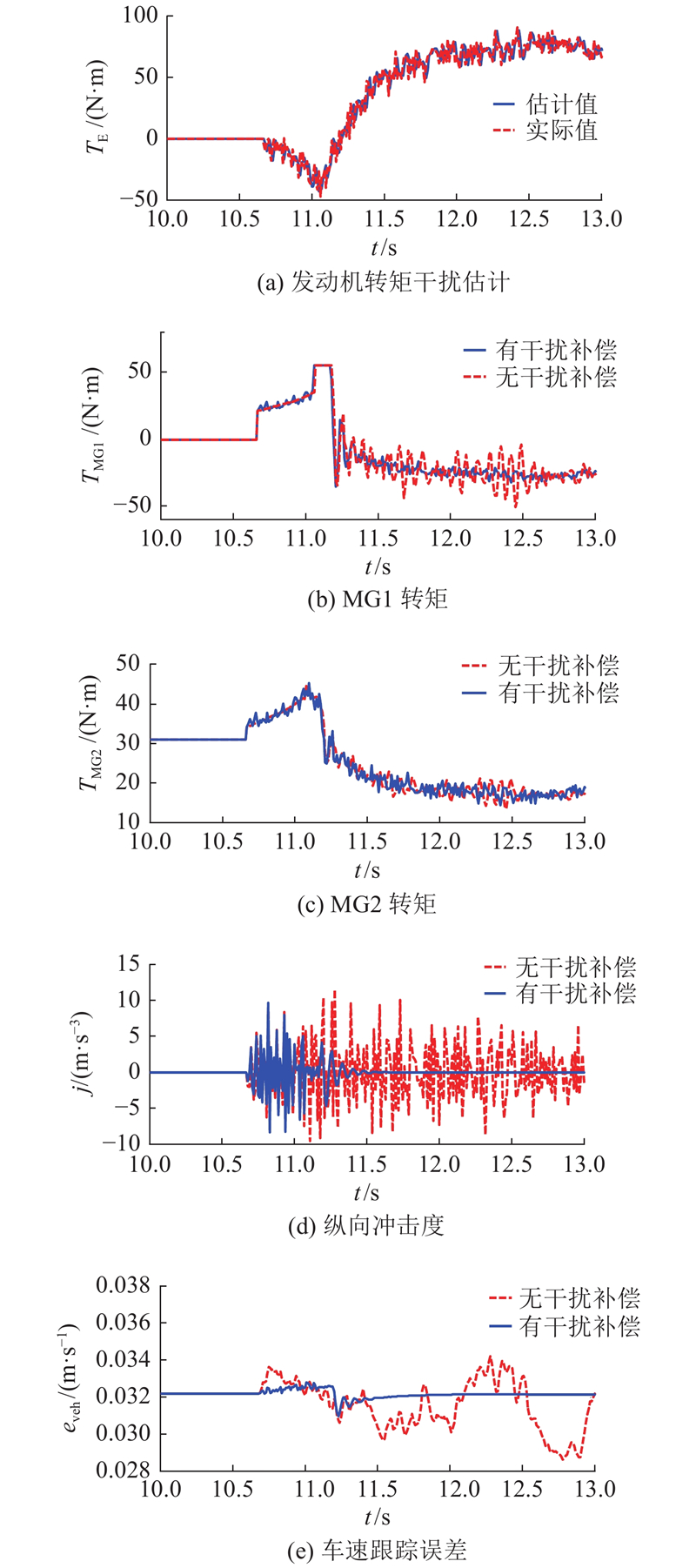
通过Matlab/Simulink软件平台对上述转矩协调策略进行仿真分析,可得图6所示的混合动力车辆在受到发动机转矩输出干扰下,采用基于扩张状态观测器估计补偿的协调控制和未采用干扰补偿的基础协调控制效果对比图. 图中,j为纵向冲击度,eveh为车速跟踪误差. 发动机转矩实际值为未考虑各种干扰下的基础协调控制策略的理想目标值TE-0与发动机干扰d1之和. 车辆在初始阶段工作于纯电动模式;10.67 s时车速达到32 km/h,整车控制器发出模式切换信号,进入发动机拖转阶段;11.07 s时发动机转速达到怠速,发动机喷油点火进入混合驱动模式.
图 6
图 6 发动机转矩干扰下2种协调控制效果的对比
Fig.6 Comparison of two kinds of coordinated control effects under engine torque disturbance
从图6(d)、(e)可知,当混合动力汽车没有采用任何干扰补偿协调控制策略时,发动机转矩干扰恶化了阶段2和3的平顺性及整车车速跟踪的平稳性,且这种干扰没有被上层控制器监测到,电机MG1和MG2的转矩命令由事先设定好的基础协调控制器发出(图6(b)、(c)的虚线). 采用包含扩张状态观测器的干扰补偿协调控制策略,可以快速、精准地估计当前的干扰信号值. 虽然存在一定的估计误差,但误差比最大只达到9.5%,在可接受范围内(见图6(a)). 通过式(56)~(58)所示的干扰补偿动力源再分配策略,重新确定电机MG1和MG2的转矩输出(图6(b)、(c)的实线),大幅度降低了混合驱动模式的纵向冲击度,提高了车速跟踪的稳定性(见图6(d)、(e)).
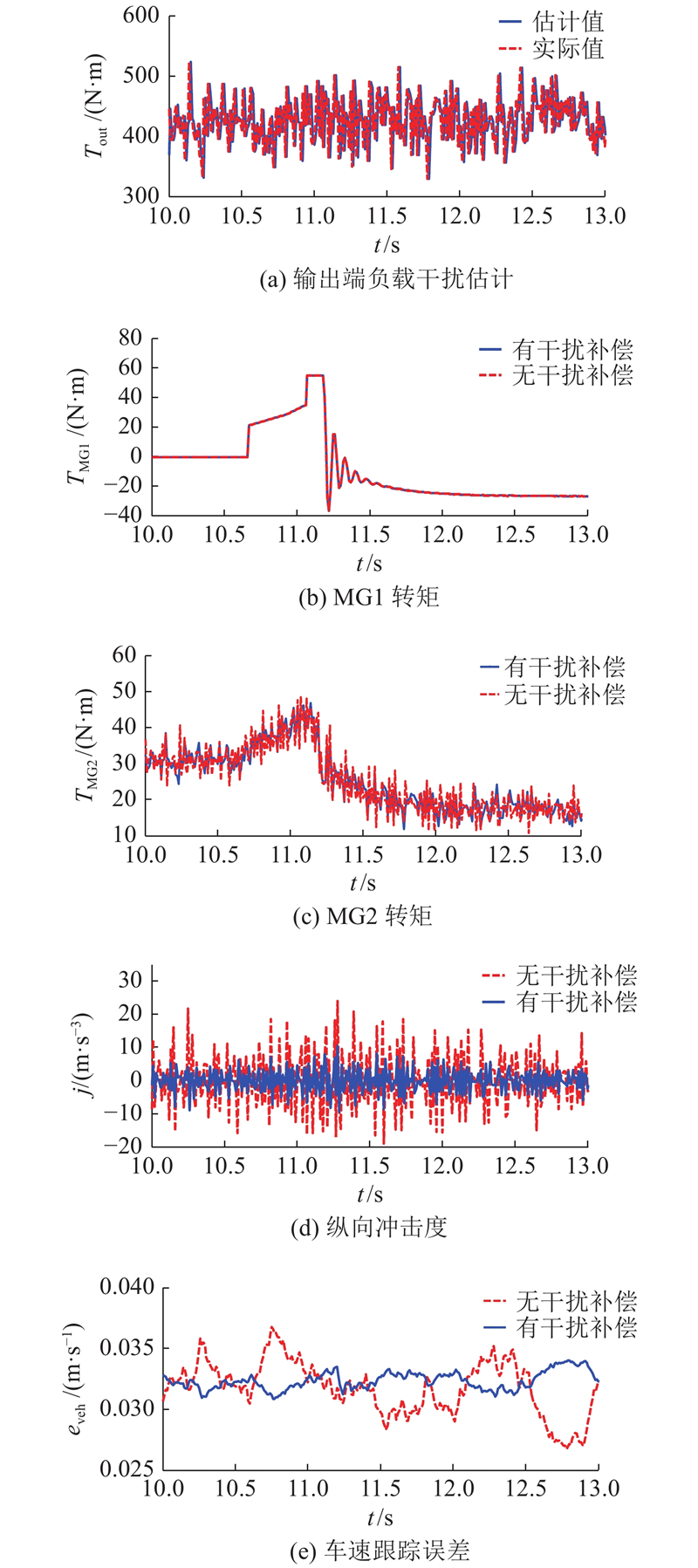
图 7
图 7 输出端负载干扰下2种协调控制效果的对比
Fig.7 Comparison of two kinds of coordinated control effects under load disturbance
4. 结 论
(1)通过研究功率分流式混合动力汽车的E-H模式切换过程的动态特性,搭建对应的整车瞬态模型,通过实验数据的对比验证了模型的准确性.
(2)考虑到发动机执行器和行驶工况2种外界干扰特性,提出由多变量线性扩张状态观测器和外界干扰补偿的转矩再分配模块构成的协调控制策略. 通过Matlab/Simulink仿真平台,验证了该策略对外部干扰的适应性和改善模式切换品质的有效性.
(3)后续研究将综合考虑系统时滞和参数摄动因素,开展HEV模式切换过程的稳定性分析研究,探求具有优异抗干扰能力的鲁棒协调控制器,这对于未来的工程实践具有一定的指导意义和参考价值.
参考文献
系统效率最优的功率分流式混合动力汽车非线性预测控制
[J].
Nonlinear predictive control of power split hybrid electric vehicle with optimal system efficiency
[J].
A comprehensive review on energy management strategies of hybrid energy storage system for electric vehicles
[J].
混联式混合动力系统动态响应协调控制
[J].DOI:10.11918/j.issn.0367-6234.2016.01.011 [本文引用: 1]
Torque coordinated control for the multi-power in parallel-series HEV
[J].DOI:10.11918/j.issn.0367-6234.2016.01.011 [本文引用: 1]
Mode shift control for a hybrid heavy-duty vehicle with power-split transmission
[J].DOI:10.3390/en10020177 [本文引用: 1]
Dynamic modelling and systematic control during the mode transition for a multi-mode hybrid electric vehicle
[J].DOI:10.1177/0954407013477027 [本文引用: 1]
Control strategy for all the mode-switches of hybrid electric vehicle
[J].
A novel torque coordination control strategy of a single-shaft parallel hybrid electric vehicle based on model predictive control
[J].
Dynamic coordinated control during mode transition process for a compound power-split hybrid electric vehicle
[J].DOI:10.1016/j.ymssp.2018.01.023 [本文引用: 1]
HEV多领域物理建模与模式切换控制仿真
[J].
Multi-domain physical modeling and mode switching control simulation of HEV
[J].
Robust control of mode transition for a single-motor full hybrid electric vehicle
[J].
机电复合传动系统基于μ-综合方法的鲁棒协调控制
[J].DOI:10.3901/JME.2017.14.088 [本文引用: 1]
Coordination control based on μ-synthesize for electro-mechanical transmission
[J].DOI:10.3901/JME.2017.14.088 [本文引用: 1]
Torque coordination control during mode transition for a series–parallel hybrid electric vehicle
[J].DOI:10.1109/TVT.2012.2200305 [本文引用: 1]
基于李雅普诺夫函数法的扩张状态观测器参数优化
[J].DOI:10.3969/j.issn.1007-2683.2012.01.011 [本文引用: 1]
Parameter optimization of extended state observer based on Lyapunov function method
[J].DOI:10.3969/j.issn.1007-2683.2012.01.011 [本文引用: 1]
基于参考模型的复合功率分流系统模式切换中的转矩协调控制
[J].
Torque coordinated control during mode switching of a compound power-split hybrid system based on reference model
[J].