图 1
目前,机器人加工系统广泛使用的测量仪器包括激光跟踪仪、室内GPS、机器视觉等. Joubair等[16]利用激光跟踪仪标定机器人. Nguyen等[17]利用激光跟踪仪,基于神经网络补偿的方法提高工业机器人的位置精度. Norman等[18]利用室内GPS测量机器人的位姿信息. Rao等[19]提出基于点云的工件表面法向测量方法,利用结构光视觉测量系统结合激光跟踪仪测量机器人末端工具的位置. Cao等[20]基于机器视觉,提高机器人的绝对定位精度. Galetto等[21]利用相机和激光跟踪仪的数据,计算出测量点的三维位置. 李瑛等[22]采用双相机视觉测量系统,在线测量销孔的加工精度. 毕运波等[23]提出基于视觉测量的沉头孔垂直度检测方法. 评定机器人加工系统的定位精度必须考虑仪器测量误差在系统单元间变换时产生的误差累积问题,只考虑系统中单一误差传递路径的误差减小效果不明显.
综上所述,针对机器人加工系统中由单元间基准变换产生的累积误差问题,提出逐级闭环优化策略. 在机器人、测量仪器、工件等单元中构造3个闭环,构建神经网络模型,使用数据驱动的方式融合3个闭环独立优化的结果,提高系统闭环优化的稳定性. 逐级闭环优化策略,达到减小机器人末端工具和工件间的相对位姿误差、提高机器人加工系统定位精度的目的.
1. 机器人加工系统的累积误差
1.1. 机器人加工系统
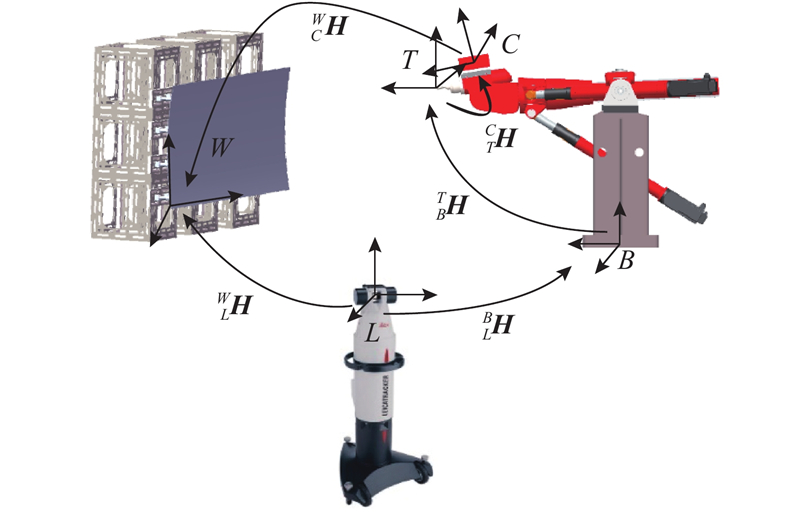
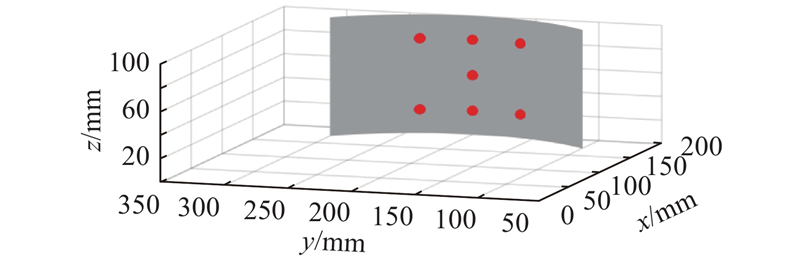
机器人加工系统如图1所示. 图中,
机器人加工系统加工作业时,末端工具需要不断变换位姿,到达工件预定的目标点进行加工. 末端工具的定位过程如下. 1)将目标点坐标和当前末端工具坐标转换至
1.2. 末端工具的累积误差
系统中各单元坐标先变换到
式中:
根据式(1)、(2)并结合末端工具的定位过程,为了减小末端工具的误差累积效应,提高末端工具的定位精度,需要提高
2. 累积误差的逐级闭环优化策略
2.1. 逐级闭环优化
为了提高末端工具的定位精度,在系统的单元中构建3个与
分别构建以激光跟踪仪坐标系、机器人基坐标系和末端工具坐标系组成的核心闭环(
2.1.1. 核心闭环优化
在
式中:
考虑到
误差方程为
目标函数J为
2.1.2. 辅助闭环优化
与核心闭环优化方法相同,在
考虑到
2.1.3. 相关性闭环优化
与核心和辅助闭环优化方法相同. 在
设置仿真实验证明,逐级闭环优化可以减小末端工具的位姿误差,探究机器人位姿数对优化效果的影响. 仿真数据和结果分析见3.1节的逐级闭环优化仿真.
2.2. 神经网络融合
逐级闭环优化后,得到每个闭环的局部最优解
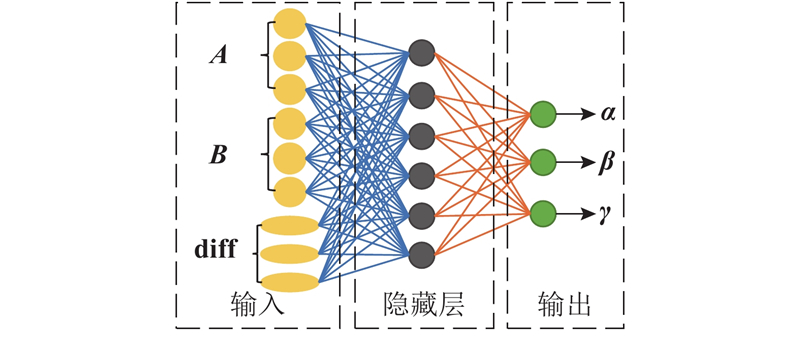
3层全连接神经网络模型如图2所示. 输入层包括辅助闭环优化后点的坐标矩阵
图 2
图 2 融合闭环优化结果的全连接神经网络模型
Fig.2 Fully connected neural network model fusing closed-loop optimization results
神经网络的训练目标是最小化
在训练过程中最小化Loss函数时,神经网络通过梯度反向传播优化模型的每个参数,使得输出点的坐标与理论坐标
采集1 000个样本作为训练集,200个样本作为验证集,200个样本作为测试集. 经过50个周期的优化,模型训练至收敛. 测试结果表明,
3. 仿真实验
3.1. 逐级闭环优化仿真
分别用30、50、70个机器人位姿下的数据优化核心闭环,用30个位姿检验闭环优化,检验结果如表1所示. 表中,
表 1 核心闭环优化检验结果
Tab.1
| 位姿数 | 平均位置误差 | 平均角度误差 | |||||
| | | Φ /% | | | Φ /% | ||
| 30 | 0.076 | 0.064 | 15.39 | 0.116 | 0.083 | 28.45 | |
| 50 | 0.073 | 0.053 | 27.40 | 0.119 | 0.089 | 25.21 | |
| 70 | 0.068 | 0.056 | 17.65 | 0.128 | 0.094 | 26.56 | |
| 位姿数 | 最大位置误差 | 最大角度误差 | |||||
| | | Φ /% | | | Φ /% | ||
| 30 | 0.123 | 0.109 | 11.38 | 0.198 | 0.169 | 14.65 | |
| 50 | 0.105 | 0.088 | 16.19 | 0.190 | 0.161 | 15.26 | |
| 70 | 0.104 | 0.098 | 5.77 | 0.234 | 0.185 | 20.94 | |
图 3
图 3
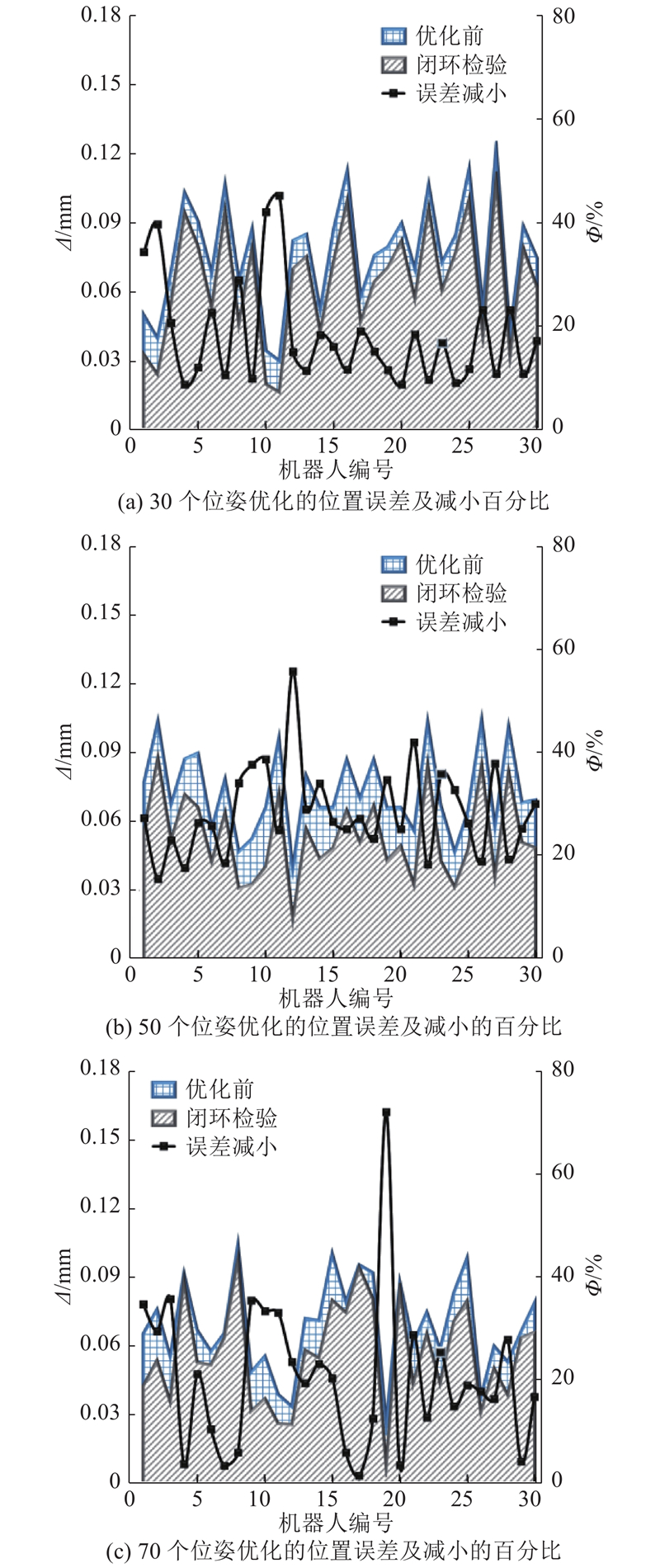
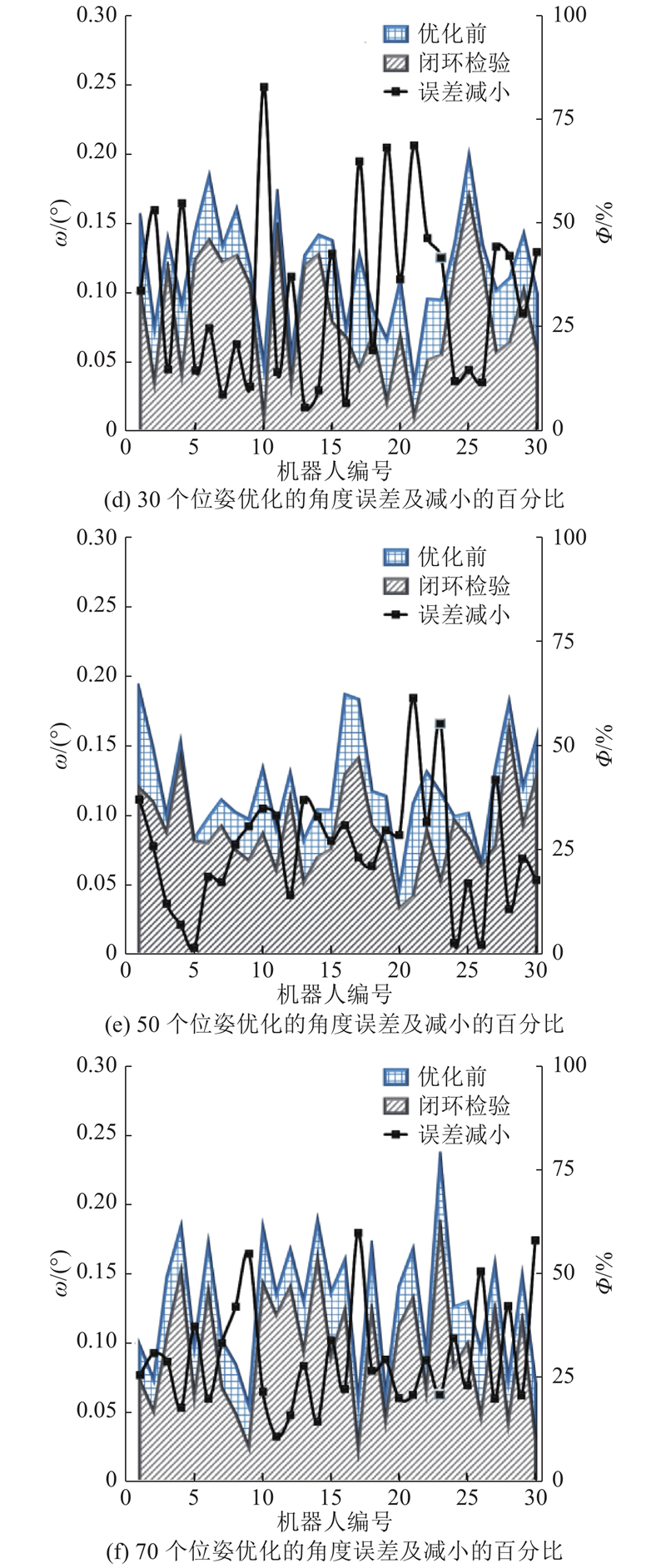
图 3 不同机器人位姿的核心闭环优化效果
Fig.3 Core closed-loop optimization effects of different robot poses
通过核心闭环优化,末端工具位置误差平均减小了20.15%,角度误差平均减小了26.74%. 将核心闭环优化仿真方法用于辅助和相关性闭环优化,末端工具位置误差平均减小了14.56%和7.99%,角度误差平均减小了24.59%和26.24%.
根据实验结果可知,样本点闭环优化前误差最大,优化后误差最小,闭环检验的误差小于优化前的误差. 逐级闭环优化后,末端工具位置误差平均减小了14.23%,角度误差平均减小了25.86%,表明使用有限的机器人位姿进行闭环优化的有效性和泛化能力. 对比不同机器人位姿数3个闭环优化后的效果可见,没有明显的规律,说明机器人位姿数对闭环优化的影响不明显,在实际工程中可以使用较少的机器人位姿优化闭环.
3.2. 神经网络融合仿真
测试集包含200个样本点,测试神经网络(neural networks, NN)的融合效果. 样本点分别经过闭环优化和NN融合后点的误差如图4所示. NN融合后
图 4
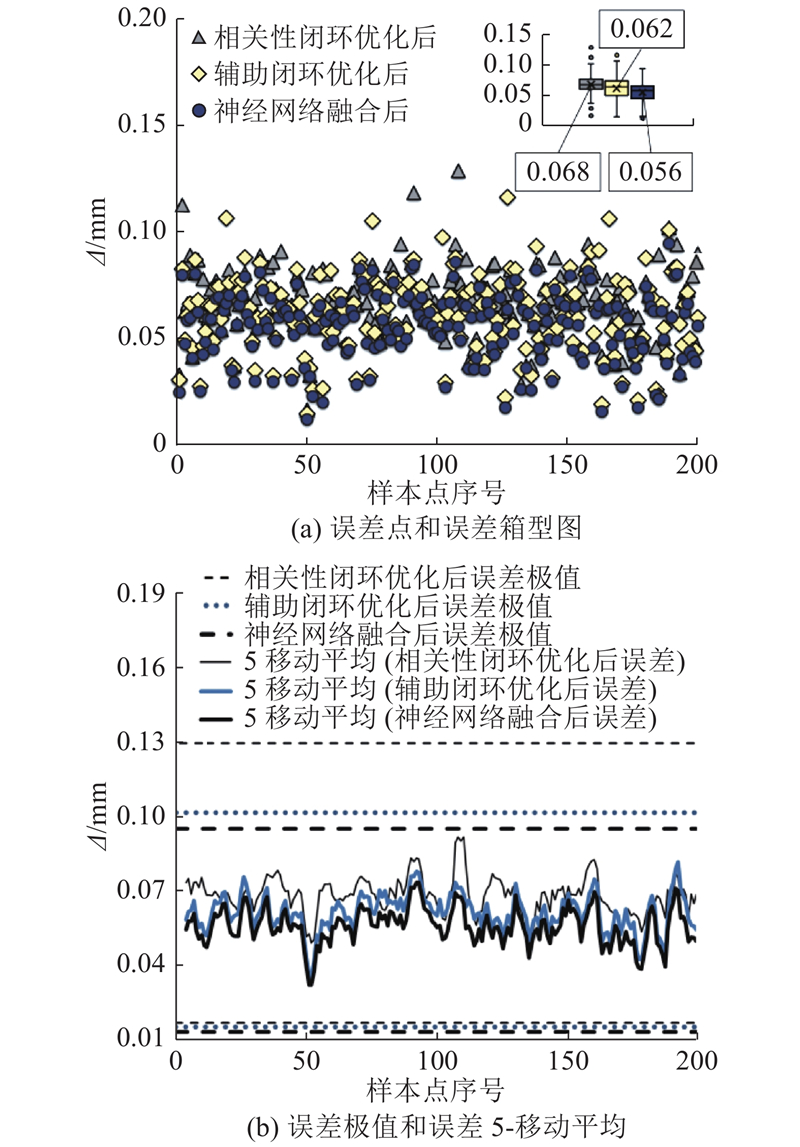
图 4 样本点分别经过闭环优化和神经网络融合后的误差
Fig.4 Errors of sampling points after closed-loop optimization and neural network fusion
根据图4(a)可知,辅助闭环优化后点的平均误差为0.062 mm,相关性闭环优化后点的平均误差为0.068 mm,NN融合后点的平均误差为0.056 mm,且NN融合后点的误差的上四分位数、下四分位数和中位数比闭环优化后均明显减小. 以均方根误差(root mean squared error, RMSE)为评估指标,NN融合后的RMSE比辅助和相关性闭环优化后的RMSE分别减小了10.61%和5.04%.
根据图4(b)可知,NN融合后点的误差的最大值、最小值和5-移动平均明显下降,误差的波动范围缩小且误差极值沿着y轴下移,误差的标准差没有明显变化. 仿真结果表明,神经网络融合提高了辅助和相关性闭环优化的稳定性.
图 5
图 5 神经网络融合辅助和相关性闭环优化的效果
Fig.5 Neural network fusion effect of auxiliary and correlational closed-loop optimization
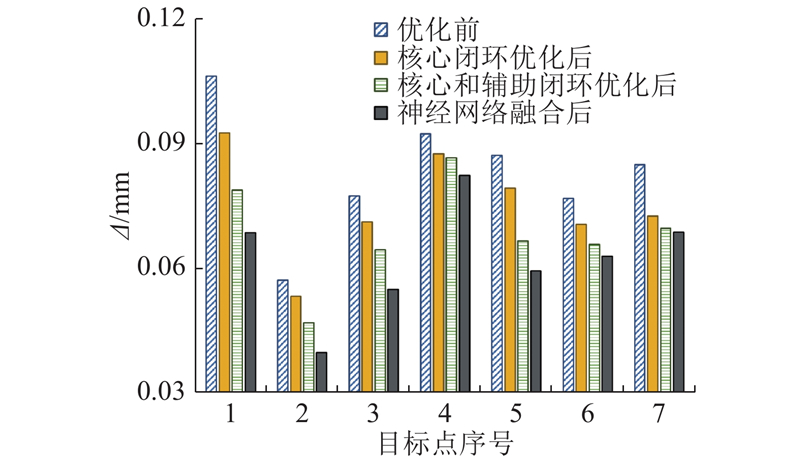
图 6
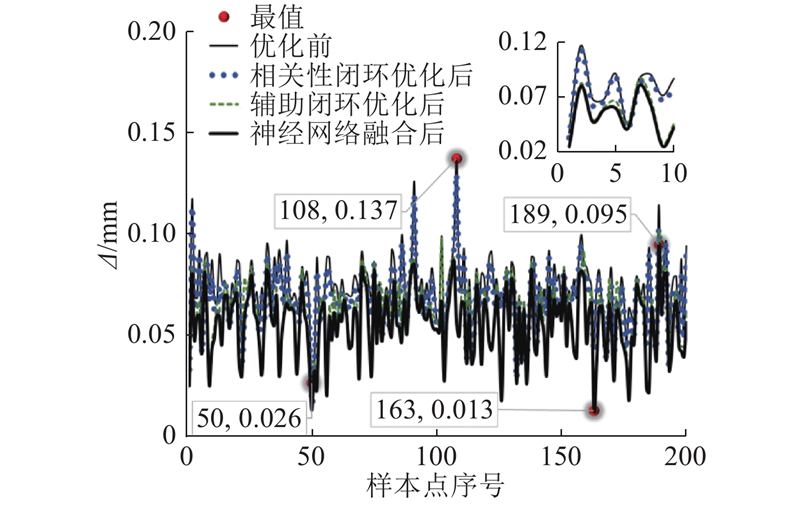
图 6 样本点优化前、经过闭环优化和神经网络融合后的误差
Fig.6 Errors of sampling points before optimization, after closed-loop optimization and neural network fusion
图 7
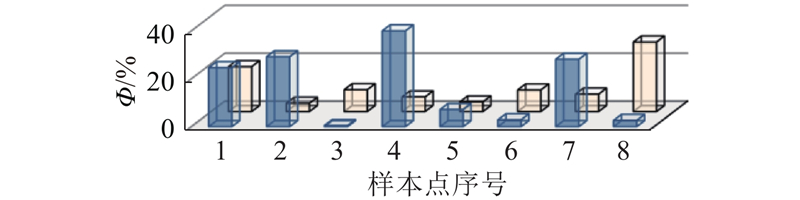
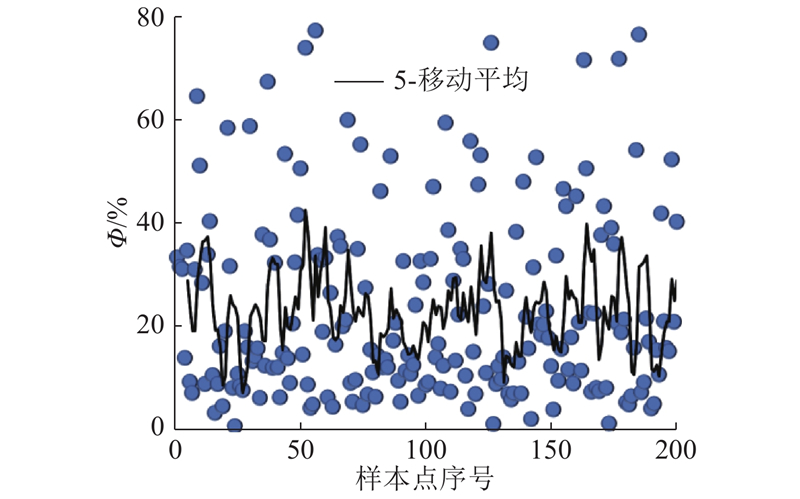
图 7 神经网络融合后点的误差比优化前减小的百分比
Fig.7 Reduced percentage of point errors after neural network fusion than before optimization
3.3. 末端工具定位仿真
图 8
图 8 工件局部及工件上预定的目标点
Fig.8 Part of workpiece and predetermined target points on workpiece
图 9
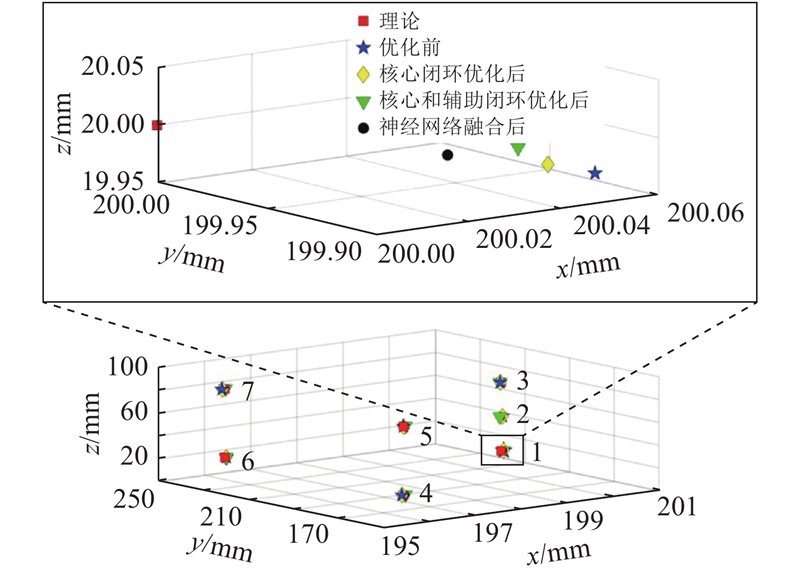
机器人末端工具的位置误差如图10所示. 比较逐级闭环优化策略和只考虑单一误差传递路径优化方法的误差减小效果可知,前者优化后的误差更小. 根据末端工具定位的仿真结果可知,优化前的末端工具位置误差最大,神经网络融合后的末端工具位置误差最小,逐级闭环优化策略有助于指导后续样机实验和实际加工应用.
图 10
4. 结 论
(1)面向机器人、测量仪器以及精密工装组成的机器人加工系统的定位误差问题,只考虑单一误差传递路径的误差减小效果不明显,提出逐级闭环优化策略. 基于核心闭环、辅助闭环和相关性闭环独立优化,构建神经网络模型,使用数据驱动的方式融合闭环优化结果. 利用该方法有效解决了误差通过坐标系变换累积传递的问题,提高了机器人末端工具的定位精度.
(2)闭环优化仿真显示,优化后末端工具位置误差平均减小了14.23%,角度误差平均减小了25.86%,表明闭环优化的有效性和泛化能力. 神经网络融合的仿真结果表明,神经网络融合提高了闭环优化的稳定性,使用数据驱动的方式融合闭环优化结果,可以减小点的误差. 综合比较闭环优化和神经网络融合可知,神经网络融合后比闭环优化前点的误差平均减小了23.38%.
(3)根据末端工具定位的仿真结果可知,优化前的末端工具位置误差最大,神经网络融合后的末端工具位置误差最小,逐级闭环优化策略比单一误差传递路径优化方法的误差减小效果明显. 该结果有助于指导后续样机实验和实际加工应用.
参考文献
Structural design and analyses of a fabric-covered wind turbine blade
[J].DOI:10.1080/09243046.2019.1626187 [本文引用: 1]
Mobile-robotic machining for large complex components: a review study
[J].DOI:10.1007/s11431-019-9510-1 [本文引用: 1]
A theoretical approach on determining the geometrical errors in case of articulated robot structures
[J].
A PSO-tuned fuzzy logic system for position tracking of mobile robot
[J].
A novel loop closure detection approach using simplified structure for low-cost LiDAR
[J].DOI:10.3390/s20082299 [本文引用: 1]
Road side unit location optimization for optimum link flow determination
[J].DOI:10.1111/mice.12490 [本文引用: 1]
Real-time quality monitoring and predicting model based on error propagation networks for multistage machining processes
[J].DOI:10.1007/s10845-012-0703-0 [本文引用: 1]
Modified steepest descent method for nonlinear irregular operator equations
[J].DOI:10.1134/S1064562415030187 [本文引用: 1]
Gauss-Newton methods with approximate projections for solving constrained nonlinear least squares problems
[J].DOI:10.1016/j.jco.2020.101459 [本文引用: 1]
Trajectory tracking control of wheeled mobile manipulator based on fuzzy neural network and extended Kalman filtering
[J].
GNSS/INS/LiDAR-SLAM integrated navigation system based on graph optimization
[J].DOI:10.3390/rs11091009 [本文引用: 1]
Deep learning in neural networks: an overview
[J].DOI:10.1016/j.neunet.2014.09.003 [本文引用: 1]
Calibration efficiency analysis based on five observability indices and two calibration models for a six-axis industrial robot
[J].DOI:10.4271/2013-01-2117 [本文引用: 1]
A new calibration method for enhancing robot position accuracy by combining a robot model-based identification approach and an artificial neural network-based error compensation technique
[J].
Validation of iGPS as an external measurement system for cooperative robot positioning
[J].DOI:10.1007/s00170-012-4004-8 [本文引用: 1]
Normal direction measurement and optimization with a dense 3D point cloud in robotic drilling
[J].
A novel indirect calibration approach for robot positioning error compensation based on neural network and hand-eye vision
[J].DOI:10.3390/app9091940 [本文引用: 1]
Cooperative fusion of distributed multi-sensor LVM (large volume metrology) systems
[J].DOI:10.1016/j.cirp.2015.04.003 [本文引用: 1]
采用结构光的大跨度销孔加工精度在线测量
[J].
Machining precision online measurement of large span pin hole using structured light
[J].