工业机器人线缆为通体柔性,会随着边界条件的改变发生局部弯曲、扭转等非线性变形,同时其受空间约束力的影响,受力状况复杂,而目前尚无成熟的方法能够全面分析其在服役过程中的动态特性。
目前,国内外许多学者对线缆等柔性体进行了建模和仿真研究。如:Terzopoulos等[4]提出了一种基于Lagrange方程的线缆物理模型,考虑了外载荷,并对几何约束进行了处理,分析了包含线缆重力、抗拉伸和抗弯曲三部分的物理变形能;Grégoire等[5]基于Cosserat理论对机电产品的线缆进行了仿真分析,在仿真模型中考虑了电缆的重力和接触摩擦力,但没考虑线缆的拉伸变形;Loock等[6]将质点-弹簧系统应用于线缆装配仿真中,用扭转弹簧表征线缆的动态弯曲特性,但是由于模型的参数较多,数值求解过程较复杂;金望韬等[7]基于弹性细杆静力学理论,提出了一种光滑平面约束下的活动线缆物理建模与仿真方法。以上研究考虑了线缆的物理属性,并对其静态特性进行了建模和分析,使柔性线缆模型在仿真和布局过程中更具真实性,但没考虑线缆活动时所产生的动态应力问题。杨炜烽等[8]基于位置动力学,对线缆离散Cosserat杆模型的位姿进行连续的预估和修正,完成了线缆的运动过程仿真,仿真结果受位姿修正迭代次数的影响。此外,还有不少利用多刚体链法[9-11]、有限元法[12-13]等进行线缆类柔性体建模的研究。然而,在上述研究中,建模过程都较复杂,数值求解效率较低。因此,需要对工业机器人线缆的动态特性进行建模优化。
在线缆布局设计方面,国内外学者也进行了研究。如:Park等[14]提出了利用多智能体系统进行协作规划的方法,研发了一种用于导弹线缆布线的线缆并行设计系统;Conru[15]利用人工智能方法研究了在复杂空间环境中线缆路径的搜索问题;Zhu等[16]利用基于知识的工程(knowledge based engineering, KBE)技术对飞机线缆的自动布局设计进行了研究,利用离散优化等技术分析了线缆长度约束和布线区域约束等,进行了线缆路径搜索;刘潇等[17-18]利用改进的运动规划算法,快速获得了单根线缆和分支线满足一定约束的线缆路径;杨啸东等[19]针对复杂机电产品的线缆装配序列规划问题,提出了装配优先关系矩阵(assembly priority matrix, APM)的概念,对标准粒子群算法的初始化加以改进,并引入了混沌算法,提高了算法的搜索效率;王发麟等[20]提出了基于数字孪生的动态建模与仿真方法,将基于随机有限集(random finite set, RFS)的同步定位与地图构建(simultaneous localization and mapping, SLAM)方法应用于线缆装配路径与位姿的估计,来构建以动态数据驱动的线缆装配工艺模型。上述线缆布局规划研究主要集中在复杂空间中线缆的可行路径搜索上,同样未考虑线缆本身处于实时运动状态的工况。特别对于工业机器人线缆而言,其在机器人第2、第3关节处通常仅有2个固定点,大部分线缆的服役特性为动态反复弯曲导致的应力动态变化和疲劳损伤,因此,上述研究成果并不适用于工业机器人关节处运动线缆的空间布局与优化。
综上,尽管目前对于线缆动态建模和布局设计的研究取得了一定的成果,但仍没有一种适合工业机器人线缆建模和布局设计的优化算法。因此,本文提出了基于弹簧阻尼链式等效的柔性线缆建模方法,并考虑了线缆动力学模型参数的取值对最终仿真精度的影响,避免了根据经验确定线缆动力学模型的参数值而造成仿真误差。通过线缆仿真参数识别技术来确定线缆力学模型的最优参数,使模型具有所需参数少而精度高的优势,实现了工业机器人线缆的运动仿真;以线缆最大应力最小为优化目标,对工业机器人线缆布局进行优化设计;通过实验,将线缆动力学模型仿真形态与工业机器人线缆的真实运动形态进行对比,来验证线缆模型的准确性。
1 工业机器人线缆动力学建模
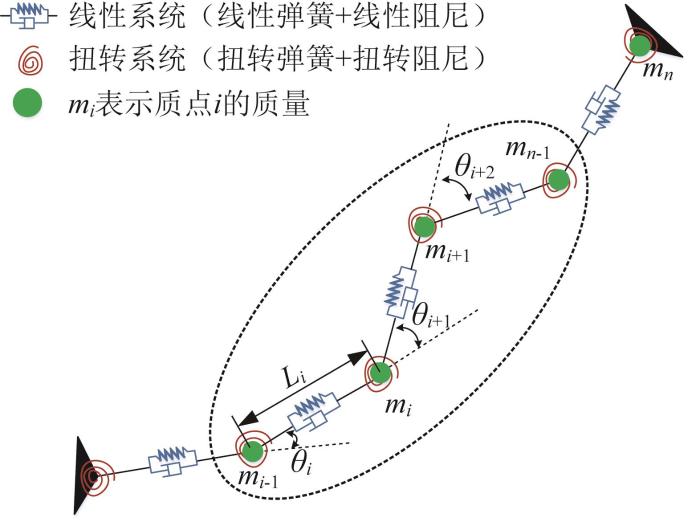
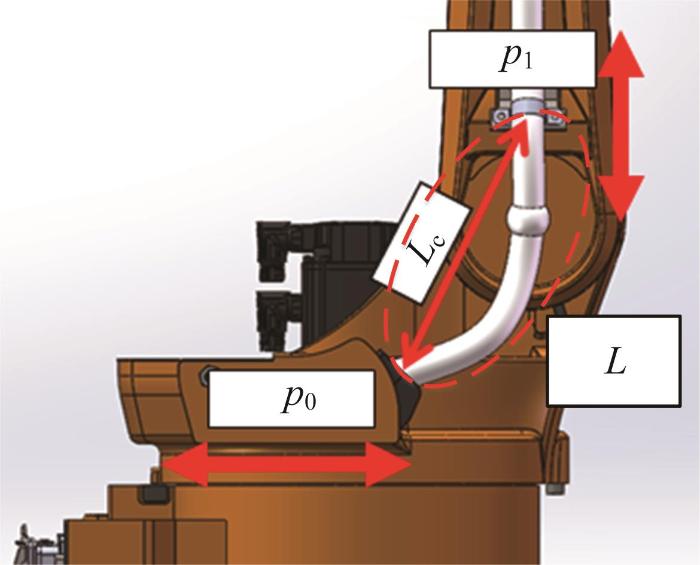
工业机器人本体线缆如图1所示。本文主要针对工业机器人本体关节处柔性线缆的变形特性进行研究,并对其进行合理布局,以提高线缆寿命。
图1
1.1 柔性线缆简化模型
图2
1.2 柔性线缆受力分析
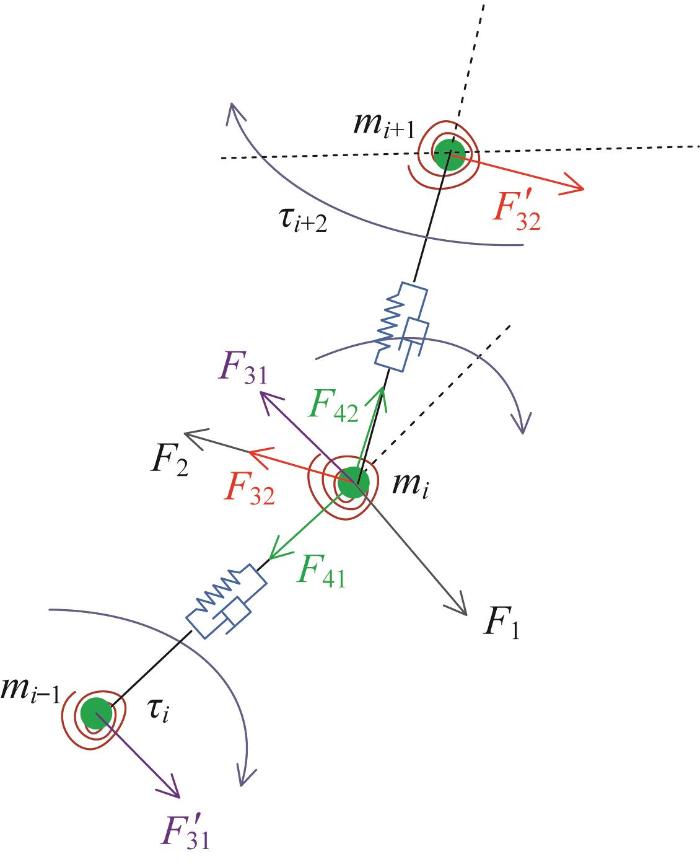
采用牛顿法对线缆进行受力分析。以任意非特定质点i (i
图3
针对图3所示的质点i,设其线性系统的拉力为
1)质点
2)质点
3)质点
4)质点
5)质点
6)质点
因此,当i
1.3 柔性线缆上各质点分力的计算方法
1.3.1 τtor, i 和ηlin, i 的计算
τtor, i 仅与其当前连杆转角θi 有关,即:
式中:ktor为扭转弹簧的弹性系数。
ηlin, i 仅与其当前连杆长度Li 有关,即:
式中:klin为线性弹簧的弹性系数,Li0为连杆原长。
1.3.2 τdam, i 和ηdam, i 的计算
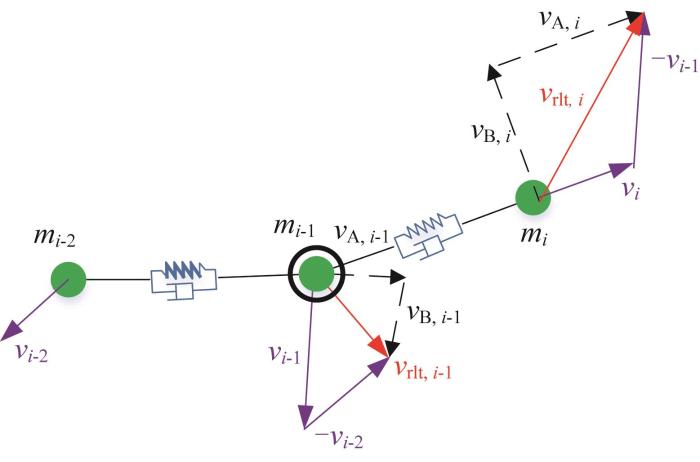
求解τdam, i 和ηdam, i,首先需要得到质点i的速度。质点i的速度分解如图4所示。设某时刻质点i及其下方两质点i-1和i-2的速度分别为vi 、vi-1和vi-2。
图4
以连杆i下方的质点i-1作为参照,则连杆i的相对速度
式中:Clin为线性阻尼系数。
同理,以连杆i-1的下方质点i-2为参照,则连杆i-1的相对速度
则:
式中:Ctor为扭转阻尼系数。
基于上述质点分力的计算,可求得每个质点所受的合力。随后,利用这些合力,可进一步求得当前时刻线缆上所有质点的加速度。
在传统基于质点-弹簧的线缆建模与仿真中,由于弹簧数量较多,仿真时求解速度慢且容易出现失真的情况。本文提出的基于弹簧阻尼链式等效的柔性线缆建模方法,可以用较少的弹簧来模拟线缆,并提高求解效率。同时,该模型还能描述线缆两端固定点运动引起的各质点作用力的变化,从而适用于描述工业机器人线缆的被动变形特征。
2 柔性线缆仿真参数识别技术
工业机器人线缆可分为2种形态:机器人处于稳固静止状态时的静态形态和机器人在执行工作任务时的动态形态。在不同的形态下,选取的线缆模型的弹性系数和阻尼系数不同。因此,利用粒子群算法对上述参数进行识别。通过实验测得线缆的真实形态,并与线缆仿真模型的形态进行对比,对仿真结果与实验结果之间的误差不断迭代来调整模型参数,直至误差值足够小,从而精确识别出最优的模型参数。对线缆弹性系数和阻尼系数的精确识别可以有效提升线缆模型的准确性,对于后续工业机器人线缆仿真与优化具有重要意义。
2.1 线缆弹性系数辨识技术
2.1.1 线缆静态形态仿真
运用最小势能原理求解线缆模型在约束条件下的静态形态。线缆处于稳定平衡状态时,其势能为最小值,线缆静态形态即线缆模型的重力势能、线性弹簧和扭转弹簧的弹性势能之和为最小值时的线缆形态。
线缆模型的重力势能Ep为:
式中:
线缆模型线性弹簧的弹性势能Elin为:
式中:klin为线性弹簧的弹性系数。
线缆模型扭转弹簧的弹性势能Etor为:
式中:ktor为扭转弹簧的弹性系数。
2.1.2 线缆静态实验与参数识别
图5
表1 线缆上端位置信息
Table 1
| 实验组号 | 坐标(X, Y, Z)/mm | 姿态(XOZ平面上与X轴的夹角/(°)) |
|---|---|---|
| 1 | (100.0, -35.0, 220.0) | 90 |
| 2 | (120.0, -35.0, 210.0) | 70 |
| 3 | (150.0, -35.0, 190.0) | 50 |
| 4 | (160.0, -35.0, 170.0) | 30 |
表2 线缆各标记点的坐标 (mm)
Table 2
| 实验组号 | 标记点1 | 标记点2 | 标记点3 | 标记点4 |
|---|---|---|---|---|
| 1 | (49.9, 7.8, 27.2) | (94.6, -1.7, 66.6) | (110.4, -18.7, 127.0) | (104.4, -35.1, 187.4) |
| 2 | (50.4, 6.9, 26.8) | (96.6, -3.0, 64.6) | (117.5, -19.8, 234.2) | (118.5, -32.7, 184.6) |
| 3 | (56.7, 6.7, 22.2) | (102.6, -3.9, 54.9) | (128.9, -20.0, 110.9) | (137.1, -29.6, 172.3) |
| 4 | (55.3, 6.2, 16.2) | (108.5, -6.1, 42.4) | (136.3, -23.1, 95.6) | (147.0, -30.6, 156.6) |
采用2.1.1节中介绍的线缆静态形态仿真方法对线缆模型进行相应场景的仿真,得到与标记点相同位置的坐标。以仿真结果与实验结果的差值最小为优化目标,目标函数F为:
式中:
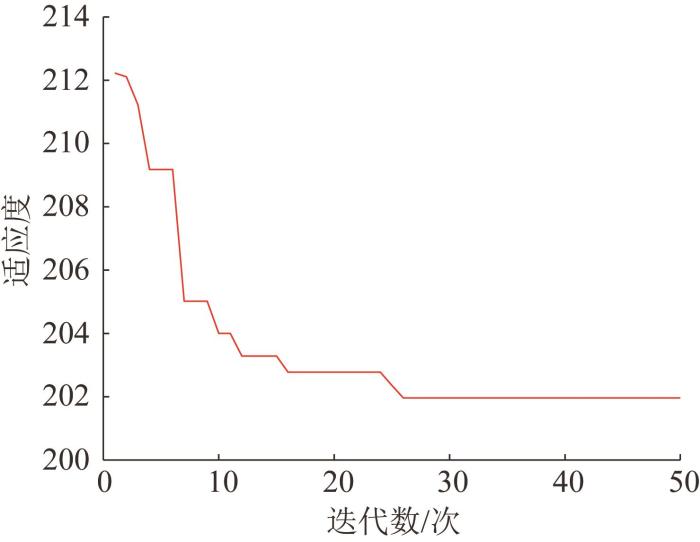
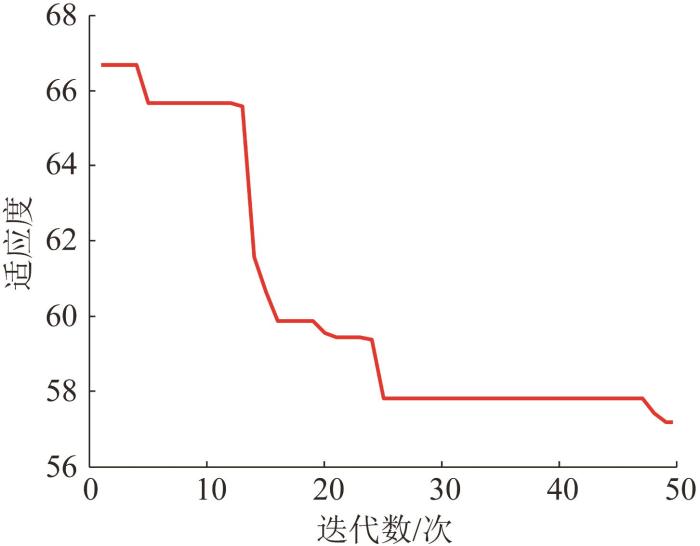
将所有数据和目标函数值代入粒子群优化算法,对线缆的弹簧参数进行识别。根据识别结果调整线性弹簧和扭转弹簧的弹性系数,得到klin=218 485 N/m,ktor=28 N/m。种群的适应度变化如图6所示。由图可知,第50代种群的适应度为202,表示上述参数与实验结果的误差为202 mm,各点的平均误差为12.6 mm。
图6
图6
线缆弹性系数识别中种群适应度的变化
Fig.6
Change of population fitness during identification of elasticity coefficient of cable
2.2 线缆阻尼系数辨识技术
2.2.1 线缆动态形态仿真
给定线缆模型某一质点的运动位置和速度,根据1.2节中线缆质点受力分析,可得到当前时刻所有质点的加速度。将线缆运动分为若干个微小时间单元,由牛顿法可得到下一时间单元的质点位置、姿态、速度并进行受力分析,得到新的质点位置,按此方法依次迭代便可实现线缆的动态形态仿真。
2.2.2 线缆动态实验与参数识别
通过线缆的动态实验识别线缆的阻尼系数。取一个线束进行动态实验,测量线缆在运动过程中的空间变形。将线缆下端固定,线缆上端运动,并用DIC相机测量线缆运动时中间4个标记点相对初始位置的位移。在线缆运动过程中每隔0.1 s选取一组数据,共取6个时刻,得到6组数据,如表3所示。
表3 线缆运动过程中各标记点的相对位移
Table 3
| 运动时间/s | 相对位移/mm | |||
|---|---|---|---|---|
| 标记点1 | 标记点2 | 标记点3 | 标记点4 | |
| 0.1 | 2.4 | 5.3 | 12.1 | 20.2 |
| 0.2 | 7.9 | 16.5 | 26.7 | 38.3 |
| 0.3 | 15.7 | 31.7 | 44.6 | 56.4 |
| 0.4 | 8.2 | 17.1 | 26.7 | 38.0 |
| 0.5 | 2.6 | 5.6 | 10.9 | 18.5 |
| 0.6 | 0.2 | 0.4 | 0.3 | 0.4 |
对线缆模型进行相应场景的动态仿真,得到与实验相同时刻的标记点位移。以仿真结果与实验结果的差值最小为优化目标,将所有数据和目标函数值代入粒子群优化算法,对线缆的阻尼参数进行识别。根据识别结果调整线性阻尼系数和扭转阻尼系数,得到Clin=45 N/(m·s-1),Ctor=28 N/(m·s-1)。种群的适应度变化如图7所示。由图可知,第50代种群的适应度为57.1,表示上述参数与实验结果的误差为57.1 mm,各点的平均误差为14.3 mm,其占线缆总长度的4.8%。
图7
图7
线缆阻尼系数识别中种群适应度的变化
Fig.7
Change of population fitness during identification of damping coefficient of cable
3 工业机器人线缆仿真模型实验验证
3.1 实验设计
为了验证线缆物理简化模型与运动仿真的准确性,进行实际工况下工业机器人关节处线缆运动的仿真和实验。实验装置如图5所示。将线缆下端在台架上用卡箍固定,上端夹持在六轴机器人的末端执行器中。通过调整机器人的末端轨迹,可模拟实际工况下线缆在机械臂上安装位置不同导致的运动特性差异。以六轴机器人末端执行器为线缆运动端,通过编程即可实现模拟工业机器人某一关节处线缆的运动。在实验过程中,用DIC相机对线缆表面的标记点进行追踪拍摄,从而得到标记点的位移。
3.2 线缆运动实验与仿真结果的对比及分析
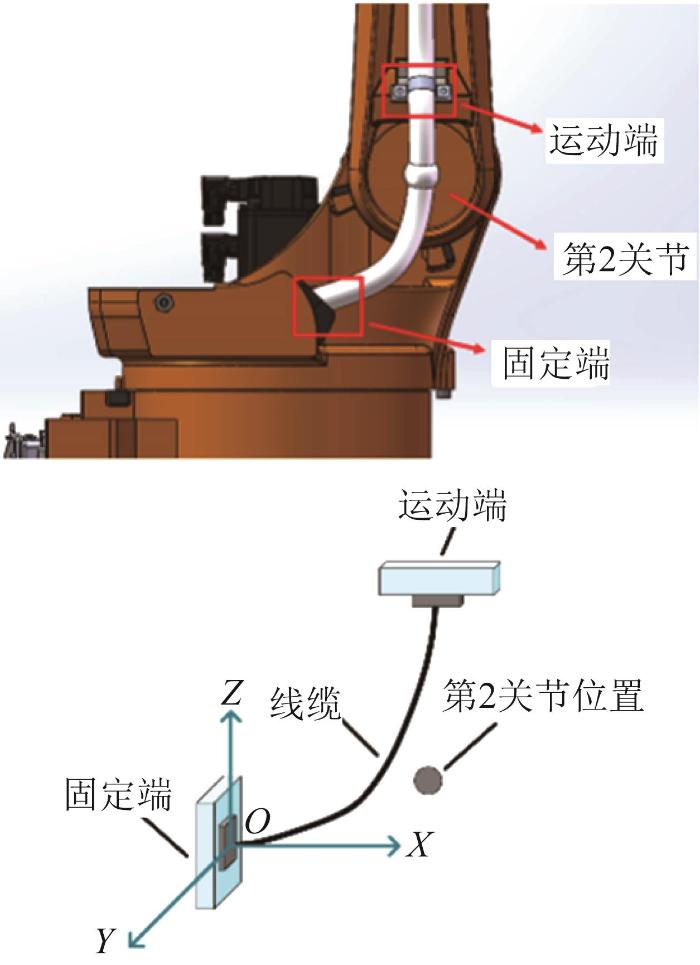
图8
图8
工业机器人第2关节处的线缆示意
Fig.8
Schematic of cable at second joint of industrial robot
图9
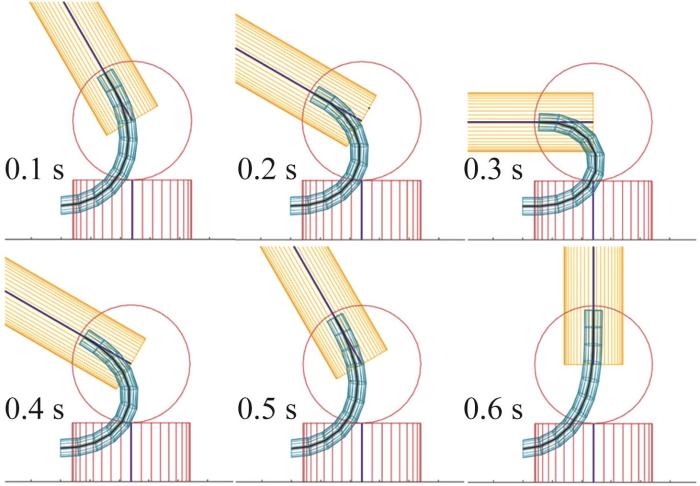
根据所建立的线缆动态模型及所识别的仿真参数,在MATLAB软件中进行线缆运动仿真。仿真中将线缆模型的质点数量设定为10个,线缆长度为0.3 m,直径为0.028 m,质量为0.9 kg,与真实线缆保持一致,并且线缆两端的相对位置及其与工业机器人第2关节的相对位置均与实验一致。线缆运动仿真结果如图10所示。
图10
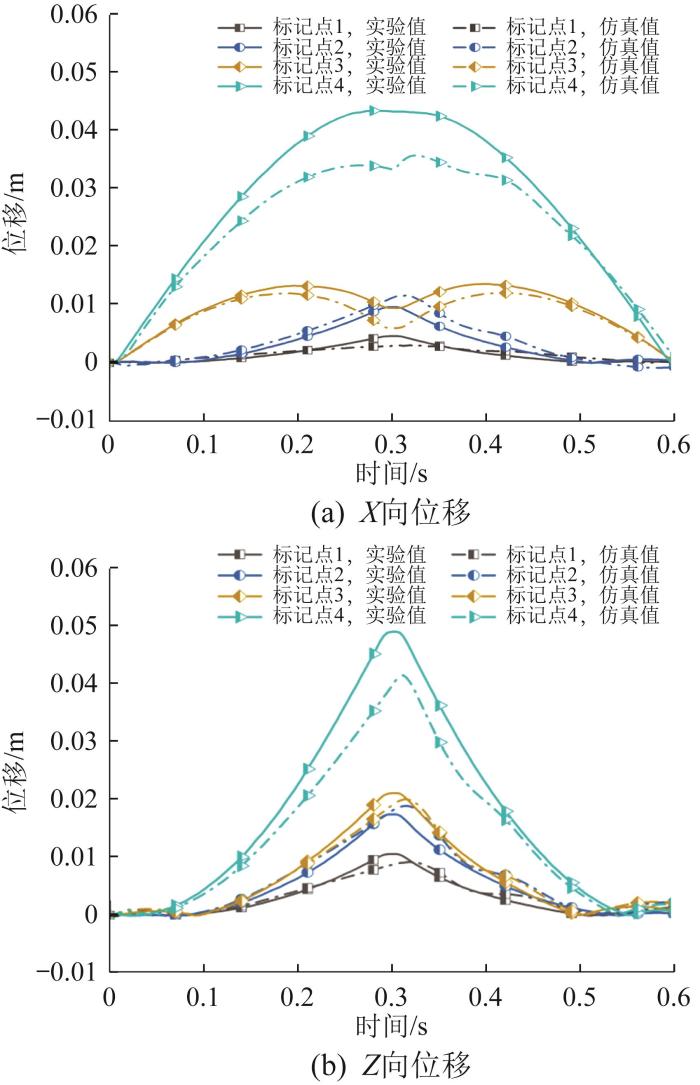
线缆运动实验与仿真结果的对比如图11所示。由图可知,实验与仿真结果存在一定差值,最大误差为10.5 mm,占线缆总长度的3.5%,符合预期要求,验证了线缆模型的准确性。
图11
图11
线缆运动实验与仿真结果的对比
Fig.11
Comparison of experimental result and simulation result of cable movement
4 工业机器人线缆布局优化
4.1 布局优化策略
在工业机器人工作时,其关节处线缆的应力随线缆两端的固定位置、运动端出线方向及活动线缆长度的变化而变化。为了优化线缆布局,提高线缆寿命,可通过优化线缆两端的固定位置、运动端出线方向及活动线缆的长度来减小线缆应力。基于线缆动态模型求得各个质点处的应力,建立使线缆最大应力最小为优化目标的线缆布局优化模型。目标函数F1为:
式中:p0为线缆固定端沿X向的位移,pl为线缆运动端沿Z向的位移,ql为线缆运动端的出线方向与机械臂在XOZ平面的夹角,L为活动线缆长度,
p0、pl、ql和L为线缆布局优化模型的主要优化参数,如图12所示。
图12
4.2 线缆模型各质点的应力计算
根据第1.2节中线缆的受力分析,对线缆各质点所受的应力进行计算。以质点
质点
式中:
质点
式中:
当i=n时,质点仅受
4.3 布局优化设计
对3.2节所示的工业机器人第2关节处的线缆进行布局优化设计,对线缆两端的固定位置、运动端出线方向及活动线缆长度进行调节。设定p0=-5~5 cm,pl=-5~5 cm,ql=-45°~45°。根据企业调研总结,线缆长度的设计要求为:活动线缆长度应大于线缆两端距离的1.1倍,且不宜过长,故取L=1.1~1.4Lc,其中Lc为线缆两端之间的距离,如图12所示。
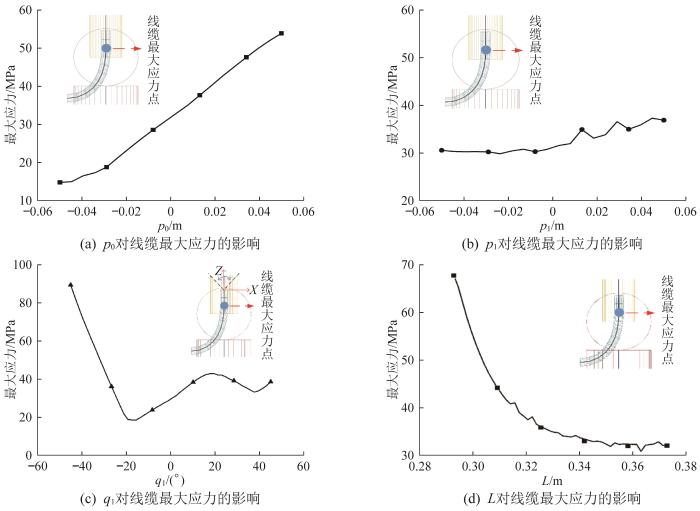
改变其中一个线缆布局优化参数,保持其余参数不变,则线缆最大应力的变化趋势如图13所示。
图13
图13
线缆布局优化参数对线缆最大应力的影响
Fig.13
Effect of cable layout optimization parameters on maximum stress on cable
由图13可得:p0越大,线缆最大应力越大;pl对线缆最大应力的影响不大;ql≈
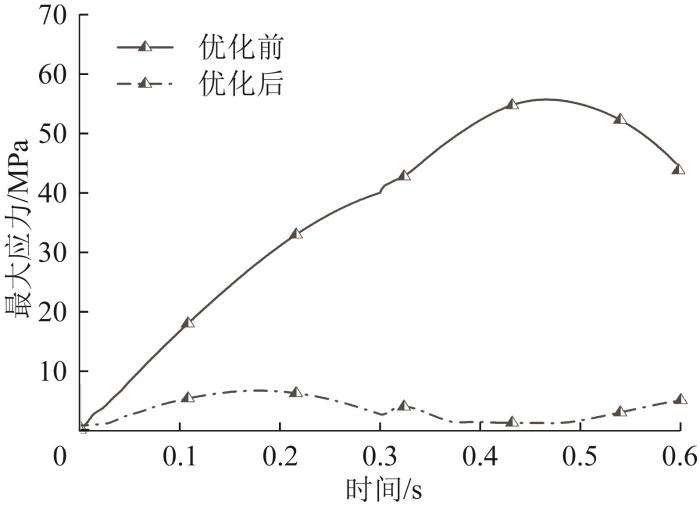
通过线缆各质点应力的仿真计算,得到工业机器人第2关节处线缆在布局优化前后最大应力的变化,如图14所示。由图可知,相较于布局优化前,布局优化后线缆的最大应力约减小了83%。
图14
图14
布局优化前后线缆最大应力变化曲线
Fig.14
Change curves of maximum stress on cable before and after layout optimization
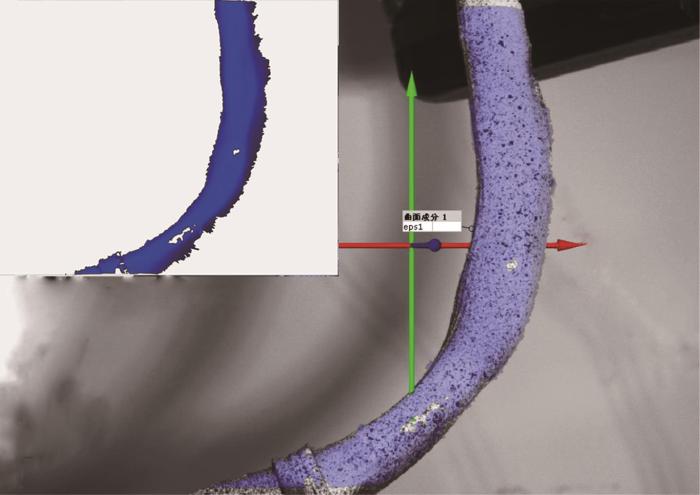
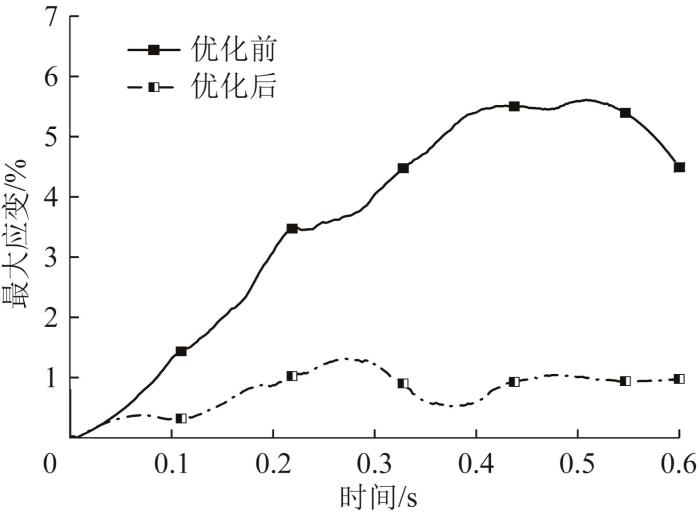
4.4 线缆最大应变测量
图15
图16
图16
布局优化前后线缆最大应变变化曲线
Fig.16
Change curves of maximum strain of cable before and after layout optimization
5 结 论
1)本文提出了基于弹簧阻尼链式等效的柔性线缆建模方法,将线缆通过线性弹簧、线性阻尼、扭转弹簧和扭转阻尼进行分割,实现了其质点动力学描述。
2)基于建立的线缆模型,通过最小势能法实现了线缆的静态形态仿真,并通过对线缆各质点的受力分析,由牛顿法解得此时质点的动力学参数,经过一个微小时间内的运动后即可得到下一时刻各质点的位置,迭代上述步骤即可实现线缆动态形态仿真。而后,通过线缆静态和动态实验,利用粒子群算法对仿真结果与实验结果的误差进行迭代,直至误差值足够小,从而得到线缆动力学模型的最优参数。搭建了模拟工业机器人第2关节处线缆运动的实验平台,用DIC相机测得线缆运动形态,将实验结果与仿真结果进行对比,验证了线缆动力学模型的准确性。
3)提出了工业机器人线缆布局优化策略,计算了线缆动力学模型各质点处的应力。通过改变线缆两端的安装位置、运动端出线方向及活动线缆的长度,使得线缆的最大应力最小,从而实现线缆的布局优化。通过对布局优化前后线缆运动过程中线缆最大应力、最大应变的对比,验证了所提出的工业机器人线缆布局优化方案的可行性。
参考文献
Vibration cascade control for motor-driven deep-sea robot cable system with actuator fault
[J].
Global sensitivity analysis of dynamic parameters to industrial robots considering spacetime two-dimensional output responses
[J].
基于Kriging模型的工业机器人定位精度补偿方法
[J].
A compensation method for positioning accuracy of industrial robot based on Kriging model
[J].
Dynamic NURBS with geometric constraints for interactive sculpting
[J].
Interactive simulation of one-dimensional flexible parts
[J].
A virtual environment for interactive assembly simulation: from rigid bodies to deformable cable
[C]//
光滑平面约束下的活动线缆物性建模与运动仿真技术
[J].
Motional cable harness physical characteristic oriented modeling and kinetic simulation technology under smooth plane constraints
[J].DOI:10.3901/JME.2016.03.118 [本文引用: 1]
基于位置动力学的线缆运动过程仿真方法
[J].
Method of cable dynamic simulation based on PBD
[J].
Real-time virtual cables based on kinematic simulation
[C]//
Large-scale dynamic simulation of highly constrained strands
[J].
A feedback tracking system for robot
[J].
Dynamic modeling of cable system using a new nodal position finite element method
[J].
A finite element/quaternion/asymptotic numerical method for the 3D simulation of flexible cables
[J].
Computational support for concurrent engineering of cable harnesses
[C]//
A genetic approach to the cable harness routing problem
[C]//
A KBE application for automatic aircraft wire harness routing
[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference,
基于改进RRT算法的线缆自动布线技术
[J].
Improved RRT based cable automatic routing
[J].DOI:10.3901/jme.2015.17.096 [本文引用: 1]
基于改进随机路径图的分支线缆自动布局技术
[J].
Multi-branch cable automatic routing based on improved PRM
[J].
基于混沌-粒子群算法的柔性线缆装配序列规划技术
[J].
Cable assembly sequence planning based on chaos-particle swarm optimization
[J].
基于数字孪生的复杂机电产品线缆装配工艺模型动态构建方法
[J].
Dynamic construction method of cable assembly process model for complex mechatronic products based on digital twin
[J].