风电塔筒的外壁面通常为圆柱面或圆锥面,传统爬壁机器人无法适应变曲率壁面。针对爬壁机器人的变曲率自适应问题,国内外学者展开了深入研究[10-11],目前主要有4种解决方案。一是基于足式结构的曲面高适应性。沈阳工业大学的崔晓森[12]设计了一种适用于风电塔筒外壁面运维的四足伸缩式爬壁机器人,其具备全向运动特性,可用于风电机组外表面的检测与修复。但是,足式移动机构存在移动速度缓慢、运动灵活性低和平稳性差等不足。二是基于多体式设计理念。多体式爬壁机器人的母体通过串接多个独立的子结构,利用机器人母体、子结构及壁面之间的空间约束关系来实现机器人系统整体的姿态调整,从而提高对变曲率壁面的适应性。清华大学的崔宗伟等[13]研制了由机械臂串联而成的两端吸附式双体爬壁机器人;卡内基梅隆大学的Seo等[14-15]研制了双体履带式爬壁机器人,该机器人采用被动定向柔性接头连接2组履带机构,采用扁平黏性聚合物制成的轮胎驱动,以实现在复杂变曲率壁面上的灵活、稳定移动。尽管多体式设计增强了爬壁机器人在变曲率壁面上的自适应能力,但其复杂结构导致转弯半径增大,机动性下降,从而增加了机器人在复杂壁面上的运动规划难度。三是基于柔性力学原理。自适应爬壁机器人利用柔性材料替换部分刚性材料,通过柔性材料的形变来实现在变曲率壁面上的自适应运动。中国科学院沈阳自动化研究所的Song等[16]研制了基于被动柔顺机制的爬壁机器人,可自主适应变曲率壁面;广州大学的Zhang等[17]研制了仿水蛭模块化爬壁机器人,该机器人通过多个运动模块与内部柔性材料结构的耦合来实现步距可变,以提高对变曲率壁面的适应性。采用柔性材料的自适应爬壁机器人姿态灵活且能够对壁面的曲率变化做出敏感响应,但柔性材料的形变难以精确控制,且容易受到负载和吸附力等因素的影响,导致机器人可能会出现姿态偏移或不稳定的情况。四是采用环抱式结构。区别于前3种独立式爬壁机器人,环抱式爬壁机器人横向360°包裹塔筒,通过预紧力来适应变曲率壁面。华北电力大学的韩强[18]设计了一种由6个爬升单元串联组成的抱撑式爬升装置,该装置虽可通过各单元连接装置的伸缩来适应塔筒壁面的曲率变化,但在实际作业中,操作难度大且成本高。
综上所述,现有爬壁机器人普遍通过增加本体结构的姿态灵活性来提高变曲率适应性,但难以实现姿态自适应变化与运动稳定性之间的平衡。因此,需要从结构角度出发探索单体机器人在变曲率环境下的姿态变化规律,以提升其在复杂壁面上的运动性能,但目前相关研究尚不足。为此,本文通过分析轮式爬壁机器人在变曲率壁面上作纵向和转弯运动时的姿态变化规律,提出了一种采用分体式柔性变曲率自适应设计理念的新型爬壁机器人。首先,基于爬壁机器人在风电塔筒变曲率壁面上的多种运动状态,对柔性铰链处的摆角与铰链安装位置及壁面曲率的关系进行分析;然后,通过参数化分析对爬壁机器人的磁吸附模块进行结构优化;最后,通过实验来测试爬壁机器人整体结构设计的合理性和可靠性。
1 变曲率自适应爬壁机器人结构设计
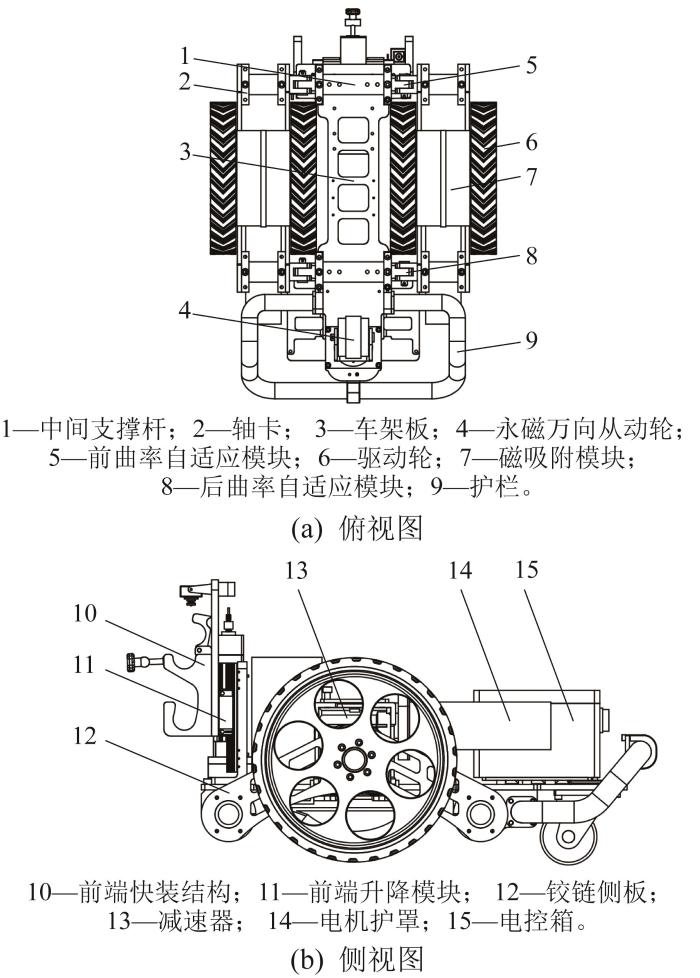
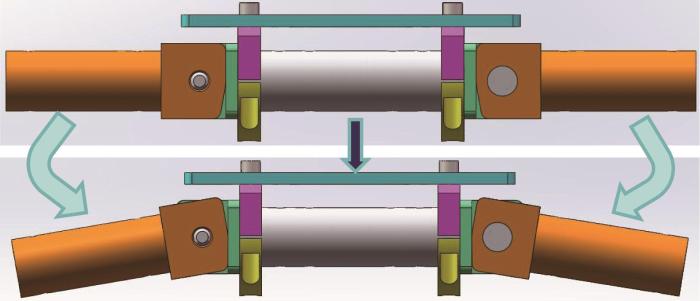
风电塔筒的外壁面通常具有较大的曲率变化。为了实现在复杂变曲率环境中的可靠吸附,本文选择采用轮式移动方式和永磁吸附技术。然而,由于风电塔筒外壁面的曲率变化较大,爬壁机器人磁吸附模块与壁面之间的间隙会发生显著变化,而间隙变化会直接影响吸附稳定性。这是因为磁吸附模块与壁面之间的间隙会影响磁力强度:若间隙过大,则磁力减弱,导致吸附力不足;反之,吸附力过大,则可能会导致机器人损害壁面涂漆甚至难以解附。为了克服这一难题,本文设计了一种新型的分体式柔性变曲率自适应爬壁机器人,其结构如图1所示。区别于传统爬壁机器人刚性一体化的特点,所设计的爬壁机器人将驱动模块、磁吸附模块与本体分解形成左右2个独立的集成模块并采用柔性连接。柔性连接模块的结构如图2所示,其具有一个翻转0°~10°的自由度,以适应壁面的曲率变化。柔性连接模块通过侧板与驱动模块相连,左右4个驱动轮分别由2个电机驱动。磁吸附模块分别安装于左右驱动模块底盘上并采用间隙式永磁吸附方式,使得机器人整体形成左右对称结构且重心在本体中轴线上;在面对变曲率环境时,磁吸附模块与壁面之间的间隙始终保持不变,以保证机器人的吸附稳定性。机器人尾部安装永磁万向从动轮,起支撑作用。
图1
图1
分体式柔性变曲率自适应爬壁机器人结构
Fig.1
Structure of split-type flexible variable curvature adaptive wall-climbing robot
图2
图3
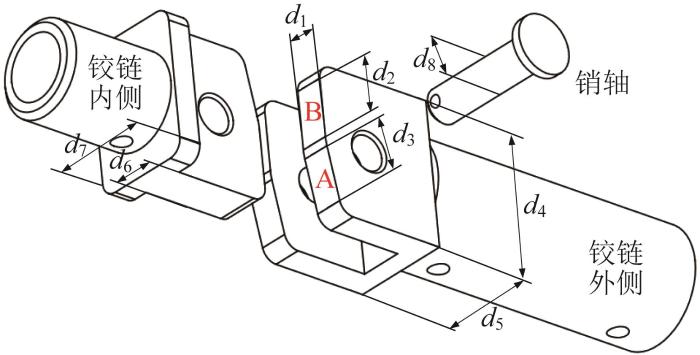
表1 柔性铰链关键尺寸参数 (mm)
Table 1
| 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|
| d1 | 10 | d5 | 35 |
| d2 | 20 | d6 | 15 |
| d3 | 18 | d7 | 35 |
| d4 | 50 | d8 | 12 |
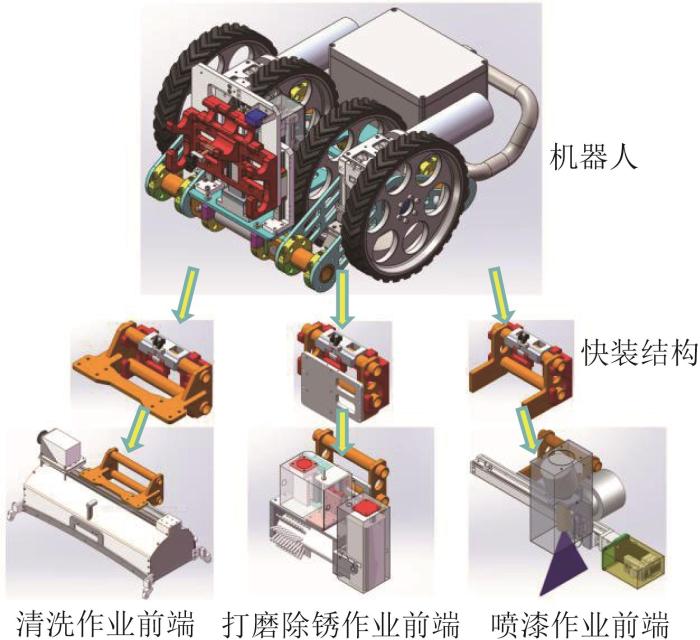
此外,因所设计的爬壁机器人面向风电塔筒维护作业,为弥补传统爬壁机器人作业功能单一的不足,设计了3款模块化作业前端:清洗作业前端、打磨除锈作业前端和喷漆作业前端。如图4所示,采用模块化设计理念,通过快装结构将作业前端与机器人本体相连,即可实现“一车三用”。
图4
图4
作业前端快速换装示意图
Fig.4
Schematic diagram of rapid replacement of front operation end
2 变曲率自适应爬壁机器人曲面运动姿态分析
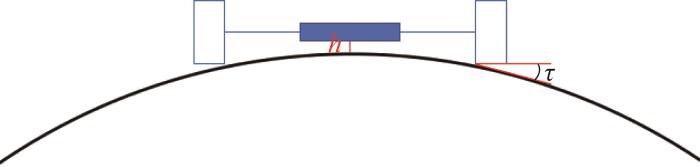
如图5所示,当传统爬壁机器人(采用刚性移动机构)沿风电塔筒壁面纵向移动时,其驱动轮的边缘与壁面发生接触,但是胎面并没有完全贴合壁面,驱动轮与壁面之间形成夹角
图5
图5
传统爬壁机器人的曲面姿态简图
Fig.5
Sketch of curved attitude of conventional wall-climbing robot
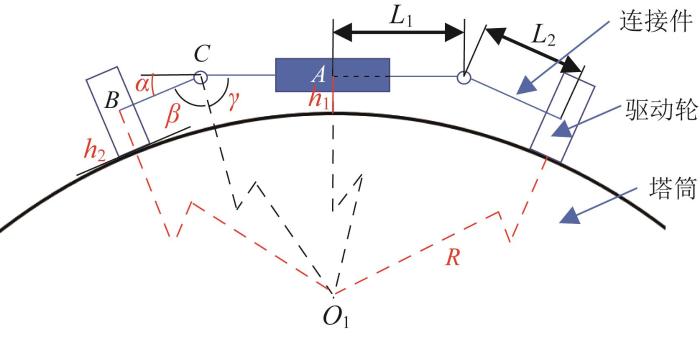
为提高爬壁机器人在变曲率壁面上的运动稳定性,在设计移动机构时引入了一种增加驱动轮自由度的方法,即采用多段式结构设计。如图6所示,在移动机构的两侧各设置了柔性铰链,这些铰链通过连接件分别与驱动轮相连。驱动轮连接件与机器人本体之间的夹角为
图6
图6
变曲率自适应爬壁机器人曲面姿态简图
Fig.6
Sketch of curved attitude of variable curvature adaptive wall-climbing robot
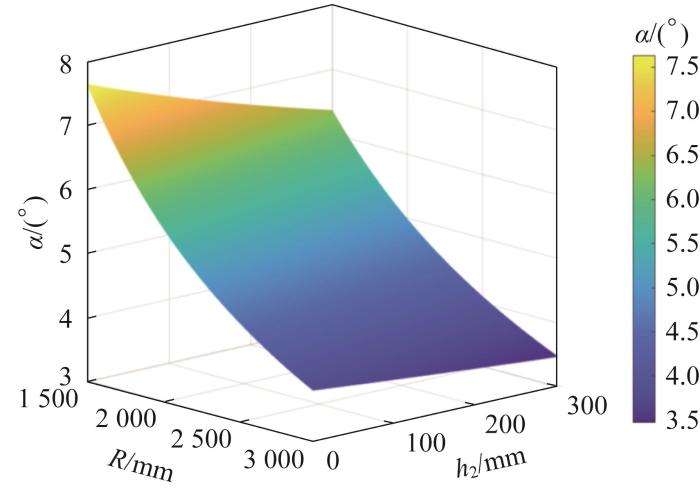
根据图6,塔筒曲率半径R与铰链处摆角α的几何关系可表示为:
机器人本体中心到塔筒壁面的距离
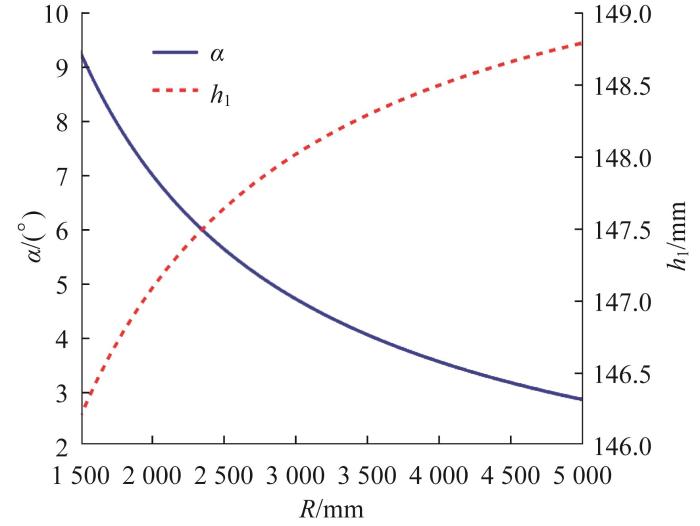
图7
由
图8
图8
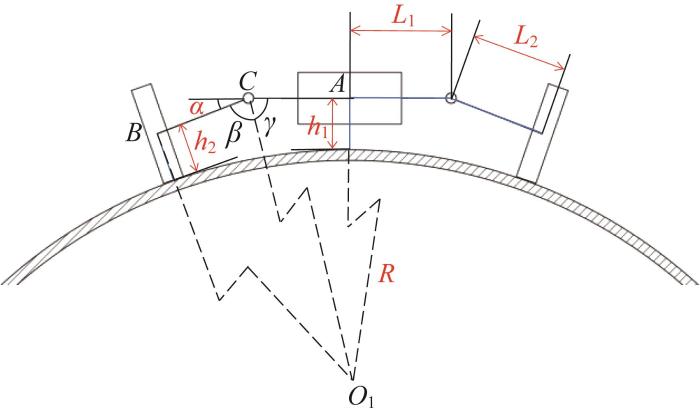
优化后变曲率自适应爬壁机器人曲面姿态简图
Fig.8
Sketch of curved attitude of optimized variable curvature adaptive wall-climbing robot
在机器人移动机构的结构参数满足
其中:
式中:
由
将已知的结构参数代入
图9
3 变曲率自适应爬壁机器人转弯运动特性分析
根据上述研究结果,在机器人本体半宽
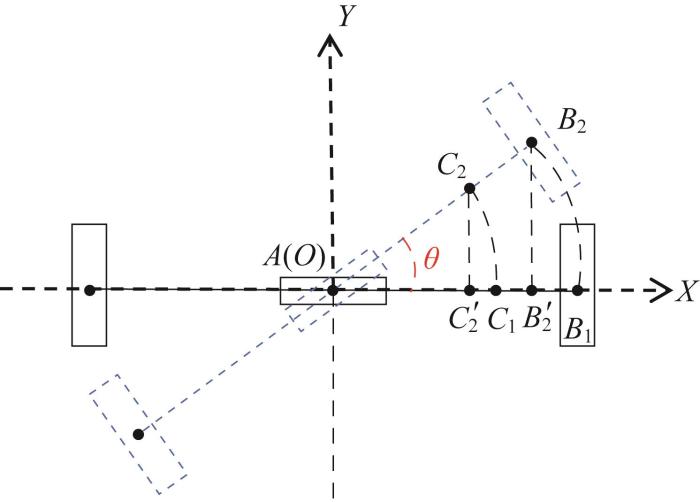
为分析爬壁机器人在变曲率壁面上转弯时的运动特性,绘制其原地转弯示意图(以机器人本体中心A为原点构建坐标系O-XYZ)。机器人在壁面上原地转弯的XOY面投影如图10所示。图中:
图10
图10
爬壁机器人原地转弯的 XOY 面投影
Fig.10
XOY surface projection of wall-climbing robot turning in place
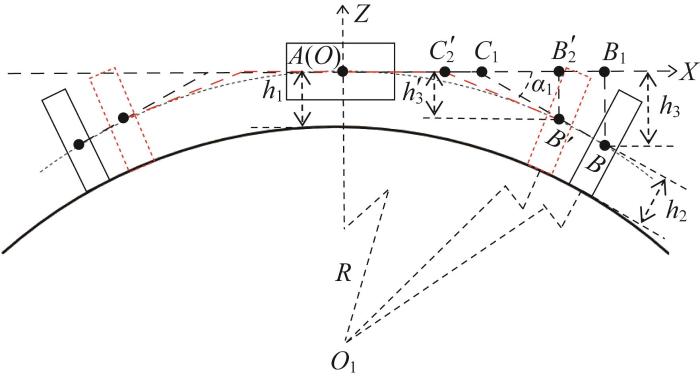
机器人在壁面上原地转弯时的XOZ面投影如图11所示。图中:
图11
图11
爬壁机器人原地转弯的 XOZ 面投影
Fig.11
XOZ surface projection of wall-climbing robot turning in place
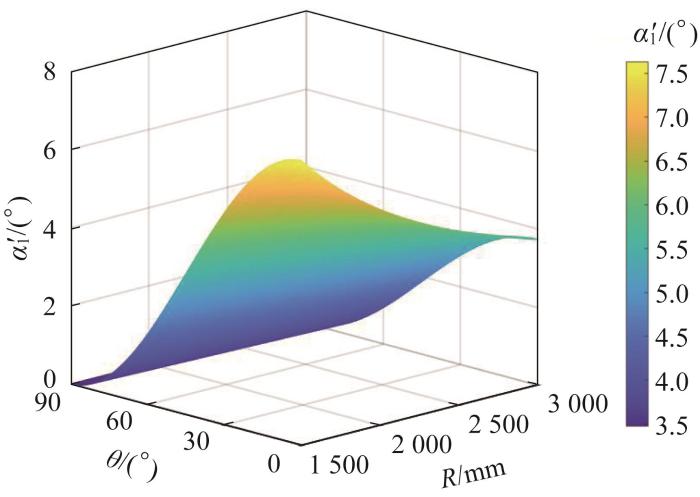
假设机器人原地转弯
式中:
根据图11,机器人原地转弯后驱动轮中心到XOY面的距离
其中:
式中:
图12
图13
图14
综上所述,铰链相对于机器人本体的位置高低对机器人运动的灵活性、稳定性有重要影响,这主要涉及机器人在壁面上的姿态控制和稳定性。
1)低位置铰链。铰链位置较低时可降低机器人的重心,低重心可使机器人更好地抵抗外部扰动,不易翻倒,从而提高稳定性。此外,铰链位置较低时机器人更容易进行姿态调整与控制,运动响应更加灵活,有利于应对不同曲率半径和倾斜角度的壁面。但是,铰链安装位置不宜过低,这是因为机器人在小曲率半径条件下转弯时,铰链易与壁面发生剐蹭。
2)高位置铰链。铰链位置较高可能会导致机器人的重心相对较高,增加了翻倒的风险。尤其是在垂直壁面上,高重心可能会导致机器人更容易失去平衡。此外,较高位置处的铰链可能需要更精密的姿态控制,以确保机器人在不同条件下保持稳定。在不同曲率的壁面上,铰链安装位置较高可能会使机器人面临更大的稳定性挑战。
因此,在设计爬壁机器人柔性连接模块的结构参数时,应保证在机器人转弯时铰链与塔筒壁面之间保持安全距离,以避免剐蹭。综上所述,当机器人本体中心到壁面的距离
4 变曲率自适应爬壁机器人磁吸附模块优化
为了提高变曲率自适应爬壁机器人磁吸附模块的吸附效率,基于Halbach阵列单侧磁场聚集能力强的特性,分析磁吸附模块结构参数对吸附力的影响并优化结构参数[19]。
表2 NdFeB-N48性能参数
Table 2
| 性能参数 | 数值 |
|---|---|
| 剩磁感应强度 | |
| 矫顽力 | 923 |
| 最大磁能 | |
| 最高工作温度 |
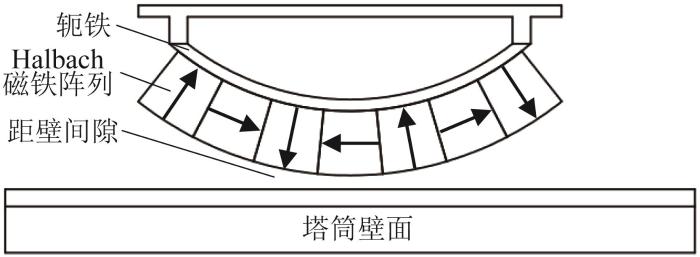
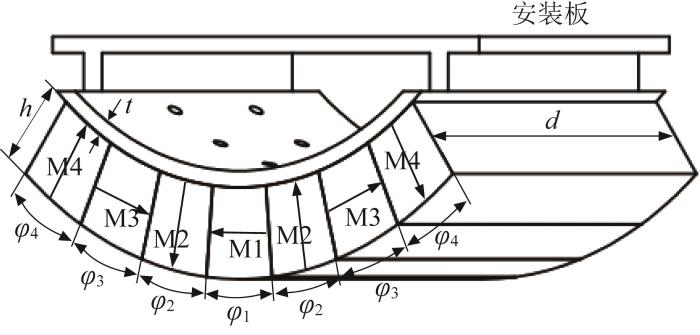
磁吸附模块由7块小的弧形磁铁和1块轭铁组成,采用Halbach阵列充磁技术。如图15所示,从左至右第1、3、5、7块磁铁采用径向充磁,第2、4、6块磁铁采用切向充磁。弧形磁铁内径为120 mm,距塔筒壁面8 mm;Q235低碳钢材质的塔筒壁面曲率半径为1 500 mm,厚度为20 mm。
图15
图15
磁吸附模块结构示意图
Fig.15
Schematic diagram of magnetic adsorption module structure
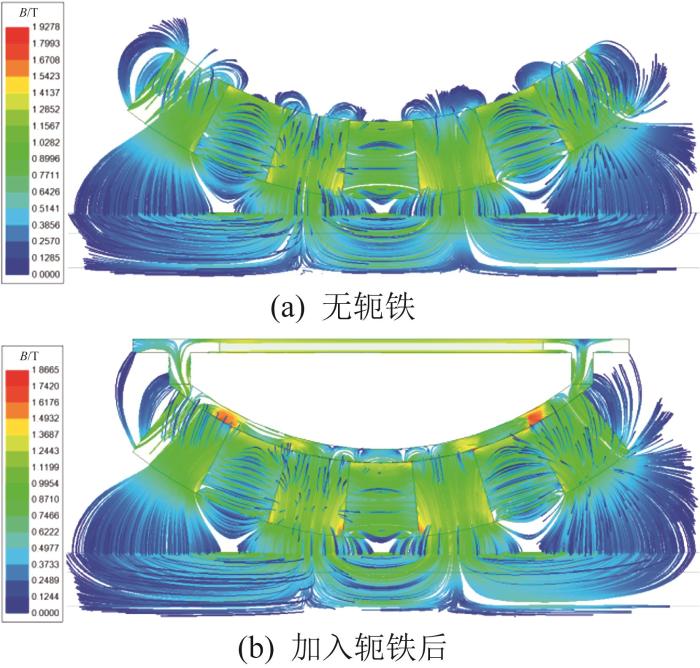
使用ANSYS Maxwell软件对上述磁吸附模块进行仿真分析,得到其磁感应强度云图,如图16所示。从图16(a)中可以看出,在不含轭铁时,采用径向充磁的弧形磁铁的磁感线穿过间隙和塔筒壁面后回到磁铁内部,对壁面产生吸附力;而切向充磁使得磁感线沿磁铁表面流动并汇聚在塔筒壁面处,形成靠近壁面一侧的回路,从而增强吸附力。由此可知,磁吸附模块远离壁面一侧存在磁场泄漏现象,部分磁感线未形成回路,磁感应强度明显弱于靠近壁面形成聚磁效应的这一侧。为此,在弱磁侧安装1块轭铁来引导磁感线,以减少磁场的泄漏。从图16(b)中可以看出,在加入轭铁后,弱磁侧的磁感线得到有效引导,改善了磁场泄漏现象,使得弱磁侧的磁感应强度增大,从而优化了磁吸附模块的性能。
图16
图16
磁吸附模块的磁感应强度云图
Fig.16
Magnetic induction intensity cloud map of magnetic adsorption module
磁吸附模块的结构参数如图17所示。其中:
图17
利用控制变量法,系统地分析不同结构尺寸的弧形Halbach磁铁阵列和轭铁对磁吸附模块吸附效率的影响。
磁吸附模块结构参数的初始值如表3所示,结构优化目标为在一定的距壁间隙下,通过调整结构参数来实现吸附效率最大化,即实现单位质量吸附力
表3 磁吸附模块结构参数初始值
Table 3
| 参数 | 初始值 | 参数 | 初始值 |
|---|---|---|---|
| 11 | 28 | ||
| 11 | 105 | ||
| 11 | 5 | ||
| 11 |
在距壁间隙
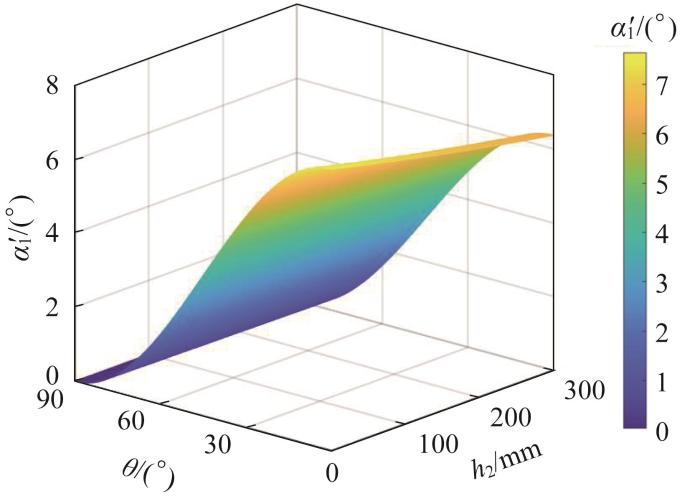
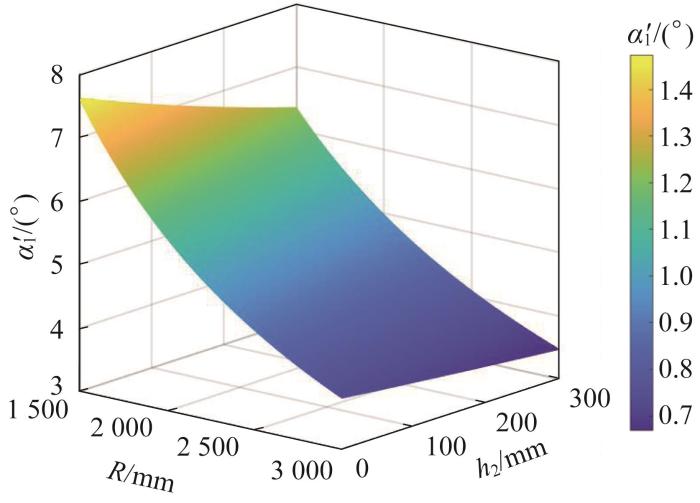
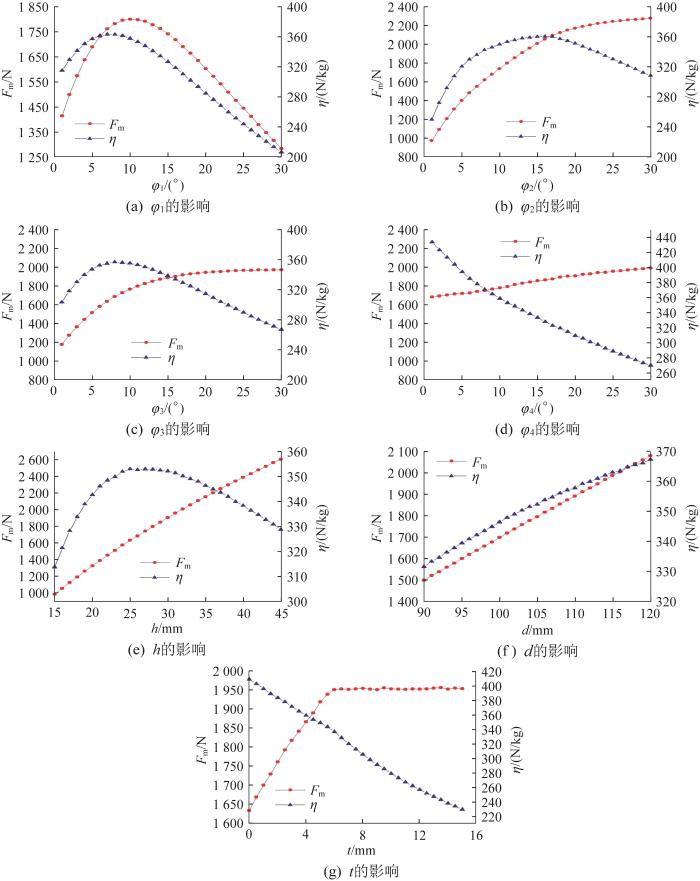
要求所设计的磁吸附模块可为风电塔筒维护用爬壁机器人提供至少1 600 N的吸附力,以满足其在距壁间隙为8 mm的情况下负载20 kg的作业要求。使用ANSYS Maxwell软件对磁吸附模块进行参数化分析,以确定其最佳结构参数。磁吸附模块的参数化分析结果如图18所示。
图18
图18
磁吸附模块参数化分析结果
Fig.18
Parameterized analysis results of magnetic adsorption module
由图18(a)可知,在磁铁M1的角度
由图18(b)可知,在磁铁M2的角度
由图18(c)可知,在磁铁M3的角度
由图18(d)可知,磁铁M4的角度
由图18(e)可知,磁铁厚度
由图18(f)可知,磁铁宽度d与磁吸附模块的总吸附力和单位质量吸附力均呈正相关,但单位质量吸附力的增大趋势逐渐变缓。由此可见,磁铁宽度对磁吸附模块的总吸附力和吸附效率均有显著影响,可根据所需吸附力设定合适的磁铁宽度。
由图18(g)可知,当轭铁厚度
根据上述磁吸附模块的参数化分析结果,对其结构参数进行优化,以提高其吸附效率。优化前后各结构参数和性能参数的对比如表4所示。结果表明,结构参数优化后,磁吸附模块的单位质量吸附力从350.7 N/kg提高到了403.9 N/kg,提升了15.17%。
表4 磁吸附模块优化结果
Table 4
| 参数 | 优化前 | 优化后 |
|---|---|---|
| 11 | 8 | |
| 11 | 16 | |
| 11 | 10 | |
| 11 | 6 | |
| 28 | 26 | |
| d | 105 | 105 |
| t | 5 | 6 |
| 1 796.2 | 1 833.6 | |
| 350.7 | 403.9 |
图19
图19
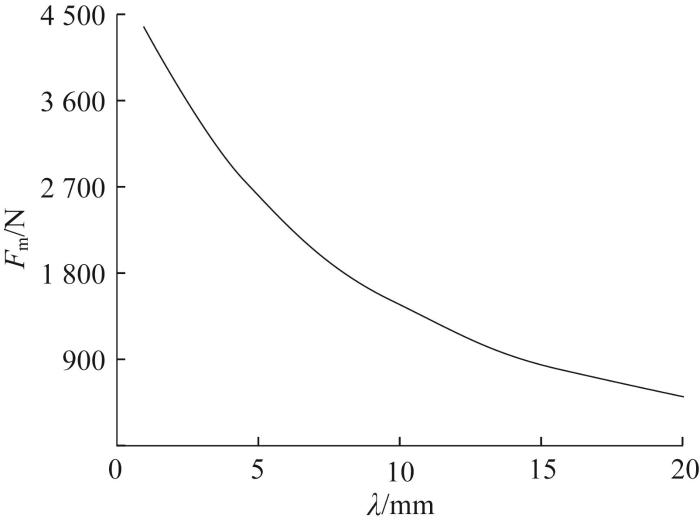
磁吸附模块总吸附力随距壁间隙的变化曲线
Fig.19
Variation curve of total adsorption force of magnetic adsorption module with clearance from wall
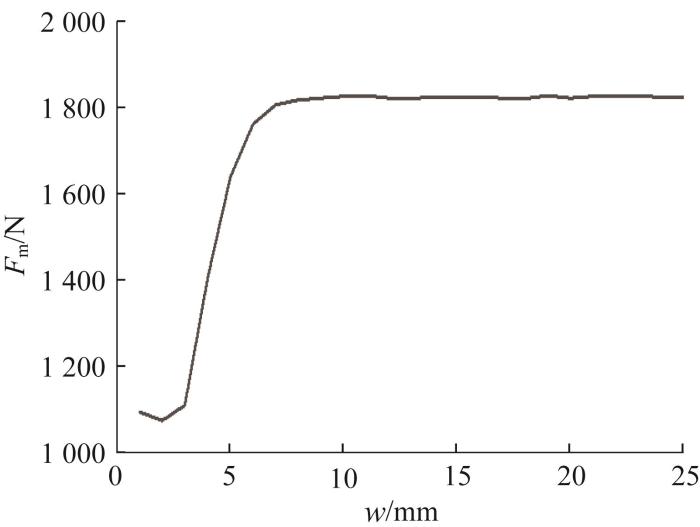
塔筒壁面厚度也会对磁吸附模块的吸附力产生一定影响。设定距壁间隙为8 mm,通过仿真获得优化后磁吸附模块的总吸附力Fm随壁面厚度w的变化曲线,如图20所示。结果显示,当壁面厚度超过8 mm后,磁吸附模块的磁路达到饱和,其总吸附力基本保持不变。风电塔筒整体由多段小塔筒组成,在变曲率环境下,不同段小塔筒的壁面厚度不同,但均大于10 mm。因此,针对在风电塔筒变曲率壁面上作业的机器人,壁面厚度变化对其影响甚微。
图20
图20
磁吸附模块总吸附力随壁面厚度的变化曲线
Fig.20
Variation curve of total adsorption force of magnetic adsorption module with wall thickness
5 变曲率自适应爬壁机器人实验测试
图21
图21
变曲率自适应爬壁机器人系统
Fig.21
Variable curvature adaptive wall-climbing robot system
表5 爬壁机器人参数
Table 5
| 参数 | 数值 |
|---|---|
| 机身尺寸①/(mm | 680 |
| 质量/kg | 55 |
| 最大负载/kg | 110 |
| 载重自重比 | 2 |
| 可适应曲率半径/mm | |
| 最大移动速度/(m/min) | 8 |
① 尺寸为长×宽×高。
面向风电塔筒维护的爬壁机器人在塔筒外壁面上作业时,需根据作业需求选择搭载清洗、打磨、喷漆等作业前端,同时移动电缆随着机器人的爬升被拖得越来越长,导致机器人负重增加,这会对其稳定性产生影响,增加了倾覆风险。因此,须对机器人进行极限负载测试,如图22所示。实验结果表明,该机器人可搭载约110 kg的重物进行作业,满足技术要求。
图22
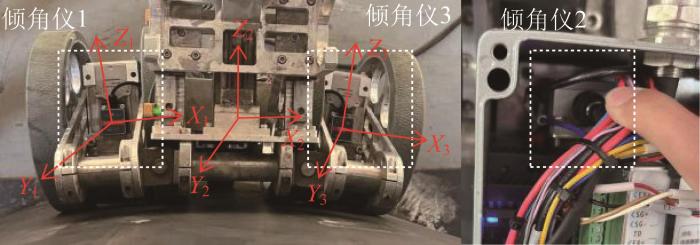
针对在变曲率壁面上的运动实验,按1∶1比例搭建了仿照风电塔筒顶部的实验壁面,其材质为Q235钢,顶部曲率半径为1 500 mm,底部曲率半径为1 800 mm,壁面厚度为20 mm。在机器人的不同位置处安装3个倾角仪,如图23所示。倾角仪1与倾角仪3分别对称安装在左驱动模块与右驱动模块处,用于测量左右2个柔性铰链外侧的角度;倾角仪2安装于机器人本体中间后端的控制箱内,用于测量柔性铰链内侧的角度。利用上位机软件实时记录测量数据,并基于倾角仪1的X向偏转角读数与倾角仪2的X向偏转角读数计算得到铰链处摆角
图23
图23
爬壁机器人变曲率自适应运动实验
Fig.23
Variable curvature adaptive motion experiment of wall-climbing robot
图24
图24
爬壁机器人稳定性与灵活性测试实验
Fig.24
Stability and flexibility test experiment of wall-climbing robot
图25
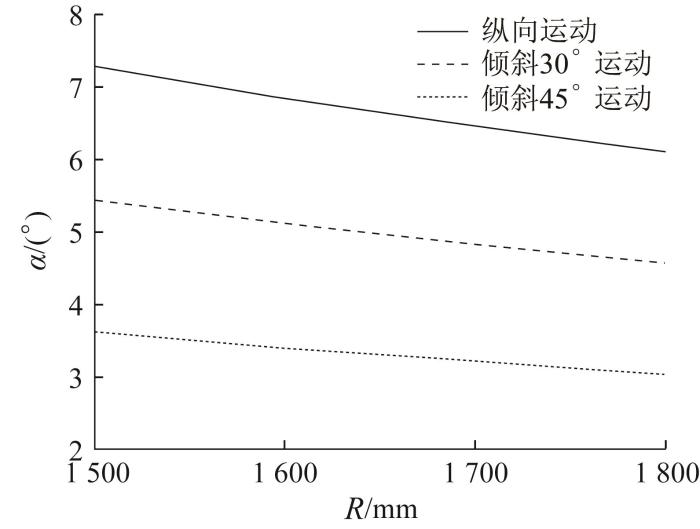
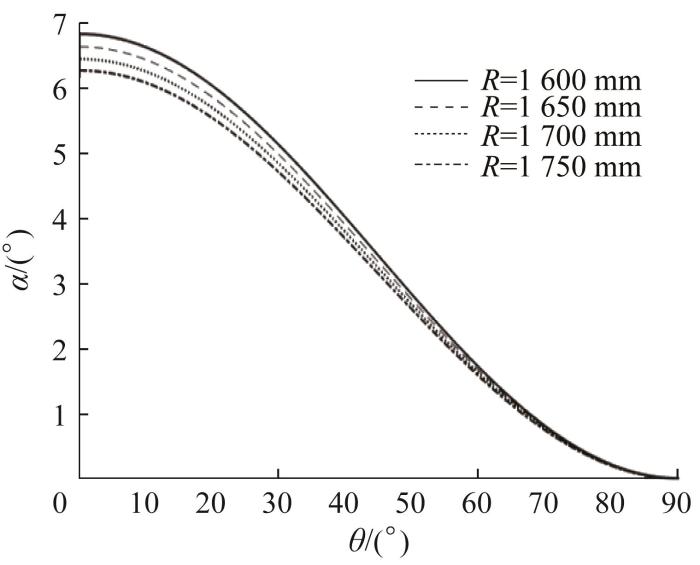
图25
爬壁机器人纵向、斜向运动时铰链处摆角的变化情况
Fig.25
Change of swing angle at the hinge during longitudinal and oblique motion of wall-climbing robot
图26
图27
图27
爬壁机器人转弯时铰链处摆角的变化情况
Fig.27
Change of swing angle at the hinge during turning of wall-climbing robot
综合上述实验结果可知,本文所设计的面向风电塔筒维护的变曲率自适应爬壁机器人能够在变曲率环境下进行灵活、稳定的大负载作业。
6 结 论
本文在分析了风电塔筒的变曲率环境与维护作业需求的基础上,基于模块化设计理念提出了一种新型的变曲率自适应爬壁机器人。该爬壁机器人采用分体轮式移动方式和间隙式永磁吸附技术,通过柔性连接模块的柔性机制被动地调整姿态,以适应塔筒壁面的曲率变化。同时,建立了多状态下的爬壁机器人运动模型,分析了机器人在自适应壁面曲率变化时铰链处摆角的变化趋势,以及转弯时铰链安装位置对机器人稳定性的影响,并优化了铰链的安装位置。基于Halbach阵列充磁对磁吸附模块进行了参数化仿真分析,并优化了其结构参数,提高了吸附效率。另外,还分析了变曲率环境下距壁间隙和壁面厚度对磁吸附模块吸附力的影响。
实验测试结果表明:所设计的爬壁机器人具有变曲率自适应能力,可通过其柔性连接模块的柔性机制,在风电塔筒变曲率环境下进行稳定、可靠的大负载作业。
参考文献
爬壁机器人研究现状及发展趋势
[J].
Research status and development trend of wall climbing robot
[J].DOI:10.3901/jme.2023.05.011 [本文引用: 1]
轮腿式爬壁机器人的永磁吸附装置设计与优化
[J].
Design and optimization of permanent magnet adsorption device for wheel-legged wall-climbing robot
[J].
A survey of wall climbing robots: recent advances and challenges
[J].
Path planning for detection robot climbing on rotor blade surfaces of wind turbine based on neural network
[J].
风电塔筒爬壁机器人吸附结构优化设计及试验研究
[J].
Optimization design and experimental research on adsorption structure of wind power tower wall climbing robot
[J].
船体清洗机器人的开发现状与展望
[J].
Development status and prospect of ship hull cleaning robot
[J].
大型球罐壁面除漆机器人设计与实验研究
[J].
Design and experimental study of a large spherical tank wall paint removal robot
[J].
管道全位置焊接机器人结构设计与运动学分析
[J].
Structural design and kinematics analysis of pipeline all-position welding robot
[J].
Design and analysis of a passive adaptive wall-climbing robot on variable curvature ship facades
[J].
Proposed locomotion strategy for a traveling-wave-type omnidirectional wall-climbing robot for spherical surfaces
[C]//
Design and analysis of a wall-climbing robot for passive adaptive movement on variable-curvature metal facades
[J].
风电塔筒运维用四足伸缩式爬壁机器人设计与分析研究
[D].
Design and analysis of a quadruped telescopic wall climbing robot for the operation and maintenance of wind power tower
[D].
两端吸附式焊缝修形爬壁机器人研制
[J].
Wall climbing robot based on two-end adsorption for weld seam amending
[J].
Tank-like module-based climbing robot using passive compliant joints
[J].
Under-actuated tank-like climbing robot with various transitioning capabilities
[C]//
Design and analysis of a wall-climbing robot with passive compliant mechanisms to adapt variable curvatures walls
[J].
Optimization design and trajectory error compensation of a facade-adaptive wall-climbing robot
[J].
风电塔筒爬升装置及叶片与塔筒检测管理系统的开发
[D].
Development on the wind turbine tower climbing device and blades with towers detection management system
[D].
爬壁机器人悬摆式磁吸附机构的设计与优化
[J].
Design and optimization of pendulous magnetic adsorption mechanism for wall-climbing robots
[J].