音圈电机驱动的三自由度大行程柔性偏摆台设计与分析

doi:10.3785/j.issn.1006-754X.2025.04.108

音圈电机驱动的三自由度大行程柔性偏摆台设计与分析

徐智皓^,^,¹, 陆晓伟², 谢雨欣¹, 赖磊捷^,^,¹

1.上海工程技术大学机械与汽车工程学院，上海 201620

2.华立科技股份有限公司，浙江杭州 310023

Design and analysis of three-degree-of-freedom large-stroke flexible tip-tilt stage driven by voice coil motor

XU Zhihao^,^,¹, LU Xiaowei², XIE Yuxin¹, LAI Leijie^,^,¹

1.School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China

2.Holley Technology Ltd. , Hangzhou 310023, China

通讯作者: 赖磊捷（1984—），男，副教授，博士，从事微位移驱动控制、微纳制造装备等研究，E-mail: lailj@sues.edu.cn，https://orcid.org/0000-0002-8767-4715

收稿日期: 2024-01-30 修回日期: 2024-03-29

基金资助:

国家自然科学基金资助项目.  52475063
国家自然科学基金重点项目.  U2013211
国家自然科学基金青年科学基金资助项目.  51605275
上海市自然科学基金资助项目.  21ZR1426000

Received: 2024-01-30 Revised: 2024-03-29

作者简介 About authors

徐智皓（1999—），男，硕士生，从事柔性机构设计研究，E-mail:hankxu99@163.com，https://orcid.org/0009-0002-5174-2111 , E-mail：hankxu99@163.com

摘要

为解决传统压电驱动偏摆台因行程较小而无法适应诸多毫米级大行程应用场景的问题，设计了一种音圈电机驱动的三自由度大行程柔性偏摆台，并对其进行了柔度建模与性能测试。首先，介绍了三自由度大行程柔性偏摆台的结构构型，该构型包含3组呈120°均匀排布的垂直驱动支链，并利用柔性球铰和平行四边形机构实现各驱动支链的运动解耦和电机动子的直线导向；同时，根据各驱动支链的几何关系建立了偏摆台动平台的运动学方程。然后，利用柔度矩阵法推导了柔性球铰、驱动支链和整个偏摆台的柔度解析模型。接着，通过对偏摆台进行静力学有限元仿真分析，验证了所推导的柔度解析模型的准确性。最后，通过搭建偏摆台测试系统来测量偏摆台的最大行程以及沿Z轴的平移柔度和绕X、Y轴的旋转柔度，验证了偏摆台结构设计以及所推导柔度解析模型的有效性和合理性。结果表明：柔度解析模型计算结果与有限元仿真结果、实测结果的相对误差均在10%以内；偏摆台的最大行程范围为±0.054 3 rad×±0.047 2 rad×±4.45 mm，具有行程大、结构紧凑等优点。所设计的偏摆台适用于多种需要大行程空间定位的场景，具有广阔的应用前景。

关键词： 偏摆台 ; 大行程 ; 柔度 ; 音圈电机 ; 柔性球铰 ; 有限元仿真

Abstract

In order to solve the problem that the traditional piezoelectric-driven tip-tilt stage cannot adapt to many millimeter-level large-stroke application scenarios due to its small stroke, a three-degree-of-freedom large-stroke flexible tip-tilt stage driven by voice coil motor is designed, and its compliance modeling and performance testing are carried out. Firstly, the structural configuration of the three-degree-of-freedom large-stroke flexible tip-tilt stage was introduced, which included three sets of 120° uniformly arranged vertical driving chains, and the motion decoupling of each driving chain and the linear guidance of the motor rotor were achieved by using flexible spherical hinges and parallelogram mechanisms. At the same time, the kinematics equation of the dynamic platform of the tip-tilt stage was established according to the geometric relationship of each driving chain. Then, the compliance matrix method was used to derive the compliance analytical models for the flexible spherical hinge, the driving chain and the overall tip-tilt stage. Subsequently, the accuracy of the derived compliance analytical model was verified through the statics finite element simulation analysis for the tip-tilt stage. Finally, a tip-tilt stage testing system was built to measure its maximum stroke, as well as the translational compliance along the Z-axis and the rotational compliance around the X and Y axes, so as to verify the effectiveness and rationality of the structural design of the tip-tilt stage and the derived compliance analytical model. The results showed that the relative error between the calculation results of the compliance analytical model and the finite element simulation results, as well as the experimental results, was within 10%. The maximum stroke range of the tip-tilt stage was ±0.054 3 rad×±0.047 2 rad×±4.45 mm, which had the advantages of large-stroke and compact structure. The designed tip-tilt stage can be used in various situations that require large-stroke spatial positioning, demonstrating broad application prospects.

Keywords： tip-tilt stage ; large-stroke ; compliance ; voice coil motor ; flexible spherical hinge ; finite element simulation

PDF (4097KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

徐智皓, 陆晓伟, 谢雨欣, 赖磊捷. 音圈电机驱动的三自由度大行程柔性偏摆台设计与分析[J]. 工程设计学报, 2025, 32(1): 82-91 doi:10.3785/j.issn.1006-754X.2025.04.108

XU Zhihao, LU Xiaowei, XIE Yuxin, LAI Leijie. Design and analysis of three-degree-of-freedom large-stroke flexible tip-tilt stage driven by voice coil motor[J]. Chinese Journal of Engineering Design, 2025, 32(1): 82-91 doi:10.3785/j.issn.1006-754X.2025.04.108

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2025.04.108

具有空间偏转功能的三自由度偏摆台在快速反射镜、增材制造技术和激光加工工艺中发挥着重要作用^[1-3]。目前，以压电陶瓷驱动器为驱动单元的偏摆台已有成熟产品并实现了较普遍的应用。但是，由于压电陶瓷驱动器的行程较小，压电驱动偏摆台无法适应毫米级的大行程应用场景^[4-6]。现阶段，以音圈电机为代表的电磁微驱动器具有结构简单、行程大、响应快、线性度好和分辨率高等优点，能够实现大行程范围内的快速定位和平滑运动^[7-9]。此外，柔性机构依靠柔性单元的弹性变形实现运动，其相较于传统的刚性机构具有结构简单、无磨损、无需润滑及无间隙等优点，在精密定位领域得到了广泛应用^[10]。因此，以音圈电机为驱动器、以柔性机构为导向部件的大行程偏摆台具有广阔的应用前景。

近年来，国内外众多学者针对压电陶瓷驱动器和音圈电机驱动的偏摆台开展了大量研究。Han等^[11]设计了一种由环形柔性铰链引导的压电驱动微型快速反射镜，能够实现高精度的偏转与运动解耦。Wang等^[12]通过结合柔性万向支架与压电陶瓷驱动器，有效地缩减了快速反射镜旋转轴系统的排列空间。汪奎等^[13]设计了基于十字形柔性铰链的两轴柔性支撑结构，并研制了音圈电机驱动的快速反射镜，该反射镜具有空间利用率高、中心漂移小等优点。徐宁^[14]设计了一种两轴转动柔性机构，用于提高快速反射镜的精度和带宽。由当前研究现状可知，大部分音圈电机驱动的偏摆台存在缺少导向机构或导向机构刚度过大等问题。导向机构缺失容易使音圈电机动子产生横向位移，从而导致动子与定子产生摩擦；而导向机构刚度过大则会使音圈电机的有效行程和驱动效率降低，无法实现偏摆台结构尺寸与行程的平衡。

为解决上述问题，本文设计了一种音圈电机驱动的三自由度大行程柔性偏摆台。该偏摆台具有3组呈120°均匀并联排布的垂直驱动支链，每一组驱动支链由音圈电机、平行四边形机构和柔性球铰组成。在设计驱动支链结构时，将音圈电机整体嵌入平行四边形机构内部，以实现紧凑化设计以及提升电机的驱动效率和有效行程；同时，通过柔性球铰来实现各驱动支链的运动解耦。本文先对大行程柔性偏摆台的结构构型进行介绍，并根据各驱动支链的几何关系推导动平台的运动学方程。随后，基于柔度矩阵法对柔性球铰、驱动支链及整个偏摆台进行柔度解析建模，并通过静力学有限元分析和搭建测试系统来获取偏摆台的最大行程和柔度，以验证偏摆台结构设计与所推导的柔度解析模型的有效性和合理性。

1 偏摆台结构设计与运动学模型构建

1.1　偏摆台结构构型

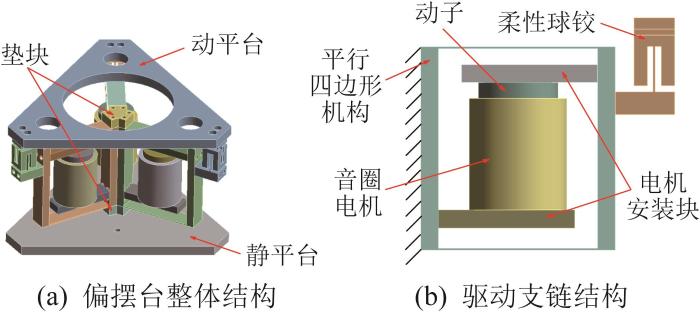
音圈电机驱动的三自由度大行程柔性偏摆台的结构如图1(a)所示。该偏摆台由3组并联排布的全簧片驱动支链组成（相邻2组驱动支链的夹角为120°），通过2个垫块将驱动支链固定在静平台上。在每组驱动支链中，音圈电机通过上下2块安装块与平行四边形机构连接；平行四边形机构的输出端通过柔性球铰与偏摆台的动平台相连，如图1(b)所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三自由度大行程柔性偏摆台结构

Fig.1 Structure of three-degree-of-freedom large-stroke flexible tip-tilt stage

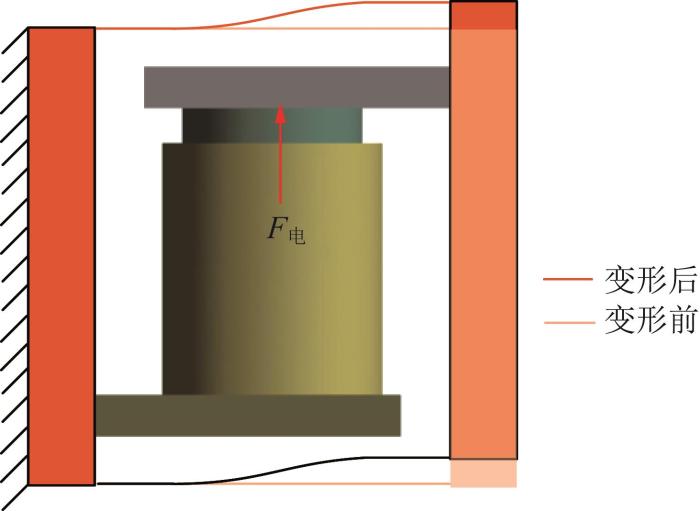
如图2所示，在音圈电机推力F_电的作用下，平行四边形机构中上下2组平行簧片梁同时发生弯曲变形。由于簧片梁沿水平方向具有较高的刚度，可忽略其在变形过程中产生的寄生位移，因此利用平行四边形机构可对音圈电机动子的输出位移实现较好的导向作用，从而限制其横向位移，避免动子与定子产生摩擦。为了在增大偏摆台行程范围的同时限制其整体尺寸，将音圈电机整体嵌入平行四边形机构内部，实现紧凑化设计。偏摆台通过3组驱动支链不同的位移输出以及柔性球铰对驱动支链输出位移的运动解耦，最终实现绕X、Y轴旋转和沿Z轴平移的空间三自由度大行程微纳米定位。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 平行四边形机构的导向原理

Fig.2 Guiding principle of parallelogram mechanism

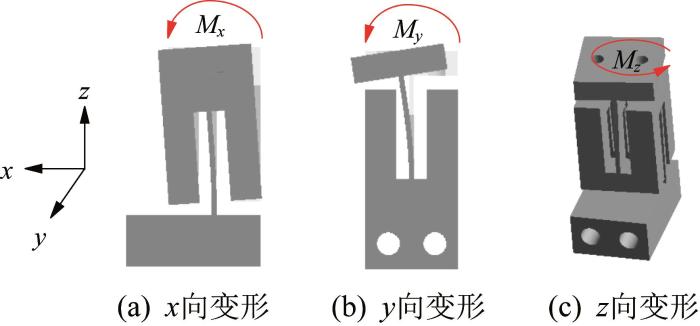
图3所示为簧片型柔性球铰的变形原理。该柔性球铰通过簧片梁的正交组合形成柔性虎克铰，能够产生绕x、y、z三轴的旋转位移。与传统柔性球铰相比，簧片型柔性球铰依靠簧片梁的弯曲变形，能够增大偏摆台动平台的运动范围，并使其应力分布更加均匀，从而有效提高偏摆台的运行稳定性和使用寿命^[15]。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 簧片型柔性球铰变形原理

Fig.3 Deformation principle of reed-type flexible spherical hinge

1.2　偏摆台运动学模型

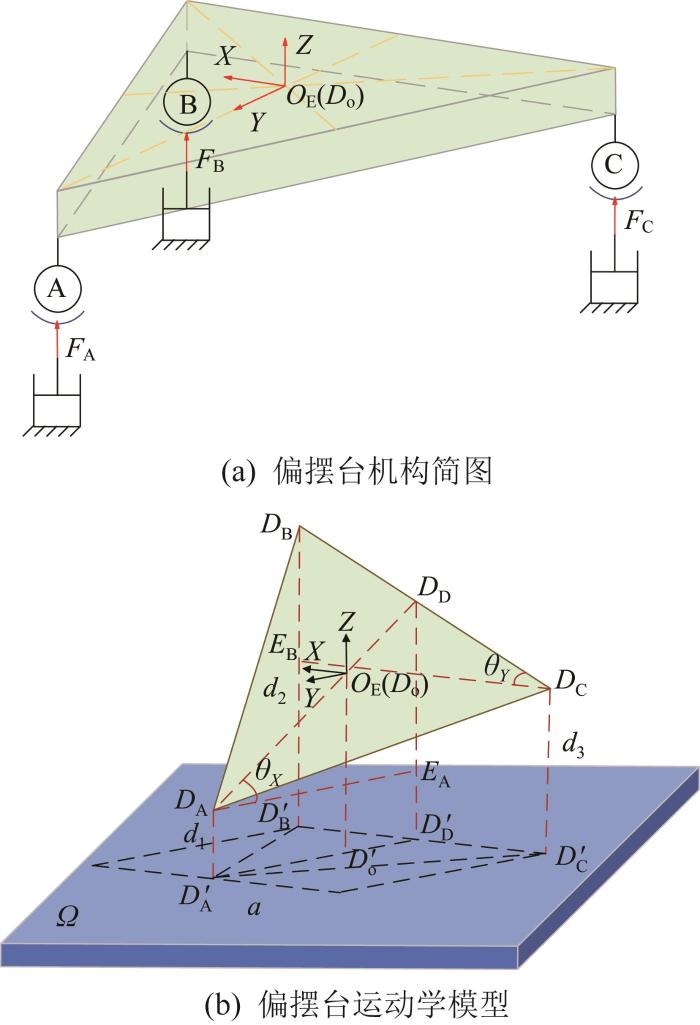
偏摆台的机构简图和运动学模型分别如图4(a)和图4(b)所示。图4(a)中：F_A、F_B和F_C分别为3组驱动支链（记为A、B、C）中音圈电机产生的推力。图4(b)中：D_A、D_B和D_C分别为3组驱动支链与动平台的连接点，三点构成等边三角形； $D_{A}^{'}$ 、 $D_{B}^{'}$ 和 $D_{C}^{'}$ 分别为音圈电机未驱动时动平台上D_A、D_B和D_C三点在起始平面（Ω平面）上的点， $D_{A}^{'} D_{B}^{'}$ = $D_{B}^{'} D_{C}^{'}$ = $D_{A}^{'} D_{C}^{'}$ =a=190 mm；d₁、d₂和d₃分别为音圈电机驱动后D_A、D_B和D_C三点所改变的位移，d₁= $D_{A} D_{A}^{'}$ ，d₂= $D_{B} D_{B}^{'}$ ，d₃= $D_{C} D_{C}^{'}$ ；D_o为△D_AD_BD_C的几何中心， $D_{o}^{'}$ 为△ $D_{A}^{'} D_{B}^{'} D_{C}^{'}$ 的几何中心。为了简化计算，忽略驱动支链末端产生的沿水平方向的极小位移量。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 偏摆台的机构简图和运动学模型

Fig.4 Mechanism schematic and kinematics model of tip-tilt stage

根据图4(b)所示的几何关系，可得偏摆台动平台的运动学方程：

\{\begin{array}{l} δ_{Z} = \frac{d_{1} + d_{2} + d_{3}}{3} \\ θ_{X} \approx t a n θ_{X} = \frac{2}{\sqrt[]{3} a} (\frac{d_{2} + d_{3}}{2} - d_{1}) = \\ \frac{- 2 \sqrt[]{3} d_{1} + \sqrt[]{3} d_{2} + \sqrt[]{3} d_{3}}{3 a} \\ θ_{Y} \approx t a n θ_{Y} = \frac{d_{2} - d_{3}}{a} \end{array}

(1)

式中：δ_Z 、θ_X 和θ_Y 分别为动平台沿Z轴平移的位移、绕X轴旋转和绕Y轴旋转的角度。

由此可得，音圈电机的输出位移与偏摆台动平台位姿之间的关系用矩阵形式可表示为^[16]：

[\begin{matrix} δ_{Z} \\ θ_{X} \\ θ_{Y} \end{matrix}] = [\begin{matrix} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{- 2 \sqrt[]{3}}{3 a} & \frac{\sqrt[]{3}}{3 a} & \frac{\sqrt[]{3}}{3 a} \\ 0 & \frac{1}{a} & - \frac{1}{a} \end{matrix}] [\begin{matrix} d_{1} \\ d_{2} \\ d_{3} \end{matrix}]

(2)

2 偏摆台柔度解析建模

2.1　簧片梁柔度建模

本文采用柔度矩阵法对偏摆台进行柔度建模，该方法适用于各类柔性机构构型，具有计算快速、精度高等优势，可用于描述载荷与位移之间的关系^[17]。偏摆台动平台的运动依靠簧片梁的弹性变形来实现，因此需要先对簧片梁进行柔度建模。

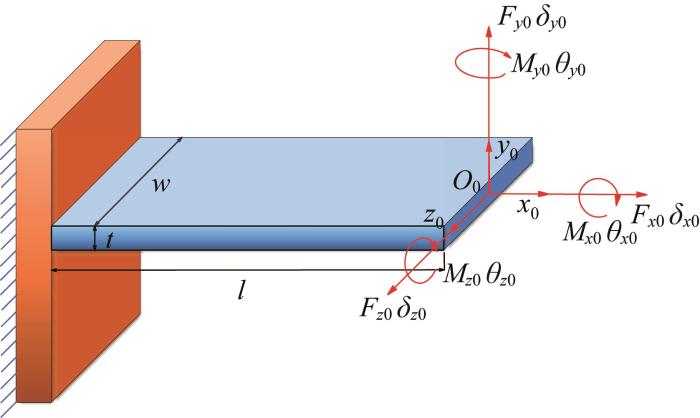
图5所示为簧片梁受力示意，坐标系O₀-x₀y₀z₀的原点位于簧片梁末端中心处。当外载荷 F =［F_x₀F_y₀F_z₀M_x₀M_y₀M_z₀］作用于簧片梁自由端时，簧片梁末端会产生6个自由度方向上的变形 δ =［δ_x₀δ_y₀δ_z₀θ_x₀θ_y₀θ_z₀］，即沿x₀、y₀、z₀轴的变形和绕x₀、y₀、z₀轴的变形，则载荷与变形的关系可表示为：

δ = C_{i}^{0} F

(3)

式中： $C_{i}^{0}$ 为簧片梁i在其末端坐标系O₀-x₀y₀z₀中的柔度矩阵。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 簧片梁受力示意图

Fig.5 Schematic diagram of reed beam under force

根据材料力学中的欧拉-伯努利梁理论^[18]，求解簧片梁末端分别单独作用F_x₀、F_y₀、F_z₀、M_x₀、M_y₀和M_z₀时坐标系原点O₀处的变形量，并根据叠加原理获得总变形量，从而求得簧片梁的柔度矩阵：

C_{i}^{0} = [\begin{matrix} \frac{l}{E t w} & 0 & 0 & 0 & 0 & 0 \\ 0 & \frac{4 l^{3}}{E t^{3} w} & 0 & 0 & 0 & \frac{6 l^{2}}{E t^{3} w} \\ 0 & 0 & \frac{4 l^{3}}{E t w^{3}} & 0 & - \frac{6 l^{2}}{E t w^{3}} & 0 \\ 0 & 0 & 0 & \frac{l}{G J} & 0 & 0 \\ 0 & 0 & - \frac{6 l^{2}}{E t w^{3}} & 0 & \frac{12 l}{E t w^{3}} & 0 \\ 0 & \frac{6 l^{2}}{E t^{3} w} & 0 & 0 & 0 & \frac{12 l}{E t^{3} w} \end{matrix}]

(4)

其中：

G = \frac{E}{2 (1 + ν)}

J = \frac{β t^{3} w}{12}

β = 12 \{\frac{1}{3} - 0.21 \frac{t}{w} [1 - \frac{1}{12} {(\frac{t}{w})}^{4}]\}

式中：l、t和w分别为簧片梁的长度、厚度和宽度，E、G、J和ν分别为簧片梁的弹性模量、剪切模量、扭转系数和泊松比。本文簧片梁的材料选择7075铝合金，其参数如下：E=71.7 GPa，G=26.69 GPa，ν=0.33。

2.2　柔性球铰柔度建模

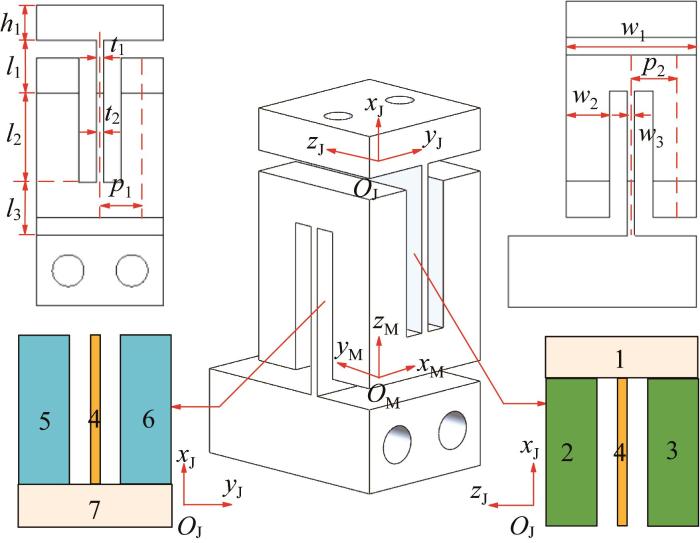
柔性球铰由7个簧片梁组成，在柔度建模时为了更好地区分不同簧片梁，对其进行编号（依次为1~7）。柔性球铰的剖面结构和结构参数如图6所示，其中：基坐标系O_M-x_My_Mz_M的原点位于簧片梁7的底部中心。簧片梁1，7的长度分别为l₁和l₃，两者的厚度和宽度均为t₁和w₁；簧片梁2，3，5，6的长度、厚度和宽度均为l₂、t₂和w₂；簧片梁4的长度、厚度和宽度为l₂、t₂和w₃；簧片梁5，6和簧片梁2，3的中心线到簧片梁4中心线的距离分别为p₁和p₂；柔

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 柔性球铰的剖面结构和结构参数

Fig.6 Section structure and structural parameters of flexible spherical hinge

性球铰顶部厚度为h₁。柔性球铰各结构参数的取值如表1所示。

表1 柔性球铰结构参数的取值 (mm)

Table 1 Values of structural parameters of flexible spherical hinge

结构参数	数值
l₁、l₃	7.5
l₂	12.5
t₁、t₂	1.0
w₁	18.0
w₂	6.0
w₃	1.0
p₁、p₂	6.0
h₁	5.0

新窗口打开| 下载CSV

在对柔性球铰进行柔度建模时，需要将柔性球铰中所有簧片梁的柔度矩阵均转换到同一个坐标系中。为了方便计算，引入全局坐标系O_J-x_Jy_Jz_J，其原点O_J位于柔性球铰的上端面中心。通过坐标变换^[19]，可将第i个簧片梁在其末端局部坐标系中的柔度矩阵 $C_{i}^{0}$ 转换为在全局坐标系O_J-x_Jy_Jz_J中的柔度矩阵 $C_{i}^{J}$ ，转换过程如下：

C_{i}^{J} = T_{i}^{J} C_{i}^{0} {(T_{i}^{J})}^{T}

(5)

其中：

T_{i}^{J} = [\begin{matrix} R_{i}^{J} & S (r_{i}^{J}) R_{i}^{J} \\ 0 & R_{i}^{J} \end{matrix}]

式中： $T_{i}^{J}$ 、 $R_{i}^{J}$ 、 $r_{i}^{J}$ 分别为每个簧片梁末端的局部坐标系相对于全局坐标系O_J-x_Jy_Jz_J的转换矩阵、旋转矩阵和位移矩阵， $S (r_{i}^{J})$ 为 $r_{i}^{J}$ 的反对称算子^[20]。限于篇幅，下文中仅上下标不同的量符号不再重复说明。

旋转矩阵 $R_{i}^{J}$ 可表示为：

R_{i}^{J} = R_{x} (α) R_{y} (β) R_{z} (γ)

(6)

其中：

\{\begin{array}{l} R_{x} (α) = [\begin{matrix} 1 & 0 & 0 \\ 0 & c o s α & - s i n α \\ 0 & s i n α & c o s α \end{matrix}] \\ R_{y} (β) = [\begin{matrix} c o s β & 0 & s i n β \\ 0 & 1 & 0 \\ - s i n β & 0 & c o s β \end{matrix}] \\ R_{z} (γ) = [\begin{matrix} c o s γ & - s i n γ & 0 \\ s i n γ & c o s γ & 0 \\ 0 & 0 & 1 \end{matrix}] \end{array}

式中：α、β和γ分别为簧片梁末端局部坐标系O₀-x₀y₀z₀相对于全局坐标系O_J-x_Jy_Jz_J绕x_J、y_J和z_J轴旋转的角度。

反对称算子 $S (r_{i}^{J})$ 可表示为：

S (r_{i}^{J}) = [\begin{matrix} 0 & - r_{z} & r_{y} \\ r_{z} & 0 & - r_{x} \\ - r_{y} & r_{x} & 0 \end{matrix}]

（7）

式中：r_x 、r_y 和r_z 分别为簧片梁末端局部坐标系O₀-x₀y₀z₀相对于全局坐标系O_J-x_Jy_Jz_J沿x_J、y_J和z_J轴方向的位移。

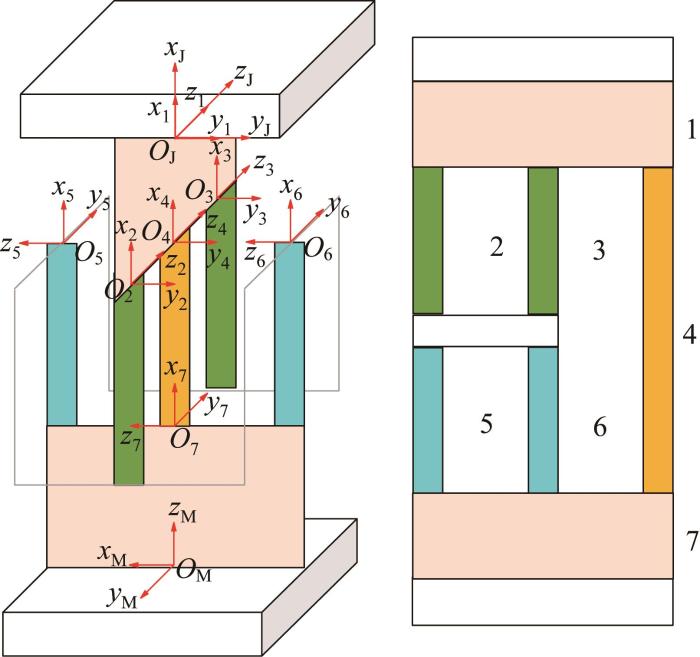
图7所示为柔性球铰中各个簧片梁的连接关系及其局部坐标系的示意图。将柔性球铰中7个簧片梁的柔度矩阵都转换到全局坐标系O_J-x_Jy_Jz_J中，对应的旋转矩阵和位置矩阵可分别表示为：

R_{1}^{J} = I, r_{1}^{J} = (0, 0, 0)

(8)

R_{2}^{J} = I, r_{2}^{J} = (- l_{1}, 0, p_{2})

(9)

R_{3}^{J} = I, r_{3}^{J} = (- l_{1}, 0, - p_{2})

(10)

R_{4}^{J} = I, r_{4}^{J} = (- l_{1}, 0, 0)

(11)

R_{5}^{J} = R_{x} (\frac{π}{2}), r_{5}^{J} = (- l_{1}, - p_{1}, 0)

(12)

R_{6}^{J} = R_{x} (\frac{π}{2}), r_{6}^{J} = (- l_{1}, p_{1}, 0)

(13)

R_{7}^{J} = R_{x} (\frac{π}{2}), r_{7}^{J} = (- l_{1} - l_{2}, 0, 0)

(14)

式中： I 为3×3单位矩阵。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 柔性球铰中各簧片梁的连接关系及其局部坐标系

Fig.7 Connection relationship and local coordinate system of each reed beam in flexible spherical hinge

柔性球铰中的簧片梁2，3并联，簧片梁5，6并联，簧片梁2，3与簧片梁5，6串联后再与簧片梁4并联，簧片梁2，3，4，5，6构成整体后与簧片梁1，7串联。根据柔度矩阵在串、并联机构中的传递规律，可得整个柔性球铰在全局坐标系O_J-x_Jy_Jz_J中的柔度矩阵 $C_{S}^{J}$ ：

C_{S}^{J} = C_{1}^{J} + C_{2 ~ 6}^{J} + C_{7}^{J}

(15)

其中：

C_{2 ~ 6}^{J} = {[{(C_{2356}^{J})}^{- 1} + {(C_{4}^{J})}^{- 1}]}^{- 1}

C_{2356}^{J} = C_{23}^{J} + C_{56}^{J}

C_{23}^{J} = {[{(C_{2}^{J})}^{- 1} + {(C_{3}^{J})}^{- 1}]}^{- 1}

C_{56}^{J} = {[{(C_{5}^{J})}^{- 1} + {(C_{6}^{J})}^{- 1}]}^{- 1}

将柔性球铰在全局坐标系O_J-x_Jy_Jz_J中的柔度矩阵转换到基坐标系O_M-x_My_Mz_M中，可得：

C_{S}^{M} = T_{J}^{M} C_{S}^{J} {(T_{J}^{M})}^{T}

(16)

其中：

T_{J}^{M} = [\begin{matrix} R_{J}^{M} & S (r_{J}^{M}) R_{J}^{M} \\ 0 & R_{J}^{M} \end{matrix}]

R_{J}^{M} = R_{x} (\frac{π}{2}) R_{z} (\frac{π}{2})

r_{J}^{M} = (0, 0, l_{1} + l_{2} + l_{3})

2.3　驱动支链柔度建模

图8所示为驱动支链的结构参数。其中：l₄为簧片梁8，9的长度，l₅为O_M点到O₈和O₉点（O₈、O₉点分别位于簧片梁8，9的末端中心）的水平距离，l₆为O₈和O₉点到动平台几何中心的水平距离，p₃、p₄分别为O_M到O₈、O₉点的竖直距离。各结构参数的具体数值如表2所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 驱动支链的结构参数

Fig.8 Structural parameters of driving chain

表2 驱动支链结构参数取值 (mm)

Table 2 Values of structural parameters of driving chain

结构参数	数值
l₄	70.0
l₅	25.0
l₆	84.7
p₃	19.5
p₄	69.5

新窗口打开| 下载CSV

簧片梁8，9并联形成的平行四边形机构与柔性球铰串联，由此可得单个驱动支链在坐标系O_M-x_My_Mz_M中的柔度矩阵 $C_{D}^{M}$ ：

C_{D}^{M} = C_{S}^{M} + {[{(C_{8}^{M})}^{- 1} + {(C_{9}^{M})}^{- 1}]}^{- 1}

(17)

其中：

R_{8}^{M} = R_{x} (- \frac{π}{2}) R_{y} (\frac{π}{2}), r_{8}^{M} = (0, l_{5}, p_{3})

R_{9}^{M} = R_{x} (- \frac{π}{2}) R_{y} (\frac{π}{2}), r_{9}^{M} = (0, l_{5}, - p_{4})

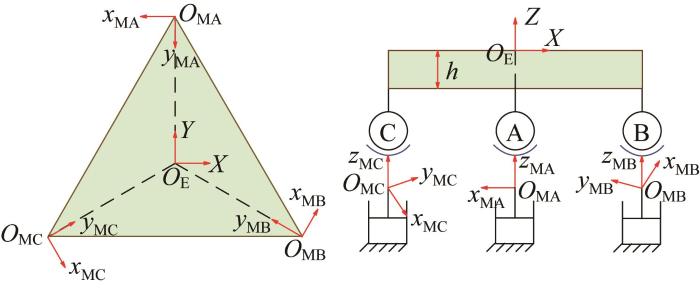
2.4　偏摆台整体柔度建模

偏摆台整体柔度的计算模型如图9所示。其中：动平台厚度h=10 mm，音圈电机可视为竖直运动的移动副。设3个驱动支链的坐标系分别为O_MA-x_MAy_MAz_MA、O_MB-x_MBy_MBz_MB和O_MC-x_MCy_MCz_MC，则各驱动支链在自身局部坐标系下的柔度矩阵 $C_{A}^{M A}$ 、 $C_{B}^{M B}$ 和 $C_{C}^{M C}$ 可表示为：

C_{A}^{M A} = C_{B}^{M B} = C_{C}^{M C} = C_{D}^{M}

(18)

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 偏摆台整体柔度计算模型

Fig.9 Overall compliance calculation model of tip-tilt stage

将驱动支链A的柔度矩阵转换到动平台的坐标系O_E-XYZ中，可得：

C_{A}^{E} = T_{M A}^{E} C_{A}^{M A} {(T_{M A}^{E})}^{T}

(19)

其中：

R_{M A}^{E} = R_{Z} (π)

r_{M A}^{E} = (0, l_{5} + l_{6}, - h - h_{1} - l_{1} - l_{2} - l_{3})

根据旋转对称性，将驱动支链B和C的柔度矩阵转换到动平台的坐标系O_E-XYZ中，可得：

C_{B}^{E} = T_{B}^{E} C_{A}^{E} {(T_{B}^{E})}^{T}

(20)

C_{C}^{E} = T_{C}^{E} C_{A}^{E} {(T_{C}^{E})}^{T}

(21)

其中：

R_{B}^{E} = R_{Z} (- \frac{2 π}{3})

r_{B}^{E} = (0, 0, 0)

R_{C}^{E} = R_{Z} (\frac{2 π}{3})

r_{C}^{E} = (0, 0, 0)

由此可得，整个偏摆台的柔度矩阵 $C_{S T}^{E}$ 为：

C_{S T}^{E} = [{(C_{A}^{E})}^{- 1} + {(C_{B}^{E})}^{- 1} + {{(C_{C}^{E})}^{- 1}]}^{- 1}

(22)

3 偏摆台静力学有限元仿真分析

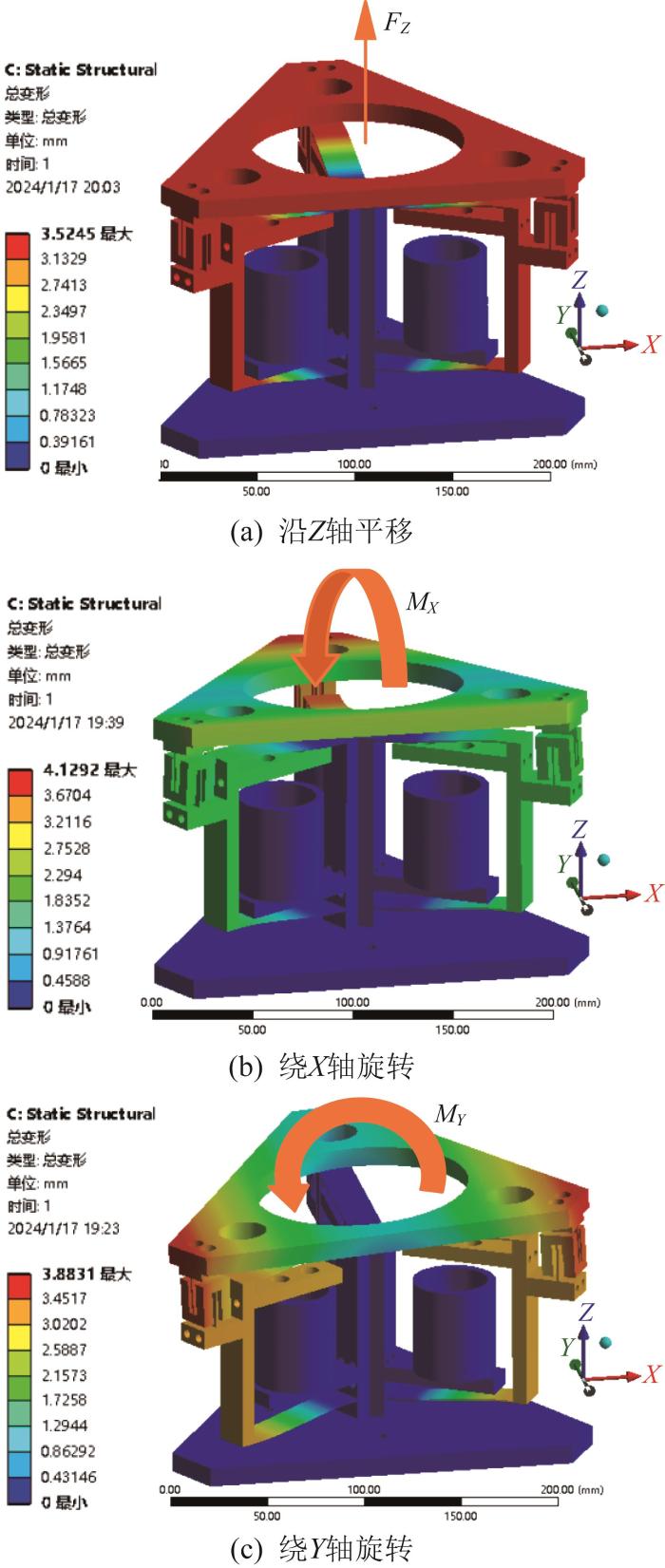
使用SolidWorks软件建立三自由度大行程柔性偏摆台的三维模型，随后将其导入有限元仿真软件ANSYS Workbench，对整个偏摆台进行静力学分析，并与柔度解析模型的计算结果进行对比。

在有限元仿真过程中，依次在偏摆台动平台上施加Z向载荷F_Z =80 N、绕X轴和Y轴的力矩M_X =M_Y =5 $N \cdot m$ 。图10所示为偏摆台的静力学有限元仿真结果。根据所施加的载荷和偏摆台动平台所产生的位移，求解偏摆台沿Z轴的平移柔度 $C_{δ Z}$ 和绕X、Y轴的旋转柔度 $C_{θ X}$ 和 $C_{θ Y}$ ，并与柔度解析模型的计算结果进行对比，如表3所示。由表3可以看出，偏摆台柔度的解析计算结果与仿真结果的相对误差均在10%以内，验证了柔度解析模型的准确性。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 偏摆台静力学有限元仿真结果

Fig.10 Statics finite element simulation results of tip-tilt stage

表3 偏摆台柔度的计算值与仿真值对比

Table 3 Comparison between calculated and simulated values of compliance of tip-tilt stage

对比项

$C_{δ Z}$ /

(mm/N)

$C_{θ X}$ /

［rad/(N·m)］

$C_{θ Y}$ /

［rad/(N·m)］

相对误差/%

2.64

7.84

5.10

计算值

0.044 76

0.006 70

仿真值

0.043 61

0.007 27

0.007 06

新窗口打开| 下载CSV

4 实验测试

4.1　偏摆台测试系统搭建

为了进一步验证偏摆台结构设计和所推导的柔度解析模型的有效性与合理性，搭建偏摆台测试系统。偏摆台样机和偏摆台测试系统各组成部分的连接示意图分别如图11和图12所示。偏摆台测试系统主要由三自由度大行程柔性偏摆台、电流线性放大器、激光位移传感器、数据采集卡及LabVIEW测试软件等组成。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 偏摆台样机

Fig.11 Prototype of tip-tilt stage

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 偏摆台测试系统各组成部分连接示意

Fig.12 Connection schematic of various components of tip-tilt stage testing system

本文偏摆台选用VCAR0070-0149-00 A音圈电机，该电机能够实现70 N的最大推力和40 N的持续推力，最大输入电流为4.0 A，力常数为17.7 N/A，总行程为14.9 mm；选用的激光位移传感器型号为HL-G103-S-J，其分辨率达到0.5 μm，测量范围为±4 mm（0 V→-4 mm，10 V→4 mm）。3个激光位移传感器测量得到的3组驱动支链的模拟量位移信号通过数据采集卡转化为数字信号并在LabVIEW测试软件界面上显示。LabVIEW测试软件通过数据采集卡将-10~10 V的电压传送给CH808电流线性放大器，该放大器的输出电流可设为-2~2 A，-4~4 A，-6~6 A和-8~8 A四种量程范围。为了提升偏摆台动平台的运动分辨率，同时考虑音圈电机的最大输入电流，选择将-10~10 V的电压线性转换为-2~2 A的电流后用于驱动3个音圈电机，则单个音圈电机最大能够输出35.4 N的推力，3个音圈电机对偏摆台动平台最大可输出106.2 N的推力。

4.2　偏摆台最大行程测量

鉴于激光位移传感器的测量范围为±4 mm，为了避免出现超量程现象，对偏摆台的3个自由度方向分别进行2次独立的单向最大行程测量，即对沿Z轴正、负方向的平移位移和绕X、Y轴顺时针、逆时针方向的旋转位移分别进行测量，则位移传感器可实现8 mm以内的位移测量。最后，将2次测量结果相结合，即可得到偏摆台在每个自由度方向上的最大行程。考虑到偏摆台的实际结构和装配尺寸的限制，同时结合开环系统测试结果，可测得当音圈电机输出35.4 N（电流为2 A）推力时，其对应的驱动支链到达最大极限位置。若继续增大推力，则平行四边形机构中的簧片梁会与音圈电机的安装机架产生干涉，容易导致偏摆台损坏。因此，通过驱动不同支链到达各自的最大极限位置（沿Z轴平移：3个音圈电机同时输出35.4 N的推力；绕X轴旋转：驱动支链B、C的音圈电机同时输出35.4 N的推力，驱动支链A的音圈电机输出-35.4 N的推力；绕Y轴旋转：驱动支链B、C的音圈电机分别输出35.4 N和-35.4 N的推力，驱动支链A的音圈电机输出0 N的推力），即可获得偏摆台的最大有效行程，为±0.054 3 rad×±0.047 2 rad×±4.45 mm。

4.3　偏摆台柔度测量

当测量偏摆台沿Z轴的平移柔度时，分别对3组驱动支链中的3个音圈电机输入相同电流，以使其产生相同的推力。当测量偏摆台绕X轴的旋转柔度时，在令驱动支链A的音圈电机产生向下的推力的同时令驱动支链B、C的音圈电机产生向上的推力，以使偏摆台产生绕X轴的旋转力矩。使用相同方法测量偏摆台绕Y轴的旋转柔度，在测量过程中，在令驱动支链A的音圈电机不产生推力的同时分别令驱动支链B、C的音圈电机产生方向相反、大小相同的推力，以使偏转台产生绕Y轴的旋转力矩。偏摆台动平台的位移和转角由安装在驱动支链末端的激光位移传感器测量获得。通过对偏摆台动平台依次施加不同的推力，并同步记录动平台的位移和转角，最终得到其沿Z轴平移的力—位移曲线和绕X、Y轴旋转的力矩—转角曲线，结果如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 偏摆台动平台所受力/力矩与位姿的关系曲线

Fig.13 Relationship curve between force/torque and pose of dynamic platform of tip-tilt stage

根据图13所示结果，利用最小二乘法拟合得到直线斜率，即可得到偏摆台沿Z轴的平移柔度 $C_{δ Z}$ 和绕X、Y轴的旋转柔度 $C_{θ X}$ 、 $C_{θ Y}$ ，并与柔度解析模型的计算结果进行对比，如表4所示。由表4可知，两者的相对误差均在10%以内，充分验证了所推导的柔度解析模型的准确性以及偏摆台结构设计的有效性和合理性。

表4 偏摆台柔度的计算值与实测值对比

Table 4 Comparison between calculated and measured values of compliance of tip-tilt stage

对比项

$C_{δ Z}$ /

(mm/N)

$C_{θ X}$ /

［rad/(N·m)］

$C_{θ Y}$ /

［rad/(N·m)］

相对误差/%

8.88

1.76

3.32

计算值

0.044 76

0.006 70

实测值

0.041 11

0.006 82

0.006 93

新窗口打开| 下载CSV

5 结论

本文针对传统压电驱动偏摆台因压电陶瓷驱动器行程小而无法适用于毫米级大行程场合的问题，提出了一种音圈电机驱动的三自由度大行程柔性偏摆台。该偏摆台含3组由音圈电机、平行四边形机构和柔性球铰组成的垂直驱动支链，通过引入柔性球铰与平行四边形机构成功实现了偏摆台的运动解耦和电机动子的直线导向。同时，基于柔度矩阵法推导了柔性球铰、驱动支链与整个偏摆台的柔度解析模型，并通过静力学有限元仿真和实验测试验证了其准确性。结果表明：柔度解析模型的计算结果与有限元仿真结果和实测结果的相对误差均在10%以内，表明所推导的柔度解析模型的精度较高；偏摆台的最大行程范围为±0.054 3 rad×±0.047 2 rad×±4.45 mm，具有行程大、结构紧凑的特点。由此说明，本文所设计的偏摆台适用于多种需要大行程空间定位的场合。

随着精密工程技术的不断发展，对以三自由度偏摆台为代表的精密定位平台提出了更高的定位精度和控制带宽要求。因此，对偏摆台驱动和控制方式进行创新设计，同时寻求解耦性能更强、动态性能更好的多自由度柔性机构是目前柔性精密定位平台的发展趋势和未来方向。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

范大鹏，谭若愚.

快速反射镜中柔顺传动机构应用与研究现状

［J］. 中国机械工程， 2020， 31（24）： 2899-2909.