两栖仿海龟机器人动力学建模与运动控制研究

doi:10.3785/j.issn.1006-754X.2023.00.007

两栖仿海龟机器人动力学建模与运动控制研究

芮宏斌^,^,, 李路路, 王天赐, 段凯文

西安理工大学机械与精密仪器工程学院，陕西西安 710048

Research on dynamic modeling and motion control of amphibious turtle inspired robot

RUI Hong-bin^,^,, LI Lu-lu, WANG Tian-ci, DUAN Kai-wen

College of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China

收稿日期: 2022-05-17 修回日期: 2022-06-27

基金资助:

国家自然科学基金面上项目.  51775432
陕西省技术创新引导专项.  2018ZKC-160
陕西省教育厅重点科研计划项目.  22JY051
陕西省科技计划重点研发项目.  2023-YBGY-357

Received: 2022-05-17 Revised: 2022-06-27

作者简介 About authors

芮宏斌（1978—），男，陕西西安人，副教授，博士，从事车辆系统动力学与控制技术、特种移动机器人设计研究，E-mail:Hongbin.rui@126.com，https://orcid.org/0000-0002-2718-831X , E-mail：Hongbin.rui@126.com

摘要

为了提高两栖仿海龟机器人行走的稳定性，对其进行动力学建模，并基于PID（proportional integral derivative，比例积分微分）反馈控制策略提出了一种力/位控制模型。首先，根据机器人的运动学模型，得到了支腿的变换矩阵和雅可比矩阵，并利用虚功原理建立了足端与液压缸之间的力传递模型。然后，利用拉格朗日法对机器人进行动力学建模，推导了支腿的动力学方程，同时进行了动力学仿真，并将实时的足端受力导入动力学方程进行计算，验证了动力学模型的正确性。最后，搭建了液压仿真模型，并在ADAMS‒AMESim‒MATLAB联合仿真环境中开展了机器人运动仿真。仿真结果显示：与纯位置控制模式相比，力/位控制模式下机器人膝关节的转动更加平稳，液压缸的动力输出更稳定且功耗更小。研究结果对提高机器人运动的稳定性、增强运动控制系统的鲁棒性和提高液压系统的总效率具有借鉴意义。

关键词： 机器人 ; 动力学 ; 力/位控制 ; 联合仿真

Abstract

In order to improve the walking stability of amphibious turtle inspired robot, a dynamics model was established, and a force/position control model was proposed based on the PID (proportional integral derivative) feedback control strategy. Firstly, according to the kinematics model of the robot, the transformation matrix and Jacobian matrix of the outrigger were obtained, and a force transfer model between foot end and hydraulic cylinder was established by the virtual work principle. Then, the Lagrange method was used to model the dynamics of the robot, and the dynamics equation of the outrigger was derived. At the same time, the dynamics simulation was carried out, and the real-time force on the foot end was introduced into the dynamics equation for calculation, which verified the correctness of the dynamics model. Finally, a hydraulic simulation model was built, and the robot motion simulation was carried out in the ADAMS‒AMESim‒MATLAB co-simulation environment. The simulation results showed that compared with the pure position control mode, the rotation of the robot knee joint under the force/position control mode was more stable, and the power output of the hydraulic cylinder was more stable and the power consumption was less. The research results have reference significance for improving the stability of robot motion, enhancing the robustness of motion control system and improving the overall efficiency of hydraulic system.

Keywords： robot ; dynamics ; force/position control ; co-simulation

PDF (4081KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

芮宏斌, 李路路, 王天赐, 段凯文. 两栖仿海龟机器人动力学建模与运动控制研究. 工程设计学报[J], 2023, 30(1): 73-81 doi:10.3785/j.issn.1006-754X.2023.00.007

RUI Hong-bin, LI Lu-lu, WANG Tian-ci, DUAN Kai-wen. Research on dynamic modeling and motion control of amphibious turtle inspired robot. Chinese Journal of Engineering Design[J], 2023, 30(1): 73-81 doi:10.3785/j.issn.1006-754X.2023.00.007

近年来，我国生态环境失调，洪涝灾害频发。据国家自然灾害灾情管理系统统计，河南郑州“7·20”特大暴雨灾害在10日内造成1 616个乡镇、1 391.28万人受灾，倒塌房屋达1.8万户。洪水阻断、毁坏了交通要道，对救援和灾后重建工作带来极大影响^[1]。为了应对此等灾害，国家在《国务院办公厅关于加快应急产业发展的意见》《“十四五”机器人产业发展规划》等文件中明确指出了研发应急救援装备和救援机器人的重要性^[2-3]。因此，救援机器人的设计开发对促进国家应急产业发展具有重要意义。

救援机器人按移动机构的形式可分为履带式、腿式和轮‒腿复合式。其中，履带式救援机器人的机动性强，可以轻松通过松软地面和不稳定介质，主要用于在室外执行搜救和运送伤员的任务，如日本东京工业大学的Ueda等^[4]提出的HELIOS Ⅸ机器人、美国iRobot公司的Yamauchi^[5]提出的PackBot机器人和德国波鸿鲁尔大学的Neumann等^[6]提出的一种蛇形履带移动机器人等。但是，该类救援机器人只能在相对平坦的地面上移动，越障能力有限。腿式救援机器人能够克服这个缺点，它可以像动物一样攀越障碍，并在一定程度上摆脱地面摩擦力和粗糙度的限制，主要用于执行建筑物内部和复杂地面环境下的救援任务，如波士顿动力公司开发的Atlas机器人^[7]、瑞士苏黎世机器人系统实验室设计的ANYmal机器人^[8]等。但是，该类机器人移动机构的自由度较多，控制相对困难。轮‒腿复合式救援机器人具有更为综合且优越的移动性能，其救援能力强大。如：韩国科学技术高级研究院的Jung等^[9]提出的DRC-HUBO+机器人同时具备双足步行模式和车轮模式，对灾害现场的环境适应性很强；德国波恩大学的Schwarz等^[10]提出的Momaro机器人具备轮‒腿复合式移动机构，能够轻松跨越灾害现场的障碍。

救援机器人在救援过程中会进行人机交互，为了防止对伤员造成二次伤害，保证其移动机构和末端执行器的稳定控制尤为重要。郭冰菁等^[11]、张琦等^[12]、宛敏红等^[13]、王学军等^[14]和Koolen等^[15]通过多种方法建立了机器人的动力学模型，实现了其稳定控制。笔者在文献[16]中提出的两栖仿海龟机器人即为一种救援机器人。为实现其轮‒腿复合式移动机构的稳定控制，本文拟对其运动学模型进行更深层次的分析，并通过虚功原理和拉格朗日法建立该机器人的动力学模型，以推导支腿的动力学方程，最后将动力学方程引入支腿的控制系统，建立力/位控制模型，并在ADAMS‒AMESim‒MATLAB联合仿真环境中开展机器人的运动仿真。

1 机器人的机械结构和运动学模型

1.1　机械结构

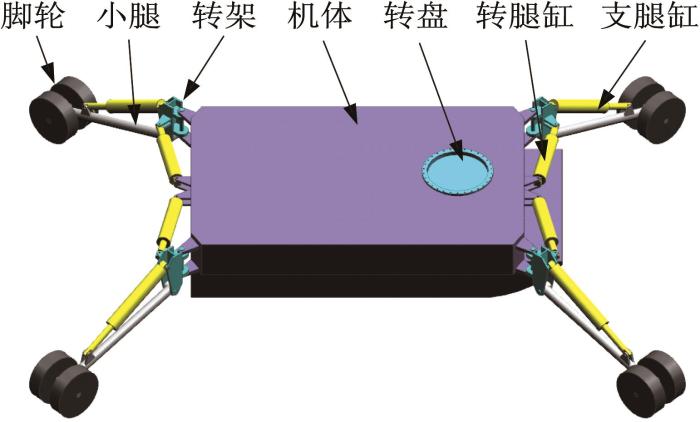
两栖仿海龟机器人的三维模型如图1所示，其整体上主要包括机体和4条支腿。4条支腿分布在机体四角，用于驱动机器人运动。每条支腿均由转架、小腿和脚轮组成，通过转架铰接在机体一角，其具有水平转动和竖直转动两个自由度，转动的动力分别由转腿缸和支腿缸这2个液压缸提供。脚轮为自由轮，由2个轮胎组成，可分别自由转动。机器人主要的尺寸参数以及液压缸的主要技术性能参数分别如表1和表2所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 两栖仿海龟机器人三维模型

Fig.1 Three-dimensional model of amphibious turtle inspired robot

表1 两栖仿海龟机器人的主要尺寸参数 (mm)

Table 1 Main dimensional parameters of amphibious turtle inspired robot

参数	数值
机体（长×宽×高）	1 006×620×245
转架长度	42
小腿长度	430
脚轮直径	150

新窗口打开| 下载CSV

表2 液压缸的主要技术性能参数

Table 2 Main technical performance parameters of hydraulic cylinder

参数	转腿缸	支腿缸
工作压力/MPa	10	10
缸径/mm	16	25
杆径/mm	8	10
最小安装距/mm	210	250
最大行程/mm	110	150
最大推力/N	2 010	4 906
最大拉力/N	1 507	4 121

新窗口打开| 下载CSV

1.2　运动学模型

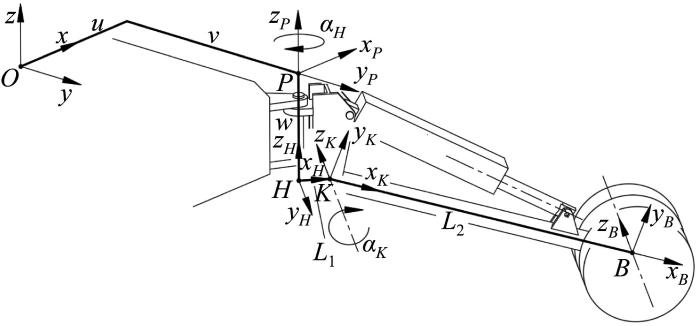
以两栖仿海龟机器人的右前腿为例，构建其运动学模型。建立的支腿运动坐标系如图2所示。其中，坐标系{O}为整个机器人的基坐标系，原点O位于机体重心处，x轴指向机体头部，y轴指向机体右侧，z轴指向机体上端面。坐标系{P}为支腿的基坐标系，原点P位于机体一角，与基坐标系{O}处于同一高度，其坐标轴的指向与基坐标系{O}一致。坐标系{H}为髋关节坐标系，与膝关节处于同一高度，z_H 轴为髋关节的转动轴，x_H 轴由髋关节指向膝关节。坐标系{K}为膝关节坐标系，z_K 轴为膝关节的转动轴，x_K 轴由膝关节指向脚轮。坐标系{B}为足端坐标系，原点B位于小腿末端，各坐标轴的指向与膝关节坐标系{K}一致。图中：α_H 表示x_H 轴与x_P 轴之间的夹角，即髋关节转角，α_K 表示x_K 轴与x_H 轴之间的夹角，即膝关节转角，其正方向已在图中标出；u、v、w分别表示原点O到原点H在x、y、z方向上的距离；L₁表示髋关节与膝关节之间的距离，即转架长度，L₂表示小腿长度。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 支腿运动坐标系

Fig.2 Motion coordinate system of outrigger

经文献[16]分析可得，机器人基坐标系{O}到足端坐标系{B}的齐次变换矩阵 ${}_{B}^{O}$ T 为：

_{B}^{O} T = [\begin{matrix} c α_{H} c α_{K} & c α_{H} s α_{K} & s α_{H} & L_{2} c α_{H} c α_{K} + L_{1} c α_{H} + u \\ s α_{H} c α_{K} & s α_{H} s α_{K} & - c α_{H} & L_{2} s α_{H} c α_{K} + L_{1} s α_{H} + v \\ - s α_{K} & c α_{K} & 0 & - L_{2} s α_{K} - w \\ 0 & 0 & 0 & 1 \end{matrix}]

(1)

式中：c表示cos，s表示sin，下文矩阵中同。

基于式(1)可得，足端B的正运动学方程为：

\{\begin{array}{l} B_{x} = L_{2} c o s α_{H} c o s α_{K} + L_{1} c o s α_{H} + u \\ B_{y} = L_{2} s i n α_{H} c o s α_{K} + L_{1} s i n α_{H} + v \\ B_{z} = - L_{2} s i n α_{K} - w \end{array}

(2)

式中：B_x 、B_y 、B_z 分别表示足端B的x、y、z坐标。

由式(2)可得，支腿的雅可比矩阵 J $(α)$ 为：

J (α) = {[\begin{matrix} \frac{\partial B_{x}}{\partial α_{H}} & \frac{\partial B_{y}}{\partial α_{H}} & \frac{\partial B_{z}}{\partial α_{H}} \\ \frac{\partial B_{x}}{\partial α_{K}} & \frac{\partial B_{y}}{\partial α_{K}} & \frac{\partial B_{z}}{\partial α_{K}} \end{matrix}]}^{T} = [\begin{matrix} - L_{2} s α_{H} c α_{K} - L_{1} s α_{H} & - L_{2} c α_{H} s α_{K} \\ L_{2} c α_{H} c α_{K} + L_{1} c α_{H} & - L_{2} s α_{H} s α_{K} \\ 0 & - L_{2} c α_{K} \end{matrix}]

(3)

1.3　关节力传递模型

基于虚功原理，足端B与支腿关节之间的力传递关系可表示为：

{[\begin{matrix} T_{H} & T_{K} \end{matrix}]}^{T} = J^{T} (α) {[\begin{matrix} Q_{x} & Q_{y} & Q_{z} \end{matrix}]}^{T}

(4)

式中：T_H 、T_K 分别表示髋关节和膝关节所受的力矩；Q_x 、Q_y 、Q_z 分别表示地面作用在足端B上的外负载Q在x、y、z方向上的分力。

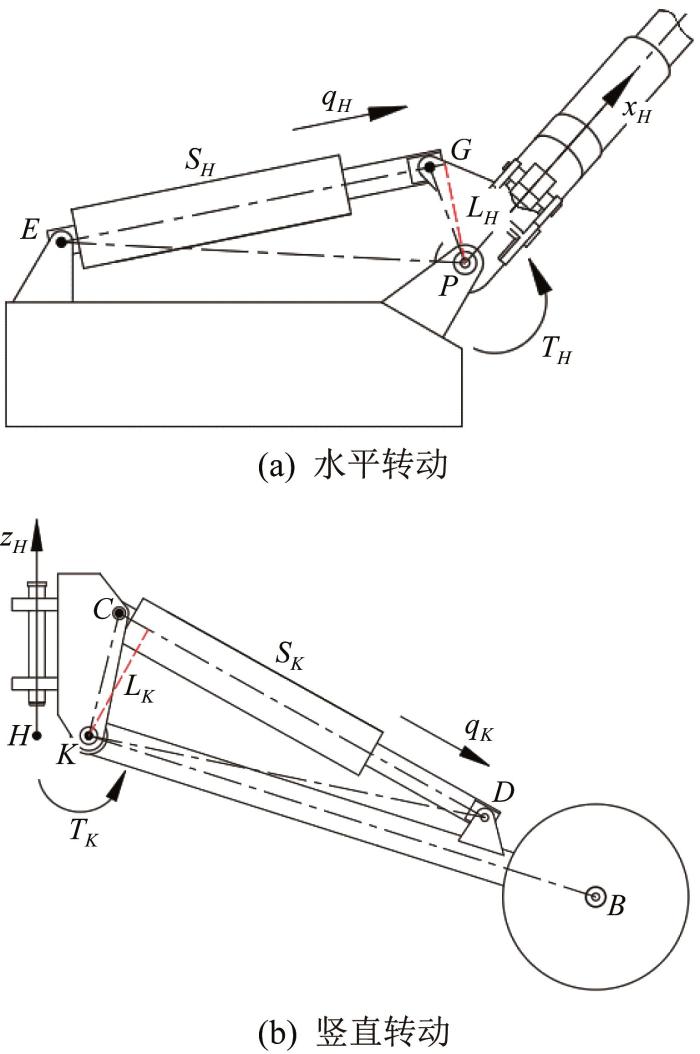
鉴于机器人的支腿由转腿缸和支腿缸这2个液压缸驱动，若要完全解析力的传递模型，则需建立液压缸与对应关节之间的力传递关系。图3所示为机器人支腿的运动图解，图中坐标系与图2一致。设外负载作用下转腿缸和支腿缸的输出力分别为q_H 和q_K，则液压缸与髋、膝关节之间的力传递关系可表示为：

q_{H} = \frac{T_{H}}{L_{H}}

(5)

q_{K} = \frac{T_{K}}{L_{K}}

(6)

其中：

L_{H} = \frac{\sqrt[]{4 L_{P E}^{2} S_{H}^{2} - {(L_{P E}^{2} + S_{H}^{2} - L_{P G}^{2})}^{2}}}{2 S_{H}}

(7)

L_{K} = \frac{\sqrt[]{4 L_{K C}^{2} S_{K}^{2} - {(L_{K C}^{2} + S_{K}^{2} - L_{K D}^{2})}^{2}}}{2 S_{K}}

(8)

式中：L_H 、L_K 分别表示转腿缸和支腿缸的力臂长度；S_H 、S_K 分别表示转腿缸和支腿缸的两端长度；L_PE 、L_PG 、L_KC 和L_KD 分别表示对应点之间的距离。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 支腿的运动图解

Fig.3 Diagram of outrigger movement

2 机器人的动力学模型

力是改变物体运动状态的原因，动力学相对于静力学和运动学能更加全面地分析物体的运动，从而更加完整地研究物体所受力系与物体运动之间的关系^[17]。对于两栖仿海龟机器人而言，其运动完全依靠各支腿上的2个液压缸驱动。因此，建立该机器人的动力学模型，并将动力学模型引入控制系统，可大大改善机器人的运动性能。

以机器人右前腿为例，利用拉格朗日法对其进行动力学建模^[18-19]。为简化动力学模型，将支腿各部件均看作刚体，并忽略弹性形变与转动惯量。支腿各部件的质心位置如图4所示。令j=1, 2, …, 7分别表示转架、小腿、脚轮、转腿缸缸体、转腿缸推杆、支腿缸缸体和支腿缸推杆；m_j 表示各部件的质量，其标示位置对应点即为部件质心；L_m_j 表示各部件质心到相应铰点的距离（即质心位置）；θ_H 为杆件EG与y轴正向的夹角，θ_K 为杆件CD与x_H 轴正向的夹角。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 支腿各部件质心位置示意

Fig.4 Schematic diagram of centroid position of each component of outrigger

根据图4，可得：

\{\begin{array}{l} L_{m 5} = L_{m 50} + I_{H} \\ L_{m 7} = L_{m 70} + I_{K} \end{array}

式中：L_m50和L_m70分别表示活塞杆完全缩回时转腿缸和支腿缸的活塞杆质心到相应铰点的距离，分别为151 mm和171 mm；I_H 、I_K 分别表示转腿缸和支腿缸的工作行程。

支腿各部件的质量及质心位置如表3所示。机体质量为80 kg，机体的质心坐标(u, v, w)=(503, 310, 26) mm。

表3 支腿各部件的质量及质心位置

Table 3 Mass and centroid position of each component of outrigger

部件j	质量m_j /kg	质心位置L_m_j /mm
1	0.5	30
2	1.5	215
3	1.0	430
4	0.8	102
5	0.4	—
6	1.0	122
7	0.5	—

新窗口打开| 下载CSV

设支腿各部件质心的位置矩阵为 c_j，表示为该部件质心在基坐标系中的坐标(x_j, y_j, z_j )，则由齐次坐标变换计算可得：

c_{1} = [\begin{array}{l} L_{m 1} c α_{H} + u \\ L_{m 1} s α_{H} + v \\ z_{1} \end{array}]

c_{2} = [\begin{matrix} L_{m 2} c α_{H} c α_{K} + L_{1} c α_{H} + u \\ L_{m 2} s α_{H} c α_{K} + L_{1} s α_{H} + v \\ - L_{m 2} s α_{K} - w \end{matrix}]

c_{3} = [\begin{matrix} L_{m 3} c α_{H} c α_{K} + L_{1} c α_{H} + u \\ L_{m 3} s α_{H} c α_{K} + L_{1} s α_{H} + v \\ - L_{m 3} s α_{K} - w \end{matrix}]

c_{4} = [\begin{array}{l} L_{m 4} s θ_{H} + E_{x} \\ L_{m 4} c θ_{H} + E_{y} \\ E_{z} \end{array}]

c_{5} = [\begin{matrix} (L_{m 50} + I_{H}) s θ_{H} + E_{x} \\ (L_{m 50} + I_{H}) c θ_{H} + E_{y} \\ E_{z} \end{matrix}]

c_{6} = [\begin{matrix} L_{m 6} c α_{H} c θ_{K} + C_{x H} c α_{H} + u \\ L_{m 6} s α_{H} c θ_{K} + C_{x H} s α_{H} + v \\ - L_{m 6} s θ_{K} + C_{z H} - w \end{matrix}]

c_{7} = [\begin{matrix} (L_{m 70} + I_{K}) c α_{H} c θ_{K} + C_{x H} c α_{H} + u \\ (L_{m 70} + I_{K}) s α_{H} c θ_{K} + C_{x H} s α_{H} + v \\ - (L_{m 70} + I_{K}) s θ_{K} + C_{z H} - w \end{matrix}]

式中：E_x 、E_y 、E_z 分别表示铰点E的x、y、z坐标；C_xH 、C_zH 分别表示铰点C的x_H 和z_H 坐标。这些参数均为固定值。

设支腿各部件的速度为v_j，则有：

v_{j} = \sqrt[]{{(\frac{d x_{j}}{d t})}^{2} + {(\frac{d y_{j}}{d t})}^{2} + {(\frac{d z_{j}}{d t})}^{2}}

设支腿各部件的动能为E_k_j，则有：

E_{k j} = \frac{1}{2} m_{j} v_{j}^{2}

设支腿各部件的势能为E_p_j，则有：

E_{p j} = m_{j} g z_{j}

则拉格朗日算子 $ℒ$ 为：

ℒ = \sum_{j = 1}^{7} E_{k j} - E_{p j}

设无外负载作用下转腿缸和支腿缸的输出力分别为f_H 和f_K，由拉格朗日函数计算可得：

f_{H} = \frac{d}{d t} (\frac{\partial ℒ}{\partial {\dot{I}}_{H}}) - \frac{\partial ℒ}{\partial I_{H}} = A_{1} {\dot{I}}_{H}^{2} + A_{2} {\dot{I}}_{H} {\dot{I}}_{K} + A_{3} {\ddot{I}}_{H}

f_{K} = \frac{d}{d t} (\frac{\partial ℒ}{\partial {\dot{I}}_{K}}) - \frac{\partial ℒ}{\partial I_{K}} = A_{4} {\dot{I}}_{H}^{2} + A_{5} {\dot{I}}_{K}^{2} + A_{6} {\ddot{I}}_{K} - A_{7}

式中：A₁~A₇表示各变量的系数； ${\dot{I}}_{H}$ 和 ${\dot{I}}_{K}$ 分别表示转腿缸和支腿缸的工作速度； ${\ddot{I}}_{H}$ 和 ${\ddot{I}}_{K}$ 分别表示转腿缸和支腿缸的工作加速度。

联立式(5)和式(6)以及式(14)和式(15)，可将支腿的动力学方程表示为：

F = f + q

式中：F表示支腿运动时液压缸的输出力；f表示无外负载作用下支腿运动时液压缸的输出力；q表示外负载作用下足端运动时液压缸的输出力。

按照相同方法，建立其他支腿的运动坐标系，求解拉格朗日算子，即可获得机器人的动力学模型。

3 机器人动力学模型验证

鉴于本文所建立动力学方程的复杂性，通过仿真来验证动力学方程的正确性。借助ADAMS（automatic dynamic analysis of mechanical systems，机械系统动力学自动分析）软件建立两栖仿海龟机器人的虚拟样机，并进行动力学仿真。笔者在文献[20]中规划了所研究机器人的仿海龟爬行步态，其具体动作的解析图如图5所示。图中：足端实心表示足端支撑地面，机体悬空；足端空心表示机体支撑地面，足端悬空。将整个步态周期划分为支撑相和摆动相：机器人从姿态1运动到姿态2的过程为支撑相，在此期间机器人向前爬行的距离为s，其余过程为摆动相。在ADAMS软件中开展机器人仿海龟爬行仿真，采用位移驱动控制液压缸的工作行程，仿真结果如图6所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 仿海龟爬行步态示意

Fig.5 Schematic diagram of imitation turtle crawling gait

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 仿海龟爬行步态仿真结果

Fig.6 Simulation results of imitation turtle crawling gait

机器人动力学模型正确性仿真验证的技术路线如图7所示。通过ADAMS仿真测量机器人足端外负载Q在x_B 、y_B 、z_B 三个方向上的分力Q_xB、Q_yB 、Q_zB。由式(1)可得，[Q_xBQ_yBQ_zB ]与[Q_xQ_yQ_z ]的映射关系为：

[\begin{matrix} Q_{x} \\ Q_{y} \\ Q_{z} \end{matrix}] = [\begin{matrix} c α_{H} c α_{K} & c α_{H} s α_{K} & s α_{H} \\ s α_{H} c α_{K} & s α_{H} s α_{K} & - c α_{H} \\ - s α_{K} & c α_{K} & 0 \end{matrix}] [\begin{matrix} Q_{x B} \\ Q_{y B} \\ Q_{z B} \end{matrix}]

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 机器人动力学模型仿真验证技术路线

Fig.7 Technical route of robot dynamics model simulation verification

将上述外负载测量结果、式(3)至式(8)及式(14)至式(16)导入MATLAB软件进行计算，即可得到机器人爬行过程中液压缸动力输出的理论值。然后，将所得理论值与利用ADAMS软件测量得到的液压缸动力输出仿真值进行比较，以验证动力学模型的正确性。

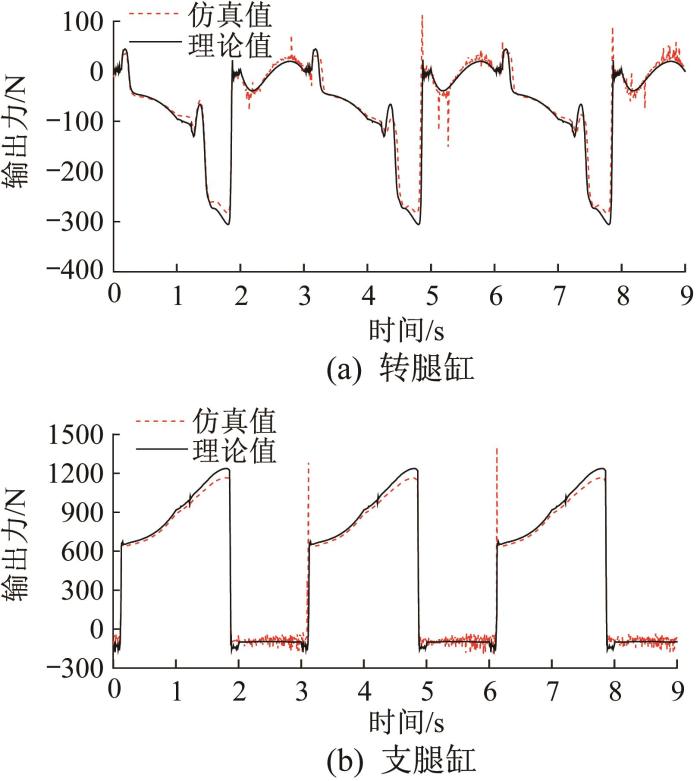
通过理论计算和仿真得到的液压缸动力输出曲线如图8所示。由图可知，机器人在9 s内完成了3个爬行步态周期，每个步态周期的前2 s为支撑相，后1 s为摆动相。从图中还可以看出，液压缸动力输出的理论曲线与仿真曲线的变化趋势基本一致，且具有较高的重合度。排除仿真过程中产生的系统误差，转腿缸动力学方程的最大相对误差为7.7%，支腿缸动力学方程的最大相对误差为6.3%，误差均在每个步态周期的支撑相向摆动相过渡的时刻产生，即姿态2对应的时刻。推测产生误差的原因是机器人机体与地面的刚性接触，但总体误差很小，足以验证动力学方程的正确性。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 液压缸动力输出曲线对比

Fig.8 Comparison of power output curve of hydraulic cylinder

4 机器人运动仿真

4.1　仿真模型构建

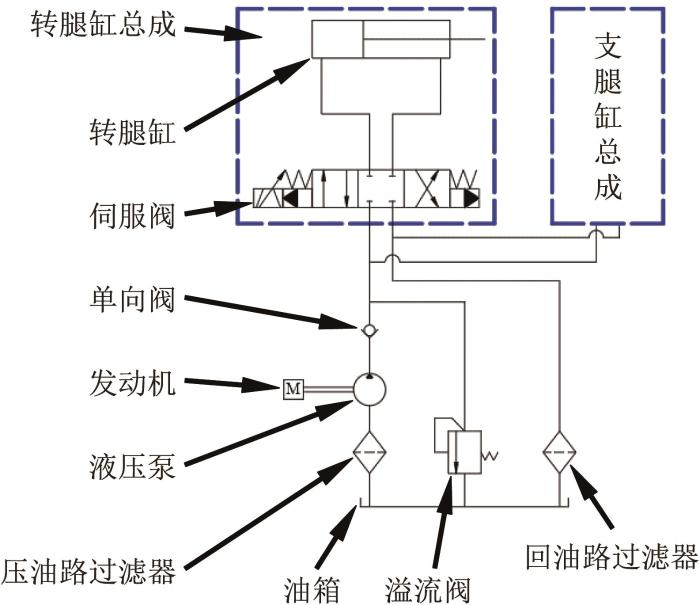
两栖仿海龟机器人每条支腿的液压回路完全相同，单支腿的液压原理如图9所示。支腿液压系统的动力元件主要包括液压泵、发动机等，可为系统提供10 MPa的压力油；控制元件主要包括伺服阀、溢流阀、单向阀、传感器和控制器等，控制元件通过反馈控制液压缸工作；执行元件主要包括转腿缸和支腿缸，用于驱动支腿运动。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 单支腿的液压原理

Fig.9 Hydraulic principle of single outrigger

同样以机器人右前腿为例，搭建单支腿液压系统仿真模型，如图10所示。其中，点划线表示信号传输线，实线表示液压系统的油路。该仿真模型主要包括ADAMS、MATLAB和AMESim三个模块。ADAMS模块用于搭建机器人虚拟样机，该模块需要测量足端外负载Q_xB 、Q_yB 、Q_zB，关节转角α_H 、α_K 和液压缸工作行程I_H 、I_K，并将这3类数据传输给AMESim模块。AMESim模块中的位移传感器将液压缸的工作行程数据传输给液压缸，PID（proportional integral derivative，比例积分微分）控制器以关节转角为反馈信号控制伺服阀活塞的位置。在动力源的驱动下和伺服阀的控制下，液压缸产生可控的输出力，并由力传感器将输出力数据传输给ADAMS模块，从而驱动虚拟样机运动。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 单支腿液压系统仿真模型

Fig.10 Simulation model of single outrigger hydraulic system

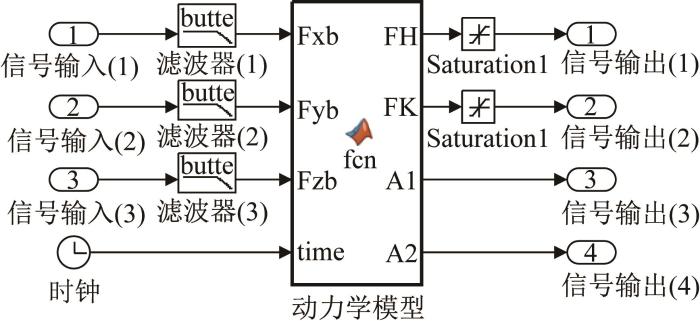
图11所示为基于机器人动力学方程的MATLAB计算模型。AMESim模块将足端外负载数据导入MATLAB模块，经滤波后代入动力学模型计算得到液压缸动力输出理论值，同时将仿真时间代入动力学模型以计算关节转角的理论值，并将其作为目标信号代入PID控制器，实现支腿关节的反馈控制。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 基于机器人动力学方程的MATLAB计算模型

Fig.11 MATLAB calculation model based on robot dynamics equation

4.2　运动仿真

根据所搭建的仿真模型，分别开展纯位置控制模式下和力/位控制模式下的机器人运动仿真。2种控制模式的不同之处在于：前者的动力源保持10 MPa压力不变；后者根据MATLAB模块计算得到的液压缸动力输出理论值对动力源油压进行调控，实现高负载时液压缸在高压下工作，低负载时液压缸在低压下工作。

通过分析可得，液压缸在支撑相阶段处于高负载，在摆动相阶段处于低负载，则力/位控制模式下支腿液压系统的供油压力为：

P = \{\begin{array}{l} \frac{4 |F|}{π d_{i}^{2}} K_{s u} + P_{m i n}, t \in (0, 2] \\ \frac{4 |F|}{π d_{o}^{2}} K_{s w} + P_{m i n}, t \in (2, 3] \end{array}

(18)

式中：P表示液压系统的供油压力；K_su和K_sw分别表示支撑相和摆动相阶段对液压系统油压添加的增益；d_i、d_o分别表示液压缸的内、外径；P_min表示对液压系统限制的最小油压。

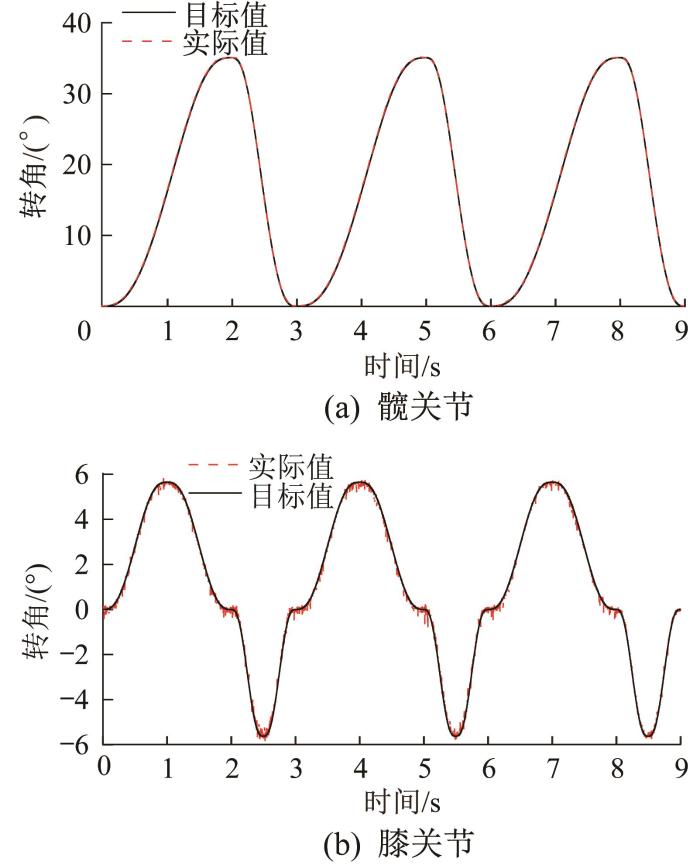
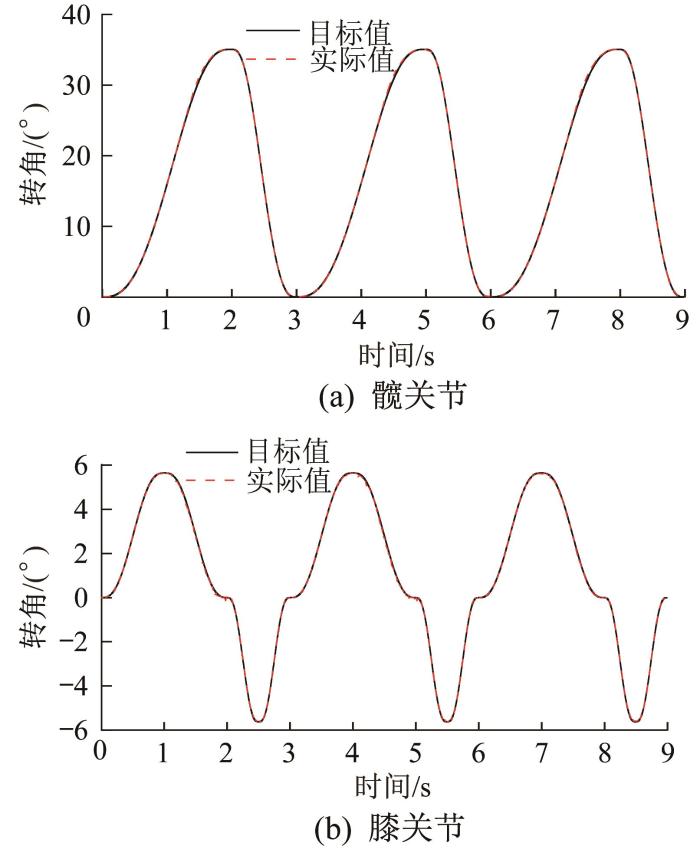
设定仿真时间为9 s，即机器人完成3次完整爬行，通过仿真得到不同控制模式下机器人髋、膝关节转角的变化曲线，分别如图12和图13所示。由图可以看出，2种控制模式下髋关节的控制效果良好，其转角的实际曲线与目标曲线几乎完全重合，说明髋关节能够完全按照预先规划的轨迹转动。但是，纯位置控制模式下膝关节的转动产生了噪声信号，且在每个爬行步态周期的第1秒、第2秒、第2.5秒和第3秒最为明显。分析原因在于，液压系统持续在10 MPa高压下工作会出现以下现象：1）液压缸的推力过大，脚轮与地面接触时产生了较大的碰撞力；2）脚轮悬空的瞬间支腿缸的合外力急剧变化；3）液压缸活塞杆换向时有杆腔和无杆腔的压力不稳定。上述3种现象均会导致液压缸的工作行程发生突变，从而影响伺服阀的控制效果。而力/位控制模式下液压系统的工作压力由动力学模型控制，可调整支腿缸的实际输出力和合外力，使得膝关节能够完全按照预先规划的轨迹转动，取得更好的控制效果。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 纯位置控制模式下支腿关节转角的变化曲线

Fig.12 Variation curve of outrigger joint angle under pure position control mode

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 力/位控制模式下支腿关节转角的变化曲线

Fig.13 Variation curve of outrigger joint angle under force/position control mode

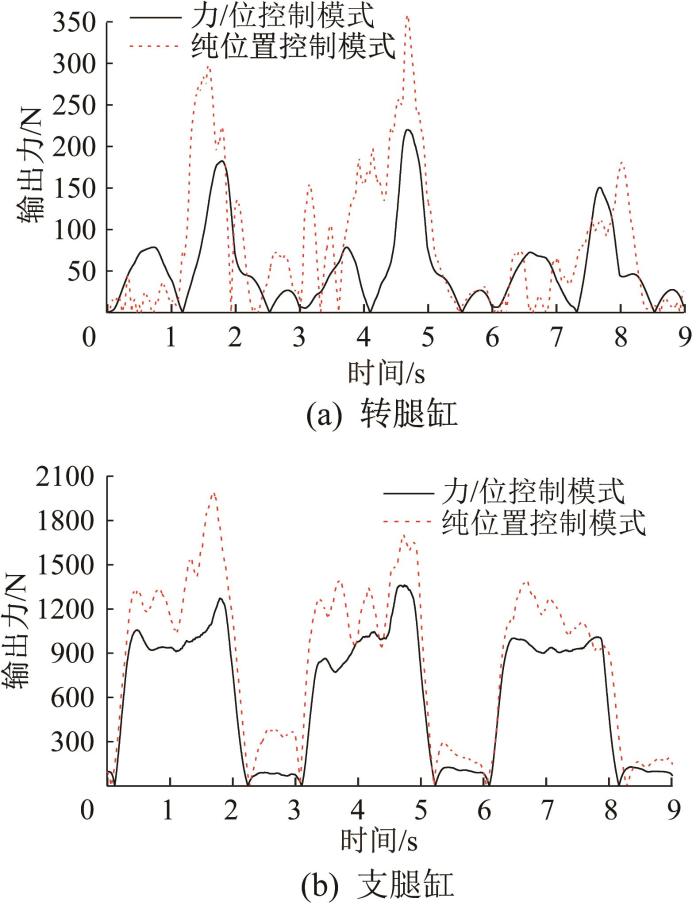
图14所示为2种控制模式下液压缸的动力输出曲线对比。由图可以看出，力/位控制模式下液压缸的动力输出曲线更加规则且平缓，未产生瞬时突变和多余的振荡信号，说明液压缸的动力输出稳定，有利于提高机器人的稳定性。通过对比图中2条曲线对应的动力输出值可知，纯位置控制模式下转腿缸和支腿缸的最大输出力分别达到了359 N和1 989 N，而力/位控制模式下分别为220 N和1 361 N。2种控制模式下液压缸的工作行程相等，因此力/位控制模式下液压缸的功耗更小，有利于节约能源，减小能量损耗，提高液压系统的总效率。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同控制模式下液压缸动力输出曲线对比

Fig.14 Comparison of hydraulic cylinder power output curves under different control modes

5 结论

1）基于虚功原理建立了两栖仿海龟机器人支腿足端与液压缸之间的力传递模型，得到了外负载作用下液压缸的力学方程。

2）利用拉格朗日法建立了两栖仿海龟机器人的动力学模型，得到了支腿的动力学方程，并在ADAMS软件中开展了仿海龟爬行仿真，验证了动力学模型的正确性。

3）建立了两栖仿海龟机器人的液压控制模型，并开展了纯位置控制模式下和力/位控制模式下的运动仿真。结果显示，力/位控制模式下机器人支腿关节的控制效果更好，液压缸的动力输出更加稳定，减小了液压缸的功耗，提高了液压系统的总效率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

牛少杰

河南因水灾遇难

99人［N］.天津日报，2021-07-03（7）.