水下装备的重浮力特性是影响装备姿态和运动的重要因素。大多数水下装备都要求具备良好的静平衡特性，以满足装备水下稳定运动的要求。许多学者对水下装备的静平衡特性进行了研究。如：蒋新松等^［1］指出，有缆水下机器人的稳心高应大于7 cm，同时给出了重浮心总体布置的设计准则，在回转型自主水下机器人（autonomous underwater vehicle， AUV）的静平衡设计阶段，主要通过质浮心表进行重浮力的粗略配置，再在实际水池中由人工加铅块和配浮力材料进行配重，水下的精细调控则一般采用浮力调节装置^［2］；罗阳等^［3］设计了水下焊接机器人的重浮心补偿控制方案；孙烨等^［4］利用重心调节装置实现了水下拖曳体姿态角的调节，消除了其静俯仰力矩，保持了其自稳定性能。同时，静不平衡也可以作为水下装备的动力来源。如：水下滑翔机器人可以借助静不平衡实现锯齿形运动，完成大范围、低能耗的扫测勘探任务^［5］；深渊着陆器、预置系统的无动力下潜和上浮，也是借助了水下装备的静平衡敏感性^［6］。

在AUV水下对接中，导向罩式水下接驳坞站因具有容错性高、缓冲保护性能及水动力特性优良等特点而被广泛应用^［7］。目前针对坞站式接驳装置重浮心配置的相关研究并不多。现有的一些悬浮对接、移动对接装备，由于设计的空间较为开放，易具有较大的稳心高和质量，装备水下自稳定性较好^［8］；而对于一些常用的流线型水下拖体，一般应用于水下扫测声阵，常采用多拖点现场配置方式试错配重，再加上辅助的重心调节或者舵面调节来保证拖体的运动稳定性^［9］。这些水下装备经过主动调节重浮心之后，并无被动的质浮心偏移，因此重浮心的配置依据经验便可以满足使用要求。然而，针对有严格重浮心配置要求的水下装备，须在设计阶段进行优化配置。如：水下球形机器人的对称性有严格要求^［10］；深海着陆器上浮和下潜时抛载重物块的质量和位置须优化设计^［6］；再入航天器更是对质心位置、惯性矩和惯性积有严格的设计要求^［11］。

对于应用于水下单点系泊悬浮对接AUV场景的开合式接驳装置，由于其设计空间有限，限制了稳心高；同时，在对接过程中，导向罩开合对接驳装置的悬浮平衡纵倾角有较大影响，为了保证接驳装置有良好的悬浮自稳定性，其纵倾角的波动应在-8°~8°内。为了设计满足单点系泊悬浮对接自稳特性的开合式接驳装置，对接驳装置的开合机构进行质浮心位移分析，并根据静平衡计算结果，着重分析拖点位置和稳心高对接驳装置悬浮平衡纵倾角的影响；基于悬浮平衡分析，提出稳心高设计要求，并以接驳装置悬浮平衡纵倾角及其波动幅值较小和接驳装置质量最小为设计目标，对配重铅块、浮力材的特征尺寸和拖点位置进行优化配置。

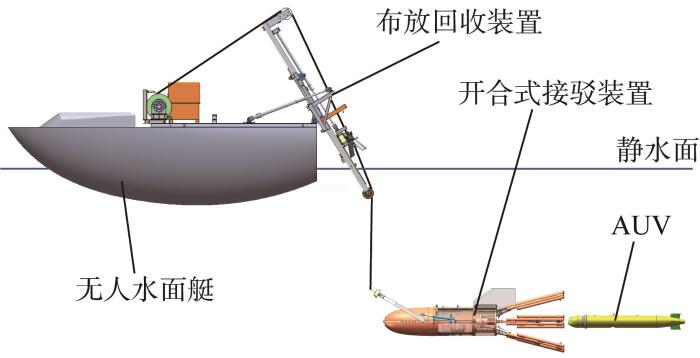
无人水面艇（unmanned surface vehicle， USV）自主部署AUV一体化系统如图1所示。其中布放回收装置（置于USV甲板上）与开合式接驳装置由拖缆连接，共同组成一套完整的拖曳式布放对接回收系统。当USV停泊于水面处于非机动状态时，开合式接驳装置被系泊悬浮于水下，其导向罩打开，等待与AUV对接并完成后续的电量补充、数据交换或者将AUV回收至甲板等任务。同样，接驳装置也可以系泊于水面固定或漂浮的结构物上，共同组成单点系泊悬浮对接系统。

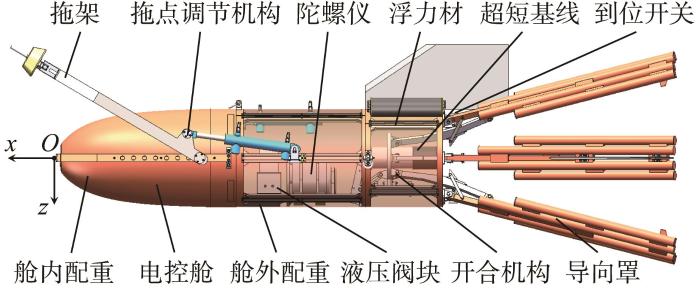
开合式接驳装置的结构如图2所示。其主要由电控舱、液压系统、开合机构、拖点调节机构、传感设备和衡重部件六部分组成。舱艏外形光顺，导向罩打开后接驳装置外形为伞状，水动力性能良好；导向罩合拢后，装置的周身为圆柱形，可以匹配滑道式布放回收方式，有助于实现接驳的自动化。除此之外，为了提高AUV被动导向效率，将传统的固定罩导引方式改为动态开合导引方式。当到位开关检测到AUV就位时，开合机构驱动导向罩合拢，AUV逐渐被约束、定位和夹紧，以便进一步进行水下非接触式充电、无线数据传输及回收等工作。

考虑接驳装置自动化布放回收的可靠性和便捷性，接驳装置的设计空间被限制为直径为534 mm的圆柱形，因此装置的稳心高会受到限制；同时，为了使回收便捷，避免给布放回收架的主滑道施加过多负载，要求接驳装置的质量越小越好。最为关键的是，在系泊悬浮对接过程中，要求接驳装置的悬浮平衡纵倾角的波动在-8°~8°内，这就须合理设计和优化衡重区域，进行舱内配重、舱外配重和浮力材特征尺寸以及拖点位置的确定，以使接驳装置满足基本静平衡设计要求。

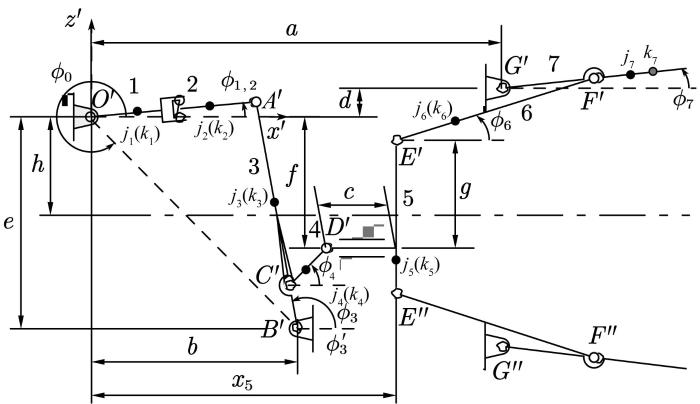
打开状态下的导向罩分为6瓣。由于6瓣导向叶片的运动规律一致，可将空间开合对接机构简化为平面机构，如图3所示。简化后开合对接机构是一种由降程机构O′A′B′和开合机构D′E′F′G′组成的7杆机构。杆1和2所示的液压缸部件推动降程杆3；在降程机构的作用下，液压缸200 mm长的行程经杆4输出推程；推板滑块5的短程位移经推杆6推动导向罩7张开，满行程下对称导向罩的最大张角约为34°。液压缸回程，则导向罩合拢。

如图3所示，建立机构的基准坐标系O′-x′z′。把各构件当作杆矢量，构建开合对接机构闭环O′A′B′、B′C′D′、E′FG′的角位移方程组，并按坐标系分量形式展开，可得：

式中：x_O′A′为机构的输入位移；x₅为推板滑块的位移；l为各杆件的长度，l₃=A′B′， l₃′=B′C′， l₄=C′D′， l₆=E′F′， l₇=G′F′； ϕ_i （i=1， 2， 3， 4， 6， 7）为各杆件的角位移大小，规定各杆件绕其旋转轴逆时针旋转的方向为正，杆件与x′向的夹角即为各杆件的角位移大小，其中ϕ₁=ϕ₂，ϕ₃′=ϕ₃-C₀，C₀=23.062°；a、b、c、d、e、f、g、h为各机架的长度。

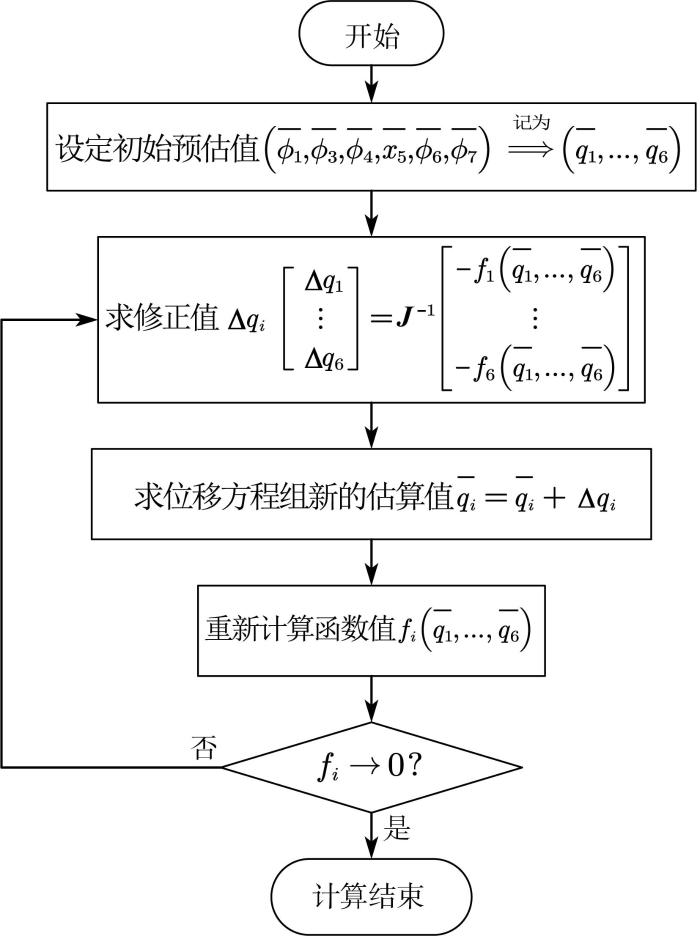
式（1）是一个非线性超越方程组，很难直接求出其解析解，故采用牛顿‒辛普森数值算法对其进行数值迭代求解^［12］。牛顿‒辛普森数值算法如图4所示。

将式（1）记为：

则可得方程组雅可比矩阵为：

式中：

利用MATLAB软件按照上述算法的流程不断迭代，可以获得开合对接机构各杆件的角位移变化曲线。

将接驳装置分为运动部件、非运动部件和配重部件三类，分别计算各部件的重浮力，叠加后可以获得接驳装置整体的重浮力。为了方便配重优化设计，首先分析配重前在导向罩开合过程中接驳装置的重浮心位移。以接驳装置首部中心O为原点，建立随体坐标系O-xyz，如图2中所示。其中，x轴的方向为沿装置中轴线指向前方，z轴与接驳装置纵中剖面重合且垂直于x轴向下，y轴方向满足右手定则，图中未标注。

接驳装置的运动部件主要包括开合对接机构的活动构件。各活动构件的质心和浮心分别记为j_i 、k_i （i=1，…，7），如图3所示。在基准坐标系O′-x′z′下，开合对接机构运动部件的质心矢量和浮心矢量分别为 rj'、rk'，那么在随体坐标系O-xyz下运动部件质心矢量 r_GJ和浮心矢量 r_BJ分别为：

式中： r_O′ 为机构基准坐标系原点在O-xyz中的位置向量； rji'、 rki'分别为各杆在O′-x′z′中的质心位置矢量和浮心位置矢量，其中，杆1至杆6均为均质实心材质，则 rji'= rki'_{（i=1， 2，…， 6），而导向罩存在空心结构，则 rj7'≠ rk7'；mi 、mbi 分别为各杆件的质量和排水质量；mJ、mBJ分别为接驳装置运动部件的质量和排水质量。}

记O'j1=r1,O'j2=r2,B'j3=r3,C'j4=r4,D'j5=r5,F'j6=r6,G'j7=r7,G'k7=r7'。考虑机构实际的结构分布，推杆6和导向罩7关于图3中的中心线圆周均布，数量为6，合算后实际质浮心的x′坐标为 rj6'、 rj7'和 rk7'的实部，即对应矢量关于x′轴的投影。z′坐标落在图3所示的机构中心线上，即z′坐标为-h。那么，开合对接机构各杆件质浮心位置在基准坐标系O′-x′z′下的坐标分量可以表示为：

将式（5）代入式（4），可以得到接驳装置运动部件的质浮心位置。

接驳装置非运动部件主要包括电控舱部件、框架、阀块、稳定翼和装置外挂的传感器设备等。借助三维设计软件，定义好接驳装置各零件的几何物理参数，可以获得O-xyz中接驳装置非运动部件的质浮心位置矢量 r_Gfix和 r_Bfix，以及非运动部件的质量m_fix和排水质量m_Bfix。

接驳装置配重部件的重浮力是主要的设计参数，将在下一节通过定义的配重优化设计变量进行详细描述。

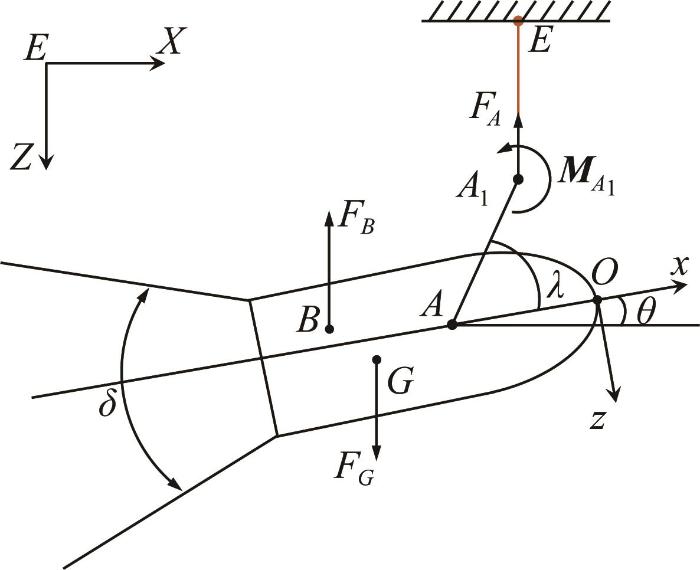
由于接驳装置整体结构关于纵垂面xOz对称，质浮心y向的坐标值非常小，可以将悬浮静平衡分析转化为平面力系分析。接驳装置悬浮平衡受力分析如图5所示。图中，拖架AA₁与装置框架铰接于A，系泊缆绳分别栓于拖点A₁和水面静止结构物上E点。当拖架角固定时，接驳装置整体的实际拖点A₁与理论拖点重合；当拖架与装置主体为自由铰接状态时，接驳装置系泊悬浮理论拖点近似为A点，等价于拖架AA₁的长度为0。

设在O-xyz中拖点A₁的位置矢量 r_A1=（x_A1， 0， z _A1）^T，铰接点A的位置矢量 r_A =（x_A， 0， 0）^T。记拖架长度为L_AA1，拖架角为λ，则 r_A1= r_A +（L_AA1cos λ， 0， - L_AA1sin λ）^T。重心G的位置矢量 r_G =（x_G， 0， z_G ）^T，浮心B 的位置矢量 r_B =（x_B， 0， z_B ）^T。设接驳装置重力为 F_G，方向垂直向下，大小F_G =mg，其中：m为接驳装置总质量，g为重力加速度，g=9.8 m/s²；浮力为 F_B，方向与重力方向相反，大小F_B =ρVg，其中：ρ为水的密度，ρ=1 000 kg/m³；V为接驳装置排水体积。那么，在静平衡状态下，系泊缆绳的张力FA=FG-FB，方向为大地坐标系E-XZ的负Z方向。接驳装置重力 F_G 在O-xyz下的矢量形式为：

式中：ROE-1为随体坐标系旋转变换矩阵ROE的逆矩阵；θ为接驳装置悬浮平衡纵倾角，即x向与X向的夹角，规定抬艏为正，埋艏为负。同理可得浮力 F_B 在O-xyz下的矢量形式为：

于是，接驳装置重力对A₁点的力矩向量 τ_G 和浮力对A₁点的力矩向量 τ_B 可以分别表示为：

由此，可以得到接驳装置水下悬浮静平衡方程为：

求解式（10），可以得到接驳装置悬浮平衡纵倾角与重浮力大小、质浮心位置以及拖点位置之间的关系。

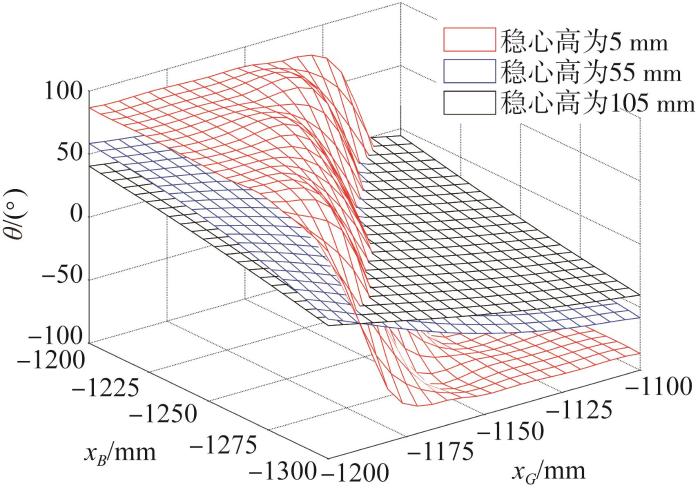
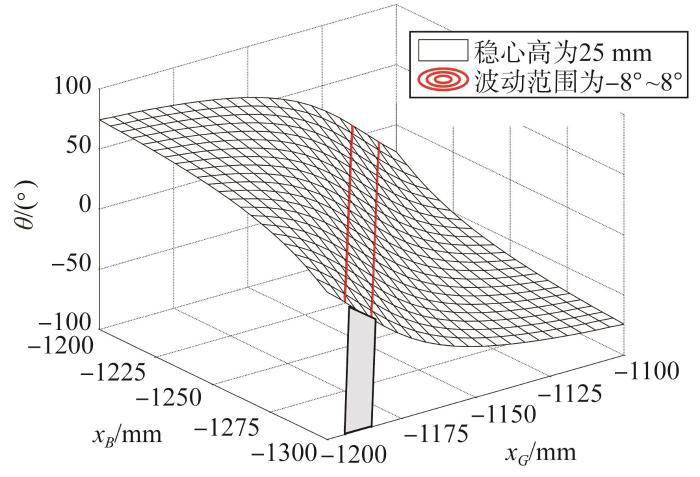
为了更好地建立配重优化模型，根据按经验配重后接驳装置质量m=371 kg及其排水质量m_B=293 kg，来分析稳心高和拖点位置对悬浮平衡纵倾角的影响。当x_A =-770 mm，在自由拖架工况下，重浮心位置与悬浮平衡纵倾角的关系如图6所示。由图可知，稳心高越大，θ关于质浮心x向坐标的响应曲面越平缓。也就是说，在单点系泊悬浮工况下，接驳装置的稳心高越大，允许质浮心x向的变动范围越大，接驳装置运动部件动作带来的扰动影响就越小。重浮心相对位置变动可行域如图7所示。考虑在接驳装置单点系泊悬浮过程中θ的波动范围为-8°~8°，对应图7可以得到，当接驳装置稳心高为25 mm时，等高线所截曲面的投影区域为重浮心相对位置变动可行域，当重浮心位置超出该区域时，接驳装置的纵倾波动过大。在该工况下，接驳装置浮力臂变动可行域在0~8.8 mm范围内，与开合机构动作导致的重浮心变化在同一量级。因此，在配重优化设计时装置稳心高应大于25 mm。

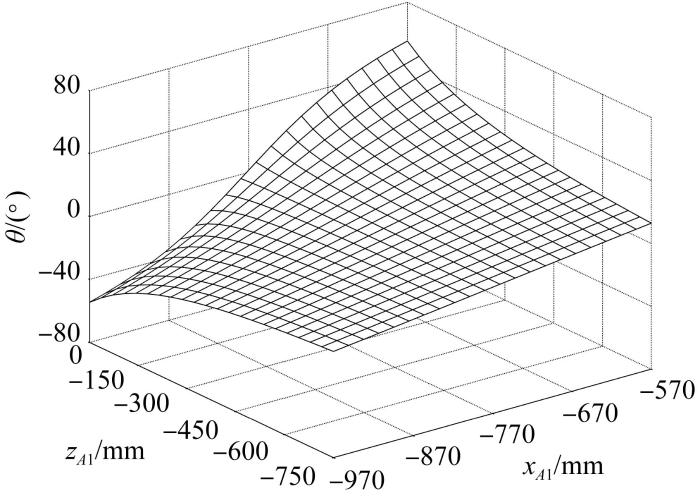
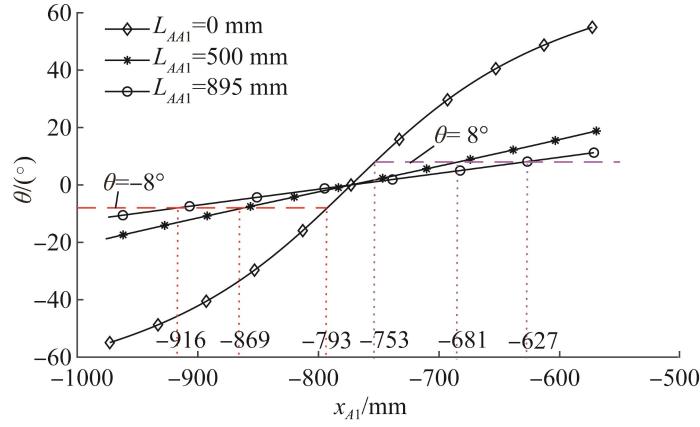
对于拖点可调的情况，假设接驳装置质心的位置矢量 r_G =（-1 162 mm， 0 mm， 21 mm）^T，浮心的位置矢量 r_B =（-1 265 mm， 0 mm， -11 mm）^T，则拖点位置与悬浮平衡纵倾角的关系如图8所示。由图可知：当x_A1≈-773 mm时，接驳装置处于θ = 0°的理想平衡状态，此时z_A1的变化基本不对θ造成影响；随着x_A1向-773 mm的两侧偏移，在不同z_A1下，θ有不同幅度的变化：z_A1的绝对值越大，θ变化越平缓，并逐渐趋于线性缓慢变化。由此可见，采用固定拖架方式，适当加大接驳装置拖架的长度，对单点系泊接驳装置的悬浮静平衡是极为有利的。拖架长度对悬浮平衡纵倾角的影响如图9所示。图9中：L_AA1=0 mm时的曲线表示在自由拖架工况下拖架铰接在不同位置时所对应的θ；L_AA1=500 mm和L_AA1=895 mm时的曲线表示在固定拖架工况下长度为500 mm和895 mm的拖架在不同x_A1时所对应的θ。由图可得，在θ的波动范围为-8°~8°的设计要求下，L_AA1越大，所允许的x_A1的变化范围越大，其中，在自由拖架工况下x_A1允许设计裕度仅为［-793， -753］ mm。因此，下文仅针对采用可调固定拖架形式的接驳系统展开配重优化设计。

结合上述接驳装置悬浮静平衡分析，接驳装置的配重优化有如下设计要求：在有限的设计空间内，在开合机构动作过程中接驳装置悬浮平衡纵倾角的波动幅值和装置总质量尽可能小，θ在-8°~8°范围内波动，稳心高大于25 mm。

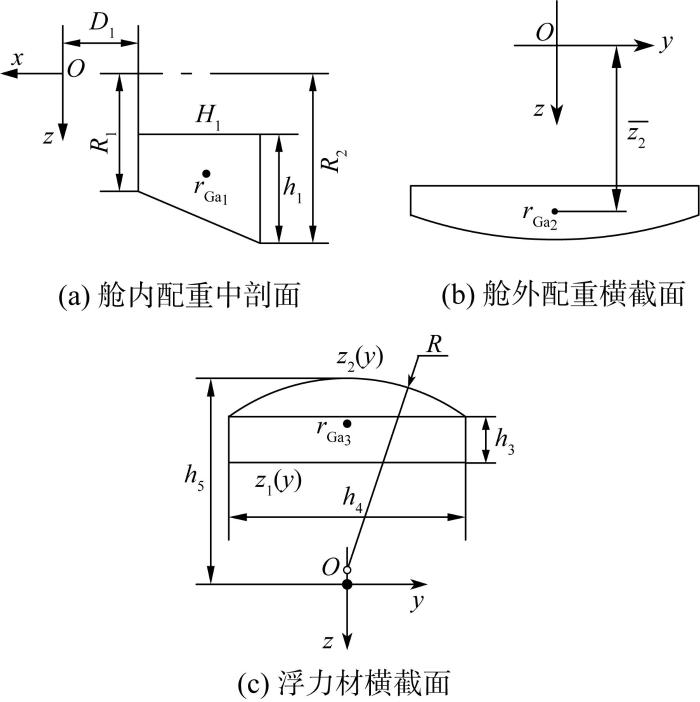
接驳装置的配重部件分为舱内配重、舱外配重和浮力材，其特征截面如图10所示。

设计舱内配重的目的是平衡电控舱浮力，使接驳装置的重心大幅前移。为了方便装配和固定，将舱内配重设计为一横切圆台。如图10（a）所示：圆台的顶圆半径为R₁，底圆半径为R₂，高为H₁，在O-xyz中的定位尺寸为D₁； h₁为横切定位量，为设计变量。记舱内配重质心的位置矢量rGa1=x1¯,0,z1¯^T。因处于密封舱中，无须计算其浮心位置。

舱外配重和浮力材的形状均为拉伸体，且沿xOz面对称布置，其横截面积分别记为S₂和S₃。记舱外配重z向坐标为z2¯，其拉伸长度h₂为设计变量，用于配置接驳装置质浮心的x向坐标，其质浮心位置相同，记为rGa2=x2¯,0,z2¯^T。

浮力材的质浮心位置也相同，记为rGa3=x3¯,0,z3¯^T，其拉伸长度为H₂，横截面为由曲线z₁（y）、z₂（y）围成的曲边梯形。其中z₂（y）为一圆心为 （0， R-h₅）、半径R的圆弧，z₁（y）为一平行于y向的直线。

为方便计算，采用三次多项式来拟合舱内配重质量m_a1及其质心位置矢量 r_Ga1关于设计变量h₁的函数：

舱外配重质量m_a2、排水质量m_Ba2及其质浮心位置矢量 r_Ga2可以表示为：

浮力材质量m_a3、排水质量m_Ba3及其质浮心位置矢量 r_Ga3可以表示为：

式（12）和式（13）中：ρ₁、ρ₂、ρ₃分别为配重铅块、水和浮力材的密度；D为浮力材横截面区域。

浮力材横截面区域的面积S₃为：

联立式（11）至式（13），通过计算可得配重部件质量m_a、排水质量m_Ba、质心位置矢量 r_Ga和浮心位置矢量 r_Ba分别为：

依据实际情况，拖架的铰接点A为固定点，x_A =-781 mm，取拖架长度L_AA1=895 mm，则 r_A1可以用拖架角λ单独表示。

综上，汇总接驳装置配重优化设计变量，记为 h =［h₁， h₂， h₃， h₄， h₅， λ］^T。

配重后接驳装置总质量m、排水质量m_B和质心位置矢量 r_G和浮心位置矢量 r_B分别为：

由于接驳装置的设计空间有限，配重部件各特征截面尺寸均有上下限，同时，为了发挥拖点调节机构在单点系泊悬浮对接过程中调节接驳装置悬浮平衡纵倾角的作用，要求：0°≤λ≤95°；质心、浮心、拖点的相对位置满足x_{A> xG > xB，稳心高zGB= zG- zB≥25 mm；θ的波动范围为-8°~8°。}

针对单点系泊悬浮接驳装置的设计要求，接驳装置配重优化问题可以描述为：在满足约束条件的设计空间内搜索合适的1组或多组设计变量 h，使得在开合机构动作过程中接驳装置悬浮平衡纵倾角波动幅值θ_v和装置总质量m最小。联立式（1）、（4）、（5）和（10）可求得一组不同导向罩张角δ所对应的θ（δ），该数组的最大元素与最小元素之差即为θ_v。

求解多目标优化设计问题的方法有多种，如约束法、分层序列法、评价函数法和Pareto方法等^［13］。将m作为主要优化目标，θ_v作为次要优化目标，采用约束法将次要优化目标转换为优化问题的约束条件，可将配重优化多目标问题转化为单目标优化问题。则接驳装置配重优化数学模型可以表示为：

式中：c₁、c₂分别为θ和θ_v的约束控制常数，均大于0°，可以根据实际求解结果将其调小以作加强约束处理。

式（16）是一个有约束非线性规划问题。MATLAB最优化工具箱提供了强大的非线性规划搜索算法，不过其求解结果对最优化搜索的初值有很大的依赖性^［14］。经过实际调试，当初值差异大时，直接采用序列二次规划（sequential quadratic programming， SQP）方法或者内点法来求出不同的局部最优解。

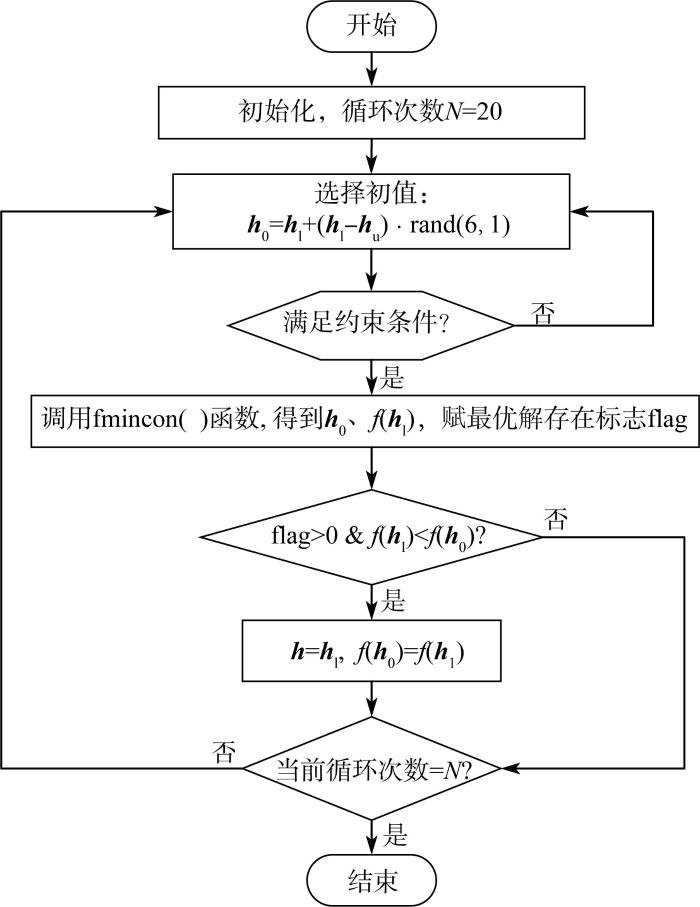
为避免出现局部最小值问题，采用图11所示的求解流程对式（16）所示优化问题作全局寻优。用随机的方式在变量上下限约束区域（ h_l， h_u）选择初值，并预先判定初值是否满足其他非线性约束条件，如果满足，通过调用fmincon （ ）函数并采用SQP优化算法得到候选最优解 h₁及其目标函数值f（ h₁），如果得出的最优目标值比已经得到的小，则记录该最优值。重复20次求解过程，则得出原始问题的全局最优解。

配重优化前后设计变量值和目标值如表1所示。

通过试配法得到在自由铰接拖架工况下导向罩处于打开状态且接驳装置悬浮平衡纵倾角趋于0°时的初始设计值 h₀=［210 mm， 200 mm， 60 mm， 260 mm， 310 mm， 90°］。对于拖架处于自由铰接状态的接驳装置，开合机构动作导致θ从-7.37°变化到0.124 7°，变化幅值较大。当拖架受到拖点调节机构控制时，在同样的初始设计值下，θ的变化幅值可减小至0.493 7°。这再次说明，可调固定拖架形式非常有利于接驳装置悬浮平衡纵倾角的稳定。

加入对接驳装置悬浮平衡纵倾角的要求，取c₁=1°， c₂=0.5°，可以获得优化配重后的设计参数，取整后得 h₁=［178 mm， 213 mm， 130 mm， 320 mm， 380 mm， 95°］，对应的接驳装置总质量m=357.935 5 kg，θ的波动范围为（0.110 7°， 0.785 9°），稳心高约为25 mm。相比试配法得到的经验设计，m约减小13.4 kg，θ_v约减小90.68%，稳心高约增加7.63 mm。对比设计参数和配重优化后设计参数上限值可知，为满足优化设计要求，浮力材设计参数h₃、h₅均已取到上限。这说明，在设计时，要适当留足浮力材配重空间，有利于满足配重优化设计要求。

为了验证单点系泊静力平衡模型的准确性，并在一定程度上反映优化后设计变量的合理性，对配重优化后的接驳装置进行单点系泊悬浮实验。实验现场如图12所示，图中字母的标注同图5。实验所用的水池长为20 m，宽为10 m，深为10 m。接驳装置系泊在静止拖车桁架E点，系泊缆绳长约为6 m，没入水中的部分长约为2 m。接驳装置的运动数据由PHINS6000惯组陀螺仪模块采集，频率为5 Hz，拖架角λ由磁感应角位移霍尔传感器监测。实验中以“三摇三荡”的形式描述接驳装置在水中的悬浮位姿。“三摇”分别指纵倾、横摇和艏摇，即接驳装置分别在随体坐标系中绕y、x、z轴的转动；“三荡”分别指纵荡、横荡和垂荡，即接驳装置分别在随体坐标系中沿x、y、z轴的平动。

经悬吊称重，接驳装置的质量为361 kg，利用悬吊法测得x_G ≈-1 150 mm；接驳装置在水中的质量约为71 kg。实际测得的接驳装置的质量、重心位置、接驳装置在水中的质量与理论值的相对误差分别为0.85%、2.67%、9.87%，均在工程设计允许的误差范围内。

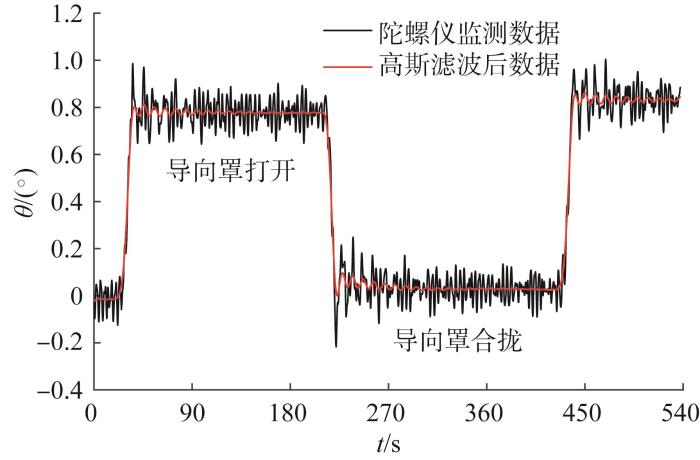
当λ=95°时导向罩动作对悬浮平衡纵倾角的影响如图13所示。由图可知，导向罩从合拢到打开，接驳装置略微抬艏，θ由0°逐渐增大到0.77°，与理论上的变化范围（0.110 7°， 0.785 9°）大致吻合。根据经验可知，在对接过程中约0.8°的纵倾摆动对接驳基本没有影响，因此可以忽略由开合机构动作引起的质浮心位置变化所导致的悬浮平衡纵倾角的变化。

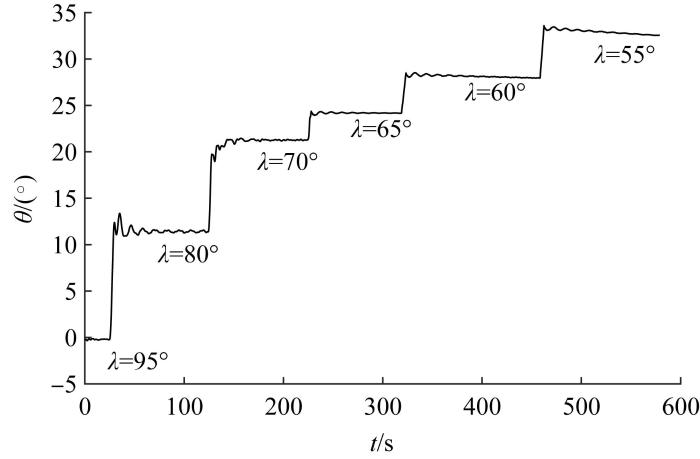
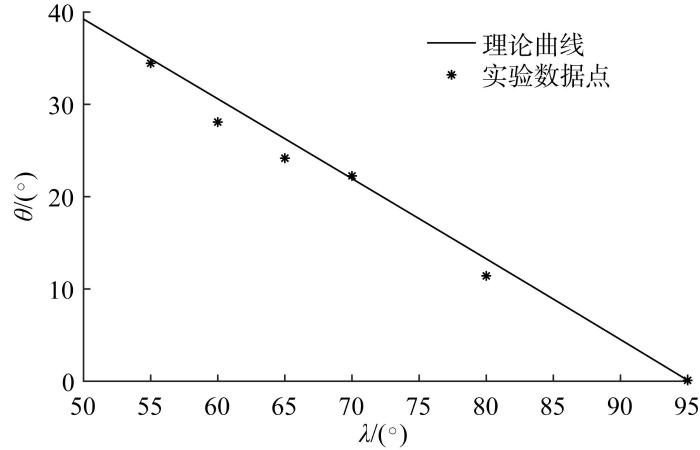
拖架位置对悬浮平衡纵倾角的影响如图14所示。拖架角λ分5个阶段从95°调整至55°，每次调整后，接驳装置均能在50 s左右的时间内调整至新的平衡状态。悬浮平衡纵倾角与拖架角的关系如图15所示。由图可知：θ与λ基本呈线性关系，实验数据点基本在理论曲线附近，实验结果与理论分析结果大致吻合。

本文设计了一种具有开合导向罩和拖点调节机构的AUV水下接驳装备。通过开合对接机构位移分析和接驳装置质浮心计算，结合接驳装备水下悬浮静平衡分析，建立了装备重心、浮心和拖点的相对位置与悬浮平衡纵倾角之间的数学模型。着重分析了拖点位置和稳心高对悬浮平衡纵倾角的影响。基于此模型，结合接驳装置设计要求，为使接驳装置悬浮平衡纵倾角及其波动幅值尽可能小，且接驳装置配重后质量最小，建立了接驳装置配重优化数学模型，并通过非线性规划方法进行模型求解，对配重铅块、浮力材的特征尺寸和拖点位置等配重参数进行优化设计。最后，通过接驳装置单点系泊悬浮实验，验证了悬浮平衡模型的正确性和优化设计结果的准确性。配重优化模型的建立，有利于快速且灵活地针对具体工况展开接驳装置的配重设计。通过AUV接驳装置悬浮平衡分析与配置优化设计，得出如下结论：

1） 通过悬浮平衡分析可知，对于负浮力拖体，稳心高越大，越有利于悬浮平衡。然而稳心高的微小增大会大大增大装置的整体质量，且10 mm左右稳心高的增大对减小悬浮平衡纵倾角的效果并不显著，所以，单点系泊悬浮接驳装置选择合适的稳心高即可。

2） 相比于增大稳心高来增强悬浮接驳装置的稳定性，增大理论拖点与质心的垂向距离是一种更为有效且经济的办法。通过拖点调节机构增大拖架的长度，有利于大幅度减小接驳装置悬浮平衡残余纵倾角，增强装置悬浮平衡的稳定性。

3） 基于配重优化模型，可以根据实际工况合理配置约束条件，快速完成对配重铅块、浮力材的特征尺寸和拖点位置等配重参数的优化设计。

4） 理论分析和实验表明，合理的重心、浮心和拖点位置的配置能够减小开合对接机构动作对悬浮平衡纵倾角的影响。相比经验配重设计，优化配重设计后，接驳装置总质量减小约13.4 kg，平衡悬浮纵倾角的波动值约减小90.68%，稳心高约增加7.63 mm。

5） 所设计的单点系泊悬浮接驳装置的平衡悬浮纵倾角与拖架角基本呈线性关系，可以通过控制拖点位置实现对纵倾角的快速调节。