[1]
GRIGORESCU S, TRASNEA B, COCIAS T, et al A survey of deep learning techniques for autonomous driving
[J]. Journal of Field Robotics , 2020 , 37 (3 ): 362 - 386
DOI:10.1002/rob.21918
[本文引用: 1]
[2]
陈文强, 王东丹, 朱文英, 等 基于时空图注意力网络的车辆多模态轨迹预测模型
[J]. 浙江大学学报: 工学版 , 2025 , 59 (3 ): 443 - 450
[本文引用: 2]
CHEN Wenqiang, WANG Dongdan, ZHU Wenying, et al Vehicle multimodal trajectory prediction model based on spatiotemporal graph attention network
[J]. Journal of Zhejiang University: Engineering Science , 2025 , 59 (3 ): 443 - 450
[本文引用: 2]
[3]
LEFÈVRE S, VASQUEZ D, LAUGIER C A survey on motion prediction and risk assessment for intelligent vehicles
[J]. ROBOMECH Journal , 2014 , 1 (1 ): 1
[本文引用: 1]
[4]
LEFKOPOULOS V, MENNER M, DOMAHIDI A, et al Interaction-aware motion prediction for autonomous driving: a multiple model Kalman filtering scheme
[J]. IEEE Robotics and Automation Letters , 2021 , 6 (1 ): 80 - 87
DOI:10.1109/LRA.2020.3032079
[本文引用: 1]
[5]
WANG Y, WANG C, ZHAO W, et al Decision-making and planning method for autonomous vehicles based on motivation and risk assessment
[J]. IEEE Transactions on Vehicular Technology , 2021 , 70 (1 ): 107 - 120
DOI:10.1109/TVT.2021.3049794
[本文引用: 1]
[6]
LI J, DAI B, LI X, et al A dynamic Bayesian network for vehicle maneuver prediction in highway driving scenarios: framework and verification
[J]. Electronics , 2019 , 8 (1 ): 40
DOI:10.3390/electronics8010040
[本文引用: 1]
[7]
STREUBEL T, HOFFMANN K H. Prediction of driver intended path at intersections [C]//Proceedings of the IEEE Intelligent Vehicles Symposium . [S. l. ]: IEEE, 2014: 134−139.
[本文引用: 1]
[8]
TRAN Q, FIRL J. Online maneuver recognition and multimodal trajectory prediction for intersection assistance using non-parametric regression [C]//2014 IEEE Intelligent Vehicles Symposium . Dearborn: IEEE, 2014: 118−123.
[本文引用: 1]
[9]
SCHREIER M, WILLERT V, ADAMY J. Bayesian, maneuver-based, long-term trajectory prediction and criticality assessment for driver assistance systems [C]//Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems . Qingdao: IEEE, 2014: 334–341.
[本文引用: 1]
[10]
REN Y Y, ZHAO L, ZHENG X L, et al A method for predicting diverse lane-changing trajectories of surrounding vehicles based on early detection of lane change
[J]. IEEE Access , 2022 , 10 : 17451 - 17472
[本文引用: 1]
[11]
LI J, MA H, ZHAN W, et al. Generic probabilistic interactive situation recognition and prediction: from virtual to real [C]//Proceedings of the 21st International Conference on Intelligent Transportation Systems . Maui: IEEE, 2018: 3218–3224.
[本文引用: 1]
[12]
DEO N, TRIVEDI M M. Convolutional social pooling for vehicle trajectory prediction [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops . Salt Lake City: IEEE, 2018: 1549–15498.
[本文引用: 5]
[13]
GUPTA A, JOHNSON J, LI F F, et al. Social GAN: socially acceptable trajectories with generative adversarial networks [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 2255–2264.
[本文引用: 1]
[14]
ZHAO T, XU Y, MONFORT M, et al. Multi-agent tensor fusion for contextual trajectory prediction [C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2020: 12118–12126.
[本文引用: 2]
[15]
LI X, YING X, CHUAH M C. GRIP: graph-based interaction-aware trajectory prediction [C]//Proceedings of the IEEE Intelligent Transportation Systems Conference . Auckland: IEEE, 2019: 3960–3966.
[本文引用: 3]
[16]
ZHANG K, ZHAO L, DONG C, et al AI-TP: attention-based interaction-aware trajectory prediction for autonomous driving
[J]. IEEE Transactions on Intelligent Vehicles , 2023 , 8 (1 ): 73 - 83
[本文引用: 1]
[17]
MO X, XING Y, LV C. Graph and recurrent neural network-based vehicle trajectory prediction for highway driving [C]//Proceedings of the IEEE International Intelligent Transportation Systems Conference . Indianapolis: IEEE, 2021: 1934−1939.
[本文引用: 1]
[18]
HELBING D, MOLNÁR P Social force model for pedestrian dynamics
[J]. Physical Review E , 1995 , 51 (5 ): 4282 - 4286
[本文引用: 1]
[19]
ALAHI A, GOEL K, RAMANATHAN V, et al. Social LSTM: human trajectory prediction in crowded spaces [C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 961–971.
[本文引用: 1]
[20]
MESSAOUD K, YAHIAOUI I, VERROUST-BLONDET A, et al Attention based vehicle trajectory prediction
[J]. IEEE Transactions on Intelligent Vehicles , 2021 , 6 (1 ): 175 - 185
DOI:10.1109/TIV.2020.2991952
[本文引用: 2]
[21]
LIN L, LI W, BI H, et al Vehicle trajectory prediction using LSTMs with spatial–temporal attention mechanisms
[J]. IEEE Intelligent Transportation Systems Magazine , 2022 , 14 (2 ): 197 - 208
DOI:10.1109/MITS.2021.3049404
[本文引用: 1]
[22]
GUO H, MENG Q, CAO D, et al Vehicle trajectory prediction method coupled with ego vehicle motion trend under dual attention mechanism
[J]. IEEE Transactions on Instrumentation and Measurement , 2022 , 71 : 2507516
[本文引用: 1]
[23]
LI C, LIU Z, YANG N, et al Regional attention network with data-driven modal representation for multimodal trajectory prediction
[J]. Expert Systems with Applications , 2023 , 232 : 120808
[本文引用: 1]
[24]
CHEN X, ZHANG H, ZHAO F, et al Intention-aware vehicle trajectory prediction based on spatial-temporal dynamic attention network for Internet of vehicles
[J]. IEEE Transactions on Intelligent Transportation Systems , 2022 , 23 (10 ): 19471 - 19483
DOI:10.1109/TITS.2022.3170551
[本文引用: 2]
[25]
DIEHL F, BRUNNER T, LE M T, et al. Graph neural networks for modelling traffic participant interaction [C]//Proceedings of the IEEE Intelligent Vehicles Symposium . Paris: IEEE, 2019: 695–701.
[本文引用: 2]
[26]
CHEN H. STGCN for modeling vehicle trajectory in highway scenario [C]//Proceedings of the 5th International Conference on Mechanical, Control and Computer Engineering . Harbin: IEEE, 2020: 1115−1118.
[本文引用: 1]
[27]
SHENG Z, XU Y, XUE S, et al Graph-based spatial-temporal convolutional network for vehicle trajectory prediction in autonomous driving
[J]. IEEE Transactions on Intelligent Transportation Systems , 2022 , 23 (10 ): 17654 - 17665
DOI:10.1109/TITS.2022.3155749
[本文引用: 3]
[28]
LI F J, ZHANG C Y, PHILIP CHEN C L STS-DGNN: vehicle trajectory prediction via dynamic graph neural network with spatial–temporal synchronization
[J]. IEEE Transactions on Instrumentation and Measurement , 2023 , 72 : 2525413
[本文引用: 3]
[29]
VASWANI A, SHAZEER N, PARMAR N, et al Attention is all you need
[J]. Advances in Neural Information Processing Systems , 2017 , 30 : 5998 - 6008
[本文引用: 3]
[30]
QUINTANAR A, FERNÁNDEZ-LLORCA D, PARRA I, et al. Predicting vehicles trajectories in urban scenarios with transformer networks and augmented information [C]//Proceedings of the IEEE Intelligent Vehicles Symposium . Nagoya: IEEE, 2021: 1051–1056.
[本文引用: 2]
[31]
GENG M, LI J, XIA Y, et al A physics-informed Transformer model for vehicle trajectory prediction on highways
[J]. Transportation Research Part C: Emerging Technologies , 2023 , 154 : 104272
DOI:10.1016/j.trc.2023.104272
[本文引用: 1]
[32]
GAO K, LI X, CHEN B, et al Dual transformer based prediction for lane change intentions and trajectories in mixed traffic environment
[J]. IEEE Transactions on Intelligent Transportation Systems , 2023 , 24 (6 ): 6203 - 6216
DOI:10.1109/TITS.2023.3248842
[本文引用: 1]
[33]
CHEN X, ZHANG H, ZHAO F, et al Vehicle trajectory prediction based on intention-aware non-autoregressive transformer with multi-attention learning for Internet of vehicles
[J]. IEEE Transactions on Instrumentation and Measurement , 2022 , 71 : 2513912
[本文引用: 2]
[34]
XU D, SHANG X, LIU Y, et al Group vehicle trajectory prediction with global spatio-temporal graph
[J]. IEEE Transactions on Intelligent Vehicles , 2023 , 8 (2 ): 1219 - 1229
DOI:10.1109/TIV.2022.3200338
[本文引用: 1]
[35]
徐东伟, 程千兵, 顾同成, 等 基于时空交互特征融合的车辆轨迹预测方法研究
[J]. 中国公路学报 , 2025 , 38 (11 ): 447 - 458
[本文引用: 1]
XU Dongwei, CHENG Qianbing, GU Tongcheng, et al Research on vehicle trajectory prediction method based on spatio-temporal interaction feature fusion
[J]. China Journal of Highway and Transport , 2025 , 38 (11 ): 447 - 458
[本文引用: 1]
[36]
CHEN C, CHEN X, GUO C, et al Trajectory prediction for autonomous driving based on structural informer method
[J]. IEEE Transactions on Automation Science and Engineering , 2025 , 22 : 17452 - 17463
[本文引用: 2]
[37]
WANG W, CHEN W, QIU Q, et al CrossFormer: a versatile vision transformer hinging on cross-scale attention
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2023 , 45 (8 ): 10260 - 10276
[本文引用: 2]
[38]
WANG J, WU J, ZHENG X, et al Driving safety field theory modeling and its application in pre-collision warning system
[J]. Transportation Research Part C: Emerging Technologies , 2016 , 72 : 306 - 324
DOI:10.1016/j.trc.2016.10.003
[本文引用: 1]
[39]
MA H, AN B, LI L, et al Anisotropy safety potential field model under intelligent and connected vehicle environment and its application in car-following modeling
[J]. Journal of Intelligent and Connected Vehicles , 2023 , 6 (2 ): 79 - 90
DOI:10.26599/JICV.2023.9210006
[本文引用: 1]
[40]
袁阳阳. 基于近似模型的汽车尾部结构减阻优化 [D]. 重庆: 重庆交通大学, 2018.
YUAN Yangyang. Drag reduction optimization of vehicle rear structure based on approximate model [D]. Chongqing: Chongqing Jiaotong University, 2018.
[41]
李文中, 王立, 李振兴, 等 不同尺寸车身轻量化评价及重量目标设定
[J]. 汽车实用技术 , 2020 , 45 (19 ): 122 - 124
DOI:10.16638/j.cnki.1671-7988.2020.19.039
[本文引用: 1]
LI Wenzhong, WANG Li, LI Zhenxing, et al BIW lightweight evaluation and weight target setting method for different size vehicle
[J]. Automobile Applied Technology , 2020 , 45 (19 ): 122 - 124
DOI:10.16638/j.cnki.1671-7988.2020.19.039
[本文引用: 1]
[42]
WOLF M T, BURDICK J W. Artificial potential functions for highway driving with collision avoidance [C]//Proceedings of the IEEE International Conference on Robotics and Automation . Pasadena: IEEE, 2008: 3731–3736.
[本文引用: 1]
[43]
LI L, GAN J, JI X, et al Dynamic driving risk potential field model under the connected and automated vehicles environment and its application in car-following modeling
[J]. IEEE Transactions on Intelligent Transportation Systems , 2022 , 23 (1 ): 122 - 141
DOI:10.1109/TITS.2020.3008284
[本文引用: 1]
[44]
LV P, WANG W, WANG Y, et al SSAGCN: social soft attention graph convolution network for pedestrian trajectory prediction
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2024 , 35 (9 ): 11989 - 12003
DOI:10.1109/TNNLS.2023.3250485
[本文引用: 1]
[45]
LIU Y, HU T, ZHANG H, et al. iTransformer: inverted transformers are effective for time series forecasting [EB/OL]. [2025−09−10]. https://arxiv.org/abs/2310.06625.
[本文引用: 2]
[46]
DAS A, KONG W, LEACH A, et al. Long−term forecasting with TiDE: time−series dense encoder [EB/OL]. [2025−09−10]. https://arxiv.org/abs/2304.08424.
[本文引用: 1]
A survey of deep learning techniques for autonomous driving
1
2020
... 随着汽车智能化水平从非自动驾驶(L0级)向辅助驾驶(L2级)和有条件自动驾驶(L3级)技术迈进,车辆轨迹预测作为自动驾驶的核心关键技术,对行车安全至关重要[1 -2 ] . 在混合交通环境中,驾驶员行为具有显著的不确定性和个性化特征,使得高精度、强泛化的车辆轨迹预测仍是一项极具挑战的课题. ...
基于时空图注意力网络的车辆多模态轨迹预测模型
2
2025
... 随着汽车智能化水平从非自动驾驶(L0级)向辅助驾驶(L2级)和有条件自动驾驶(L3级)技术迈进,车辆轨迹预测作为自动驾驶的核心关键技术,对行车安全至关重要[1 -2 ] . 在混合交通环境中,驾驶员行为具有显著的不确定性和个性化特征,使得高精度、强泛化的车辆轨迹预测仍是一项极具挑战的课题. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
基于时空图注意力网络的车辆多模态轨迹预测模型
2
2025
... 随着汽车智能化水平从非自动驾驶(L0级)向辅助驾驶(L2级)和有条件自动驾驶(L3级)技术迈进,车辆轨迹预测作为自动驾驶的核心关键技术,对行车安全至关重要[1 -2 ] . 在混合交通环境中,驾驶员行为具有显著的不确定性和个性化特征,使得高精度、强泛化的车辆轨迹预测仍是一项极具挑战的课题. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
A survey on motion prediction and risk assessment for intelligent vehicles
1
2014
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
Interaction-aware motion prediction for autonomous driving: a multiple model Kalman filtering scheme
1
2021
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
Decision-making and planning method for autonomous vehicles based on motivation and risk assessment
1
2021
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
A dynamic Bayesian network for vehicle maneuver prediction in highway driving scenarios: framework and verification
1
2019
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
1
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
1
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
1
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
A method for predicting diverse lane-changing trajectories of surrounding vehicles based on early detection of lane change
1
2022
... 为了准确地预测车辆轨迹,现有方法大致归为以下3类:基于物理模型的方法、基于机动意图的方法和基于时空感知的方法[3 ] . 基于物理模型的轨迹预测方法依赖严密的数学和统计基础,主要包括动力学模型、卡尔曼滤波器[4 ] 和马尔可夫模型[5 ] 等,但常忽略车辆与周围环境的时空交互,在长期轨迹预测中表现受限[6 ] . 基于机动意图的轨迹预测方法以行为推理为核心[7 ] ,通过高斯过程回归[8 ] 、贝叶斯网络[9 ] 和连续马尔可夫过程[10 ] 等技术对车辆的驾驶意图进行识别与分类,实现轨迹预测. ...
1
... 与上述2类方法相比,基于时空感知的模型因同时考虑时间依赖性与车辆间空间交互,在复杂场景中表现出更高的可靠性和鲁棒性[11 ] . 该类研究早期多采用递归神经网络(RNN)对车辆轨迹的时间动态进行建模,通过聚合隐藏状态,捕捉车辆之间基于位置的空间关系[12 -14 ] . 近年来,学者们逐步引入图神经网络(GNN)表征车辆间的拓扑结构,并在多个基准上取得了具有竞争力的性能[15 -17 ] . ...
5
... 与上述2类方法相比,基于时空感知的模型因同时考虑时间依赖性与车辆间空间交互,在复杂场景中表现出更高的可靠性和鲁棒性[11 ] . 该类研究早期多采用递归神经网络(RNN)对车辆轨迹的时间动态进行建模,通过聚合隐藏状态,捕捉车辆之间基于位置的空间关系[12 -14 ] . 近年来,学者们逐步引入图神经网络(GNN)表征车辆间的拓扑结构,并在多个基准上取得了具有竞争力的性能[15 -17 ] . ...
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
... 车辆轨迹预测可以表述为:基于已观测到的车辆历史轨迹,预测未来的运动状态. 与Gupta等[13 , 29 , 12 ] 针对单一车辆进行预测不同,本文提出并行预测框架,能够同时推断场景中所有相邻车辆的未来轨迹. 令$ X $
... 在数据划分方面,2个数据集均按7∶1∶2的比例划分为训练集、验证集和测试集. 每条轨迹被切分为时长为8 s的片段,其中前3 s作为历史观测轨迹,后5 s作为用于预测的未来轨迹真值. 为了保持对比的公平性,遵循Deo等[12 ] 的做法,对每个片段进行2倍降采样,最终的采样率为5帧/s. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
1
... 车辆轨迹预测可以表述为:基于已观测到的车辆历史轨迹,预测未来的运动状态. 与Gupta等[13 , 29 , 12 ] 针对单一车辆进行预测不同,本文提出并行预测框架,能够同时推断场景中所有相邻车辆的未来轨迹. 令$ X $
2
... 与上述2类方法相比,基于时空感知的模型因同时考虑时间依赖性与车辆间空间交互,在复杂场景中表现出更高的可靠性和鲁棒性[11 ] . 该类研究早期多采用递归神经网络(RNN)对车辆轨迹的时间动态进行建模,通过聚合隐藏状态,捕捉车辆之间基于位置的空间关系[12 -14 ] . 近年来,学者们逐步引入图神经网络(GNN)表征车辆间的拓扑结构,并在多个基准上取得了具有竞争力的性能[15 -17 ] . ...
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
3
... 与上述2类方法相比,基于时空感知的模型因同时考虑时间依赖性与车辆间空间交互,在复杂场景中表现出更高的可靠性和鲁棒性[11 ] . 该类研究早期多采用递归神经网络(RNN)对车辆轨迹的时间动态进行建模,通过聚合隐藏状态,捕捉车辆之间基于位置的空间关系[12 -14 ] . 近年来,学者们逐步引入图神经网络(GNN)表征车辆间的拓扑结构,并在多个基准上取得了具有竞争力的性能[15 -17 ] . ...
... 图神经网络(GNN)近年来被广泛应用于交通场景中车辆空间依赖关系的提取. 基于GNN的交互建模方法将交通场景构建为图结构,车辆及其相互作用关系被描述为节点和边,避免了池化操作或注意力机制将周围车辆视为整体而导致的噪声干扰[25 ] . Li等[15 ] 基于多图卷积网络(GCN)捕捉空间交互特征,引入LSTM编码器-解码器框架,实现多车轨迹的并行预测. 时空图卷积神经网络(STGCN)[26 ] 整合时域与空域卷积模块,协同提取车辆轨迹中的时空依赖特征. Zhang等[16 ] 结合图注意网络(GAT)与卷积门控循环单元(ConvGRU),实现对不同车辆间交互权重的差异化建模. Sheng等[27 ] 以车辆间欧式距离的倒数作为临近矩阵,构建GCN以区分车辆之间动态交互的影响. Li等[28 ] 依据车辆间的欧氏距离构建指数衰减权重作为GAT的邻接矩阵,通过结合门控循环单元和图神经网络来共同表征车辆动态交互行为. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
AI-TP: attention-based interaction-aware trajectory prediction for autonomous driving
1
2023
... 图神经网络(GNN)近年来被广泛应用于交通场景中车辆空间依赖关系的提取. 基于GNN的交互建模方法将交通场景构建为图结构,车辆及其相互作用关系被描述为节点和边,避免了池化操作或注意力机制将周围车辆视为整体而导致的噪声干扰[25 ] . Li等[15 ] 基于多图卷积网络(GCN)捕捉空间交互特征,引入LSTM编码器-解码器框架,实现多车轨迹的并行预测. 时空图卷积神经网络(STGCN)[26 ] 整合时域与空域卷积模块,协同提取车辆轨迹中的时空依赖特征. Zhang等[16 ] 结合图注意网络(GAT)与卷积门控循环单元(ConvGRU),实现对不同车辆间交互权重的差异化建模. Sheng等[27 ] 以车辆间欧式距离的倒数作为临近矩阵,构建GCN以区分车辆之间动态交互的影响. Li等[28 ] 依据车辆间的欧氏距离构建指数衰减权重作为GAT的邻接矩阵,通过结合门控循环单元和图神经网络来共同表征车辆动态交互行为. ...
1
... 与上述2类方法相比,基于时空感知的模型因同时考虑时间依赖性与车辆间空间交互,在复杂场景中表现出更高的可靠性和鲁棒性[11 ] . 该类研究早期多采用递归神经网络(RNN)对车辆轨迹的时间动态进行建模,通过聚合隐藏状态,捕捉车辆之间基于位置的空间关系[12 -14 ] . 近年来,学者们逐步引入图神经网络(GNN)表征车辆间的拓扑结构,并在多个基准上取得了具有竞争力的性能[15 -17 ] . ...
Social force model for pedestrian dynamics
1
1995
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
1
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
Attention based vehicle trajectory prediction
2
2021
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
Vehicle trajectory prediction using LSTMs with spatial–temporal attention mechanisms
1
2022
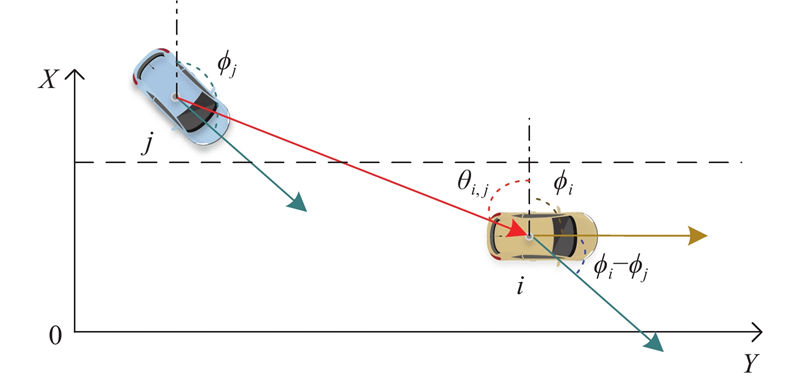
... 3)车辆之间的交互与运动方向高度相关[44 ] ,前车对后车的影响远远大于后车对前车的影响,而在变道时,目标车道上的车辆对变道车辆的影响更显著[21 ] . 如图3 所示,当车辆j 变道时,其受到目标车道前车i 的影响更大,而直行车辆i 受到变道车辆j 的影响较小. 利用车辆之间运动航向角的差值与车辆间距离角度的相似度,描述运动方向对车辆的交互影响. 利用车辆间纵向距离y 的差值表示车辆前、后的运动方向,修正车辆相对位置对交互的影响,如下所示: ...
Vehicle trajectory prediction method coupled with ego vehicle motion trend under dual attention mechanism
1
2022
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
Regional attention network with data-driven modal representation for multimodal trajectory prediction
1
2023
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
Intention-aware vehicle trajectory prediction based on spatial-temporal dynamic attention network for Internet of vehicles
2
2022
... 在空间交互建模方面,Helbing等[18 ] 提出社会力模型,通过排斥力和吸引力来建模行人及车辆之间的空间互动. 该模型依赖人工设计,难以灵活适用于多样化复杂的交通场景. 随着深度学习技术的发展,诸多基于神经网络的空间交互方法被提出. Alahi等[19 ] 提出Social-LSTM,通过社会池化操作整合行人之间的交互信息. Deo等[12 ] 引入卷积社会池化机制(CS-LSTM),增强车辆间交互的建模能力. Zhao等[14 ] 提出多智能体张量融合(multi-agent tensor fusion, MATF)网络,通过构建统一的空间张量表征车辆间的结构化空间关系. 此外,注意力机制被广泛应用于车辆空间交互建模. 部分研究将多头注意力机制融入基于LSTM的编码器-解码器框架中,以自适应捕捉周围车辆对目标车辆轨迹的影响[20 -22 ] . Li等[23 ] 利用卷积网络提取车辆特征,构建基于意图的区域注意力机制,实现不同交互区域内车辆特征的差异化聚合. Chen等[24 ] 提出双层注意力机制,能够在每个时间戳动态捕获车辆之间的动态交互,将提取的交互特征自适应地融合于多模态轨迹预测中. ...
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
2
... 图神经网络(GNN)近年来被广泛应用于交通场景中车辆空间依赖关系的提取. 基于GNN的交互建模方法将交通场景构建为图结构,车辆及其相互作用关系被描述为节点和边,避免了池化操作或注意力机制将周围车辆视为整体而导致的噪声干扰[25 ] . Li等[15 ] 基于多图卷积网络(GCN)捕捉空间交互特征,引入LSTM编码器-解码器框架,实现多车轨迹的并行预测. 时空图卷积神经网络(STGCN)[26 ] 整合时域与空域卷积模块,协同提取车辆轨迹中的时空依赖特征. Zhang等[16 ] 结合图注意网络(GAT)与卷积门控循环单元(ConvGRU),实现对不同车辆间交互权重的差异化建模. Sheng等[27 ] 以车辆间欧式距离的倒数作为临近矩阵,构建GCN以区分车辆之间动态交互的影响. Li等[28 ] 依据车辆间的欧氏距离构建指数衰减权重作为GAT的邻接矩阵,通过结合门控循环单元和图神经网络来共同表征车辆动态交互行为. ...
... 与以往transformer架构中引入位置编码的做法不同,本研究采用基于多层感知机(MLP)的前馈神经网络结构,对输入的变量的时间维度进行变换[25 , 46 ] . 该方法能够有效捕捉时间系列的中长期依赖关系,避免传统位置编码的归纳偏差. ...
1
... 图神经网络(GNN)近年来被广泛应用于交通场景中车辆空间依赖关系的提取. 基于GNN的交互建模方法将交通场景构建为图结构,车辆及其相互作用关系被描述为节点和边,避免了池化操作或注意力机制将周围车辆视为整体而导致的噪声干扰[25 ] . Li等[15 ] 基于多图卷积网络(GCN)捕捉空间交互特征,引入LSTM编码器-解码器框架,实现多车轨迹的并行预测. 时空图卷积神经网络(STGCN)[26 ] 整合时域与空域卷积模块,协同提取车辆轨迹中的时空依赖特征. Zhang等[16 ] 结合图注意网络(GAT)与卷积门控循环单元(ConvGRU),实现对不同车辆间交互权重的差异化建模. Sheng等[27 ] 以车辆间欧式距离的倒数作为临近矩阵,构建GCN以区分车辆之间动态交互的影响. Li等[28 ] 依据车辆间的欧氏距离构建指数衰减权重作为GAT的邻接矩阵,通过结合门控循环单元和图神经网络来共同表征车辆动态交互行为. ...
Graph-based spatial-temporal convolutional network for vehicle trajectory prediction in autonomous driving
3
2022
... 图神经网络(GNN)近年来被广泛应用于交通场景中车辆空间依赖关系的提取. 基于GNN的交互建模方法将交通场景构建为图结构,车辆及其相互作用关系被描述为节点和边,避免了池化操作或注意力机制将周围车辆视为整体而导致的噪声干扰[25 ] . Li等[15 ] 基于多图卷积网络(GCN)捕捉空间交互特征,引入LSTM编码器-解码器框架,实现多车轨迹的并行预测. 时空图卷积神经网络(STGCN)[26 ] 整合时域与空域卷积模块,协同提取车辆轨迹中的时空依赖特征. Zhang等[16 ] 结合图注意网络(GAT)与卷积门控循环单元(ConvGRU),实现对不同车辆间交互权重的差异化建模. Sheng等[27 ] 以车辆间欧式距离的倒数作为临近矩阵,构建GCN以区分车辆之间动态交互的影响. Li等[28 ] 依据车辆间的欧氏距离构建指数衰减权重作为GAT的邻接矩阵,通过结合门控循环单元和图神经网络来共同表征车辆动态交互行为. ...
... 2)Sheng等[27 -28 ] 利用车辆间欧式距离的倒数表示距离与风险的负相关关系. 在实际驾驶中,车辆通常会在自己的车道上与前车保持较远的距离,但可能会相对靠近车道边界处的障碍物[42 ] . 为了更准确地描述车辆从不同角度接近目标车辆时的风险水平,引入等效距离[43 ] 的概念,对真实空间中的距离进行改变,如下所示: ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
STS-DGNN: vehicle trajectory prediction via dynamic graph neural network with spatial–temporal synchronization
3
2023
... 图神经网络(GNN)近年来被广泛应用于交通场景中车辆空间依赖关系的提取. 基于GNN的交互建模方法将交通场景构建为图结构,车辆及其相互作用关系被描述为节点和边,避免了池化操作或注意力机制将周围车辆视为整体而导致的噪声干扰[25 ] . Li等[15 ] 基于多图卷积网络(GCN)捕捉空间交互特征,引入LSTM编码器-解码器框架,实现多车轨迹的并行预测. 时空图卷积神经网络(STGCN)[26 ] 整合时域与空域卷积模块,协同提取车辆轨迹中的时空依赖特征. Zhang等[16 ] 结合图注意网络(GAT)与卷积门控循环单元(ConvGRU),实现对不同车辆间交互权重的差异化建模. Sheng等[27 ] 以车辆间欧式距离的倒数作为临近矩阵,构建GCN以区分车辆之间动态交互的影响. Li等[28 ] 依据车辆间的欧氏距离构建指数衰减权重作为GAT的邻接矩阵,通过结合门控循环单元和图神经网络来共同表征车辆动态交互行为. ...
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
... 2)Sheng等[27 -28 ] 利用车辆间欧式距离的倒数表示距离与风险的负相关关系. 在实际驾驶中,车辆通常会在自己的车道上与前车保持较远的距离,但可能会相对靠近车道边界处的障碍物[42 ] . 为了更准确地描述车辆从不同角度接近目标车辆时的风险水平,引入等效距离[43 ] 的概念,对真实空间中的距离进行改变,如下所示: ...
Attention is all you need
3
2017
... 在时间特征建模方面,Transformer模型凭借近似人类思维过程的注意力机制,能够高效捕捉数据中的长程依赖关系[29 ] ,被广泛应用在车辆轨迹预测任务中. Quintanar等[30 ] 对标准Transformer进行修改,实现对单车轨迹的独立建模. Geng等[31 ] 提出融合物理信息的Transformer车辆轨迹预测模型,在长时预测范围内表现出较高精度、强泛化能力与良好的可解释性. Gao等[32 ] 设计双分支Transformer结构,其中一分支用于提取车辆状态的时间相关性以预测车辆换道意图,另一分支融合变道意图向量生成车辆未来轨迹. Chen等[33 ] 利用稀疏自注意机制对车辆轨迹长期依赖关系进行建模,引入意图感知解码器查询生成模块,有效克服了Transformer在推理速度和多模态预测方面的局限性. ...
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
... 车辆轨迹预测可以表述为:基于已观测到的车辆历史轨迹,预测未来的运动状态. 与Gupta等[13 , 29 , 12 ] 针对单一车辆进行预测不同,本文提出并行预测框架,能够同时推断场景中所有相邻车辆的未来轨迹. 令$ X $
2
... 在时间特征建模方面,Transformer模型凭借近似人类思维过程的注意力机制,能够高效捕捉数据中的长程依赖关系[29 ] ,被广泛应用在车辆轨迹预测任务中. Quintanar等[30 ] 对标准Transformer进行修改,实现对单车轨迹的独立建模. Geng等[31 ] 提出融合物理信息的Transformer车辆轨迹预测模型,在长时预测范围内表现出较高精度、强泛化能力与良好的可解释性. Gao等[32 ] 设计双分支Transformer结构,其中一分支用于提取车辆状态的时间相关性以预测车辆换道意图,另一分支融合变道意图向量生成车辆未来轨迹. Chen等[33 ] 利用稀疏自注意机制对车辆轨迹长期依赖关系进行建模,引入意图感知解码器查询生成模块,有效克服了Transformer在推理速度和多模态预测方面的局限性. ...
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
A physics-informed Transformer model for vehicle trajectory prediction on highways
1
2023
... 在时间特征建模方面,Transformer模型凭借近似人类思维过程的注意力机制,能够高效捕捉数据中的长程依赖关系[29 ] ,被广泛应用在车辆轨迹预测任务中. Quintanar等[30 ] 对标准Transformer进行修改,实现对单车轨迹的独立建模. Geng等[31 ] 提出融合物理信息的Transformer车辆轨迹预测模型,在长时预测范围内表现出较高精度、强泛化能力与良好的可解释性. Gao等[32 ] 设计双分支Transformer结构,其中一分支用于提取车辆状态的时间相关性以预测车辆换道意图,另一分支融合变道意图向量生成车辆未来轨迹. Chen等[33 ] 利用稀疏自注意机制对车辆轨迹长期依赖关系进行建模,引入意图感知解码器查询生成模块,有效克服了Transformer在推理速度和多模态预测方面的局限性. ...
Dual transformer based prediction for lane change intentions and trajectories in mixed traffic environment
1
2023
... 在时间特征建模方面,Transformer模型凭借近似人类思维过程的注意力机制,能够高效捕捉数据中的长程依赖关系[29 ] ,被广泛应用在车辆轨迹预测任务中. Quintanar等[30 ] 对标准Transformer进行修改,实现对单车轨迹的独立建模. Geng等[31 ] 提出融合物理信息的Transformer车辆轨迹预测模型,在长时预测范围内表现出较高精度、强泛化能力与良好的可解释性. Gao等[32 ] 设计双分支Transformer结构,其中一分支用于提取车辆状态的时间相关性以预测车辆换道意图,另一分支融合变道意图向量生成车辆未来轨迹. Chen等[33 ] 利用稀疏自注意机制对车辆轨迹长期依赖关系进行建模,引入意图感知解码器查询生成模块,有效克服了Transformer在推理速度和多模态预测方面的局限性. ...
Vehicle trajectory prediction based on intention-aware non-autoregressive transformer with multi-attention learning for Internet of vehicles
2
2022
... 在时间特征建模方面,Transformer模型凭借近似人类思维过程的注意力机制,能够高效捕捉数据中的长程依赖关系[29 ] ,被广泛应用在车辆轨迹预测任务中. Quintanar等[30 ] 对标准Transformer进行修改,实现对单车轨迹的独立建模. Geng等[31 ] 提出融合物理信息的Transformer车辆轨迹预测模型,在长时预测范围内表现出较高精度、强泛化能力与良好的可解释性. Gao等[32 ] 设计双分支Transformer结构,其中一分支用于提取车辆状态的时间相关性以预测车辆换道意图,另一分支融合变道意图向量生成车辆未来轨迹. Chen等[33 ] 利用稀疏自注意机制对车辆轨迹长期依赖关系进行建模,引入意图感知解码器查询生成模块,有效克服了Transformer在推理速度和多模态预测方面的局限性. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
Group vehicle trajectory prediction with global spatio-temporal graph
1
2023
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
基于时空交互特征融合的车辆轨迹预测方法研究
1
2025
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
基于时空交互特征融合的车辆轨迹预测方法研究
1
2025
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
Trajectory prediction for autonomous driving based on structural informer method
2
2025
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
... 基于NGSIM和HighD 2个真实世界数据集,对提出的RGMA模型与当前7种代表性轨迹预测方法进行综合对比实验. 参与对比的基线模型包括卷积社交长短期记忆网络[12 ] (CS-LSTM)、多头注意力LSTM [20 ] (MHA-LSTM)、时空动态注意力网络[36 ] (STDAN)、交互感知Transformer [33 ] (iNATran)、图注意力网络[2 ] (STGAMT)、图轨迹预测模型[15 ] (GRIP)和图时空卷积网络[27 ] (GSTCN). 这些模型分别代表基于卷积社交池化、注意力机制、时空分层建模、图结构交互及多模态特征融合等不同的技术路线. ...
CrossFormer: a versatile vision transformer hinging on cross-scale attention
2
2023
... 尽管基于时空感知的车辆轨迹预测方法在引入图神经网络与Transformer架构后已取得显著进展,现有研究仍存在若干关键局限性. 在空间交互建模上,驾驶行为往往受到视野内多个车辆的复杂影响,仅依靠简单的图结构难以充分建模多层次、多因素的交互机制[34 ] . 以往研究方法大多以车辆间的欧氏距离作为交互权重[28 ] ,缺乏对多源交互特征,如相对速度、加速度、视角等多种时空因素的系统性融合与推理,从而限制了模型的泛化能力. 在时间特征建模上,大多数现有模型仅以最终时间步的轨迹信息作为输入,忽略了完整轨迹蕴含的时间依赖特性. Transformer模型通过自注意力机制能够有效捕捉学习特征在不同时刻之间的长程依赖与耦合关系[29 ] ,已被广泛应用于车辆轨迹时序数据处理中[35 ] ,其自注意力机制可以对目标车辆轨迹的动态变化进行有效建模[24 ,30 ] . Transformer的变形网络Informer[36 ] 提出的自注意力提取操作,减少了计算冗余和模型的时空复杂度. 这些方法往往忽视了对多变量间跨维度依赖性的捕捉[37 ] . 另外,当捕捉数据沿时间维度的长期相关性时,传统Transformer模型依赖位置编码,面临性能退化和计算成本激增的问题. ...
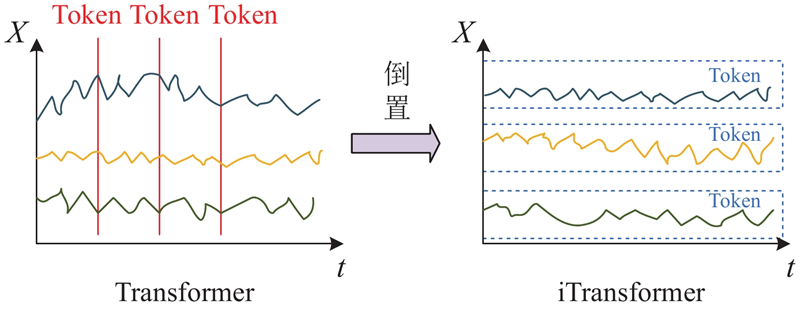
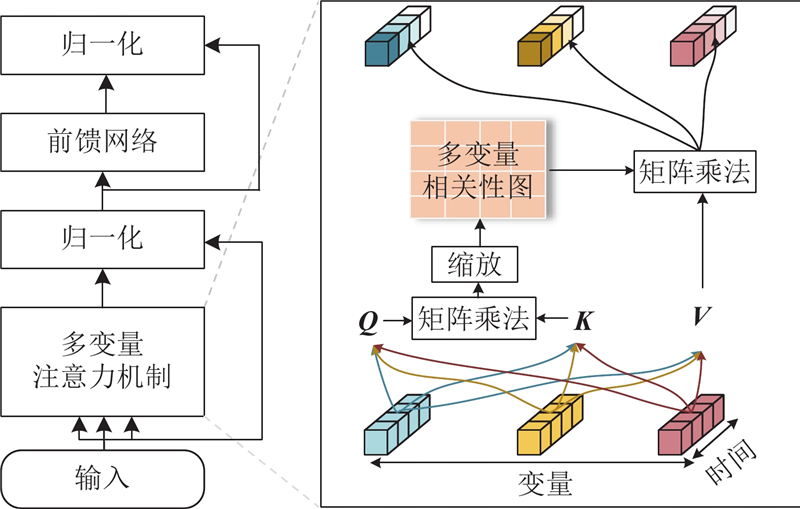
... 车辆未来轨迹的预测高度依赖于其历史时序轨迹. 传统基于Transformer的轨迹预测方法一般将特定时间步长的所有维度数据嵌入单个向量中,随着历史窗口长度的增加,Transformer将面临性能下降和计算量激增的挑战[37 ] . 此外,Transformer将多个变量在相同时间戳下进行对齐,这种编码方式会导致多变量之间的相关性丧失,无法充分、明确地挖掘和利用变量间的依存关系[45 ] . ...
Driving safety field theory modeling and its application in pre-collision warning system
1
2016
... 1)在车辆运动过程中,车辆的质量可以定义为等效质量,它与车辆当前的速度有关,反映了车辆在特定速度下的行驶风险程度[38 ] . 在实际驾驶过程中,很难实时获取车辆的精确质量信息. 采用车辆的尺寸作为质量的替代指标[39 -41 ] ,等效质量的数学表达式为 ...
Anisotropy safety potential field model under intelligent and connected vehicle environment and its application in car-following modeling
1
2023
... 1)在车辆运动过程中,车辆的质量可以定义为等效质量,它与车辆当前的速度有关,反映了车辆在特定速度下的行驶风险程度[38 ] . 在实际驾驶过程中,很难实时获取车辆的精确质量信息. 采用车辆的尺寸作为质量的替代指标[39 -41 ] ,等效质量的数学表达式为 ...
不同尺寸车身轻量化评价及重量目标设定
1
2020
... 1)在车辆运动过程中,车辆的质量可以定义为等效质量,它与车辆当前的速度有关,反映了车辆在特定速度下的行驶风险程度[38 ] . 在实际驾驶过程中,很难实时获取车辆的精确质量信息. 采用车辆的尺寸作为质量的替代指标[39 -41 ] ,等效质量的数学表达式为 ...
不同尺寸车身轻量化评价及重量目标设定
1
2020
... 1)在车辆运动过程中,车辆的质量可以定义为等效质量,它与车辆当前的速度有关,反映了车辆在特定速度下的行驶风险程度[38 ] . 在实际驾驶过程中,很难实时获取车辆的精确质量信息. 采用车辆的尺寸作为质量的替代指标[39 -41 ] ,等效质量的数学表达式为 ...
1
... 2)Sheng等[27 -28 ] 利用车辆间欧式距离的倒数表示距离与风险的负相关关系. 在实际驾驶中,车辆通常会在自己的车道上与前车保持较远的距离,但可能会相对靠近车道边界处的障碍物[42 ] . 为了更准确地描述车辆从不同角度接近目标车辆时的风险水平,引入等效距离[43 ] 的概念,对真实空间中的距离进行改变,如下所示: ...
Dynamic driving risk potential field model under the connected and automated vehicles environment and its application in car-following modeling
1
2022
... 2)Sheng等[27 -28 ] 利用车辆间欧式距离的倒数表示距离与风险的负相关关系. 在实际驾驶中,车辆通常会在自己的车道上与前车保持较远的距离,但可能会相对靠近车道边界处的障碍物[42 ] . 为了更准确地描述车辆从不同角度接近目标车辆时的风险水平,引入等效距离[43 ] 的概念,对真实空间中的距离进行改变,如下所示: ...
SSAGCN: social soft attention graph convolution network for pedestrian trajectory prediction
1
2024
... 3)车辆之间的交互与运动方向高度相关[44 ] ,前车对后车的影响远远大于后车对前车的影响,而在变道时,目标车道上的车辆对变道车辆的影响更显著[21 ] . 如图3 所示,当车辆j 变道时,其受到目标车道前车i 的影响更大,而直行车辆i 受到变道车辆j 的影响较小. 利用车辆之间运动航向角的差值与车辆间距离角度的相似度,描述运动方向对车辆的交互影响. 利用车辆间纵向距离y 的差值表示车辆前、后的运动方向,修正车辆相对位置对交互的影响,如下所示: ...
2
... 车辆未来轨迹的预测高度依赖于其历史时序轨迹. 传统基于Transformer的轨迹预测方法一般将特定时间步长的所有维度数据嵌入单个向量中,随着历史窗口长度的增加,Transformer将面临性能下降和计算量激增的挑战[37 ] . 此外,Transformer将多个变量在相同时间戳下进行对齐,这种编码方式会导致多变量之间的相关性丧失,无法充分、明确地挖掘和利用变量间的依存关系[45 ] . ...
... 借鉴iTransformer[45 ] 的设计思路,在不改变transformer网络结构框架的前提下,提出变量分离的编码策略. 该方法将一个变量的整个序列视为一个独立的token,利用注意力机制建模不同变量之间的依赖关系. 利用前馈神经网络深度提取变量内部沿时间维度的动态特征,从而实现对多变量时序轨迹更充分、更具判别性的表征. Transformer和iTransformer的数据处理方式比较如图4 所示. ...
1
... 与以往transformer架构中引入位置编码的做法不同,本研究采用基于多层感知机(MLP)的前馈神经网络结构,对输入的变量的时间维度进行变换[25 , 46 ] . 该方法能够有效捕捉时间系列的中长期依赖关系,避免传统位置编码的归纳偏差. ...