针对车辆队列稳定性控制问题,宋家成等[4]提出基于数据驱动的鲁棒自适应巡航控制算法,保证了车辆的跟踪精度和鲁棒性能. 针对车辆外部扰动问题,Zhu等[5-6]提出自适应协同队列控制算法. 由上述文献可知,队列控制器的设计依赖于传感器输出的精确车辆状态. 考虑传感器量测过程往往伴随着扰动和噪声,Vargas等[7]研究了加性噪声下车辆队列的链式稳定性问题. Liu等[8]通过Riccati方程求解系统矩阵与噪声方差的关系,推导了外部扰动下车辆队列一致性稳定的充要条件. 在车辆队列实际行驶过程中,受传感器成本和数据采集精度的限制,车辆的部分状态信息(如速度、加速度)往往不易准确获取[9],增加了控制器的设计难度. 输出反馈作为仅利用输出信息对控制器进行设计的方法,为部分状态信息未知的车辆队列控制提供了新思路[10]. 如Jiang等[11]仅用领航车辆的相对输出信息来实现巡航控制. Wang等[12]针对模型存在未知扰动和不确定性的问题,提出基于分布式输出反馈的车辆队列协同控制算法. 行驶中的车辆队列多采用周期性连续采样的时间触发机制进行状态的测量与更新,给带宽有限的车载网络信道带来沉重负担. 对于稳定行驶的车辆队列,周期性采样将使大量无用的重复信息散布在有限信道中,造成通信网络的冗余和计算资源的浪费[13]. 不同于时间触发机制,事件触发机制仅在违背触发条件时执行控制任务,能够有效降低控制任务执行数量并节约通信资源[14]. Yang等[15]提出基于相对控制输入的事件触发机制,用于减少控制器到执行器的通信传输数据. Kang等[16]根据状态波动引起的控制输入变化设计事件触发策略,仅当系统状态变化足够大时进行传感器信息传输. 静态事件触发机制阈值固定,灵活性低. 自适应触发机制引入时变参数,根据系统状态在一定范围内对触发阈值进行动态调整[17]. Shi等[18]通过预设自适应最大阈值建立自适应事件触发机制,有效减少了控制信号的传输次数. Wang等[19]基于车辆状态变化设置触发条件,避免了车辆间的无效数据传输. 此外,动态触发机制通过在触发条件中引入非负的动态变量,使平均触发间隔时间延长,可进一步减少通信资源消耗[20]. 如Wang等[21]提出动态事件触发鲁棒控制方法,降低了多车辆协同过程中的通信资源消耗. 事件触发机制虽然能够节省通信资源,但是造成了控制性能下降[22]. 在触发间隙,若参考信号发生突变,车辆队列可能会错过关系系统性能的重要量测信息,导致控制性能下降甚至失稳[23]. 如何综合时间触发和事件触发的优势,在保证控制性能的同时有效节约通信资源,是值得深入研究的问题. Liu等[24-25]针对网络攻击下控制系统的稳定性问题,设计时间-事件混合触发机制,使得系统在保证控制性能的同时有效节省了通信资源. 上述混合触发机制假设切换变量服从伯努利(Bernoulli)分布,无法根据系统当前状态进行自适应切换,难以满足车辆队列的实际行车需求.
本文研究传感器与通信资源受限下的车辆队列控制问题. 通过构造状态观测器,仅利用位置信息实现对车辆状态的估计;提出基于时间-事件混合触发机制的车辆队列输出反馈控制算法. 相较于已有研究,本研究仅基于车辆位置信息可实现车辆队列跟踪控制,有助于降低车辆传感器成本. 此外,单一事件触发机制可能造成系统性能下降,本研究提出的时间-事件混合触发机制能够在保证车辆跟踪性能的前提下显著降低通信资源消耗.
1. 问题描述
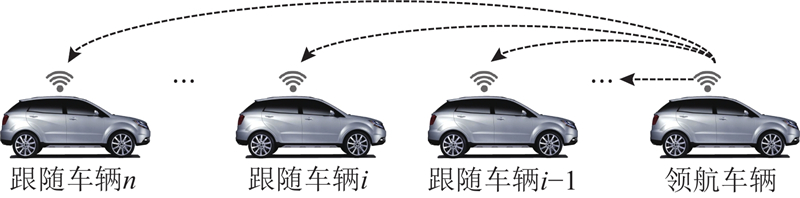
图 1
式中:
式中:
引理1[27]
引理2[28] 对于任意
2. 基于时间-事件混合触发的车辆队列输出反馈控制方法
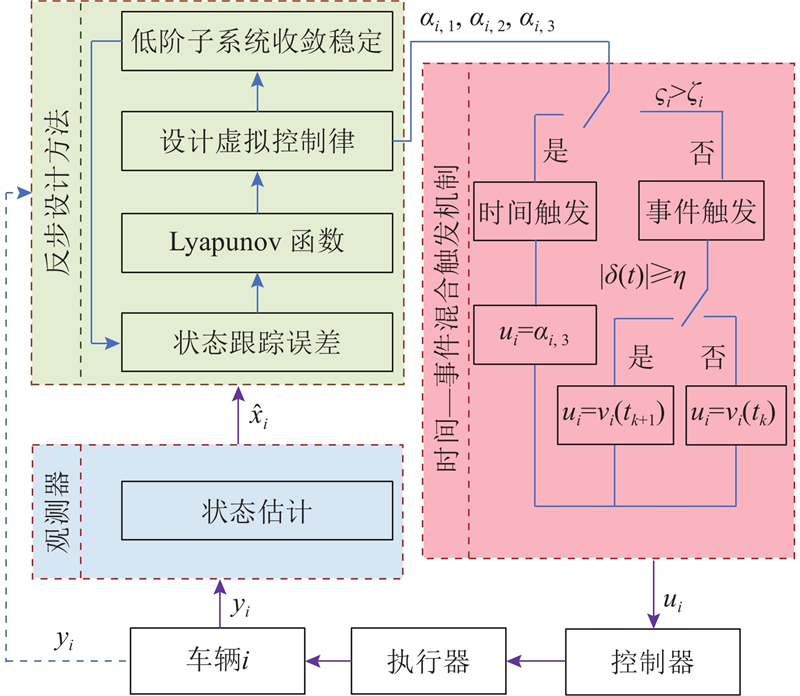
针对基于时间-事件触发的车辆队列输出反馈控制问题,1)利用车辆输出的位置信息设计状态观测器,对未知的速度和加速度信息进行估计;2)基于估计的状态信息,通过反步法设计控制器保持系统稳定;3)由跟踪误差
图 2
2.1. 状态观测器设计
针对车辆部分状态信息不可测量的问题,设计观测器对未知状态进行估计. 选取变量
式中:
令
通过选择适当参数,使
式中:
其中
注1 由式(6)和式(7)可知,
2.2. 时间-事件混合触发机制设计
为了节省通信资源并保证控制性能,设计基于跟踪误差的时间-事件混合触发机制. 定义参数
情况1 当
情况2 当
定义
式中:
式中:
在事件触发机制下,输入信号
注2 本研究设计的时间-事件混合触发机制根据触发信号
2.3. 输出反馈控制器设计
针对车辆动力学式(1),采用反步法设计车辆队列控制器,主要步骤如下.
1)定义
选择李雅普诺夫函数
设计虚拟控制律
其中
因此,当
2)定义
选择李雅普诺夫函数
设计虚拟控制律
其中
因此,当
3)定义
选择李雅普诺夫函数
设计虚拟控制律
其中
根据本研究设计的时间-事件混合触发机制可知,车辆会根据当前状态自动选择触发方式,因此存在以下2种情况.
情况1 当
将式(24)代入式(25),得到
情况2 当
因此,控制器
其中,
将式(27)代入式(22)得到
至此,完成基于时间-事件触发的车辆队列的控制器设计. 如果设计的控制器可以保证
2.4. 稳定性分析
选择李雅普诺夫函数
对
其中
进一步得到
则跟踪误差满足
因此,
对混合触发机制不会产生芝诺(Zeno)现象进行证明. 对于情况1,混合触发机制切换为时间触发机制. 此时有
其中常数
根据式(36)得到
定义
注3 本研究采用仅跟随领航车辆的通信拓扑. 当车辆队列中发生扰动时,车辆能够使用领航车辆信息校正跟踪误差,扰动不会沿队列传播,车辆队列的链式稳定性得以保证.
3. 仿真验证
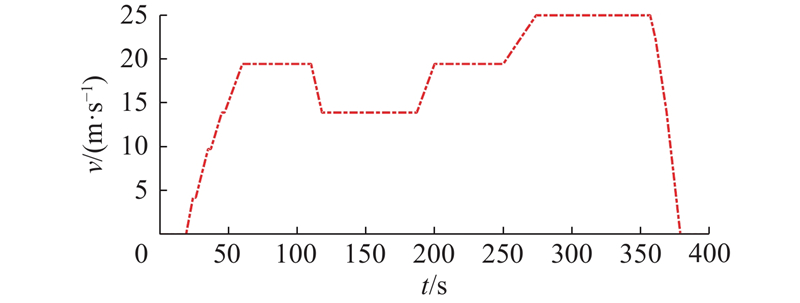
为了验证所提方法的有效性,利用Matlab开展仿真研究. 考虑由1辆领航车和5辆跟随车组成的车辆队列. 假设车辆的初始速度和加速度均为零,初始位置
图 3
3.1. 仿真结果
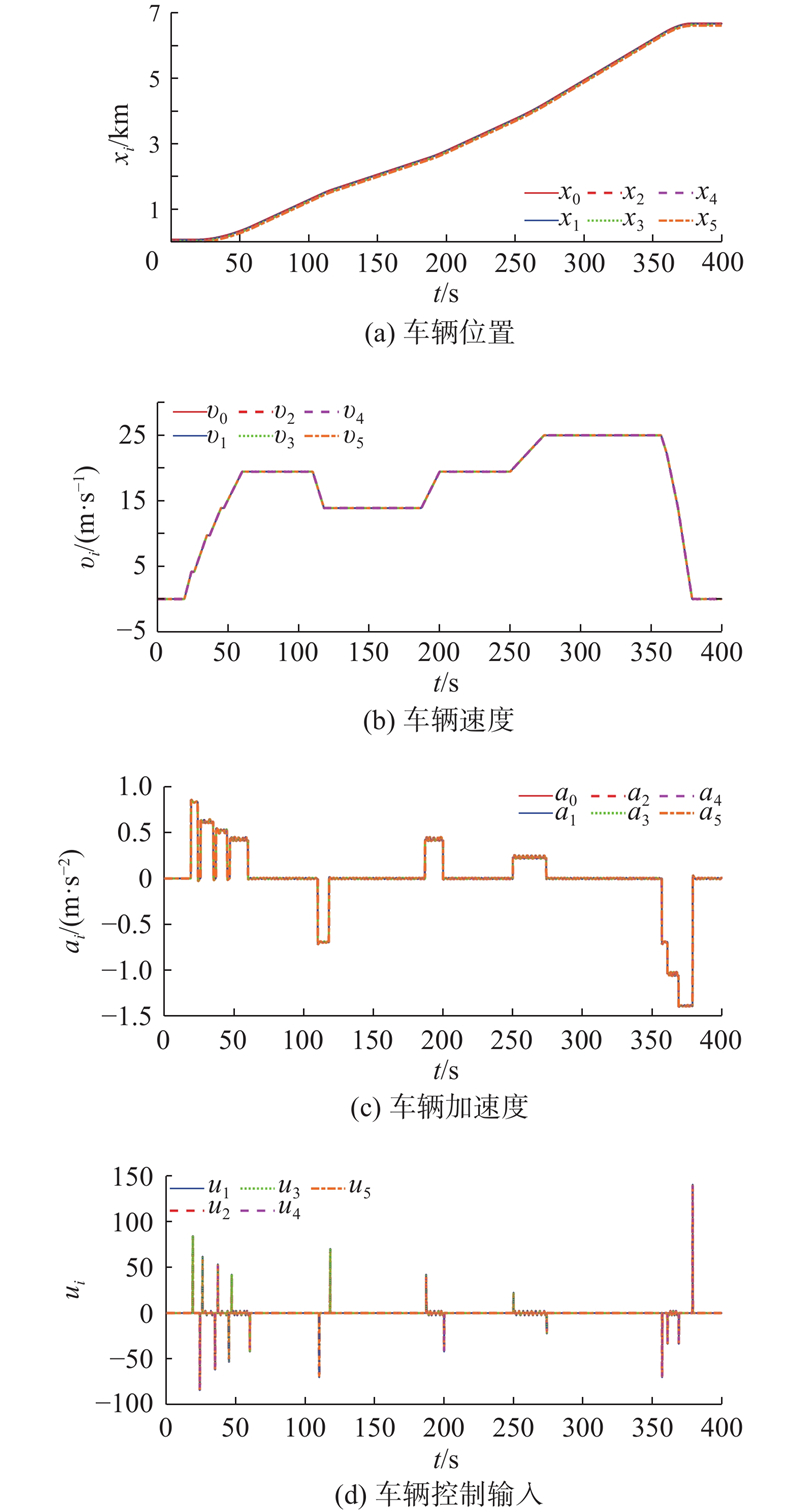
如图4所示为车辆队列控制仿真结果. 可以看出,在仿真过程中车辆位置曲线没有发生交叉,表明车辆间未发生碰撞,每辆车可以保持与前车固定的间距进行队列行驶. 车辆速度曲线与给定参考信号一致,可以实现对给定速度的精确跟踪. 车辆的加速度和控制输入的变化与车辆速度变化的规律保持一致.
图 4
如图5所示为每辆车的采样间隔. 结合车辆速度曲线可以看出,在加速和减速阶段,车辆状态变化较为剧烈,需要频繁更新控制输入以保证控制性能,因此该阶段以时间触发为主;反观匀速行驶阶段,车辆状态变化很小,因此采用事件触发方式,节约通信资源.
图 5
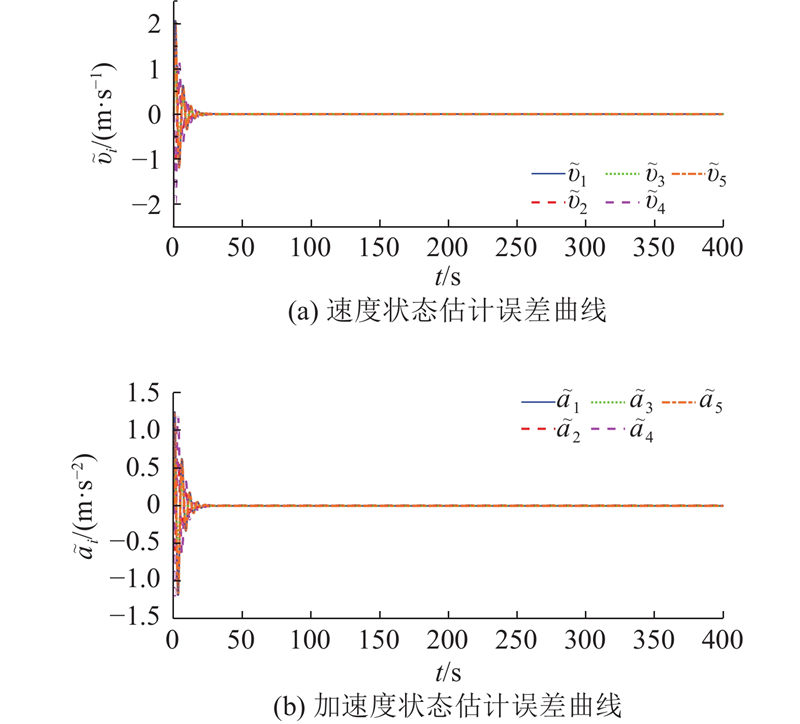
如图6所示为每辆车速度和加速度的估计值与实际值的误差曲线. 可以看出,速度误差能快速收敛到0,状态估计效果良好. 加速度的状态估计误差虽然存在一定的波动,但能满足队列行驶要求.
图 6
图 6 速度与加速度的状态估计误差曲线
Fig.6 State estimation error curve of velocity and acceleration
以上仿真结果表明,本研究设计的状态观测器能够实现对车辆速度和加速度的准确估计,设计的控制器可以根据车辆行驶状态自动调节采样方式,实现车辆队列的跟踪控制,且整个闭环系统稳定,所有控制信息以及误差均有界.
3.2. 对比分析
表 1 不同触发机制下的触发次数
Tab.1
以车辆2作为参考,3种触发机制下车辆的状态误差如图7所示. 可以看出,在时间触发机制下,由于采样频率较高,车辆队列控制器周期性地执行控制信号,跟踪性能最好. 在单一事件触发机制下,由于采样间隔较大,在领航车辆突然加减速情况下,车辆的位置、速度与加速度跟踪误差最大值分别为
图 7
4. 结 语
本研究1)仅利用车辆位置信息,通过设计状态观测器实现对车辆速度与加速度信息的准确估计,摆脱了对专用传感器的依赖,有效降低了系统状态的量测与感知成本. 2)设计时间-事件混合触发机制,在车辆队列平稳运行时采用事件触发模式以节省通信资源,在状态剧烈变化时采用时间触发模式以保证控制性能,实现了控制性能与通信资源的有效平衡. 3)在时间-事件混合触发架构下,基于反步控制的思想,设计仅基于位置信息的车辆队列输出反馈控制器,实现了车辆队列的稳定控制. 本研究提出的时间-事件混合触发机制初步实现了车辆队列控制性能与通信资源的有效平衡,未来计划针对触发阈值的设计、触发机制对系统性能的影响机理与数理关系问题深入开展研究.
参考文献
Evolution of road traffic congestion control: a survey from perspective of sensing, communication, and computation
[J].DOI:10.23919/JCC.2021.12.010 [本文引用: 1]
DeepGAL: intelligent vehicle control for traffic congestion alleviation at intersections
[J].DOI:10.1109/TITS.2023.3257199 [本文引用: 1]
Unknown input observer based neuro-adaptive fault-tolerant control for vehicle platoons with sensor fault and output quantization
[J].DOI:10.1016/j.conengprac.2024.106007 [本文引用: 1]
基于数据驱动的鲁棒反步自适应巡航控制
[J].DOI:10.3785/j.issn.1008-973X.2022.03.007 [本文引用: 1]
Robust backstepping adaptive cruise control based on data-driven
[J].DOI:10.3785/j.issn.1008-973X.2022.03.007 [本文引用: 1]
Finite-time cooperative control for vehicle platoon with sliding-mode controller and disturbance observer
[J].DOI:10.1109/TITS.2024.3418631 [本文引用: 1]
Disturbance observer-based cooperative control of vehicle platoons subject to mismatched disturbance
[J].DOI:10.1109/TIV.2023.3237703 [本文引用: 1]
On stochastic string stability with applications to platooning over additive noise channels
[J].DOI:10.1016/j.automatica.2024.111923 [本文引用: 1]
Consensus of linear discrete-time connected autonomous vehicle systems with time delays and multiplicative noise
[J].DOI:10.1109/TITS.2023.3330823 [本文引用: 1]
Observer design for continuous-time dynamical systems
[J].DOI:10.1016/j.arcontrol.2021.11.002 [本文引用: 1]
Output feedback stabilization of linear systems with infinite distributed input and output delays
[J].DOI:10.1016/j.ins.2021.06.060 [本文引用: 1]
Containment control of discrete-time multi-agent systems with application to escort control of multiple vehicles
[J].DOI:10.1002/rnc.6176 [本文引用: 1]
Distributed output-feedback control of unmanned container transporter platooning with uncertainties and disturbances using event-triggered mechanism
[J].DOI:10.1109/TVT.2021.3130006 [本文引用: 1]
Distributed adaptive event-triggered control and stability analysis for vehicular platoon
[J].DOI:10.1109/TITS.2020.2974280 [本文引用: 1]
状态时延和全状态约束下的多智能体系统自适应事件触发控制
[J].DOI:10.13195/j.kzyjc.2020.1046 [本文引用: 1]
Adaptive event-triggered control for multi-agent systems with state time-delays and full state constraints
[J].DOI:10.13195/j.kzyjc.2020.1046 [本文引用: 1]
Fixed time event-triggered control for high-order nonlinear uncertain systems with time-varying full state constraints
[J].DOI:10.1002/rnc.6998 [本文引用: 3]
Event-triggered stabilization for large-scale interconnected systems with time delays
[J].DOI:10.1002/rnc.6225 [本文引用: 1]
Connectivity-preserving consensus: an adaptive event-triggered strategy
[J].DOI:10.1002/rnc.7169 [本文引用: 1]
Improved adaptive dynamic event-triggered consensus of multi-agent systems
[J].
Distributed adaptive event-triggered control of connected automated vehicle platoon systems with spoofing cyber attacks
[J].DOI:10.1109/TVT.2024.3436052 [本文引用: 1]
Data-driven dynamic event-triggered control
[J].DOI:10.1109/TAC.2024.3417088 [本文引用: 1]
Nonlinear consensus-based autonomous vehicle platoon control under event-triggered strategy in the presence of time delays
[J].DOI:10.1016/j.amc.2021.126246 [本文引用: 1]
Hybrid-triggered consensus for multi-agent systems with time-delays, uncertain switching topologies, and stochastic cyber-attacks
[J].DOI:10.1088/1674-1056/ab38a8 [本文引用: 1]
An overview of recent advances in event-triggered consensus of multiagent systems
[J].DOI:10.1109/TCYB.2017.2771560 [本文引用: 1]
Stabilization of networked control systems with hybrid-driven mechanism and probabilistic cyber attacks
[J].DOI:10.1109/TSMC.2018.2888633 [本文引用: 1]
Dynamic hybrid-triggered-based fuzzy control for nonlinear networks under multiple cyberattacks
[J].DOI:10.1109/TFUZZ.2021.3134745 [本文引用: 1]
参数不确定和扰动下智能汽车路径跟踪控制
[J].DOI:10.3785/j.issn.1008-973X.2023.04.007 [本文引用: 1]
Intelligent vehicle path tracking control under parametric uncertainties and external disturbances
[J].DOI:10.3785/j.issn.1008-973X.2023.04.007 [本文引用: 1]
Distributed integrated sliding mode control for vehicle platoons based on disturbance observer and multi power reaching law
[J].DOI:10.1109/TITS.2020.3035764 [本文引用: 1]
A robust adaptive nonlinear control design
[J].DOI:10.1016/0005-1098(95)00147-6 [本文引用: 1]
Prescribed-time adaptive state observer approach for distributed output-feedback formation tracking of networked uncertain underactuated surface vehicles
[J].DOI:10.1007/s11071-024-10014-1 [本文引用: 2]