随着机器人导航、无人驾驶汽车和增强现实等人工智能技术的兴起,同步定位与建图(simultaneous localization and mapping,SLAM)技术得到迅速发展[1]. 在众多SLAM方法中,视觉SLAM因其能够通过图像获取丰富的环境信息而成为研究重点. 通过摄像头获取环境中的大量特征信息,视觉SLAM能够精准地估计相机的位姿,实现机器人的定位与导航.
根据所采集的图像特征不同,视觉SLAM可以分为直接法和特征点法[2]. 直接法如DSO[3],依赖灰度不变假设,对光线的影响较为敏感. 基于特征点的方法,如ORB-SLAM[4-6],能够在纹理丰富的场景下提取具有尺度不变性和旋转不变性的特征点,实现有效的位姿估计. 在低纹理环境(如白墙、走廊、地板等场景)中,基于点特征的视觉SLAM通常只能提取较少的点特征,容易出现定位丢失的情况[7]. 除了点特征提取之外,相关研究还探索了通过提取线段和平面[8]特征来提高视觉SLAM性能的方法. 与点特征相比,线特征和面特征的几何信息更丰富,能够更好地应对环境纹理和光照的变化,提高视觉SLAM在低纹理环境下的鲁棒性. Pumarola等[9]提出基于点线特征融合的PL-SLAM算法,该方法结合ORB特征点和LSD[10]线特征,使用点特征和线特征进行融合的SLAM系统,在相机位姿局部优化时考虑点、线2种特征约束,提高了算法的精度和鲁棒性. 由于线特征数量的增加以及部分短线特征的不稳定性,线特征提取和匹配的计算时间增加,导致PL-SLAM系统的实时性较差. Qian等[11]在PL-SLAM的基础上提出Line-SLAM算法,该方法融入点线词袋(BoPLW)回环检测模块,存在过度提取线特征以及线特征质量不高的问题,导致特征匹配误差增加,并且计算时间显著提高. 平面特征通常提取自点云[12],点云从RGB-D相机[13]或激光雷达传感器[14]中获取. 由于3D信息有限,单目相机的平面特征提取非常困难. 相比之下,双目相机可以通过立体匹配获得点云提取平面特征,但过程耗时较长[15]. 黄宁生等[16]提出基于平面约束的RGB-D SLAM系统,它在关键帧中提取平面特征,通过构建平面特征之间的约束关系来优化相机位姿. Zhang等[17]提出SP-SLAM算法,该方法同时提取平面和平面边缘,以增加平面观测和约束. 以上方法仅对单一的平面特征进行优化,未进行点特征与面特征的联合优化,导致无法充分利用点特征和面特征之间的几何约束. Wang等[18]提出基于点面联合约束的RS-SLAM算法,通过设计具有严格离群点剔除机制的新型平面提取算法,结合Sobel算子优化支持点分布,实现鲁棒的平面特征检测. Yan等[19]提出基于点线面特征自适应融合的PLPF-VSLAM系统,通过多特征耦合优化框架与动态融合策略,在纹理变化场景中自适应选择最优特征组合进行位姿估计. Shu等[20]提出PLP-SLAM系统,紧密地结合语义信息和几何特征(点线面特征)以提高前端位姿跟踪和后端地图优化.
为了提高在低纹理环境下视觉SLAM的定位精度,本研究提出融合点线面特征的双目视觉SLAM算法. 1)考虑到高质量的线特征能改善SLAM系统在低纹理环境中的性能,对EDLines[21]线特征提取算法进行改进,通过引入短线抑制和相似直线合并策略提高线段提取的质量. 2)提出基于相交直线的平面特征提取方法,通过筛选可靠的线特征以增强平面计算的稳定性,有效提取平面特征. 3)提出点线面特征的联合优化方法,通过融合点线面特征的几何约束,提高位姿估计的准确性,从而提高视觉机器人在低纹理环境下定位与建图的精度和鲁棒性.
1. 算法框架
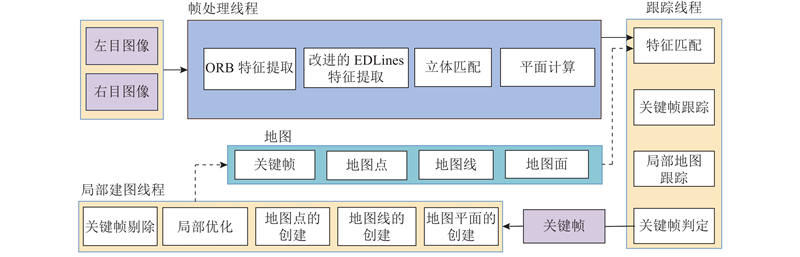
融合点线面特征的双目视觉SLAM算法在ORB-SLAM2结构的基础上增加了线、面特征信息,使线特征和面特征在特征跟踪、局部地图构建中发挥作用. 如图1所示,该算法框架主要由帧处理线程、跟踪线程和局部建图线程3个部分组成. 1)在帧处理线程中,利用ORB算法从左右目图像中提取点特征,使用特征描述子对提取的点特征进行匹配. 与此同时,使用改进的EDLines算法提取线特征,获取场景中的显著直线信息. 为了进一步丰富几何信息,通过对提取的线特征进行筛选,识别出相交的线对,进而构建平面特征. 线特征与平面特征为系统提供了更加全面的几何约束,有效地解决了低纹理环境中点特征稀缺的问题. 同时,线面特征的结合增强了特征匹配过程中几何约束的稳定性,确保了特征跟踪的稳定性. 2)跟踪线程的主要任务是特征匹配、关键帧跟踪、局部地图跟踪以及关键帧判定,以确保系统能够稳定、准确地估计相机位姿. 特征匹配通过对图像中的点线面特征进行匹配来获得相机位姿的初步估计. 关键帧跟踪将当前帧与之前的关键帧进行比对,以优化相机位姿的连续性,并通过局部地图中的已知特征进一步调整位姿估计. 在局部地图跟踪阶段,系统通过与局部地图中存储的点线面特征进行匹配来提升跟踪过程的鲁棒性. 关键帧判定基于当前帧与前一帧之间的位姿变化和跟踪质量,决定何时插入新的关键帧,以保证系统在长时间运行中的精度和效率. 3)在局部建图线程中,点线面特征被有效地融合并存储在局部地图中. 局部地图由关键帧及其对应的地图点线面特征组成. 该线程的主要任务是维护局部地图的信息,包括关键帧的插入、删除及其特征的管理. 通过光束平差法,结合重投影误差进行局部位姿优化,实现更精确的姿态估计. 为了避免地图冗余,系统根据新旧关键帧之间的相似性,决定是否删除重复率过高的关键帧. 最终,优化得到的局部地图特征会返回跟踪线程,支持实时的相机位姿更新以及对新图像帧的重新跟踪.
图 1
图 1 融合点线面特征的双目视觉SLAM算法框架
Fig.1 Framework of stereo visual SLAM algorithm for fusing point-line-plane features
2. 算法原理
2.1. 基于改进的EDLines线特征提取算法
EDLines线段提取算法是无参数的线段提取算法,因其在提取过程中具有较低的计算耗时和误提取率,广泛应用于线段检测. EDLines算法在一些特定场景下存在局限性. 1)该算法提取过程中常常产生大量无效线特征,尤其是较短线段,这不仅增加了后续特征匹配和提取的计算成本,还可能影响系统的整体效率. 2)低质量的线特征缺乏足够的几何信息(如短小或噪声干扰的线段难以稳定跟踪),导致在动态场景中的位姿估计误差增大. 直接将EDLines算法应用于视觉SLAM系统中,会面临效率低下和准确性不足的问题. 本研究提出改进的EDLines线特征提取算法. 该算法通过抑制短线段的产生来有效减少无效线特征的数量,从而提升线特征的整体质量. 具体而言,抑制短线段的产生通过设定线段长度阈值实现. 当提取的线段长度小于该阈值时,这些线段会被舍弃,避免了短线段对特征匹配的干扰. 此外,通过判断相似线段是否满足合并条件,进行线段合并,减少线特征的数量,加速匹配过程,降低定位过程中的漂移误差.
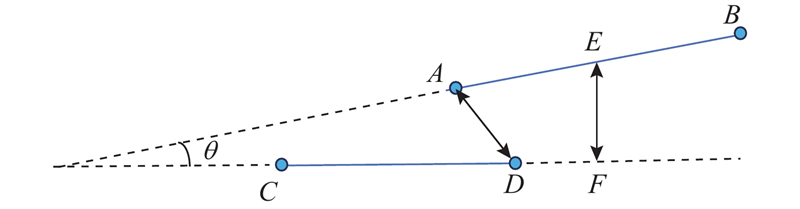
如图2所示为线段合并原理图. 假设LAB和LCD是需要合并的2条线段. 判断它们是否可以合并的3个条件如下. 1)在图像坐标系下,LAB与LCD的夹角小于设定的角度阈值θ(实验中设置θ=5°):
图 2
2)LAB的中点到LCD的距离小于设定的垂直距离阈值LEF(实验中设置LEF=10 pixel):
3)LAB和LCD端点之间的距离小于设定的端点距离阈值LAD(实验中设置LAD=40 pixel):
式中:mid(·)为线段中点到另一条线段的垂直距离,d(·)为两线段端点的最短距离. 基于改进的EDLines线特征提取算法如算法1所示.
算法1 基于改进的EDLines线特征提取算法
输入:图像I,阈值T
输出:线特征集合
1.对输入图像应用高斯平滑,降低噪声影响.
2.在图像的每个像素处利用Sobel算子计算梯度幅度和方向.
3.细化边缘点并通过梯度方向进行边缘跟踪,生成初步边缘.
4.对每条边缘线段进行直线拟合,将长的边缘线段分割为多个直线段.
5.输出满足误检数量小于1的线段.
6.遍历图像中的每个直线段:
a.计算每条线段的长度.
b.若直线段的长度大于T(实验中设置为15 pixel):
c.若直线段满足式(1)~(3),则与相邻的直线段合并继续循环,否则丢弃该线段.
7.返回符合条件的直线段.
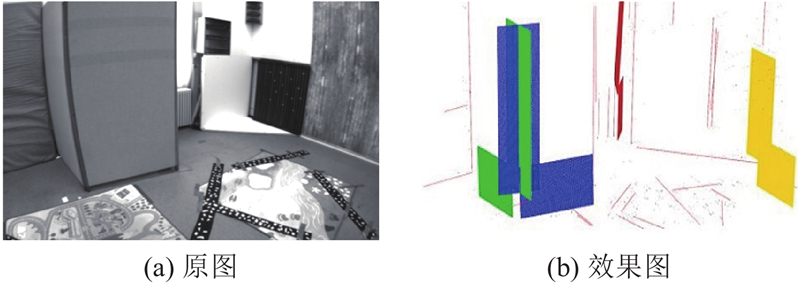
对比改进EDLines线特征提取算法与原始EDLines算法的线特征提取效果,结果如图3所示. 可以看出,原始EDLines算法提取的线段数量较多,大部分线段较短且缺乏明显的梯度,导致算法几何信息较为贫乏,难以提供有效的几何约束. 采用改进的EDLines算法后,提取的线段质量显著提高,主要集中为明显的水平和竖直线段.实验结果表明,改进的EDLines算法在线特征提取效率与匹配精度上均有显著提升. 具体而言,原始算法提取783条线特征,正确匹配436条,用时35 ms;改进后算法仅提取107条线特征,即实现105条正确匹配,用时3 ms. 由此可见,改进方法在特征数量减少约86%的情况下,匹配正确率从约55.7%提升至98.1%,同时处理速度提升了约11.7倍. 尽管提取的线特征数量有所减少,但改进后的算法更加注重线段的质量,优先保留具有较长长度、直线度高、几何稳定性强的线段,这些线段为后续的位姿估计和特征跟踪过程提供了更精炼的几何信息. 线特征匹配率的提升使得估计相机位姿的约束更加准确,从而降低了匹配误差对位姿计算的影响,提高了SLAM系统的精度和鲁棒性.
图 3
图 3 不同算法的线特征提取效果对比
Fig.3 Performance comparison of line feature extraction between two algorithms
2.2. 基于相交直线的平面特征提取方法
虽然系统中已经加入线特征,这些特征能够在一定程度上弥补低纹理环境中点特征的稀缺性,但是在某些场景下,尤其是在具有大面积平面或几何结构较简单的环境中,线特征的数量和分布可能不足以提供足够的几何约束. 为了进一步提高系统的鲁棒性和定位精度,本研究提出基于相交直线的平面特征提取方法,利用相交直线构成的平面特征,进一步增强系统的几何约束能力. 从双目相机的左右图像中提取线段,通过匹配线段及其端点,计算线段的方向向量nl和端点
图 4
式中:
2)中点距离约束:2条直线的中点间距小于直线的长度.
3)共面性约束:2条直线的4个端点在同个平面上. 直线的中点pc由直线的端点ps和pe计算得到. 通过前2个条件约束,就可以找到相符合的相交直线. 由2条直线的方向向量
使用平面的法向量
平面系数的范围计算式为
如果D小于阈值(实验中设置阈值为2 cm),则这2条直线满足共面性条件约束,并且可以计算出平面特征
图 5
2.3. 点线面特征的联合优化方法
为了提高视觉SLAM系统在低纹理环境中的鲁棒性和定位精度,本研究提出点线面特征的联合优化方法,通过融合多种特征的几何关系来减少由单一特征带来的误差累积. 在SLAM系统中,若C={ci},P={pj},L={lk},Π={πm}分别为相机姿态、点特征、线特征和平面特征的集合,则优化问题可以表示为
式中:C*,P*,L*,Π*分别为优化后的相机姿态、点特征、线特征和平面特征的位置,e(c,p)、e(c,l),e(c,π)为相机到点、相机到线和相机到面的测量误差,
式中:TCW为从世界坐标系到相机坐标系的变换矩阵,Pw为世界坐标系中的三维点,uc为相机图像中的二维观测点,ρ为将三维点投影到图像平面的投影模型. 在优化过程中,TCW被映射到李代数
式中:
式中:k为相机的内部参数,TCW为从世界坐标系到相机坐标系的变换矩阵,P为3D线段的端点,L为二维直线方程的参数. TCW和L对应的雅可比矩阵计算式分别为
式中:
使用最小参数化的重投影误差表示相机到平面的测量误差:
式中:πw为世界坐标系中的平面参数,πc为相机坐标系中的平面观测值. 相机-平面误差定义了在相机坐标系中平面地标与其对应观测点之间的差值,通过对相机到点线面的测量误差最小化实现定位精度的提升.
3. 实验结果与分析
实验选用EuRoC[23]、KITTI[24]和UMA-VI[25]数据集,涉及室内和室外场景. EuRoC数据集包含微型飞行器在3种不同的室内环境中飞行所记录的双目相机序列,其中包括1个工业机械大厅和2个Vicon房间. 根据速度、光照和场景纹理,将序列分为简单、中等和困难. 该数据集还提供来自激光跟踪系统和运动捕捉系统的地面真实情况. KITTI数据集中的立体序列由自动驾驶平台采集,场景覆盖城市与高速公路,地面真值由GPS和IMU定位单元给出. UMA-VI数据集是使用手持定制传感器装置收集的视觉-惯性立体序列,包含低纹理环境和动态光照场景. 所有实验都在搭载Ubuntu18.04系统的笔记本电脑中进行测试,该笔记本配备Intel i5-9300H CPU和NVIDIA GTX 1650 GPU. 在实验中估计不同数据集的轨迹和地图信息,并将所提算法与其他视觉SLAM算法进行比较. ORB-SLAM2[5]是基于点特征的视觉SLAM算法,PL-SLAM和Line-SLAM是基于点线特征的SLAM算法,RS-SLAM是基于点面特征的视觉SLAM算法,这3类算法均是常见的SLAM系统,具有较好的性能. 绝对位姿误差APE用于评估SLAM算法在估计单一位姿时的准确性,通过计算估计位姿与地面真值之间的差异来量化算法的精度,常用于分析长序列中的位姿估计误差,能够准确反映算法在室外场景以及低纹理环境下的定位精度. 在实验中,主要通过APE的均方根误差RMSE来比较不同SLAM算法的定位精度.
本研究的SLAM算法主要集中在特征提取和局部优化阶段,因此实验关闭了回环检测来对比轨迹漂移误差.
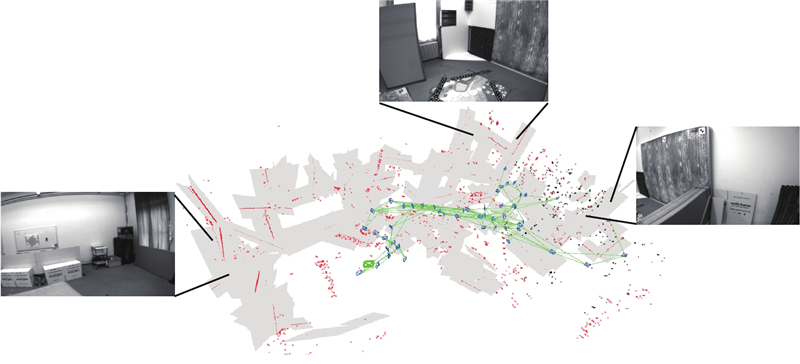
3.1. 特征提取
表 1 不同场景的点线面特征数量
Tab.1
| 场景 | nf | ||
| 点 | 线 | 面 | |
| 走廊 | 199 | 28 | 5 |
| 大厅 | 305 | 32 | 6 |
| 楼梯 | 212 | 32 | 10 |
图 6
3.2. KITTI数据集测试结果分析
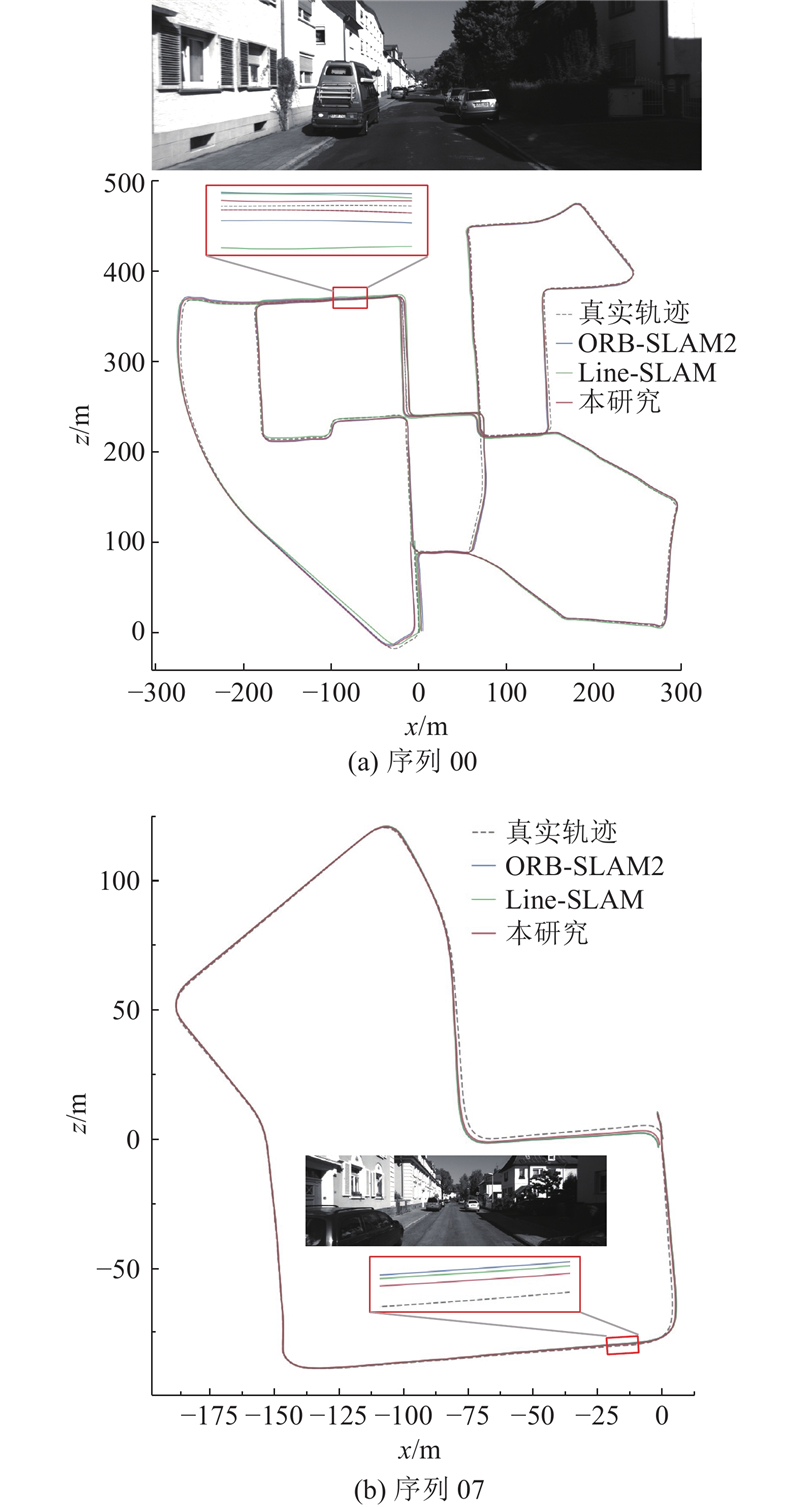
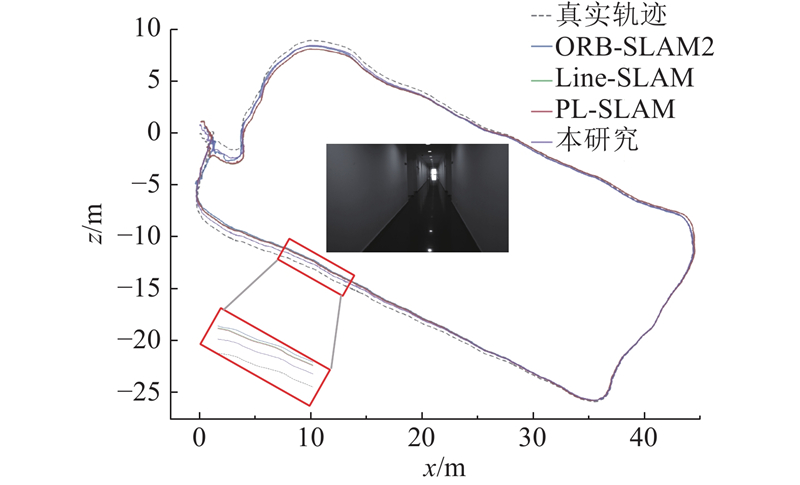
如表2所示为5种视觉SLAM算法在KITTI数据集00-10序列上的平移均方根误差,加粗数据表示每个序列的最小误差. 可以看出,除了00、03和04序列,本研究所提算法在其他序列中的表现均优于对比算法,11个序列上的最优结果为8项,证明了所提算法在提高姿态估计精度方面的有效性. 在03和04序列中,道路沿线存在大量杂乱的树木,导致错误的平面提取以及不准确的平面约束. 在其他序列中,线段和平面很容易从人造结构(如房屋墙面与道路)中提取出来,这也体现了所提算法的有效性. 为了更直观地展示所提算法在轨迹估计中的效果,在00和07序列上绘制对比算法的2D轨迹,不同算法在00和07序列上的位姿估计轨迹对比如图7所示. 可以看出,所提算法的结果比对比算法的更接近真实轨迹. 在纹理信息重复的场景下(如白墙),对比算法无法有效提取特征点,导致位姿估计误差较大,而所提算法能够有效提取线面特征,实现更稳定和准确的位姿估计,显著减小定位误差并提高系统的鲁棒性.
表 2 不同视觉SLAM算法在KITTI 数据集上的平移均方根误差比较
Tab.2
| 序列 | RMSE/m | ||||
| ORB-SLAM2 | Line-SLAM | PL-SLAM | RS-SLAM | 本研究 | |
| 00 | 4.958 | 3.903 | 4.565 | 3.754 | 3.795 |
| 01 | 6.210 | 9.078 | 8.816 | 10.574 | 5.704 |
| 02 | 9.552 | 9.887 | 9.946 | 9.728 | 8.052 |
| 03 | 0.261 | 0.243 | 0.255 | 0.654 | 0.271 |
| 04 | 0.172 | 0.175 | 0.192 | 0.199 | 0.232 |
| 05 | 1.957 | 1.911 | 1.856 | 2.056 | 1.800 |
| 06 | 2.695 | 2.428 | 2.553 | 2.152 | 1.927 |
| 07 | 1.577 | 1.469 | 1.428 | 1.309 | 1.109 |
| 08 | 3.137 | 3.163 | 3.089 | 3.625 | 2.788 |
| 09 | 2.901 | 2.865 | 2.875 | 3.200 | 2.373 |
| 10 | 0.989 | 0.954 | 0.818 | 1.073 | 0.795 |
| 平均值 | 3.128 | 3.279 | 3.308 | 3.395 | 2.622 |
图 7
图 7 不同视觉SLAM算法在KITTI数据集2种序列中的位姿估计轨迹对比
Fig.7 Pose-trajectory comparison of different visual SLAM algorithms on two KITTI-dataset sequences
3.3. EuRoC数据集测试结果分析
如表3所示为5种视觉SLAM算法在EuRoC数据集2种不同类型序列上的平移均方根误差,加粗数据表示每个序列的最小误差. 可以看出,ORB-SLAM2算法在10个序列上均无最优表现,原因是EuRoC数据集包含大量低纹理和快速运动的场景,导致ORB-SLAM2无法有效提取和匹配足够的特征点,从而影响位姿估计精度. Line-SLAM算法在1个序列上取得最优结果,原因是点线特征的融合在一定程度上缓解了特征点不足的问题,提高了系统在低纹理环境下的鲁棒性. 相较而言,所提算法在10个序列中的最优结果达到8项. 这主要得益于本研究提出的点线面特征联合优化方法利用面特征提供的全局几何约束,使得系统在低纹理以及光照变化环境下仍能保持较高的定位精度和鲁棒性.
表 3 不同视觉SLAM算法在EuRoC数据集上的平移均方根误差比较
Tab.3
| 序列 | RMSE/m | ||||
| ORB-SLAM2 | Line-SLAM | PL-SLAM | RS-SLAM | 本研究 | |
| MH_01_easy | |||||
| MH_02_easy | |||||
| MH_03_medium | |||||
| MH_04_difficult | |||||
| MH_05_difficult | |||||
| V1_01_easy | |||||
| V1_02_medium | |||||
| V1_03_difficult | |||||
| V2_01_easy | |||||
| V2_02_medium | |||||
| 平均值 | |||||
图 8
图 8 不同视觉SLAM算法在序列V2_01_easy中的位姿估计轨迹对比
Fig.8 Pose-trajectory comparison of different visual SLAM algorithms on sequence V2_01_easy
图 9
3.4. UMA-VI数据集测试结果分析
如表4所示为4种SLAM算法在UMA-VI数据集7个序列上的平移均方根误差,加粗数据表示每个序列的最小误差. 这7个序列包含了大量低纹理的场景,如走廊、楼梯和大厅等. 可以看出,ORB-SLAM2算法在7个序列上均未取得最优,主要原因是这些序列都存在大量白墙场景,影响了系统的跟踪稳定性和定位精度,尤其在hall-eng和third-floor-eng这2个低纹理场景较多的序列中,ORB-SLAM2甚至出现跟踪失败的情况. Line-SLAM和PL-SLAM在一定程度上缓解了特征点不足的问题,提高了系统在低纹理环境下的鲁棒性. 由于它们对线特征的提取质量较低,并且线特征本身的几何约束能力有限,难以有效抑制累积误差,导致整体定位精度较差. 相较而言,所提算法在7个序列中的定位精度均优于其他SLAM算法. 这主要得益于所提算法在提取高质量线特征的同时引入面特征,补充了低纹理环境下的几何信息,使特征提取更加稳定和均匀;其次点线面特征的联合优化充分利用面特征的全局几何约束,有效减少了累积误差,使系统在低纹理环境下仍能保持较高的定位精度和鲁棒性.
表 4 不同视觉SLAM算法在UMA-VI数据集上的平移均方根误差比较
Tab.4
| 序列 | RMSE/m | |||
| ORB-SLAM2 | Line-SLAM | PL-SLAM | 本研究 | |
| corridor-eng | ||||
| class-csc1 | ||||
| class-csc2 | ||||
| parking-csc1 | ||||
| hall1-rev-eng | ||||
| hall1-eng | — | |||
| third-floor-eng | — | |||
| 平均值 | ||||
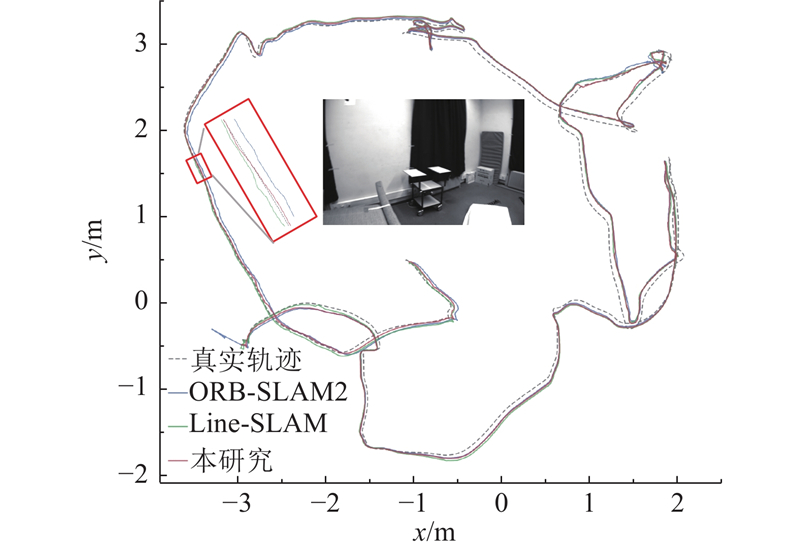
如图10所示为所提算法与对比算法在corridor-eng序列上的位姿估计轨迹. 可以看出,所提算法的结果比对比算法的更接近真实轨迹,进一步直观证明了所提算法在低纹理环境下具有更好的估计一致性与全局几何保持能力. 特别是在走廊这种结构化低纹理场景中,所提算法通过引入面特征增强了几何约束的完整性,从而有效抑制了轨迹漂移,提升了所提算法的定位精度与鲁棒性.
图 10
图 10 不同视觉SLAM算法在序列corridor-eng中的位姿估计轨迹比较
Fig.10 Pose-trajectory comparison of different visual SLAM algorithms on sequence corridor-eng
4. 结 语
本研究提出融合点线面特的双目视觉SLAM算法,将点线面特征约束结合并在后端进行联合优化,在3个公共数据集上的算法性能测试结果证明了所提算法的鲁棒性和有效性. 实验结果表明,所提算法可以在纹理欠缺的苛刻条件下,显著增加前端线面特征提取的数量,对定位过程中的漂移产生明显的抑制效果,在室内白墙的单一且纹理重复环境中仍然能够保持较高的定位精度与跟踪稳定性. 所提算法可以提取丰富的点线面特征以真实反映场景结构特征,实现高精度定位. 未来计划通过引入基于深度学习的线面特征提取网络,进一步提高线特征和平面特征的提取精度,在系统中加入基于线面特征的回环检测模块,以增强系统的鲁棒性.
参考文献
Past, present, and future of simultaneous localization and mapping: toward the robust-perception age
[J].DOI:10.1109/TRO.2016.2624754 [本文引用: 1]
Visual SLAM algorithms: a survey from 2010 to 2016
[J].DOI:10.1186/s41074-017-0027-2 [本文引用: 1]
Direct sparse odometry
[J].DOI:10.1109/TPAMI.2017.2658577 [本文引用: 1]
ORB-SLAM: a versatile and accurate monocular SLAM system
[J].DOI:10.1109/TRO.2015.2463671 [本文引用: 1]
ORB-SLAM2: an open-source SLAM system for monocular, stereo, and RGB-D cameras
[J].DOI:10.1109/TRO.2017.2705103 [本文引用: 2]
ORB-SLAM3: an accurate open-source library for visual, visual–inertial, and multimap SLAM
[J].DOI:10.1109/TRO.2021.3075644 [本文引用: 1]
A point-line VIO system with novel feature hybrids and with novel line predicting-matching
[J].DOI:10.1109/LRA.2021.3113987 [本文引用: 1]
LSD: a fast line segment detector with a false detection control
[J].DOI:10.1109/TPAMI.2008.300 [本文引用: 1]
Visual SLAM with BoPLW pairs using egocentric stereo camera for wearable-assisted substation inspection
[J].DOI:10.1109/JSEN.2019.2947275 [本文引用: 1]
Efficient organized point cloud segmentation with connected components
[J].
Lidar SLAM with plane adjustment for indoor environment
[J].DOI:10.1109/LRA.2021.3092274 [本文引用: 1]
基于平面约束的RGB-D SLAM系统
[J].DOI:10.19734/j.issn.1001-3695.2019.03.0100 [本文引用: 1]
RGB-D SLAM system based on plane constraint
[J].DOI:10.19734/j.issn.1001-3695.2019.03.0100 [本文引用: 1]
Point-plane SLAM using supposed planes for indoor environments
[J].DOI:10.3390/s19173795 [本文引用: 2]
RSS: robust stereo SLAM with novel extraction and full exploitation of plane features
[J].DOI:10.1109/LRA.2024.3388854 [本文引用: 1]
PLPF-VSLAM: an indoor visual SLAM with adaptive fusion of point-line-plane features
[J].DOI:10.1002/rob.22242 [本文引用: 1]
EDLines: a real-time line segment detector with a false detection control
[J].DOI:10.1016/j.patrec.2011.06.001 [本文引用: 1]
An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency
[J].DOI:10.1016/j.jvcir.2013.05.006 [本文引用: 1]
The EuRoC micro aerial vehicle datasets
[J].DOI:10.1177/0278364915620033 [本文引用: 1]
Vision meets robotics: the KITTI dataset
[J].DOI:10.1177/0278364913491297 [本文引用: 1]
The UMA-VI dataset: visual–inertial odometry in low-textured and dynamic illumination environments
[J].DOI:10.1177/0278364920938439 [本文引用: 1]