仓储业作为物流过程中的重要环节，负责货物存储、管理和分拣，以确保供应链的高效运转. 随着企业对交付时间和效率要求不断提高^[1]，智能仓储的渗透率不断提升，市场需求快速增长，行业迎来了蓬勃发展的关键时期^[2]. 中国仓储行业正从自动化仓储发展阶段向智能仓储加速转型^[3]. 在智能叉车密集仓储系统中，货物存储在箱式料框内，由于料框的密集堆叠，出库作业时面临复杂的翻箱问题，严重制约了系统的出库效率. 可以看出，优化料框翻箱策略对提高整个系统的作业效率至关重要.

针对密集仓储系统调度问题的研究主要集中在多设备协同调度^[4]、订单排序^[5]和路径规划^[6-7]等方面. Azadeh等^[8]对不同类型的仓储系统进行分类和分析，概述了自动化仓储的发展趋势. 张牧仁等^[9]针对四向车式密集仓储系统的货位分配问题，提出面向低能耗的货位分配优化模型以及自适应的差分进化求解算法. 马云峰等^[10]针对四向穿梭车仓储系统中双端出库翻箱问题，设计启发式上界和估值函数来改进A*算法求得最优解. 许丽丽等^[11]针对四向穿梭车系统复合作业调度问题，构建以出入库作业时间最短为目标的数学模型，设计改进的遗传算法来求解. 占翔南等^[12]针对多深度四向穿梭车仓储系统调度优化问题，采用Hopcroft-Tarjan算法制定路径定向策略，以最小作业时间为目标构建出入库作业调度模型，并设计混合遗传算法进行求解；Roy等^[13]基于四向车的密集仓储系统，研究货位停留点和交叉通道位置对系统性能的影响. 翻箱问题大多是针对集装箱装卸时的翻箱问题展开研究，智能叉车密集仓储系统的料框翻箱问题与集装箱堆场的集装箱翻箱问题(container relocation problem, CRP)具有相似性，其核心目标都是最小化总翻箱次数. Carlo等^[14-15]对相关研究工作进行系统分类和总结. Kim等^[16]提出CRP并给出该问题下界的计算方法，采用分支定界算法求解该问题的最优解. Zhu等^[17]基于文献[16]中的下界，提出2种改进的下界计算方法，并在迭代深化A*算法中采用探测机制来更新已知的最优解决方案. Tanaka等^[18]基于文献[17]提出更加严格的下界，构建快速求解的分支定界算法. CRP也被称为块重定位问题(block relocation problem, BRP)，Caserta等^[19]阐述BRP的定义并证明该问题属于NP难题（NP-hard），同时提出2种不同的二进制混合整数规划模型；有研究指出Caserta等构建的BRP模型的错误，并给出修正和改进的BRP模型^[20-22]. 为了快速求解大规模BRP，Jovanovic等^[23-25]开发出大量的启发式方法来寻找近似最优解. 张艳伟等^[26]构建堆场翻箱动态决策模型，提出基于逆向强化学习的智能决策算法. Jin等^[27]为非限制性CRP设计2个可以快速求解的下界和1组相互一致的优势规则，提出高效的迭代深化分支定界算法. Đurasević等^[28]通过引入新的终端节点和几种解的构造方法，基于遗传规划方法自动对翻箱规则进行设计.

在集装箱堆场中，集装箱搬运设备通常能运行至各堆栈并对最上方的集装箱进行吊取作业，翻箱时只考虑竖直方向上阻塞箱，因此大多数研究集中于单贝位内的二维翻箱问题. 在智能叉车密集仓储系统中，当要从密集堆叠的堆料区中检索位于内部堆栈中的料框时，由于叉车作业范围的限制，不仅要对该堆栈竖直方向上的阻塞料框进行翻箱，通常还要考虑在四周出库路径上阻塞堆栈中料框的翻箱操作. 智能叉车密集仓储系统中出库路径和落位堆栈的选择使得料框的三维翻箱问题复杂度显著增加. 本研究1）针对料框翻箱问题，以最小化有序取出堆料区中须出库料框翻箱次数为目标，提出快速求解料框翻箱方案的启发式方法并给出该问题下界的求解方法. 2）构建具有深度优先和回溯策略的分支定界算法以获得最优解，通过大量随机算例验证算法的有效性和实用性.

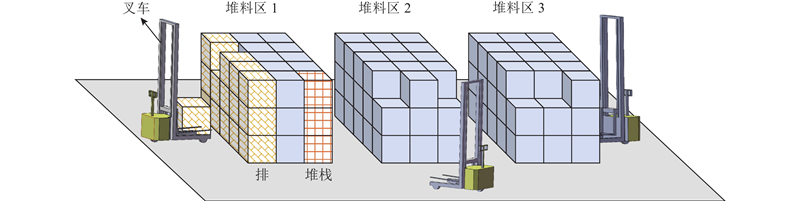
智能叉车密集仓储系统的仓库布局如图1所示，货物存储区域由多个堆料区组成，每个堆料区被划分为$ r\left(r\geqslant 3\right) $排，且每排有$ c(c\geqslant 3) $个堆栈，每个堆栈可以堆放多层料框. 若某个堆料区由$ S(S= r\times c) $个堆栈组成，每个堆栈编号为$ i(i=\mathrm{1,2},3,\cdots ,S) $，最大堆存层数被限制为$ H $，每层编号为$ j(j=\mathrm{1,2}, 3,\cdots ,H) $，则该堆料区的布局为$ r\times c\times H $. 堆料区中存储有$ N $个大小相同的料框，其中有$ M(M\leqslant N) $个料框等待出库，堆栈$ i $中料框的数量为$ {N}_{i}({N}_{i}\leqslant H) $，则有$ N=\displaystyle{\sum} _{i=1}^{S}{N}_{i} $. 位于堆栈$ i $第$ j $层料框的储位表示为$ (i,j) $. 位于$ (i,j) $的料框编号为$ {n}_{ij}({1\leqslant n}_{ij}\leqslant N) $，当$ {n}_{ij}\leqslant M $时，该编号也表示对应料框的出库序号$ {P}_{ij} $，出库序号越小表示需要越早出库，当$ {n}_{ij} > M $时，对应料框的出库序号为$ {P}_{ij}=M+1 $，即表示料框无需出库. 料框出库可以看成多步任务，每步执行以下操作之一：1）将位于$ (i,j) $的料框移动至另一储位$ ({i}{'},{j}{'}) $，该操作称为翻箱；2）将位于$ (i,j) $的料框从堆料区中移除，该操作称为检索. 本研究针对使用单台前移式智能叉车对单个堆料区中的料框进行出库作业的限制性翻箱问题，1）翻箱操作只发生在出库作业期间，不允许采取任何预先操作以减少料框翻箱次数；2）限制性翻箱特指在执行翻箱操作时，仅针对目标料框出库路径上的阻碍料框进行.

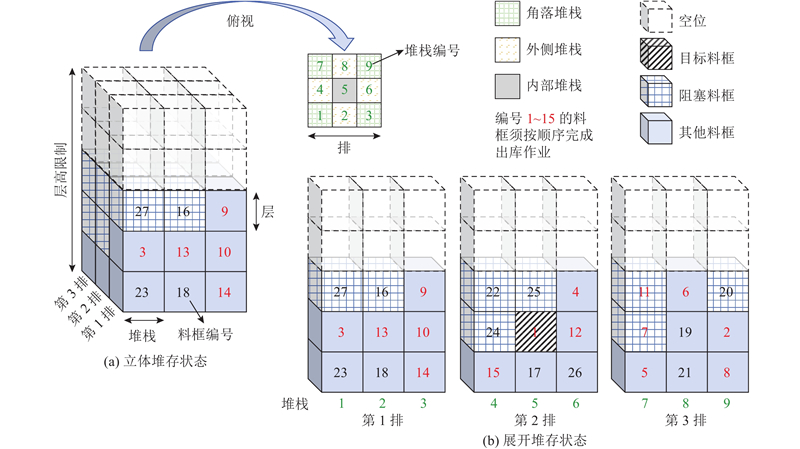
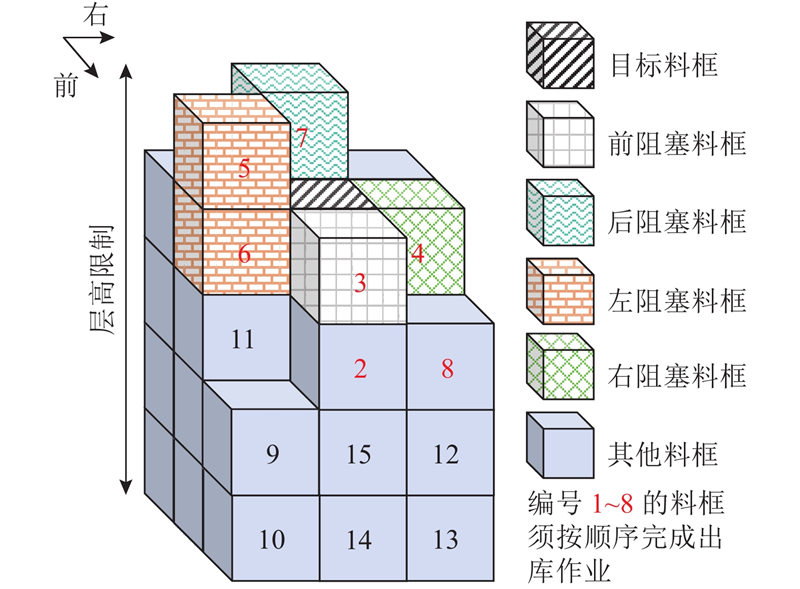
如图2所示，3×3×5布局的堆料区中储存有27个料框，其中编号1~15的料框须按序出库. 为了方便描述料框翻箱问题进行如下定义：当前堆存状态下出库序号最小的料框称为目标料框；各堆栈中大编号料框位于小编号料框之上且小编号料框需要出库时，大编号料框称为阻塞料框；当某堆栈中料框数量为0时称为空堆栈，否则为非空堆栈；当某堆栈四周都存在其他堆栈（包括空堆栈）时称为内部堆栈，其余堆栈则称为外侧堆栈，外侧堆栈中若某堆栈周围与之相邻的只有2个堆栈时称之为角落堆栈. 当前移式智能叉车在堆料区的狭窄空间内进行操作时，为了保证操作安全，每次只能沿直线叉取1个料框，且最多只能叉取（放）到2个料框长度方向上的物料. 当目标料框位于内部堆栈且无法仅通过对该堆栈阻塞料框进行翻箱后完成检索操作时，对目标料框所处堆栈四周某一侧出库路径上的料框进行翻箱操作以开辟通路. 出库路径上的堆栈称为阻塞堆栈. 出库路径选取规则：优先选择翻箱料框数量最少的一侧；若多侧需翻箱料框数量相等，则按该堆栈前后左右的顺序决定. 如图3所示，目标料框位于堆料区内部堆栈最顶层，前后左右出库路径上的阻碍料框数分别为1、2、2、1，根据上述规则，检索目标料框须先对料框3进行翻箱操作. 智能叉车密集仓储系统中料框的翻箱问题可以简单归纳如下：将堆料区中的部分料框按给定顺序依次进行检索操作，在整个检索过程中为须进行翻箱操作的料框选择合适的落位堆栈，最小化检索操作所需的总翻箱次数.

考虑到密集仓储系统中料框翻箱操作的可行性和实际应用场景，进行如下合理假设. 1）料框的检索和翻箱操作由单台前移式智能叉车在单个堆料区内独立执行，且堆料区有足够的空储位以满足最小料框翻箱操作的空间需求. 2）料框在堆料区中的存储位置和检索顺序已知且固定，在整个操作过程中，不考虑有新的料框被添加到堆料区. 3）每次翻箱操作仅针对目标料框出库路径上的阻碍料框进行.

智能叉车密集仓储系统料框翻箱问题数学模型中的符号定义如表1所示.

基于问题描述与假设，构建数学规划模型，目标函数用决策变量表示为

(1)$ Z = \min \sum\limits_{i = 1}^S {\sum\limits_{j = 1}^H {\sum\limits_{i' = 1}^S {\sum\limits_{j' = 1}^H {\sum\limits_{n = 1}^N {\sum\limits_{t = 0}^T {y_{iji'j'n}^t} } } } } } . $

智能叉车密集仓储系统料框出库翻箱问题模型约束条件为

(2)$ \sum\limits_{j = 1}^H {\sum\limits_{n = t}^N {x_{ijn}^t} } \leqslant H;\;\; i \in B,t \in D. $

(3)$ \sum\limits_{n = t}^N {x_{ijn}^t} \leqslant 1;\;\; i \in B,j \in C,t \in D. $

(4)$ \left. \begin{gathered} \sum\limits_{i = 1}^S {\sum\limits_{j = 1}^H {x_{ijn}^t} +v_n^t} = 1;\;\; t \in D;n = 1,\cdots ,M. \\ \sum\limits_{i = 1}^S {\sum\limits_{j = 1}^H {x_{ijn}^t} } = 1;\;\; t \in D;n = M+1,\cdots ,N. \\ \end{gathered} \right\} $

(5)$ \begin{split}& \sum\limits_{n = t}^N {x_{ijn}^t} \geqslant \sum\limits_{n = t}^N {x_{ij+1n}^t} ;\;\; \\ &\qquad\quad i \in B, t \in D;j = 1,\cdots ,H - 1. \end{split} $

(6)$ \sum\limits_{i = 1}^S {\sum\limits_{j = 1}^H {\sum\limits_{n = t}^N {r_{ijn}^t} } } = 1;\;\; t \in D. $

(7)$ v_n^t = \sum\limits_{i = 1}^S {\sum\limits_{j = 1}^H {\sum\limits_{t' = 0}^t {r_{ijn}^{t'}} } } ;\;\; t \in D;n = 1,\cdots ,M. $

(8)$ \begin{split} x_{ijn}^t =& x_{ijn}^{t - 1}+\sum\limits_{i' = 1}^S {\sum\limits_{j' = 1}^H {y_{i'j'ijn}^t} } - \sum\limits_{i' = 1}^S {\sum\limits_{j' = 1}^H {y_{iji'j'n}^t} } - r_{ijn}^t; \\ & i \in B,j \in C,n \in A;t = 1,\cdots ,T. \end{split} $

(9)$ \begin{split}& \lambda \left(1 - \sum\limits_{n = t+1}^N {y_{iji'j'n}^t} \right) \geqslant \sum\limits_{l = j+1}^H {\sum\limits_{l' = j'+1}^H {\sum\limits_{n = t+1}^N {y_{ili'l'n}^t} } } ; \\ &\qquad i,i' \in B,t \in D;j,j' = 1,\cdots ,H - 1. \end{split} $

(10)$ \begin{split}& \lambda \left(1 - \sum\limits_{j = 1}^H {x_{ijt}^t} \right) \geqslant \sum\limits_{i' \notin {E_t}}^S {\sum\limits_{j = 1}^H {\sum\limits_{k = 1}^S {\sum\limits_{l = 1}^H {\sum\limits_{n = t+1}^N {y_{i'jkln}^t} } } } } ; \\ &\qquad\qquad\qquad\qquad i \in B,t \in D. \end{split} $

(11)$ y_{ijij'n}^t = 0;\;\; i \in B,j,j' \in C,n \in A,t \in D. $

(12)$ \sum\limits_{t = 0}^T {v_n^t} \geqslant \sum\limits_{t = 0}^T {v_{n+1}^t} +1;\;\;n = 1,\cdots ,M - 1. $

式(1)表示最小化料框翻箱次数；式(2)确保每个堆栈中料框的数量不超过层高限制；式(3)确保每个储位最多只能放置1个料框；式(4)表明每个料框都有具体位置，要么在堆料区内，要么已经被检索；式(5)确保堆料区中没有料框处于悬空状态；式(6)确保每个阶段都只执行1次检索操作；式(7)表示决策变量$ {v}_{n}^{t} $与$ {r}_{ijn}^{t} $之间的关系；式(8)表示每个料框从第$ t-1 $阶段到第$ t $阶段的状态变化应满足的条件；式(9)确保在同一阶段从某堆栈翻箱至其他同一堆栈的料框中，后翻箱的料框位于先翻箱料框的上方；式(10)确保每次翻箱操作仅针对目标料框出库路径上的阻碍料框进行；式(11)要求在执行翻箱操作时，料框的落位堆栈不能为原堆栈；式(12)确保出库料框必须按出库序号1~M的顺序完成检索任务.

针对智能叉车密集仓储系统仓库的布局特征和仓储设备的取货特点，根据堆料区料框的堆存状态，制定不同情况下料框的翻箱操作落位堆栈的选取规则，基于这些规则提出快速求解智能密集仓储系统中料框翻箱数上界的启发式方法. 定义启发式方法中的相关概念.

定义1　堆栈优先序号$ {Q}_{i} $. 当堆栈$ i $为空堆栈或堆栈中的料框都不出库时，堆栈的优先序号$ {Q}_{i}=M+1 $，否则，堆栈$ i $中出库序号最小的料框的出库序号为该堆栈的优先序号，即$ {Q}_{i}=\mathop {\min }\limits_{1\leqslant j\leqslant {N}_{i}}{P}_{ij} $.

定义2　待翻箱料框. 3种情形下待翻箱料框的确定方法如下. 1）当目标料框位于外侧堆栈时，待翻箱料框为该堆栈最上方的阻塞料框. 2）当目标料框位于内部堆栈，且四周存在某一路径能够直接对该堆栈的阻塞料框进行翻箱后完成检索任务时，待翻箱料框为该堆栈最上方的阻塞料框. 3）当目标料框位于内部堆栈，且须对出库路径上阻塞堆栈中的料框进行翻箱操作后才能完成检索任务时，待翻箱料框为出库路径上由外到内第1个阻塞堆栈最上方的料框.

定义3　可选落位堆栈. 除了目标料框所在堆栈及出库路径上阻碍目标料框检索的堆栈外，未达到高度限制的能够直接进行叉放作业的其他堆栈.

定义4　$ \mathrm{G} $类可选落位堆栈和$ \mathrm{B} $类可选落位堆栈. 在可选落位堆栈中，堆栈优先序号$ {Q}_{i}=M+1 $及堆栈优先序号高于待翻箱料框出库序号的堆栈为$ \mathrm{G} $类可选落位堆栈，其余堆栈为$ \mathrm{B} $类可选落位堆栈.

基于上述定义，针对不同待翻箱料框和可选落位堆栈的特点，制定6条翻箱操作落位堆栈的选取规则.

规则1　存在$ \mathrm{G} $类可选落位堆栈，且待翻箱料框需要出库，则最终落位堆栈为$ \mathrm{G} $类可选落位堆栈中堆栈优先序号最小的堆栈.

规则2　存在$ \mathrm{G} $类可选落位堆栈，且待翻箱料框不需要出库，同时内部堆栈中存在$ \mathrm{G} $类可选落位堆栈，则最终落位堆栈在内部堆栈的$ \mathrm{G} $类可选落位堆栈中选取，若存在多个，则选择其中编号最小的堆栈.

规则3　存在$ \mathrm{G} $类可选落位堆栈，且待翻箱料框不需要出库，同时角落堆栈中存在$ \mathrm{G} $类可选落位堆栈但内部堆栈中不存在$ \mathrm{G} $类可选落位堆栈，则最终落位堆栈在角落堆栈的$ \mathrm{G} $类可选落位堆栈中选取. 若存在多个，则选择其中编号最小的堆栈.

规则4　存在$ \mathrm{G} $类可选落位堆栈，且待翻箱料框不需要出库，但内部堆栈和角落堆栈中都不存在$ \mathrm{G} $类可选落位堆栈，则最终落位堆栈为$ \mathrm{G} $类可选落位堆栈中堆栈优先序号最大的堆栈.

规则5　可选落位堆栈全为$ \mathrm{B} $类，并且其中堆栈优先序号最大的堆栈只有1个空储位时，则最终落位堆栈为$ \mathrm{B} $类可选落位堆栈中堆栈优先序号次大的堆栈.

规则6　可选落位堆栈全为$ \mathrm{B} $类，并且其中堆栈优先序号最大的堆栈空储位数大于1时，则最终落位堆栈为$ \mathrm{B} $类可选落位堆栈中堆栈优先序号最大的堆栈.

基于上述规则的启发式算法见算法1. 根据该流程算出启发式算法的时间复杂度为$ O\left(2M{SH}^{2}\right) $.

算法1　　启发式算法

输入：堆料区布局$ r\times c\times H $、料框数量$ N $、需出库料框数量$ M $、料框检索优先级$ {P}_{ij} $等相关参数

输出：翻箱路径$ \delta $和总翻箱次数$ Z $

1：初始化堆料区堆存状态

2：while $ M > 0 $ do

3：确定目标料框在堆料区中的位置

4：if 目标料框能被检索 do

5：检索目标料框，更新堆料区堆存状态，$ M-- $

6：else do

7：选择出库路径并确定待翻箱料框

8：根据翻箱操作落位堆栈选取规则1~6确定最终落位堆栈并进行翻箱操作

9：获取本次翻箱路径并更新堆料区堆存状态，Z++

10：end if

11：end while

12：输出翻箱路径$ \delta $和总翻箱次数$ Z $

智能叉车密集仓储系统中料框翻箱问题的下界是指在最理想的情况下至少进行多少次翻箱操作才能按要求完成出库作业任务. 下界的计算在分支定界算法中至关重要，通过计算各分支的下界，可以对分支进行修剪，从而减少搜索空间，加快算法的搜索效率，且计算获得的下界越接近实际下界，算法的性能越好. 在对下界进行计算时，必须确保计算值不高于真实下界，这样所得的下界才能被接受.

料框翻箱次数的下界与堆料区中阻塞料框的数量及其翻箱操作后对落位堆栈中料框的影响有关. 当目标料框位于内部堆栈且须对出库路径上阻塞堆栈中的料框进行翻箱时，可能会产生额外翻箱. 在本研究中，料框翻箱次数下界的计算方法分成3个部分，先在初始布局下直接计算，接着在布局更新过程中进行逐步计算，具体说明如下. 1）堆料区内的料框必须按照给定的出库顺序完成检索任务，当存在出库序号较大的料框位于出库序号较小且需要出库的料框的上方时，须对上方的阻塞料框至少进行1次翻箱操作. 2）当目标料框位于内部堆栈且不能仅通过对该堆栈的阻塞料框进行翻箱后完成其检索任务时，须对出库路径上阻塞堆栈中某些料框进行翻箱操作. 若该目标料框为当前布局中最先出库的料框或在检索该目标料框之前的其他料框时未发生翻箱操作，则可以考虑阻塞堆栈中料框翻箱时产生的额外翻箱次数（注意不要重复计算该堆栈中部分1）已经计入下界的阻塞料框数量）. 3）当某待翻箱料框的出库序号大于所有可选落位堆栈的堆栈优先序号时，说明该料框之后会再次称为阻塞料框，产生二次翻箱. 部分3）下界计算方法：从当前目标料框开始，检查对应阻塞料框在翻箱后是否一定会产生二次翻箱，之后将目标料框和对应的阻塞料框从堆料区中移除，重复上述操作直至堆料区中所有需要出库的料框均被移除. 需要注意的是，当为了检索内部堆栈的料框而对出库路径上阻塞堆栈中的料框进行翻箱，且在此之前存在翻箱操作时，该部分下界值的计算应终止，原因是此时已经无法确定检索内部堆栈中目标料框的出库路径.

使用分支定界算法求解智能叉车密集仓储系统料框翻箱问题的基本思路：将问题的解空间划分为多个子空间，对每个子空间进行搜索并进行剪支，找到问题的最优解. 使用分支定界算法求解该问题的具体步骤如下.

1）初始化. 初始化堆料区料框的堆存状态和检索顺序，使用启发式方法和料框翻箱次数下界求解方法计算初始布局的上界$ {\mathrm{U}\mathrm{B}}_{0} $和下界$ {\mathrm{L}\mathrm{B}}_{0} $，设该布局当前最优上界$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{U}\mathrm{B}}_{0} $，当前最优下界$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{L}\mathrm{B}}_{0} $. 若$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $，则此时启发式求解结果即为最优解；当$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} < {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $时，则须进行多轮迭代深化搜索来获得最优解，且每轮迭代开始时都以初始堆存状态为根节点.

2）分支. 在限制性料框出库翻箱问题中，每次翻箱有1个待翻箱料框和1~$ S-1 $个可选落位堆栈，根据当前节点对应的堆存状态，确定目标料框、待翻箱料框和可选落位堆栈，将待翻箱料框翻箱至每个可选落位堆栈，形成新的堆存状态作为新的分支.

3）剪支. 分支定界算法的搜索树中深度为$ k $的分支集合表示堆料区中料框从初始状态开始经$ k $次翻箱后得到的分支节点集合，对于步骤2）中产生的每个新的分支状态$ \varphi $，都使用料框翻箱次数下界计算方法求解该分支状态的下界$ \mathrm{L}\mathrm{B}(\varphi ) $，若某分支状态的下界与搜索深度的和大于当前最优下界（$ \mathrm{L}\mathrm{B}(\varphi )+k > {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $），则在该轮搜索中将该分支节点剪除.

4）更新界限. 当搜索树中的分支满足下界与搜索深度的和等于当前最优下界减1（$ \mathrm{L}\mathrm{B}(\varphi )+ k= {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}-1 $）时，将使用快速求解的启发式方法求解该分支状态的上界$ \mathrm{U}\mathrm{B}(\varphi ) $；当该分支状态的上界与搜索深度的和小于当前最优上界（$ \mathrm{U}\mathrm{B}(\varphi )+ k < {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $）时，更新当前最优上界$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=\mathrm{U}\mathrm{B}(\varphi )+ k $；若$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}= {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $，则根据搜索树中到达该节点的分支路线和当前节点的启发式结果即可找到最优解.

5）选择分支. 从当前节点未被剪除和遍历的分支节点集合中选择下界值最小的分支节点作为新的当前节点. 若新的当前节点为叶子节点，即所需出库料框均已被检索，则达到该叶子节点的分支路线即为最优解；否则，重复步骤2）~5）. 若当前节点的所有分支都被剪除或遍历，则将该当前节点标为已遍历，并回溯至上一层继续寻找下界最小的分支节点作为新的当前节点，直至回溯到根节点. 当回溯到根节点时，当前最优下界自增1，即$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}+1 $，若此时$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $，则当前最优上界对应节点的启发式结果为最优解；否则，返回步骤2），以初始堆存状态为根节点开始新一轮的搜索.

综上所述，找到最优解的终止条件有2个：1）在遍历某节点时，当前最优上界等于当前最优下界，即$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $，则最优策略为该节点对应的启发式求解结果；2）迭代搜索到叶子节点，则最优策略为达到该叶子节点的分支路线. 为了防止求解时间过长，可以预设求解时限，则最优策略由到达预设时限时当前最优上界$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $对应节点的分支路线和启发式结果确定. 使用分支定界算法求解智能叉车密集仓储系统料框出库翻箱问题的整体流程见算法2. 根据该流程算出分支定界算法的时间复杂度为$ O\left(2{M}^{2}{{S}^{2H}H}^{2}\right) $.

算法2　　分支定界算法

输入：堆料区布局$ r\times c\times H $、料框数量$ N $、需出库料框数量$ M $、料框检索优先级$ {P}_{ij} $等相关参数

输出：全局最优解B

1：初始化堆料区堆存状态

2：计算初始布局启发式上界$ {\mathrm{U}\mathrm{B}}_{0} $和下界$ {\mathrm{L}\mathrm{B}}_{0} $，令$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{U}\mathrm{B}}_{0} $，$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{L}\mathrm{B}}_{0} $

3：while $ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $> $ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $ do

4：初始化搜索深度$ k=0 $

5：while $ M > 0 $ do

6：确定目标料框在堆料区中的位置

7：if 目标料框能被检索 do

8：检索目标料框，更新堆料区堆存状态，$ M-- $

9：else do

10：选择出库路径并确定待翻箱料框、可选落位堆栈

11：将待翻箱料框翻箱至所有可选落位堆栈形成新的分支

12：计算各分支下界$ \mathrm{L}\mathrm{B}(\varphi ) $，并对该层分支进行修剪

13：对有希望的分支进一步探索，更新当前最优上界$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $

14：if $ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}={\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}} $ do

15：当前解为最优解，结束搜索，输出全局最优解B

16：end if

17：选择分支继续迭代搜索，更新搜索深度$ k $

18：if $ k==0 $ do

19：更新下界，即$ {\mathrm{L}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}++ $，返回第3步进行下一轮搜索

20：end if

21：end if

22：end while

23：最优解为从初始状态到该叶节点的分支路线，$ {\mathrm{U}\mathrm{B}}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=k $

24：end while

25：输出全局最优解B

为了验证算法的有效性和实用性，基于某公司仓储系统的实际运行情况，随机生成不同堆料区布局、不同储量、不同空位数以及不同出库量下的大量算例，对比分支定界算法与随机、就近策略下的翻箱次数和出库效率. 算例中堆料区规模为3×3×5~3×8×5和4×4×5~4×7×5，为了满足翻箱空位数要求，空储位数设置在总储位数的20%~40%，出库量设置在存储量的30%~70%. 共生成算例28组，每组算例随机生成10个符合条件的不同堆存状态. 算法使用C语言在Visual Studio 2022软件上进行编码. 求解采用Intel i7-12700 CPU@2.1 GHz、16 GB RAM台式电脑，操作系统为Windows 11，每个算例的求解时间上限为300 s.

启发式方法、分支定界算法及下界求解方法的算例计算结果如表2、表3所示，表中数据为每组算例中10种不同堆存状态下求解结果的平均值，R为翻箱次数，t_a为算法耗时，t_opt为分支定界算法获得限定时间内最优解的实际耗时. 其中阻塞料框数量均值大小反映该组算例初始堆存状态下作业的难易程度，通常来说，阻塞料框数量越多，求解难度越高. 由表2可以看出，在小规模算例中（料框数量为0~45），启发式方法和分支定界算法都能在极短的时间内求解，甚至接近于0 s，且启发式方法平均13.88次翻箱与分支定界算法平均13.62次翻箱较为接近，表明这2种方法都能够高效求解小规模问题. 随着堆料区规模的增大和料框数量的增加，在中型规模算例中（料框数量为46~70），启发式方法仍能在较短的时间给出结果；相比之下，分支定界算法的求解时间增加，但能够在给定时间内获得问题的最优解或近似最优解. 随着堆料区规模的增大和出库需求的不断增加，阻塞料框和翻箱次数增加，问题的求解难度也随之增加. 由表3可以看出，在大规模算例中（料框数量为71~120），分支定界算法平均39.79次翻箱优于启发式方法41.55次翻箱，但启发式方法仍能快速提供有效的翻箱方案；相反，分支定界算法难以在短时间内求得理论最优解. 原因是随着问题规模的增大，计算量呈指数级增长，求解时间急剧增加. 但计算结果表明，分支定界算法能够在给定计算时间内对启发式结果进一步优化并给出较好的翻箱方案.

为了深入分析堆料区规模和布局对分支定界算法性能的影响以及存储密度（存储密度=料框数量/总储位数）和出库率（出库率=出库需求/料框数量）对料框翻箱次数的影响，对表2、表3中的数据进行详细分析. 分析结果表明，在存储密度和出库率保持不变的情况下，随堆料区规模的增大，分支定界算法的求解时间明显增加（如表2中的第3和第7组算例）；随堆料区布局复杂度的提升，分支定界算法求得最优解耗时延长（如表3中的第6和第10组算例）. 在堆料区布局保持一致的情况下，当出库需求相同，存储密度提高时，料框的堆积更紧密，会导致料框翻箱次数增加（如表2中的第10和11组算例）；当存储密度相同，出库率增加时，阻塞料框的数量随之增加，进而增加料框翻箱次数（如表2中的第11和12组算例）. 由表2和表3可知，分支定界算法求解时间对堆料区规模、料框数量以及料框出库需求非常敏感. 特别是当堆料区规模超过4×6×5时，所有算例求解时间都超出预设的时间限制. 进一步分析实验结果，在各组算例中，分支定界算法能够在较短的时间内对初始方案进行优化并给出设定时间内的近似最优解，平均优化耗时均不超过40 s.

综上所述，启发式方法具有计算速度快、适应性强的特点，适用于实时性要求较高的场景；分支定界算法虽然需要更长的求解时间，但在精度要求较高的情况下，能够提供更为精确的解. 在实际应用中，可根据具体需求合理设置求解时间，以确保算法在有限时间内提供高质量的解决方案.

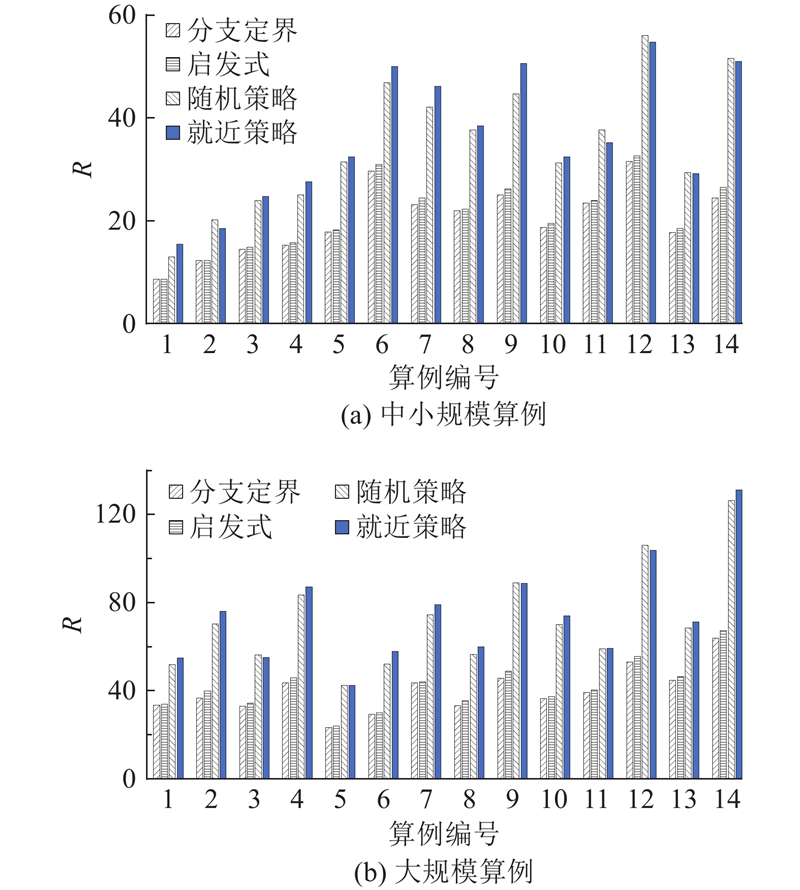
经调研发现，在某些企业的密集仓储系统中，使用前移式智能叉车进行料框翻箱作业时，翻箱落位堆栈的选择通常采用随机策略或就近策略. 随机策略即在可选落位堆栈中随机选择最终落位堆栈，就近策略即在可选落位堆栈中选择距离（本实验选用曼哈顿距离）最近的堆栈作为最终落位堆栈. 为了验证启发式方法和分支定界算法的性能表现，使用上述2种翻箱策略对算例进行求解. 如图4所示，在中小规模和大规模布局下，采用随机策略平均分别需要34.90和71.66次翻箱，采用就近策略平均分别需要36.01和74.05次翻箱，分支定界算法相较于随机翻箱策略翻箱次数平均减少了42.16%、44.48%. 结果表明，相比随机策略和就近策略，采用启发式和分支定界算法求解智能叉车密集仓储系统料框出库翻箱问题能明显减少料框出库翻箱次数，极大提高了仓储系统的作业效率.

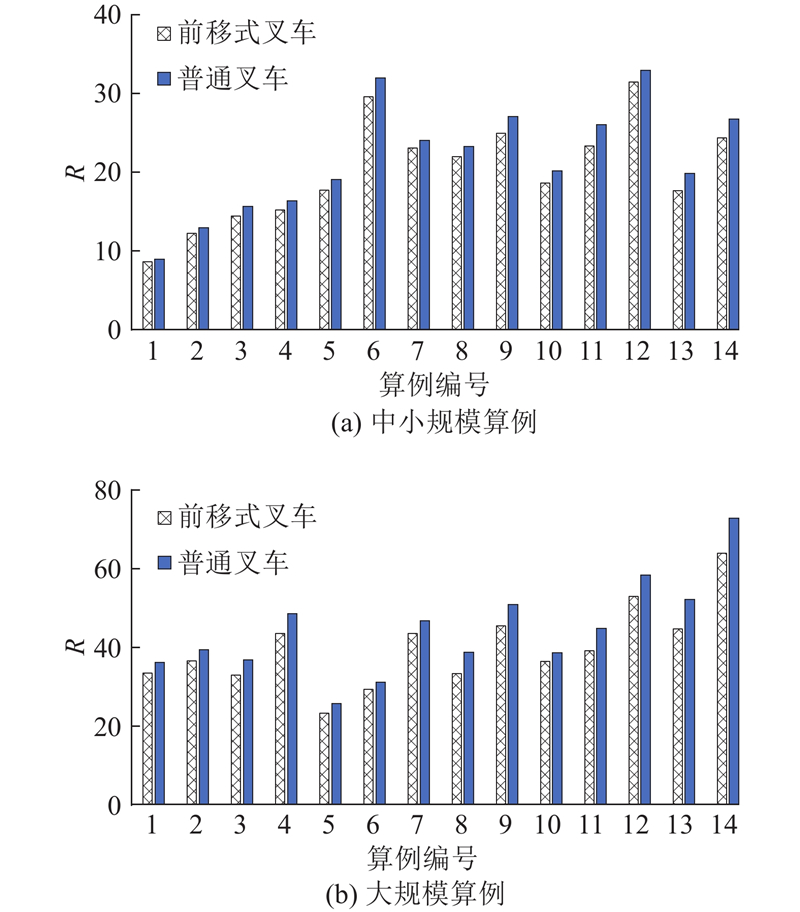
仓储设备的选择也会影响出库效率. 与普通叉车相比，前移式智能叉车具备可伸缩的货叉，能够适应多个料框长度方向上物料的搬运需求，在处理位于内部堆栈中的料框时具有明显优势. 为了对比分析不同仓储设备的出库性能，针对使用普通叉车的仓储环境，采用分支定界算法求解算例，对比实验结果如图5所示. 在中小规模和大规模布局下，使用普通叉车平均分别需要21.74和44.23次翻箱，前移式智能叉车相较于普通叉车翻箱次数平均分别减少了7.13%、10.05%. 结果表明，使用前移式智能叉车能在一定程度上减少检索内部堆栈料框产生的额外翻箱，有效提升密集仓储系统的吞吐量和出入库效率.

本研究针对智能叉车密集仓储系统中料框的翻箱问题，在考虑料框堆存约束、作业优先约束和智能叉车存取约束的基础上，构建问题的数学规划模型，提出快速求解料框翻箱方案的启发式方法，并给出该问题下界的计算方法，利用启发式方法作为上界的求解算法，设计相应的分支定界算法. 算例分析表明，启发式方法和分支定界算法均能够在小规模算例中进行高效率求解；在处理中大规模算例时，使用分支定界算法寻找问题的最优解需要更多的时间，但能够在较短时间内对初始翻箱方案进行有效优化，得到较优解. 将所提算法与随机和就近翻箱策略的性能进行对比分析，结果表明所提算法能够减少超过40%的翻箱次数，验证了算法的有效性和实用性. 开展对比分析实验，研究不同类型仓储设备对料框出库效率的具体影响. 结果表明，前移式智能叉车相较于普通叉车能够减少超过7%的翻箱次数，展现了前移式智能叉车在密集仓储系统中的显著优势. 本研究通过优化翻箱策略来减少料框翻箱次数，大幅提升了仓储系统的作业效率和质量，整体研究成果可以为智能叉车密集仓储系统的高质量管理提供参考. 本研究在探索智能叉车密集仓储系统料框出库翻箱问题的有效解决方案方面取得了初步成果，但要为智能仓储系统提供更全面和高效的优化策略还存在一定挑战. 为了适应不断变化的仓储需求和条件，未来的研究计划从以下几个方面进行深化与拓展：1）探寻更优的翻箱规则，设计更高效的启发式算法，提高问题下界的精度，增强分支定界算法的性能. 2）针对大规模布局翻箱次数较多的问题，考虑设置临时存储堆栈以减少料框翻箱次数提高货物出库效率. 3）深入探讨动态仓储环境下料框出库作业时的翻箱与调度优化问题.