文献[8]的研究表明,可达集方法适用于动态不确定的结构化场景. 该方法通过车辆运动模型计算时空可达状态集,在最后时刻选择最优行驶区域,基于后向可达集生成驾驶走廊[9]. 然而,基于可达集的传统方法本质上属于被动反应式规划,因忽视整体交通效率常导致保守驾驶行为,进而造成交通拥堵. 近来可达集的发展趋势是采用更多的场景语义信息[10-11]. 在复杂场景下,为了提升智能体与其他交通参与者的行为交互能力,常采用基于学习的决策规划算法. 其中,模仿学习多用于端到端规划构型;而考虑到安全性和可解释性,强化学习更适合分层架构中的行为决策[12]. 强化学习在智能体与环境的交互中寻找一种状态到动作的映射,通过试错最大化长期奖励达到学习的目的,其基础模型框架是马尔科夫决策过程(Markov decision process, MDP). 基于强化学习的决策模型可在强交互场景下输出安全高效的宏观驾驶行为[13],并作为生成驾驶走廊的重要启发信息. 然而,其不具备明确的时间信息,难以为路径规划提供高质量的启发函数与边界约束,故当前研究趋势是将强化学习与规则型方法融合[14-16].
传统可达集方法通常包括4个步骤:前向可达集生成、可行驶区域分割、驾驶走廊生成、轨迹优化. 本研究针对区域分割与走廊生成环节进行优化,即避免过多的划分子集和对子集的计算处理,从而避免同一种行为下的子集过多;利用多步强化学习决策明确关键行为的时间帧,以更准确地生成驾驶走廊. 本研究的主要贡献在于将强化学习和可达集方法相结合,将强化学习预训练的结果作为先验知识,通过横纵向语义谓词实现可行域的高效分割,从而在动态不确定场景中生成更优驾驶走廊并提升计算效率. 相比于单一规划方法,本研究首次提出基于集合+学习的融合型决策规划框架,充分发挥两者的优点,一方面利用强化学习模型的多步决策引导可达集规划,避免现有可达集方法在驾驶走廊生成过程中的保守和低效;另一方面,可达集的轨迹优化过程为上层强化学习的行为决策提供安全校验,从而使决策规划算法更好地满足安全性、舒适性、高效性和实时性等综合性能要求.
1. 结合强化学习的可达集总体框架
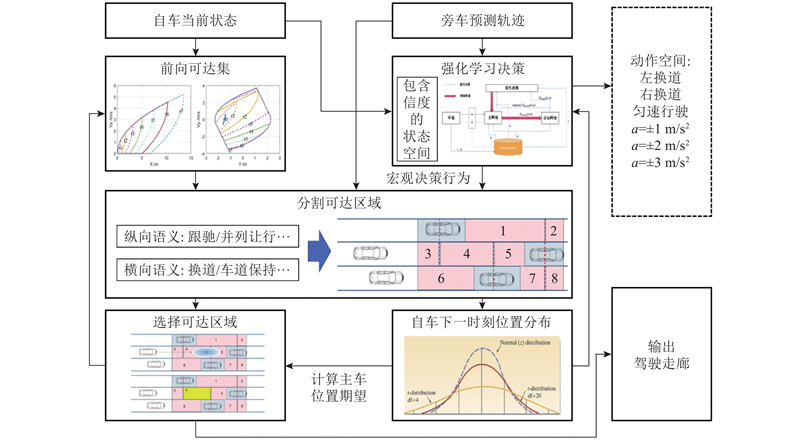
强化学习多步决策结合可达集时空耦合规划的算法架构如图1所示. 该算法由考虑不确定性的强化学习决策和基于驾驶语义的行驶区域划分2个部分组成,两者都有各自的控制闭环并且共同决定驾驶走廊的生成. 其中,强化学习决策模块基于每一时刻的车辆状态(包括位置、速度及不确定性等),进行自车行为决策,输出离散驾驶动作,决定车辆的宏观运动意图. 行驶区域划分模块则根据不同行为语义,将当前可达区域细分为多个具有驾驶语义的凸空间,为最优区域的选择提供候选集合.
图 1
图 1 强化学习决策引导下的可达集规划架构
Fig.1 Reachable set programming architecture guided by reinforcement learning decision
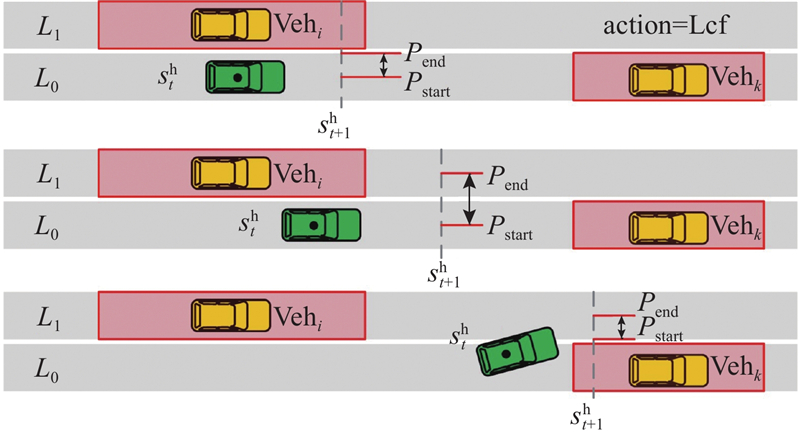
所提算法的输入为自车的当前状态、旁车的预测轨迹及各时刻位置分布. 其中,自车状态用于生成下一时刻的前向可达集;自车与旁车的位置及其不确定性分布则作为强化学习模型的输入,以输出行为决策. 整体规划流程如下. 1)通过自车上一时刻所选择的最优行驶区域集合计算当前时刻车辆的前向可达空间,同时基于上一时刻的自车和障碍物状态通过强化学习决策模型获得上一时刻的最优驾驶行为;2)基于前向可达空间以及车辆上一时刻驾驶行为进行基于驾驶语义的区域分割,将前向驾驶区域分割为代表不同驾驶语义的有限个可行驶空间;3)根据决策驾驶行为计算自车在本时刻的期望位置分布,据此计算自车处于每个可行驶区域的概率期望,并选取期望值最高的区域作为当前最优行驶区域;4)将本时刻的最优行驶区域及自车位置分布反馈至模型,用于迭代计算下一时刻的可达集与决策行为. 通过可达集规划输出驾驶走廊,即可完成凸空间的构建. 由于篇幅所限,在驾驶走廊内进行轨迹凸优化的具体求解过程请见文献[8].
2. 强化学习决策模型
抽象的行为决策主要依据每时刻的障碍物位置、速度、自身的位置、速度以及交通规则等信息,作出宏观的驾驶行为判断,从而引导车辆选择正确的驾驶行为[17]. 根据行为决策的特点,采用DDQN(Double Deep Q-Leaning)强化学习算法选择离散的驾驶行为,并从状态空间、动作空间、奖励函数3个方面进行驾驶决策的MDP建模.
2.1. 状态空间
状态空间中包含智能汽车所需的自车信息以及周围旁车信息,表达式如下:
式中:
2.2. 动作空间
考虑到宏观行为的可解释性,驾驶动作选择离散动作,分为纵向动作以及横向动作,表达式如下:
式中:
2.3. 奖励函数
本研究MDP模型中的奖励函数主要由以下几个方面组成.
1)发生碰撞. 当智能汽车与其他车辆发生碰撞时,将立即终止当前回合并给予较大的负奖励,表达式如下:
2)安全性. 考虑TTC与THW这2个指标来对碰撞风险进行评估,各自对应的风险值定义表达式如下:
式中:TTC为考虑2辆车继续按照当前的车速以及车道行驶发生碰撞的时间;THW为跟车时距,即自车与前车之间的时间间隔;
式中:
3)期望速度. 智能汽车希望尽可能以期望车速行驶,因此期望车速项设置表达式如下:
式中:
4)行驶舒适性. 过于频繁或者幅度过大的加减速会影响乘坐舒适性,同时为了避免不必要的换道,设定行驶舒适性指标表达式如下:
式中:
3. 基于驾驶语义的可行驶区域分割
3.1. 横向可行域分割
横向语义主要通过自车实际位置
基于车辆横向驾驶行为所定义的谓词
表 1 横向需搜索的谓词
Tab.1
| 决策出的驾驶行为 | 需搜索谓词 |
图 2
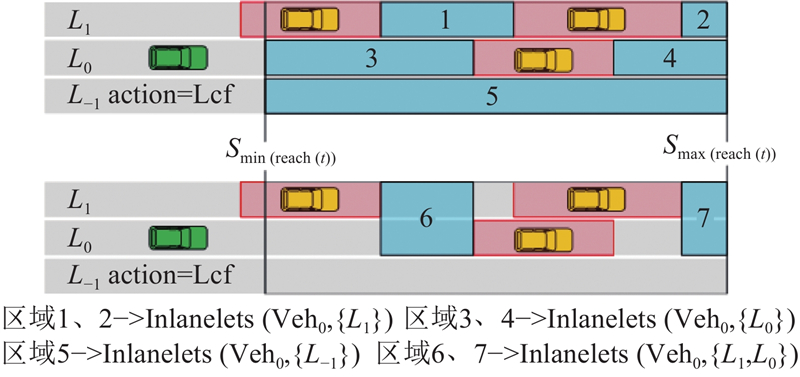
图 2 横向语义分割结果示意图
Fig.2 Schematic diagram of horizontal semantic segmentation results
3.2. 纵向可行域分割
在横向语义模块将可达区域分割为有限个可行驶区域集合后,基于纵向意图对区域集合做进一步分割. 其中,纵向意图主要考虑与自车道车辆的相对位置,以及与潜在目标车道上旁车的相对位置. 纵向驾驶语义分割也分为2种情况:当目前车辆并没有处在换道过程中时,自车所在车道的区域划分考虑两侧车道的所有旁车;当目前车辆正处于换道过程中时,仅考虑本车道和目标车道的旁车. 对于和旁车的相对位置,采用3个谓词进行描述:
式中:
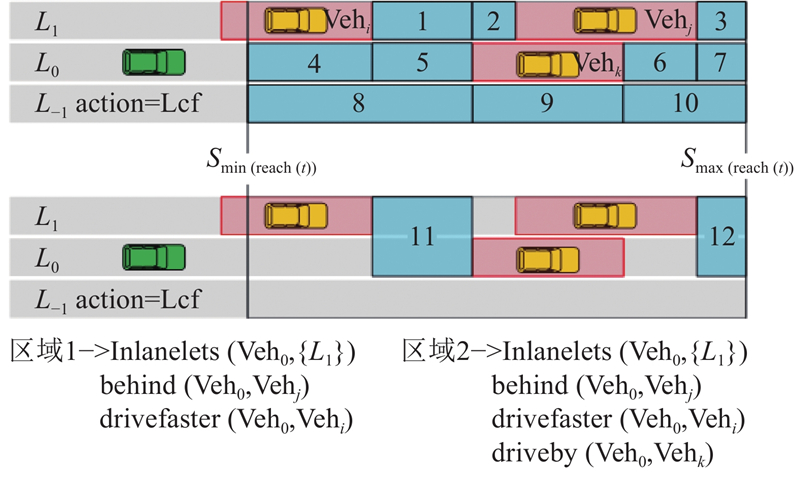
将横向语义区域分割得到的区域逐个输入进行遍历搜索,进一步分割出使得特定参数下满足纵向谓词定义的区域,以上节横向语义区域分割结果为例,决策行为依然为向左侧换道,最终的备选区域的分割结果如图3所示. 每个区域内的所有状态点均满足相同的谓语定义,以保证可行驶区域内驾驶语义的一致性.
图 3
4. 驾驶走廊生成
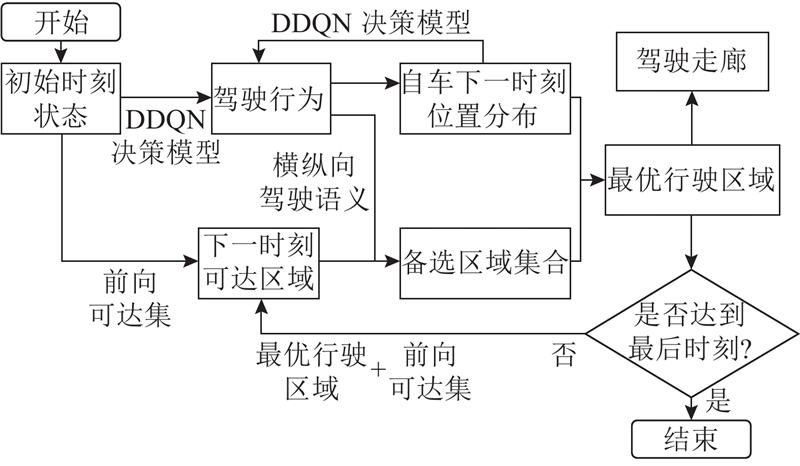
在得到强化学习决策模型和基于驾驶语义的可行驶区域分割模型后,便可进行驾驶走廊的生成,并进一步在驾驶走廊内完成轨迹凸优化,具体流程如图4所示.
图 4
从初始状态开始,通过计算自车初始状态的前向可达集获得第1个时刻的可达区域. 通过初始状态得出第1个驾驶动作,得到驾驶行为之后在对可达区域进行分割的同时,要对自车的当前时刻的状态进行推算. 推算出的新状态与此时刻的旁车状态一起,作为下一次决策模型的输入量,也是这一时刻下最优行驶区域的选择依据.
自车状态推算分为纵向和横向2部分. 首先进行纵向部分计算,根据决策动作的加速度和当前纵向位置可得出:
式中:
横向位置基于自车当前的换道状态得出. 强化学习模型在输出一次换道动作后,认为在未来3 s内车辆会以固定横向速度完成换道动作. 但实际换道过程中的具体轨迹和换道速度须依据周围车辆的状态决定,横向位移
式中:
图 5
在得到车辆下一时刻的位置后,通过前3个时刻的自车状态计算下一时刻的自车的位置分布. 本研究通过3个位置点进行多项式拟合来得到自车在下一时刻的曲率和加速度,然后根据自车位置的二维高斯分计算其在每个备选区域内的期望值,并选取期望值最高的区域作为该时刻的最优行驶区域.
5. 实验结果
5.1. 动态不确定测试场景
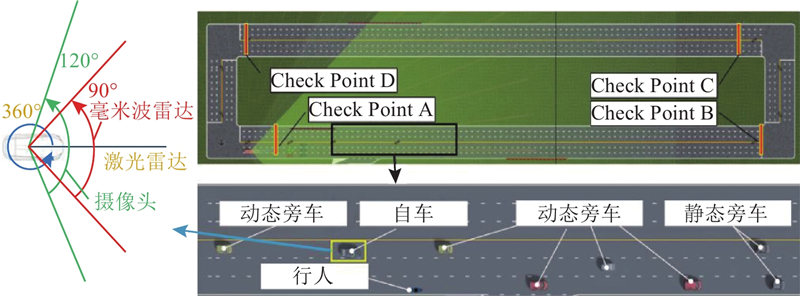
设计了一个可随机生成交互式交通参与者的环形测试场景,并通过长时间测试结果的统计分析及典型corner case对比,验证所提出算法的有效性与鲁棒性. 如图6所示,直线路段总长为750 m,限速为15 m/s. 路中设置4个检查点,当主车经过检查点A、C时,会自动生成分布在3个车道的9辆动态车辆和2辆静态车辆和1个行人. 静态车辆的位置为随机生成,行人生成位置固定,并且以1 m/s的速度横穿马路. 动态车辆生成位置、初始速度、期望车速均为随机分布,并分别通过MOBIL(minimizing overall braking induced by lane-changes)和IDM(intelligent driver model)模型进行换道决策以及速度控制[20-21].
图 6
表 2 测试场景随机变量分布参数
Tab.2
| 参数 | 随机变量 |
| 1)注:U表示随机变量服从区间( )上的均匀分布. | |
| 车辆初始位置(前)/m | |
| 车辆初始位置(中)/m | |
| 车辆初始位置(后)/m | |
| 静止车辆初始位置/m | |
| 静止车辆压线概率/% | |
| 车辆初始车速/(m·s−1) | |
5.2. 强化学习模型训练
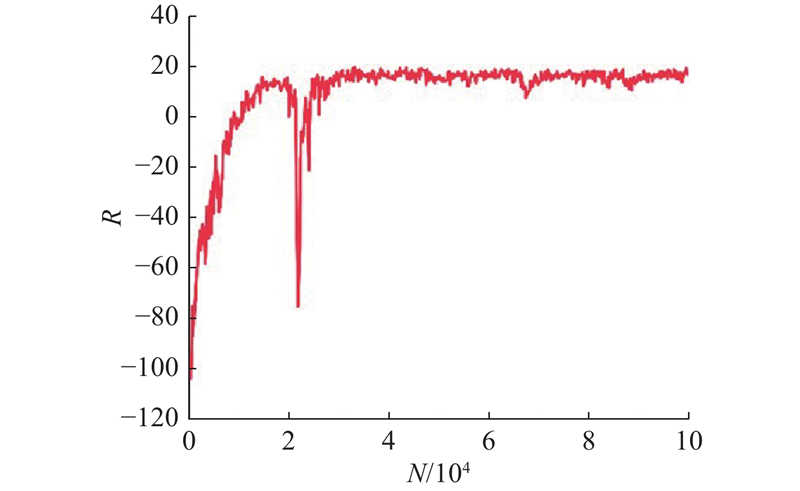
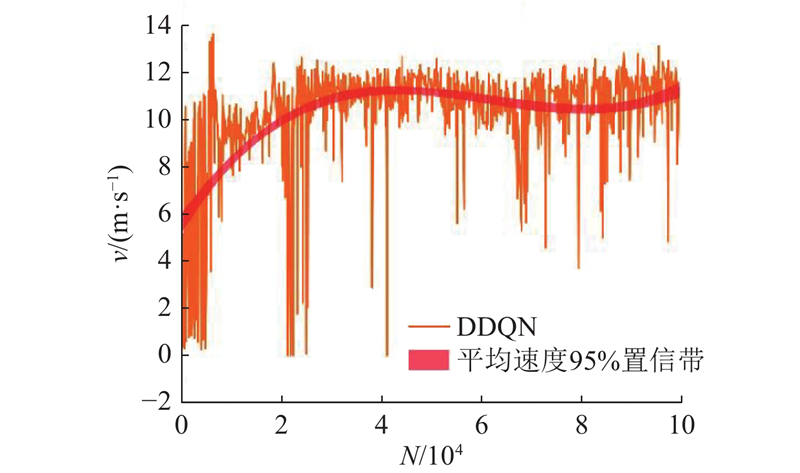
为了便于针对上述场景开展强化学习决策模型的训练,在SUMO仿真平台中同样搭建了3车道直道,总共11辆旁车的训练环境. 其中,2辆静止车辆会在3个车道内随机刷新位置,而9辆动态车辆的初始速度和期望速度均为8~12 m/s的随机值,其驾驶行为由SUMO自带的IDM和LC2013模块控制. 最后,将第2章搭建的强化学习模型在该仿真场景下进行训练,将MDP建模中的换道时长和表征纵向动作的期望加速度分别设为3 s和[4,−2,−1,0,1,2] m/s2,而模型中超参数选取如表3所示.
表 3 强化学习模型的主要超参数
Tab.3
| 参数名称 | 描述 | 参数值 |
| 隐藏层参数 | 各层神经元数 | (256,128) |
| 折扣系数 | 计算长期折扣奖励 | 0.99 |
| 探索系数 | ε-贪心算法 | 1.0 |
| 学习率衰减率系数 | 学习率减小比例 | 0.8 |
| 最小学习率 | 学习率的最小值 | |
| 学习率衰减步 | 每隔一定训练步长减小学习率 | |
| 激活函数 | 增加神经网络的非线性 | Relu |
| 损失函数 | 计算拟合误差传播梯度 | Huber-Loss |
| 批量大小 | 单次训练抽取的样本数 | 32 |
| 软更新速率 | 目标网络更替系数 | 0.01 |
| 经验池尺寸 | 存储训练样本 | |
| 梯度截断 | 梯度传播最大值 | 10 |
| 网络优化器 | 梯度下降算法 | Adam |
图 7
图 8
5.3. 不确定场景测试结果
基于Prescan将所提出的算法与对比算法在动态不确定场景中总共运行
表 4 动态不确定场景统计对比结果
Tab.4
除了证明强化学习决策引导的可达集规划算法针对动态不确定场景的有效性和鲁棒性之外,还统计了不同算法的实时性能. 将可达集算法在配备intel i7-9700 3 GHz CPU和16 GB DDR3内存的计算机上的Matlab2020和Visual Studio Code 2017中实现,统计结果表明,虽然计算时间仍有优化空间,但所提出的可达集算法的实时性优于其他可达集算法. 与基于动态规划的可达集方法相比,所提方法同样考虑了场景不确定性,但由于省略了风险概率计算,其求解速度提升了约2倍. 因此,从表4中可以得出基于强化学习的可达集算法在安全性、舒适性、通行效率和实时性4个维度具有更好的综合性能.
5.4. 典型场景测试结果
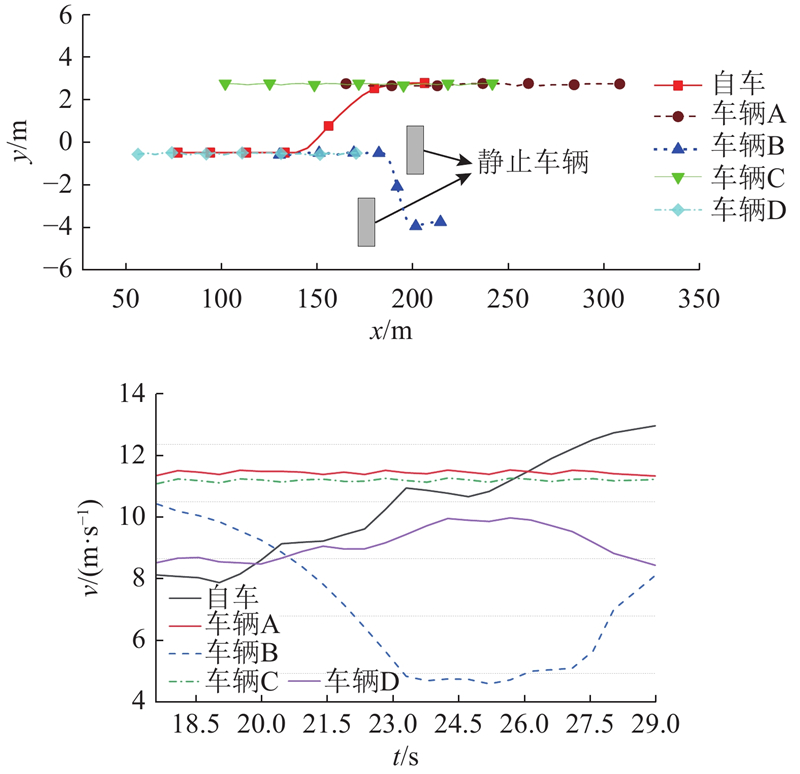
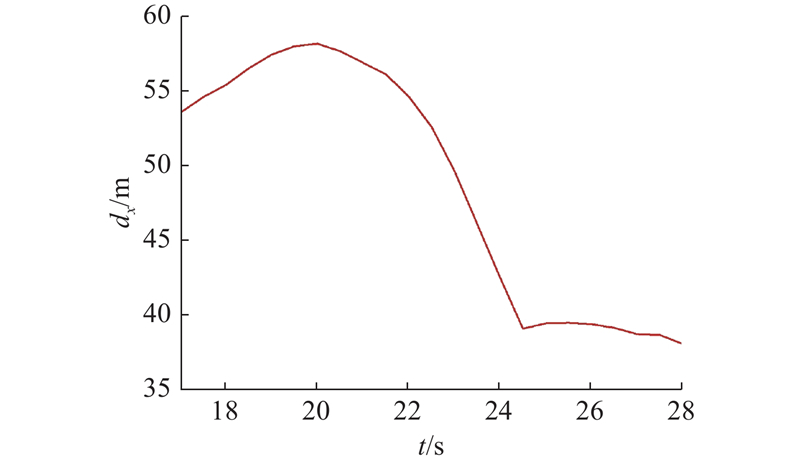
在完成长时测试的宏观统计后,提取其中一次随机产生过的典型Corner Case场景进行详细分析. 具体场景为三车道中两车道被静止车辆占据,自车须与其他动态车辆共用一条车道行驶,如图9所示.在第18 s时,自车在中间车道行驶,静止车辆分别停放在中间车道距自车125 m和右侧车道距自车100 m处. 动态旁车须通过左侧车道继续向前行驶,但旁车B由于已减速至低速,因此最终选择从2个静止车辆中间穿过,并未换道至左侧车道. 除此之外,左侧车道有2辆旁车C、A,自车后方20 m处有1辆旁车D在跟车行驶. 在第18 s,自车初速度为 8.5 m/s,其轨迹、速度变化以及与前车的车距变化如图10、11所示. 其中,t为时间. 从图中轨迹可以看出,自车在第21 s时开始向左换道,换道时长为3 s,并于第24 s 开始跟随前车行驶. 从速度曲线中可以看出,由于一开始道路被2个静止车辆影响,交通较为拥堵,自车一直处于较低车速. 但是在换道过程中和换道完成后自车一直处于加速状态,并在10 s内将车速回升到14 m/s,保证了交通效率. 从与前车的纵向距离曲线中可以看出,自车与前车车距始终大于37.5 m,车间时距为2.5 s,因此保证了车辆行驶安全性.
图 9
图 10
图 10 典型场景下的轨迹和速度结果
Fig.10 Trajectory and velocity results under a typical scenario
图 11
图 11 典型场景下自车与前向车距结果
Fig.11 Results of forward vehicle distance from vehicle in a typical scenario
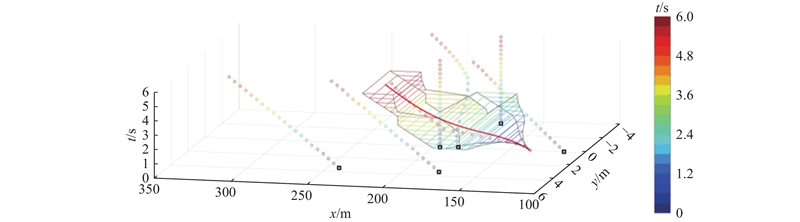
如图12所示为自车在第20 s生成的驾驶走廊以及规划轨迹结果. 可以看出,可达集算法可在强化学习决策的引导下规划出合理的驾驶走廊. 通过最终获得的三维时空轨迹可以看出,所提出的规划算法可以根据当前自车状态,在换道的同时,适当进行速度调整,从而在保证舒适性的前提下提高车辆的行驶效率.
图 12
图 12 典型场景下第21 s时的驾驶走廊
Fig.12 Driving corridor at 21 seconds in a typical scenario
6. 结 语
提出由强化学习多步决策引导的可达集算法框架,旨在提升传统可达集方法在动态不确定交通场景中的有效性与实时性. 该方法不仅引入基于离散动作空间的 DDQN 强化学习模型用于决策引导,还结合基于横纵向谓词判断的可行驶区域划分方法,有效降低了各时刻备选区域的数量,并提升了语义分割的准确性. 长时间随机测试结果表明,与其他2种可达集基线算法(传统可达集/基于动态规划的可达集)相比,所提出的强化学习引导的可达集算法在行驶效率上分别提升了22.1% 和10.9%,在行驶舒适性上分别提升了44.0% 和6.4%. 此外,该算法在动态不确定场景下亦表现出良好的安全性与实时性. 对测试过程中典型 Corner Case 场景的分析进一步验证了所提出算法在复杂交通环境中的鲁棒性与适应性,能在保证行驶安全的前提下兼顾通行效率,实现更为合理的轨迹规划结果.
本研究仅在单一场景下验证了可达集与强化学习结合的可行性,后续将考虑引入 Rainbow、DSAC(distributional soft actor-critic)等先进强化学习算法,以进一步提升算法在交叉路口、匝道、环岛等多类场景中的决策泛化能力与精度. 同时,还计划对算法进行工程化部署,集成至实车平台,与真实感知及执行系统协同工作,从而在实际道路环境中开展更加全面、真实的测试与验证.
参考文献
自动驾驶车辆决策与规划研究综述
[J].
Review of research on decision-making and planning for automated vehicles
[J].
Hierarchical motion control strategies for handling interactions of automated vehicles
[J].DOI:10.1016/j.conengprac.2023.105523 [本文引用: 1]
Integrated decision making and planning based on feasible region construction for autonomous vehicles considering prediction uncertainty
[J].DOI:10.1109/TIV.2023.3299845 [本文引用: 1]
Enable faster and smoother spatio-temporal trajectory planning for autonomous vehicles in constrained dynamic environment
[J].DOI:10.1177/0954407020906627 [本文引用: 1]
Parallel sensor-space lattice planner for real-time obstacle avoidance
[J].
Using reachable sets for trajectory planning of automated vehicles
[J].
An integrated framework of decision making and motion planning for autonomous vehicles considering social behaviors
[J].DOI:10.1109/TVT.2020.3040398 [本文引用: 1]
Trajectory planning based on spatio-temporal reachable set considering dynamic probabilistic risk
[J].DOI:10.1016/j.engappai.2023.106291 [本文引用: 3]
Computing the drivable area of autonomous road vehicles in dynamic road scenes
[J].DOI:10.1109/TITS.2017.2742141 [本文引用: 1]
A survey of deep RL and IL for autonomous driving policy learning
[J].DOI:10.1109/TITS.2021.3134702 [本文引用: 1]
Hierarchical reinforcement learning for self-driving decision-making without reliance on labelled driving data
[J].DOI:10.1049/iet-its.2019.0317 [本文引用: 1]
Hierarchical framework integrating rapidly-exploring random tree with deep reinforcement learning for autonomous vehicle
[J].DOI:10.1007/s10489-022-04358-7
智能汽车决策中的驾驶行为语义解析关键技术
[J].DOI:10.3969/j.issn.1674-8484.2019.04.001 [本文引用: 1]
Key techniques of semantic analysis of driving behavior in decision making of autonomous vehicles
[J].DOI:10.3969/j.issn.1674-8484.2019.04.001 [本文引用: 1]
Synchronous maneuver searching and trajectory planning for autonomous vehicles in dynamic traffic environments
[J].DOI:10.1109/MITS.2019.2953551 [本文引用: 2]
Congested traffic states in empirical observations and microscopic simulations
[J].
基于可达集优化的智能汽车轨迹规划研究
[J].DOI:10.3963/j.issn.1671-4431.2022.06.007 [本文引用: 1]
Trajectory planning of intelligent vehicle based on reachable set and optimization
[J].DOI:10.3963/j.issn.1671-4431.2022.06.007 [本文引用: 1]