定义状态向量$ \boldsymbol{X}={\left[\beta ,\omega ,\varphi ,x,y\right]}^{{\mathrm{T}}} $ $ u={\delta }_{\mathrm{f}} $ $ \dot{\boldsymbol{X}}=f\left(\boldsymbol{X},u\right) $ . 当前系统状态为$ {\boldsymbol{X}}_{0} $ $ {u}_{0} $ $ {u}_{0}\left(k\right)={u}_{0} $ $ {\dot{\boldsymbol{X}}}_{0}\left(k\right)=f\left({\boldsymbol{X}}_{0}\left(k\right),{u}_{0}\left(k\right)\right) $ . 对于非线性系统,在当前状态点通过泰勒展开进行线性化处理[24 ] :
[1]
李淑庆, 彭囿朗, 肖莉英, 等 道路交通事故发生机理研究现状与趋势分析
[J]. 安全与环境学报 , 2014 , 14 (3 ): 14 - 19
[本文引用: 1]
LI Shuqing, PENG Youlang, XIAO Liying, et al Analysis of the mechanism of the road traffic accidents in-situ and the future research trends
[J]. Journal of Safety and Environment , 2014 , 14 (3 ): 14 - 19
[本文引用: 1]
[2]
高轶男, 巩建强 我国道路交通事故特征及致因分析
[J]. 安全与环境学报 , 2023 , 23 (11 ): 4013 - 4023
[本文引用: 1]
GAO Yinan, GONG Jianqiang Characteristics and mechanism of road traffic accidents
[J]. Journal of Safety and Environment , 2023 , 23 (11 ): 4013 - 4023
[本文引用: 1]
[3]
ROTHFUß S, SCHMIDT R, FLAD M, et al. A concept for human-machine negotiation in advanced driving assistance systems [C]// IEEE International Conference on Systems, Man and Cybernetics . Bari: IEEE, 2019: 3116–3123.
[本文引用: 1]
[4]
ANDERSON S J, KARUMANCHI S B, IAGNEMMA K. Constraint-based planning and control for safe, semi-autonomous operation of vehicles [C]// IEEE Intelligent Vehicles Symposium . Madrid: IEEE, 2012: 383–388.
[本文引用: 4]
[5]
WU Y, WEI H, CHEN X, et al Adaptive authority allocation of human-automation shared control for autonomous vehicle
[J]. International Journal of Automotive Technology , 2020 , 21 (3 ): 541 - 553
DOI:10.1007/s12239-020-0051-6
[本文引用: 1]
[6]
方浩杰, 董红召, 林少轩, 等 多特征融合的驾驶员疲劳状态检测方法
[J]. 浙江大学学报: 工学版 , 2023 , 57 (7 ): 1287 - 1296
[本文引用: 1]
FANG Haojie, DONG Hongzhao, LIN Shaoxuan, et al Driver fatigue state detection method based on multi-feature fusion
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (7 ): 1287 - 1296
[本文引用: 1]
[8]
刘志强, 吴雪刚, 倪捷, 等 基于HMM和SVM级联算法的驾驶意图识别
[J]. 汽车工程 , 2018 , 40 (7 ): 858 - 864
[本文引用: 1]
LIU Zhiqiang, WU Xuegang, NI Jie, et al Driving intention recognition based on HMM and SVM cascade algorithm
[J]. Automotive Engineering , 2018 , 40 (7 ): 858 - 864
[本文引用: 1]
[9]
喻恺, 彭理群, 丁雪, 等 面向人机协同共驾的驾驶行为短时预测方法研究
[J]. 交通信息与安全 , 2019 , 37 (1 ): 42 - 48
[本文引用: 1]
YU Kai, PENG Liqun, DING Xue, et al A study on the short-time forecasting method of operation behaviors of drivers for man-machine cooperative driving
[J]. Journal of Transport Information and Safety , 2019 , 37 (1 ): 42 - 48
[本文引用: 1]
[10]
BENLOUCIF A, NGUYEN A T, SENTOUH C, et al Cooperative trajectory planning for haptic shared control between driver and automation in highway driving
[J]. IEEE Transactions on Industrial Electronics , 2019 , 66 (12 ): 9846 - 9857
DOI:10.1109/TIE.2019.2893864
[本文引用: 2]
[11]
JIANG B, LI X, ZENG Y, et al Human-machine cooperative trajectory planning for semi-autonomous driving based on the understanding of behavioral semantics
[J]. Electronics , 2021 , 10 (8 ): 946
DOI:10.3390/electronics10080946
[本文引用: 2]
[12]
KOO Y, KIM J, HAN W. A method for driving control authority transition for cooperative autonomous vehicle [C]// IEEE Intelligent Vehicles Symposium . Seoul: IEEE, 2015: 394–399.
[本文引用: 1]
[13]
ZEEB K, BUCHNER A, SCHRAUF M What determines the take-over time? An integrated model approach of driver take-over after automated driving
[J]. Accident Analysis & Prevention , 2015 , 78 : 212 - 221
[本文引用: 1]
[14]
LOUW T, MARKKULA G, BOER E, et al Coming back into the loop: drivers’ perceptual-motor performance in critical events after automated driving
[J]. Accident Analysis & Prevention , 2017 , 108 : 9 - 18
[本文引用: 1]
[15]
张文镝, 周诗婕, 金海亮, 等 自动驾驶系统中人机协同的认知决策一体化机制研究
[J]. 汽车文摘 , 2023 , (9 ): 11 - 18
[本文引用: 1]
ZHANG Wendi, ZHOU Shijie, JIN Hailiang, et al Research on cognitive decision integration mechanism of human machine collaboration in automated driving system
[J]. Automotive Digest , 2023 , (9 ): 11 - 18
[本文引用: 1]
[16]
何仁, 赵晓聪, 杨奕彬, 等 基于驾驶人风险响应机制的人机共驾模型
[J]. 吉林大学学报: 工学版 , 2021 , 51 (3 ): 799 - 809
[本文引用: 1]
HE Ren, ZHAO Xiaocong, YANG Yibin, et al Man-machine shared driving model using risk-response mechanism of human driver
[J]. Journal of Jilin University: Engineering and Technology Edition , 2021 , 51 (3 ): 799 - 809
[本文引用: 1]
[17]
LI M, CAO H, LI G, et al A two-layer potential-field-driven model predictive shared control towards driver-automation cooperation
[J]. IEEE Transactions on Intelligent Transportation Systems , 2022 , 23 (5 ): 4415 - 4431
DOI:10.1109/TITS.2020.3044666
[本文引用: 1]
[18]
宗长富, 代昌华, 张东 智能汽车的人机共驾技术研究现状和发展趋势
[J]. 中国公路学报 , 2021 , 34 (6 ): 214 - 237
[本文引用: 2]
ZONG Changfu, DAI Changhua, ZHANG Dong Human-machine interaction technology of intelligent vehicles: current development trends and future directions
[J]. China Journal of Highway and Transport , 2021 , 34 (6 ): 214 - 237
[本文引用: 2]
[19]
ERLIEN S M, FUJITA S, GERDES J C Shared steering control using safe envelopes for obstacle avoidance and vehicle stability
[J]. IEEE Transactions on Intelligent Transportation Systems , 2016 , 17 (2 ): 441 - 451
DOI:10.1109/TITS.2015.2453404
[本文引用: 5]
[20]
HUANG C, HANG P, WU J, et al. Reference-free human-automation shared control for obstacle avoidance of automated vehicles [C]// IEEE International Conference on Systems, Man, and Cybernetics . Toronto: IEEE, 2020: 4398–4403.
[本文引用: 1]
[21]
CONSTANTIN A, PARK J, IAGNEMMA K. A margin-based approach to threat assessment for autonomous highway navigation [C]// IEEE Intelligent Vehicles Symposium Proceedings . Dearborn: IEEE, 2014: 234–239.
[本文引用: 1]
[22]
FALCONE P, BORRELLI F, TSENG H E, et al Linear time-varying model predictive control and its application to active steering systems: stability analysis and experimental validation
[J]. International Journal of Robust and Nonlinear Control , 2008 , 18 (8 ): 862 - 875
DOI:10.1002/rnc.1245
[本文引用: 1]
[23]
BHARILYA V, KUMAR N Machine learning for autonomous vehicle’s trajectory prediction: a comprehensive survey, challenges, and future research directions
[J]. Vehicular Communications , 2024 , 46 : 100733
DOI:10.1016/j.vehcom.2024.100733
[本文引用: 2]
[24]
闫宏阳. 基于限定Delaunay三角剖分的移动机器人路径规划[D]. 北京: 北京工业大学, 2008.
[本文引用: 2]
YAN Hongyang. Path planning for mobile robots based on constrained Delaunay triangulation [D]. Beijing: Beijing University of Technology, 2008.
[本文引用: 2]
[25]
CUI Q, DING R, WEI C, et al Path-tracking and lateral stabilisation for autonomous vehicles by using the steering angle envelope
[J]. Vehicle System Dynamics , 2021 , 59 (11 ): 1672 - 1696
DOI:10.1080/00423114.2020.1776344
[本文引用: 1]
[26]
龚建伟, 刘凯, 齐建永. 无人驾驶车辆模型预测控制[M]. 北京: 北京理工大学出版社, 2020: 189–191.
[本文引用: 1]
[27]
GUO W, TENG Z, SONG X, et al Toward consumer acceptance of cooperative driving systems: a human-centered shared steering control approach within a hierarchical framework
[J]. IEEE Transactions on Consumer Electronics , 2024 , 70 (1 ): 635 - 645
DOI:10.1109/TCE.2024.3357985
[本文引用: 1]
[28]
KIM G, KIM D, AHN Y, et al Hybrid approach for vehicle trajectory prediction using weighted integration of multiple models
[J]. IEEE Access , 2021 , 9 : 78715 - 78723
DOI:10.1109/ACCESS.2021.3083918
[本文引用: 1]
道路交通事故发生机理研究现状与趋势分析
1
2014
... 驾驶员作为交通的主要参与者,承担着繁重的驾驶任务,其行为是造成交通事故的主要原因之一[1 -2 ] . 自动驾驶将驾驶员部分或全部地从驾驶任务中解放出来,在降低驾驶员劳动强度的同时有效减少交通事故,提升了整体交通效率. 尽管自动驾驶受到追捧,但是由于技术发展水平的限制和相关法律法规的不健全与滞后性,要实现完全自动驾驶仍面临许多挑战. 因此,短期内驾驶员依然是主要的交通参与者. 驾驶员在环境感知、场景情境化以及信息归纳推理方面具有天然优势,而自动化系统擅长快速准确地响应定义良好的目标[3 -4 ] ;在尚未真正实现自动驾驶的过渡时期,有效发挥两者优势的人机共驾系统是最佳选择之一. ...
道路交通事故发生机理研究现状与趋势分析
1
2014
... 驾驶员作为交通的主要参与者,承担着繁重的驾驶任务,其行为是造成交通事故的主要原因之一[1 -2 ] . 自动驾驶将驾驶员部分或全部地从驾驶任务中解放出来,在降低驾驶员劳动强度的同时有效减少交通事故,提升了整体交通效率. 尽管自动驾驶受到追捧,但是由于技术发展水平的限制和相关法律法规的不健全与滞后性,要实现完全自动驾驶仍面临许多挑战. 因此,短期内驾驶员依然是主要的交通参与者. 驾驶员在环境感知、场景情境化以及信息归纳推理方面具有天然优势,而自动化系统擅长快速准确地响应定义良好的目标[3 -4 ] ;在尚未真正实现自动驾驶的过渡时期,有效发挥两者优势的人机共驾系统是最佳选择之一. ...
我国道路交通事故特征及致因分析
1
2023
... 驾驶员作为交通的主要参与者,承担着繁重的驾驶任务,其行为是造成交通事故的主要原因之一[1 -2 ] . 自动驾驶将驾驶员部分或全部地从驾驶任务中解放出来,在降低驾驶员劳动强度的同时有效减少交通事故,提升了整体交通效率. 尽管自动驾驶受到追捧,但是由于技术发展水平的限制和相关法律法规的不健全与滞后性,要实现完全自动驾驶仍面临许多挑战. 因此,短期内驾驶员依然是主要的交通参与者. 驾驶员在环境感知、场景情境化以及信息归纳推理方面具有天然优势,而自动化系统擅长快速准确地响应定义良好的目标[3 -4 ] ;在尚未真正实现自动驾驶的过渡时期,有效发挥两者优势的人机共驾系统是最佳选择之一. ...
我国道路交通事故特征及致因分析
1
2023
... 驾驶员作为交通的主要参与者,承担着繁重的驾驶任务,其行为是造成交通事故的主要原因之一[1 -2 ] . 自动驾驶将驾驶员部分或全部地从驾驶任务中解放出来,在降低驾驶员劳动强度的同时有效减少交通事故,提升了整体交通效率. 尽管自动驾驶受到追捧,但是由于技术发展水平的限制和相关法律法规的不健全与滞后性,要实现完全自动驾驶仍面临许多挑战. 因此,短期内驾驶员依然是主要的交通参与者. 驾驶员在环境感知、场景情境化以及信息归纳推理方面具有天然优势,而自动化系统擅长快速准确地响应定义良好的目标[3 -4 ] ;在尚未真正实现自动驾驶的过渡时期,有效发挥两者优势的人机共驾系统是最佳选择之一. ...
1
... 驾驶员作为交通的主要参与者,承担着繁重的驾驶任务,其行为是造成交通事故的主要原因之一[1 -2 ] . 自动驾驶将驾驶员部分或全部地从驾驶任务中解放出来,在降低驾驶员劳动强度的同时有效减少交通事故,提升了整体交通效率. 尽管自动驾驶受到追捧,但是由于技术发展水平的限制和相关法律法规的不健全与滞后性,要实现完全自动驾驶仍面临许多挑战. 因此,短期内驾驶员依然是主要的交通参与者. 驾驶员在环境感知、场景情境化以及信息归纳推理方面具有天然优势,而自动化系统擅长快速准确地响应定义良好的目标[3 -4 ] ;在尚未真正实现自动驾驶的过渡时期,有效发挥两者优势的人机共驾系统是最佳选择之一. ...
4
... 驾驶员作为交通的主要参与者,承担着繁重的驾驶任务,其行为是造成交通事故的主要原因之一[1 -2 ] . 自动驾驶将驾驶员部分或全部地从驾驶任务中解放出来,在降低驾驶员劳动强度的同时有效减少交通事故,提升了整体交通效率. 尽管自动驾驶受到追捧,但是由于技术发展水平的限制和相关法律法规的不健全与滞后性,要实现完全自动驾驶仍面临许多挑战. 因此,短期内驾驶员依然是主要的交通参与者. 驾驶员在环境感知、场景情境化以及信息归纳推理方面具有天然优势,而自动化系统擅长快速准确地响应定义良好的目标[3 -4 ] ;在尚未真正实现自动驾驶的过渡时期,有效发挥两者优势的人机共驾系统是最佳选择之一. ...
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
... [4 ],这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
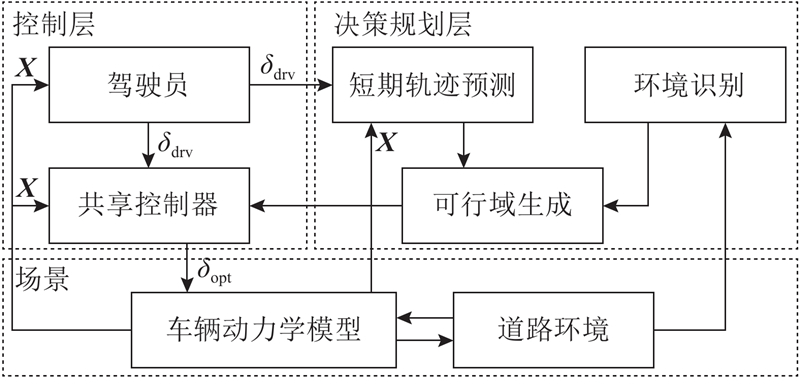
... 将驾驶员意图纳入决策规划,并构建具有与驾驶员意图相匹配的控制器的人机共驾框架,如图1 所示. 驾驶员根据车辆状态$ {\boldsymbol{X}} $ $ {\delta }_{\mathrm{d}\mathrm{r}\mathrm{v}} $ X [10 -11 ] ,以表征驾驶员的驾驶意图. 然后,采用德洛内三角剖分(Delaunay triangulation)算法对环境识别结果进行离散化,并设计匹配驾驶员意图的启发式图搜索算法,得到符合驾驶员偏好的车辆可通行区域,将可行域作为决策规划层的结果输出给控制层[4 ,21 ] . 最后,基于线性时变模型预测控制理论构建共享控制器[22 ] ,建立人机输出偏差代价函数. 在满足可行域边界和车辆稳态约束的前提下,自动化系统优化前轮转向角输出$ {\delta }_{\mathrm{o}\mathrm{p}\mathrm{t}} $
Adaptive authority allocation of human-automation shared control for autonomous vehicle
1
2020
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
多特征融合的驾驶员疲劳状态检测方法
1
2023
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
多特征融合的驾驶员疲劳状态检测方法
1
2023
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
基于自然驾驶数据的分心驾驶行为识别方法
1
2020
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
基于自然驾驶数据的分心驾驶行为识别方法
1
2020
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
基于HMM和SVM级联算法的驾驶意图识别
1
2018
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
基于HMM和SVM级联算法的驾驶意图识别
1
2018
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
面向人机协同共驾的驾驶行为短时预测方法研究
1
2019
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
面向人机协同共驾的驾驶行为短时预测方法研究
1
2019
... 人机共驾是自然驾驶人和自动化系统协同完成驾驶任务的技术框架. 国内外学者针对人机共驾系统中的驾驶员因素、人机交互和共驾策略等方向展开研究. 不同驾驶员具有不同的驾驶风格,在不同场景下表现各异,而基于固定规则的人机共驾策略难以满足多样化需求,因此,充分考虑驾驶员因素是人机共驾系统的必然要求. 为了满足这一要求,通常需要对驾驶员状态进行监测,或对其驾驶意图进行识别. 驾驶员状态监测一般利用生理信号[5 ] 、图像[6 ] 和车辆状态[7 ] 等数据实现;驾驶意图识别包含战略行为的识别和短时行为的预测. 刘志强等[8 ] 通过分析驾驶样本之间的差异来确定意图识别指标,并运用隐马尔可夫模型和支持向量机级联算法建立驾驶意图识别模型. 喻恺等[9 ] 利用线性最优二次型方法建立驾驶操纵序贯链的优化目标函数,并结合恒定加速度模型提出短时驾驶行为预测模型. 在实际场景中,驾驶员的真实意图无法直接获取;基于行驶数据学习的方法虽然能够有效识别意图,但是其准确度取决于驾驶样本,且受到场景复杂程度的影响. 驾驶员对车辆的实时操纵是基于车辆状态和自身期望的决策结果,因此,车辆的短期行驶轨迹在一定程度上反映了驾驶意图,可以作为驾驶意图的真值. ...
Cooperative trajectory planning for haptic shared control between driver and automation in highway driving
2
2019
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
... 将驾驶员意图纳入决策规划,并构建具有与驾驶员意图相匹配的控制器的人机共驾框架,如图1 所示. 驾驶员根据车辆状态$ {\boldsymbol{X}} $ $ {\delta }_{\mathrm{d}\mathrm{r}\mathrm{v}} $ X [10 -11 ] ,以表征驾驶员的驾驶意图. 然后,采用德洛内三角剖分(Delaunay triangulation)算法对环境识别结果进行离散化,并设计匹配驾驶员意图的启发式图搜索算法,得到符合驾驶员偏好的车辆可通行区域,将可行域作为决策规划层的结果输出给控制层[4 ,21 ] . 最后,基于线性时变模型预测控制理论构建共享控制器[22 ] ,建立人机输出偏差代价函数. 在满足可行域边界和车辆稳态约束的前提下,自动化系统优化前轮转向角输出$ {\delta }_{\mathrm{o}\mathrm{p}\mathrm{t}} $
Human-machine cooperative trajectory planning for semi-autonomous driving based on the understanding of behavioral semantics
2
2021
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
... 将驾驶员意图纳入决策规划,并构建具有与驾驶员意图相匹配的控制器的人机共驾框架,如图1 所示. 驾驶员根据车辆状态$ {\boldsymbol{X}} $ $ {\delta }_{\mathrm{d}\mathrm{r}\mathrm{v}} $ X [10 -11 ] ,以表征驾驶员的驾驶意图. 然后,采用德洛内三角剖分(Delaunay triangulation)算法对环境识别结果进行离散化,并设计匹配驾驶员意图的启发式图搜索算法,得到符合驾驶员偏好的车辆可通行区域,将可行域作为决策规划层的结果输出给控制层[4 ,21 ] . 最后,基于线性时变模型预测控制理论构建共享控制器[22 ] ,建立人机输出偏差代价函数. 在满足可行域边界和车辆稳态约束的前提下,自动化系统优化前轮转向角输出$ {\delta }_{\mathrm{o}\mathrm{p}\mathrm{t}} $
1
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
What determines the take-over time? An integrated model approach of driver take-over after automated driving
1
2015
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
Coming back into the loop: drivers’ perceptual-motor performance in critical events after automated driving
1
2017
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
自动驾驶系统中人机协同的认知决策一体化机制研究
1
2023
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
自动驾驶系统中人机协同的认知决策一体化机制研究
1
2023
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
基于驾驶人风险响应机制的人机共驾模型
1
2021
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
基于驾驶人风险响应机制的人机共驾模型
1
2021
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
A two-layer potential-field-driven model predictive shared control towards driver-automation cooperation
1
2022
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
智能汽车的人机共驾技术研究现状和发展趋势
2
2021
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
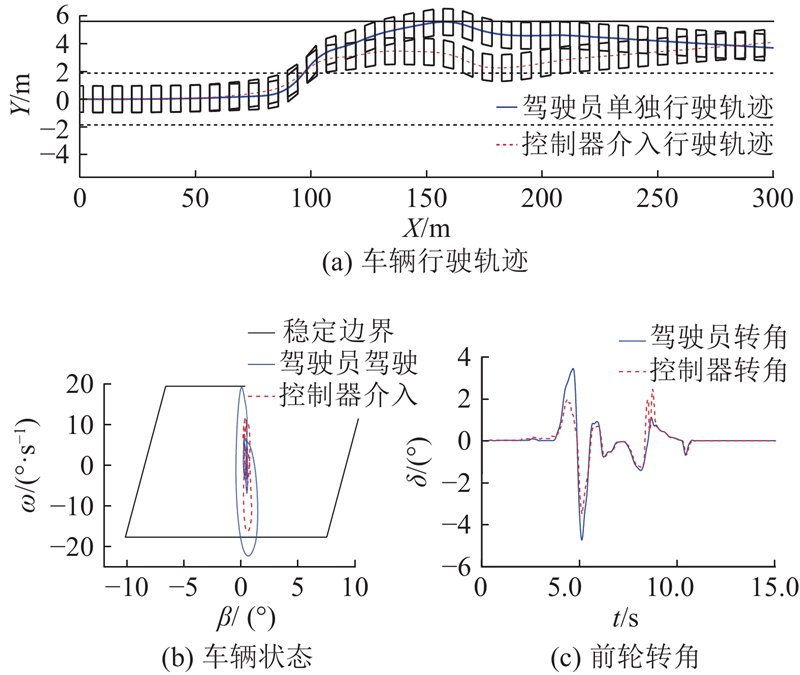
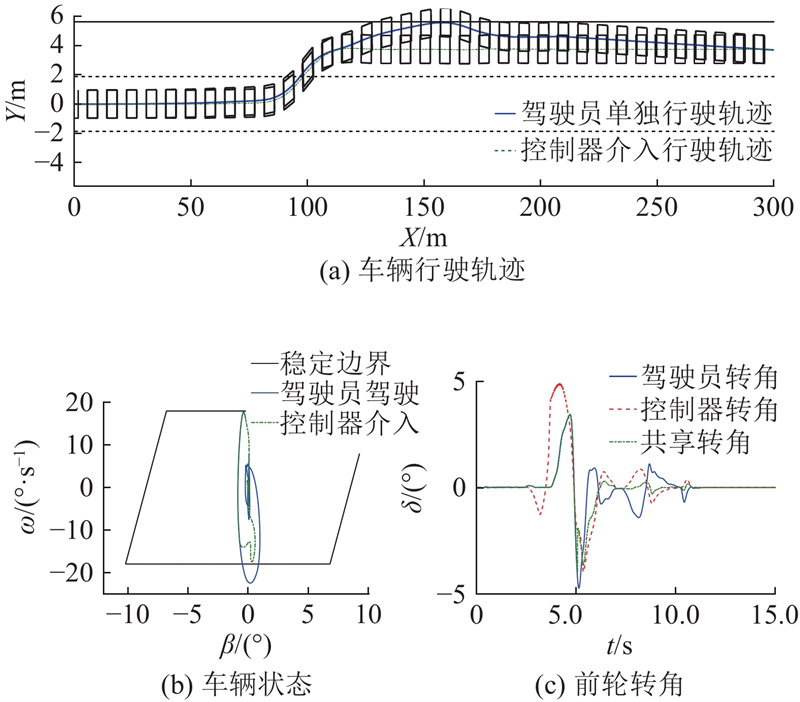
... 在建立的优化问题中,驾驶员与控制器转向命令偏差代价是实现人机共驾的关键,构建了间接型双驾双控共享结构[18 -19 ] . 自动化系统在获得驾驶员操纵命令后,在约束条件限制下求解得到最终的车辆控制命令,而构建的代价函数保证自动化系统输出的控制命令贴近驾驶员对车辆的操纵,从而实现了驾驶员实时在环的人机共驾系统. ...
智能汽车的人机共驾技术研究现状和发展趋势
2
2021
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
... 在建立的优化问题中,驾驶员与控制器转向命令偏差代价是实现人机共驾的关键,构建了间接型双驾双控共享结构[18 -19 ] . 自动化系统在获得驾驶员操纵命令后,在约束条件限制下求解得到最终的车辆控制命令,而构建的代价函数保证自动化系统输出的控制命令贴近驾驶员对车辆的操纵,从而实现了驾驶员实时在环的人机共驾系统. ...
Shared steering control using safe envelopes for obstacle avoidance and vehicle stability
5
2016
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
... 轮胎具有强非线性,尤其在中、高速工况下,简单线性化会产生较大偏差. 如图6 所示,针对轮胎模型进行局部线性化处理,建立近似线性模型[19 ] : ...
... 在稳态转向工况中,考虑到路面附着系数$ \mu $ [19 ] 为 ...
... 可行域由空闲环境单元构成,车辆可在其中自由行驶,一旦超出边界将可能与障碍物和道路边界发生碰撞. 因此,将可行域边界作为约束条件,确保车辆横向位置位于可行域上、下边界之间,从而实现避障行驶[19 ] : ...
... 在建立的优化问题中,驾驶员与控制器转向命令偏差代价是实现人机共驾的关键,构建了间接型双驾双控共享结构[18 -19 ] . 自动化系统在获得驾驶员操纵命令后,在约束条件限制下求解得到最终的车辆控制命令,而构建的代价函数保证自动化系统输出的控制命令贴近驾驶员对车辆的操纵,从而实现了驾驶员实时在环的人机共驾系统. ...
1
... 驾驶员状态监测和意图识别为驾驶模式的选择和控制权限的分配提供了必要信息. Benloucif等[10 ] 针对多项式轨迹库建立包含期望轨迹偏离代价的评价指标,根据驾驶员的操纵意图不断地调整规划轨迹. Jiang等[11 ] 通过比较特定行为语义对应的虚拟轨迹与短期预测轨迹之间的偏差来确定行为语义,然后根据多项式轨迹库和评价指标确定最优轨迹. Koo等[12 ] 根据通过视觉识别得到的驾驶员状态结果切换驾驶模式. 切换控制存在由接管时间[13 ] 和驾驶员反应差异[14 ] 导致的响应延迟或操作失误的问题,而驾驶员实时在环的共享控制能够整合驾驶员和自动化系统的能力,提高了系统适用性. 此外,考虑驾驶意图的人机共驾系统有利于保证决策一致性[15 ] . 何仁等[16 ] 基于典型驾驶片段的量化风险建立安全响应策略曲面,并根据策略偏差构建控制权柔性切换模型. Li等[17 ] 采用两层模糊策略确定协作和权重系数,实现控制权限分配以避免碰撞,并实现代价权重调整以解决人机冲突问题. 基于权限分配的共享策略一般以车辆行驶效果为导向,而考虑驾驶意图的策略以驾驶员为主,最大程度地发挥驾驶员的能力和满足驾驶期望[18 ] . 不同于上述共享控制形式,采用优化求解形式可以将驾驶员操纵信号纳入优化问题进行求解,无须建立驾驶员模型. Anderson等[4 ] 和Erlien等[19 ] 依据模型预测控制(model predictive control, MPC)理论构建驾驶员和自动化系统输出的偏差代价,结合稳定性和包络约束,最大程度地保证控制结果符合驾驶员期望. Huang等[20 ] 建立无参考轨迹的共享控制框架,优化驾驶员操纵命令,使得车辆满足避障和稳定性要求. 与自动化系统严格规划并精确跟踪特定路线的特点不同,驾驶员在目标区域内的驾驶行为表现出高度的自由性和随机性[4 ] ,这一特性难以通过传统方法准确建模. 优化求解的方式能够结合驾驶员的特性灵活建立优化问题,有助于缓解因目标不一致引发的人机冲突,为构建一致性更高的人机共驾策略提供了具有创新性的解决方案. ...
1
... 将驾驶员意图纳入决策规划,并构建具有与驾驶员意图相匹配的控制器的人机共驾框架,如图1 所示. 驾驶员根据车辆状态$ {\boldsymbol{X}} $ $ {\delta }_{\mathrm{d}\mathrm{r}\mathrm{v}} $ X [10 -11 ] ,以表征驾驶员的驾驶意图. 然后,采用德洛内三角剖分(Delaunay triangulation)算法对环境识别结果进行离散化,并设计匹配驾驶员意图的启发式图搜索算法,得到符合驾驶员偏好的车辆可通行区域,将可行域作为决策规划层的结果输出给控制层[4 ,21 ] . 最后,基于线性时变模型预测控制理论构建共享控制器[22 ] ,建立人机输出偏差代价函数. 在满足可行域边界和车辆稳态约束的前提下,自动化系统优化前轮转向角输出$ {\delta }_{\mathrm{o}\mathrm{p}\mathrm{t}} $
Linear time-varying model predictive control and its application to active steering systems: stability analysis and experimental validation
1
2008
... 将驾驶员意图纳入决策规划,并构建具有与驾驶员意图相匹配的控制器的人机共驾框架,如图1 所示. 驾驶员根据车辆状态$ {\boldsymbol{X}} $ $ {\delta }_{\mathrm{d}\mathrm{r}\mathrm{v}} $ X [10 -11 ] ,以表征驾驶员的驾驶意图. 然后,采用德洛内三角剖分(Delaunay triangulation)算法对环境识别结果进行离散化,并设计匹配驾驶员意图的启发式图搜索算法,得到符合驾驶员偏好的车辆可通行区域,将可行域作为决策规划层的结果输出给控制层[4 ,21 ] . 最后,基于线性时变模型预测控制理论构建共享控制器[22 ] ,建立人机输出偏差代价函数. 在满足可行域边界和车辆稳态约束的前提下,自动化系统优化前轮转向角输出$ {\delta }_{\mathrm{o}\mathrm{p}\mathrm{t}} $
Machine learning for autonomous vehicle’s trajectory prediction: a comprehensive survey, challenges, and future research directions
2
2024
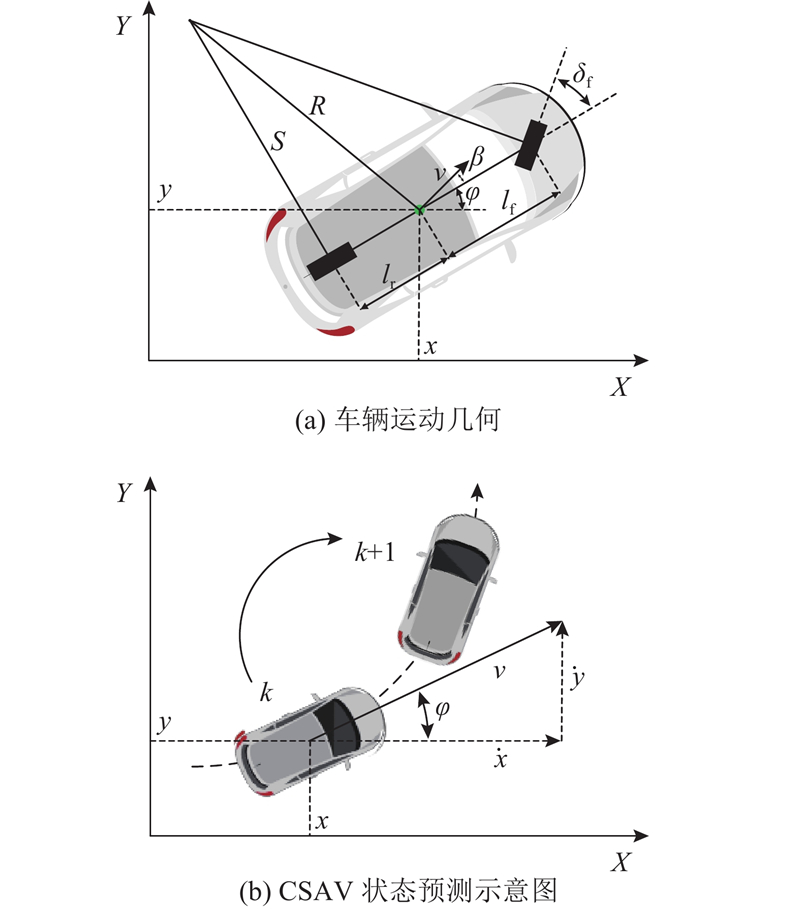
... 由于研究对象为车辆的横向共享控制,假设纵向车速恒定,且短时间内驾驶员的转向操纵保持不变,即车辆转向角和车辆速度恒定. 建立恒定转向角和速度(constant steering angle and velocity, CSAV)模型,如图2 所示. 采用车辆单轨迹模型进行车辆轨迹预测,该模型可解释性强、性能稳定,且计算简单[23 ] . ...
... 通过对当前人机共驾问题的深入分析,明确了人机冲突和整体性框架研究不足的现状. 为此,提出以驾驶员意图为基准的共驾框架,覆盖从决策规划到控制的全流程. 在仿真场景中,提出的规划算法能够实时生成行驶区域,不仅符合驾驶员的决策倾向,同时满足了无碰撞的安全要求. 此外,基于MPC的共享控制器在确保行驶安全的同时,最大程度地保留了驾驶员的驾驶自由. 所构建的算法框架能够实时求解可行域及其对应的最优控制律,这一过程贴近驾驶员的实际驾驶行为,更符合驾驶员的预期. 然而,该共驾框架使用物理模型方法进行轨迹预测,预测时域较短,并且驾驶员操作中的细微抖动可能导致意图预测结果的波动,从而影响后续问题的求解. 基于机器学习的方法在轨迹预测和意图识别方面已成为当前研究热点[23 ,28 ] . 未来研究可以利用驾驶员操作和车辆行驶数据集,探索物理模型与数据驱动模型的融合框架,以拓展轨迹预测时域并提高结果的可信度,从而进一步完善共驾框架. ...
2
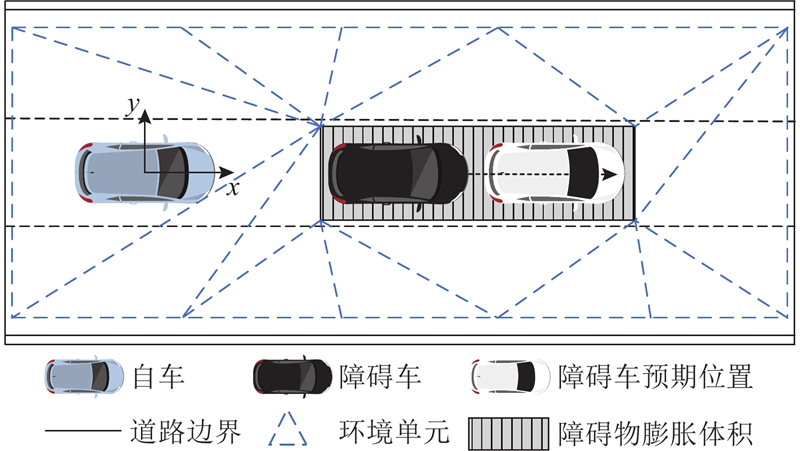
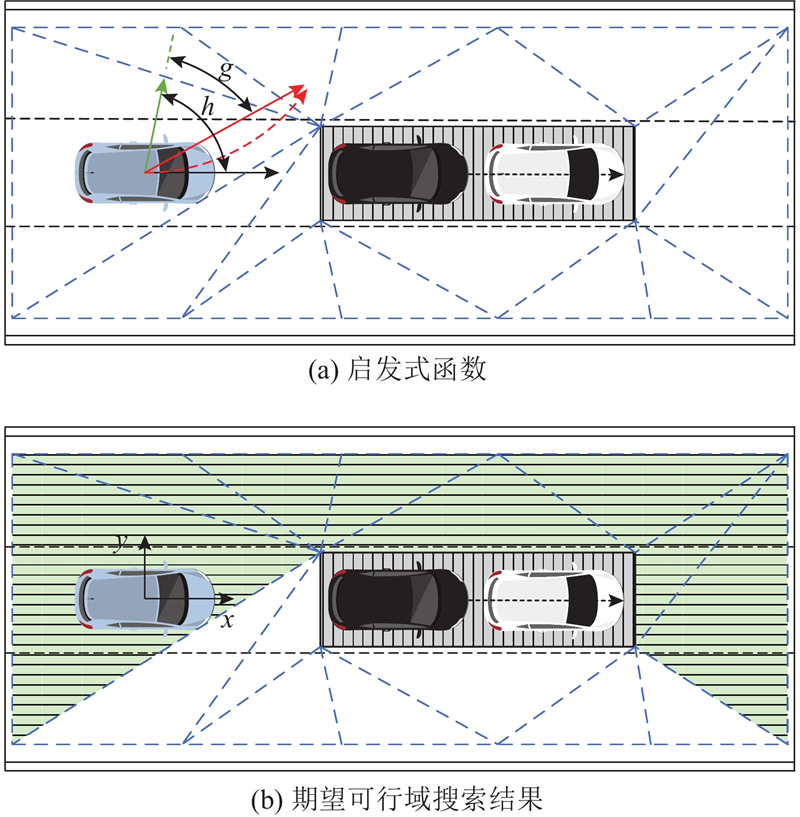
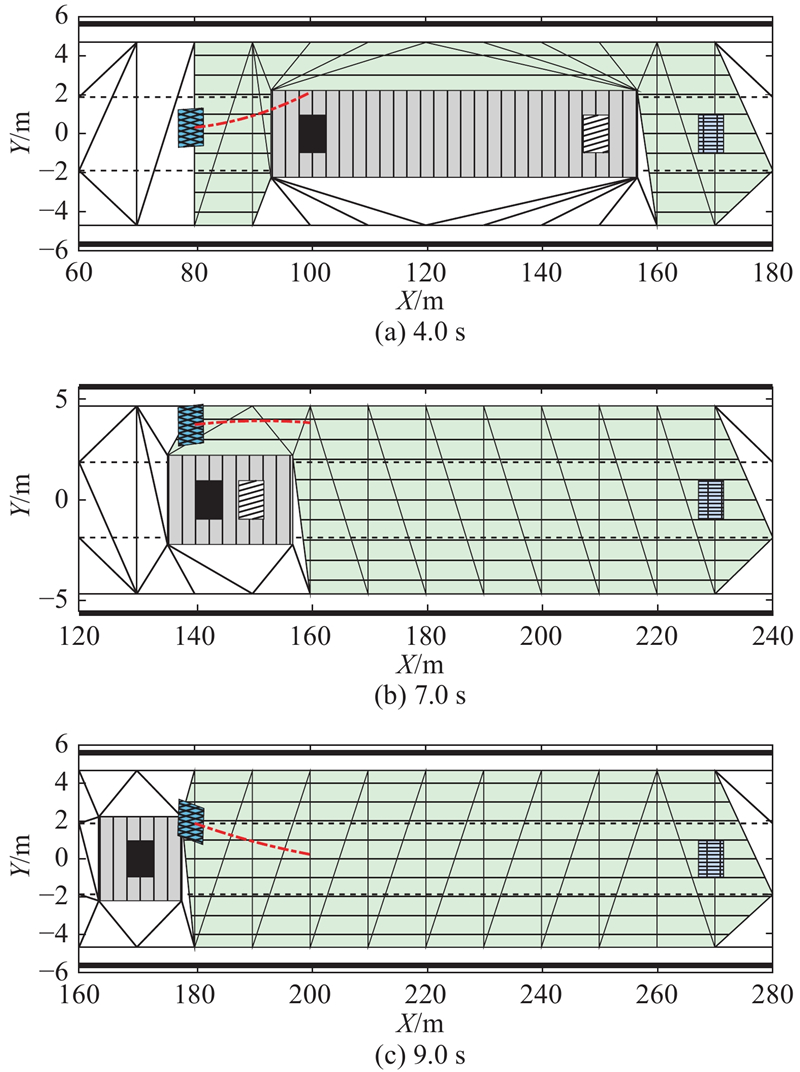
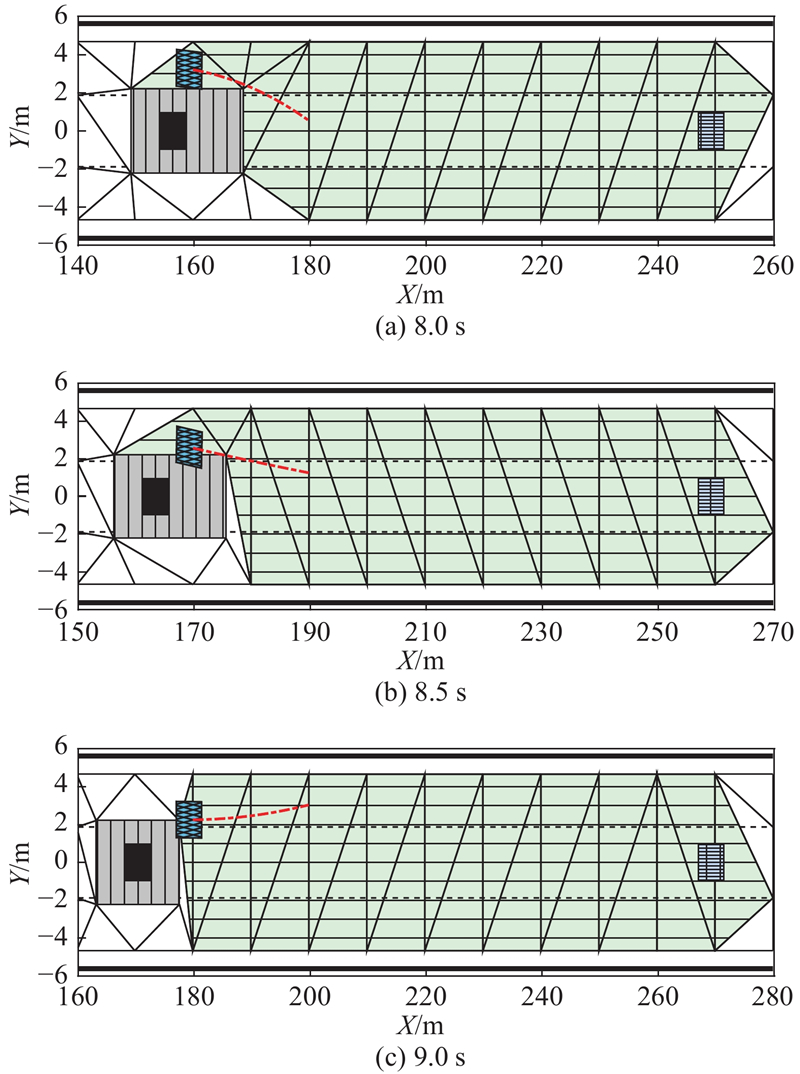
... 基于环境识别结果,设计可行域搜索算法. 为了确保环境单元准确反映实际的占用情况,采用德洛内三角剖分方法构建环境分解模型[24 ] . 考虑到碰撞风险和驾驶舒适性,对障碍物体积进行膨胀处理. 根据自车与障碍车在路面投影面积的重叠情况来判断两者碰撞与否,因此,保证$ X $ $ Y $ $ X $ $ {T}_{\mathrm{C}} $ . 当自车与前方障碍车的距离小于一定值时,认为障碍车已进入预警区域;将$ {T}_{\mathrm{C}} $ $ \Delta {x}_{\mathrm{o}\mathrm{b}\mathrm{s}} $ $ \Delta {y}_{\mathrm{o}\mathrm{b}\mathrm{s}} $ ) : ...
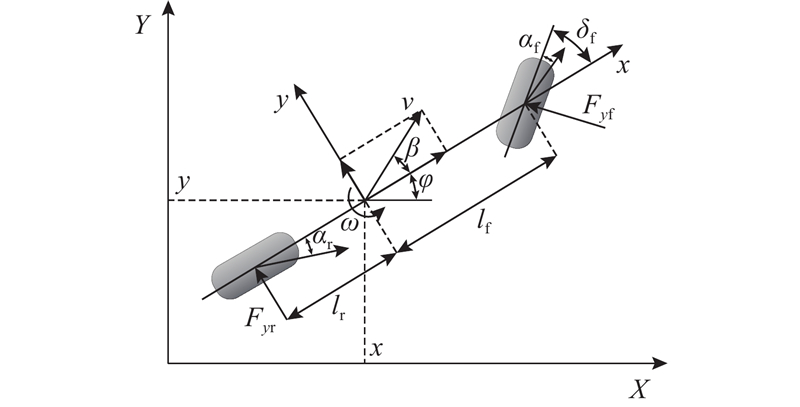
... 定义状态向量$ \boldsymbol{X}={\left[\beta ,\omega ,\varphi ,x,y\right]}^{{\mathrm{T}}} $ $ u={\delta }_{\mathrm{f}} $ $ \dot{\boldsymbol{X}}=f\left(\boldsymbol{X},u\right) $ . 当前系统状态为$ {\boldsymbol{X}}_{0} $ $ {u}_{0} $ $ {u}_{0}\left(k\right)={u}_{0} $ $ {\dot{\boldsymbol{X}}}_{0}\left(k\right)=f\left({\boldsymbol{X}}_{0}\left(k\right),{u}_{0}\left(k\right)\right) $ . 对于非线性系统,在当前状态点通过泰勒展开进行线性化处理[24 ] : ...
2
... 基于环境识别结果,设计可行域搜索算法. 为了确保环境单元准确反映实际的占用情况,采用德洛内三角剖分方法构建环境分解模型[24 ] . 考虑到碰撞风险和驾驶舒适性,对障碍物体积进行膨胀处理. 根据自车与障碍车在路面投影面积的重叠情况来判断两者碰撞与否,因此,保证$ X $ $ Y $ $ X $ $ {T}_{\mathrm{C}} $ . 当自车与前方障碍车的距离小于一定值时,认为障碍车已进入预警区域;将$ {T}_{\mathrm{C}} $ $ \Delta {x}_{\mathrm{o}\mathrm{b}\mathrm{s}} $ $ \Delta {y}_{\mathrm{o}\mathrm{b}\mathrm{s}} $ ) : ...
... 定义状态向量$ \boldsymbol{X}={\left[\beta ,\omega ,\varphi ,x,y\right]}^{{\mathrm{T}}} $ $ u={\delta }_{\mathrm{f}} $ $ \dot{\boldsymbol{X}}=f\left(\boldsymbol{X},u\right) $ . 当前系统状态为$ {\boldsymbol{X}}_{0} $ $ {u}_{0} $ $ {u}_{0}\left(k\right)={u}_{0} $ $ {\dot{\boldsymbol{X}}}_{0}\left(k\right)=f\left({\boldsymbol{X}}_{0}\left(k\right),{u}_{0}\left(k\right)\right) $ . 对于非线性系统,在当前状态点通过泰勒展开进行线性化处理[24 ] : ...
Path-tracking and lateral stabilisation for autonomous vehicles by using the steering angle envelope
1
2021
... 进一步对轮胎侧向力进行约束,以确保轮胎力在安全范围内,从而保证车辆的行驶稳定性. 忽略行驶过程中轮胎载荷变化,前、后轴轮胎饱和侧偏角分别为$ {\alpha }_{\mathrm{f}}^{\mathrm{s}\mathrm{a}\mathrm{t}} $ $ {\alpha }_{\mathrm{r}}^{\mathrm{s}\mathrm{a}\mathrm{t}} $ [25 ] 为 ...
1
... 在模型预测控制中,较长的预测时域能够提供更准确的预测结果和更优的控制效果,但也显著增加了计算量,从而影响实时性. 因此,可以采用变步长方法设计控制器. 通过保持短步长时域与控制时域一致,可以在保证控制精度的同时,以更低的计算性能实现较长的预测时域[26 ] . 车辆的位置约束可以通过对可行域边界采样得到. 然而,当车辆靠近不平滑边界时,约束条件可能存在突变的情况,而在采用短步长的控制时域内无法显著调整车辆位置,可能导致优化问题无解. 为了解决这一问题,在短步长时域内不对车辆位置施加约束,同时适当膨胀障碍物体积以保证安全. 优化问题的代价函数由二次项组成,因此,可以将其转化为标准的二次规划问题,并利用MATLAB提供的quadprog求解器进行高效求解. ...
Toward consumer acceptance of cooperative driving systems: a human-centered shared steering control approach within a hierarchical framework
1
2024
... 在共享控制框架中,控制器的介入辅助驾驶员驾驶车辆,但过度的介入会干扰驾驶员的正常驾驶行为. 为了验证提出的共享框架在解决人机冲突方面的优势,将其与文献[27 ]提出的共享控制权限分配策略进行对比,并选择干预程度作为人机冲突评价指标. 该指标定义为 ...
Hybrid approach for vehicle trajectory prediction using weighted integration of multiple models
1
2021
... 通过对当前人机共驾问题的深入分析,明确了人机冲突和整体性框架研究不足的现状. 为此,提出以驾驶员意图为基准的共驾框架,覆盖从决策规划到控制的全流程. 在仿真场景中,提出的规划算法能够实时生成行驶区域,不仅符合驾驶员的决策倾向,同时满足了无碰撞的安全要求. 此外,基于MPC的共享控制器在确保行驶安全的同时,最大程度地保留了驾驶员的驾驶自由. 所构建的算法框架能够实时求解可行域及其对应的最优控制律,这一过程贴近驾驶员的实际驾驶行为,更符合驾驶员的预期. 然而,该共驾框架使用物理模型方法进行轨迹预测,预测时域较短,并且驾驶员操作中的细微抖动可能导致意图预测结果的波动,从而影响后续问题的求解. 基于机器学习的方法在轨迹预测和意图识别方面已成为当前研究热点[23 ,28 ] . 未来研究可以利用驾驶员操作和车辆行驶数据集,探索物理模型与数据驱动模型的融合框架,以拓展轨迹预测时域并提高结果的可信度,从而进一步完善共驾框架. ...