电动公交已成为城市公共交通系统的重要组成部分,在缓解城市交通拥堵、实现交通节能、促进经济与社会可持续发展方面具有显著优势. 鉴于这些优势,许多国家都采取补贴政策来提高电动公交渗透率[1-5]. 电动公交在运营过程中面临着诸多挑战,如电池续航里程有限、充电基础设施不足以及充电时间过长等. 这些挑战直接影响到公交系统的运营效率和服务质量. 配置大容量电池会导致公交能耗与运营成本显著增加,而配置小容量电池又会增加驾驶人的“里程焦虑”[6]. 如何在现有电池容量的条件下保证电动公交的正常运行,即通过保证电动公交的电量需求来减少因电量不足而导致的运营中断情形的发生,从而降低因应对中断情形而需要额外购置车辆所产生的运营成本,已成为一个紧迫而关键的问题.
网联电动公交(connected electric buses, CEBs)的相关研究主要包括网联公交轨迹规划和电动公交充电策略2个方面.在CEBs轨迹规划方面,相关研究主要集中在如何通过车路协同技术实现公交的精细化控制[7-8]. 赵琥等[9]提出基于车速诱导的动态公交调度模型. 该模型结合各线路独立运行时的乘客需求和车头时距,避免重叠区域站点的公交串车现象,同时尽可能地保持各线路原有的车头时距,以提高运行效率. 任晗啸等[10]提出基于云控系统的两车协同换道策略,根据换道收益准则,采用两段式滚动时域轨迹规划方法,有效提升公交车在进、出站时强制换道的成功率和安全性. 网联公交轨迹规划通常也涉及其与交叉口信号的协同优化[11-12]. Yang等[13]建立网联环境下交叉口信号与公交车速度诱导协同优化模型,该模型可以在改善公交运行状态的同时最大程度地减少对社会车辆的影响. Estrada等[14]基于公交实时轨迹数据开发动态公交控制策略,旨在减少车头时距波动对路线运载能力的影响. 该策略通过调整车辆速度对公交进行调度,并在信号交叉口处为明显延误的公交提供信号优先.
电动公交充电策略主要分为4个类别:1)静态有线充电策略. 熊杰等[15]提出基于混合整数规划的公交充电计划优化方法,通过考虑分时电价、不完全充电策略和电池的非线性充电特性,同步优化充电时段与充电起始时间以降低系统成本. 2)动态无线充电策略. Yang等[16]提出基于无线充电的电动公交充电调度优化方案,旨在最小化系统运营电力成本. 该方案结合电力市场模型、公交速度和电价波动,设计最优的充电调度算法,并通过仿真验证其有效性. 3)电池快速更换策略. Ayad等[17]提出基于电池更换的电动公交充电系统优化模型,该模型采用多目标混合整数非线性规划方法,考虑电池容量、充电功率、电池数量、交通状况、电价波动等因素,最小化运营成本. 4)静态无线充电(static wireless charging, SWC)策略. 别一鸣等[6]提出电动公交线路SWC设施布局优化方法,通过建立电动公交运行状态模型并综合考虑时间控制点、剩余电量与准点率等约束条件,优化公交充电设施布局.
综上所述,已有的关于CEBs的研究虽然对运行与充电问题提供了一定参考,但仍然存在以下不足. 1)车路协同技术为公交精细化控制与充电优化提供了新的思路,但是现有研究没有充分利用网联环境下CEBs与常规车辆 (regular vehicles, RVs)各自的运行特点和进行兼顾二者运行效率的干线信号协调控制. 2)在实际应用中,动态无线充电技术与电池快速更换技术仍然存在挑战[18]. 大多数现有的电动公交系统主要采取基于首末站的静态有线方式进行充电,并且必须配备较大尺寸的电池才能维持一天的正常运行. 因此,现有的固定充电式电动公交系统存在电池成本高、每次充电里程有限、充电时间长等问题.
SWC技术可以很好地避免桩式充电和机架式充电对场地的要求,克服了部署成本高的缺点[19]. 将基于网联环境下CEBs运行特点的轨迹控制技术与SWC技术相结合,可以解决上述问题. 具体而言,根据CEBs的运行特点推导出CEBs的交叉口不停车约束条件,并基于Multiband模型构建兼顾CEBs和RVs运行效率的干线信号协调控制模型. 在干线信号协调控制环境下,构建CEBs轨迹控制与站点充电协同优化模型,使CEBs在保持良好运行效率和秩序的同时,可以在停靠站采用SWC方式充电,并灵活调整充电时长.
1. CEBs轨迹控制与站点充电协同模型
1.1. 假设条件
为了便于问题的研究,进行如下假设.
1)在混合交通环境下,CEBs在公交专用车道上运行,RVs在常规车道运行.
2)公交停靠站处每次只允许1辆CEB停靠[9].
3)不考虑CEBs在停靠站停车时的加减速过程所消耗的时间.
1.2. 干线信号协调控制模型
为了充分发挥CEBs的优势,同时兼顾RVs的运行效率,信号控制方案应同时考虑2类车辆的运行效率. 在干线信号协调优化方面,Maxband[20]和Multiband[21]是2种具有代表性的方法. 相比之下,Multiband方法更加灵活,可以根据流量得到加权带宽,从而大大提高控制效率. RVs具有离散到达和行驶异质性的特点,本研究参考Multiband模型,建立RVs的干线信号协调优化模型. 具体而言,采用道路通行能力手册(highway capacity manual, HCM)[22]中的信号配时方法获得各交叉口的信号配时方案,并基于Multiband方法构建RVs干线信号协调控制模型. 与RVs不同的是,CEBs具有网联化和自动化的优势,可以对其行驶轨迹进行实时、精细的控制. 因此,根据CEBs的运行特点,构建公交车专用道场景下CEBs的不停车约束,使所有在绿灯期间从上游交叉口通过的CEBs均可以不停车地通过下游交叉口.
干线信号协调控制模型的优化目标是使得RVs双向绿波带的带宽最大,目标函数为
式中:B为最大双向绿波带宽,
干线信号协调控制模型的约束条件包括RVs绿波带宽约束和CEBs交叉口不停车约束2类.
1)RVs绿波带宽约束.
在构建RVs绿波带宽约束条件之前,首先定义1组二元整数变量
式中:
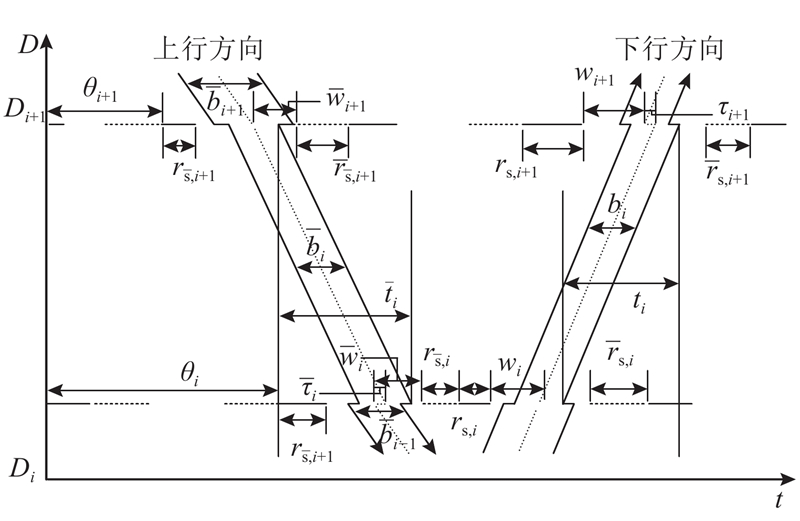
采用Multiband模型构建绿波带基础模型,RVs在交叉口之间的运行时空图如图1所示. 其中,Di为第i个交叉口的位置坐标. 相应的绿波带约束为
图 1
式中:
式中:
2)CEBs交叉口不停车约束.
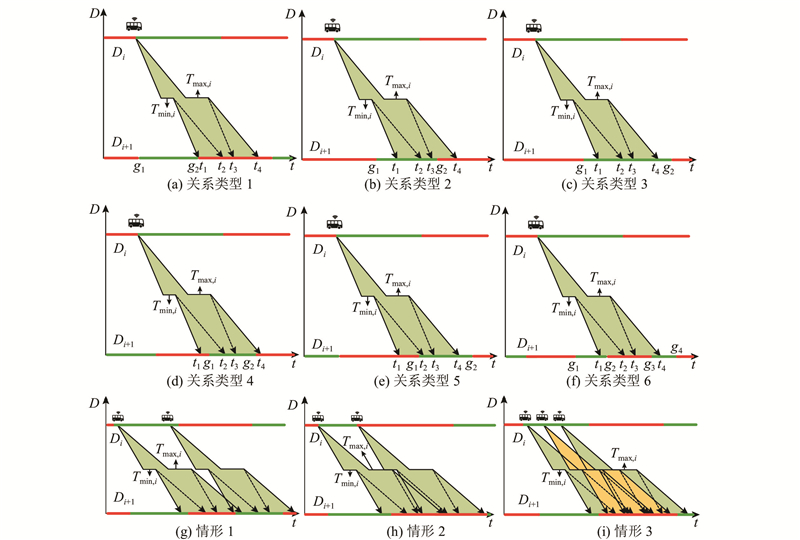
通过分析CEBs离开上游交叉口与到达下游交叉口时刻之间的关系,得出CEBs可以不停车地通过下游交叉口的必要条件. 如图2(a)~(f)所示为CEBs从上游交叉口绿灯时出发,经过行驶与停靠过程,到达下游交叉口时的信号灯的所有可能状态. 其中2条黑色实线分别表示以最快速度行驶并以最短停站时间停车的车辆轨迹,以及以最慢速度行驶并以最长停站时间停车的车辆轨迹,即单个CEB行程时间的2个边界(到达时刻分别为t1和t4). 为了表示本研究中速度控制策略下CEBs的时空运行特征,使t1与t4更充分地表达CEBs的速度与到达区间的关系,引入CEBs在总到达区间[t1, t4]内的2个特殊到达时刻,即t2和t3,分别表示CEBs首先以最快速度行驶并以最短停站时间停车,然后又以最慢速度行驶到达下游交叉口的时刻,以及首先以最慢速度行驶并以最长停站时间停车,然后又以最快速度行驶到达下游交叉口的时刻. g1和g2分别表示绿灯区间的2个边界. 在图2(a)中,CEBs的到达区间[t1, t4]与交叉口绿灯区间[g1, g2]显然没有重叠关系,即不论CEBs以何种速度行驶或停站时间停靠,其到达交叉口时都会遇到红灯,因此无法不停车地通过交叉口. 图2(b)~(f)中,CEBs的到达区间[t1, t4]与交叉口绿灯区间[g1, g2]显然存在重叠关系,即CEBs可以通过控制速度与停站时间在绿灯期间[g1, g2]到达交叉口,从而实现不停车通过交叉口.
图 2
图 2 CEBs到达区间与绿灯区间之间的关系
Fig.2 Relationship between arrival interval of CEBs and green-phase interval
综上所述,若要实现CEBs不停车地通过交叉口,其必要条件是CEBs的到达区间[t1, t4]与交叉口绿灯区间[g1, g2]存在重叠,即满足
CEBs不停车通过交叉口是一个连续建模问题,而建立连续约束比建立带宽约束要困难得多. 首先根据到达区间与绿灯区间的重叠关系将公交离开与到达划分成不同场景,然后对不同场景中的特征点进行数学描述,实现连续问题的离散化,在此基础上构建CEBs不停车约束. 根据对到达区间与绿灯区间的比较结果,将公交到达情况分成3种情形,并以下行方向为例进行分析.
情形1:
式中:
类似地,CEBs在路段i上行方向的平均行程时间的取值范围为
通过计算平均行程时间的差值,可以得到下行方向的CEBs在交叉口i+1到达时间区间长度为
情形2:
交叉口i绿灯结束时刻离开的CEBs不停车通过交叉口i+1的约束为
式(24)~(27)可以合并为
同理,上游方向CEBs的不停车约束如下:
情形3:
1.3. CEBs轨迹控制与站点充电协同策略
1.2节中的干线信号协调控制模型为同时存在CEBs与RVs的混合交通流提供了统一的交通信号环境,即通过相位相序、相位差及绿灯时长协调2类车辆的有序运行,同时为CEBs轨迹控制与站点充电协同策略的制定提供了信号基础. 在此框架下,制定CEBs轨迹控制与站点充电协同策略,使CEBs在保持良好运行秩序与效率的同时,优化其在停靠站进行静态无线充电的时长. 根据CEBs在每个路段上的不同位置,将协同策略的控制过程分为3个阶段:第1个控制阶段是从当前路段的上游交叉口停车线到当前路段的公交停靠站;第2个控制阶段是公交的停靠过程;第3个控制阶段是从当前路段公交停靠站到下游交叉口停车线.
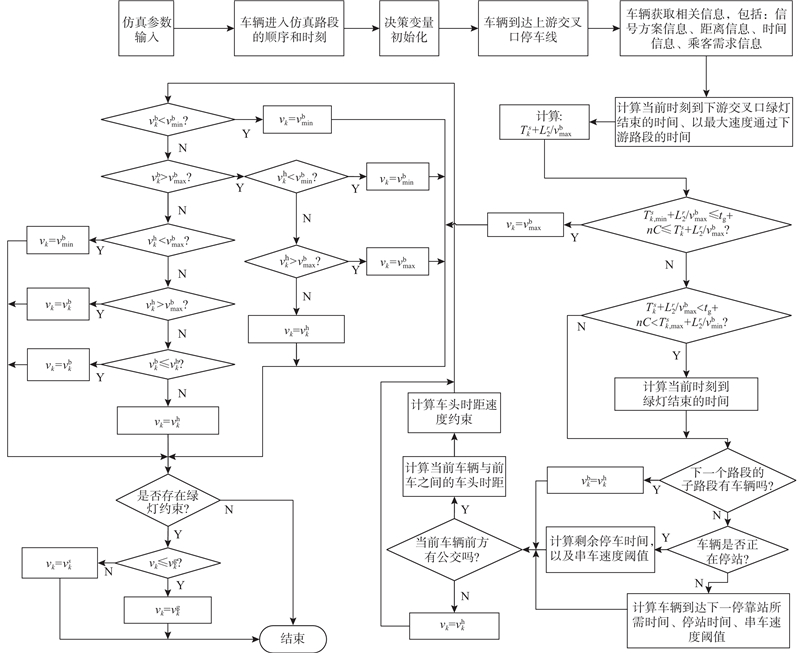
阶段1的控制逻辑如图3所示,其中,
图 3
图 3 各运行路段第1阶段中CEBs的轨迹控制逻辑
Fig.3 CEBs trajectory control logic at first stage for each operational section
1)串车:需要计算串车速度阈值
2)车头时距:需要判断当前车辆与前方车辆的车头时距与计划车头时距的偏差. 如果当前车头时距小于计划车头时距,则当前车辆速度为
式中:H为计划车头时距,
如果当前车头时距大于计划车头时距,则当前车辆速度为
3)CEBs速度限值:CEBs的速度始终在最大值与最小值的范围内.
式中:
对于控制阶段2,如果在公交站正常停靠而不影响公交车不停车通过下游交叉口,则公交的车速不受公交站停车时长影响. 反之,公交采取提前离站或者推迟离站策略. 当采取提前离站策略时,最短停站时长使公交的实际停站时间满足绝大部分停靠站的乘客上下车需求. 当采取推迟离站策略时,公交的实际停站时间满足所有停靠站的乘客上下车时间需求. 当下游交叉口是绿灯时,停站时长的计算方法如下:
式中:
式中:
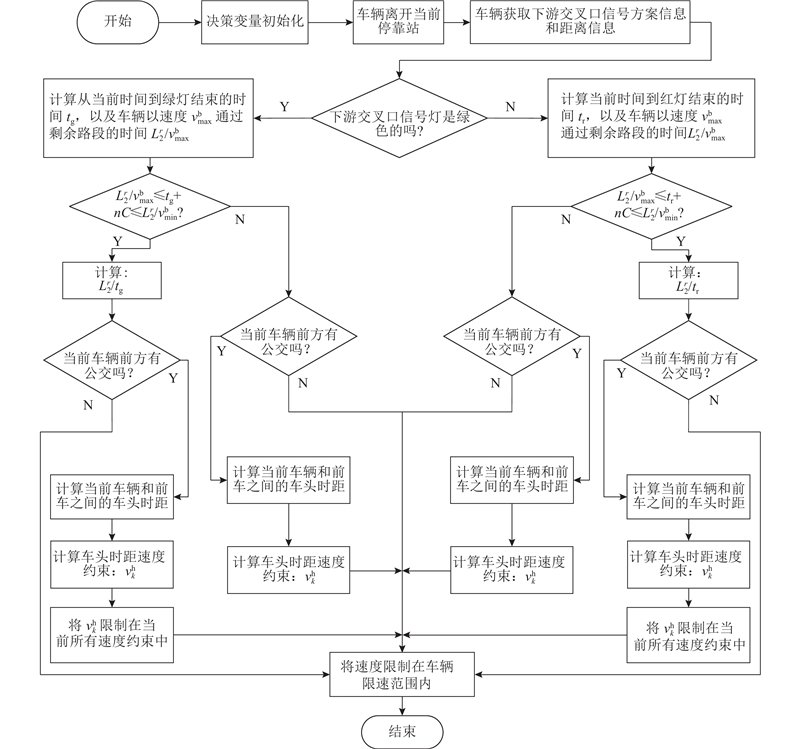
阶段3控制逻辑如图4所示,当车辆离开停靠站时,可以获得下游交叉口的信号配时方案、当前位置与下游路口的距离. 阶段3车辆速度的确定受到如下因素的影响.
图 4
图 4 各运行路段第3阶段中CEBs的轨迹控制逻辑
Fig.4 CEBs trajectory control logic at third stage for each operational section
1) 车头时距:与阶段1中车头时距速度约束相同.
2) 不停车速度约束:使车辆不停车通过交叉口. 当下游交叉口是绿灯时,不停车速度约束如下.
式中:
3) CEBs速度限值:CEBs的速度始终在最大值与最小值的范围内,与阶段1相同.
对于CEBs轨迹控制与站点充电协同策略,采用Python与SUMO仿真软件的TraCI接口对公交的运行、停靠和充电过程进行仿真.
2. 仿真验证
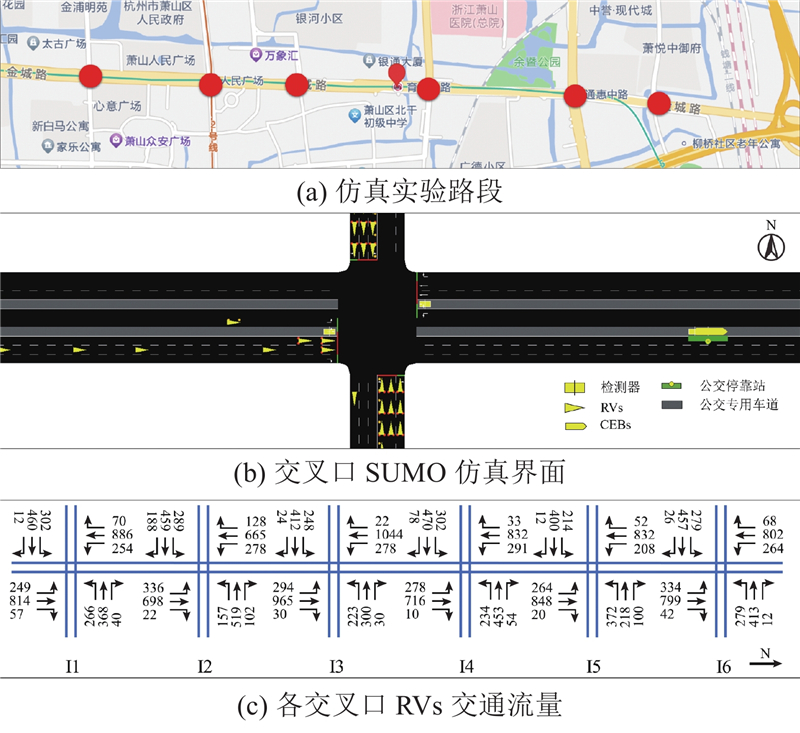
2.1. 仿真环境构建
图 5
2.2. 方案对比分析
采用提出的方法和不考虑站点充电协同的方法进行比较. 提出的方法同时采用干线信号协调、CEBs轨迹控制与站点充电协同(signal-trajectory-charging, STC)的策略,不考虑站点充电协同的方法仅采用干线信号协调与CEBs轨迹控制(signal-trajectory, ST)策略.
首先,根据HCM中的方法计算每个交叉口的信号配时方案. 其次,将公共周期长度设为最大周期长度,计算出最大周期长度为215 s. 最后,采用改进后的Multiband模型对实验路段上的相位相序和相位差进行优化. 模型采用Gurobi 9.5.2求解器与Python 3.9.8,在配备AMD Ryzen 5 pro处理器的Windows 10操作系统上进行联合求解;求解器的求解时间限制设为“inf”,相对最优间隙的终止条件为0.01%. 在干线信号协调方案中,RVs的运行速度设定为40 km/h,CEBs的速度区间定义为13~60 km/h. 在Python与SUMO的TraCI接口构建的仿真环境下,基于优化后的信号协调方案和设计的轨迹控制策略,实现CEBs的运行控制.
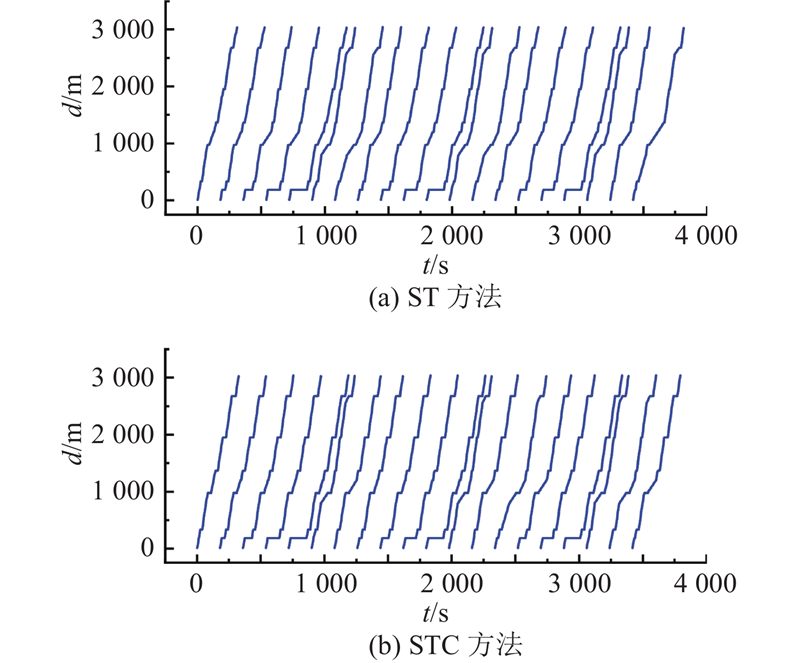
根据历史乘客需求数据和公交排班方案,重构工作日早高峰8:00—9:00期间20辆CEBs进入第1个车站时的时间. 相邻2辆CEBs的进入时间间隔为180 s,所有CEBs以统一的时间间隔进入仿真路段. STC和ST方法下的CEBs运行轨迹如图6所示.
图 6
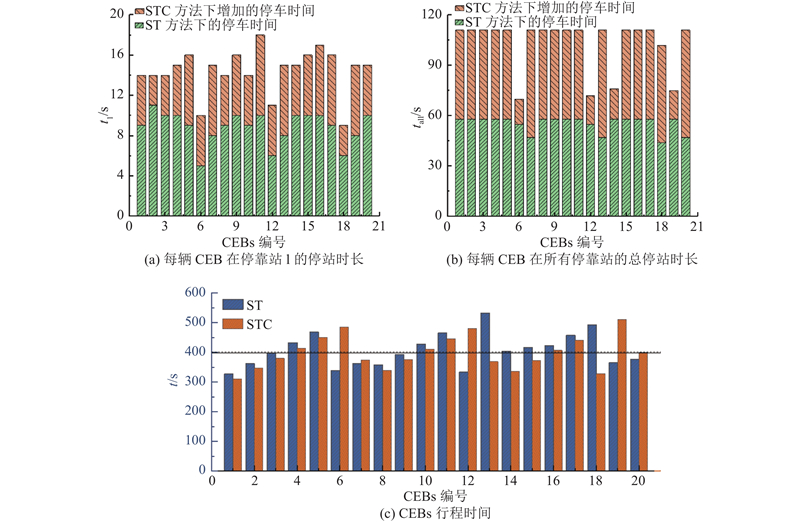
可以看出,在CEBs轨迹控制与站点充电协同策略下,车辆的停站时长明显大于采用常规调度方法时的停站时长. 此外,定量分析2种控制策略下每辆CEB的充电时长的增加以及每辆车的停车时间总和,如图7中(a)、(b)所示. 其中,t1为车辆在停靠站1的充电时长,tall为车辆在所有停靠站的总充电时长. 通过计算可得,对于停靠站1,STC方法与ST方法下的平均停车时间分别为14.5 s和8.9 s,即STC可以使CEBs的充电时长增加62.9%. 类似地,对于所有停靠站,STC与常规ST方法下的停车平均时间总和分别为103.1 s和55.6 s,即STC策略可以使CEBs的充电时长增加85.4%. 另一方面,对每辆公交的总行程时间进行分析,结果如图7(c)所示. STC和ST方法下的车辆平均行程时间分别为406.8 s和399.1 s. 在STC策略下,平均行程时间仅增加了7.7 s. 由此可见,提出的STC策略在提升CEBs静态无线充电时长的同时,几乎不会影响CEBs的运行效率.
图 7
图 7 STC和ST策略下CEBs充电时长与行程时间
Fig.7 Charging time and travel time of CEBs under STC and ST strategies
2.3. 适用性分析
2.3.1. 不同公交流量下的模型分析
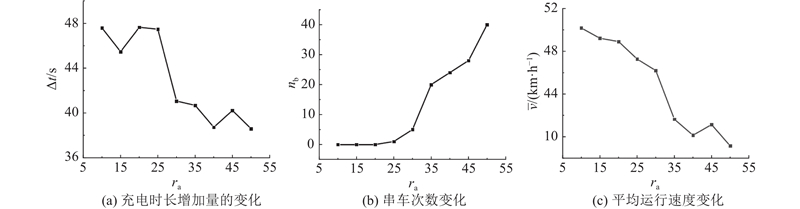
为了分析CEBs流量对模型性能的影响,将公交流量从每小时10辆逐步提升至每小时50辆进行对比分析. 在每个场景中,充电需求系数都设置为1.0. 仿真时车辆的实际停站时间为乘客上下车需求时间与附加停站时间之和. 其中,站台1~10的实际的乘客上下车需求时间分别为9.0、14.0、9.0、12.0、14.0、14.0、12.0、9.0、14.0、9.0 s,附加的停站时间是车辆在满足实际的乘客上下车需求时间与不停车通过交叉口约束的前提下所延长的停站时间. 随着流量的增加,平均停车时长增加量
图 8
图 8 不同CEBs流量下的运行指标变化
Fig.8 Changes in operation indicators under different traffic flows of CEBs
从图8可以看出,随着CEBs流量的增加,能够增加的充电时长有所减小(从47.6 s下降为38.6 s). 这是由于在流量较低时,前后2辆CEBs之间的距离较大,前方的车辆不会对后方车辆的速度产生影响,或只产生较小的影响. 因此,后方车辆的停车时长有更大的优化空间. 在本节的场景中,更大的停车时长优化空间意味着CEBs可以在停靠站停靠更长的时间来进行静态无线充电. 随着流量的增加,前后2辆CEBs之间的距离较小,后方车辆的停车时长优化空间减小,公交串车次数也逐渐增多. 这是由于当流量增加时,前后2辆车之间的车头时距减小,从而提高了串车情况的发生概率. 此外,随着流量的增加,CEBs平均行驶速度呈现下降的趋势. 这是由于更大的流量意味着更小的计划车头时距,而更小的计划车头时距会导致前车对后车产生更多的影响. 在本研究提出的模型中,为了减少串车情况,后车将以更小的速度行驶,以尽量保持计划车头时距.
2.3.2. 不同乘客需求下的模型分析
为了分析乘客需求对模型性能的影响,设置4种乘客需求场景进行分析,从场景1(ST1)至场景4(ST4)乘客需求逐渐增大,如表1所示. 其中,ts为站台s的停站时间,1~10表示10个不同的站台. 在每个场景中,充电需求系数都设置为1.0,公交流量为20 veh/h,且以均匀的车头时距(180.0 s)发车.
表 1 不同需求场景下的CEBs停站时间
Tab.1
| 场景 | ts/s | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| ST1 | 6.0 | 8.0 | 5.0 | 5.0 | 6.0 | 6.0 | 5.0 | 5.0 | 8.0 | 6.0 |
| ST2 | 9.0 | 14.0 | 9.0 | 12.0 | 14.0 | 14.0 | 12.0 | 9.0 | 14.0 | 9.0 |
| ST3 | 12.0 | 20.0 | 13.0 | 19.0 | 22.0 | 22.0 | 19.0 | 13.0 | 20.0 | 12.0 |
| ST4 | 15.0 | 25.0 | 16.0 | 25.0 | 30.0 | 30.0 | 25.0 | 16.0 | 25.0 | 15.0 |
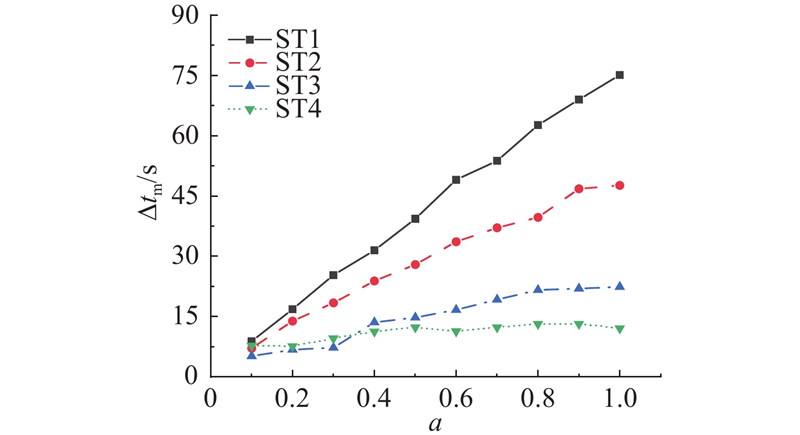
图9为4种乘客需求场景下CEBs停站时间的提升情况. 一方面,随着乘客需求从场景ST1变化到场景ST4,平均停站时长增加量
图 9
图 9 不同乘客需求场景与充电需求系数下充电时间增加量的变化
Fig.9 Changes in increased charging time under different passenger demand scenarios and charging demand coefficients
2.4. 敏感性分析
为了分析不同充电需求系数下的模型在充电时长增加方面的潜力,对充电需求系数a进行敏感性分析. 具体地,以0.1为间隔在0.0~1.0之间设置11种不同的充电需求系数进行分析,CEBs流量都为20 bus/h. 采取不同系数a时的CEBs平均停站时间
图 10
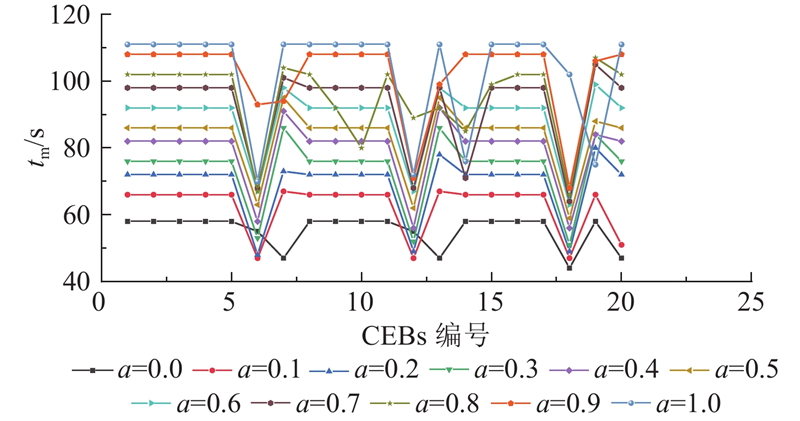
图 10 不同充电需求系数下的CEBs平均充电时长
Fig.10 Average charging time with different values of charging demand coefficient
对于同一辆CEB而言,随着a的增加,总的充电时长基本呈线性增加. 当a=0.0时,相当于此过程没有考虑充电时长的增加,CEBs正常运行,不同CEBs的平均停站时长为55.0 s;当a=1.0时,平均停站时长为103.0 s,说明提出的控制方法可以提升87.3%的充电时长. 当采取相同的a时,大部分CEBs的充电时长基本保持不变,而第6、12、18辆CEBs的充电时长提升值较小,这是因为交叉口不停车约束使得这些车辆在达到基本停车时长后,须尽早离开车站,从而实现不停车通过下个交叉口,因此无法获得理论上的最大停站时长.
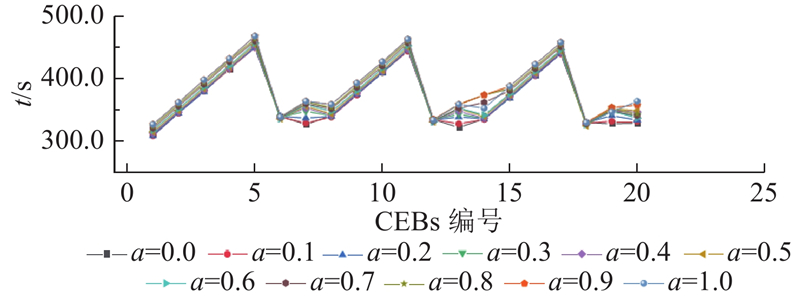
图11为不同充电需求系数下每辆CEB的行程时间与所有CEBs的平均行程时间. 首先,在相同a下,不同CEBs的行程时间存在近似于周期性的变化,这是由交叉口信号方案的周期性导致的. 其次,对于同一辆CEB,随着a增加,行程时间都在较小的时间范围内变化(行程时间的最小时间差为4.0 s,最大时间差为39.0 s,平均行程时间差为20.4 s). 这表明在不同a下,提出的方法均可以在几乎不对CEBs效率产生影响的同时,提升CEBs的充电时长. 最后,对比不同a下所有CEBs的平均行程时间. 最小平均行程时间为367.0 s,最大为385.5 s,这进一步表明不同a下,提出的方法不会对CEBs运行效率产生较大影响.
图 11
图 11 不同充电需求系数下的CEBs行程时间
Fig.11 CEBs operation time under different values of charging demand coefficients
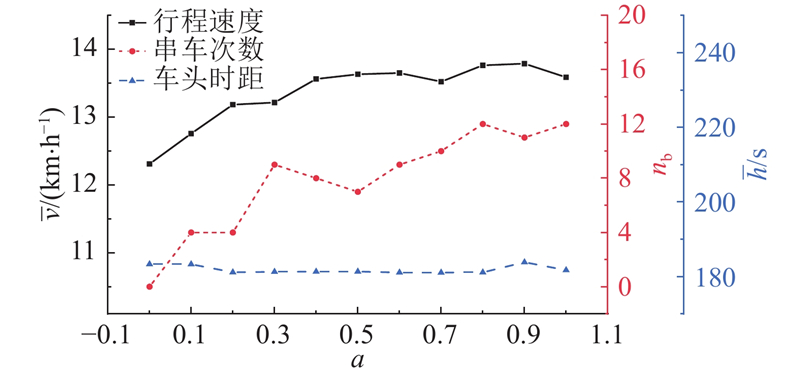
图12为CEBs平均行驶速度
图 12
图 12 不同充电需求系数下的CEBs运行指标变化
Fig.12 Changes in CEBs operation indicators under different charging demand coefficients
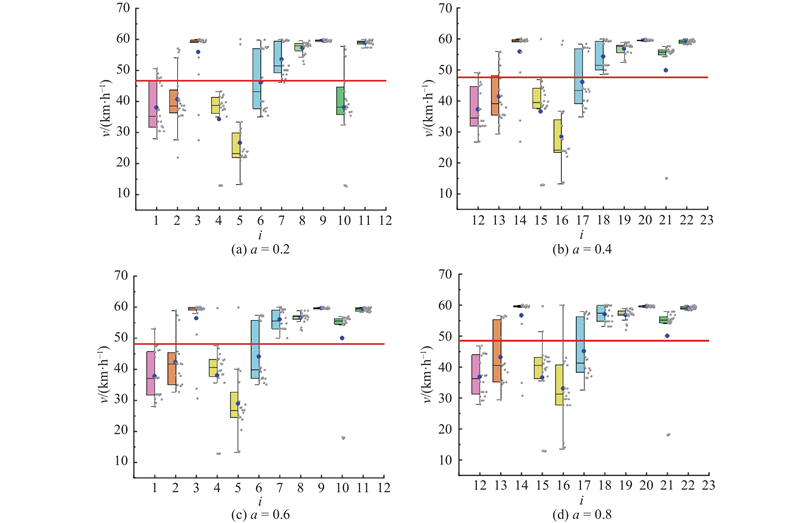
图 13
图 13 当充电需求系数分别为0.2、0.4、0.6、0.8时的CEBs速度分布
Fig.13 Speed distribution of CEBs with charging demand coefficients of 0.2, 0.4, 0.6 and 0.8
3. 结 语
构建考虑干线信号协调的网联电动公交轨迹控制与站点充电协同优化模型,该模型同时考虑了干线信号协调、车速诱导和充电时长优化. 基于实际场景的仿真分析结果表明,提出的模型可以在几乎不对公交总体运行效率产生影响的情况下,提升85%的静态无线充电时长. 适用性分析结果表明,提出的模型可以很好地适用于不同公交流量与乘客需求场景. 敏感性分析结果表明,协同模型中引入的充电需求系数使得公交可以根据实际运行过程中不同的电量状态进行充电时长的动态调整. 为了聚焦研究重点,模型中没有考虑左转或右转公交车的不停车约束,这些约束的加入可能会对RVs效率产生影响,未来的研究将重点关注这一影响.
参考文献
Cooperative optimization of bus service and charging schedules for a fast-charging battery electric bus network
[J].DOI:10.1109/TITS.2023.3243105 [本文引用: 1]
电动公交车电池荷电状态的Seq2Seq预测方法
[J].
Seq2Seq prediction method of state of charge of electric bus battery
[J].
电动公交车队规模与充电桩配置协同优化
[J].
Collaborative optimization of electric bus fleet size and charger deployment
[J].
面向资源约束的电动公交车充电调度策略
[J].
Resource constraint-oriented charging scheduling strategy for electric buses
[J].
考虑充电需求的电动公交车运营优化模型与算法
[J].
Optimization model and algorithm for electric bus operation considering charging demand
[J].
专用道条件下电动公交线路静态无线充电设施布局优化
[J].DOI:10.3969/j.issn.1001-7372.2023.01.016 [本文引用: 2]
Layout optimization of static wireless charging facilities for electric bus routes with dedicated bus lanes
[J].DOI:10.3969/j.issn.1001-7372.2023.01.016 [本文引用: 2]
智能网联车借用公交专用道的轨迹与信号协同优化
[J].
Collaborative optimization for signals and trajectories of connected automated vehicles on dedicated bus lanes
[J].
智能网联车和人驾车辆混合交通流排队长度估计模型
[J].
Queue length estimation model for mixed traffic flow of intelligent connected vehicles and human-driven vehicles
[J].
车路协同环境下重叠线路公交车速诱导策略
[J].DOI:10.3969/j.issn.1001-7372.2021.07.004 [本文引用: 2]
Speed guidance strategy for buses run on overlapping route segments under cooperative vehicle infrastructure
[J].DOI:10.3969/j.issn.1001-7372.2021.07.004 [本文引用: 2]
面向进出站强制换道过程的智能网联公交车两车协同换道策略
[J].
Two-vehicle cooperative lane change strategy for intelligent and connected buses in the mandatory lane change process of entry and exit
[J].
考虑路口上游停靠站影响的公交延误模型
[J].
Bus delay model considering influence of stop at upstream of intersection
[J].
兼顾社会车辆多路径协调的干线公交优先信号协调方法
[J].
An arterial bus signal priority strategy considering multi-path coordination of social vehicles
[J].
Collaborative optimization of intersection signals and speed guidance for buses run on overlapping route segments under connected environment
[J].DOI:10.1111/mice.13289 [本文引用: 1]
Bus control strategies in corridors with signalized intersections
[J].DOI:10.1016/j.trc.2016.08.013 [本文引用: 1]
考虑非线性充电的纯电动公交充电计划优化
[J].
Charging schedule optimization of battery electric bus considering nonlinear charging profile
[J].
On charging scheduling optimization for a wirelessly charged electric bus system
[J].DOI:10.1109/TITS.2017.2740329 [本文引用: 1]
Optimal design of battery swapping-based electrified public bus transit systems
[J].DOI:10.1109/TTE.2021.3083106 [本文引用: 1]
Deployment of stationary and dynamic charging infrastructure for electric vehicles along traffic corridors
[J].DOI:10.1016/j.trc.2017.01.021 [本文引用: 1]
Trip energy consumption estimation for electric buses
[J].DOI:10.1016/j.commtr.2022.100069 [本文引用: 1]
MAXBAND: a program for setting signals on arteries and triangular networks
[J].
A multi-band approach to arterial traffic signal optimization
[J].DOI:10.1016/0191-2615(91)90013-9 [本文引用: 1]