在多智能体系统的研究中，多智能体路径规划问题（multi-agent path finding，MAPF）是目前研究的重点之一. 多智能体路径规划算法按照解决方式主要可以分为快速MAPF算法、最优MAPF算法与次优MAPF算法.

快速MAPF算法的主要方式是用尽可能少的交互，将MAPF问题解耦成若干个单智能体的路径规划问题. 其中优先级规划算法是应用最广泛的方法. 优先级规划算法为每个智能体分配一个优先等级，根据智能体的优先等级依次进行单智能体路径规划. Bnaya等^[1]提出多种设置优先级的方法来提高算法效率，虽然优先级规划可以用于解决MAPF问题，但优先级规划的解决方案不能保证最佳，也不能保证完整性，即这类快速MAPF算法在可行解存在的MAPF问题实例中存在求解失败的可能性.

最优MAPF算法是用于求解具有完整性与最优性的MAPF算法. 最优MAPF算法可以分为扩展A*搜索、代价增长树搜索与基于冲突搜索3类. Wagner等^[2]针对扩展A*搜索提出M*算法，通过动态地改变搜索过程中每一次扩展的分支数量，解决状态空间爆炸的问题. Sharon等^[3]提出代价增长树搜索（increasing cost tree search, ICTS）算法，将搜索过程分为上、下2层，对MAPF问题进行求解. ICTS上层搜索基于全局优化目标，为智能体$ {a_i} \in A $生成路径代价上限$ {C_i} $，其中$ A $表示智能体集合，下层搜索根据路径代价进行搜索，使用多值决策图^[4]验证是否存在一条路径代价等于$ {C_i} $且不与其他路径发生冲突的路径. 基于冲突搜索算法^[5]，采用分层结构对MAPF问题进行求解. Cohen等^[6]通过将搜索时间分成几部分，在每部分打乱智能体顺序后重新规划，提高规划成功率. 虽然最优MAPF算法的求解质量高，但随着问题规模的不断扩大，时间复杂度呈现指数级增长的特性，这将导致该类算法无法满足实际应用的需求.

次优MAPF算法通常由快速MAPF算法与最优MAPF算法推广而来，增强冲突搜索算法^[7]（enhanced CBS, ECBS）通过采用焦点搜索^[8]引入次优性. 焦点搜索在每次迭代中选择不大于$ (1+\omega ) $倍最优代价且冲突最少的节点进行扩展，这使得ECBS算法在保证次优边界的同时，大大缩短了搜索时间. 综上所述，利用次优MAPA算法能够得到具有一定次优边界的解，在解质量与计算时间中找到平衡点，同时具备求解速度快和质量高的优势.

在算法研究不断深化的同时，多智能体路径规划问题因其在仓库自动化^[9]、自动交通管理^[10]、物流配送^[11-12]和电弧增材制造^[13]等领域的广泛应用而备受关注. 典型应用场景如分拣机器人系统，其中每个智能体需要从一个或多个货物存储位置取下产品，并将其交付到一个或多个请求存储该产品的库存站点. 在此过程中，智能体需要按照特定顺序访问多个目标位置. 针对该多目标应用场景，该算法可以用于求解多目标体任务分配与路径规划（multi-goal task assignment and path finding, MG-TAPF）问题^[14].

现有技术存在的缺陷在于对每个智能体的路径进行规划时采用了离散的时间步长，无论是移动还是原地等待，都强制规定智能体在单个时间步长内持续占用当前所在的网格单元，导致智能体到达目标花费的时间较长且成功率较低. 针对上述问题，本文提出连续时间下用于求解MG-TAPF问题的高效算法，优化了现有算法中因采用离散时间所导致的智能体到达目标花费时间较长的问题，求解得到更优的解决方案. 引入冲突分级策略，提高了算法的求解成功率.

在MG-TAPF问题中，先为所有智能体进行任务分配，再为每个智能体规划出一条依次经过任务目标的路径.

MG-TAPF问题主要由以下3部分组成.

1）无向图$ G = (V,E) $用于描述智能体的运行环境. 其中$ V $为一组位置的集合，表示智能体可以占据的位置；$ E $为连接不同位置间的边，$ E = \{ (x,y)|x \in V, y \in V,x \ne y\} $，智能体可以从$ x $移动到$ y $而不经过其他顶点. $ {i_{xy}} $为决策变量，若智能体$ {a_i} $经过边$ (x,y) $，则$ {i_{xy}} = 1 $，否则$ {i_{xy}} = 0 $.

2）$ m $个智能体$ \{ {a_1},{a_2},\cdots ,{a_m}\} $，其中每个智能体$ {a_i} $对应一个起始位置$ {s_i} \in V $.

3）$ m $个任务$ \{ {g_1},{g_2},\cdots ,{g_m}\} $，其中每个任务$ {g_j} $由一个大小为$ {K_j} $的目标点序列组成，$ {g_j} = \{ {g_j}(1),{g_j}(2),\cdots , {g_j}({K_j})\} $. 当智能体在执行此任务时，必须按照目标点序列中的顺序进行访问，不能改变次序. 所有任务不存在优先级，即每个智能体$ {a_i} $可以被分配去完成任意任务$ {g_j} $.

$ {\pi _i}(t) $表示智能体$ {a_i} $在$ t $时刻所在的位置，智能体$ {a_i} $的路径可以由一组由位置组成的序列表示，即$ {\pi _i} = \{ {\pi _i}(0),{\pi _i}(1),\cdots ,{\pi _i}({T_i}),{\pi _i}({T_i}+1),\cdots \} $.除此之外，每个智能体路径满足以下约束条件.

1）智能体路径从其起始位置开始，即$ {\pi _i}(0) = {s_i} $.

2）在每一个时间步长t，智能体只能执行2种动作：移动到相邻位置或在当前位置原地等待，$ ({\pi }_{i}(t),{\pi }_{i}(t+1))\in E或{\pi }_{i}(t)={\pi }_{i}(t+1) $，$ {\pi _i}(t+1) \in V $.

3）智能体到达其被分配任务$ {g_j} $的位置，并在$ {T_i} $时刻停留在目标位置，则$ {T_i} $为当前智能体的最短完成时间. 智能体在$ {T_i} $时刻后始终停留在目标位置，即$ {\pi _i}(t) = {g_j} $，$ t = {T_i},\cdots ,\infty $.

连续时间下，MG-TAPF问题中的每个智能体设定如下.

1）设定所有智能体都以相同的速度进行运动.

2）不考虑智能体运动所涉及的惯性问题，智能体可以立即开始或停止运动.

3）某一时刻2个或多个智能体的轮廓存在重叠，表示智能体间的路径存在冲突. 为了方便计算碰撞的开始时间与结束时间，设定所有智能体具有相同的形状与大小.

4）采用一系列运动与等待的动作序列，对智能体路径进行描述. 每个智能体动作序列中每个动作持续时间的总和构成解决方案的总成本.

若每个智能体按照规划好的路径进行运动，且在运动过程中不会与其他智能体发生冲突，则每个智能体路径的集合为当前MG-TAPF的一个可行解. MG-TAPF问题解的评价指标主要为路径总成本与最大完成时间^[15]. 路径总成本指所有智能体到达目标位置的路径长度总和. 路径总长度越小，反映了解的质量越高. 最大完成时间指每个智能体完成各自任务所需的最大用时. 最大完成时间越短，反映了解的质量越高.

结合任务分配的冲突搜索（conflict-based search with optimal task assignment, CBS-TA）算法^[16]是TAPF问题中常用的最优求解算法.

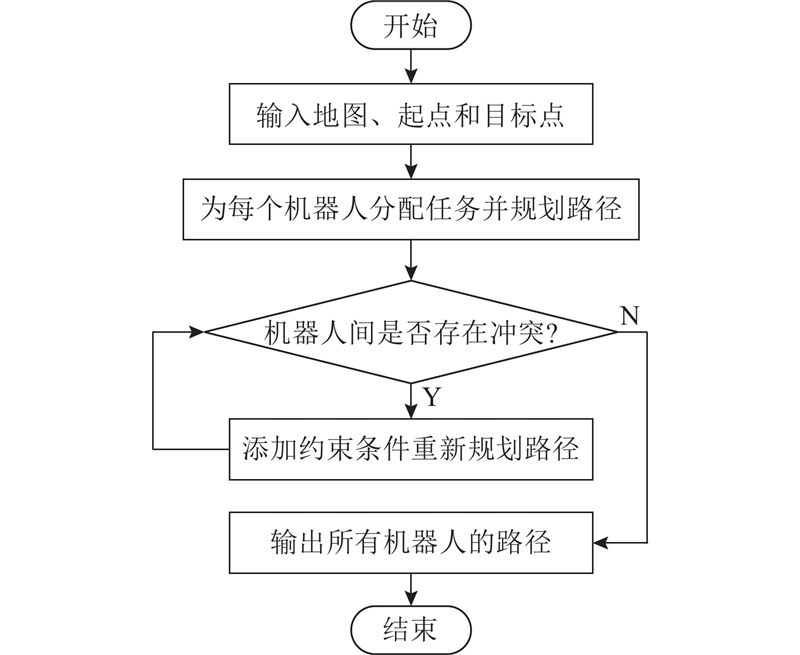
该算法采用分层结构，对TAPF问题进行求解. 上层规划器采用多个二叉约束树结构进行组织，树上的每个节点包含一个约束条件集合与一个满足约束集合的多智能体路径规划方案. 智能体间的冲突采用元组$ \{ {a_i},{a_j},v,t\} $进行描述，表示智能体$ {a_i} $与智能体$ {a_j} $在$ t $时刻同时占据了顶点$ v $.针对每个智能体的约束由一个元组$ \{ {a_i},v,t\} $进行描述，表示智能体$ {a_i} $禁止在$ t $时刻占据顶点$ v $. 该算法检查当前节点规划方案中是否存在冲突. 若存在，则在当前约束树节点生成2个子节点，分别在2个子节点的约束条件集合中添加用于解决父节点冲突的约束条件. 下层规划器常采用A*算法作为路径规划算法，根据上层规划器的约束条件，为每个智能体规划出满足约束的最优路径. CBS-TA算法的基本流程如图1所示.

CBS-TA算法可以用于求解TAPF问题的最优解，但算法的整体流程都基于以下设定.

1）每个智能体的运动都为相同速度的匀速运动，时间被离散为固定的时间步长，通常为智能体从当前栅格运动至相邻栅格的时间.

2）智能体无论是移动至相邻栅格或是原地等待，都为固定的时间步长.

3）在每个时间步长中，智能体始终占据当前顶点.

由此，下层规划器常采用4邻域作为路径规划时的搜索范围. 由于使用栅格与时间步长描述智能体的路径，智能体在当前时间段内始终在某一栅格，下一时刻始终在相邻栅格，这省略了智能体运动的过程. 这些简化的设定限制了算法在实际应用中的适用性.

针对上述CBS-TA算法的不足，作出以下改进：定义连续时间下智能体间的冲突与解冲突方式，在下层规划器中引入安全间隔与标签的概念，引入冲突分级策略.

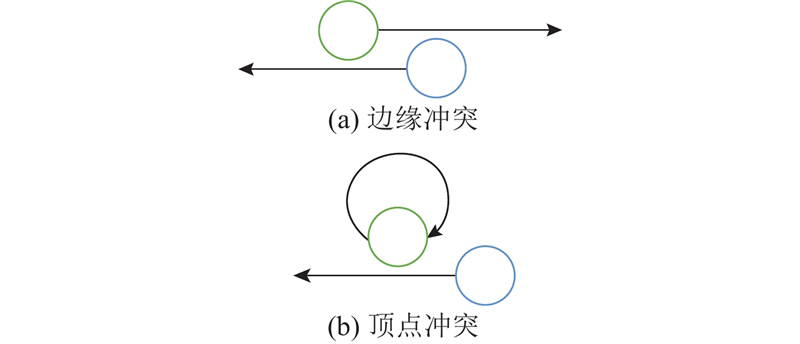
在连续时间下，由于需要考虑智能体的形状，边缘冲突不仅发生在2个智能体沿同一条边对向运动时，还可能因它们在不同边上运动但间距过小而触发，如图2(a)所示. 顶点冲突不仅在2个智能体同时占据同一顶点时发生，一个运动的智能体与另一个在顶点执行等待动作的智能体也会发生顶点冲突，如图2(b)所示. 在离散时间下，边缘冲突与顶点冲突通常使用元组$ \{ {a_i},{a_j},u,v,t\} $或$ \{ {a_i},{a_j},v,t\} $进行描述，其中$ {a_i} $、$ {a}_{j} $为智能体，$ u $、$ v $为顶点，$ t $为时间. 由于连续时间下使用动作与持续时间代替顶点与时间描述智能体路径，改用元组$ \{ {a_i},({v_i},{u_i}),{t_i},{a_j},({v_j},{u_j}),{t_j}\} $进行描述. 该元组表示若智能体$ {a_i} $在$ {t_i} $时刻执行动作$ ({v_i},{u_i}) $且智能体$ {a_j} $在$ {t_j} $时刻执行动作$ ({v_j},{u_j}) $，则两者将发生碰撞. 其中动作$ ({v_i},{u_i}) $由2个无向图中的2个顶点组成，若$ {v_i} = {u_i} $，则表示原地等待动作；若$ {v_i} \ne {u_i} $，则表示从顶点$ {v_i} $向顶点$ {u_i} $运动. 算法中的冲突采用模拟的方式进行检测. 由于连续时间下智能体路径为连续的曲线，依据不同的智能体大小选择不同的路径间隔，将连续路径离散化为路径点序列，采用模拟的方式进行碰撞检测.

将算法推广至连续时间后，采用最佳优先搜索，在每次迭代中选择约束树中路径成本总和最小的节点. 若检测到碰撞，则生成2个子节点，并为2个节点分别添加解冲突的约束. 在连续时间下，智能体等待时间无须为时间步长的整数倍. 仿照冲突定义的修改，将用于解决冲突$ \{ {a_i},({v_i},{u_i}),{t_i},{a_j}, ({v_j},{u_j}),{t_j}\} $的约束修改为$ \{ {a_i},({v_i},{u_i}),({t_i},{t_{i\_{\mathrm{end}}}})\} $与$ \{ {a_j},({v_j}, {u_j}),({t_j},{t_{j\_{\mathrm{end}}}})\} $. 以$ \{ {a_i},({v_i},{u_i}),({t_i},{t_{i\_{\mathrm{end}}}})\} $为例，表示智能体$ {a_i} $在$ {t_i} $至$ {t_{i\_{\mathrm{end}}}} $的时间段内（$ ({t_i},{t_{i\_{\mathrm{end}}}}) $为智能体$ {a_i} $与智能体$ {a_j} $发生冲突的最小时间间隔）不能执行动作$ ({v_i},{u_i}) $，但在$ {t_{i\_{\mathrm{end}}}} $时刻之后开始执行动作可以避免冲突.

针对发生冲突的最小时间间隔$ ({t_i},{t_{i\_{\mathrm{end}}}}) $，已有一些算法可以进行求解^[17]，但由于智能体的形状不确定，目前还不存在较通用的计算方式. 通过多次仿真的方式，计算最小时间间隔. 设置每次增加的时间步长$ \Delta t $，以冲突$ \{ {a_i},({v_i},{u_i}),{t_i},{a_j},({v_j},{u_j}),{t_j}\} $为例，在$ {t_i} $的基础上不断累加$ \Delta t $，每次累加后，通过仿真判断是否会和$ {a_j} $发生冲突，直至不会发生冲突，由此得到最小时间间隔.

根据输入无向图$ G = (V,E) $计算每个智能体到达每个目标位置的最短路径，得到代价矩阵$ {c_{xy}} $，利用匈牙利算法得到最优任务分配结果. 根据任务分配结果与路径代价总和，生成首棵约束树的根节点. 判断当前解决方案是否存在冲突，若存在冲突，则需要对根节点进行扩展. 根据当前根节点的任务分配方案，额外生成次优的任务分配方案，且该次优分配方案为所有次优解中路径代价总和最小的方案，根据该方案生成另外一棵约束树的根节点. 这使得搜索过程中若当前解决方案解冲突后的子节点代价高于次优方案的代价，则扩展次优方案，因为此时潜在的全局最优解在次优方案中. 当扩展次优方案约束树的根节点时，额外生成进一步次优的任务分配方案. 如此循环，扩展得到的第一个无冲突节点为输出的全局最优的任务分配方案.

为了规划得到满足上层规划器约束的最优路径，以A*算法作为基础，引入安全间隔. 若智能体在某一节点从开始时刻起始终停留在此处，且不会与其他智能体发生碰撞，则该节点的安全间隔为$ [0,\infty ] $. 若从某一时刻$ {t_i} $开始至之后的某一时刻$ {t_j} $会与其他智能体发生冲突，则将安全间隔定义为$ [0,{t_i}] \cup [{t_j},\infty ) $. $ (t_i^{},{t_j}) $为碰撞区间，智能体在碰撞区间的任一时刻都会发生冲突.

利用改进后的算法，可以规划得到满足上层规划器约束的最优路径. 若约束$ \{ {a_i},({v_i},{u_i}),({t_i},{t_{i\_{\mathrm{end}}}})\} $为运动动作，规划过程中，智能体在$ ({t_i},{t_{i\_{\mathrm{end}}}}) $时间段内到达$ {v_i} $，计算智能体到达$ {u_i} $的代价，可以使其等待至$ {t_{i\_{\mathrm{end}}}} $时刻再运动至$ {u_i} $，并判断是否可行. 若约束$ \{ {a_i},({v_i},{u_i}),({t_i},{t_{{i\_{{\mathrm{end}}}}}})\} $为等待动作，则将节点$ {v_i} $的$ ({t_i},{t_{{i\_{{\mathrm{end}}}}}}) $时间段设置为碰撞区间，更新节点的安全间隔后再进行规划.

将A*算法中搜索后继节点的过程进行如下更改.

1）获取节点邻域内的所有节点，根据当前位置到节点间的距离，得到运动至每个节点所需的时间$ t $. 针对运动动作的约束，需要额外考虑等待的时间.

2）根据当前所在节点的安全间隔，分别加上$ t $，得出到达相邻节点的可能时间范围$ [{t_{{\mathrm{start}}}},{t_{{\mathrm{end}}}}] $.

3）与每个节点的每个安全间隔$ [{t_i},{t_j}] $进行比较. 若$ {t_{{\text{start}}}} > {t_j} $或$ {t_{{\text{end}}}} < {t_i} $，则无法在此安全间隔内到达；反之，则可以到达.

4）计算到达相邻节点对应安全间隔的最早时间$ {t_{{\text{early}}}} $. 若$ {t_{{\text{early}}}} $在当前节点的安全间隔内，则表示去往目标节点的过程中不会发生冲突；反之，则表示存在冲突，跳过该相邻节点.

在MG-TAPF问题中，下层规划器需要规划出智能体$ {a}_{i} $从当前位置顺序访问任务$ {g_j} $中目标点序列的最短路径. 多目标A*算法（multi-label A*，MLA*）^[18]是用于规划顺序访问所有目标位置的最优路径规划方法. 结合MLA*算法与引入安全间隔的A*算法，将算法扩展至求解MG-TAPF问题. 该算法的下层规划器伪代码如下所示.

算法 1　下层规划器输入：起点s，目标点g输出：机器人路径 Path1. insert s to OPEN2. while g is not in OPEN do3. P←best node from OPEN4. Insert P_neighbor to OPEN5. while P_Arrive ∩ P_Safe=ϕ do6. P ← next node from OPEN7. insert P to Path8. end while9. end while10. return Path

提出连续时间下引入安全间隔的路径规划算法，改进后的算法虽然减少了路径总成本，但由于碰撞检测与冲突避免需要较大的计算量，在智能体分布较密集的场景下，该算法需要较长的求解时间. 除此之外，将该算法推广至求解MG-TAPF后，多目标位置将带来更大的计算量，这对该算法的求解效率提出了更高的要求.

在上层规划器中，针对当前路径中的多个冲突，往往选择优先解决最早发生的冲突，但这有时会导致扩展更多的节点. 随着碰撞检测代价的提高，扩展较多节点会大大延长找到最优解所需的时间. 由此，引入冲突分级的概念，将冲突分类为重要冲突、次要冲突与非重要冲突.

重要冲突指解决冲突后的2个子节点的路径总成本都高于父节点. 次要冲突指解决冲突后的2个子节点的路径总成本一个高于父节点，一个与父节点成本相同. 非重要冲突指解决冲突后2个子节点的总成本都与父节点相同.

对约束树扩展过程进行修改，当对节点进行扩展时，检查所有存在的冲突. 若检查到重要冲突，则解决该冲突并生成子节点. 若无重要冲突，则优先解决次要冲突，若无次要冲突则解决非重要冲突. 通过对智能体间的冲突进行分级，减少约束树扩展的节点个数，以缩短算法的求解时间.

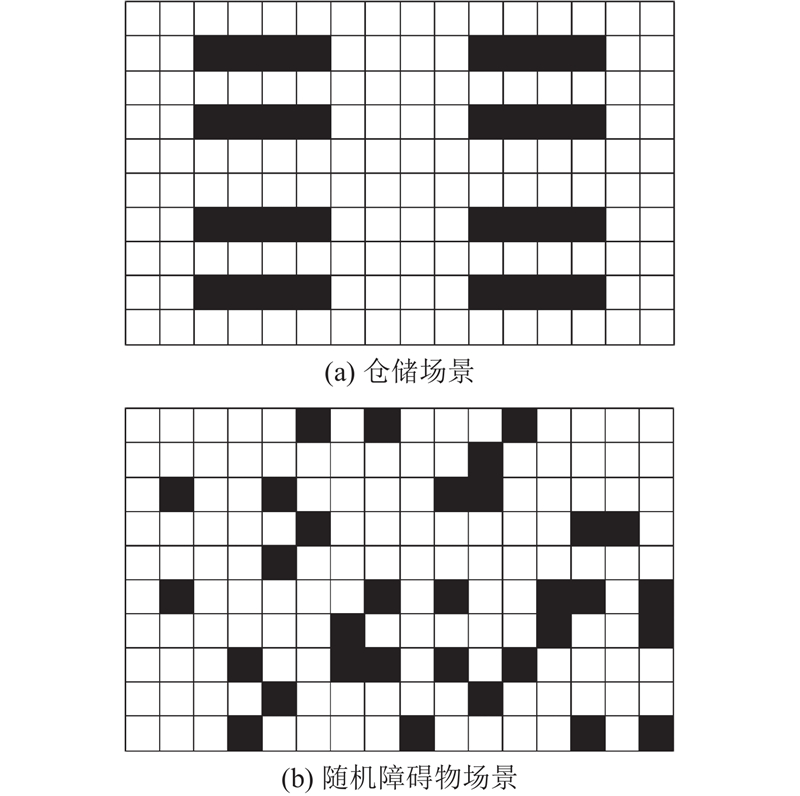
基于C++实现了连续时间内结合任务分配路径规划算法，其中代码使用Boost库用于数学计算. 本次测试采用3种场景：10 m×10 m的空旷场景、10 m×16 m的随机障碍物的场景与10 m×16 m的仓储场景. 其中，设定地图中每个栅格为1 m，在随机障碍物场景的栅格地图中随机选取20%的栅格设置为障碍物，在仓储场景中选取20%的栅格设置为障碍物，障碍物用黑色方块表示. 仓储场景与随机障碍物场景如图3所示. 在不同场景中，随机初始化智能体的起始位置与任务的目标位置，保证所有起始位置和目标位置不重叠. 将智能体的形状设置为半径为$ \sqrt 2 /4 $ m的圆形，该半径是在4连通栅格内2个智能体相互跟随时不会发生碰撞的最大半径. 除此之外，每个智能体在执行运动动作时，始终为1 m/s的匀速运动. 将求解时间限制为30 s，若在30 s内解出，则求解成功. 成功率是指求解成功的次数占100次求解总数的比率，具体表达式为：成功率R=（求解成功的次数/100）×100%. 成功率越高，表示算法的求解时间越短. 取100次测试中所有智能体完成任务的路径总成本的均值作为平均路径总成本，平均路径成本越小，表示智能体走过的路程越短，算法的解质量越高. 分别测试在4，6，8，······，20个智能体的情况下，解决100个不同的TAPF问题的成功率和平均路径总成本. 通过测试不同场景下的算法表现，验证算法的适用性. 所有测试都在一台配有AMD Ryzen 3600@3. 60 GHz处理器、16 GB内存的运行Ubuntu 18. 04操作系统的计算机上执行.

使用2种算法作为实验的对比算法：TA-CBS与CBS-TA. TA-CBS为TAPF问题的常用解决方式，将问题分解为任务分配与多智能体路径规划^[5]2个部分单独进行求解. CBS-TA为离散时间下的TAPF问题最优求解器. TA-CBS算法通过在CBS-TA算法中移除约束树根节点的初始任务分配预处理机制，转而采用动态优先级分配策略，可以保证两者具有相同的运算效率. 由于两者都是基于离散时间的算法，下层规划器都采用搜索范围为4邻域的A*算法. TA-ICTS^[3]采用任务分配与代价增长树搜索算法对问题进行求解，整数线性规划（integer linear program, ILP）算法^[19]通过将TAPF问题转化为线性规划问题进行求解. 下层规划器的节点搜索范围采用8邻域，并将冲突时间间隔计算的精准度设置为10⁻⁷ s.

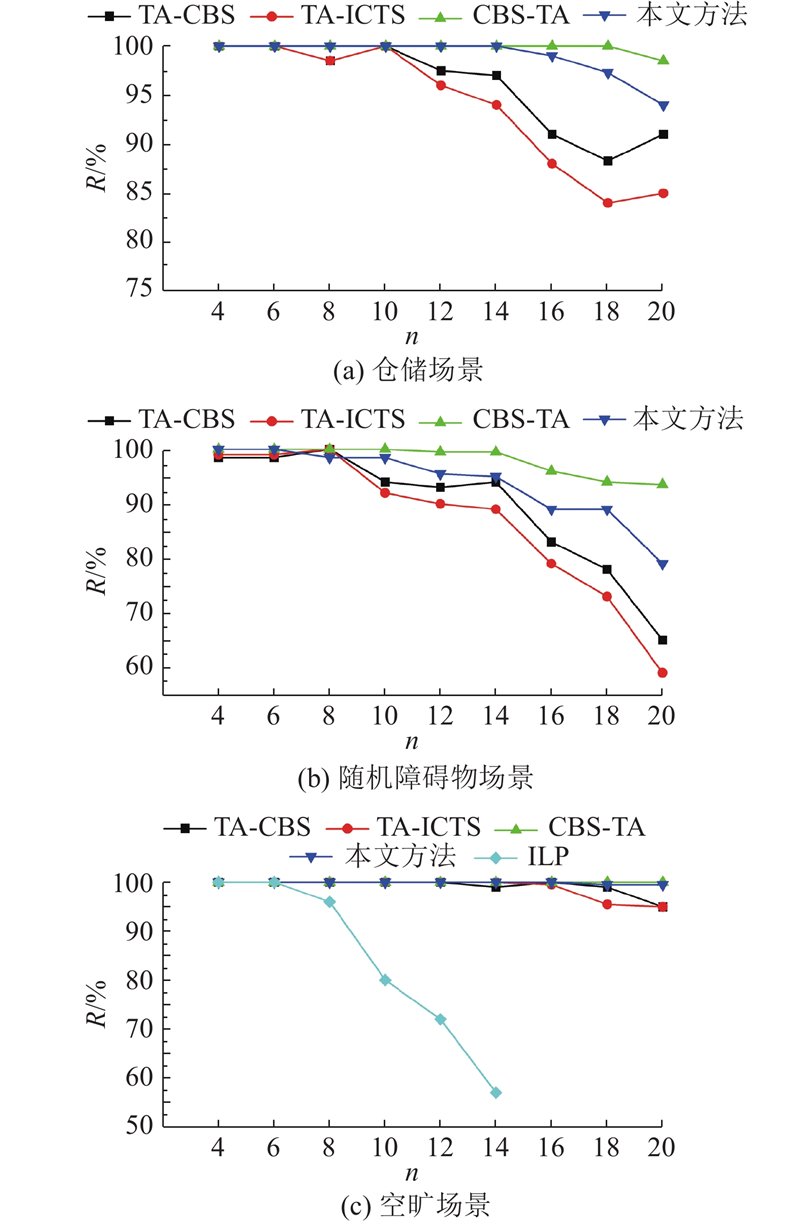
将每个实例的求解时间限制为30 s，在不同场景、不同智能体数量$ n $下的算法求解成功率$ R $如图4所示. TA-CBS算法存在无法求得最优解甚至无法找到可行解的问题，所以随着n的增加，求解成功率较低. TA-ICTS算法由于采用与TA-CBS算法相同解耦的方式进行求解，且ICTS的运算效率低于CBS算法，TA-ICTS的求解成功率进一步低于TA-CBS. ILP由于求解TAPF问题时需要对所有任务分配情况进行求解，即使在空旷场景中求解成功率也显著低于其余算法. 随着智能体数量的增加，CBS-TA算法与TA-CBS算法的差距逐步增大，具有更高的求解成功率. 由于在连续时间下进行冲突检测与安全间隔计算往往需要较大的计算量，本文算法在智能体较密集、冲突较多的情况下，求解成功率略低于CBS-TA算法，但相较于TA-CBS具有显著的优势.

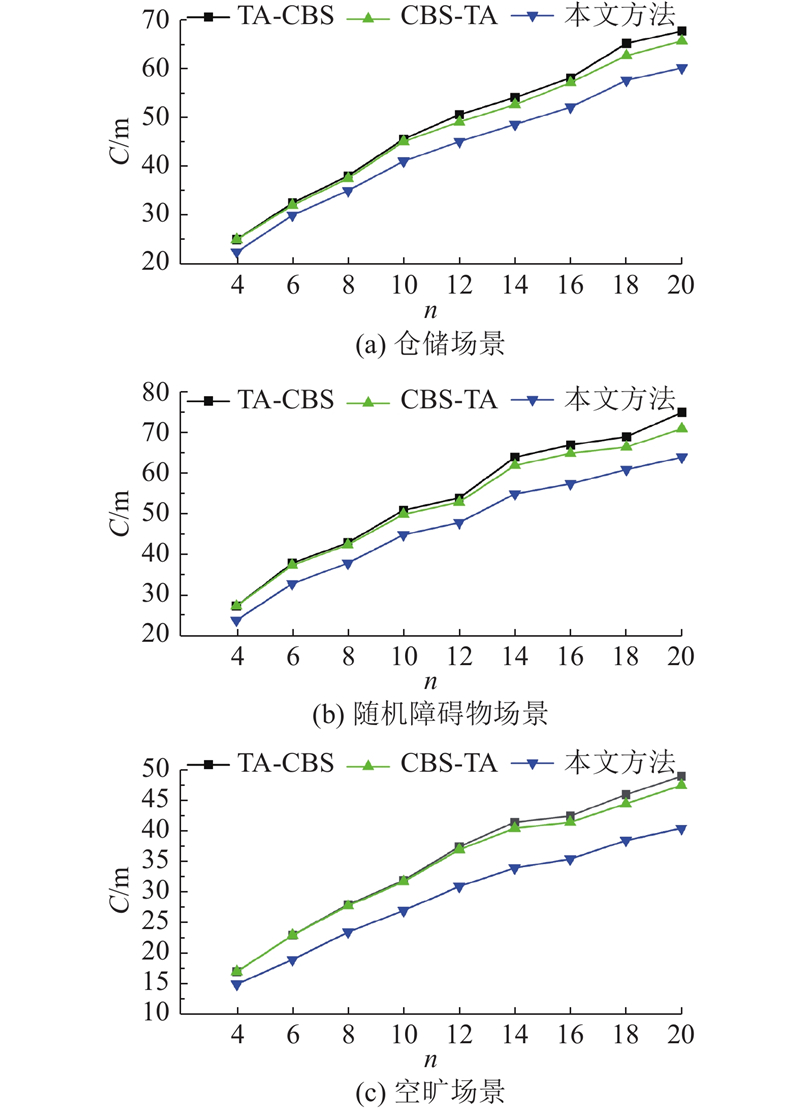
如图5所示为该算法在不同场景、不同$ n $下求解成功实例的平均路径总成本$ C $. 通过实验数据可以看出，在3种不同场景下，TA-CBS算法大部分测试结果的平均总路径成本都高于CBS-TA算法，且随着智能体数量的增多，差距更加明显. 在智能体数量较少的情况下，两者性能没有较大的差距. 此时场景内智能体分布较稀疏，以4邻域作为路径规划的扩展节点范围，往往存在多种从当前位置到达目标位置的最优路径. 针对新添加的约束，可以在路径成本不变的情况下找到避免冲突的路径. 在场景内智能体分布较密集后，随着冲突的增多，任务分配与路径规划之间的关系更加紧密，CBS-TA算法与TA-CBS算法的性能差距逐渐拉大，且在仓储与随机障碍物场景中，两者的差距更加明显. 可以看出，结合任务分配与冲突搜索算法后，在应对复杂场景与智能体分布密集的情况时，可以得到更优的解决方案. 与TA-CBS、CBS-TA算法相比，提出的扩展至连续时间后的算法的最优路径的路径成本显著减小，使得解决方案的路径总时间显著减小. 在智能体数量较少的情况下，冲突较小，路径总成本降低的主要原因是路径长度变短. 随着智能体的增多，连续时间下的等待时间不再为固定时间，使得路径总成本低于CBS-TA算法.

如表1所示为3种算法在3种场景下平均路径总成本的总和S. 可以看出，以TA-CBS作为基准，3种场景下，通过将任务分配与冲突搜索融合，在空旷场景下路径总成本降低了2.14%，在随机障碍物场景下降低了2.57%，仓储场景下降低了2.22%. 本文提出的算法在空旷场景下路径总成本降低了16.13%，在随机障碍物场景下降低了12.57%，在仓储场景下降低了9.80%. 由于在仓储场景下障碍物集中分布，场景中存在较多宽度仅为一个栅格大小的可通行区域，所以下层规划器采用8邻域，较4邻域搜索不会降低理想的路径成本开销，这使得本文算法在仓储场景下的解质量提升低于另外2种场景. 综合3种场景，利用提出的算法，显著降低了路径总成本.

在基于栅格地图的图搜索路径规划算法中，可以通过扩大搜索范围进一步优化解的质量. 如表2所示为算法在随机障碍物场景中不同邻域大小下的平均路径总成本$ C $. 总体而言，随着搜索范围的增大，算法求解的路径总成本更小. 随着邻域的扩展，路径总成本降低的幅度逐渐减小，考虑到求解时间随之增长，需要权衡两者选择合适的搜索邻域.

在随机障碍物场景下，4、10、16个智能体的实例在不同搜索邻域大小^[20]下的平均求解时间T如表3所示. 可以看出，当智能体数为4时，算法的平均求解时间随着搜索邻域的扩大而增长.当智能体数为10时，8邻域的平均求解时间较4邻域更少. 当智能体数增加至16时，8邻域的平均求解时间更加显著地少于4邻域，同时16邻域与32邻域的平均求解时间始终多于8邻域. 测试结果表明，随着搜索邻域的扩大，计算量增大，求解时间增长. 同时，4邻域虽然可以在较短的时间内完成路径规划，但求解的路径长度较长，增大了发生冲突的概率. 当智能体分布较密集时，上层规划器需要扩展更多的节点以解决冲突，这使得4邻域下算法需要更长的时间进行求解. 在智能体分布密集的场景下，本文算法的路径总成本与求解时间更少.

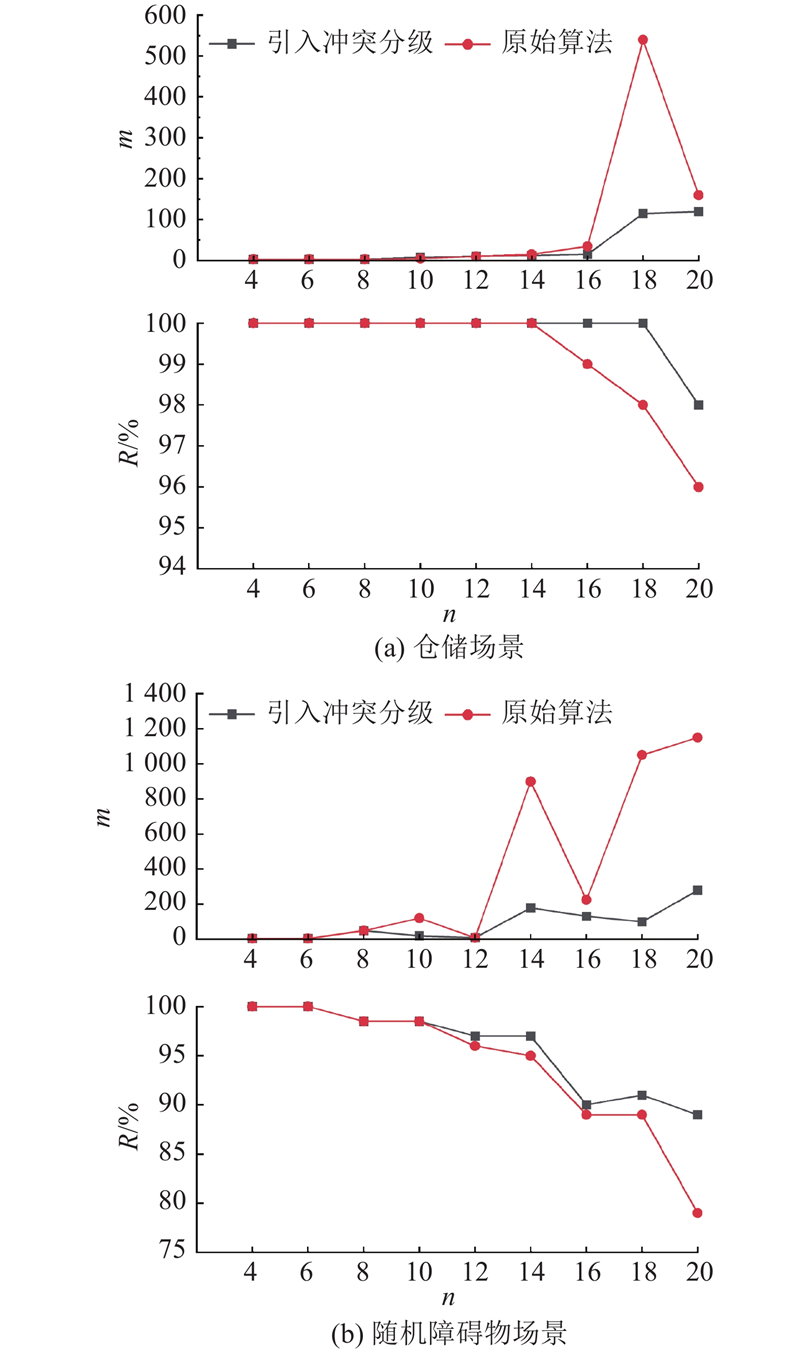
在仓储与随机障碍物场景中，测试了引入冲突分级的算法与原始算法的表现，如图6所示. 可以看出，在2种不同的场景下，引入冲突分级的算法都具有更少的平均扩展节点数$ m $与更高的求解成功率$ R $. 在多数场景下，随着$ n $的增多，潜在冲突数量随之增多，引入冲突分级的算法与原始算法的差距更加明显.

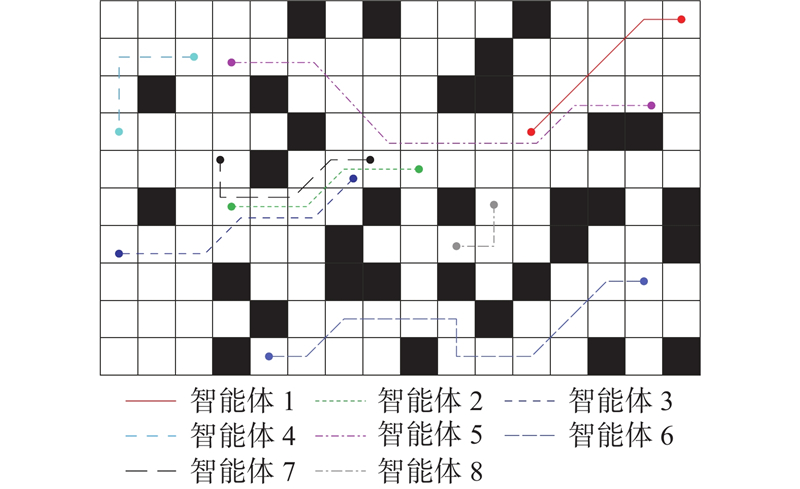
如图7~9所示分别为利用TA-CBS算法、CBS-TA算法与提出算法解决某一包含8个智能体的TAPF问题的求解结果. 图中，每条路径的方形端点为智能体的初始位置，圆形端点为智能体被分配的任务位置. 设定图7~9中左上栅格坐标为(0,0)，右下栅格坐标为(9,15). 利用TA-CBS算法计算任务分配，最终的任务分配方式如图7所示. 可以看出，根据任务分配规划对应路径后，智能体2、智能体3与智能体7存在冲突. 在智能体2达到任务位置(4,6)后，智能体3与智能体7无法按照原有规划到达任务位置. 为了解决该冲突，最终的求解结果为智能体2在坐标为(4, 5)的栅格原地等待5个时间步长，等待完成后，智能体7已到达任务位置(4,8)，智能体3到达(4,6)栅格，下个时间步长智能体2从(4,5)运动至(4,6). 此时3个智能体间不存在冲突，直接输入所有智能体路径得到问题的解，最终的路径总成本为66 m. CBS-TA算法的初始任务分配与TA-CBS算法相同，但利用CBS-TA算法探索冲突场景下的全局最优解，将生成额外的任务分配方案. 从图8可以看出，CBS-TA算法在额外的任务分配方案中找到了问题的最优解. 相较于初始任务分配方案，智能体2、3、6、7、8所分配的任务发生了变化，最终路径总成本为61 m，低于TA-CBS算法. 由于下层规划器采用8邻域，利用提出算法得到了更低的路径代价，最终的解决方案如图9所示，路径总成本为53.38 m，显著低于TA-CBS算法与CBS-TA算法.

多智能体任务分配与路径规划问题作为多智能体系统中的重要部分，本文提出连续时间下可用于求解多目标任务的多智能体路径规划算法. 在原有的算法框架下，提出连续时间下的碰撞检测方式、冲突定义与解冲突方式. 在下层规划器中为每个路径点引入安全间隔与标签概念，改进算法搜索流程. 提出冲突分级策略，加快算法的求解速度. 实验表明，与CBS-TA算法相比，提出算法的路径总成本在空旷场景下降低了13.99%，在随机障碍物场景下降低了10.00%，在仓储场景下降低了7.58%. 利用提出算法可以求解得到更优的解决方案，具有更高的适用性.