单目3D目标检测在自动驾驶、机器人导航和智能监控等领域有广泛的应用. 相比使用激光雷达或双目相机的3D目标检测方法，单目3D目标检测的优点是节省大量时间和成本，在实际应用中部署灵活，缺点是空间信息在投影到图像平面的过程中丢失严重.

Liu等^[1-2]探索了从单目图像检测3D目标的固有不适定性问题，指出准确地预测深度信息是提高单目3D目标检测性能的关键. Pseudo-LiDAR^[3]、PatchNet^[4]直接借助专门的深度预测模型来预测每个像素的深度值，将图像特征转换成伪点云，输入已有基于激光点云的3D目标检测模型中，实现目标的检测和定位. 这些方法的预测准确度严重依赖深度预测模型预测的深度结果，且整体模型参数量和复杂度很大，不利于实际应用部署. LPCG-Monoflex^[5]利用基于激光点云的3D目标检测模型从大量激光雷达数据中生成伪标签，再用这些伪标签进一步监督单目3D目标检测模型训练；CMKD^[6]以知识蒸馏的方式，利用基于激光雷达的3D目标检测模型对单目3D目标检测模型进行监督训练. 以上2种方法只在训练阶段涉及基于激光雷达的3D目标检测模型，在实际应用推理时仅使用单目3D目标检测模型，模型的大小和性能都大幅度提升，但是需要大量数据支撑，且在一定程度上依赖基于激光雷达的3D目标检测模型的性能. 为了避免使用基于激光雷达的检测模型，AutoShape^[7]、MSAC^[8]、DCD^[9]等模型利用目标的几何关系和投影约束来提升深度预测的准确性，改善目标的定位和姿态估计，但是几何关系和投影约束的计算复杂度非常高，对相机的内、外参数要求精确，还存在投影误差放大的问题. Lu等^[10]提出几何不确定性投影方法来减小投影误差放大对深度预测造成的不可控影响. 还有一些模型，如SMOKE^[11]和M3D-RPN^[12]利用卷积神经网络直接回归预测目标3D中心点在图像上的投影坐标、深度、尺寸和朝向角；在实际推理阶段，通过结合相机的内、外参数和预测的深度值，将投影坐标转换，得到3D中心点的空间坐标. 虽然SMOKE和M3D-RPN的模型较小且计算复杂度较低，符合实际部署的要求，但是深度信息预测不准确，模型的准确性有待提升.

上述单目3D目标检测方法均基于卷积神经网络构建，通过串联多个小卷积核的卷积来扩大感受野，增强上下文信息的提取能力. Transformer结构被引入计算机视觉任务，通过自注意力机制捕捉长距离依赖关系，提取丰富的上下文信息，在图像分类、分割和检测等多个领域中显著提升了模型的性能. MonoDETR^[13]、MonoDTR^[14]利用自注意力机制全局聚合上下文信息和深度特征，通过深度线索得到位置编码嵌入模型以得到更好的深度预测结果. 但是，Transformer结构的计算复杂度较高，尤其在3D目标检测中，输入图像的分辨率一般为384×1 280，Transformer结构如何高效处理高分辨率图像成为目标检测的挑战. 在卷积神经网络中，大核卷积有效地扩大感受野，提取丰富的上下文信息，如何将大核卷积应用于单目3D目标检测值得深入研究. 为了准确预测目标的3D属性，本研究构建高效的上下文信息增强模块，利用大核卷积捕捉图像的上下文信息；为了降低大核卷积的参数量和计算量，采用深度可分离卷积和条形卷积进一步优化大核卷积. 为了探索3D预测框各个属性的预测结果对目标检测精度的影响，进行数据和实验分析，提出基于深度误差的损失权重，监督目标的长度和深度预测，提高长度和深度预测的准确性.

如图1所示，上下文信息增强和深度引导模型主要由5个部分组成：特征编码、高效的上下文信息增强模块、2D预测、特征对齐和3D预测. 特征编码部分以由单个相机捕获的RGB图像$ {\boldsymbol{I}} \in {{\bf{R}}^{H \times W \times 3}} $作为输入（H为图像的高度，W为图像的宽度），经过单目3D目标检测模型中应用最广泛的特征提取主干网络^[15]（特征编码器DLA34和特征解码器DLAup）得到特征图$ {\boldsymbol{F}} \in {{\bf{R}}^{H/4 \times W/4 \times C}} $，C为通道数；经过本研究构建模块进一步扩大感受野，并在不同尺度上自适应地聚合丰富的上下文信息，得到增强后的特征图. 在2D预测部分，基于CenterNet^[16]无锚框的方法预测2D目标框属性，包括热力图、2D中心点偏差和2D尺寸. 在特征对齐部分，为了更好地在目标区域内进行预测，减少背景噪声干扰，根据2D检测结果得到每个目标在特征图中的对应区域，利用特征提取（RoIAlign）操作将每个目标对应区域的特征统一对齐成7×7大小的特征图，按照GUPNet^[10]将目标的空间坐标(coord maps)与目标特征图进行拼接，为后续3D目标检测提供空间位置信息. 3D属性预测包括3D尺寸、3D中心点投影偏差、朝向角和深度及其不确定度，其中深度及其不确定度预测按照DID-M3D^[17]模型中提出的方式进行预测，将实例深度分解为属性深度和视觉深度，同时预测对应深度的不确定度. 通过深度误差加权损失进一步监督深度和长度的预测，最终得到目标框的预测结果.

在目标检测领域中，上下文场景信息对目标的识别和定位至关重要. 每个目标像素点对应的感受野越大，包含的上下文信息越丰富. 在DID-M3D单目3D目标检测网络中，经过主干网络编码提取后特征图的分辨率通常为原图的1/4，该特征图缺乏丰富的上下文信息，影响了目标的精确定位. 在图像中，目标距离自身车辆的距离不同，目标在图像中所占的像素大小差异大. 本研究构建高效的上下文信息增强模块，在主干网络提取的特征图上利用不同大小的大核卷积自适应地增强不同尺度目标像素对应的上下文信息. 为了避免参数量和复杂度大幅度增加，高效地增强目标的上下文信息，采用深度可分离卷积和条形卷积对大核卷积进行优化.

在本研究构建模块中，来自主干网络特征编码后的特征图${\boldsymbol{F}} $先经过卷积核大小为5×5的卷积进一步扩大感受野、聚合局部信息，得到特征图${\boldsymbol{F}}_1 $，再分别经过大核卷积中较为常用的大小为7、11和21的卷积来感知不同大小的目标，得到不同尺度的上下文特征. 为了进一步降低参数量和复杂度，采用深度可分离卷积代替普通卷积，同时对卷积核大小为7、11和21的大核卷积进行卷积分解，将k×k大小的卷积分解为1×k和k×1的2个条形卷积：

(1)$ {{\boldsymbol{F}}_i} = \left\{ {\begin{array}{*{20}{l}} {{\mathrm{DCon}}{{\mathrm{v}}_{5 \times 5}}\left( {\boldsymbol{F}} \right)},&{}&{i = 1;} \\ {{\mathrm{DCon}}{{\mathrm{v}}_{k \times 1}}\left( {{\mathrm{DCon}}{{\mathrm{v}}_{1 \times k}}\left( {{{\boldsymbol{F}}_1}} \right)} \right)},&{}&{i \in \left\{ {2,3,4} \right\}.} \end{array}} \right. $

式中：$ {\mathrm{D}\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}}_{k\times k}\left(\cdot \right) $为卷积核大小为k×k的深度可分离卷积，F_i为不同卷积操作得到不同感受野大小的特征图. 将不同分支得到的特征图对应元素相加后经过1×1卷积建模不同通道间的关系，再对输入该模块之前的原始特征图进行加权，自适应地增强不同尺度目标的上下文信息：

(2)$ {{\boldsymbol{F}}_{\mathrm{c}}} = {\boldsymbol{F}} \otimes {\mathrm{Conv}}\left(\sum\limits_{i = 1}^4 {({{\boldsymbol{F}}_i})} \right). $

式中：$ \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v}\left(\cdot \right) $为1×1的普通卷积，$ \otimes $为矩阵逐元素相乘操作，F_c为高效的上下文信息增强模块输出的特征图.

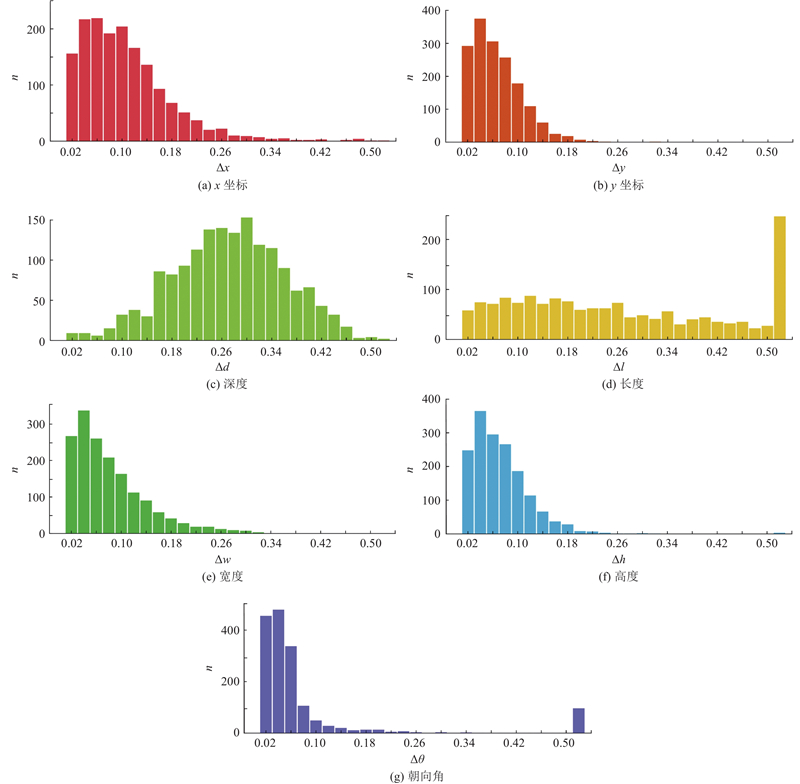
为了探索对模型检测结果影响较大的潜在因素，在KITTI^[18]数据集上统计基线模型的3D预测框各个属性{x, y, d, l, w, h, θ}的预测误差，各个属性的预测误差等于预测值与真实值之差的绝对值. 其中{x, y, d}为3D框中心点在相机坐标系下的位置坐标，l、w、h为3D框的长、宽、高，θ为3D框的朝向角. 判断目标是否被正确检测的标准是计算预测框与真实框之间的交并比（intersection over union, IoU）. 当IoU$ \geqslant $0.7时，说明预测框较好地检测出对应目标；当交并比IoU$ \leqslant $0.5时，说明预测框与目标真实框误差很大. 对于现有方法IoU$ \in $(0.5, 0.7)的预测框，如果能够提高3D属性的预测精度，则有希望使预测框与真实框的IoU$\geqslant $0.7，从而提升算法检测效果. 本研究以DID-M3D方法为基线方法，对IoU$ \in $(0.5, 0.7)的预测框各个属性的预测误差进行直方图统计，统计结果如图2所示. 由图可知， 3D属性{x, y, w, h, θ}的预测误差分布趋势基本一致，大部分预测误差集中在较小的数值范围内. 目标的朝向角在误差超过0.5时的数量激增，进一步观察朝向角预测误差较大的情况，发现当朝向角接近0、±π/2和±π时，由于目标几何场景特征信息严重丢失，模型对朝向角的预测值与真实值之间符号相反，导致预测误差较大. d和l的预测误差分布存在明显不同. 在自动驾驶场景中，3D目标通过相机投影到2D图像平面时，深度信息会严重丢失；对于大部分同向或逆向行驶的车辆，长度信息投影到2D图像平面上也会受到较大影响. 因此，深度和长度比其他3D属性更难预测，对应的预测误差相对较大. 针对以上实验结果分析，本研究认为：减小目标长度和深度的预测误差能够提升预测框的准确性，使得原来在IoU阈值边缘的预测框符合目标检测的要求. 本研究提出深度误差加权损失函数，进一步监督长度和深度预测，提高模型的预测精度. 深度误差加权损失函数表达式为

(3)$ {L_{\mathrm{r}}} = \lambda \cdot ({{\mathrm{SmoothL}}_1}(\Delta l)+{{\mathrm{SmoothL}}_1}(\Delta d)). $

式中：$ \Delta l $为预测的长度误差，$ \Delta d $为预测的深度误差，$ \lambda $为自适应的深度误差权重. 注意到深度误差的统计结果呈现中间高两边低的分布趋势，为此设计$ \lambda $，加强模型对靠近高分布区域预测框的关注：

(4)$ \lambda = {\mathrm{exp}}\;( - ||\Delta d| - \alpha |). $

式中：$ \alpha $为超参数，根据消融实验取$ \alpha $=0.35. 当深度误差接近$ \alpha $时，$ \lambda $接近于1，模型更加专注该预测框；当深度误差逐渐远离$ \alpha $时，$ \lambda $逐渐减小，模型也逐渐减少对该预测框的关注.

上下文信息增强和深度引导模型的损失函数主要包括2D目标检测的损失和3D目标检测的损失. 其中2D检测部分与CenterNet中损失设计保持一致，分别得到热力图损失$ {L}_{\mathrm{H}} $、2D中心点偏差损失$ {L}_{\mathrm{O},2\mathrm{d}} $和2D尺寸损失$ {L}_{\mathrm{S},2\mathrm{d}} $. 热力图$ {\boldsymbol{F}}_{\mathrm{H}}\in {\bf{R}}^{{H}/4\times {W}/4\times {C}} $预测图像上目标的粗中心点位置. 2D检测的总损失表达式为

(5)$ {L_{\mathrm{H}}} = - \frac{1}{N}\sum\limits_i^{} {\left\{ {\begin{array}{*{20}{l}} {{{(1 - {Y_i})}^\beta }{\mathrm{lb}}\;{({Y_i})}},&{Y_i^{{\mathrm{gt}}} = 1;} \\ {{{(1 - Y_i^{{\mathrm{gt}}})}^\gamma }{{({Y_i})}^\beta }{\mathrm{lb}}\;{(1 - {Y_i})}},&{{\text{其他}}.} \end{array}} \right.} $

(6)$ L_{{\mathrm{O}},2{{\mathrm{d}}}} = \frac{1}{N}\sum\limits_{{p^{{\mathrm{gt}}}}}^{} {|{O_{\mathrm{p}}} - {O_{{\mathrm{p}},{\mathrm{gt}}}}|} , $

(7)$ {L_{{\mathrm{S}},2{\mathrm{d}}}} = \frac{1}{N}\sum\limits_{k = 1}^N {|{S_k} - {S_{k,{\mathrm{gt}}}}|} , $

(8)$ {L_{2{\mathrm{d}}}} = {L_{\mathrm{H}}}+{L_{{\mathrm{O}},2{\mathrm{d}}}}+{L_{{\mathrm{S}},2{\mathrm{d}}}}. $

式中：N为热力图中关键点的个数；Y_i为热力图中i位置的预测值；$ {Y}_{i}^{\mathrm{g}\mathrm{t}} $为对应真值热力图中的值；β、γ均为超参数，按照CenterNet取β=2，γ=4；$p^{{\mathrm{gt}}} $为真实框，$ {O}_{\mathrm{p}} $为预测的2D中心点偏差，$ {O}_{\mathrm{p},\mathrm{g}\mathrm{t}} $为对应2D中心点偏差的真值，$ {S}_{k} $为预测的2D尺寸大小，$ {S}_{k,\mathrm{g}\mathrm{t}} $为对应2D尺寸的真值. 3D检测部分与基线DID-M3D模型设计保持一致，将目标的实例深度$ {d}_{\mathrm{i}\mathrm{n}\mathrm{s}} $分解为视觉深度$ {d}_{\mathrm{v}\mathrm{i}\mathrm{s}} $和属性深度$ {d}_{\mathrm{a}\mathrm{t}\mathrm{t}} $，同时模型还预测对应深度及其不确定度. 为了结合不确定度优化深度预测，采用不确定性回归损失进行监督，原深度损失的表达式为

(9)$ {{L_{d,{j_{}}}} = \frac{{\sqrt 2 }}{{{u_j}}}|{d_j} - d_j^{{\mathrm{gt}}}|+{\mathrm{lb}}\;{({u_j})}},\quad{j \in } \{ {\mathrm{ins,vis,att}}\} . $

(10)$ {L_d} = {L_{d,{\mathrm{ins}}}}+{L_{d,{\mathrm{vis}}}}+{L_{d,{\mathrm{att}}}}. $

式中：$ {d}_{j} $为深度的预测值，$ {d}_{j}^{\mathrm{g}\mathrm{t}} $为对应的真值，$ {u}_{j} $为对应的预测不确定度. 对于朝向角损失$ {L}_{\theta } $，使用multi-bin损失^[19]监督，将$ \left[-\text{π},\text{π}\right] $划分成n个有重叠的格子，网络预测目标的朝向角属于每个格子的置信度$ {L}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}} $和对应的残差角度$ {L}_{\mathrm{l}\mathrm{o}\mathrm{c}} $. 最终目标的朝向角等于置信度最高格子的中心角度加上残差角度.

(11)$ {L_{{\mathrm{conf}}}} = - \sum\limits_i^{} {y_i^{{\mathrm{gt}}}} {\mathrm{lb}}\;{({y_i})}, $

(12)$ {L_{{\mathrm{loc}}}} = - \frac{1}{{{n_\theta }}}\sum\limits_{}^{} {\cos \;(\theta - {c_i} - \Delta {\theta _i})} , $

(13)$ {L_\theta } = {L_{{\mathrm{conf}}}}+m \times {L_{{\mathrm{loc}}}}. $

式中：$ {y}_{i} $为第i个格子的预测值；$ {y}_{i}^{\mathrm{g}\mathrm{t}} $为对应的真实值；$ {n}_{\theta } $为包含目标真实朝向角的格子数量；$ {c}_{i} $为第i个格子的中心角度值；$ {\Delta \theta }_{i} $为预测的残差角；m为超参数权重，按照multi-bin损失取m=1. 3D尺寸损失$ {L}_{\mathrm{S},3\mathrm{d}} $和3D中心点在图像平面上的投影点的偏移损失$ {L}_{\mathrm{O},3\mathrm{d}} $分别与式（7）和式（6）类似. 采用L₁损失函数进行监督，结合深度误差加权损失，模型总损失表达式为

(14)$ L = {L_{{\mathrm{2d}}}}+{L_{{\mathrm{S,3d}}}}+{L_{{\mathrm{O,3d}}}}+{L_\theta }+{L_d}+{L_{\mathrm{r}}}. $

使用单目3D目标检测任务中常用的数据集KITTI、Waymo^[20]进行模型训练和性能对比.

KITTI有7 481张训练数据样本和7 518张测试数据样本，其中训练样本的标签由数据集官网下载得到，测试集的标签官网不提供，须将模型预测结果提交官网进行评估和排名，每个账号每月限制最多提交3次. 为了方便验证各个模块是否有效，官网提供了将7 481张训练数据样本划分为3 712个训练样本和3 769个验证样本的文件，研究者可以利用训练集训练，在验证集上验证模块是否有效和参数调优等. KITTI根据目标的2D框高度、目标被遮挡程度和截断程度将目标进一步划分为简单（easy）、中等（moderate）和困难（hard）共3个级别，规定官网上的排名顺序以中等级别的准确度为基准.

Waymo是3D目标检测领域中规模较大的公开数据集，包含798个训练序列和202个验证序列，每个序列包含2.0×10⁵个样本. CaDNN^[21]是在该数据集上进行实验的单目3D目标检测模型，它以每3帧采样一次的方式构建训练数据集，考虑到硬件资源和时间成本，本研究以50帧为间隔进行采样，以构建相应的数据集. 由于Waymo标签中没有遮挡程度和截断程度，评价检测精度时除了整体的检测精度，通常还会按照目标深度值划分为(0, 30]、(30, 50]和(50, +∞)共3个级别进行评价.

本研究所提模型基于Pytorch框架构建，模型在KITTI上使用NVIDIA RTX 2080Ti GPU进行训练，输入模型的图像分辨率大小为384×1 280，批量大小设置为8，训练总轮数为150，采用Adam优化器，初始学习率设置为1.0×10⁻⁵，采用warm-up训练策略在前5轮迭代逐渐增加到9.0×10⁻⁴，同时采用衰减策略，在模型训练到90轮和120轮时，以0.1的比率对学习率进行衰减. 在Waymo上使用NVIDIA RTX 3090 GPU进行训练，输入模型的图像分辨率大小为1 280×1 920，批量大小设置为5，其他策略与KITTI数据集上训练保持一致.

所有实验都按照单目3D目标检测标准的评价指标平均检测精度AP进行评估和对比，对于汽车(Car)类别设置IoU=0.7. 在计算汽车类别的平均精度时，对准确率-召回率曲线的横坐标采样40个点来计算平均检测精度，表示为AP|R₄₀，避免采样11个点计算的AP|R₁₁在召回率较低时带来的较大偏差. 实验结果对比方法与其他模型保持一致，均在相机3D空间视角和鸟瞰图（bird-eye-view, BEV）视角下进行对比评估.

如表1所示为本研究与主流单目3D目标检测模型在KITTI测试集上检测汽车类别的单目3D目标检测精度. 可以看到，与主流的单目3D目标检测方法相比，本研究所提模型在3D目标检测的简单、中等和困难级别中平均检测精度均最高；在BEV目标检测中，简单和中等级别中平均检测精度最高，困难级别中平均检测精度第二高. 所提高效的上下文信息增强模块自适应地增强了模型对不同尺度目标上下文信息提取的能力，深度误差加权损失有效地提升了深度和长度属性的预测精度. 相比于基线模型DID-M3D，在3D目标检测的简单、中等和困难级别上的平均检测精度分别提升了2.34、0.38和0.58个百分点. 以上分析有效验证了所提模型的优越性.

对方法的组合，大核卷积核大小的选择和深度误差加权损失超参数的设置进行消融实验. 为了验证深度误差加权损失的普适性，在Waymo上进行深度误差加权损失的消融实验.

验证不同方法对模型性能影响的消融实验结果如表2所示. 表中，ECIE表示高效的上下文信息增强模块，$ {L}_{r}^{l} $表示用深度误差权重对目标长度预测进行细化损失监督，$ {L}_{r}^{d} $表示用深度误差权重对目标深度预测进行细化损失监督. 实验1是对基线模型DID-M3D复现的结果. 实验2在基线模型上加入高效的上下文信息增强模块，通过不同大小的大核卷积提升模型对多尺度目标上下文信息的提取能力，进而提升目标检测性能. 实验3在基线模型上加入深度误差加权的深度损失，对深度预测进行细化监督，提升模型深度预测的准确性，进而提升目标平均检测精度；实验4在基线模型上加入深度误差加权的长度损失，对长度预测进行细化监督，提升模型长度预测的准确性，进而提升目标平均检测精度；实验5在基线模型上加入深度误差加权的深度和长度损失，对深度和长度都进行细化监督，模型对深度和长度信息的预测更加准确，进而提升模型的检测性能. 实验6、7在高效的上下文信息增强模块基础上，利用深度误差权重分别加权深度损失和长度损失，在上下文信息增强后的模型上分别提升对深度和长度的预测精度，进一步提升了模型的检测性能. 实验8在基线模型上加入所有方法，增强了模型的特征表达能力，提升了深度和长度预测性能，平均准确度最高.

为了验证大核卷积的大小对实验结果的影响，对大核卷积特征增强模块中不同的大核卷积组合进行消融实验，实验结果如表3所示. 可以看出，随着卷积核大小的增大，模型的性能逐渐提升，卷积核大小越大，提取的上下文信息越丰富，模型对目标的识别和定位越准确. 通过组合不同大小的大核卷积，预测的平均检测精度比单独使用任意单个卷积核的平均检测精度高，同时组合的卷积核大小越大，对应的性能越好，当3个不同大小的大核卷积组合在一起时，模型取得最高的平均检测精度. 该实验结果证明了多尺度目标感知的重要性，在实际检测中，随着目标距离相机的深度增加，在图像中所占的像素大小差异巨大，采用多个尺度的大核卷积可以自适应地提取不同大小目标的上下文信息.

深度误差加权损失涉及超参数α，为了验证超参数的取值对模型预测平均检测精度的影响，根据深度预测误差直方图分布情况，对α以0.05为取值间隔，在0.20~0.45取值，统计对应的实验结果如图3所示. 由图可知，当α=0.35时，模型的平均检测精度最高. 本研究的深度误差加权损失取α=0.35.

为了验证深度可分离卷积和条形卷积的有效性，统计不同卷积操作的参数量和复杂度，结果如表4所示. 相比于普通卷积，通过将大核卷积替换为深度可分离卷积，该模块的参数量和复杂度大幅度降低. 在此基础上，将大核卷积分解为条形卷积，参数量和复杂度得到进一步优化.

为了验证深度误差加权损失在其他数据集上的有效性，在Waymo上进行消融实验，实验结果如表5所示. 在IoU=0.7、0.5时，相比基线模型，加入深度误差加权损失后，模型对目标深度和长度的整体预测更加精确，显著提升了模型的平均检测精度. 特别是d=0~30 m的目标，深度误差加权损失可以大幅度提升目标的深度和长度预测性能. 对于d>30 m的目标，由于目标预测较为困难，深度误差加权损失在深度和长度的预测性能提升上受到限制，模型的平均检测精度与基线模型基本一致或略有提升. 由深度误差加权损失实验结果及分析可知，深度误差加权损失对单目3D目标检测具有一定的普适性.

对模型的预测结果在KITTI验证集上进行可视化展示，结果如图4所示. 在图像平面上绘制3D目标框存在投影偏差，不容易观察到预测框的准确性，但可以提供丰富的场景语义信息. 相比之下，鸟瞰图视角下观察预测结果的准确性更方便，为此提供在图像和鸟瞰图视角下对预测结果的对比展示. 所有可视化图均绘制了数据集提供的真值框、基线模型DID-M3D的预测结果和所提模型预测的结果. 图4（a）中，对比基线模型，所提模型能够较好进行较远目标的预测. 图4（b）中，所提模型能够预测一些近距离由于相机视角导致部分信息截断的目标. 图4（c）和图4（d）中，相比基线模型，所提模型在近处和远处对目标的3D位置坐标预测更准确，尤其是对距离相对较远的目标或者存在部分遮挡的目标，所提模型也能够得出较好的预测结果.

本研究将大核卷积引入单目3D目标检测模型中，提出高效的上下文信息增强模块，利用多个大核卷积对不同尺度的目标自适应地提取丰富的上下文特征；结合深度可分离卷积和条形卷积，使模块的设计更符合实际部署要求，目标的识别和定位性能得到有效提升. 在探索对模型检测结果影响较大的潜在因素中，本研究发现目标的长度预测结果对模型整体准确性有较大影响，为单目3D目标检测的研究方法提供了新的解决方向. 本研究提出深度误差加权损失函数，基于深度误差对目标的长度和深度进一步监督，提高长度和深度预测的准确性. 在KITTI数据集上开展实验，验证了所提方法的优越性能. 未来将继续探索加权损失函数的优化设计，充分利用和预测目标的长度和深度信息；探索大核卷积在特征提取网络中的应用，进一步优化模型，提升模型在KITTI数据集上的预测精度.