[1]
LUO Y, CAI P, BERA A, et al Porca: modeling and planning for autonomous driving among many pedestrians
[J]. IEEE Robotics and Automation Letters , 2018 , 3 (4 ): 3418 - 3425
DOI:10.1109/LRA.2018.2852793
[本文引用: 1]
[2]
RUDENKO A, PALMIERI L, HERMAN M, et al Human motion trajectory prediction: a survey
[J]. The International Journal of Robotics Research , 2020 , 39 (8 ): 895 - 935
DOI:10.1177/0278364920917446
[本文引用: 1]
[3]
ALAHI A, GOEL K, RAMANATHAN V, et al. Social LSTM: human trajectory prediction in crowded spaces [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE , 2016: 961–971.
[本文引用: 1]
[4]
XUE H, HUYNH D Q, REYNOLDS M. SS-LSTM: a hierarchical LSTM model for pedestrian trajectory prediction [C]// 2018 IEEE Winter Conference on Applications of Computer Vision (WACV) . Lake Tahoe: IEEE, 2018: 1186–1194.
[5]
ZHANG P, OUYANG W L, ZHANG P F, et al. SR-LSTM: state refinement for LSTM towards pedestrian trajectory prediction [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 12085–12094.
[本文引用: 1]
[6]
孔玮, 刘云, 李辉, 等 基于图卷积网络的行为识别方法综述
[J]. 控制与决策 , 2021 , 36 (7 ): 1537 - 1546
[本文引用: 1]
KONG Wei, LIU Yun, LI Hui, et al A survey of action recognition methods based on graph convolutional network
[J]. Control and Decision , 2021 , 36 (7 ): 1537 - 1546
[本文引用: 1]
[7]
MOHAMED A, QIAN K, ELHOSEINY M, et al. Social-STGCNN: a social spatio-temporal graph convolutional neural network for human trajectory prediction [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 14424–14432.
[本文引用: 4]
[8]
SHI L, WANG L, LONG C, et al. SGCN: sparse graph convolution network for pedestrian trajectory prediction [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 8994–9003.
[本文引用: 6]
[9]
WU Z, PAN S, CHEN F, et al A comprehensive survey on graph neural networks
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2020 , 32 (1 ): 4 - 24
[本文引用: 1]
[10]
GUPTA A, JOHNSON J, FEI-FEI L, et al. Social GAN: socially acceptable trajectories with generative adversarial networks [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Salt Lake: IEEE, 2018: 2255–2264.
[本文引用: 2]
[11]
BAE I, PARK J H, JEON H G. Non-probability sampling network for stochastic human trajectory prediction [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 6477–6487.
[本文引用: 9]
[12]
MA Y J, INALA J P, JAYARAMAN D, et al. Likelihood-based diverse sampling for trajectory forecasting [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2021: 13279–13288.
[本文引用: 1]
[13]
VEMULA A, MUELLING K, OH J. Social attention: modeling attention in human crowds [C]// 2018 IEEE International Conference on Robotics and Automation . Brisbane: IEEE, 2018: 4601–4607.
[本文引用: 1]
[14]
KOSARAJU V, SADEGHIAN A, MARTÍN-MARTÍN R, et al. Social-bigat: multimodal trajectory forecasting using bicycle-gan and graph attention networks [C]// Proceedings of the Annual Conference on Neural Information Processing Systems . Vancouver: NeurIPS, 2019: 1–10.
[本文引用: 3]
[15]
MANGALAM K, GIRASE H, AGARWAL S, et al. It is not the journey but the destination: endpoint conditioned trajectory prediction [C]// Computer Vision–ECCV 2020: 16th European Conference . Glasgow: Springer International Publishing, 2020: 759–776.
[本文引用: 5]
[16]
LIANG J, JIANG L, NIEBLES J C, et al. Peeking into the future: predicting future person activities and locations in videos [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 5725–5734.
[本文引用: 3]
[17]
HUANG Y, BI H, LI Z, et al. Stgat: modeling spatial-temporal interactions for human trajectory prediction [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 6272–6281.
[本文引用: 3]
[18]
YU C, MA X, REN J, et al. Spatio-temporal graph transformer networks for pedestrian trajectory prediction [C]// Computer Vision-ECCV 2020: 16th European Conference . Glasgow: Springer International Publishing, 2020: 507–523.
[本文引用: 2]
[19]
YUAN Y, WENG X, OU Y, et al. Agentformer: agent-aware transformers for socio-temporal multi-agent forecasting [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2021: 9813–9823.
[本文引用: 2]
[20]
SHI L, WANG L, LONG C, et al. Social interpretable tree for pedestrian trajectory prediction [C]// Proceedings of the AAAI Conference on Artificial Intelligence . [s.l.]: AAAI, 2022, 36(2): 2235–2243.
[本文引用: 2]
[21]
BAE I, JEON H G. A set of control points conditioned pedestrian trajectory prediction [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Washington D. C.: AAAI , 2023, 37(5): 6155–6165.
[本文引用: 4]
Porca: modeling and planning for autonomous driving among many pedestrians
1
2018
... 行人轨迹预测是一项关键技术,旨在根据行人的历史轨迹和当前状态,准确预测其未来的位置坐标序列. 这项技术在自动驾驶[1 ] 和智能监控系统[2 ] 领域具有广泛的应用前景. 在智能监控系统中,行人轨迹预测可用于异常情况检测,有助于及时发现潜在的安全问题. 在自动驾驶领域,行人轨迹预测则提供了关键的行人运动信息,为车辆路径规划和行车安全性提供了必要的参考依据. ...
Human motion trajectory prediction: a survey
1
2020
... 行人轨迹预测是一项关键技术,旨在根据行人的历史轨迹和当前状态,准确预测其未来的位置坐标序列. 这项技术在自动驾驶[1 ] 和智能监控系统[2 ] 领域具有广泛的应用前景. 在智能监控系统中,行人轨迹预测可用于异常情况检测,有助于及时发现潜在的安全问题. 在自动驾驶领域,行人轨迹预测则提供了关键的行人运动信息,为车辆路径规划和行车安全性提供了必要的参考依据. ...
1
... 由于行人之间的复杂互动和环境的不确定性,行人轨迹预测是一项具有挑战性的任务. 随着深度学习的发展,许多基于深度学习的方法在这个领域中出现. 最初的研究主要集中在循环神经网络(recurrent neural network,RNN)[3 -5 ] 上,并取得了显著的成果. 然而,尽管RNN具备显著的序列建模能力,但在处理行人运动时存在无法直观地表达时空结构的问题. 在这方面,图结构成为一种表示行人之间的交互行为的更为自然的方法,相比之下,图卷积网络(graph convolutional network,GCN)方法更加直观和有效. 尽管目前许多方法[6 -8 ] 都将GCN作为基本组成部分,但现有的大多数研究中存在以下问题:1)行人在连续时间内的移动是连贯的,而不是随机的. 为了准确预测未来的行人位置,必须同时考虑行人之间的空间关系和时间上的连续性. 2)在轨迹采样的过程中通常采用高斯分布方法,但往往容易受到采样偏差的影响,导致性能被低估. ...
1
... 由于行人之间的复杂互动和环境的不确定性,行人轨迹预测是一项具有挑战性的任务. 随着深度学习的发展,许多基于深度学习的方法在这个领域中出现. 最初的研究主要集中在循环神经网络(recurrent neural network,RNN)[3 -5 ] 上,并取得了显著的成果. 然而,尽管RNN具备显著的序列建模能力,但在处理行人运动时存在无法直观地表达时空结构的问题. 在这方面,图结构成为一种表示行人之间的交互行为的更为自然的方法,相比之下,图卷积网络(graph convolutional network,GCN)方法更加直观和有效. 尽管目前许多方法[6 -8 ] 都将GCN作为基本组成部分,但现有的大多数研究中存在以下问题:1)行人在连续时间内的移动是连贯的,而不是随机的. 为了准确预测未来的行人位置,必须同时考虑行人之间的空间关系和时间上的连续性. 2)在轨迹采样的过程中通常采用高斯分布方法,但往往容易受到采样偏差的影响,导致性能被低估. ...
基于图卷积网络的行为识别方法综述
1
2021
... 由于行人之间的复杂互动和环境的不确定性,行人轨迹预测是一项具有挑战性的任务. 随着深度学习的发展,许多基于深度学习的方法在这个领域中出现. 最初的研究主要集中在循环神经网络(recurrent neural network,RNN)[3 -5 ] 上,并取得了显著的成果. 然而,尽管RNN具备显著的序列建模能力,但在处理行人运动时存在无法直观地表达时空结构的问题. 在这方面,图结构成为一种表示行人之间的交互行为的更为自然的方法,相比之下,图卷积网络(graph convolutional network,GCN)方法更加直观和有效. 尽管目前许多方法[6 -8 ] 都将GCN作为基本组成部分,但现有的大多数研究中存在以下问题:1)行人在连续时间内的移动是连贯的,而不是随机的. 为了准确预测未来的行人位置,必须同时考虑行人之间的空间关系和时间上的连续性. 2)在轨迹采样的过程中通常采用高斯分布方法,但往往容易受到采样偏差的影响,导致性能被低估. ...
基于图卷积网络的行为识别方法综述
1
2021
... 由于行人之间的复杂互动和环境的不确定性,行人轨迹预测是一项具有挑战性的任务. 随着深度学习的发展,许多基于深度学习的方法在这个领域中出现. 最初的研究主要集中在循环神经网络(recurrent neural network,RNN)[3 -5 ] 上,并取得了显著的成果. 然而,尽管RNN具备显著的序列建模能力,但在处理行人运动时存在无法直观地表达时空结构的问题. 在这方面,图结构成为一种表示行人之间的交互行为的更为自然的方法,相比之下,图卷积网络(graph convolutional network,GCN)方法更加直观和有效. 尽管目前许多方法[6 -8 ] 都将GCN作为基本组成部分,但现有的大多数研究中存在以下问题:1)行人在连续时间内的移动是连贯的,而不是随机的. 为了准确预测未来的行人位置,必须同时考虑行人之间的空间关系和时间上的连续性. 2)在轨迹采样的过程中通常采用高斯分布方法,但往往容易受到采样偏差的影响,导致性能被低估. ...
4
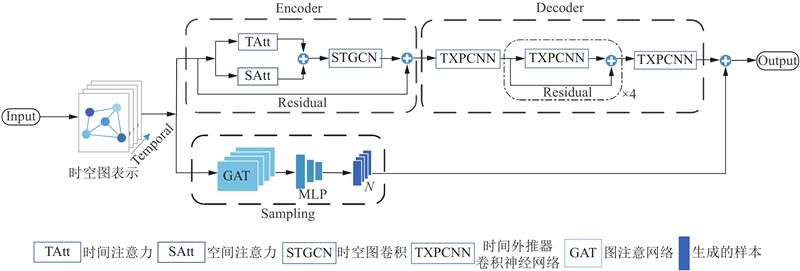
... Social-STGCNN[7 ] :先由STGCN提取特征,然后通过TXPCNN来预测未来的轨迹. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of results on SDD dataset
Tab.2 模型 年份 ADE FDE STGAT[17 ] 2019 18.80 31.30 Social-STGCNN[7 ] 2020 20.76 33.18 PECNET[15 ] 2020 9.96 15.88 SGCN[8 ] 2021 11.67 19.10 Social-STGCNN+NPSN 2022 11.80 18.43 SGCN+NPSN[11 ] 2022 17.12 28.97 Graph-TERN[21 ] 2023 8.43 14.26 本研究模型 — 9.16 15.21
针对不同数据集体现出的各自的优越性,发现采用NPSN方法实现的轨迹采样,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. 其次,为了解决行人前后帧之间的时空相关性,将时间注意力和空间注意力结合在一起,以提取有价值的信息并降低无价值信息的影响. 此外,通过改进邻接矩阵的计算方式,也可以有效地提取行人之间的信息,进一步提升模型的性能. 这些是未来改进的方向之一. ...
... Comparison of model parameters and inference time
Tab.3 模型 M /103 t /sPITF[16 ] 360.0 0.1145 PECNET[15 ] 21.0 0.1376 Social-STGCNN[7 ] 7.6 0.0020 SGCN[8 ] 25.0 0.1146 SGCN+NPSN[11 ] 30.4 0.2349 Graph-TERN[21 ] 48.5 0.0945 TAtt+SAtt 1.1 — STGCN+6层TXPCNN 7.7 — Sampling 5.1 — 本研究模型 13.9 0.0879
3.5. 消融研究 为了验证本研究方法的有效性,进行了一系列消融实验,分别在ETH、UCY和SDD数据集上对每个子模块的效果进行评估,同时保持其他模块的设置与最终模型一致. ...
6
... 由于行人之间的复杂互动和环境的不确定性,行人轨迹预测是一项具有挑战性的任务. 随着深度学习的发展,许多基于深度学习的方法在这个领域中出现. 最初的研究主要集中在循环神经网络(recurrent neural network,RNN)[3 -5 ] 上,并取得了显著的成果. 然而,尽管RNN具备显著的序列建模能力,但在处理行人运动时存在无法直观地表达时空结构的问题. 在这方面,图结构成为一种表示行人之间的交互行为的更为自然的方法,相比之下,图卷积网络(graph convolutional network,GCN)方法更加直观和有效. 尽管目前许多方法[6 -8 ] 都将GCN作为基本组成部分,但现有的大多数研究中存在以下问题:1)行人在连续时间内的移动是连贯的,而不是随机的. 为了准确预测未来的行人位置,必须同时考虑行人之间的空间关系和时间上的连续性. 2)在轨迹采样的过程中通常采用高斯分布方法,但往往容易受到采样偏差的影响,导致性能被低估. ...
... 为了验证本研究方法的有效性,使用3个真实世界的数据集:ETH、UCY和斯坦福无人机数据集(SDD). ETH/UCY数据集为行人轨迹预测邻域的经典基准,其中ETH数据集包含ETH和HOTEL共2个场景,UCY数据集包含ZARA1、ZARA2和UNIV共3个场景. 这些数据集包含了上千条真实的行人轨迹,展现了多种多样的行人交互情况. 在ETH/UCY数据集中,轨迹坐标以m为单位进行计算,并采用留一法交叉验证[8 ] ,将数据集分成5个子集,每次使用4个子集进行训练和验证,1个子集用于测试. 此外,为了验证所提方法在各种场景下的适用性,还在包含大量不同场景的SDD数据集上进行了实验. SDD数据集是行人轨迹预测领域提出的第1个大规模数据集,由无人机从鸟瞰图的角度捕获了大学校园的几个大区域,它被分成60个记录,展示了复杂的行人动态和与周围环境的强烈互动. 在该数据集中,轨迹坐标以像素为单位进行计算,并采用与NPSN[11 ] 方法相同的数据分割方式. ...
... SGCN[8 ] :提出新的稀疏图卷积网络,它将稀疏有向交互和运动趋势相结合. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of results on SDD dataset
Tab.2 模型 年份 ADE FDE STGAT[17 ] 2019 18.80 31.30 Social-STGCNN[7 ] 2020 20.76 33.18 PECNET[15 ] 2020 9.96 15.88 SGCN[8 ] 2021 11.67 19.10 Social-STGCNN+NPSN 2022 11.80 18.43 SGCN+NPSN[11 ] 2022 17.12 28.97 Graph-TERN[21 ] 2023 8.43 14.26 本研究模型 — 9.16 15.21
针对不同数据集体现出的各自的优越性,发现采用NPSN方法实现的轨迹采样,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. 其次,为了解决行人前后帧之间的时空相关性,将时间注意力和空间注意力结合在一起,以提取有价值的信息并降低无价值信息的影响. 此外,通过改进邻接矩阵的计算方式,也可以有效地提取行人之间的信息,进一步提升模型的性能. 这些是未来改进的方向之一. ...
... Comparison of model parameters and inference time
Tab.3 模型 M /103 t /sPITF[16 ] 360.0 0.1145 PECNET[15 ] 21.0 0.1376 Social-STGCNN[7 ] 7.6 0.0020 SGCN[8 ] 25.0 0.1146 SGCN+NPSN[11 ] 30.4 0.2349 Graph-TERN[21 ] 48.5 0.0945 TAtt+SAtt 1.1 — STGCN+6层TXPCNN 7.7 — Sampling 5.1 — 本研究模型 13.9 0.0879
3.5. 消融研究 为了验证本研究方法的有效性,进行了一系列消融实验,分别在ETH、UCY和SDD数据集上对每个子模块的效果进行评估,同时保持其他模块的设置与最终模型一致. ...
A comprehensive survey on graph neural networks
1
2020
... 近年来,GCN被广泛应用于视觉追踪、视频轨迹预测和人类交互行为识别等任务中[9 ] . 在行人轨迹预测中,GCN可以有效地学习行人之间复杂的空间关系,有效提高预测的准确性. 在之前的研究中,如Social-STGCNN首次将STGCN应用到行人轨迹预测中,来处理时空图数据. 尽管利用STGCN可以较好地表示行人之间的相互关系,但通常将所有交互影响视为相同,而实际情况是不同行人之间交互的影响是不同的. SGCN是在Social-STGCNN基础上的改进,它提出了稀疏有向交互作用算法,解决了行人之间交互作用无向的问题. 然而之前的方法没有考虑如何通过时空注意力机制优化行人间的社会交互关系,从而减少模型冗余度. 因此,本研究提出了一种新方法,将STGCN和时空注意力机制相结合应用于行人轨迹预测,以更充分地考虑行人之间的时空相关性,并减少模型的冗余程度. ...
2
... 轨迹采样在行人轨迹预测中具有重大作用,有助于模型更精确地预测未来行人的轨迹. 早期研究常采用确定性轨迹预测方法进行轨迹采样,但这种单一预测无法完全反映行人之间的复杂性和不确定性. 为了解决这个问题,Social-GAN[10 ] 提出多模态轨迹预测的方法,使用随机抽样的方式进行轨迹采样,但由于采样数量有限,随机采样可能无法覆盖所有可能的模态[11 ] . 为了使采样的轨迹可以覆盖更多的模态且更加均匀,一些先进的采样方法被提出. 例如,Ma等[12 ] 提出似然多元采样的方法,通过平衡可能性和空间分离来训练采样模型,以提高方法的质量和多样性并使其适用于其他框架. Bae等[11 ] 则利用Quasi-Monte Carlo方法的非概率抽样网络(non-probability sampling network,NPSN),该方法能够覆盖样本空间并生成均匀分布的轨迹样本,从而实现更有效的轨迹预测. 本研究受到Bae等[11 ] 的启发,采用NPSN方法来实现轨迹采样,通过对输入的信息提取特征生成多条均匀分布的轨迹样本,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. ...
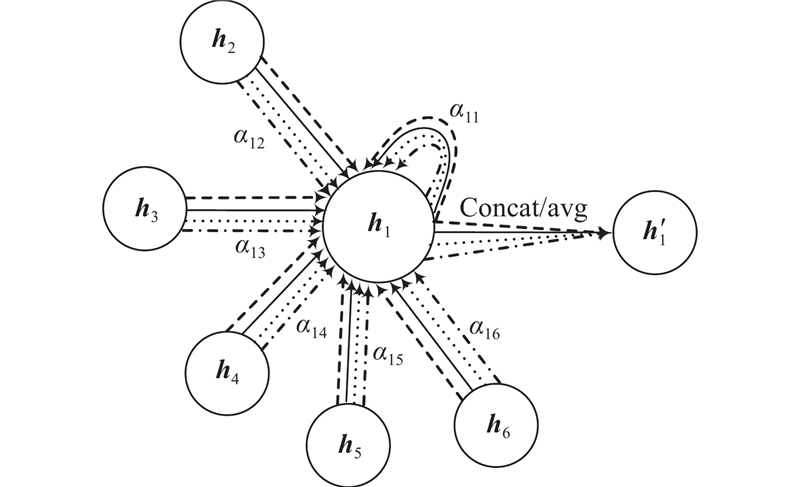
... 目前,注意力机制已成为各种序列建模任务中引人注目的组成部分,在行人轨迹预测中,先前的研究工作已经广泛采用了注意力机制来提高模型的性能. 例如Social Attention[13 ] 提出使用社交池化和自注意力模块来学习行人之间的关系,并在预测过程中使用注意力机制聚焦于最相关的行人. Social GAN[10 ] 提出GAN的方法,用于生成符合社交规则的行人轨迹. 在生成过程中,模型使用注意力机制来考虑其他行人的影响,并生成与社交规则一致的轨迹. Social-BIGAT[14 ] 利用图注意网络(graph attention network,GAT)和图像上的自注意力机制来考虑场景的社交和物理特征. PECNET[15 ] 提出符合社会标准的以端点为条件的变分自动编码器,并利用基于自注意力的社交池化来实现行人轨迹预测. 与上述工作不同,本研究在轨迹编码器阶段采用了时间和空间注意力结合的双重注意力机制,这一机制能够高效地捕获行人之间的动态时空相关性. 它通过聚焦于重要信息,同时降低对不重要信息的关注,显著提高了任务处理的效率和准确性. ...
9
... 轨迹采样在行人轨迹预测中具有重大作用,有助于模型更精确地预测未来行人的轨迹. 早期研究常采用确定性轨迹预测方法进行轨迹采样,但这种单一预测无法完全反映行人之间的复杂性和不确定性. 为了解决这个问题,Social-GAN[10 ] 提出多模态轨迹预测的方法,使用随机抽样的方式进行轨迹采样,但由于采样数量有限,随机采样可能无法覆盖所有可能的模态[11 ] . 为了使采样的轨迹可以覆盖更多的模态且更加均匀,一些先进的采样方法被提出. 例如,Ma等[12 ] 提出似然多元采样的方法,通过平衡可能性和空间分离来训练采样模型,以提高方法的质量和多样性并使其适用于其他框架. Bae等[11 ] 则利用Quasi-Monte Carlo方法的非概率抽样网络(non-probability sampling network,NPSN),该方法能够覆盖样本空间并生成均匀分布的轨迹样本,从而实现更有效的轨迹预测. 本研究受到Bae等[11 ] 的启发,采用NPSN方法来实现轨迹采样,通过对输入的信息提取特征生成多条均匀分布的轨迹样本,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. ...
... [11 ]则利用Quasi-Monte Carlo方法的非概率抽样网络(non-probability sampling network,NPSN),该方法能够覆盖样本空间并生成均匀分布的轨迹样本,从而实现更有效的轨迹预测. 本研究受到Bae等[11 ] 的启发,采用NPSN方法来实现轨迹采样,通过对输入的信息提取特征生成多条均匀分布的轨迹样本,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. ...
... [11 ]的启发,采用NPSN方法来实现轨迹采样,通过对输入的信息提取特征生成多条均匀分布的轨迹样本,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. ...
... 为了验证本研究方法的有效性,使用3个真实世界的数据集:ETH、UCY和斯坦福无人机数据集(SDD). ETH/UCY数据集为行人轨迹预测邻域的经典基准,其中ETH数据集包含ETH和HOTEL共2个场景,UCY数据集包含ZARA1、ZARA2和UNIV共3个场景. 这些数据集包含了上千条真实的行人轨迹,展现了多种多样的行人交互情况. 在ETH/UCY数据集中,轨迹坐标以m为单位进行计算,并采用留一法交叉验证[8 ] ,将数据集分成5个子集,每次使用4个子集进行训练和验证,1个子集用于测试. 此外,为了验证所提方法在各种场景下的适用性,还在包含大量不同场景的SDD数据集上进行了实验. SDD数据集是行人轨迹预测领域提出的第1个大规模数据集,由无人机从鸟瞰图的角度捕获了大学校园的几个大区域,它被分成60个记录,展示了复杂的行人动态和与周围环境的强烈互动. 在该数据集中,轨迹坐标以像素为单位进行计算,并采用与NPSN[11 ] 方法相同的数据分割方式. ...
... NPSN[11 ] :提出非概率抽样网络,利用行人过去的路径和社会互动产生样本序列. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... [
11 ]
2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38 如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of results on SDD dataset
Tab.2 模型 年份 ADE FDE STGAT[17 ] 2019 18.80 31.30 Social-STGCNN[7 ] 2020 20.76 33.18 PECNET[15 ] 2020 9.96 15.88 SGCN[8 ] 2021 11.67 19.10 Social-STGCNN+NPSN 2022 11.80 18.43 SGCN+NPSN[11 ] 2022 17.12 28.97 Graph-TERN[21 ] 2023 8.43 14.26 本研究模型 — 9.16 15.21
针对不同数据集体现出的各自的优越性,发现采用NPSN方法实现的轨迹采样,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. 其次,为了解决行人前后帧之间的时空相关性,将时间注意力和空间注意力结合在一起,以提取有价值的信息并降低无价值信息的影响. 此外,通过改进邻接矩阵的计算方式,也可以有效地提取行人之间的信息,进一步提升模型的性能. 这些是未来改进的方向之一. ...
... Comparison of model parameters and inference time
Tab.3 模型 M /103 t /sPITF[16 ] 360.0 0.1145 PECNET[15 ] 21.0 0.1376 Social-STGCNN[7 ] 7.6 0.0020 SGCN[8 ] 25.0 0.1146 SGCN+NPSN[11 ] 30.4 0.2349 Graph-TERN[21 ] 48.5 0.0945 TAtt+SAtt 1.1 — STGCN+6层TXPCNN 7.7 — Sampling 5.1 — 本研究模型 13.9 0.0879
3.5. 消融研究 为了验证本研究方法的有效性,进行了一系列消融实验,分别在ETH、UCY和SDD数据集上对每个子模块的效果进行评估,同时保持其他模块的设置与最终模型一致. ...
1
... 轨迹采样在行人轨迹预测中具有重大作用,有助于模型更精确地预测未来行人的轨迹. 早期研究常采用确定性轨迹预测方法进行轨迹采样,但这种单一预测无法完全反映行人之间的复杂性和不确定性. 为了解决这个问题,Social-GAN[10 ] 提出多模态轨迹预测的方法,使用随机抽样的方式进行轨迹采样,但由于采样数量有限,随机采样可能无法覆盖所有可能的模态[11 ] . 为了使采样的轨迹可以覆盖更多的模态且更加均匀,一些先进的采样方法被提出. 例如,Ma等[12 ] 提出似然多元采样的方法,通过平衡可能性和空间分离来训练采样模型,以提高方法的质量和多样性并使其适用于其他框架. Bae等[11 ] 则利用Quasi-Monte Carlo方法的非概率抽样网络(non-probability sampling network,NPSN),该方法能够覆盖样本空间并生成均匀分布的轨迹样本,从而实现更有效的轨迹预测. 本研究受到Bae等[11 ] 的启发,采用NPSN方法来实现轨迹采样,通过对输入的信息提取特征生成多条均匀分布的轨迹样本,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. ...
1
... 目前,注意力机制已成为各种序列建模任务中引人注目的组成部分,在行人轨迹预测中,先前的研究工作已经广泛采用了注意力机制来提高模型的性能. 例如Social Attention[13 ] 提出使用社交池化和自注意力模块来学习行人之间的关系,并在预测过程中使用注意力机制聚焦于最相关的行人. Social GAN[10 ] 提出GAN的方法,用于生成符合社交规则的行人轨迹. 在生成过程中,模型使用注意力机制来考虑其他行人的影响,并生成与社交规则一致的轨迹. Social-BIGAT[14 ] 利用图注意网络(graph attention network,GAT)和图像上的自注意力机制来考虑场景的社交和物理特征. PECNET[15 ] 提出符合社会标准的以端点为条件的变分自动编码器,并利用基于自注意力的社交池化来实现行人轨迹预测. 与上述工作不同,本研究在轨迹编码器阶段采用了时间和空间注意力结合的双重注意力机制,这一机制能够高效地捕获行人之间的动态时空相关性. 它通过聚焦于重要信息,同时降低对不重要信息的关注,显著提高了任务处理的效率和准确性. ...
3
... 目前,注意力机制已成为各种序列建模任务中引人注目的组成部分,在行人轨迹预测中,先前的研究工作已经广泛采用了注意力机制来提高模型的性能. 例如Social Attention[13 ] 提出使用社交池化和自注意力模块来学习行人之间的关系,并在预测过程中使用注意力机制聚焦于最相关的行人. Social GAN[10 ] 提出GAN的方法,用于生成符合社交规则的行人轨迹. 在生成过程中,模型使用注意力机制来考虑其他行人的影响,并生成与社交规则一致的轨迹. Social-BIGAT[14 ] 利用图注意网络(graph attention network,GAT)和图像上的自注意力机制来考虑场景的社交和物理特征. PECNET[15 ] 提出符合社会标准的以端点为条件的变分自动编码器,并利用基于自注意力的社交池化来实现行人轨迹预测. 与上述工作不同,本研究在轨迹编码器阶段采用了时间和空间注意力结合的双重注意力机制,这一机制能够高效地捕获行人之间的动态时空相关性. 它通过聚焦于重要信息,同时降低对不重要信息的关注,显著提高了任务处理的效率和准确性. ...
... BIGAT[14 ] :基于GAN的方法,利用GAT和图像上的self-attention来考虑场景的社交和物理特征. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
5
... 目前,注意力机制已成为各种序列建模任务中引人注目的组成部分,在行人轨迹预测中,先前的研究工作已经广泛采用了注意力机制来提高模型的性能. 例如Social Attention[13 ] 提出使用社交池化和自注意力模块来学习行人之间的关系,并在预测过程中使用注意力机制聚焦于最相关的行人. Social GAN[10 ] 提出GAN的方法,用于生成符合社交规则的行人轨迹. 在生成过程中,模型使用注意力机制来考虑其他行人的影响,并生成与社交规则一致的轨迹. Social-BIGAT[14 ] 利用图注意网络(graph attention network,GAT)和图像上的自注意力机制来考虑场景的社交和物理特征. PECNET[15 ] 提出符合社会标准的以端点为条件的变分自动编码器,并利用基于自注意力的社交池化来实现行人轨迹预测. 与上述工作不同,本研究在轨迹编码器阶段采用了时间和空间注意力结合的双重注意力机制,这一机制能够高效地捕获行人之间的动态时空相关性. 它通过聚焦于重要信息,同时降低对不重要信息的关注,显著提高了任务处理的效率和准确性. ...
... PECNET[15 ] :提出符合社会标准以端点为条件的变分自动编码器,以及结合自注意力机制的社交池层. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of results on SDD dataset
Tab.2 模型 年份 ADE FDE STGAT[17 ] 2019 18.80 31.30 Social-STGCNN[7 ] 2020 20.76 33.18 PECNET[15 ] 2020 9.96 15.88 SGCN[8 ] 2021 11.67 19.10 Social-STGCNN+NPSN 2022 11.80 18.43 SGCN+NPSN[11 ] 2022 17.12 28.97 Graph-TERN[21 ] 2023 8.43 14.26 本研究模型 — 9.16 15.21
针对不同数据集体现出的各自的优越性,发现采用NPSN方法实现的轨迹采样,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. 其次,为了解决行人前后帧之间的时空相关性,将时间注意力和空间注意力结合在一起,以提取有价值的信息并降低无价值信息的影响. 此外,通过改进邻接矩阵的计算方式,也可以有效地提取行人之间的信息,进一步提升模型的性能. 这些是未来改进的方向之一. ...
... Comparison of model parameters and inference time
Tab.3 模型 M /103 t /sPITF[16 ] 360.0 0.1145 PECNET[15 ] 21.0 0.1376 Social-STGCNN[7 ] 7.6 0.0020 SGCN[8 ] 25.0 0.1146 SGCN+NPSN[11 ] 30.4 0.2349 Graph-TERN[21 ] 48.5 0.0945 TAtt+SAtt 1.1 — STGCN+6层TXPCNN 7.7 — Sampling 5.1 — 本研究模型 13.9 0.0879
3.5. 消融研究 为了验证本研究方法的有效性,进行了一系列消融实验,分别在ETH、UCY和SDD数据集上对每个子模块的效果进行评估,同时保持其他模块的设置与最终模型一致. ...
3
... PITF[16 ] :利用人的行为模块和人的交互模块,将丰富的视觉语义编码为特征. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of model parameters and inference time
Tab.3 模型 M /103 t /sPITF[16 ] 360.0 0.1145 PECNET[15 ] 21.0 0.1376 Social-STGCNN[7 ] 7.6 0.0020 SGCN[8 ] 25.0 0.1146 SGCN+NPSN[11 ] 30.4 0.2349 Graph-TERN[21 ] 48.5 0.0945 TAtt+SAtt 1.1 — STGCN+6层TXPCNN 7.7 — Sampling 5.1 — 本研究模型 13.9 0.0879
3.5. 消融研究 为了验证本研究方法的有效性,进行了一系列消融实验,分别在ETH、UCY和SDD数据集上对每个子模块的效果进行评估,同时保持其他模块的设置与最终模型一致. ...
3
... STGAT[17 ] :在对行人运动进行建模的背景下,将GAT与LSTM结合起来的首次尝试. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of results on SDD dataset
Tab.2 模型 年份 ADE FDE STGAT[17 ] 2019 18.80 31.30 Social-STGCNN[7 ] 2020 20.76 33.18 PECNET[15 ] 2020 9.96 15.88 SGCN[8 ] 2021 11.67 19.10 Social-STGCNN+NPSN 2022 11.80 18.43 SGCN+NPSN[11 ] 2022 17.12 28.97 Graph-TERN[21 ] 2023 8.43 14.26 本研究模型 — 9.16 15.21
针对不同数据集体现出的各自的优越性,发现采用NPSN方法实现的轨迹采样,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. 其次,为了解决行人前后帧之间的时空相关性,将时间注意力和空间注意力结合在一起,以提取有价值的信息并降低无价值信息的影响. 此外,通过改进邻接矩阵的计算方式,也可以有效地提取行人之间的信息,进一步提升模型的性能. 这些是未来改进的方向之一. ...
2
... STAR[18 ] :在2个编码块中交叉使用空间Transformer和时间Transformer提取时空行人依赖关系,同时还使用外部可读可写图形存储模块. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
2
... AGENTFORMER[19 ] :设计了一种独特的agent-ware注意力,同时采用时间编码减少时间损失. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
2
... SIT[20 ] :提出简单而有效的基于树的方法,首先构建粗轨迹树,然后采用由粗到细的策略获得最终的多模态未来轨迹. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
4
... Graph-TERN[21 ] :提出通过预测的一组控制点确定行人的最终目的地,接着通过轨迹优化进一步提升路径预测的准确性. ...
... Comparison of results (ADE/FDE) on ETH and UCY datasets
Tab.1 模型 年份 ADE/FDE ETH HOTEL UNIV ZARA1 ZARA2 平均值 PITF[16 ] 2019 0.73/1.65 0.30/0.59 0.60/1.27 0.38/0.81 0.31/0.68 0.46/1.00 STGAT[17 ] 2019 0.50/0.84 0.26/0.46 0.51/1.07 0.33/0.64 0.30/0.61 0.38/0.72 BIGAT[14 ] 2019 0.69/1.29 0.49/1.01 0.55/1.32 0.30/0.62 0.36/0.75 0.48/1.00 Social-STGCNN[7 ] 2020 0.64/1.11 0.49/0.85 0.44/0.79 0.34/0.53 0.30/0.48 0.44/0.75 PECNET[15 ] 2020 0.54/0.87 0.18/0.24 0.35/0.60 0.22/0.39 0.17/0.30 0.29/0.48 STAR[18 ] 2020 0.36/0.65 0.17 /0.360.31/0.62 0.26/0.55 0.22/0.46 0.26/0.53 SGCN[8 ] 2021 0.63/1.03 0.32/0.55 0.37/0.70 0.29/0.53 0.25/0.45 0.37/0.65 AGENTFORMER[19 ] 2021 0.45/0.75 0.14 /0.22 0.25/0.45 0.18/0.30 0.14 /0.24 0.23/0.39 SIT[20 ] 2022 0.42/0.60 0.21/0.37 0.51/0.94 0.20/0.34 0.17/0.30 0.30/0.51 Social-STGCNN+NPSN[11 ] 2022 0.44/0.65 0.21/0.34 0.27/0.44 0.24/0.43 0.21/0.37 0.28/0.44 SGCN+NPSN[11 ] 2022 0.35/0.58 0.15 /0.250.22/0.39 0.18/ 0.31 0.13/0.24 0.21/0.36 Graph-TERN[21 ] 2023 0.42/0.58 0.14 /0.230.26/0.45 0.21/0.37 0.17/0.29 0.24/0.38 本研究模型 — 0.37/0.60 0.17/0.30 0.23 /0.39 0.19 /0.330.14/0.26 0.22/0.38
如表1 所示展示了本研究模型在ETH/UCY数据集上的性能. 实验结果表明,本研究模型的整体性能(AVG)处于第2优. 与AGENTFORMER相比,本研究模型在ADE和FDE上分别降低4.0%和2.5%,与Social-STGCNN+NPSN模型相比,本研究模型在ADE指标上降低了21.0%,在FDE指标上降低了15.0%. 与SGCN+NPSN模型相比,本研究模型在ADE指标和FDE指标上有所提升,但是本研究模型在模型参数量方面减少1.65×104 ,并且推理时间也减少0.147 s. 如表2 所示为本研究模型在SDD数据集上的性能对比结果. 实验结果表明,本研究模型的性能明显优于SGCN、Social-STGCNN+NPSN、SGCN+NPSN等模型;但是与Graph-TERN模型相比,本研究模型在ADE和FDE指标上有所提升,这是因为Graph-TERN模型首先通过预测一组控制点来确定最终目的地,然后通过模型优化轨迹,从而显著提高模型的预测精度. ...
... Comparison of results on SDD dataset
Tab.2 模型 年份 ADE FDE STGAT[17 ] 2019 18.80 31.30 Social-STGCNN[7 ] 2020 20.76 33.18 PECNET[15 ] 2020 9.96 15.88 SGCN[8 ] 2021 11.67 19.10 Social-STGCNN+NPSN 2022 11.80 18.43 SGCN+NPSN[11 ] 2022 17.12 28.97 Graph-TERN[21 ] 2023 8.43 14.26 本研究模型 — 9.16 15.21
针对不同数据集体现出的各自的优越性,发现采用NPSN方法实现的轨迹采样,能更好地反映行人之间的复杂性和不确定性,提高预测的准确性和鲁棒性. 其次,为了解决行人前后帧之间的时空相关性,将时间注意力和空间注意力结合在一起,以提取有价值的信息并降低无价值信息的影响. 此外,通过改进邻接矩阵的计算方式,也可以有效地提取行人之间的信息,进一步提升模型的性能. 这些是未来改进的方向之一. ...
... Comparison of model parameters and inference time
Tab.3 模型 M /103 t /sPITF[16 ] 360.0 0.1145 PECNET[15 ] 21.0 0.1376 Social-STGCNN[7 ] 7.6 0.0020 SGCN[8 ] 25.0 0.1146 SGCN+NPSN[11 ] 30.4 0.2349 Graph-TERN[21 ] 48.5 0.0945 TAtt+SAtt 1.1 — STGCN+6层TXPCNN 7.7 — Sampling 5.1 — 本研究模型 13.9 0.0879
3.5. 消融研究 为了验证本研究方法的有效性,进行了一系列消融实验,分别在ETH、UCY和SDD数据集上对每个子模块的效果进行评估,同时保持其他模块的设置与最终模型一致. ...