(4) $ f{_{P,j}^{m,i}} = \left\{ \begin{array}{*{20}{l}} 0,& | {(x,y)}_j^i - {C_n^m} | \geqslant {R^m_{\max,n}}; \\ K_{_{{\mathrm{thr}}}}^m| {R_{\max n}^m - | {(x,y)} _j^i - {C_n^m} |} |,& 其他. \\ \end{array} \right. $
(14) $ C_{i,j}^{\text{t}} = \left\{ \begin{gathered} P/\left| {{t_i} - {t_j}} \right|,\max \left[ {{t_{i,\min }},{t_{j,\min }}} \right] < \min \left[ {{t_{i,\max }},{t_{j,\max }}} \right]; \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他. \\ \end{gathered} \right. $
式中:P 、P ' 均为足够大的常数,本研究均取为100;|t i t j i 和无人机j 到达目标点的时间差;$C_{i,j}^{\mathrm{t}} $ t i ,mint j ,mint i ,maxt j ,maxd k k 个航迹点的欧氏距离,n 为航迹点数. 假设有M 架无人机,则第i 架无人机与第j 架无人机的协同时空约束代价函数为
(20) $ \begin{split} {\boldsymbol\varOmega _i} =& \left[{{\rho _{i1}},{\psi _{i1}},{\phi _{i1}},{\rho _{i2}},{\psi _{i2}},{\phi _{i2}}, \cdots ,{\rho _{iN}},{\psi _{iN}},{\phi _{iN}}} \right],\\& N = n - 2.\end{split} $
(21) $ \left. \begin{gathered} {x_{i,j}} = {x_{i,j - 1}}+{\rho _{ij}}\sin {\psi _{ij}}\cos {\phi _{ij}}{\text{,}} \\ {y_{i,j}} = {y_{i,j - 1}}+{\rho _{ij}}\sin {\psi _{ij}}\cos {\phi _{ij}}{\text{,}} \\ {z_{i,j}} = {z_{i,j - 1}}+{\rho _{ij}}\cos {\psi _{ij}}. \\ \end{gathered} \right\} $
(24) $ {p}_{i,\text{n}}=\left\{ \begin{array}{*{20}{l}}G\text{(}{p}_{i,\text{m}},\varsigma \text{)}+\text{(}{r}_{1}{p}_{i,\text{m}}-{r}_{2}{p}_{i}\text{),}& {p}_{i}=\dfrac{1}{3}p;\\{\mathrm{rand}} {p}_{\text{b}}+{\delta }_{x}+{\delta }_{y}\text{,}& {p}_{i}=\dfrac{2}{3}p.\end{array} \right.$
模型1:选取2架UAV进行仿真实验,建立100 km×100 km×5 km的模拟地形区域,实验参数如表4 所示. 第一架无人机记作UAV1,航线起点为(15,20,2),终点为(80,80,2). UAV2的航线起点为(40,10,1),终点为(90,55,1). 2架无人机型号相同. 威胁源数量为5个,其中雷达威胁为2个,作用中心分别为(30,40)和(70,60),作用半径为10 km,作用效果等效为螺旋线. 禁飞区、地空导弹和防空火炮数量均为1个,作用中心分别为(35,20)、(65,75)和(50,60),作用半径分别为7、8和5 km,作用效果等效为圆柱体. 如图8 所示为各算法航迹规划结果,各算法求解质量比较如表5 所示,l m 为平均路径长度,f m 为平均威胁代价,l s 为最短路径长度,f s 为最小威胁代价. NSGA-Ⅱ规划出的路径较短,但多次穿过威胁源,威胁代价极高,规划效果差;其他算法均能规划出满足约束的路径. 由表5 可知,所提算法稳定性更高,无论是航程代价还是威胁代价,均得到最优的规划效果. 由图8 可以看出,所提算法规划的路径中,UAV1和UAV2飞行路径没有发生交叉和重合,这说明所提算法在对无人机路径协同规划问题进行寻优时实现了无人机之间的空间协同,算法的寻优效果能够让飞行路径更短,威胁代价更小,耗时最短.
[1]
ZHANG Z, WU J, DAI J, et al A novel real-time penetration path planning algorithm for stealth UAV in 3D complex dynamic environment
[J]. IEEE Access , 2020 , 8 : 122757 - 122771
DOI:10.1109/ACCESS.2020.3007496
[本文引用: 1]
[2]
王建峰, 贾高伟, 郭正, 等. 多无人机协同任务规划方法研究综述[EB/OL]. (2023−04−19)[2024−07−29]. https://kns.cnki.net/kcms/detail/11.2422.TN.20230419.1331.010.html.
[本文引用: 1]
[3]
PUENTE-CASTRO A, RIVERO D, PAZOS A, et al A review of artificial intelligence applied to path planning in UAV swarms
[J]. Neural Computing and Applications , 2022 , 34 : 153 - 170
DOI:10.1007/s00521-021-06569-4
[本文引用: 1]
[4]
YU X, LI C, YEN G G A knee-guided differential evolution algorithm for unmanned aerial vehicle path planning in disaster management
[J]. Applied Soft Computing , 2021 , 98 : 106857
DOI:10.1016/j.asoc.2020.106857
[本文引用: 1]
[5]
HUO L, ZHU J, WU G, et al A novel simulated annealing based strategy for balanced UAV task assignment and path planning
[J]. Sensors , 2020 , 20 (17 ): 4769
DOI:10.3390/s20174769
[本文引用: 1]
[6]
YANG L, GUO J, LIU Y Three-dimensional UAV cooperative path planning based on the MP-CGWO algorithm
[J]. International Journal of Innovative Computing, Information and Control , 2020 , 16 (3 ): 991 - 1006
[本文引用: 1]
[7]
PAN J, LIU N, CHU S A hybrid differential evolution algorithm and its application in unmanned combat aerial vehicle path planning
[J]. IEEE Access , 2020 , 8 : 17691 - 17712
DOI:10.1109/ACCESS.2020.2968119
[本文引用: 1]
[8]
黄鹤, 李潇磊, 杨澜, 等 引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划
[J]. 西安交通大学学报 , 2022 , 56 (7 ): 9 - 18
DOI:10.7652/xjtuxb202207002
[本文引用: 1]
HUANG He, LI Xiaolei, YANG Lan, et al Three dimensional path planning of unmanned underwater vehicle based on improved manta ray foraging optimization algorithm
[J]. Journal of Xi’an Jiaotong University , 2022 , 56 (7 ): 9 - 18
DOI:10.7652/xjtuxb202207002
[本文引用: 1]
[9]
EUN Y, BANG H Cooperative task assignment/path planning of multiple unmanned aerial vehicles using genetic algorithm
[J]. Journal of Aircraft , 2009 , 46 (1 ): 338 - 343
DOI:10.2514/1.38510
[本文引用: 1]
[10]
杜云, 彭瑜, 邵士凯, 等 基于改进粒子群优化的多无人机协同航迹规划
[J]. 科学技术与工程 , 2020 , 20 (32 ): 13258 - 13264
DOI:10.3969/j.issn.1671-1815.2020.32.025
[本文引用: 1]
DU Yun, PENY Yu, SHAO Shikai, et al Cooperative path planning of multi-unmanned aerial vehicle based on improved particle swarm optimization
[J]. Science Technology and Engineering , 2020 , 20 (32 ): 13258 - 13264
DOI:10.3969/j.issn.1671-1815.2020.32.025
[本文引用: 1]
[11]
闫少强, 杨萍, 刘卫东, 等. 基于GPSSA算法的复杂地形多无人机航迹规划[EB/OL]. (2023–04–12)[2024–07–29]. https://doi.org/10.13700/j.bh.1001-5965.2022.0984.
[本文引用: 1]
[12]
袁梦顺, 陈谋, 吴庆宪 基于NSGA-III算法的多无人机协同航迹规划
[J]. 吉林大学学报: 信息科学版 , 2021 , 39 (3 ): 295 - 302
[本文引用: 1]
YUAN Mengshun, CHEN Mou, WU Qingxian Cooperative path planning for multiple UAVs based on NSGA-III algorithm
[J]. Journal of Jilin University: Information Science Edition , 2021 , 39 (3 ): 295 - 302
[本文引用: 1]
[13]
ALSATTAR H A, ZAIDAN A A, ZAIDAN B B Novel meta-heuristic bald eagle search optimisation algorithm
[J]. Artificial Intelligence Review , 2020 , 53 : 2237 - 2264
DOI:10.1007/s10462-019-09732-5
[本文引用: 1]
[14]
YANG C, TSAI M, KANG S, et al UAV path planning method for digital terrain model reconstruction: a debris fan example
[J]. Automation in Construction , 2018 , 93 : 214 - 230
DOI:10.1016/j.autcon.2018.05.024
[本文引用: 1]
[15]
RADMANESH M, KUMAR M, GUENTERT P H, et al Overview of path-planning and obstacle avoidance algorithms for UAVs: a comparative study
[J]. Unmanned Systems , 2018 , 6 (2 ): 95 - 118
DOI:10.1142/S2301385018400022
[本文引用: 1]
[16]
WAHAB S H A, CHEKIMA A, SAAD N, et al. Path planning of UAV based on fluid computing via accelerated method [J]. International Journal of Engineering Trends and Technology , 2020, 76–80.
[本文引用: 1]
[17]
黄鹤, 李文龙, 吴琨, 等 基于ALCE-SSA优化的三维无人机低空突防
[J]. 南京大学学报: 自然科学 , 2022 , 58 (3 ): 448 - 459
[本文引用: 1]
HUANG He, LI Wenlong, WU Kun, et al 3D UAV low altitude penetration optimization based on ALCE-SSA
[J]. Journal of Nanjing University: Natural Science , 2022 , 58 (3 ): 448 - 459
[本文引用: 1]
[18]
PHUNG M D, HA Q P Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization
[J]. Applied Soft Computing , 2021 , 107 : 107376
DOI:10.1016/j.asoc.2021.107376
[本文引用: 2]
[19]
周德云, 王鹏飞, 李枭扬, 等 基于多目标优化算法的多无人机协同航迹规划
[J]. 系统工程与电子技术 , 2017 , 39 (4 ): 782 - 787
DOI:10.3969/j.issn.1001-506X.2017.04.13
[本文引用: 1]
ZHOU Deyun, WANG Pengfei, LI Xiaoyang, et al Cooperative path planning of multi-UAV based on multi-objective optimization algorithm
[J]. Systems Engineering and Electronics , 2017 , 39 (4 ): 782 - 787
DOI:10.3969/j.issn.1001-506X.2017.04.13
[本文引用: 1]
[20]
SHAKIBA A A novel randomized one-dimensional chaotic Chebyshev mapping for chosen plaintext attack secure image encryption with a novel chaotic breadth first traversal
[J]. Multimedia Tools and Applications , 2019 , 78 (24 ): 34773 - 34799
DOI:10.1007/s11042-019-08071-5
[本文引用: 1]
[22]
XUE J, SHEN B A novel swarm intelligence optimization approach: sparrow search algorithm
[J]. Systems Science and Control Engineering , 2020 , 8 (1 ): 22 - 34
DOI:10.1080/21642583.2019.1708830
[本文引用: 2]
[23]
TROJOVSKÝ P, DEHGHANI M Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications
[J]. Sensors , 2022 , 22 (3 ): 855
DOI:10.3390/s22030855
[本文引用: 2]
[24]
NEGI G, KUMAR A, PANT S, et al GWO: a review and applications
[J]. International Journal of System Assurance Engineering and Management , 2021 , 12 : 1 - 8
[本文引用: 2]
[25]
XUE J, SHN B Dung beetle optimizer: a new meta-heuristic algorithm for global optimization
[J]. The Journal of Supercomputing , 2023 , 79 : 7305 - 7336
DOI:10.1007/s11227-022-04959-6
[本文引用: 2]
[26]
LIU T, YUAN Q, DING X, et al Multi-objective optimization for greenhouse light environment using Gaussian mixture model and an improved NSGA-II algorithm
[J]. Computers and Electronics in Agriculture , 2023 , 205 : 107612
[本文引用: 2]
[27]
戴晓晖, 李敏强, 寇纪淞 遗传算法的性能分析研究
[J]. 软件学报 , 2001 , 12 (5 ): 742 - 750
[本文引用: 1]
DAI Xiaohui, LI Minqiang, KOU Jisong Study on the performance analysis of genetic algorithm
[J]. Journal of Software , 2001 , 12 (5 ): 742 - 750
[本文引用: 1]
[28]
Geoscience Australia. Digital elevation model (DEM) of Australia derived from LiDAR 5 metre grid [DB/OL]. [2024–07–29]. https://doi.org/10.26186/89644.
[本文引用: 1]
[29]
MA M, WU J, SHI Y, et al Research on multi-aircrafts cooperative arraying to jam based on multi-objective moth-flame optimization algorithm
[J]. IEEE Access , 2022 , 10 : 80539 - 80554
DOI:10.1109/ACCESS.2022.3193094
[本文引用: 1]
[30]
YI J, XING L, WANG G, et al. Behavior of crossover operators in NSGA-III for large-scale optimization problems [J]. Information Sciences , 2020, 509: 470–487.
[本文引用: 1]
[31]
CHOU J, TRUONG D Multi-objective optimization inspired by behavior of jellyfish for solving structural design problems
[J]. Chaos, Solitons and Fractals , 2020 , 135 : 109738
DOI:10.1016/j.chaos.2020.109738
[本文引用: 1]
A novel real-time penetration path planning algorithm for stealth UAV in 3D complex dynamic environment
1
2020
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
1
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
A review of artificial intelligence applied to path planning in UAV swarms
1
2022
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
A knee-guided differential evolution algorithm for unmanned aerial vehicle path planning in disaster management
1
2021
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
A novel simulated annealing based strategy for balanced UAV task assignment and path planning
1
2020
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
Three-dimensional UAV cooperative path planning based on the MP-CGWO algorithm
1
2020
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
A hybrid differential evolution algorithm and its application in unmanned combat aerial vehicle path planning
1
2020
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划
1
2022
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划
1
2022
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
Cooperative task assignment/path planning of multiple unmanned aerial vehicles using genetic algorithm
1
2009
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
基于改进粒子群优化的多无人机协同航迹规划
1
2020
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
基于改进粒子群优化的多无人机协同航迹规划
1
2020
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
1
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
基于NSGA-III算法的多无人机协同航迹规划
1
2021
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
基于NSGA-III算法的多无人机协同航迹规划
1
2021
... 低空突防是无人机(unmanned aerial vehicle, UAV)作战中的重要环节[1 ] ,其目标是在满足各项约束的基础上,设计算法规划出从起点到终点能够有效避开威胁源的低能耗路线. 单无人机突防能力略显不足,因此多无人机协同规划逐渐成为无人机集群化、自主化和智能化的发展关键和研究热点[2 ] . 由于作战环境形势交错、复杂性强,且多无人机在航迹规划时受到众多条件的约束,亟须建立更精确的模型并设计更高效的算法. 元启发式算法被认为是处理单目标和多目标问题的标准优化方法[3 ] ,这些方法在复杂和动态环境(包括战场、救援任务和多无人机路径优化等场景)中表现出色. 元启发式算法大致分为4类:进化算法[4 ] 、基于物理的算法[5 ] 、基于群体的算法[6 ] 和混合元启发算法[7 ] . 其中基于群体的算法也称群体智能(swarm intelligence, SI)[8 ] 算法,它不仅克服了进化算法收敛慢和基于物理的算法受模型限制的缺陷,而且计算成本适中. 此外,该方法强调合作和信息共享处理集体智能问题,对初始条件的敏感性较低,适用于三维多无人机低空突防. 群体智能算法已被应用于多无人机航迹规划. Eun等[9 ] 在二维地图上利用遗传算法讨论多无人机组的任务分配和轨迹规划问题,但未充分考虑三维地形和威胁源约束的影响. 杜云等[10 ] 考虑无人机性能、威胁源、时空协同等约束,利用改进的粒子群算法求解最优路径集合,但利用单目标代价函数寻优时,权重设置受主观因素影响较大. 闫少强等[11 ] 提出改进麻雀搜索算法(game predatory sparrow search algorithm, GPSSA),在复杂三维地形中求解单无人机及多无人机航迹规划中都取得了较好的规划效果,但协同目标函数仍依赖单目标群智能算法的寻优性能,影响了算法效率. 袁梦顺等[12 ] 将各项约束和代价转换为非支配排序遗传算法-Ⅲ(non-dominated sorting genetic algorithm-Ⅲ, NSGA-Ⅲ) 的数值指标,避免了单目标问题加权的主观性,但算法应用的建模场景复杂程度不高. 上述研究虽然能够实现多无人机协同航迹规划,但优化效果和迭代收敛速度仍有提升空间. ...
Novel meta-heuristic bald eagle search optimisation algorithm
1
2020
... 秃鹰搜索算法(bald eagle search,BES)[13 ] 是新型元启发式算法,具有收敛速度快,适应性强,模型易修改等特点. 与同类型的如麻雀算法(sparrow search algorithm,SSA)、鹈鹕算法(pelican optimization algorithm,POA)、水母算法(jellyfish search,JS)和蜣螂算法(dung beetle optimizer,DBO)相比,BES的性能更优,且在极坐标系中进行搜索的寻优方式独特,更适用于高效搜索无人机构型空间. 多无人机航迹规划问题通常涉及多个冲突的目标,使用单目标群智能算法只能解决单个目标或通过加权方式平衡多个目标,求解精度欠缺. 多目标算法能够在优化过程中同时优化多个目标,找到一系列平衡解,提供多样化决策选择. BES本身搜索能力不足,寻优过程易趋于中心点,选取局部最优航迹时缺陷较大. 为了使多无人机在航迹规划中实现快速寻优,获取到具有高精度的较优路径,本研究提出改进的多目标秃鹰搜索算法(improved multi-objective bald eagle search algorithm,IMBES),应用于多无人机协同低空突防. ...
UAV path planning method for digital terrain model reconstruction: a debris fan example
1
2018
... 建模时地形约束有2种,分别是地势低平的平原和地势较高的山丘[14 -15 ] ,其中山丘对地形代价影响较大. 构建山丘三维模型为 ...
Overview of path-planning and obstacle avoidance algorithms for UAVs: a comparative study
1
2018
... 建模时地形约束有2种,分别是地势低平的平原和地势较高的山丘[14 -15 ] ,其中山丘对地形代价影响较大. 构建山丘三维模型为 ...
1
... 在建模无人机突防过程中,雷达探测、防空火炮、地空导弹和禁飞区等被认为是主要的威胁源. 为了简化建模,根据威胁的性质算出各威胁源的作用半径和作用空间形状,以等效地形代替[16 ] . 假设距离威胁源中心越近,威胁代价越大;反之,则越低. 将威胁源等效为数学模型,定义每个航迹点在威胁区域的计算代价为 ...
基于ALCE-SSA优化的三维无人机低空突防
1
2022
... 单无人机在飞行过程中受自身的物理约束,主要包括最大拐弯角α 、最大下滑及爬升角β、 续航时间t d 以及发动机功率W 约束[17 ] ,表达式分别为 ...
基于ALCE-SSA优化的三维无人机低空突防
1
2022
... 单无人机在飞行过程中受自身的物理约束,主要包括最大拐弯角α 、最大下滑及爬升角β、 续航时间t d 以及发动机功率W 约束[17 ] ,表达式分别为 ...
Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization
2
2021
... 路径平滑是生成路径可行的必要条件,通过计算转弯速率和爬坡速率得到[18 ] . 如图1 所示,转弯角$\phi_j^i $ o xy 的2个连续路径段$ \rightharpoonup {P{{_j^{i'}}}P{{_{j+1}^{i'}}}} $ $ \rightharpoonup {P{{_{j+1}^{i'}}}P{{_{j+2}^{i'}}}} $ k z 轴方向的单位向量,则投影向量计算式为 ...
... 设定迭代中每条更新路径由种群中的秃鹰X i x i 1x i 2x id [18 ] . 用球坐标系代替笛卡尔坐标表示秃鹰位置,因为所有路径的起点和终点固定,所以不包含在优化序列中,路径由n 个航迹点组成,选用维度为3n 的向量序列进行表示. 这些向量在球坐标系中表示为3个分量,分别为航迹距离增量ρ 、仰角Ψ ∈(−π/2,π/2)和方位角Φ ∈(−π,π). 飞行路径Ω i
基于多目标优化算法的多无人机协同航迹规划
1
2017
... 多无人机系统在执行协同打击作战任务时,须在保证同时到达同一目标点的前提下,尽可能实现各无人机的飞行路径足够分散,即实现“分散突防、集中打击”的作战效果,从战术角度保证以最小代价实现最大打击效果[19 ] . 设时间和空间协同约束系数$C_{i,j}^{\mathrm{t}} $ $C_{i,j}^{\mathrm{d}} $
基于多目标优化算法的多无人机协同航迹规划
1
2017
... 多无人机系统在执行协同打击作战任务时,须在保证同时到达同一目标点的前提下,尽可能实现各无人机的飞行路径足够分散,即实现“分散突防、集中打击”的作战效果,从战术角度保证以最小代价实现最大打击效果[19 ] . 设时间和空间协同约束系数$C_{i,j}^{\mathrm{t}} $ $C_{i,j}^{\mathrm{d}} $
A novel randomized one-dimensional chaotic Chebyshev mapping for chosen plaintext attack secure image encryption with a novel chaotic breadth first traversal
1
2019
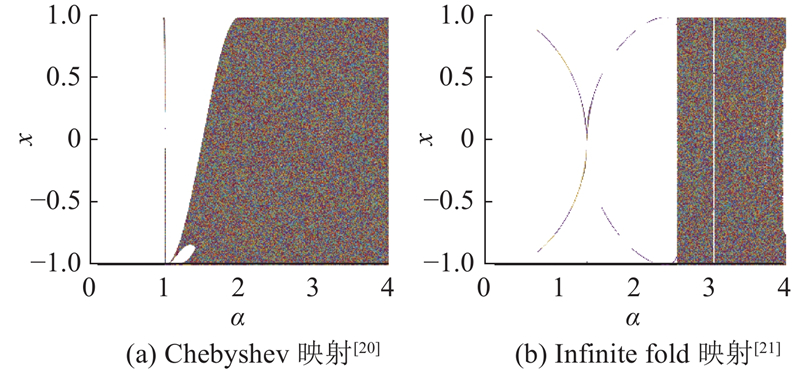
... 本研究设计耦合混沌映射,如图2 所示为各混沌映射分岔图,横轴为参数值,纵轴为映射的状态或输出值. 由Chebyshev映射[20 ] 和Infinite Fold[21 ] 混沌映射的分岔图可以看出,当2个混沌映射中的控制参数分别在大于1.0和1.8时,逐渐出现分岔现象,因此采用耦合参数c 级联这2个种子映射,对非线性映射的混沌片段进行拼接,通过交叉迭代的方式从一维扩展到多维,其中二维情况的表达式为 ...
一种有限区间内无限折叠的混沌映射
1
2002
... 本研究设计耦合混沌映射,如图2 所示为各混沌映射分岔图,横轴为参数值,纵轴为映射的状态或输出值. 由Chebyshev映射[20 ] 和Infinite Fold[21 ] 混沌映射的分岔图可以看出,当2个混沌映射中的控制参数分别在大于1.0和1.8时,逐渐出现分岔现象,因此采用耦合参数c 级联这2个种子映射,对非线性映射的混沌片段进行拼接,通过交叉迭代的方式从一维扩展到多维,其中二维情况的表达式为 ...
一种有限区间内无限折叠的混沌映射
1
2002
... 本研究设计耦合混沌映射,如图2 所示为各混沌映射分岔图,横轴为参数值,纵轴为映射的状态或输出值. 由Chebyshev映射[20 ] 和Infinite Fold[21 ] 混沌映射的分岔图可以看出,当2个混沌映射中的控制参数分别在大于1.0和1.8时,逐渐出现分岔现象,因此采用耦合参数c 级联这2个种子映射,对非线性映射的混沌片段进行拼接,通过交叉迭代的方式从一维扩展到多维,其中二维情况的表达式为 ...
A novel swarm intelligence optimization approach: sparrow search algorithm
2
2020
... 实验硬件仿真平台使用处理器为12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz,内存为16.0 GB的计算机,软件平台为Matlab R2020b. 设置种群规模为500,迭代次数为200. 在标准测试函数集上将IMBES与基于网格法的多目标麻雀算法(MOSSA)[22 ] 、多目标鹈鹕算法(MOPOA)[23 ] 、多目标灰狼算法(MOGWO)[24 ] 、基于非支配排序的多目标蜣螂算法(NSDBO)[25 ] 以及NSGA-Ⅱ[26 ] 等主流算法的求解性能进行对比测试.各测试函数具体描述如表1 所示,其中N OF 为目标函数个数. ...
... Main parameter settings of different algorithms
Tab.3 算法 主要参数 MOSSA[22 ] R 2 = 0.8, SD=0.1, PD=0.2MOPOA[23 ] β =1.5, R =2MOGWO[24 ] α =3, β =0.1NSDBO[25 ] p 1 =0.2, p 2 =0.4, p 3 =0.63, k =0.1, b =0.3NSGA-Ⅱ[26 ] 交叉率为0.7, 变异率为0.4, μ =0.02, δ =0.2
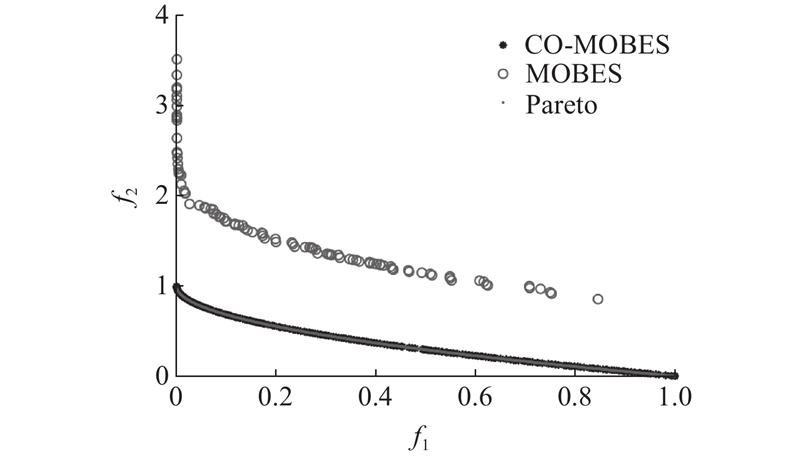
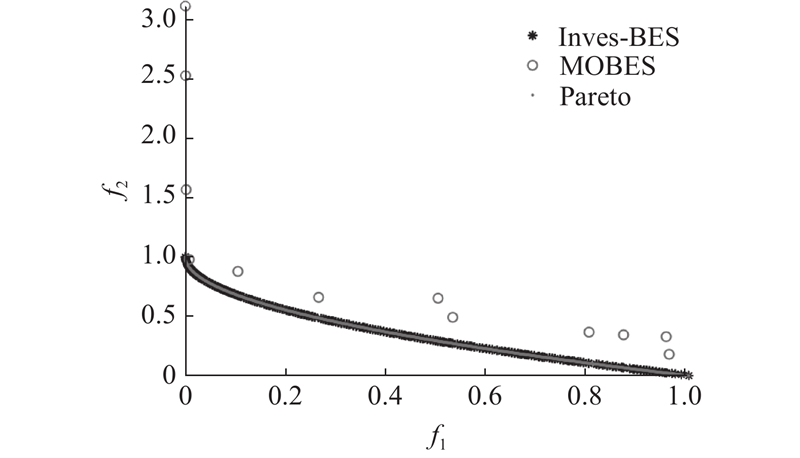
建立双模型增加算法的可信度,实验如下. ...
Pelican optimization algorithm: a novel nature-inspired algorithm for engineering applications
2
2022
... 实验硬件仿真平台使用处理器为12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz,内存为16.0 GB的计算机,软件平台为Matlab R2020b. 设置种群规模为500,迭代次数为200. 在标准测试函数集上将IMBES与基于网格法的多目标麻雀算法(MOSSA)[22 ] 、多目标鹈鹕算法(MOPOA)[23 ] 、多目标灰狼算法(MOGWO)[24 ] 、基于非支配排序的多目标蜣螂算法(NSDBO)[25 ] 以及NSGA-Ⅱ[26 ] 等主流算法的求解性能进行对比测试.各测试函数具体描述如表1 所示,其中N OF 为目标函数个数. ...
... Main parameter settings of different algorithms
Tab.3 算法 主要参数 MOSSA[22 ] R 2 = 0.8, SD=0.1, PD=0.2MOPOA[23 ] β =1.5, R =2MOGWO[24 ] α =3, β =0.1NSDBO[25 ] p 1 =0.2, p 2 =0.4, p 3 =0.63, k =0.1, b =0.3NSGA-Ⅱ[26 ] 交叉率为0.7, 变异率为0.4, μ =0.02, δ =0.2
建立双模型增加算法的可信度,实验如下. ...
GWO: a review and applications
2
2021
... 实验硬件仿真平台使用处理器为12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz,内存为16.0 GB的计算机,软件平台为Matlab R2020b. 设置种群规模为500,迭代次数为200. 在标准测试函数集上将IMBES与基于网格法的多目标麻雀算法(MOSSA)[22 ] 、多目标鹈鹕算法(MOPOA)[23 ] 、多目标灰狼算法(MOGWO)[24 ] 、基于非支配排序的多目标蜣螂算法(NSDBO)[25 ] 以及NSGA-Ⅱ[26 ] 等主流算法的求解性能进行对比测试.各测试函数具体描述如表1 所示,其中N OF 为目标函数个数. ...
... Main parameter settings of different algorithms
Tab.3 算法 主要参数 MOSSA[22 ] R 2 = 0.8, SD=0.1, PD=0.2MOPOA[23 ] β =1.5, R =2MOGWO[24 ] α =3, β =0.1NSDBO[25 ] p 1 =0.2, p 2 =0.4, p 3 =0.63, k =0.1, b =0.3NSGA-Ⅱ[26 ] 交叉率为0.7, 变异率为0.4, μ =0.02, δ =0.2
建立双模型增加算法的可信度,实验如下. ...
Dung beetle optimizer: a new meta-heuristic algorithm for global optimization
2
2023
... 实验硬件仿真平台使用处理器为12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz,内存为16.0 GB的计算机,软件平台为Matlab R2020b. 设置种群规模为500,迭代次数为200. 在标准测试函数集上将IMBES与基于网格法的多目标麻雀算法(MOSSA)[22 ] 、多目标鹈鹕算法(MOPOA)[23 ] 、多目标灰狼算法(MOGWO)[24 ] 、基于非支配排序的多目标蜣螂算法(NSDBO)[25 ] 以及NSGA-Ⅱ[26 ] 等主流算法的求解性能进行对比测试.各测试函数具体描述如表1 所示,其中N OF 为目标函数个数. ...
... Main parameter settings of different algorithms
Tab.3 算法 主要参数 MOSSA[22 ] R 2 = 0.8, SD=0.1, PD=0.2MOPOA[23 ] β =1.5, R =2MOGWO[24 ] α =3, β =0.1NSDBO[25 ] p 1 =0.2, p 2 =0.4, p 3 =0.63, k =0.1, b =0.3NSGA-Ⅱ[26 ] 交叉率为0.7, 变异率为0.4, μ =0.02, δ =0.2
建立双模型增加算法的可信度,实验如下. ...
Multi-objective optimization for greenhouse light environment using Gaussian mixture model and an improved NSGA-II algorithm
2
2023
... 实验硬件仿真平台使用处理器为12th Gen Intel(R) Core(TM) i7-12700H 2.30 GHz,内存为16.0 GB的计算机,软件平台为Matlab R2020b. 设置种群规模为500,迭代次数为200. 在标准测试函数集上将IMBES与基于网格法的多目标麻雀算法(MOSSA)[22 ] 、多目标鹈鹕算法(MOPOA)[23 ] 、多目标灰狼算法(MOGWO)[24 ] 、基于非支配排序的多目标蜣螂算法(NSDBO)[25 ] 以及NSGA-Ⅱ[26 ] 等主流算法的求解性能进行对比测试.各测试函数具体描述如表1 所示,其中N OF 为目标函数个数. ...
... Main parameter settings of different algorithms
Tab.3 算法 主要参数 MOSSA[22 ] R 2 = 0.8, SD=0.1, PD=0.2MOPOA[23 ] β =1.5, R =2MOGWO[24 ] α =3, β =0.1NSDBO[25 ] p 1 =0.2, p 2 =0.4, p 3 =0.63, k =0.1, b =0.3NSGA-Ⅱ[26 ] 交叉率为0.7, 变异率为0.4, μ =0.02, δ =0.2
建立双模型增加算法的可信度,实验如下. ...
遗传算法的性能分析研究
1
2001
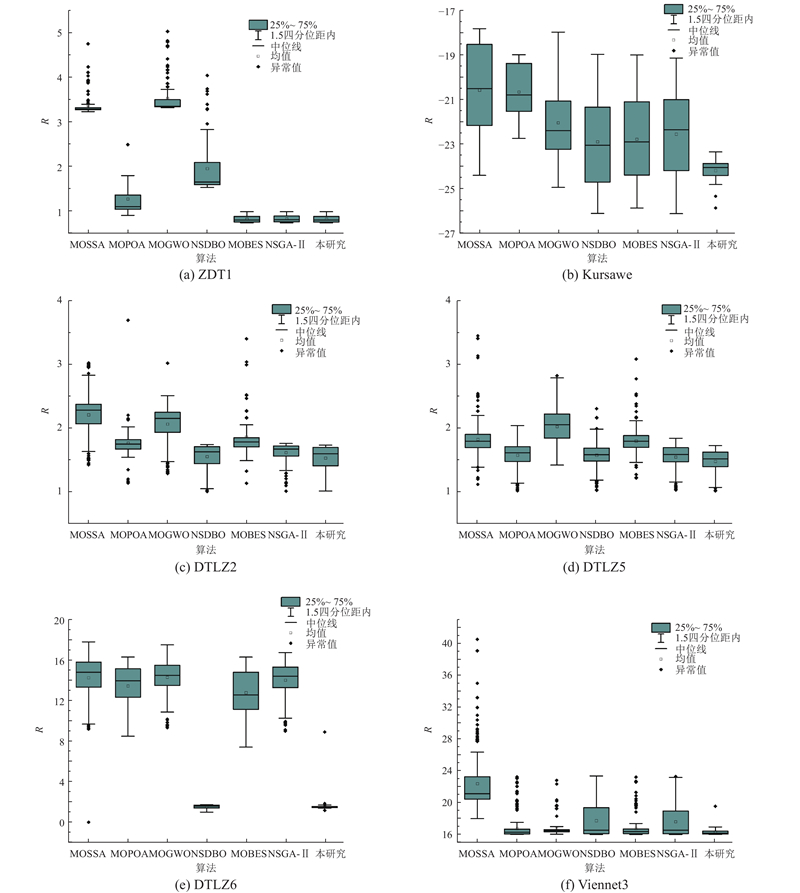
... 测试过程中,各测试函数分别运行30次,得到的pareto前沿箱线图如图7 所示,其中R 为测试结果分布范围. 可以看出,IMBES在解决各种多目标函数方面表现出色. 对于测试函数ZDT1,算法MOSSA、MOGWO和NSDBO都表现出相对较高的中位数,MOPOA在中位性能上处于中等水平. 算法NSGA-Ⅱ、MOBES和IMBES的中位数相对较低,且离散度低,表明性能相对稳定. IMBES具有最低的中位数和最佳性能. 对于Kursawe测试函数,NSGA-Ⅱ表现出总体稳定的性能,离群值较少,中位数属于中等范围. IMBES具有最低的中位数,表现出更强的鲁棒性. 对于三目标函数,所提算法收敛性和覆盖率仍占优;根据没有免费午餐定理(no free lunch, NFL) [27 ] ,不能期望算法在所有测试函数都有最好的表现,因此对于DTLZ6这样较为复杂的不连续多模态测试函数,IMBES未呈现明显优势. 但IMBES整体寻优效果较优,说明IMBES在复杂交错环境中的寻优能力较强;MOBES相较于IMBES在各个测试函数均呈现出显著优势. 6种函数的测试结果证明了所提算法的优越性. ...
遗传算法的性能分析研究
1
2001
... 测试过程中,各测试函数分别运行30次,得到的pareto前沿箱线图如图7 所示,其中R 为测试结果分布范围. 可以看出,IMBES在解决各种多目标函数方面表现出色. 对于测试函数ZDT1,算法MOSSA、MOGWO和NSDBO都表现出相对较高的中位数,MOPOA在中位性能上处于中等水平. 算法NSGA-Ⅱ、MOBES和IMBES的中位数相对较低,且离散度低,表明性能相对稳定. IMBES具有最低的中位数和最佳性能. 对于Kursawe测试函数,NSGA-Ⅱ表现出总体稳定的性能,离群值较少,中位数属于中等范围. IMBES具有最低的中位数,表现出更强的鲁棒性. 对于三目标函数,所提算法收敛性和覆盖率仍占优;根据没有免费午餐定理(no free lunch, NFL) [27 ] ,不能期望算法在所有测试函数都有最好的表现,因此对于DTLZ6这样较为复杂的不连续多模态测试函数,IMBES未呈现明显优势. 但IMBES整体寻优效果较优,说明IMBES在复杂交错环境中的寻优能力较强;MOBES相较于IMBES在各个测试函数均呈现出显著优势. 6种函数的测试结果证明了所提算法的优越性. ...
1
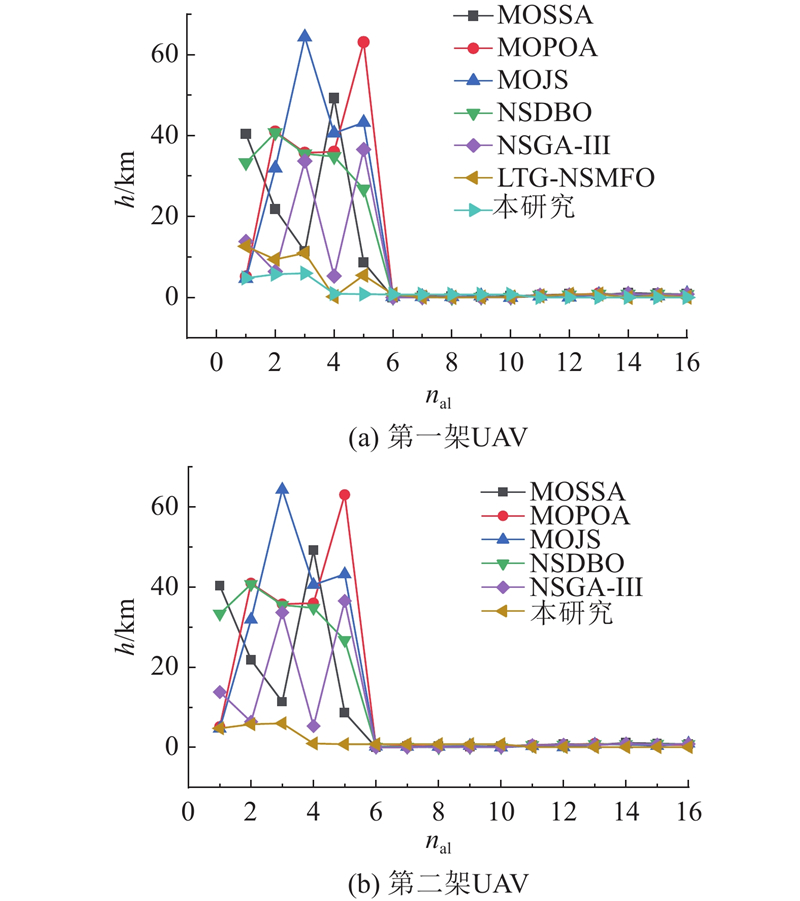
... 模型2:测试场景基于从激光雷达传感器获得的真实数字高程模型(DEM)地图[28 ] . 在此场景下,设置5个威胁. 模型2的多架无人机协同规划轨迹结果如图9 所示. 如表6 所示为每种算法的解质量的比较,度量值表示实验中所有无人机的求和结果,其中c s [29 ] 、多目标水母搜索算法(MOJS)[30 ] 、NSGA-III[31 ] 作为对比算法. 由图可知,所提算法规划了最优路径并获得最优帕累托前沿. 由表6 可知,所提算法在轨迹规划中表现出更高的稳定性以及最优的耗时性能,可以达到最优的规划效果. 与MOSSA、MOPOA、MOJS、NSDBO、NSGA-Ⅲ和LTG-NSMFO相比,所提算法将平均路径长度缩短了1.10~35.80 km,将平均威胁成本降低了0.72~302.49;结果表明,所提算法可以在复杂地形环境中提供可靠、高效的目标规划解决方案. ...
Research on multi-aircrafts cooperative arraying to jam based on multi-objective moth-flame optimization algorithm
1
2022
... 模型2:测试场景基于从激光雷达传感器获得的真实数字高程模型(DEM)地图[28 ] . 在此场景下,设置5个威胁. 模型2的多架无人机协同规划轨迹结果如图9 所示. 如表6 所示为每种算法的解质量的比较,度量值表示实验中所有无人机的求和结果,其中c s [29 ] 、多目标水母搜索算法(MOJS)[30 ] 、NSGA-III[31 ] 作为对比算法. 由图可知,所提算法规划了最优路径并获得最优帕累托前沿. 由表6 可知,所提算法在轨迹规划中表现出更高的稳定性以及最优的耗时性能,可以达到最优的规划效果. 与MOSSA、MOPOA、MOJS、NSDBO、NSGA-Ⅲ和LTG-NSMFO相比,所提算法将平均路径长度缩短了1.10~35.80 km,将平均威胁成本降低了0.72~302.49;结果表明,所提算法可以在复杂地形环境中提供可靠、高效的目标规划解决方案. ...
1
... 模型2:测试场景基于从激光雷达传感器获得的真实数字高程模型(DEM)地图[28 ] . 在此场景下,设置5个威胁. 模型2的多架无人机协同规划轨迹结果如图9 所示. 如表6 所示为每种算法的解质量的比较,度量值表示实验中所有无人机的求和结果,其中c s [29 ] 、多目标水母搜索算法(MOJS)[30 ] 、NSGA-III[31 ] 作为对比算法. 由图可知,所提算法规划了最优路径并获得最优帕累托前沿. 由表6 可知,所提算法在轨迹规划中表现出更高的稳定性以及最优的耗时性能,可以达到最优的规划效果. 与MOSSA、MOPOA、MOJS、NSDBO、NSGA-Ⅲ和LTG-NSMFO相比,所提算法将平均路径长度缩短了1.10~35.80 km,将平均威胁成本降低了0.72~302.49;结果表明,所提算法可以在复杂地形环境中提供可靠、高效的目标规划解决方案. ...
Multi-objective optimization inspired by behavior of jellyfish for solving structural design problems
1
2020
... 模型2:测试场景基于从激光雷达传感器获得的真实数字高程模型(DEM)地图[28 ] . 在此场景下,设置5个威胁. 模型2的多架无人机协同规划轨迹结果如图9 所示. 如表6 所示为每种算法的解质量的比较,度量值表示实验中所有无人机的求和结果,其中c s [29 ] 、多目标水母搜索算法(MOJS)[30 ] 、NSGA-III[31 ] 作为对比算法. 由图可知,所提算法规划了最优路径并获得最优帕累托前沿. 由表6 可知,所提算法在轨迹规划中表现出更高的稳定性以及最优的耗时性能,可以达到最优的规划效果. 与MOSSA、MOPOA、MOJS、NSDBO、NSGA-Ⅲ和LTG-NSMFO相比,所提算法将平均路径长度缩短了1.10~35.80 km,将平均威胁成本降低了0.72~302.49;结果表明,所提算法可以在复杂地形环境中提供可靠、高效的目标规划解决方案. ...