自主运动规划是现阶段智能网联车辆研究领域的核心方向之一. 考虑到无信号交叉口处周围车辆运动不确定性以及缺乏信号引导，为了保证行车安全，智能网联车辆常采取保守型通行策略^[1]. 为了平衡无信号交叉口处通行效率与安全性，须对智能网联车辆运动规划策略进行深入研究^[2]，这对于后续智能网联车辆控制系统的开发具有重要意义^[3].

现有面向交叉口场景的智能网联车辆运动规划方法大致可分为2类：基于规则和基于学习的方法. Waymo、Uber、百度等公司均从可靠性角度采用基于规则的运动规划模型，如智能驾驶模型(intelligent driver model，IDM)^[4]、最优速度模型^[5]. 该类模型仅适用预先定义的规则，缺乏处理高冲突交通场景的动态协商能力，在紧急情况下感知耗时较长可能导致反应时间不足. 近年来机器学习和深度学习算法快速发展，基于学习的运动规划方法逐渐成为热点^[6]，将环境数据直接输入由神经网络组成的运动规划模型，能够适应各种不同的环境和任务，并且无须手动设计运动规划模型. Yang等^[7]提出端到端的车辆运动规划模型，利用Udacity 数据集训练卷积神经网络，预测更新车辆速度和转向角；Thu 等^[8]采用递归神经网络和Transformer网络融合点云与图像数据，通过长短时记忆神经网络(long short term memory，LSTM)生成车辆局部路径. 上述基于深度学习的方法方需要大量数据训练神经网络模型，数据依赖性强且泛化性较差. 强化学习(reinforcement learning，RL)由于无须大量标记训练数据，在自动驾驶领域中广泛应用. Isele 等^[9]用占据栅格表示交叉口区域状态，利用RL运动规划算法计算得到车辆期望加速度，但该方法只适用特定的交叉口拓扑. Gunarathna等^[10]提出基于Q学习的RL方法用于交叉口车辆通行决策，相比基于规则的方法通行时间更短，但未考虑交叉口处车辆交互碰撞风险. 深度强化学习(deep reinforcement learning，DRL)结合RL的表征学习能力和深度学习 (deep learning, DL)的决策能力，使智能体能在更高维度的环境中学习并做出运动决策^[11-13]. Kamran等^[12]等采用深度Q网络(deep Q-network，DQN)进行交叉口车辆实时速度规划，将风险预测纳入奖励函数. 但DQN算法的动作空间离散，不适用于处理连续动作空间，为此部分学者提出采用深度确定性策略梯度(deep deterministic policy gradient，DDPG)算法解决智能车辆连续决策问题^[14-15]. Li等^[16]构建基于DDPG算法的智能汽车纵向运动决策方法，根据无信号交叉口处周围车辆运动状态更新自车加速度，但算法容易受到动作噪声和过估计问题的影响，结果不稳定. 为了提升连续动作空间下DRL算法稳定性，Fujimoto等^[17]提出双延迟深度确定性策略梯度(twin delayed DDPG,TD3)算法，较好地避免了DDPG算法过估计问题. 裴晓飞等^[18]提出构建基于TD3算法的换道决策模型，但仅以车头间距为安全性评价指标，无法准确评估动态交通环境下驾驶行为的安全性.

针对以上分析，考虑到无信号交叉口处智能网联车辆左转运动过程中可能与不同驾驶风格的周围车辆交互，且周围车辆行驶意图多变，本研究首先提出基于TCN-Transformer的周围车辆行驶意图预测模型，接着考虑车辆运动状态、行驶意图及驾驶风格等信息设计状态空间，综合行车安全性、通行效率以及舒适性等因素构建奖励函数，提出基于TD3算法的智能网联车辆运动规划模型，并通过Carla平台搭建仿真场景进行模型有效性验证.

当车辆驶近交叉口时，提前预测周围车辆的行驶意图有助于自车及时做出合理的决策. TCN ^[19]作为结合因果卷积、扩展卷积以及残差连接的网络模型，能够并行处理输入序列，并有效捕捉时序数据的长期依赖关系. 同时，Transformer能利用多头注意力机制和自注意力机制捕捉序列数据的全局特征^[20]. 因此，采用TCN-Transformer网络构建交叉口处周围车辆行驶意图预测模型，通过融合车辆运动状态序列数据中的多模态特征提高预测精度.

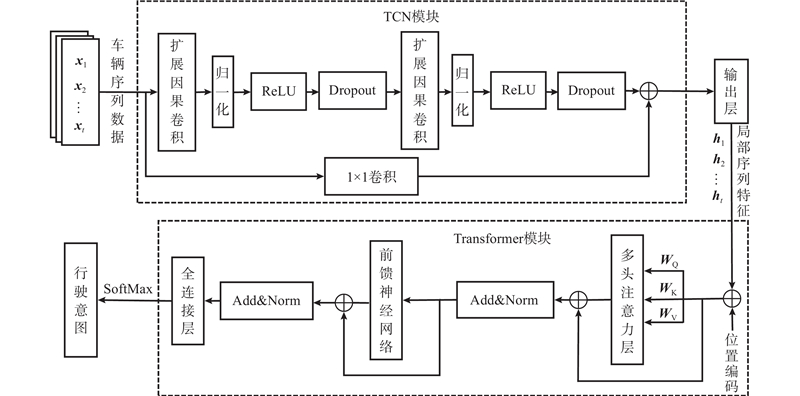
TCN-Transformer网络的整体结构如图1所示. 该网络首先通过TCN模块的多个卷积层和残差块将车辆行驶数据转换为局部特征序列，然后利用Transformer模块的多头注意力层和前馈神经网络将提取的局部特征序列转化为全局特征序列，接着采用全连接层将全局特征序列映射到预测输出空间，最后通过SoftMax函数进行归一化处理得到行驶意图预测结果. 网络输入的驾驶特征序列如下：

(1)$ x = \{ {{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2}, \cdots ,{{\boldsymbol{x}}_{t - 1}},{{\boldsymbol{x}}_t}\}, $

(2)$ {{\boldsymbol{x}}_t} = [ {l_t},{v_{x\_t}},{v_{y\_t}},{a_{x\_t}},{a_{y\_t}},{\varphi _t}]. $

式中：${{\boldsymbol{x}}_t}$表示t时刻输入的驾驶特征，${l_t}$为t时刻目标车辆到交叉口中心的距离，${v_{x\_t}}$、${v_{y\_t}}$分别为t时刻目标车辆横、纵向速度，${a_{x\_t}}$、${a_{y\_t}}$分别为t时刻目标车辆横、纵向加速度，${\varphi _t}$为t时刻目标车辆偏航角.

TCN模块采用残差块替代卷积层，通过2轮扩展因果卷积、归一化、ReLU激活函数和Dropout增强模型对驾驶序列数据的表征学习能力、减少过拟合问题、提高模型的泛化能力，然后通过一维卷积层确保输出特征维度与输入的相同. 其中，扩展因果卷积可保证训练过程不涉及未来时刻数据，同时通过增大卷积核长度和扩张因子增加卷积层的感受野，提高模型对长距离依赖关系的学习能力，具体表达式如下：

(3)$ F\left( {\boldsymbol{x}}_t \right) = \sum \nolimits_{k = 1}^K {w_k} {{\boldsymbol{x}}_{t - {{\phi}}k}}. $

式中：$ {w_k} $表示大小为k的卷积核，$\phi $为扩张因子.

TCN模块输出的局部特征序列如下：

(4)$ {\boldsymbol{h}}_t = R\left( {F\left( {\boldsymbol{x}}_t \right)} \right). $

式中：$ R\text{ } $表示全连接层的非线性激活函数.

Transformer模块主要由自注意力层和前馈神经网络组成，将TCN模块输出的局部特征序列h_t转换为全局特征序列z_t，采用LayerNorm进行数据归一化：

(5)$ {{\boldsymbol{z}}_t = {\text{LayerNorm}}\;\left( {\boldsymbol{h}}_t + {\text{MHA}}\; \left( {{\boldsymbol{h}}_t{{\boldsymbol{W}}_{{\mathrm{Q}}}},{\boldsymbol{h}}_t{{\boldsymbol{W}}_{{\mathrm{K}}}},h_t{{\boldsymbol{W}}_{{\mathrm{V}}}}} \right) + {\text{FFN}}\;\left( {\boldsymbol{h}}_t \right) \right),} $

(6)$ {\text{LayerNorm}}\;\left( {\boldsymbol{x}}_t \right) = \gamma \frac{{{\boldsymbol{x}}_t - {{\boldsymbol{\varsigma}} } }}{\sigma }+{\boldsymbol{\beta}} \text{，} $

(7)$ {\text{FFN}}\;\left( {\boldsymbol{x}}_t \right) = {\text{RELU}}\;\left( {{\boldsymbol{x}}_t{{\boldsymbol{W}}_1}+{{\boldsymbol{b}}_1}} \right){{\boldsymbol{W}}_2}+{{\boldsymbol{b}}_2}. $

式中：$ {\text{MHA}} $为多层自注意力层，$ {{\boldsymbol{W}}_{{\mathrm{Q}}}} $、$ {{\boldsymbol{W}}_{{\mathrm{K}}}} $、$ {{\boldsymbol{W}}_{{\mathrm{V}}}} $分别为查询、键、值的权重矩阵，$\gamma $和${\boldsymbol{\beta}} $分别为可学习的缩放因子和平移因子， ${\text{FFN}}$为前馈神经网络，$ {{\boldsymbol{W}}_1} $、${{\boldsymbol{W}}_2}$为权重矩阵，${{\boldsymbol{b}}_1}$、${{\boldsymbol{b}}_2}$为偏置向量，${\boldsymbol{\varsigma}} $和$\sigma $分别为均值和标准差，RELU为修正线性单元激活函数.

该网络最终通过全连接层和Softmax层获取周围车辆行驶意图预测结果：

(8)$ \hat y = \arg \mathop {\max }\limits_i \;{\text{Softmax}}\;{\left( {{\text{FC}}\left( {\boldsymbol{z}} \right)}_i \right)}\text{，} $

(9)$ {\text{FC}}\left( {\boldsymbol{z}} \right) = {\boldsymbol{z}}{{\boldsymbol{W}}_{{\text{fc}}}}+{{\boldsymbol{b}}_{{\text{fc}}}}\text{，} $

(10)$ \operatorname{Softmax}\;(\mathrm{FC}({\boldsymbol{z}})_i)={\exp\; {\left( {{\mathrm{FC}}\left( {\boldsymbol{z}} \right)}_i \right)}}\Big/{\displaystyle{\sum}_{j=1}^K \exp \;{\left( {{\mathrm{FC}}\left( {\boldsymbol{z}} \right)}_j \right)}} . $

式中：$\hat y$为行驶意图类别；${{\boldsymbol{W}}_{{\text{fc}}}}$和${{\boldsymbol{b}}_{{\text{fc}}}}$分别为全连接层的权重矩阵和偏置向量；K为类别数，取$K = 3$；$ {\text{FC}}{\left( {\boldsymbol{z}} \right)_i} $表示全连接层的第$i$个输出.

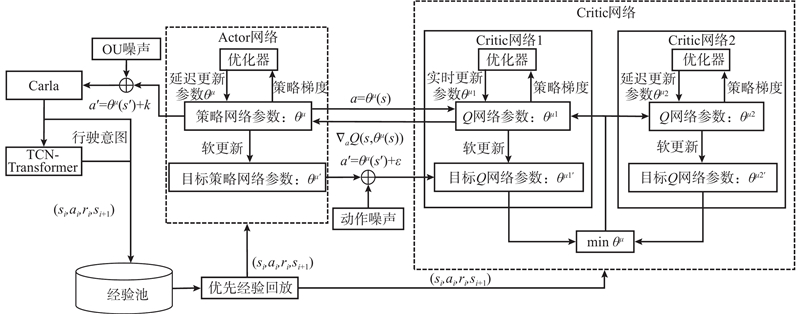
在预测周围车辆在交叉口的行驶意图基础上，采用无模型强化学习TD3算法进行无信号交叉口智能网联车辆左转运动规划，网络结构如图2所示. 强化学习的理论基础是马尔可夫决策（Markov decision process，MDP），因此将车辆左转运动规划转化为MDP最大化预期累积奖励问题，可用四元组<S，A，R，p>进行描述，其中S、A、R、p分别为状态空间、动作空间、奖励函数和状态转移概率. TD3算法在DDPG算法的基础上进行改进，DDPG算法是基于动作评价（Actor-Critic）框架的强化学习算法，包含一个Actor网络和一个Critic网络. Critic网络用于估计状态-动作对的Q值，其目标是最小化Q函数和目标Q函数之间的均方误差，其更新公式如下：

(11)$ y_i=r_i+\gamma_1 Q^{\prime}\left(s_{i+1}, \mu^{\prime}\left(s_{i+1} \big|\theta^{\mu^{\prime}}\right) \big| \theta^{Q^{\prime}}\right) , $

(12)$ L(\theta )\approx \frac{1}{N}{{\displaystyle \sum }}_{i}{\left({y}_{i}-Q\left({s}_{i},{a}_{i}\text{|}{\theta }^{Q}\right)\right)}^{2} \text{，} $

(13)$ {\theta ^{Q'}} \leftarrow \tau {\theta ^Q}+\left( {1 - \tau } \right){\theta ^{Q'}} . $

式中：$\mu^{\prime}\left(s_{i+1} \mid \theta^{\mu^{\prime}}\right) $为目标策略网络的输出，$\theta^{Q^{\prime}} $为目标Critic网络参数，$\theta^{\mu^{\prime}} $为目标Actor网络参数，N为采样的批次大小，$ {y_i} $为目标Q值，$ {r_i} $为当前回报，$ {\gamma _1} $为折扣因子，$ {s_i} $和${a_i}$为状态和动作，$Q'$为目标网络的输出，$Q$为当前网络的输出，$ L(\theta ) $为Critic网络的损失函数，$ {\theta ^Q} $为当前Critic网络参数，$ \tau $为用来平滑更新目标网络的参数.

Actor网络用于学习策略，直接输出动作信号，其目标是最大化Critic网络输出的Q值，其更新公式如下：

(14)$ {\nabla_{\theta^\mu} J \approx \dfrac{1}{N} \displaystyle\sum_i \nabla_{\theta^\mu} Q \left(s, a \mid \theta^{Q}\right) \left\lvert\, \begin{array}{l}s=s_i \\a=\mu\left(s_i \mid \theta^\mu\right) \nabla_{\theta^\mu} \mu\left(s \mid \theta^\mu\right) \mid s_i ,\end{array}\right.}$

(15)$ \theta^{\mu^{\prime}} \leftarrow \tau \theta^\mu+(1-\tau) \theta^{\mu^{\prime}} . $

式中：$J$为Actor性能度量，$\mu(s_i\left| {\mathop \theta \nolimits^\mu } \right.) $为当前策略网络的输出，$ {\theta }^{\mu } $为Actor的网络参数.

DDPG算法容易受到环境噪声的影响，目标网络的更新速度较慢，可能导致Q函数的过度估计. 针对以上问题，TD3算法主要有以下改进：1）通过2个Critic网络计算动作价值，选取两者间的较小值作为估计值，避免出现过度估计的问题；2）对网络进行延迟策略更新，使Critic网络的更新频率高于Actor网络的，降低近似动作值函数的方差；3）采用平滑目标策略，在计算Q函数时加入服从正态分布噪声用于提高算法鲁棒性.

状态空间是对智能网联车辆自身状态和周围环境信息的整体描述，是保证深度强化学习算法有效性的关键. 假设智能网联车辆通过V2V通信获取周围车辆状态信息，通过GPS和CAN总线获取自车状态信息. 在获取周围车辆行驶意图后，利用三阶贝塞尔曲线拟合自车和周围转向车辆的轨迹. 三阶贝塞尔曲线定义如下：

(16)$ \begin{split} B(q) =& {{\boldsymbol{P}}_0}{(1 - q)^3}+3{{\boldsymbol{P}}_1}q{(1 - q)^2}+\\& 3{{\boldsymbol{P}}_2}{q^2}(1 - q)+{q^3}{{\boldsymbol{P}}_3} ;\; {{q}} \in [0,1.0] .\end{split} $

式中：$ {{\boldsymbol{P}}_0} $、$ {{\boldsymbol{P}}_1} $、$ {{\boldsymbol{P}}_2} $、$ {{\boldsymbol{P}}_3} $分别表示不同控制点的坐标，$ q $表示曲线上任一点的位置.

定义冲突点为自车和周围车辆预测路径的交点，将周围第i个车辆的状态信息表示为

(17)$ \begin{split} {{\boldsymbol{s}}}_{{\rm{tar}}\_i}=&\left[{x}_{{\rm{tar}}\_i},\;{y}_{{\rm{tar}}\_i},\;{v}_{{\rm{tar}}\_i},\;{d}_{{\rm{tar}}\_i},\;{\delta }_{{\rm{tar}}\_i},\;{\gamma }_{{\rm{tar}}\_i}\right]^{{\mathrm{T}}};\\ i=& 1,2,\cdots, n.\end{split} $

式中：${{{x}}_{{\rm{tar}}\_i}}$ 、${y_{{\rm{tar}}\_i}}$ 、${v_{{\rm{tar}}\_i}}$、${\delta _{{\rm{tar}}\_i}}$、${\gamma _{{\rm{tar}}\_i}}$分别表示周围第i个车辆的横坐标、纵坐标、行驶速度、驾驶风格以及转向意图，${d_{{\rm{tar}}\_i}}$表示周围第i个车辆与冲突点间的距离.

自车状态信息表示为

(18)$ {{\boldsymbol{s}}}_{\text{ego}}={\left[{v}_{\text{ego}}\text{，}{d}_{\text{ego}}\right]}^{{\mathrm{T}}}. $

式中：${v_{{\text{ego}}}}$表示自车速度，${d_{{\text{ego}}}}$表示自车与冲突点间的距离.

故状态空间表示为

(19)$ {\boldsymbol{s}} = {\left[ {{{\boldsymbol{s}}_{{\text{ego}}}},{{\boldsymbol{s}}_{{\text{tar}}{\_1}}},{{\boldsymbol{s}}_{{\text{tar}}\_2}}, \cdots ,{{\boldsymbol{s}}_{{\text{tar}}\_n}}} \right]^{\text{T}}}. $

动作空间表示智能网联车辆可采取的动作集合. 给定无信号交叉口处智能网联车辆的行驶路径，只研究最优运动策略，因此动作空间定义如下：

(20)$ A \in ({a_{\min }},{a_{\max }}). $

式中：${a_{\min }}$和${a_{\max }}$分别为车辆能采取的加速度最小值和最大值.

1）安全性奖励函数. 为了保证智能网联车辆行驶安全性，在无信号交叉口通行过程中除了避免车辆发生碰撞外，还应使行车风险处于安全水平内. 当碰撞发生时，奖励函数给予极大惩罚；当无碰撞发生时，利用行车风险场理论^[21]计算行车风险水平. 行车风险场是表征环境中人-车-路各要素对驾驶风险影响程度的一种“物理场”，将结合驾驶风格的风险场理论用于构建奖励函数：

(21)$ E_{\mathrm{v}}=\sum_{i=1}^n M_i \lambda \frac{\exp\;\left({-\beta_1 a_i \cos \;\varphi}\right)}{\left|d_i^{\prime}\right|} \times \frac{d_i^{\prime}}{\left|d_i^{\prime}\right|}, $

(22)$ d_i^{\prime}=\delta_i \left\{{\left[\left(x^{\prime}_i-x_0\right) \xi / \exp\; ({\alpha v_i})\right]^2+\left[\left(y^{\prime}_i-y_0\right) \xi\right]^2}\right\}^{1/2},$

(23)$ \left[\begin{array}{l}x_i^{\prime} \\y_i^{\prime}\end{array}\right]=\left[\begin{array}{rr}\cos \;\psi_i & \sin\; \psi_i \\-\sin\; \psi_i & \cos \;\psi_i\end{array}\right]\left[\begin{array}{l}x_i \\y_i\end{array}\right], $

(24)$ {M_i} = {m_i} \left( {1.566 \times {{10}^{ - 14}} \times {v_i^{6.687}}+0.334\;5} \right). $

式中：E_v为当前行车风险场强，M_i为周围第i辆车的等效质量，$d'_i $为周围第i辆车的等效距离，φ为周围任意点和目标车辆质心的连线与车辆运动方向的夹角，n为周围车辆数量，a_i为周围第i辆车的加速度，$\xi $为安全距离的临界阈值，$\delta_i $为周围第i辆车驾驶风格的影响系数，α为与速度相关的参数，$\varPsi_i $为周围第i辆车的航向角，(x₀, y₀)为自车坐标，(x_i, y_i)为第i辆车的坐标，$(x'_i,y'_i) $为第i辆车沿航向角旋转后的坐标，m_i为周围第i辆车的质量，v_i为周围第i辆车的速度，λ、β₁为待定系数.

设定行车风险安全阈值为${E_{\text{t}}}$，对行车风险大于${E_{\text{t}}}$的值给予惩罚. 安全性奖励函数${R_{\text{s}}}$定义如下：

(25)$\mathop R\nolimits_{\rm{s}}= \left\{ {\begin{array}{*{20}{c}}{ - {{\mathop E\nolimits_{\rm{v}} }}/{{\mathop E\nolimits_{\rm{t}} }}},&{\mathop E\nolimits_{\rm{v}} < \mathop E\nolimits_{\rm{t}} };\\0, &{\mathop E\nolimits_{\rm{v}} \geqslant \mathop E\nolimits_{\rm{t}} }.\end{array}} \right. $

2）效率奖励函数. 为了提高无信号交叉口处智能网联车辆通行效率，定义速度奖励项${R_{{{{\mathrm{e}}\_{\mathrm{v}}}}}}$，使智能网联车辆在安全条件下尽可能按道路限定的最大速度行驶. 定义距离奖励项${R_{{{{\mathrm{e}}\_{\mathrm{d}}}}}}$，行驶距离越长，奖励越多. 效率奖励函数${R_{\text{e}}}$表达式如下：

(26)$ {R_{{{{\mathrm{e}}\_{\mathrm{v}}}}}} = {{{v_{{\text{ego}}}}}}/{{{v_{{\text{max}}}}}}, $

(27)$ {R}_{{{\mathrm{e}}\_{\mathrm{d}}}}={l}/{{l}_{0}}, $

(28)$ {R_{\text{e}}} = {R_{{{{\mathrm{e}}\_{\mathrm{v}}}}}}+{R_{{{{\mathrm{e}}\_{\mathrm{d}}}}}}. $

式中：$l$为车辆沿路径行驶的距离，${l_0}$为路径总长度，${v_{{\text{max}}}}$为道路最大限速.

3）舒适性奖励函数. 车辆频繁急加速或急减速会给乘客带来较大的惯性冲击，影响乘坐舒适性，因此定义舒适性奖励函数如下：

(29)$ R_{\mathrm{c}} = \left\{\begin{array}{lc}- \eta\left(a-a_{\mathrm{e}}\right)^2- \gamma_2\left(j- j_{\mathrm{e}}\right)^2, & a>a_{\mathrm{e}} \text { 或 } j>j_{\mathrm{e}} ; \\0, & \text { 其他 }.\end{array}\right. $

式中：a、j分别为自车的加速度、冲击度，${a_{\text{e}}}$为期望加速度，${j_{\text{e}}}$为期望冲击度，$ \eta $和$ {\gamma _2} $为权重系数.

综合考虑安全性、通行效率以及舒适性要求构建总奖励函数：

(30)$ R_{\mathrm{d}}=\left\{\begin{array}{lc}100, & \text { 成功通行 }; \\-200, & \text { 碰撞 }.\end{array}\right. $

(31)$ {R_{{\text{total}}}} = {\omega _1}{R_{\mathrm{s}}}+{\omega _2}{R_{\mathrm{e}}}+{\omega _3}{R_{\mathrm{c}}}+{R_{\mathrm{d}}}. $

式中：${\omega _1}$、${\omega _2}$、${\omega _3}$分别为对应奖励函数的权重系数，经多次测试，设定${\omega _1}$、${\omega _2}$、${\omega _3}$分别为10、9、7. 权重系数过大会导致算法无法收敛，过小会影响算法对最优通行策略的学习.

实验硬件配置为Intel(R) Core(TM) i5-12400F，基础频率为2.50 GHz，GPU使用NVIDIA GeForce RTX 3060 Ti，显存为8 G. 软件运行环境为Ubuntu20.04操作系统，使用Python3.7版本，Pytorch 1.13.1框架.

采用德国IND数据集中2个无信号交叉口实际驾驶轨迹数据进行周围车辆行驶意图预测算法训练及测试，交叉口场景如图3所示，数据采样频率为25 Hz，筛选得到左转、直行、右转各800条车辆轨迹数据，其中80%作为训练集，20%作为测试集. 基于TCN-Transformer的周围车辆行驶意图预测算法具体参数设置如下：TCN模块由3个卷积层组成，每个卷积层的卷积核大小为3，扩张因子设置为1；Transformer模块中multi-head为8，隐藏层大小为512，每个多头自注意力机制和全连接层后面都采用LayerNorm进行归一化处理，利用Dropout正则化以防止过拟合，损失函数选择交叉熵代价函数；整个算法学习率为0.001，优化器选用Adam，训练批次大小为16，训练轮次设为30.

为了验证所提TCN-Transformer算法的周围车辆意图预测性能，将所提算法与CNN-Transformer算法、LSTM算法进行对比测试，并统计车辆到达停止线时3种算法的意图预测准确率，结果如表1所示. 表中，${p_{\text{v}}}$表示车辆意图预测准确率，FPS表示每秒运行的帧数，${P_{\text{m}}}$表示模型参数量. 准确率指正确预测的样本数占总样本数的比例. 可以看出，TCN-Transformer算法的周围车辆意图预测准确率为97.3%，相较于CNN-Transformer和LSTM算法分别提升9.8%和6.2%，尤其是周围车辆转弯意图预测准确率有显著提升，这是因为TCN采用因果卷积和残差连接的结构设计可以有效捕捉时间序列中的依赖关系，提高预测准确率. 尽管TCN-Transformer模型参数量高于其他2种算法的，但经测算该模型推理速度为250帧/s，满足实时性要求.

为了进一步分析所提TCN-Transformer算法提前预测交叉口处周围车辆行驶意图的能力，将周围车辆所在车道的停止线作为参考位置，选取车辆到达停止线前20 m至通过停止线后5 m区域作为被测路段对算法进行测试，并与LSTM算法进行对比，结果如图4所示. 图中， f为频率， F为累积频率. 可以看出，2种算法对直行车辆都有较好的意图预测能力；所提算法在−7.5 m处能对超过73%的转向车辆进行准确的意图预测，但该处LSTM算法准确预测的累积频率仅为20%，在−2.5 m处所提算法的累积频率比LSTM算法的累积频率高19%. 这说明相比于LSTM算法，所提TCN-Transformer算法对转向意图有更早的预测能力且预测准确率更高，原因在于所提算法通过采用更大感受视野的卷积核、多层卷积和自注意力机制等方式处理车辆序列数据的长期依赖关系和局部特征关系，能够更为有效地捕捉转向特征.

为了验证所提算法的有效性，选用Carla驾驶模拟器Town03场景库中双向四车道交叉口场景进行算法训练和验证. 实验设定每条车道宽为3.75 m，限速为17 m/s，车辆加速度区间为 [−4, 4] m/s². 为了使仿真场景更具拟人化效果，区别于已有建模方法^[22-23]常将周围车辆设定成固定运动模式的方法，采用考虑风格的智能驾驶员模型作为周围车辆纵向运动控制算法，模型可以表示为

(32)$ {a_i} = A\left[ {1 - {{\left( {\frac{{v\left( t \right)}}{{{v_0}}}} \right)}^\delta } - {{\left( {\frac{{\bar s\left( t\right)}}{{s\left( t \right)}}} \right)}^2}} \right], $

(33)$ \bar s\left( t \right) = {s_0}+{v_0}{\sigma _t}+\frac{{v\left( t \right)}}{{2{\theta _1}}} - \frac{{{v_1}\left( t \right)}}{{2{\theta _2}}}. $

式中：$A$为车辆最大加速度，$v\left( t \right)$为车辆当前速度，${v_0}$为期望车速，$\delta $为加速度指数，$s\left( t \right)$为车辆和前车的距离，$\bar s\left( t \right)$为期望车距，$ {s_0} $为相关参数，$ {\sigma _t} $为驾驶人反应时间，${\theta _1}$为驾驶人在紧急情况下所预期的自车最大制动减速度，${\theta _2}$为驾驶人所预期的前车最大减速度，${v_1}\left( t \right)$为前车速度.

通过调整IDM算法中${v_0}$、${\theta _1}$和${\theta _2}$等参数，构建保守型、普通型、激进型3类驾驶风格的驾驶员模型，在3个模型中，${v_0}$依次设置为7.0、10.0、12.5 m/s，${\theta _1}$依次设置为3、4、5 m/s²，${\theta _2}$依次设置为5、4、3 m/s². 训练场景如图5所示. 图中，白色车辆为智能网联车辆，黑色车辆为周围车辆，带箭头的虚线和实线分别为智能网联车辆和周围车辆路径. 在每个回合开始时，智能网联车辆和周围车辆分别在路径的起点生成，其中智能网联车辆和周围车辆转向路径由三阶贝塞尔曲线生成. 为了保证交通流随机性，在周围车辆生成时随机设定其驾驶风格和行驶方向，并在 [6, 12] m/s区间内任意设定初始速度，在[1.5，3.5] s任意设定车辆生成时间. 测试场景在训练场景基础上增加交通流密度，在[1.0，2.0] s随机设定车辆生成时间，TD3算法的超参数设置如表2所示.

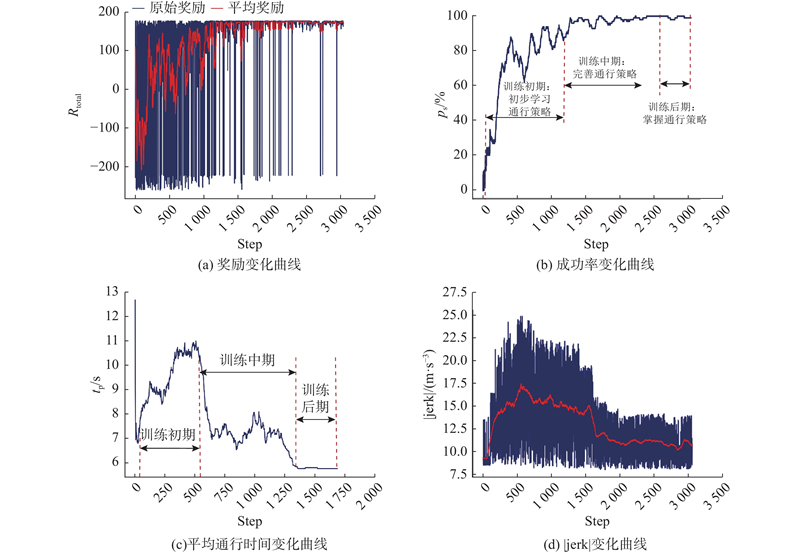
为了初步验证基于TCN-Transformer-TD3算法的智能网联车辆左转运动规划方法性能，共训练3000个回合，采用奖励、成功率、平均通行时间和加加速度绝对值（|jerk|）评估所提算法的收敛水平与学习效果. 须注意的是，这里的成功率指包括当前训练回合在内的100个训练回合的成功率；平均通行时间指训练过程中最近的100个成功通行回合的平均通行时间；加加速度绝对值是衡量舒适度的常用指标，值越小表明舒适性越好. 训练结果如图6所示. 图中，P_s为通行成功率，t_p为平均通行时间. 可以看出，前1200个训练回合的平均奖励、成功率和加加速度绝对值变化曲线均呈上升趋势，且震荡幅度较大，这些训练回合中包含550个成功回合，对应的平均通行时间曲线快速上升. 此阶段曲线变化趋势说明智能网联车辆为了获取奖励开始学习避撞策略，导致通行时间和成功率逐渐增加，此时通行策略学习并不完整，导致舒适性较差，此阶段定义为训练初期. 在第1200~2550个训练回合，奖励和成功率曲线震荡幅度减小，舒适性曲线呈下降趋势，这些训练回合中包含753个成功回合，对应的平均通行时间曲线出现小幅震荡. 这是由于此时智能网联车辆已经掌握避撞策略，为了获得更高的回合奖励开始逐渐学习如何在不发生碰撞的情况下快速且舒适地到达目的地，此阶段定义为训练中期. 在第2550~3000个回合，奖励和成功率曲线收敛至最高水平，加加速度绝对值保持在舒适性要求范围内（|jerk|<17.64 m/s³），包含的437个成功回合所对应的平均通行时间曲线也均收敛并稳定，表明此时智能网联车辆已经学会如何避免碰撞并能快速且舒适地到达目的地，此阶段定义为训练后期.

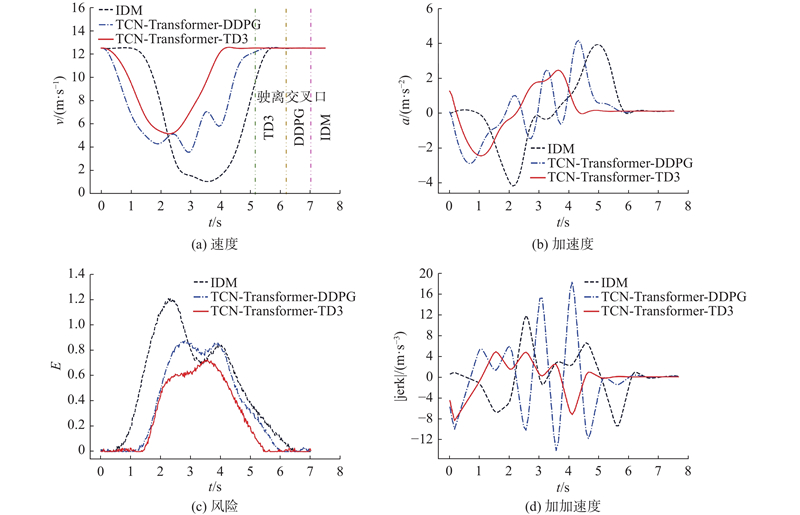
1）定性分析. 为了验证本研究所提算法在安全性、通行效率以及舒适性方面的优势，将所提算法与IDM、TCN-Transformer-DDPG进行对比，其中TCN-Transformer-DDPG与所提算法的状态空间、动作空间和奖励函数均相同. 在测试场景中为周围车辆设置相同的初始速度和驾驶风格 ，生成的运动规划结果如图7所示. 图中，3种曲线分别代表3种算法的规划结果. 可以看出，在早期进入无信号交叉口阶段，采用所提算法和TCN-Transformer-DDPG算法时智能网联车辆均选择提前减速驶近交叉口，而IDM算法此时未选择减速策略，导致行车风险迅速升至高风险状态；在与周围车辆交互阶段，所提算法选择在交叉口处低速通行，当风险值升高时实时调整自车速度平稳通过交叉口，而TCN-Transformer-DDPG算法在风险值升高时出现频繁加减速现象，使得舒适性变差， IDM在高风险状态时选择减速停车让行策略，导致通行时间最长.

在整个通行过程中，所提算法所用通行时间最短，并且加速度变化更为平稳，风险值和加加速度值始终处于安全奖励和舒适性的要求范围之内且均低于2种对比算法，说明所提算法在通行效率、安全性和舒适性方面均优于其他2种算法的.

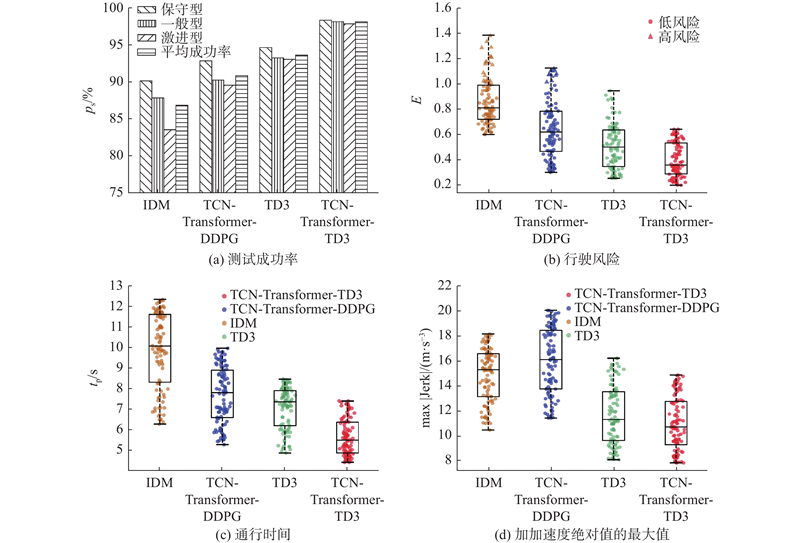
2）定量分析. 为了进一步量化分析所提算法性能，在测试场景中对IDM、TCN-Transformer-DDPG 、TD3和所提TCN-Transformer-TD3算法分别进行100个回合的测试，随机设定周围车辆驾驶风格，采用成功率、通行时间、行驶风险最大值以及加加速度绝对值的最大值作为评估指标，测试结果如图8所示. 可以看出：所提算法成功率受周围车辆驾驶风格影响最小，且平均成功率比其他3种算法分别高11%、8%和5%，说明所提算法对不同驾驶风格周围车辆的适应能力更强；所提算法和TD3算法得到的最大风险值位于安全性奖励要求范围内，没有出现风险值大于1的高风险工况，但其他2种算法均多次出现高风险工况；所提算法得到的交叉口通行时间分布区间范围明显小于其他3种算法的；所提算法的加加速度最大值的绝对值的区间范围小于其他3种算法的，且满足驾驶舒适性要求，值越小则舒适性越好. 也就是说，本研究所提算法的安全性、行驶效率以及舒适性均优于其他2种算法的. 原因在于IDM算法主要通过一些固定的规则和先验知识来生成驾驶策略，未考虑环境动态变化的不确定性，无法根据交叉口交通流交互产生的潜在碰撞风险实时动态调整通行策略，导致行驶效率和安全性较差；DDPG算法采用单个目标网络评估策略性能，使得目标网络参数更新慢同时对部分动作价值估值过高，车辆在交叉口处极可能出现不必要的加减速之类的危险行为；不带意图预测模块的TD3算法无法准确判断冲突点，容易产生非最优的车辆通行策略；所提算法根据实时预测得到的周围车辆行驶意图与运动参数信息及时调整通行策略，通过目标策略平滑化和延迟策略更新解决DDPG算法估值过高的问题，从而选择出更优动作，有效降低行驶风险水平并提升决策合理性和驾驶舒适性.

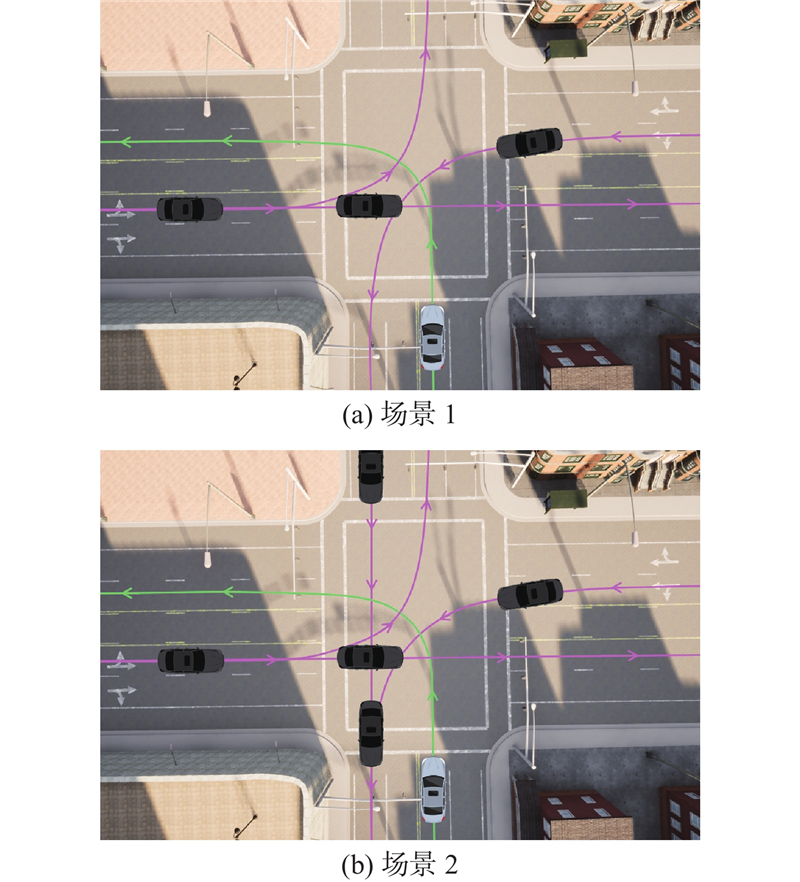
3）场景适应性验证. 为了分析所提TCN-Transformer-TD3运动规划算法对复杂场景的适应能力，设计2种不同场景将所提算法与IDM算法、不考虑意图预测的TD3算法、TCN-Transformer-DDPG算法以及LSTM-TD3算法进行对比. 场景1在原测试场景基础上加入自东向南左转交通流，每小时车流量约为2700；场景2基于场景1进一步加入自北向南直行交通流，每小时车流量约为3 600，如图9所示. 如表3所示为测试结果. 可以看出，2种场景下IDM算法的成功率分别为67.4%和59.4%，远低于其他3种算法的，这是因为IDM算法性能高度依赖于设计者的先验知识和规则，无法应对复杂多变的交通环境；不考虑意图预测的TD3算法无法判断周围车辆与自车的冲突点位置，使得复杂环境下算法运行成功率较低；TCN-Transformer-DDPG算法在场景1中成功率为89.4%，但在场景2中表现较差，可能是由于DDPG算法依赖价值函数更新策略，对稀疏奖励不敏感，容易受到超参数影响，导致无法及时响应更密集的交通流变化；LSTM-TD3算法在2种场景下的成功率均低于所提算法的，原因是LSTM算法准确识别周围车辆行驶意图的时刻较晚，导致无法提前准确判断冲突点位置；所提算法的通行时间最短且成功率最高，2种场景下成功率均大于92.1%，原因在于所提算法能够根据较早预测到的周围车辆驾驶意图与运动参数信息实时动态调整通行策略，并利用2个Q网络减小估计偏差，通过延迟策略更新有效提高算法泛化能力，使得能对密集交通流环境变化做出及时响应. 因此，相较于其他算法，所提算法能更好地适应多个方向的车流交互场景，生成更优的通行策略.

所提算法能够在周围车辆到达无信号交叉口停止线前准确识别其行驶意图，对直行、右转、左转的意图识别准确率分别为98.1%、96.3%、97.5%. 相比其他算法，通过考虑行车风险、周围车辆转向意图和驾驶风格等信息生成的交叉口最优通行策略所用通行时间最短，整个过程中加速度变化平稳，风险值和加加速度值始终处于安全奖励和舒适性的要求范围之内，能够满足安全性、通行效率和舒适性要求，且对不同车流方向和交通流密度的交叉口交互场景均有良好的适应能力. 该算法目前仅考虑了车间交互影响，今后研究中将进一步探索如何将包括行人和非机动车在内的运动障碍物的影响纳入到通行策略中，以提高智能网联车辆在复杂城市交通环境中的决策能力.