常规交叉口因左转和直行相互冲突,导致每一相位仅可使用部分进口车道,并没有充分利用交叉口道路通行资源. 为此,学者们从时间分离、空间分离的角度出发,对交叉口的几何设计进行优化改造,提出钩形转弯[1]、U型回转[2]、借道左转[3]、排阵式交叉口[4]、移位左转[5]等新型交通组织模式. 移位左转在国外应用已较普遍[6],国内已应用在深圳市彩田路-福华路、红荔路-华富路[7]交叉口. 连续流交叉口和平行流交叉口皆属于移位左转设计,能够将交叉口信号相位数减少至2个,理论上相对于常规交叉口能够提升1倍左右的容量[8],是当前研究的热点方向. Dhatrak等[9-10]的研究表明,在大部分交通场景下,两者的通行能力与车均延误相差不大,然而由于两者的运行规则存在一定区别,在部分特殊场景中各有优势.
采用移位左转设计,须在路段上设置预信号交叉口,一般要求相邻交叉口间距大于300 m,且移位左转设计对道路几何条件的要求较高,可能存在交叉口部分方向无法满足的情况. 探讨不同设置方案下平行流交叉口的运行性能,以防止在交叉口某方向几何条件受限的情况下,选择其他方向进行移位左转改造,降低通行效率. 连续流交叉口理论的研究较成熟,已有学者针对十字交叉口4个方向全设置[17]、对称双向设置[18]、非对称双向设置[19]及相邻交叉口简化设置[20]等多种方案进行探讨. 平行流交叉口的研究主要集中在4个方向全设置移位左转车道的十字交叉口,仅少数研究涉及了对称双向设置方案[15],故须开展平行流交叉口其他设置方案的研究.
本研究基于车道控制的方法[21],将单向、非对称双向、对称双向、三向、四向设置及常规交叉口整合到优化模型中,同时优化设置方案选择、车道分配和信号配时,攻克了移位左转设计中交通需求与通行能力匹配灵活度不高的难题,解决了交叉口移位左转的不合理改造可能导致通行效率降低的问题.
1. 交通特性分析
1.1. 几何设计
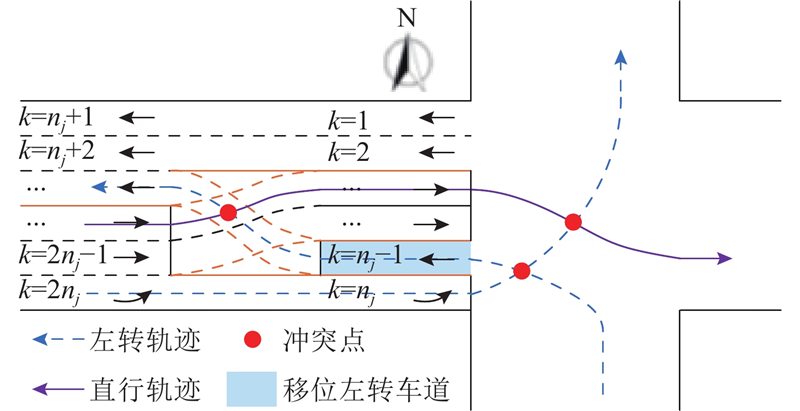
平行流交叉口某方向若采用移位左转设计,几何设计如图1所示. 在该方向路段上设置预信号交叉口,将左转车道置于直行车道右侧,部分出口车道设置在直行车道和左转车道之间,称为移位左转车道(displaced left-turn, DLT). 南向左转车流在主信号交叉口处驶入移位左转车道,避免与西向直行车流相互冲突,从而将主信号交叉口处本方向直行与相交方向左转冲突(例如图1中的西直行与南左转)转移至预信号交叉口处,即在主信号交叉口处上述2股车流不再冲突,实现主信号交叉口能够同时放行本方向直行车流和相交方向左转车流,提升了交叉口通行能力. 平行流交叉口根据移位左转车道设置方向,可以分为单向、非对称双向、对称双向、三向、四向设置方案.
图 1
图 1 平行流交叉口几何设计及车流组织的示意图
Fig.1 Diagram of geometric design and traffic flow organization at parallel flow intersection
图1中,
1.2. 交通冲突分析
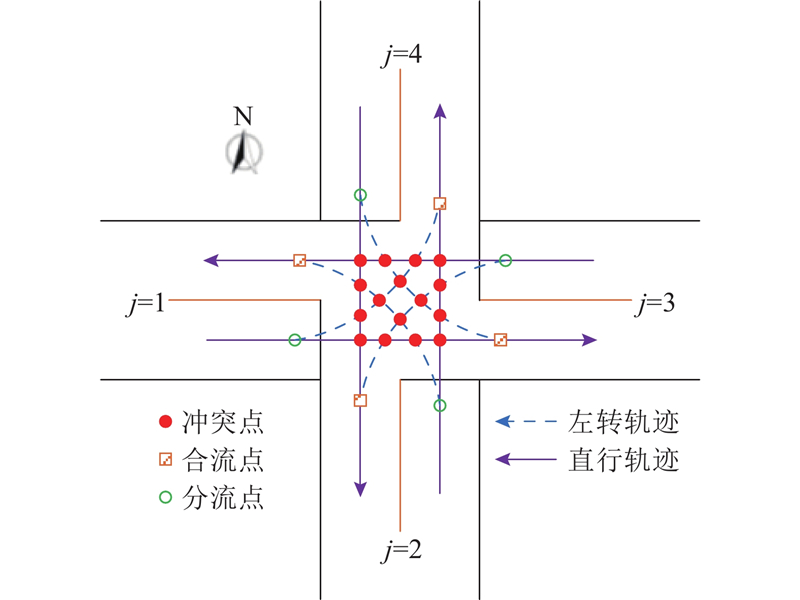
如图2所示,常规交叉口左转和直行包含4个分流点、4个合流点和16个冲突点,冲突点表示2股车流不可同时放行. 对于左转和直行之间的4个分流点,若进口车道不设置左转和直行合用车道,则可同时放行. 为了避免左转和直行合流冲突,在常规交叉口中2股合流车流一般不同时放行. 常规交叉口中影响信号相位方案设计的冲突包括16个冲突点和4个合流点,交通冲突矩阵如下:
图 2
图 2 常规交叉口各流向的交通冲突示意图
Fig.2 Diagram of traffic conflict for each flow direction at conventional intersection
式中:
若交叉口方向
式中:
平行流交叉口的交通冲突矩阵如下:
式中:
2. 模型构建
2.1. 目标函数
以交叉口储备通行能力最大化作为第1级优化目标,在各流向交通需求比例保持不变的假设下,最大化储备通行能力即最大化交叉口共用流量系数
式中:
2.2. 约束条件
2.2.1. 车道划分约束
构建如下约束集,将车道集
式中:
每条车道至少允许1股车流使用,见式(5). 每股车流行驶车道数至少有1条,见式(6). 各流向在主信号交叉口处接近车道数不大于接收车道数,见式(7)、(8). 在车道集
构建如下约束集,将车道集
常规设计在车道集
2.2.2. 信号控制约束
为了便于后续模型的构建,绿灯启亮时刻和绿灯持续时长用一个周期内的相对比例表示,周期时长、绿灯启亮时刻和绿灯持续时长应在合理的范围内,存在最小值、最大值约束.
式中:
为了保证模型生成的主信号相位相序方案可行,2股冲突车流的放行相位不可以重叠,即存在如下约束,以分配各流向放行先后顺序和绿灯持续时长.
式中:
由于式(25)~(27)仅须在2股车流存在冲突时满足,考虑到
预信号相位配时约束构建如下.
式中:
在常规设计和移位左转设计中,左转驶入和直行驶出均不受预信号控制,令上述2股车流绿灯启亮时刻为0,绿灯持续时长为1,见式(31)、(32). 在常规设计中,直行驶入和左转驶出不受预信号控制,存在式(33)、(34)的约束. 在移位左转设计中,直行驶入和左转驶出受预信号控制,在预信号交叉口处存在冲突,不可以同时放行,相位关系见式(35)、(36).
各车道控制信号方案应与相应的主预信号相位相序相同,如下.
式中:
2.2.3. 最大带宽约束
图 3
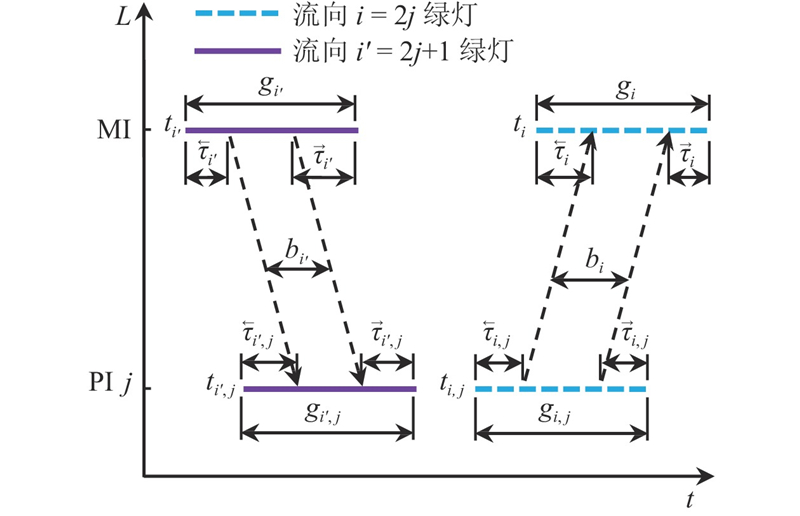
图 3 移位左转设计主预信号绿波带示意图
Fig.3 Preliminary signal green wave diagram for displaced left-turn
最大带宽约束构建如下.
式中:
式(43)为加权平均带宽计算公式. 式(44)~(46)限制相关变量的取值范围. 式(47)、(48)限制绿波带宽与绿灯持续时长的关系. 式(49)~(52)限制前、后2个信号灯处绿波带边缘的关系.
2.2.4. 流量分配约束
构建如下约束集,将各流向流量分配给各条车道.
式中:
交叉口共用流量系数不大于各流向流量系数,见式(53). 某车道只有允许某流向车辆使用,其相应流向流量才可能大于0,见式(54). 各流向在各车道上的流量之和等于该流向总流量,见式(55). 加权平均流量系数计算公式见式(56). 具有相同车道标记的一组相邻车道流量相同,见式(57). 各车道交通流量不大于通行能力,见式(58)、(59). 在移位左转设计中,左转和直行在所遇第1个信号灯处的通行能力不大于所遇第2个信号灯处,见式(60)、(61).
2.2.5. 排队长度约束
构建如下约束集,以避免车辆排队溢出破坏交叉口稳定运行的状态.
式中:
在移位左转设计中,左转和直行在所遇的第2个信号灯处都可能存在二次停车,为了避免车辆排队溢出,增加排队长度约束,见式(62)~(65). 各流向车辆二次停车形成的排队与前后2个信号灯协调效果及第1个信号灯排队消散时刻密切相关,故各流向车辆只需满足式(62)~(65)中的1个排队长度约束公式,利用排队长度约束选择0-1变量
2.3. 模型讨论
将式(4)作为目标条件,式(1)~(3)、(5)~(24)、(28)~(65)作为约束条件,将设置方案、车道标记和信号配时整合到统一的优化模型中,决策变量包括
3. 案例分析
表 1 算例中优化模型输入参数及取值
Tab.1
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | ||
| 106 | 103 | 1 | |||||
| 10 | 4 | 106 | |||||
| 60 | 120 | 7 | |||||
| 10 | 100 | 1 500 | |||||
| 10 | 30 | — | — |
图 4
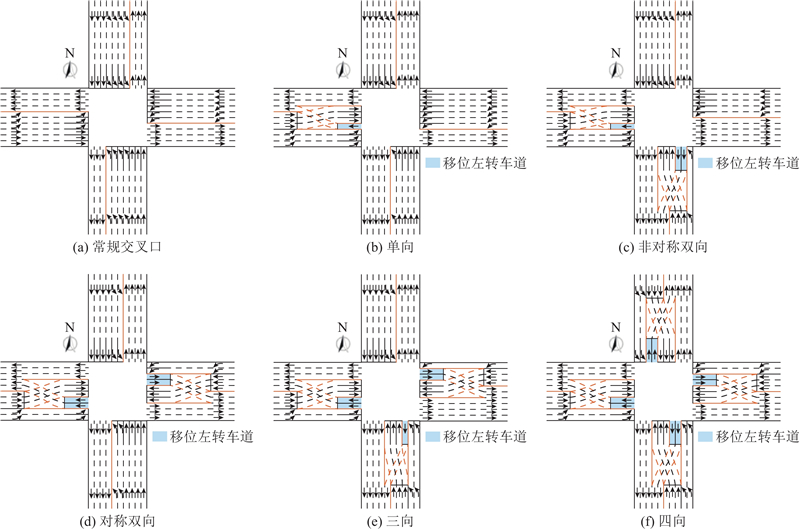
图 4 各方案的交叉口几何设计优化结果
Fig.4 Intersection geometric design optimization result for scheme
表 2 各方案的交叉口信号配时优化结果
Tab.2
| 设置方案 | 主信号 | 西预信号 | 南预信号 | 东预信号 | 北预信号 | C | ||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | |||||||
| 常规交叉口 | 启亮时刻 | 58 | 80 | 0 | 18 | 58 | 80 | 0 | 18 | — | — | — | — | — | — | — | — | 120 | ||||
| 绿灯时长 | 18 | 36 | 14 | 36 | 18 | 36 | 14 | 36 | — | — | — | — | — | — | — | — | ||||||
| 结束时刻 | 80 | 0 | 18 | 58 | 80 | 0 | 18 | 58 | — | — | — | — | — | — | — | — | ||||||
| 单向 | 启亮时刻 | 0 | 22 | 22 | 89 | 0 | 22 | 67 | 80 | 108 | 50 | — | — | — | — | — | — | 120 | ||||
| 绿灯时长 | 18 | 41 | 54 | 27 | 18 | 41 | 18 | 36 | 58 | 54 | — | — | — | — | — | — | ||||||
| 结束时刻 | 22 | 67 | 80 | 0 | 22 | 67 | 89 | 0 | 50 | 108 | — | — | — | — | — | — | ||||||
| 非对称双向 | 启亮时刻 | 0 | 22 | 22 | 80 | 80 | 22 | 62 | 80 | 104 | 46 | 29 | 103 | — | — | — | — | 120 | ||||
| 绿灯时长 | 18 | 36 | 54 | 36 | 58 | 36 | 14 | 36 | 58 | 54 | 70 | 42 | — | — | — | — | ||||||
| 结束时刻 | 22 | 62 | 80 | 0 | 22 | 62 | 80 | 0 | 46 | 104 | 103 | 29 | — | — | — | — | ||||||
| 对称双向 | 启亮时刻 | 53 | 90 | 90 | 17 | 53 | 90 | 90 | 17 | 39 | 0 | — | — | 39 | 0 | — | — | 120 | ||||
| 绿灯时长 | 33 | 43 | 43 | 32 | 33 | 43 | 43 | 32 | 77 | 35 | — | — | 77 | 35 | — | — | ||||||
| 结束时刻 | 90 | 17 | 17 | 53 | 90 | 17 | 17 | 53 | 0 | 39 | — | — | 0 | 39 | — | — | ||||||
| 三向 | 启亮时刻 | 0 | 34 | 34 | 77 | 77 | 34 | 34 | 77 | 102 | 60 | 46 | 103 | 102 | 60 | — | — | 120 | ||||
| 绿灯时长 | 30 | 39 | 39 | 39 | 73 | 39 | 39 | 39 | 74 | 38 | 53 | 59 | 74 | 38 | — | — | ||||||
| 结束时刻 | 34 | 77 | 77 | 0 | 34 | 77 | 77 | 0 | 60 | 102 | 103 | 46 | 60 | 102 | — | — | ||||||
| 四向 | 启亮时刻 | 60 | 0 | 0 | 60 | 60 | 0 | 0 | 60 | 89 | 43 | 29 | 103 | 89 | 43 | 29 | 103 | 120 | ||||
| 绿灯时长 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 70 | 42 | 70 | 42 | 70 | 42 | 70 | 42 | ||||||
| 结束时刻 | 0 | 60 | 60 | 0 | 0 | 60 | 60 | 0 | 43 | 89 | 103 | 29 | 43 | 89 | 103 | 29 | ||||||
表 3 各方案的交叉口评价指标的对比结果
Tab.3
| 设置方案 | 常规设计可展宽 | 常规设计不可展宽 | 常规设计可展宽 | ||||||||
| 常规交叉口 | 1.130 | — | 29.39 | 0.929 | — | 27.24 | 7 192 | 43.24 | — | ||
| 单向 | 1.125 | −0.48 | 32.32 | 1.000 | 7.69 | 31.23 | 7 194 | 43.99 | 1.73 | ||
| 非对称双向 | 1.125 | −0.48 | 34.29 | 1.083 | 16.67 | 32.12 | 7 198 | 41.07 | −5.02 | ||
| 对称双向 | 1.350 | 19.42 | 35.73 | 1.286 | 38.46 | 38.56 | 7 191 | 37.13 | −14.13 | ||
| 三向 | 1.227 | 8.57 | 38.68 | 1.227 | 32.17 | 36.97 | 7 200 | 35.95 | −16.86 | ||
| 四向 | 1.750 | 54.81 | 47.60 | 1.750 | 88.46 | 47.60 | 7 197 | 28.33 | −34.48 | ||
从表3可知,若常规设计可以设置展宽车道,则四向设置方案相对于常规交叉口能够提升54.81%的通行能力. 若常规设计不可以设置展宽车道,则能够提升88.46%的通行能力,说明平行流交叉口通行能力的提升优势明显. 整体来看,常规设计可设置展宽车道的通行能力大于不可设置的情况,即设置展宽车道有利于提升交叉口通行能力,故仅讨论可设置展宽车道的情况. 在常规设计可设置展宽车道中,与常规交叉口相比,对称双向、三向、四向设置方案分别提升了19.42%、8.57%、54.81%的通行能力,降低了14.13%、16.86%、34.48%的车均延误,但单向、非对称双向设置方案略微降低了交叉口通行能力,由此证明选择合适的平行流交叉口设置方案,对交叉口通行能力的提升至关重要.
4. 敏感性分析
为了分析单向、非对称双向、对称双向、三向、四向平行流交叉口设置方案在各种流量场景下对交叉口通行能力的提升效果,探讨左转流量比例
表 4 各种实验案例X、Y、Z轴的参数设计
Tab.4
| 序号 | X轴参数及 取值范围 | Y轴参数及取值范围 | Z轴参数 | 备注 |
| 1 | 左转比例10%~50% | 单向流量倍数增加(西向与南向、东向、 北向的流量比值)1.0~2.0 | 通行能力提升比例, 以常规交叉口为基准 | 南向、东向、北向流量相同 |
| 2 | 非对称双向流量倍数增加(西向、南向与东向、 北向的流量比值)1.0~2.0 | 西向、南向流量相同,东向、北向流量相同 | ||
| 3 | 对称双向流量倍数增加(西向、东向与南向、 北向的流量比值)1.0~2.0 | 西向、东向流量相同,南向、北向流量相同 | ||
| 4 | 三向流量倍数增加(西向、南向、东向与 北向的流量比值)1.0~2.0 | 西向、南向、东向流量相同 |
图 5
图 5 各方案通行能力提升比例与单向流量倍数、左转比例的分布
Fig.5 Traffic capacity enhancement, one-way flow multiplier and left turn ratio for scheme
图 6
图 6 各方案通行能力提升比例与非对称双向流量倍数、左转比例的分布
Fig.6 Traffic capacity enhancement, asymmetric two-way flow multiplier and left turn ratio for scheme
图 7
图 7 各方案通行能力提升比例与对称双向流量倍数、左转比例的分布
Fig.7 Traffic capacity enhancement, symmetric two-way flow multiplier and left turn ratio for scheme
图 8
图 8 各方案通行能力提升比例与三向流量倍数、左转比例的分布
Fig.8 Traffic capacity enhancement, three-way flow multiplier and left turn ratio for scheme
对称双向设置方案在对称双向流量倍数增加的条件下,通行能力的提升优于单向、非对称双向、三向流量倍数增加的情况,说明对称双向设置方案适用于对称流量场景. 三向设置方案在单向、非对称双向、对称双向、三向流量倍数增加的条件下,运行性能的表现相差不大,通行能力提升幅度与对称双向设置方案相近,但三向设置方案在方向流量倍数较高时的通行能力提升幅度略微大于方向流量倍数较低时,说明三向设置方案在不对称流量场景中的表现优于对称双向设置方案. 在各种流量场景下,四向设置方案的通行能力提升幅度均大于其他设置方案,且在单向、非对称双向、对称双向、三向流量倍数增加的条件下通行能力提升比例的最小值分别能够达到17.94%、20.64%、21.15%、30.99%,最大值均能达到70.51%,即平行流交叉口在工程应用中宜采用四向全设置方案.
5. 结 论
(1)提出平行流交叉口车道控制和信号配时组合优化方法,能够实现设置方案选择(包括单向、非对称双向、对称双向、三向、四向平行流交叉口设置及常规交叉口)、车道数分配和信号配时的组合优化. 案例分析表明,与常规交叉口相比,对称双向、三向、四向设置方案的通行能力分别提升了19.42%、8.57%、54.81%,车均延误降低了14.13%、16.86%、34.48%,单向、非对称双向设置方案的通行能力和车均延误均与常规交叉口相差不大.
(2) 通过敏感性分析发现,在不同左转流量比例和方向流量倍数组合的各种流量场景中,多数情况下,对称双向、三向、四向设置方案的通行能力较常规交叉口分别能够提升约20%、20%、50%,单向、非对称双向设置方案的通行能力与常规交叉口接近. 四向设置的通行能力提升幅度最大,在各种流量场景下通行能力提升比例的最小值、最大值分别为17.94%、70.51%,即采用四向设置在各种流量场景下相较于常规交叉口均具有明显的通行能力优势. 对称双向、三向设置通行能力的提升幅度次之,但对称双向设置在对称流量场景中表现更优,三向设置在不对称流量场景中表现更优. 对称双向、三向设置在各种流量场景下的通行能力提升比例最小值分别为3.48%、3.85%,最大值分别为30.55%、29.69%,即采用对称双向、三向设置在各种流量场景下均能够有效提升常规交叉口的通行能力. 单向、非对称双向设置对交叉口通行能力的提升帮助不大,即平行流交叉口不宜采用单向、非对称双向设置.
(3) 本研究仅对比单向、非对称双向、对称双向、三向、四向平行流交叉口设置方案的通行效率,可以进一步关注各种设置方案的交通安全水平,使平行流交叉口控制更符合实际的交通运行需要.
参考文献
Analysis of unconventional arterial intersection designs (UAIDs): state-of-the-art methodologies and future research directions
[J].DOI:10.1080/18128602.2012.672344 [本文引用: 1]
考虑交织路段掉头车流的邻近交叉口信号协调控制
[J].
Coordinated signal control for adjacent intersections considering U-turn movements at interweaving road sections
[J].
Stationary condition based performance analysis of the contraflow left-turn lane design considering the influence of the upstream intersection
[J].DOI:10.1016/j.trc.2020.102919 [本文引用: 1]
自动车轨迹优化以实现分转向车流串联交叉口控制
[J].
Trajectory optimization of connected and autonomous vehicles to achieve tandem intersection control
[J].
Operational assessment of continuous flow intersections in a connected vehicle environment
[J].DOI:10.1080/03081060.2022.2136177 [本文引用: 1]
移位左转交叉口研究进展
[J].
Research progress on displaced left-turn intersection
[J].
非常规交叉口设计研究现状与展望
[J].
Research status and prospect of unconventional arterial intersection design
[J].
Performance analysis of parallel flow intersection and displaced left-turn intersection designs
[J].
The parallel flow intersection: a new two-phase signal alternative
[J].
平行流交叉口信号控制策略及效益分析
[J].
Signal control strategy and benefit analysis of parallel flow intersection
[J].
平行流交叉口左转非机动车钩形转弯优化设计
[J].DOI:10.11918/202111105 [本文引用: 2]
Optimization design for left-turn non-motor vehicle crossing at parallel flow intersection with hook-turn
[J].DOI:10.11918/202111105 [本文引用: 2]
Operational and safety performance evaluation of parallel flow intersection
[J].DOI:10.1177/03611981211070283 [本文引用: 1]
Optimal operation of displaced left-turn intersections: a lane-based approach
[J].DOI:10.1016/j.trc.2015.10.012 [本文引用: 2]
T型交叉口移位左转几何设计及信号配时优化
[J].
Geometric design and signal timing optimization of displaced left-turn at T-shaped intersection
[J].
连续流交叉口左转非机动车优化设计方法
[J].
Optimization design method of left-turn bicycles crossing for continuous flow intersections
[J].
Signal control method and performance evaluation of an improved displaced left-turn intersection design in unsaturated traffic conditions
[J].DOI:10.1080/21680566.2020.1764410 [本文引用: 1]
Development of signal optimization models for asymmetric two-leg continuous flow intersections
[J].DOI:10.1016/j.trc.2016.11.021 [本文引用: 2]
A continuous-flow-intersection-lite design and traffic control for oversaturated bottleneck intersections
[J].DOI:10.1016/j.trc.2015.03.011 [本文引用: 1]
Optimal allocation of turns to lanes at an isolated signal-controlled junction
[J].DOI:10.1016/j.trb.2010.12.001 [本文引用: 1]
平行流交叉口行人过街控制策略研究
[J].
Pedestrian crossing control strategy for parallel flow intersection
[J].
考虑自行车交通的非常规交叉口通行优化设计方法
[J].DOI:10.3969/j.issn.1671-3400.2021.03.006 [本文引用: 1]
Optimization design method for bicycles at tandem unconventional arterial intersections
[J].DOI:10.3969/j.issn.1671-3400.2021.03.006 [本文引用: 1]
A restricted branch-and-bound approach for generating maximum bandwidth signal timing plans for traffic networks
[J].DOI:10.1016/S0191-2615(96)00033-1 [本文引用: 1]