制动防抱死系统是汽车行驶过程中必不可少的主动安全系统之一,而如何精准预估路面附着系数是车辆实施理想防抱死控制的前提条件之一[1]. 现有路面附着系数估计方法主要分为Cause-based识别和Effect-Based识别方法2大类[2]. Cause-based识别方法分析与路面附着系数相关的各种物理因素,如利用光学传感器[3]或者激光传感器[4],建立反映各个因素与路面附着系数关系的数学模型,通过测量相关因素,利用所设计的数学模型计算路面附着系数. 其成本较高,硬件复杂,商业推广价值不大,且识别精度过于依赖传感器信号的损失程度,在面对崎岖不平路面、行驶信号损耗严重的情况下,预估准确率不高[5]. Effect-Based识别方法通过分析路面变化引起的车辆动力学响应来估算路面附着系数. 该类方法对工作环境要求不高,仅对车辆进行动力学分析即可进行路面附着系数辨识. 其包括多种技术途径,如卡尔曼滤波估计器[6-7]、滑模观测器[8]、神经网络[9-10]等.
相比于卡尔曼滤波估计器和滑模观测器,神经网络处理非线性关系的能力更强,具有更加强大的容错性. Park等[11]采用具有传感器特征选择的深度集成网络方法在极短时间内判别路面类型;Sun等[12]提出遗传算法改进神经网络,利用路面纹理三维数据预估路面附着系数;林棻等[13]设计改进Keras模型路面附着系数估计器,极大提高了路面附着系数预估精度. 上述方法都能实现基本的估计功能,但是均无法及时感知车辆在路面较大突变情况下的路面附着系数变化,若在2类路面交界处发生紧急制动,则可能因为路面附着系数预估不准确而造成防抱死控制效果变差,甚至引发车轮抱死危险. Elman神经网络被认为是典型的动态递归神经网络,其适应时变特性能力较强,能够高效处理非线性影响下的不确定性,该类方法在路面附着系数估计领域具有更大的发展潜力[14]. 伍文广等 [15]引入Elman神经网络建立路面附着系数估计模型,与传统BP网络相比,提高了预估精度. 然而,传统Elman神经网络算法容易陷入局部极小点[16],导致路面附着系数预估不准确而引起车辆滑移率控制效果不佳,因此该方法在路面附着系数辨识应用中仍有较大提升空间.
在汽车行驶状态和路面工况时变条件下,为了克服采用传统Elman神经网络的路面附着系数估计方法可能引起路面附着系数预估不准确,进而导致车辆滑移率控制效果不佳的缺陷,设计基于变权重PSO-Elman神经网络的路面附着系数估计方法,提出将传统Elman神经网络的权值矩阵作为初始粒子群位置,以神经网络绝对误差和作为适应度值来调整粒子群位置,达到神经网络权值矩阵最优效果,以相比于传统Elman神经网络提高权值矩阵更新稳定性.
1. 基于汽车动力学分析的神经网络数据集构建
1.1. 汽车动力学建模
图 1
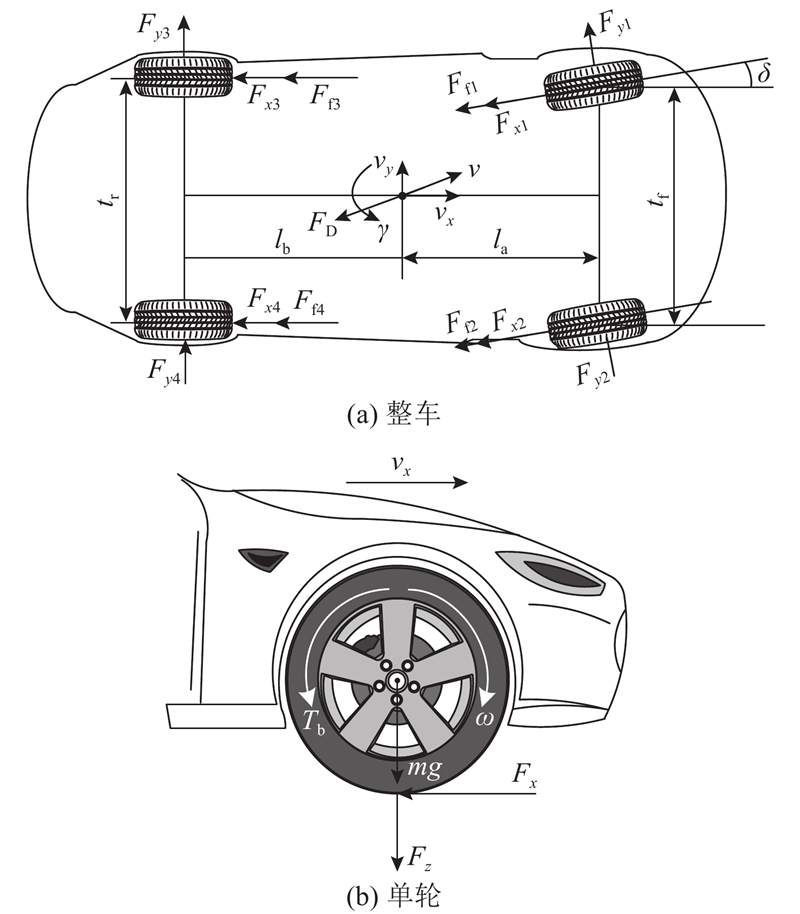
图 1 整车纵向动力学及单轮动力学建模
Fig.1 Modeling of vehicle longitudinal dynamics and single wheel
汽车动力学方程[18]如下 :
式中:
各轮胎垂直载荷满足:
式中:
各车轮纵向滑移率[19]如下:
各车轮侧偏角计算公式如下:
采用Dugoff轮胎模型描述轮胎摩擦力[20]:
式中:
1.2. 神经网络数据集构建
神经网络输入与输出应当满足一定相关性. 路面附着系数与汽车动力学模型中多种变量联系性较强,将式(10)~(12)代入式(1)~(5),获取与路面附着系数密切相关的车辆运动状态参数. 表达式如下:
由于车轮非线性状态下的分析对结果的影响相对较小,在不考虑车轮非线性状态下,将式(11)、(12)代入式(13):
可以看出,
根据式(21)确定神经网络模型的输入向量组为
表 1 车辆运动状态参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| m/kg | 1 825 | tf/m | 1.535 | |
| hg/m | 0.48 | tr/m | 1.531 | |
| Iz/(kg·m2) | 1 600 | 0.29 | ||
| la/m | 1.26 | lb/m | 1.38 | |
| CD | 0.3 | A/m2 | 2 | |
| Cσ/N | 68 900 | Cα/(N·rad−1) | 62 900 |
采集车辆制动过程中18个车辆状态参数,作为神经网络数据集. 设置路面附着系数取值范围为
2. 基于变权重PSO-Elman神经网络的路面附着系数估计系统设计
为了克服基于传统Elman神经网络的路面附着系数估计方法容易引起路面附着系数预估不准确,导致车辆滑移率控制效果不佳的问题,提出基于变权重PSO-Elman神经网络的路面附着系数估计系统.
2.1. Elman神经网络拓扑结构构建及初始权值矩阵确定
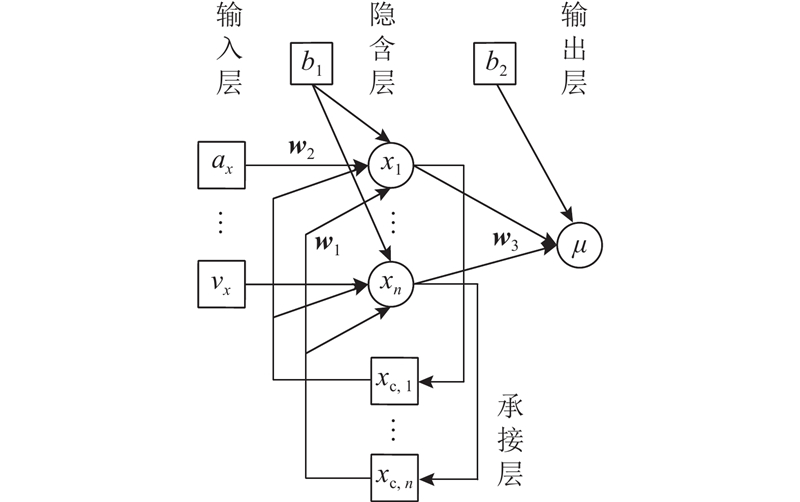
图 2
Elman神经网表达式如下:
式中:
Elman神经网络误差函数表达式如下:
式中:
进行传统Elman神经网络模型训练,并确定初始权值矩阵为
将初始权值矩阵
2.2. 基于变权重PSO的Elman神经网络权值矩阵优化
通过引入粒子群算法降低网络训练绝对误差和,实现网络权值优化,提高神经网络权值更新稳定性.
将基于Elman神经网络权值矩阵优化细分为4个步骤. 确定最大迭代次数和适应度函数;计算粒子群初始适应度函数值与初始权值矩阵;为了更有效平衡粒子全局、局部搜索能力,采用线性惯性权重递减策略对粒子群算法进行改进[22]并输出改进粒子群权重;得到优化后的神经网络权值矩阵,通过训练输出路面附着系数估计值.
1)最大迭代次数和适应度函数确定.
过少的迭代次数可能导致网络未能充分学习,而过多的迭代次数会增加训练时间和计算成本. 为了兼顾考虑网络性能、训练时间和计算成本等因素,根据文献[22],设定迭代次数
为了评价神经网络估计精度,引入神经网络绝对误差和:
神经网络绝对误差和越小,网络精度越高.
在神经网络训练过程中,以
2)初始最优适应度函数值与初始最优权值矩阵计算.
粒子群算法以群体智能为寻优原理,利用模型适应度值,使得输出值迅速向最优解靠近.
Elman神经网络误差函数对权值矩阵中的每一个值求偏导:
式中:i=1, 2,···, q,q为输入层神经元的个数;j=1, 2, ···, n,l=1, 2, ···, n,n为隐含层/承接层神经元个数;w3j表示w3第j个值,
采用梯度下降训练方法提高训练效率,各参数修正量与负梯度成正比:
式中:
为了更直观地表示神经网络权值矩阵,将式(26)代入式(27),得到
式(28)即为Elman神经网络各层之间的权值矩阵,PSO算法中每一个粒子代表权值矩阵中的一个值.
粒子群优化算法的搜索空间维度为S维,粒子的种群规模为M,其组成的粒子群为
第d个粒子的位置信息、速度信息为
式中:
当前粒子搜索的个体最优位置信息为
种群中所有粒子的最优位置信息为
初始化粒子群得到最优适应度函数值Esumy-0与最优权值矩阵
3)变权重PSO权值矩阵优化.
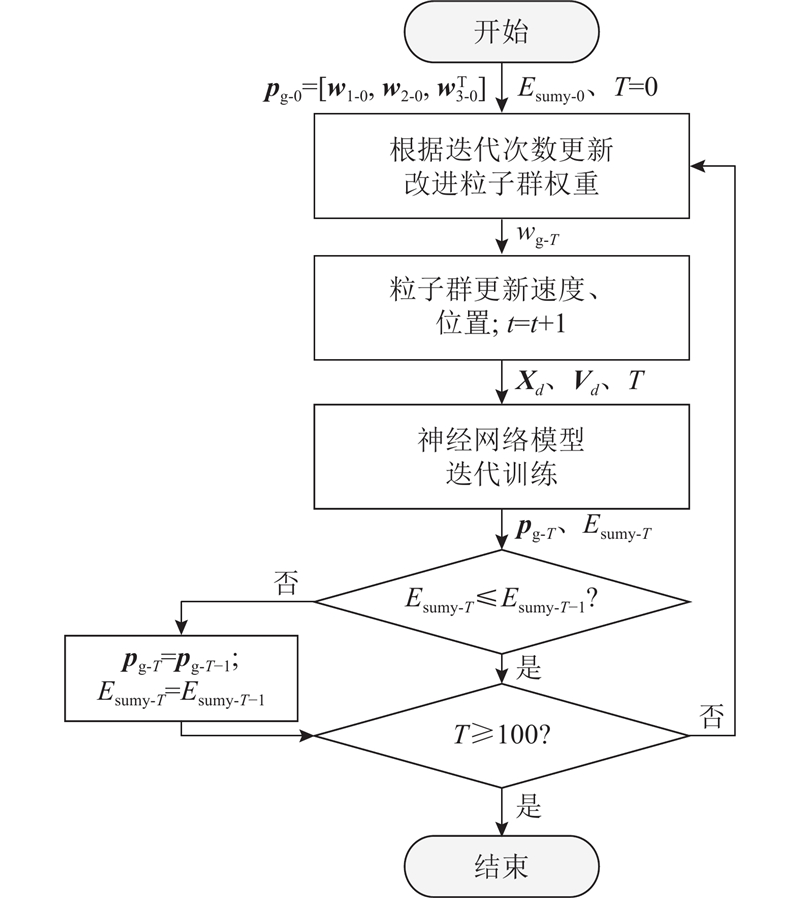
通过变权重粒子群优化算法进行神经网络权值矩阵优化,流程图详见图3.
图 3
图 3 变权重PSO权值矩阵优化流程图
Fig.3 Optimization flow chart of variable weight PSO weight arrays
粒子以适应度值为依据调整速度与位置,自发靠近最优解的粒子位置.
最优解为粒子当前的全局最优位置:
式中:
在粒子群算法的迭代寻优过程中,每个粒子分别得到在s维中的个体最优值
式中:
由于标准粒子群算法中权重固定,粒子全局搜索能力和局部搜索能力比重不能得到有效的平衡,使用线性权重递减策略对标准粒子群权重
式中:
随着每一次迭代过程,权值矩阵都会进一步被优化,直至达到最大迭代次数后得到优化后的权值矩阵.
4)神经网络模型训练.
若训练达到最大迭代次数100则训练结束,输出的最优解
3. 路面附着系数特性曲线拟合
图 4
理想滑移率估计单元具体设计步骤如下.
1)基于路面附着系数特性曲线得到实际路面附着系数
标准路面附着系数根据
式中:
根据式(39)确定实际路面附着系数和与之相对应的理想滑移率:
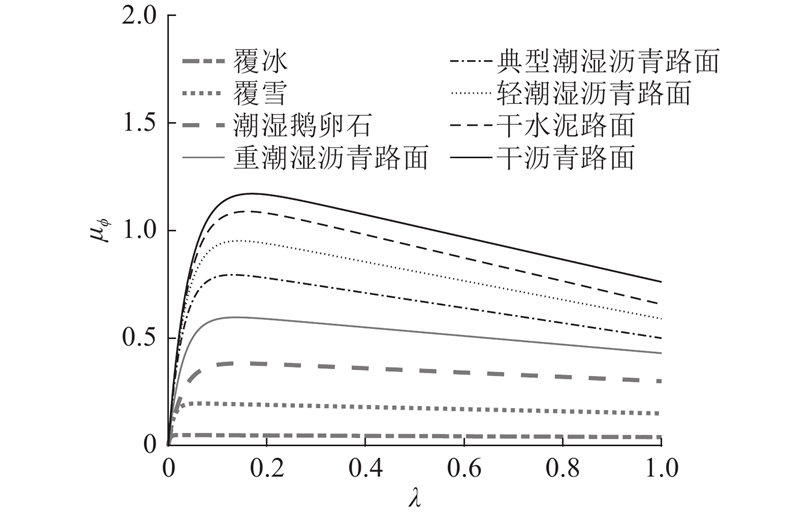
常见的典型路面主要有覆冰、覆雪、潮湿鹅卵石、重潮湿沥青、典型潮湿沥青、轻潮湿沥青、干水泥路面和干沥青路面这8类.
表 2 典型路面参数值
Tab.2
| 路面 | c1 | c2 | c3 | λp | µa |
| 覆冰 | 0.05 | 306.39 | 0.01 | 0.02 | 0.05 |
| 覆雪 | 0.20 | 94.10 | 0.05 | 0.06 | 0.19 |
| 潮湿鹅卵石 | 0.40 | 33.72 | 0.10 | 0.14 | 0.39 |
| 重潮湿沥青 | 0.63 | 33.77 | 0.20 | 0.11 | 0.60 |
| 典型潮湿沥青 | 0.85 | 33.80 | 0.35 | 0.13 | 0.80 |
| 轻潮湿沥青 | 1.03 | 29.49 | 0.44 | 0.14 | 0.95 |
| 干水泥 | 1.20 | 25.17 | 0.54 | 0.16 | 1.09 |
| 干沥青 | 1.28 | 23.99 | 0.52 | 0.17 | 1.17 |
图 5
2)
图 6
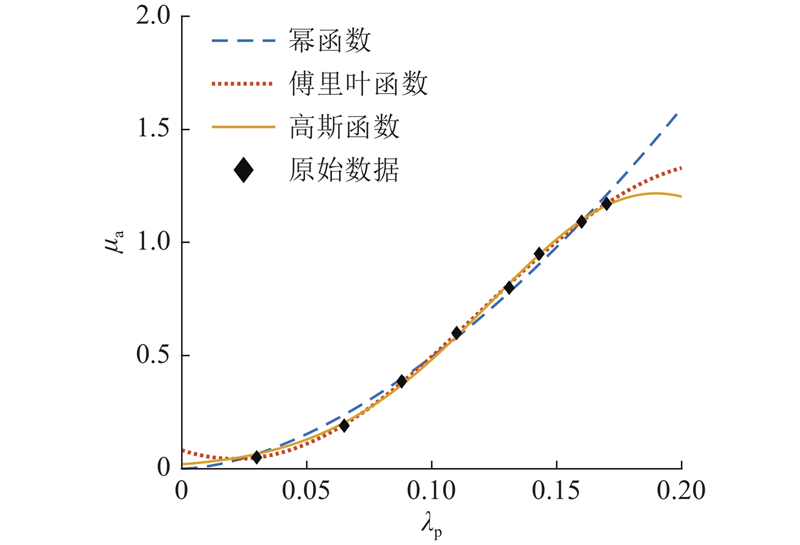
图 6 路面附着系数-滑移率拟合曲线
Fig.6 Fitted curve of road adhesion coefficient and slip rate
得到的拟合公式分别如下:
式中:
为了进一步量化评价拟合方法,采用相关系数(R2)评价上述3种方法的拟合精度:
式中:
使用MATLAB计算出拟合相关系数分别为0.9941、0.9989、0.9996. 傅里叶函数拟合相关系数更接近1.0,拟合效果最好. 因此选用傅里叶函数拟合曲线
4. 仿真分析
采用MATLAB/Simulink软件,对所提出的基于变权重PSO-Elman神经网络的路面附着系数估计方法的有效性进行仿真分析.
引入路面附着系数均方根误差
式中:N为采样频率200 Hz情况下的测试样本数量,
在仿真过程中须先对隐含层/承接层神经元个数
表 3 隐含层/承接层神经元个数试算结果
Tab.3
| n | n | |||
| 4 | 0.0109 | 9 | 0.0112 | |
| 5 | 0.0087 | 10 | 0.0100 | |
| 6 | 0.0118 | 11 | 0.5401 | |
| 7 | 0.0090 | 12 | 0.0249 | |
| 8 | 0.0086 | 13 | 0.0090 |
为了验证所提出的基于变权重PSO-Elman神经网络的路面附着系数估计方法的有效性,将参考文献[15]中Elman神经网络作为仿真对照组,更全面地评估所提出方法在路面附着系数估计方面的预估准确性和稳定性.
车轮滑移率除受到路面附着系数的影响,还受到车辆状态参数(比如轮胎状态、传感器测量精度)、防抱死控制算法等因素影响. 使用控制变量法,在不改变其他因素前提下,均采用文献[29]提出的区间二型模糊防抱死控制算法对车辆进行防抱死控制,只改变路面附着系数,以其对滑移率控制的影响评判变基于变权重PSO-Elman神经网络的路面附着系数估计方法的有效性.
4.1. 定附着系数路面
模拟防抱死应用场景下较为常见、具有代表性且相对危险的4类工况,即覆冰、覆雪、潮湿鹅卵石和典型潮湿沥青路面工况,记为工况1~4,其中车辆在工况1~3中行驶的初始速度设为15 m/s,在工况4中行驶的初始速度为30 m/s.
表 4 代表性路面参数
Tab.4
| 工况 | λp | µa |
| 1 | 0.0497 | 0.0239 |
| 2 | 0.1963 | 0.0630 |
| 3 | 0.3825 | 0.1454 |
| 4 | 0.7940 | 0.1304 |
图 7
图 7 4类工况下路面附着系数随时间变化曲线
Fig.7 Curve of value of road adhesion coefficient over time under four types of road conditions
表 5 路面附着系数预估均方根误差统计
Tab.5
| 工况 | Ermse-μ | p/% | 工况 | Ermse-μ | p/% | |||
| 传统 | 变权重 | 传统 | 变权重 | |||||
| 1 | 0.038 302 | 0.023 791 | −37.89 | 3 | 0.131 380 | 0.091 050 | −30.70 | |
| 2 | 0.071 764 | 0.037 732 | −47.42 | 4 | 0.356 060 | 0.261 800 | −26.47 | |
图 8
图 8 4类工况下车轮滑移率随时间变化曲线
Fig.8 Curve of wheel slip rate changing over time under four types of road conditions
表 6 车轮滑移率均方误差统计
Tab.6
| 工况 | 前轮 | 后轮 | |||||
| Emse_λ | q/% | Emse_λ | q/% | ||||
| 传统 | 变权重 | 传统 | 变权重 | ||||
| 1 | 0.227 8 | 0.212 6 | −6.66 | 0.227 7 | 0.212 6 | −6.64 | |
| 2 | 0.103 1 | 0.095 5 | −7.41 | 0.103 2 | 0.095 7 | −7.32 | |
| 3 | 0.067 3 | 0.064 2 | −4.83 | 0.069 0 | 0.064 7 | −6.63 | |
| 4 | 0.002 8 | 0.002 7 | −3.50 | 0.004 0 | 0.003 2 | −20.74 | |
由图7可知,基于变权重PSO-Elman神经网络的路面附着系数估计方法所估计的路面附着系数更加接近真实值,在4类工况下路面附着系数均方根误差较传统Elman神经网络分别降低37.89%、47.42%、30.70%和26.47%.
如图8所示,在4类工况中使用基于变权重PSO-Elman神经网络的路面附着系数估计方法的车辆在防抱死过程中滑移率更加接近理想滑移率,均方误差较传统Elman神经网络分别降低6.64%、7.32%、6.63%和20.74%. 仿真结果表明使用基于变权重PSO-Elman神经网络的路面附着系数估计方法的车辆在防抱死过程中路面附着系数识别更为准确,滑移率控制更为精准,波动程度更小,制动安全性更高.
4.2. 变附着系数路面
选取覆雪路面对接潮湿鹅卵石路面作为工况5进行变附着路面仿真,路面附着系数在1 s时刻由0.196突变为0.383,车辆初始速度为15 m/s.
图 9
图 9 工况5下路面附着系数随时间变化曲线
Fig.9 Curve of value of road adhesion coefficient over time under condition 5
图 10
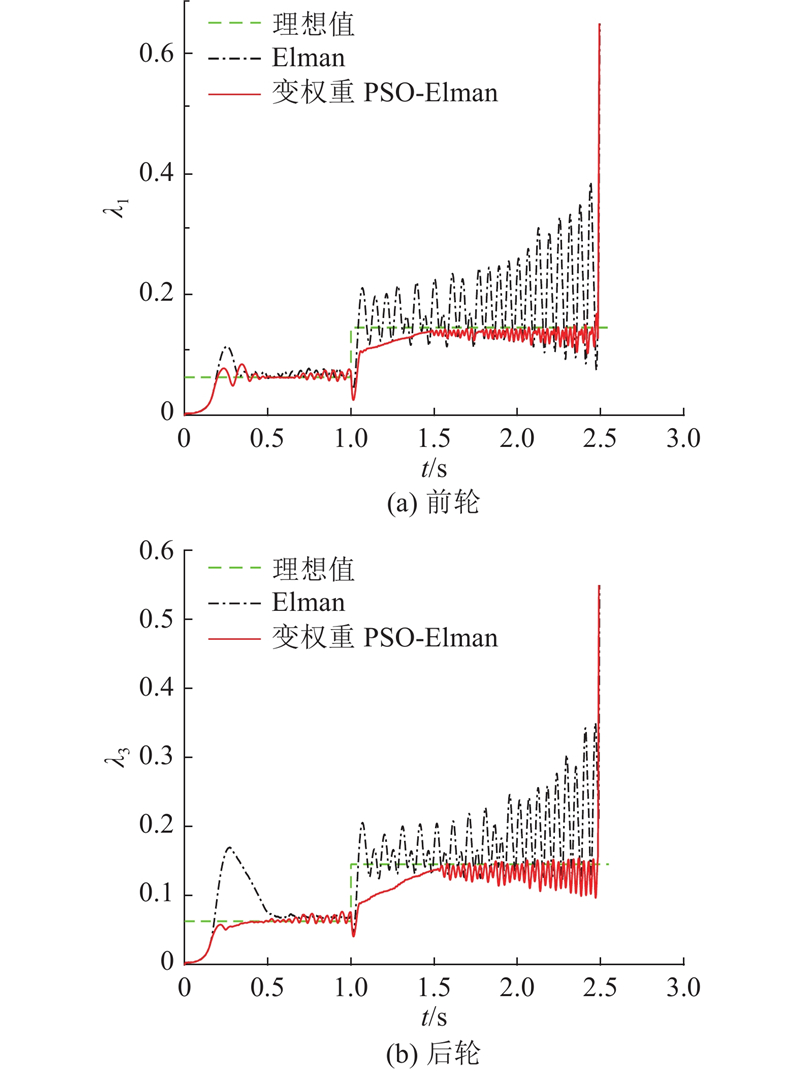
图 10 工况5下车轮滑移率随时间变化曲线
Fig.10 Curve of wheel slip rate changing over time under condition 5
如图9所示,在工况5下路面附着系数突变瞬间(由0.196上升到0.383),使用基于Elman神经网络、变权重PSO-Elman神经网络的路面附着系数估计方法得到的路面附着系数预估值随时间变化曲线的收敛时间几乎相同,而使用基于变权重PSO-Elman神经网络路面的附着系数估计方法估计的路面附着系数更加接近真实值,相比传统Elman神经网络估值方法,均方根误降低了19.2%,表明基于变权重PSO-Elman神经网络的路面附着系数估计方法估计准确度更高.
如图10所示,在工况5下使用基于变权重PSO-Elman神经网络的路面附着系数估计方法的车辆在防抱死过程中滑移率更加接近理想滑移率,均方误差较传统Elman神经网络前后轮分别降低7.39%、6.44%,说明使用基于变权重PSO-Elman神经网络的路面附着系数估计方法的车辆在防抱死过程中路面附着系数识别更为准确,滑移率能够以更小波动保持在理想滑移率附近,制动稳定性更高.
4.3. 粒子群变权重有效性验证
仿真模拟定附着与变附着2类行驶工况下,所提出的基于变权重PSO-Elman神经网络的路面附着系数估计方法的粒子群权重变化的有效性. 其中,定附着系数选用覆冰路面工况,变附着系数选取覆雪路面对接潮湿鹅卵石路面工况,初始速度皆设为15 m/s.
如图11所示为定附着工况、变附着工况下路面附着系数预估值随时间的变化曲线,路面附着系数均方根误差如表7所示. 其中,“PSO-Elman”表示基于PSO-Elman神经网络的路面附着系数估计方法(未变权重)得到的路面附着系数预估值,p1为基于PSO-Elman神经网络的路面附着系数估计方法较基于传统Elman神经网络的路面附着系数预估方法在均方根误差上的降低比率,p2为基于变权重PSO-Elman神经网络的路面附着系数估计方法较基于传统Elman神经网络的路面附着系数预估方法在均方根误差上的降低比率,p3为基于变权重PSO-Elman神经网络的路面附着系数估计方法较基于PSO-Elman神经网络的路面附着系数预估方法在均方根误差上的降低比率. 可以看出,在定附、变附工况下使用基于变权重PSO-Elman神经网络的路面附着系数估计方法估计的路面附着系数皆比基于PSO-Elman神经网络的路面附着系数估计方法所得结果更加接近真实值. 由表7可知,变权重PSO-Elman神经网络较PSO-Elman神经网络的路面附着系数均方根误差分别降低30.59%、10.02%,说明本研究针对粒子群实施“变权重”,有助于提升PSO-Elman神经网络关于路面附着系数识别的估计精度.
图 11
图 11 定附着与变附着工况路面附着系数预估值随时间变化曲线
Fig.11 Curve of predicted value of road adhesion coefficient over time under fixed-adhesion and changing-adhesion coefficient conditions
表 7 定附着与变附着工况路面附着系数预估均方根误差统计
Tab.7
| 估计方法 | Ermse_μ | p1/% | p2/% | p3/% | ||
| 传统Elman | PSO-Elman | 变权重PSO-Elman | ||||
| 定附着路面 | 0.016 080 | 0.010 914 | 0.007 576 | −32.13 | −52.89 | −30.59 |
| 变附着路面 | 0.030 281 | 0.019 156 | 0.017 237 | −36.70 | −43.08 | −10.02 |
5. 结 论
(1)设计基于变权重PSO-Elman神经网络的路面附着系数估计方法,利用变权重粒子群算法降低网络训练绝对误差和实现神经网络权值矩阵优化,克服传统Elman神经网络在汽车制动过程可能陷入局部最优的难题,提升路面附着系数的估计精度和控制系统鲁棒性.
(2)在定附着路面制动工况下,采用基于变权重PSO-Elman神经网络的路面附着系数估计方法相较于传统Elman神经网络方法,车轮滑移率控制更加接近理想滑移率,结果表明变权重PSO-Elman神经网络对于路面附着系数具有更好的估计效果.
(3)在变附着系数制动工况下,采用基于变权重PSO-Elman神经网络的路面附着系数估计方法相较于传统Elman神经网络方法,车轮滑移率控制更加接近理想滑移率,结果表明基于变权重PSO-Elman神经网络的路面附着系数估计方法鲁棒性更强.
(4)下一步,将针对所提出估计方法筹划进行路面附着系数估计实验,构建变参数动态仿真及实验对比验证与校正平台,开展面向紧急制动/非紧急制动、驱动、转向等工况的路面附着系数估计的有效性验证,循环优化相关参数,为理论研究提供更加可靠的支持和验证.
参考文献
中国汽车工程学术研究综述·2017
[J].DOI:10.19721/j.cnki.1001-7372.2017.06.001 [本文引用: 1]
Review on China’s automotive engineering research progress: 2017
[J].DOI:10.19721/j.cnki.1001-7372.2017.06.001 [本文引用: 1]
Response-based methods to measure road surface irregularity: a state-of-the-art review
[J].DOI:10.1186/s12544-018-0328-2 [本文引用: 1]
Intelligent tires: a review of tire characterization literature
[J].DOI:10.1109/MITS.2017.2666584 [本文引用: 1]
Automatic pavement defect detection using 3D laser profiling technology
[J].DOI:10.1016/j.autcon.2018.09.019 [本文引用: 1]
A novel strain-based method to estimate tire conditions using fuzzy logic for intelligent tires
[J].DOI:10.3390/s17020350 [本文引用: 1]
Terrain estimation via vehicle vibration measurement and cubature Kalman filtering
[J].
Tire road friction coefficient estimation: review and research perspectives
[J].DOI:10.1186/s10033-021-00666-0 [本文引用: 1]
Simultaneous estimation of road profile and tire road friction for automotive vehicle
[J].
基于DRBF-EKF算法的车辆质心侧偏角与路面附着系数动态联合估计
[J].
Dynamic joint estimation of vehicle sideslip angle and road adhesion coefficient based on DRBF-EKF algorithm
[J].
A comparative study of the recursive least squares and fuzzy logic estimation methods for the measurement of road adhesion coefficient
[J].DOI:10.1080/14484846.2021.1967839 [本文引用: 1]
Road surface classification using a deep ensemble network with sensor feature selection
[J].DOI:10.3390/s18124342 [本文引用: 2]
Asphalt pavement friction coefficient prediction method based on genetic-algorithm-improved neural network (GAI-NN) model
[J].DOI:10.1139/cjce-2020-0051 [本文引用: 1]
基于改进 Keras 模型的路面附着系数估计
[J].DOI:10.3901/JME.2021.12.074 [本文引用: 1]
Road friction coefficient estimation based on improved Keras model
[J].DOI:10.3901/JME.2021.12.074 [本文引用: 1]
Identification of road-surface type using deep neural networks for friction coefficient estimation
[J].DOI:10.3390/s20030612 [本文引用: 1]
基于 Elman 神经网络的路面附着系数识别
[J].
Identification of road friction coefficient based on Elman neural network
[J].
基于二次预测型横向载荷转移率的汽车侧翻预警研究
[J].
Research on vehicle rollover warning based on secondary predictive lateral load transfer ratio
[J].
Skid control of a small electric vehicle with two in-wheel motors: simulation model of ABS and regenerative brake control
[J].DOI:10.1080/13588265.2016.1147731 [本文引用: 1]
Fixed-time slip control with extended-state observer using only wheel speed for anti-lock braking systems of electric vehicles
[J].
Integrating Elman recurrent neural network with particle swarm optimization algorithms for an improved hybrid training of multidisciplinary datasets
[J].DOI:10.1016/j.eswa.2021.115441 [本文引用: 1]
PSO-based sink placement and load-balanced anycast routing in multi-sink WSNs considering compressive sensing theory
[J].DOI:10.1016/j.engappai.2021.104164 [本文引用: 2]
基于 RBF 神经网络的最佳滑移率在线计算方法
[J].DOI:10.3901/JME.2011.14.108 [本文引用: 1]
Calculation of RBF neural network based optimal slip ratio
[J].DOI:10.3901/JME.2011.14.108 [本文引用: 1]
Dynamic coordinated control for regenerative braking system and anti-lock braking system for electrified vehicles under emergency braking conditions
[J].DOI:10.1109/ACCESS.2020.3024918 [本文引用: 1]
漂移幂函数的数值拟合与理论分析
[J].
Data fitting and theoretical analysis of the shifted power function
[J].
A simple algorithm for fitting a Gaussian function [DSP tips and tricks]
[J].DOI:10.1109/MSP.2011.941846 [本文引用: 1]
Intelligent vehicle automatic stop-and-go task based on humanized learning control model
[J].
Behaviour analysis of multilayer perceptrons with multiple hidden neurons and hidden layers
[J].
Interval type-2 fuzzy logic anti-lock braking control for electric vehicles under complex road conditions
[J].DOI:10.3390/su132011531 [本文引用: 1]