为了减小位置错位,解决方向不对准的问题,本文设计具有2个自由度的穿戴式自对准人工膝关节的机械机构,通过电机主动驱动实现辅助人体运动的功能. 探讨适用于多自由度机构的人-机系统的匹配方法,应用该方法对提出的人工膝关节中部分零件进行优化. 建立自对准人工膝关节的数字虚拟样机,开展新型膝关节机构和人-机系统的匹配、优化方法的仿真验证.
1. 人工膝关节机构
1.1. 人工膝关节机构设计
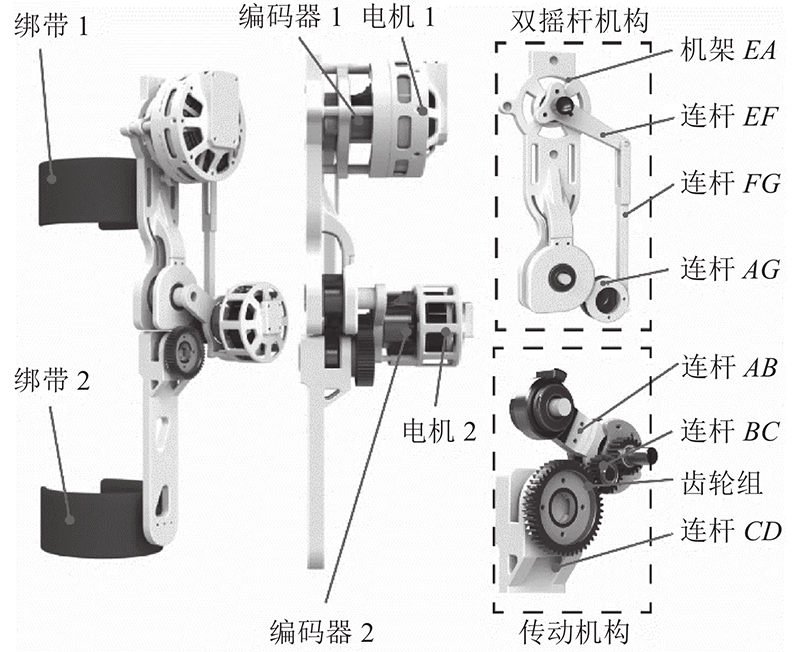
使用三维软件完成人工膝关节机械结构的设计. 如图1所示,主要的机械机构包括由连杆EA、EF、FG和AG组成的双摇杆机构和由连杆AB、BC、CD和齿轮组成的传动机构. 人工膝关节由电机 1和电机 2驱动与控制.
图 1
图 2
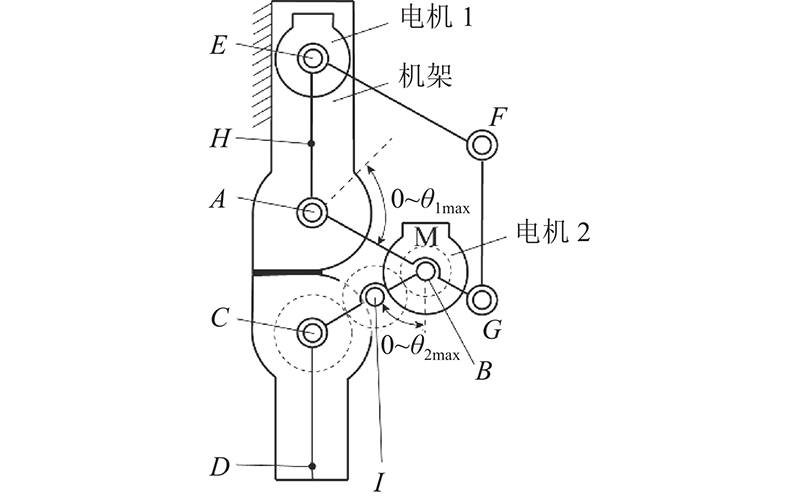
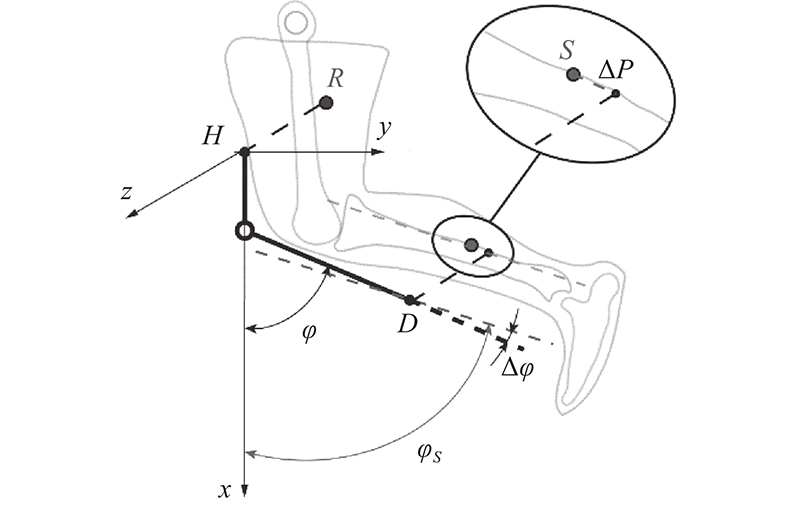
图 2 自对准人工膝关节的机构原理图
Fig.2 Mechanical diagram of self-aligning artificial knee joint
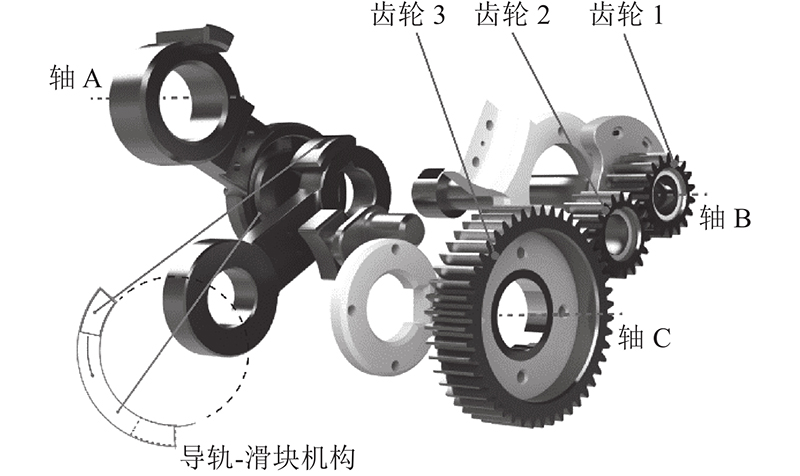
连杆AB、BC和齿轮组的详细结构如图3所示.
图 3
图 3 主要传动机构的详细机构图
Fig.3 Detailed mechanism diagram of main transmission mechanism
连杆AB与齿轮1固定安装在轴B上;齿轮3可绕轴C自由旋转. 齿轮2与齿轮1、3啮合. 连杆BC的末端设有滑块机构,与连杆AB的滑轨相互配合,实现连杆BC相对于连杆AB的转角限位,使得转角活动范围为
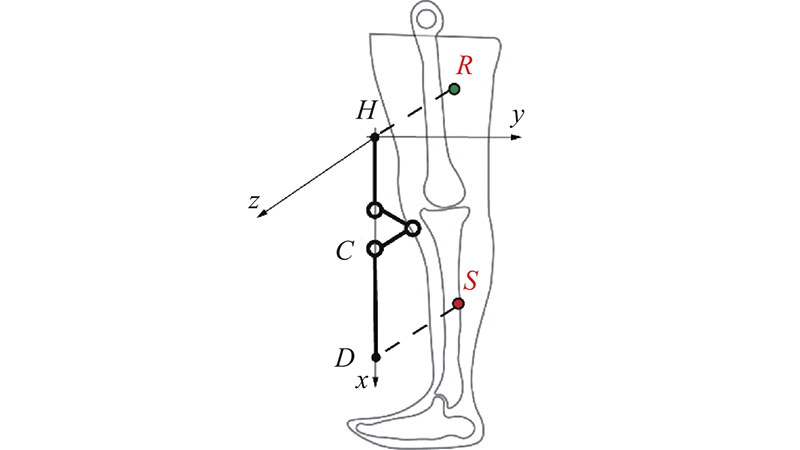
通过绑带1,将机构的大腿绑带点H与人体大腿上的参照点R固联;通过绑带2,将机构的小腿绑带点D与人体大腿上的参照点S固联. 如图4所示,直立初始状态时,R、S点是H、D点在人体上的投影.
图 4
1.2. 运动学分析
忽略机构中的虚约束,自对准人工膝关节的机构简图如图5所示. 将坐标系的原点设置在H处,参数
图 5
定义D点的位置坐标为
齿轮组传动比
摆角φ为
2. 人-机系统的运动匹配及优化方法
2.1. 人-机系统的运动匹配优化问题
将小腿视作刚体,它在空间平面中的运动可以用参照点S的坐标
自对准人工膝关节机构采用2个电机驱动,实现矢状面上绑带点D的轨迹控制. 摆角
2.2. 人-机系统运动匹配算法的设计
当人-机系统开始运动时,如图6所示,定义D点与S点位置的偏差
图 6
式中:
小腿摆动过程包括N个时刻的位姿参数:
式中:
采用逆运动学求解各个时刻的最优关节角参数
在得到优化结果
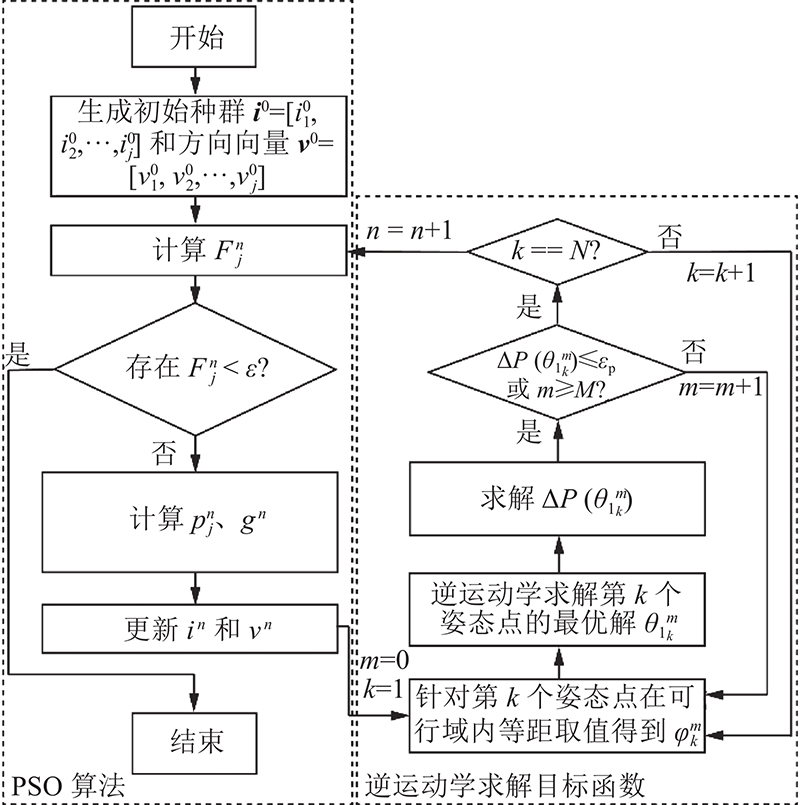
人-机系统运动匹配方法的流程如图7所示. 图中,
图 7
图 7 优化计算齿轮传动比以匹配个体小腿运动的流程图
Fig.7 Flow chart for optimally calculating gear ratio to match individual calf movement
利用粒子群算法,随机产生1组种群开始迭代. 该初始种群
采用逆运动学,求解目标函数F. 根据F计算局部最优值
式中:
2.3. 匹配个体小腿运动轨迹
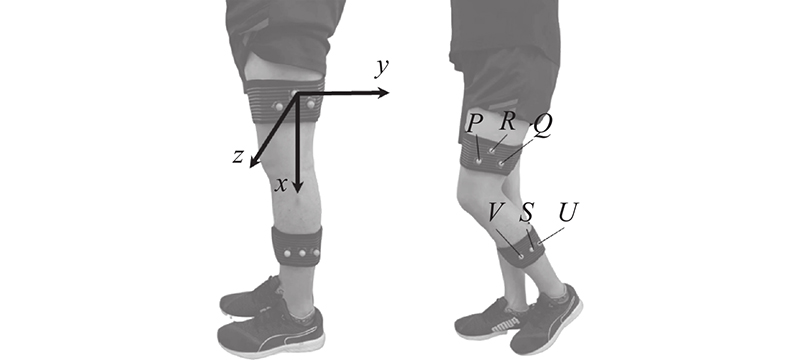
取2名身高分别为1 760、1 740 mm的健康男性作为测试对象A和测试对象B,以他们小腿的运动轨迹为参考进行人-机匹配. 在直立状态下,所有采集点通过木板和皮带固定在大腿和小腿的外侧,参照点R和S之间的竖直距离为307 mm,如图8所示.
图 8
使用高速摄像机,每隔0.02 s捕捉采集点在XY平面上的实时位置. 受试者在高速摄像机前使大腿保持静止并屈伸小腿,一次屈伸运动的角度控制在0~90°.
摄像机同时记录点R、P、Q的移动数据,利用它们来修正点S、V、U在空间中的位置坐标. 经过处理后,得到80组有效的坐标数据:S
图 9
利用下式计算小腿摆动中的角度
整合坐标和摆角数据,得到80组位姿参数:
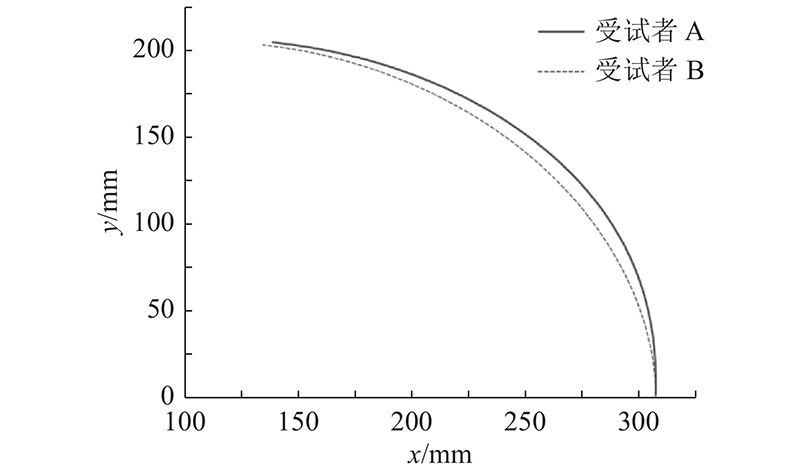
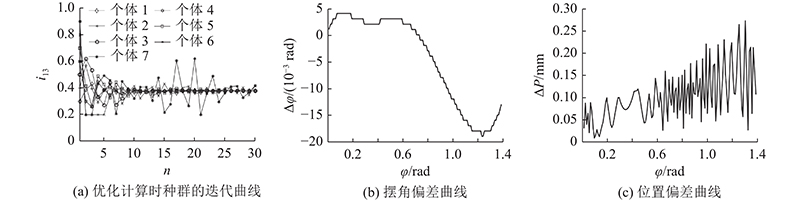
以受试者A小腿摆动时的位姿参数为目标位姿,按照如图7所示的算法求解. 建立7组传动比i13的初始值,它们的演变过程如图10(a)所示. 图中,6组迭代数据在0.378 7附近收敛. 取传动比为0.378 7,设置角度偏差的精度为0.02 rad,对点S的轨迹进行追踪. 全局角度偏差的变化如图10(b)所示;在期望摆角处,全局位置偏差的变化如图10(c)所示. 其中,最大角度偏差
图 10
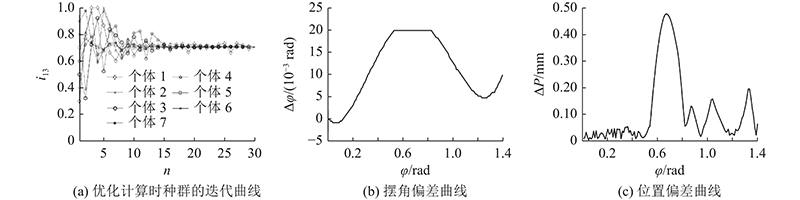
以受试者B小腿摆动时的位姿参数
图 11
利用匹配方法,人-机系统连接处点S和点D运动轨迹中的角度偏差、最大位置偏差和平均位置偏差均相对较小,说明匹配方法能够在角度对准的情况下,有效缩小人-机系统中的不匹配现象.
3. 控制系统及虚拟样机验证
3.1. 数字虚拟样机的构建
将人-机系统的3D模型导入Adams软件中,建立人工膝关节的机械机构动力学仿真模型. 主要零件的设计参数见表1. 其中,传动杆件AB和BC的杆长不唯一,主要协调缓和了膝关节尺寸大小、匹配精度与各个零件安装空间的矛盾;机架EA与杆件CD的取值依据人体上参照点而定.
表 1 人工膝关节部分零件的设计参数
Tab.1
| 杆名 | 杆长/mm | 初始角度/rad |
| EA | l0 = 100 | — |
| AB | l1 = 50 | θ10 = π/3 |
| BC | l2 = 50 | θ20 = 2π/3 |
| CD | l3 = 157 | θ30 = −π/3 |
以受试者A匹配的结果为参考进行人工膝关节的参数设计,利用前面的优化结果确定机构中3个齿轮的齿数比为18∶17∶48,对应传动比i13为0.3750. 根据文献[5]可知,平地和斜坡步态需要不到90°的膝盖弯曲. 以90°为最大运动范围,参照上述参数,对人工膝关节机构进行逆运动学解算,获取主动件的转角范围. 转角的最大活动范围为:
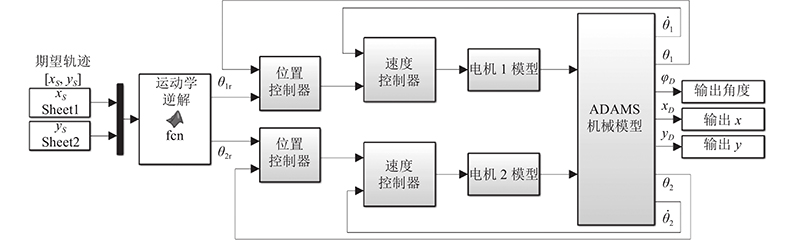
人工膝关节的控制方案是基于运动学逆解的机器人运动分解控制. 驱动人工膝关节的信号为小腿相对于大腿的摆动角度,这个摆动角度经过人工膝关节逆运动学解算,可以获得该小腿摆动角度对应的电机转动角度,以此作为人工膝关节控制指令. 控制系统采用Simulink建立,系统采样时间为0.001 s. 利用软件的联合仿真功能,将控制系统模型与机械机构模型联合起来,得到自对准人工膝关节的数字虚拟样机,如图12所示.
图 12
图 12 自对准人工膝关节与控制系统的虚拟样机
Fig.12 Virtual prototype of self-aligning artificial knee joint and control system
3.2. 仿真验证
图 13
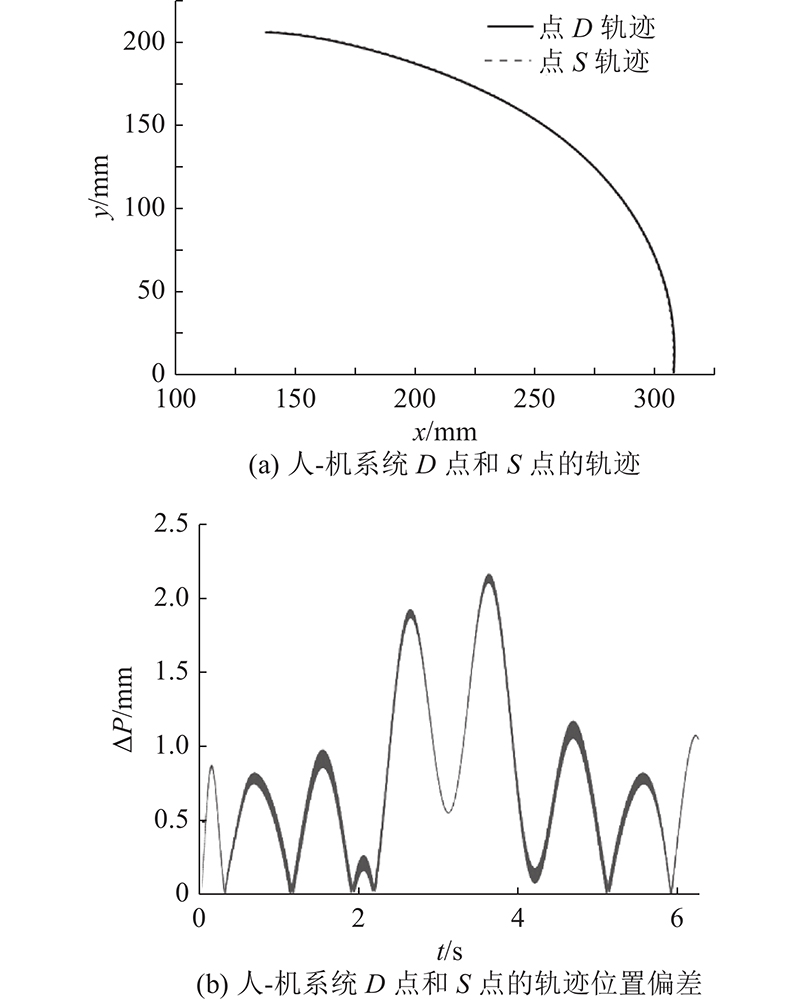
图 13 人-机系统D点和S点的轨迹比较
Fig.13 Comparison of D-point and S-point trajectories of human-robot system
图 14
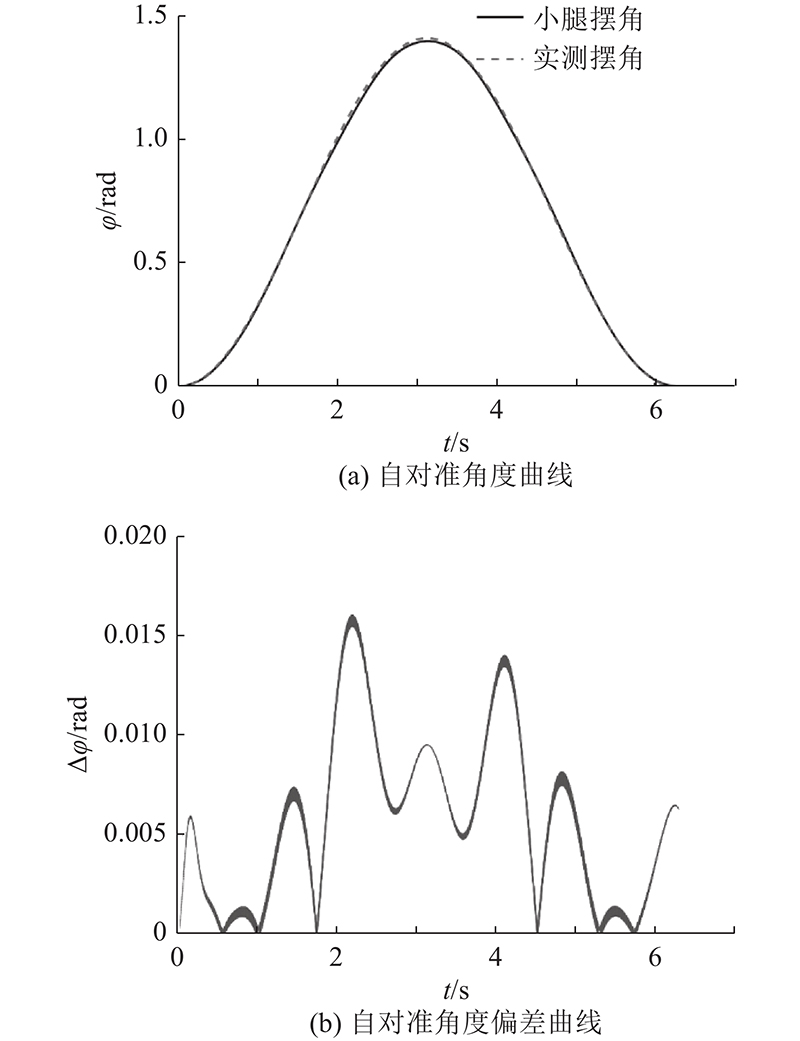
图 14 基于虚拟样机的人-机匹配实验结果
Fig.14 Experimental results of human-robot matching based on virtual prototype
4. 结 论
(1)针对人工膝关节与生物膝关节运动不匹配的问题,设计两自由度人工膝关节机构.
(2)基于粒子群算法,为这种两自由度人工膝关节设计人-机运动匹配方案,以实际测得的人体小腿运动数据为参考进行人机匹配操作.
(3)数字虚拟样机和联合仿真的结果证明,自对准人工膝关节在工作空间内可以匹配人体小腿的运动,缓解人工膝关节与人体小腿间的位置错位或方向不对准现象.
参考文献
Design and characterization of a novel knee articulation mechanism
[J].DOI:10.1515/ijame-2016-0037 [本文引用: 1]
Knee exoskeletons for gait rehabilitation and human performance augmentation: a state-of-the-art
[J].DOI:10.1016/j.mechmachtheory.2019.01.016 [本文引用: 1]
Self-alignment mechanisms for assistive wearable robots: a kineto-static compatibility method
[J].
Knee joint kinematics in gait and other functional activities measured using flexible electro-goniometry: how much knee motion is sufficient for normal daily life?
[J].DOI:10.1016/S0966-6362(00)00060-6 [本文引用: 2]
Seeing beyond morphology-standardized stress MRI to assess human knee joint instability
[J].DOI:10.3390/diagnostics11061035 [本文引用: 1]
Misalignment compensation for full human-exoskeleton kinematic compatibility: state of the art and evaluation
[J].DOI:10.1115/1.4042523 [本文引用: 2]
Tibio-femoral kinematics of the healthy knee joint throughout complete cycles of gait activities
[J].DOI:10.1016/j.jbiomech.2020.109915 [本文引用: 1]
Kinematic and dynamic analysis of an anatomically based knee joint
[J].DOI:10.1016/j.jbiomech.2010.02.001 [本文引用: 1]
Knee joint misalignment in exoskeletons for the lower extremities: effects on user’s gait
[J].DOI:10.1109/TRO.2015.2450414 [本文引用: 1]
膝关节康复外骨骼构型综合与结构设计
[J].DOI:10.11990/jheu.201601081 [本文引用: 1]
Configuration synthesis and structure design of knee rehabilitation exoskeleton
[J].DOI:10.11990/jheu.201601081 [本文引用: 1]
Biomechanical design of an agile, electricity-powered lower-limb exoskeleton for weight-bearing assistance
[J].DOI:10.1016/j.robot.2017.06.010 [本文引用: 1]
Adaptive knee joint exoskeleton based on biological geometries
[J].
变轴线生物融合式膝关节康复机构型综合
[J].DOI:10.3901/JME.2020.11.072 [本文引用: 1]
Type synthesis of rehabilitation mechanism of variable axis biofusion knee joint
[J].DOI:10.3901/JME.2020.11.072 [本文引用: 1]
The movement of the normal tibio-femoral joint
[J].DOI:10.1016/j.jbiomech.2004.02.006 [本文引用: 1]