浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(4): 702-711 doi: 10.3785/j.issn.1008-973X.2023.04.007

自动化技术、计算机技术

参数不确定和扰动下智能汽车路径跟踪控制

谭伟,, 刘景升,, 祖晖, 全洪乾

1. 重庆理工大学 车辆工程学院，重庆 400054

2. 招商局检测车辆技术研究院有限公司 国家智能网联汽车质量检验检测中心（重庆），重庆 401122

Intelligent vehicle path tracking control under parametric uncertainties and external disturbances

TAN Wei,, LIU Jing-sheng,, ZU Hui, QUAN Hong-qian

1. Vehicle Engineering Institute, Chongqing University of Technology, Chongqing 400054, China

2. National Intelligent Network Automobile Quality Inspection and Testing Center(Chongqing), China Merchants Testing Vehicle Technology Research Institute Limited Company, Chongqing 401122, China

收稿日期: 2022-04-10  

基金资助: 国家重点研发计划资助项目（2018YFB1600800）；重庆市教育委员会科学技术研究重点资助项目（KJZD-K201901103）

Received: 2022-04-10  

Fund supported: 国家重点研发计划资助项目（2018YFB1600800）；重庆市教育委员会科学技术研究重点资助项目（KJZD-K201901103）

作者简介 About authors

谭伟（1981—），男，副教授，硕导，从事车辆动力学控制的研究.orcid.org/0000-0002-0795-6086.E-mail：wtan@cqut.edu.cn , E-mail：wtan@cqut.edu.cn

摘要

针对智能汽车在路径跟踪过程中因模型参数不确定性、外部干扰、系统状态时变性非线性等导致跟踪精度较低、鲁棒性较差的问题，设计基于鲁棒预测控制（RMPC）的路径跟踪控制方法. 考虑轮胎的非线性特性，对轮胎侧偏刚度进行修正. 考虑纵向车速时变性，利用有限个多胞体顶点描述车辆纵向车速，建立离散的车辆多胞不确定模型. 根据Lyapunov渐进稳定性和无穷时域二次型性能指标，采用带松弛变量的线性矩阵不等式（LMI），求解优化问题. 利用改进后的离线鲁棒预测控制算法，提高了控制器的实时性并降低了保守性. 通过Simulink-Carsim联合仿真和硬件在环试验，验证了控制器的有效性. 仿真结果表明，所设计的控制器具有较好的跟踪精度和鲁棒性.

关键词： 智能汽车 ; 路径跟踪控制 ; 鲁棒预测控制(RMPC) ; 线性矩阵不等式（LMI） ; 参数不确定性

Abstract

A path tracking method based on robust model predictive control（RMPC） was designed aiming at the problems of low tracking accuracy and poor robustness caused by model parameter uncertainties, external disturbance, system state time-varying and nonlinearities in the process of path tracking of intelligent vehicles. The nonlinear characteristic of tire was considered, and the cornering stiffness of the tire was modified. Then the time-varying longitudinal speed was considered and a polytope with finite vertices was used to describe the longitudinal vehicle speed. A discrete vehicle polytopic uncertainty model was established. Linear matrix inequalities（LMI）with slack variables were derived to solve the optimization problem according to the Lyapunov asymptotic stability and quadratic performance index in infinite horizon. An improved offline robust model predictive control algorithm was proposed to improve the real-time performance of the controller and reduce its conservativeness. The effectiveness of the controller was verified by Simulink-Carsim co-simulation and hardware-in-the-loop tests. The simulation results showed that the designed controller had good tracking accuracy and robustness.

Keywords： intelligent vehicle ; path tracking control ; robust model predictive control (RMPC) ; linear matrix inequality (LMI) ; parameter uncertainty

PDF (2802KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

谭伟, 刘景升, 祖晖, 全洪乾. 参数不确定和扰动下智能汽车路径跟踪控制. 浙江大学学报(工学版)[J], 2023, 57(4): 702-711 doi:10.3785/j.issn.1008-973X.2023.04.007

TAN Wei, LIU Jing-sheng, ZU Hui, QUAN Hong-qian. Intelligent vehicle path tracking control under parametric uncertainties and external disturbances. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(4): 702-711 doi:10.3785/j.issn.1008-973X.2023.04.007

目前搭载先进驾驶辅助系统的智能汽车有利于减少交通事故和缓解交通压力，在未来智能交通系统中占据重要地位[1]. 路径跟踪控制是智能汽车自动驾驶技术的核心组成部分，但车辆路径跟踪系统中存在很强的非线性和时变特性，对控制算法的动态性能要求很高，如何提高控制器的跟踪精度和鲁棒性是亟须解决的重要问题.

目前已有众多学者对此进行研究并提出较多的方案. 陈亮等[2]设计基于前馈+反馈的线性二次调节器（linear quadratic regulator, LQR）控制策略，提高了车辆在高速大曲率道路上的跟踪精度和稳定性. 任玥等[3]采用最小模型误差准则降低观测器估计误差，设计基于观测器的自适应滑模控制器. 梁军等[4]利用径向基函数神经网络补偿预测误差，提高了车辆在复杂曲率变化道路下的跟踪精度. 张维刚等[5]基于轮胎侧偏角和滑移率的非线性函数设计模型预测控制器（model predictive control, MPC），提高了控制器在低附着路面下的跟踪精度和稳定性. 综上所述，模型预测控制算法的最大限制是在线计算量较大且对模型不确定性较敏感[6-7]. 为了处理模型的不确定性，吴海东等[8]在控制器设计中考虑轮胎侧偏刚度的不确定性，设计基于鲁棒预测控制的轨迹跟踪控制器，但该控制器未考虑纵向车速对控制性能的影响，在线优化较耗时. Cheng等[9]提出基于线性矩阵不等式（ linear matrix inequality, LMI）模型预测控制器的在线优化方法和离线计算方法，但忽略了外部扰动对跟踪性能的影响，且离线计算方法需要系统状态量已知，具有保守性的风险. 董晴等[10]设计基于线性变参数模型的鲁棒H∞跟踪控制器，但控制器设计中未考虑轮胎的非线性特性.

为了提高控制器的跟踪精度和鲁棒性，本文在预测模型中引入不确定因素，对轮胎侧偏刚度进行修正. 利用有限顶点多胞体描述车辆纵向车速，建立多胞不确定模型，有效地降低了模型适配问题对控制性能的影响. 在目标函数设计中，直接考虑外部扰动对控制性能的影响，将优化问题的求解转换为求解一组带松弛变量的线性矩阵不等式，增加了该优化问题的自由度，增强了所求控制律的最优性. 为了降低控制器的在线计算量和保守性，提出基于等比收缩椭圆集的离线优化方法，改进了传统基于渐进稳定椭圆不变集的离线方法较依赖已知系统状态量的缺陷.

1. 车辆多胞不确定模型

1.1. 二自由度车辆动力学模型

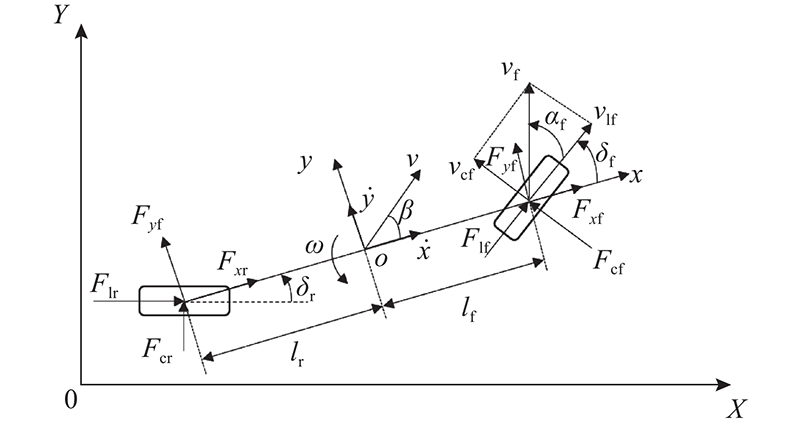
由于轮胎的非线性、模型参数的不确定性和时变性，很难建立精确的车辆模型[11]. 本文建立反映车辆侧向运动的二自由度车辆动力学模型，以便引入系统不确定性对车辆模型进行修正[12].

如图1所示，假设车辆纵向速度恒定，忽略悬架和空气阻力的影响，则车辆侧向动力学模型可以表示为

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   二自由度车辆动力学模型

Fig.1   Vehicle lateral 2-DoF dynamic model


$ \left. \begin{gathered} m({{\dot V}_y}+{{\dot V}_x}\omega ) = {F_{y{\text{f}}}}+{F_{y{\text{r}}}}, \\ {I_z}\dot \omega = {l_{\text{f}}}{F_{y{\text{f}}}} - {l_{\text{r}}}{F_{y{\text{r}}}}. \\ \end{gathered} \right\} $
(1)

式中：m和Iz分别为车辆质量和横摆转动惯量，ω为横摆角速度，Vx和Vy分别为车辆纵向车速和侧向车速，Fyf和Fyr分别为作用在车辆前、后轴的轮胎侧偏力，lf和lr分别为车辆质心到前、后轴的距离，β为车辆质心处的侧偏角.

当轮胎侧偏角较小时，轮胎侧偏力可以近似表示为轮胎侧偏角的线性函数：

$ \left. \begin{gathered} {F_{y{\text{f}}}} = {C_{\alpha_{\rm{f}}}}\left(\frac{{{l_{\text{f}}}\omega +{V_y}}}{{{V_x}}} - {\delta _{\text{f}}}\right), \\ {F_{y{\text{r}}}} = {C_{\alpha_{\rm{r}}}}\left(\frac{{{V_y} - {l_{\text{r}}}\omega }}{{{V_x}}}\right). \\ \end{gathered} \right\} $
(2)

式中：Cαf和Cαr分别为前、后轮的线性侧偏刚度，δf为前轮转角. 将式（2）代入式（1），可得二自由度车辆动力学模型.

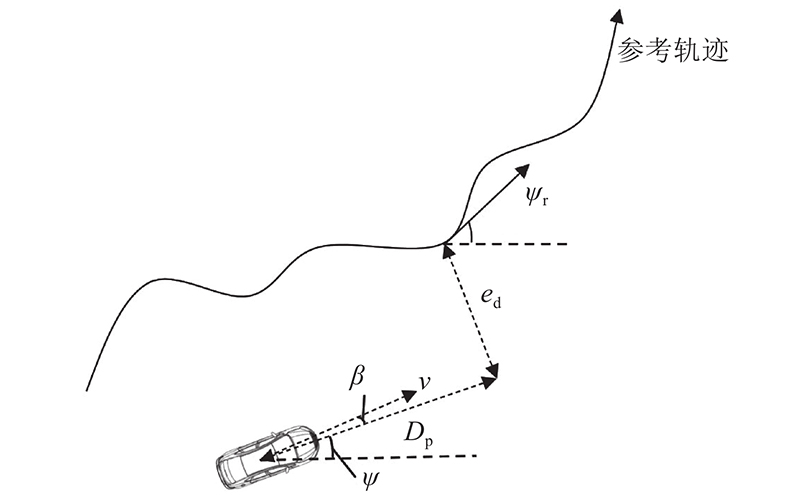
1.2. 跟踪误差模型

如图2所示，横向位移偏差ed定义为车辆当前位置到预瞄距离Dp处期望轨迹的距离，航向偏差eψ为车辆当前航向与预瞄点处期望轨迹的切线方向之间的角度误差. 预瞄距离可以根据车速和预瞄时间计算得到[13]. 采用小角度假设原则，则车辆跟踪误差模型可以表示为

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   车辆跟踪误差的模型

Fig.2   Model of vehicle tracking error


$ \left. \begin{gathered} {{\dot e}_{\text{d}}} = {e_{{{\text{ψ}} }}}{V_x}+{V_y}+\omega {D_{\text{p}}}, \\ {{\dot e}_{\text{ψ}}} = {V_x}{\rho _{\text{p}}} - \omega . \\ \end{gathered} \right\} $
(3)

式中：ρp为预瞄点处期望轨迹的曲率.

车辆实际行驶时，由于道路产生的随机扰动力作用于轮胎，使得轮胎力发生波动，称为外部扰动，常表现为道路曲率对车辆的干扰[14]. 道路曲率会影响车辆的侧向运动和横摆运动，因此需要充分考虑该因素对控制系统跟踪性能的影响.

综合式（1）~（3），取x =[ed, eψ, Vy, ω]T为系统状态变量，将δf作为控制输入，道路曲率ρp作为外部扰动输入，得到考虑道路曲率的车辆跟踪误差模型如下：

$ {\boldsymbol{\dot x}}(t) = {\boldsymbol{Ax}}(t)+{\boldsymbol{Bu}}(t)+{\boldsymbol{Ed}}(t). $
(4)

式中：u(t)为控制输入，d(t)为外部扰动输入，

$ \begin{gathered} {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&{{V_x}}&1&{ - {D_{\rm{p}}}} \\ 0&0&0&{ - 1} \\ 0&0&{\dfrac{{{C_{\alpha_{\rm{f}}}}+{C_{\alpha_{\rm{r}}}}}}{{m{V_x}}}}&{\dfrac{{{l_{\text{f}}}{C_{\alpha_{\rm{f}}}} - {l_{\text{r}}}{C_{\alpha_{\rm{r}}}}}}{{m{V_x}}} - {V_x}} \\ 0&0&{\dfrac{{{l_{\text{f}}}{C_{{\rm{\alpha_ f}}}} - {l_{\text{r}}}{C_{\alpha_{\rm{r}}}}}}{{{I_z}{V_x}}}}&{\dfrac{{{l_{\text{f}}^2}{C_{\alpha_{\rm{f}}}}+l_{\text{r}}^2{C_{{\rm{\alpha _ r}}}}}}{{{I_z}{V_x}}}} \end{array}} \right], \\ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ { - {{{C_{\alpha_{\rm{f}}}}}/m}} \\ { - {{{l_{\text{f}}}{C_{\alpha_{\rm{f}}}}}/{{I_z}}}} \end{array}} \right],\;{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{V_x}} \\ 0 \\ 0 \end{array}} \right]. \\ \end{gathered} $

1.3. 车辆多胞不确定模型

对于模型不确定性而言，即所建立的数学模型与真实的物理模型之间存在偏差，该偏差直接作用在系统控制输入上，对输入量形成扰动，常表现为模型参数不确定性[14]. 对于车辆跟踪系统而言，由于轮胎非线性和纵向车速时变性，对于车辆动力学的建模不可避免地存在误差，需要对车辆模型进行修正.

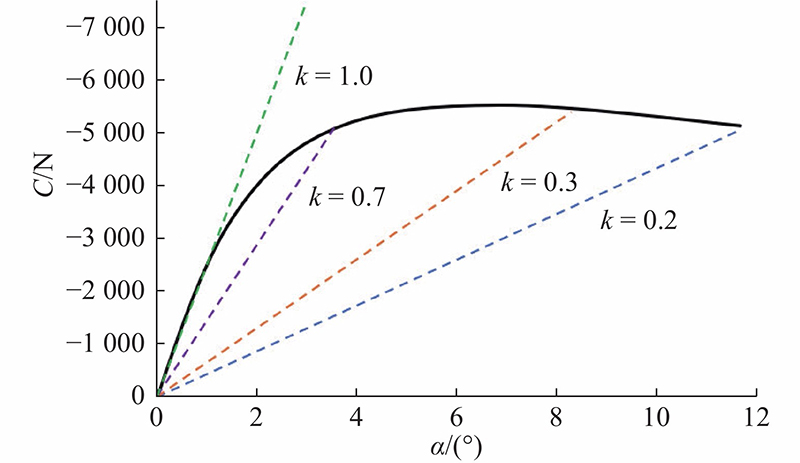
当车辆失稳时，轮胎进入非线性区域，此时线性二自由度车辆动力学模型不能准确地描述车辆的动力学特性. 当侧向加速度或轮胎侧偏角较大时，很难获得精确的轮胎侧偏力. 轮胎侧偏力受到轮胎充气压力、垂直载荷和路面附着系数等因素的影响，因此其值是不确定的[15]. 在控制器设计中，考虑侧偏刚度的变化，对轮胎侧偏刚度进行如下修正：

$ \left. \begin{gathered} {C_{\text{f}}} = {C_{\alpha_{\rm{f}}}}+{k_{\text{f}}}{{\tilde C}_{\alpha_{\rm{f}}}}, \\ {C_{\text{r}}} = {C_{\alpha_{\rm{r}}}}+{k_{\text{r}}}{{\tilde C}_{\alpha_{\rm{r}}}}. \\ \end{gathered} \right\} $
(5)

式中： ${{\tilde C}_{\alpha_{\rm{f}}}} $、 ${{\tilde C}_{\alpha_{\rm{r}}}} $分别为前、后轮侧偏刚度的调整基准值；kf和kr为轮胎侧偏刚度的调整因子，满足|kf|≤1，|kr|≤1. 为了减小计算复杂度，设定kf＝kr，该参数表明了轮胎的非线性特性.

轮胎侧偏刚度的调整因子受到轮胎侧偏角与路面附着系数因素的影响，可以根据轮胎侧偏角与轮胎侧偏力之间的关系得到.

当路面附着系数为0.85时，由于车辆前轮和后轮所处的路况通常是一致的，轮胎侧偏力（前轮或后轮）的非线性特性如图3所示。图3中，为了减小计算复杂度，根据式（5）中kf＝kr的设定，前、后轮的侧偏特性可用同一曲线表示，用C表示前、后轮的侧偏刚度，α表示前、后轮的侧偏角。调整因子的范围可以由图3的虚线得到，即0.2≤ kf、kr≤ 1.0。

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   轮胎侧偏特性

Fig.3   Tire cornering characteristic


将式（5）代入式（4），可得

$ \left. \begin{gathered} {\boldsymbol{A}}(t) = {{\boldsymbol{A}}_0}(t)+\Delta {\boldsymbol{A}}(t), \\ {\boldsymbol{B}}(t) = {{\boldsymbol{B}}_0}(t)+\Delta {\boldsymbol{B}}(t). \\ \end{gathered} \right\} $
(6)

式中：A0和B0均为系统中系数矩阵的标称项（名义项），由标称项A0和B0组成的模型称为标称模型（名义模型），即忽略了模型不确定性后得到的名义系统模型；ΔA和ΔB为系统中系数矩阵的摄动项，表征了系统的不确定特性，即轮胎侧偏刚度在一定范围内变化.

当智能汽车进行路径跟踪时，纵向车速是变化的. 考虑纵向车速一般是有界的，满足Vx,min≤Vx≤Vx,max，定义

$ \left. \begin{gathered} {V_{x,\max }} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_1},\;{V_{x,\min }} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_2}, \\ 1/{V_{x,\min }} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_1},\;1/{V_{x,\max }} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_2}. \\ \end{gathered} \right\} $
(7)

多胞体顶点的个数选择影响控制器的计算复杂度，因此选择22=4个顶点的多胞体，覆盖不确定参数{Vx, 1/Vx}的所有可能选择.

时变参数Vx和1/Vx可以通过顶点处的参数求和来计算得到：

$ \left. \begin{gathered} {V_x} = \sum\limits_{j = 1}^2 {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_j}(t){{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_j}} , \\ 1/{V_x} = \sum\limits_{j = 1}^2 {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_j}(t){{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_j}} . \\ \end{gathered} \right\} $
(8)

时变参数的权重系数通过下式计算得到：

$ \left. \begin{gathered} {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_1}(t) = \frac{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_1} - {V_x}}}{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_1} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_2}}},\;{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_2}(t) = \frac{{{V_x} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_2}}}{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_1} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } }_2}}}, \\ {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_1}(t) = \frac{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_1} - 1/{V_x}}}{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_1} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_2}}},\;{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_2}(t) = \frac{{1/{V_x} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_2}}}{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_1} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } }_2}}}. \\ \end{gathered} \right\} $

将多胞体的权重系数进行组合，作如下定义：

$ \left. \begin{gathered} {\sigma _1} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_1},\;{\sigma _2} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_1}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_2}, \\ {\sigma _3} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_2}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_1},\;{\sigma _4} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma } }_2}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma } }_2}, \\ \sum\limits_{j = 1}^4 {{\sigma _j}(t) = 1,\;{\sigma _j}(t) \geqslant 0} . \end{gathered} \right\} \\ $
(9)

综合式（4）~（9），车辆动力学模型的表达式为

$\left. \begin{gathered} {\boldsymbol{\dot x}}(t) = \sum\limits_{j = 1}^4 {{\sigma _j}(t)\left[ {{{\boldsymbol{A}}_j}{\boldsymbol{x}}(t)+{{\boldsymbol{B}}_j}{\boldsymbol{u}}(t)+{{\boldsymbol{E}}_j}{\boldsymbol{d}}(t)} \right]} , \\ {{\boldsymbol{A}}_j} = {{\boldsymbol{A}}_{0j}}+\Delta {{\boldsymbol{A}}_j},\;{{\boldsymbol{B}}_j} = {{\boldsymbol{B}}_{0j}}+\Delta {{\boldsymbol{B}}_j}. \end{gathered}\right\} $
(10)

对式（10）进行离散化，离散后的车辆多胞不确定模型表示为

$ \left. \begin{gathered} {\boldsymbol{x}}(k+1) = {\boldsymbol{Ax}}(k)+{\boldsymbol{Bu}}(k)+{\boldsymbol{Ed}}(k), \\ {\boldsymbol{A}} = \sum\limits_{j = 1}^4 {{\sigma _j}{{\boldsymbol{A}}_j},{\boldsymbol{B}} = \sum\limits_{j = 1}^4 {{\sigma _j}{{\boldsymbol{B}}_j},{\boldsymbol{E}} = \sum\limits_{j = 1}^4 {{\sigma _j}{{\boldsymbol{E}}_j}} ,} } \\ {\boldsymbol{A}},{\boldsymbol{B}},{\boldsymbol{E}} \in \varOmega , \\ \varOmega = {\rm{Co}}\left\{ {\left[ {{{\boldsymbol{A}}_1}|{{\boldsymbol{B}}_1}|{{\boldsymbol{E}}_1}} \right], \cdots, \left[ {{{\boldsymbol{A}}_4}|{{\boldsymbol{B}}_4}|{{\boldsymbol{E}}_4}} \right]} \right\}. \\ \end{gathered} \right\} $
(11)

式中：Ω定义为凸多胞体，Co表示多胞体的凸壳，[Aj, Bj]为凸壳的顶点. 多胞不确定模型常用于描述线性变参数系统，系统模型中系数矩阵在约束域Ω中变化[14]. 预测模型式（10）可以根据车辆实时速度更新顶点，该顶点可以覆盖无穷时域内系统系数矩阵变化的所有可能情况，提高预测系统未来响应的准确性，降低模型失配对控制系统的影响. 结合线性矩阵不等式的优化方法，将优化问题转换为凸优化问题进行求解.

2. 路径跟踪控制器设计

对于离散的多胞不确定系统式（11），采用“min-max”优化思想，考虑由不确定性引起的最坏情况，通过求解线性矩阵不等式获得最优控制律，保证控制系统的动态性能.

2.1. 基于RMPC的状态反馈控制器设计

考虑到系统式（11）中含有扰动项，定义无穷时域二次型性能指标：

$ {J_\infty }(k) = \sum\limits_{i = 0}^\infty {l(k+i|k)} . $
(12)

式中：

$ \begin{array}{c} l(k+i|k) ={{\boldsymbol{x}}^{\text{T}}}(k+i|k){\boldsymbol{Qx}}(k+i|k)+ \\ {{\boldsymbol{u}}^{\rm{T}}}(k+i|k){\boldsymbol{Ru}}(k+i|k) - \tau {{\boldsymbol{d}}^{\text{T}}}(k+i|k){\boldsymbol{d}}(k+i|k). \\ \end{array} $

其中矩阵Q和R为对称正定的加权矩阵，x(k+i|k)为系统在k时刻对k+1时刻的状态变量x的预测值.

该性能指标中的第1项反映了控制器对目标轨迹的跟踪性能. 第2项用于对系统控制量u进行惩罚限制，即对系统施加控制量u，使得性能指标最小化，保证系统的稳定性. 第3项为外部扰动d对控制系统的影响，扰动的存在通常使得控制系统不稳定，即使得性能指标朝相反的趋势变化，由此可知扰动量d和控制量u是对立的. 该性能指标的选取来源于鲁棒H∞控制[16- 17]. 根据文献[18]可知，τ通常为正标量，这里取τ = 1.

采用“min-max”思想，求解如下的优化问题：

$ \left.\begin{gathered} \mathop {\min }\limits_{{\boldsymbol{u}}(k+i|k),i \geqslant 0} \; \mathop {\max }\limits_{{\boldsymbol{A}}(k+i|k),{\boldsymbol{B}}(k+i|k),{\boldsymbol{E}}(k+i|k) \in \varOmega } {J_\infty }. \\ {\rm{s}}.{\rm{t}}. \\ |{\boldsymbol{u}}(k+i|k)| \leqslant {u_{\max }}, \\ ||{\boldsymbol{d}}(k)|| \leqslant \rho , \\ {\boldsymbol{x}}(k+i+1|k) = {\boldsymbol{A}}(k+i){\boldsymbol{x}}(k+i|k)+ \\ \quad {\boldsymbol{B}}(k+i){\boldsymbol{u}}(k+i|k)+{\boldsymbol{E}}(k+i){\boldsymbol{d}}(k+i|k). \end{gathered} \right\}$
(13)

式中：umax和ρ分别为控制输入约束和扰动约束.

无穷时域优化涉及到无穷个决策变量，一般无法直接求解，因此需要找到性能指标的上界，采用如下的控制律最小化该上界[19]：

$ {\boldsymbol{u}}(k+i|k) = {\boldsymbol{Kx}}(k+i|k);\;i \geqslant 0. $
(14)

为了定义性能指标的上界，定义如下的二次Lyapunov-Krasovskii函数：

$ V({\boldsymbol{x}}) = {{\boldsymbol{x}}^{\text{T}}}{\boldsymbol{Px}},{\boldsymbol{P}} > {\boldsymbol{0}}. $
(15)

该函数满足下列不等式：

$ \begin{gathered} V({\boldsymbol{x}}(k+i+1|k)) - V({\boldsymbol{x}}(k+i|k)) \leqslant - l(k+i|k). \end{gathered} $
(16)

为了使性能函数值有界，需要满足：x(∞|k)=0，V(x(∞|k))=0. 将式（16）从i = 0到i = ∞进行叠加，可得

$ - V({\boldsymbol{x}}(k|k)) \leqslant - {J_\infty }(k). $
(17)

最小化性能指标等价于最小化V(x(k|k))，即

$ \mathop {\max }\limits_{{\boldsymbol{A}}(k+i|k),{\boldsymbol{B}}(k+i|k),{\boldsymbol{E}}(k+i|k) \in \varOmega } {J_\infty } \leqslant V({\boldsymbol{x}}(k|k)). $
(18)

定义标量γ > 0，令

$ V({\boldsymbol{x}}(k|k)) \leqslant \gamma , $
(19)

则最小化RMPC性能指标J∞(k)等价于下式：

$ \min\; {J_\infty }(k) = \min\; {{\boldsymbol{x}}^{\text{T}}}(k){\boldsymbol{Px}}(k) \leqslant \gamma . $
(20)

鲁棒预测控制的核心思想如下：在每个采样时刻k，寻找状态反馈控制律u(k|k)=Kx(k|k)使得目标函数的上界V(x(k|k))最小化. 在下一个采样时刻k+1，根据测得的状态量x(k+1)，重复以上优化过程，得到新的反馈矩阵K.

对于离散的车辆多胞不确定系统（式11），若存在正定矩阵X、矩阵Gj、Yj和正标量0 < λ < 1.0，则该优化问题的求解可以转换为实时求解如下的LMI问题.

$ \begin{gathered} \mathop {\min }\limits_{\gamma ,{{\boldsymbol{X}}_j},{{\boldsymbol{Y}}_j},{{\boldsymbol{G}}_j},\lambda } \gamma . \\ {\rm{s}}.{\rm{t}}. \\ \end{gathered} $
(21)

$ \left[ {\begin{array}{*{20}{c}} 1&* \\ {{\boldsymbol{x}}(k)}&{\boldsymbol{X}} \end{array}} \right] \geqslant {\boldsymbol{0}}, $
(22)

$ \left[ {\begin{array}{*{20}{c}} {( - 1+\lambda )({{\boldsymbol{G}}_j}+{\boldsymbol{G}}_j^{\text{T}} - {\boldsymbol{X}})}&*&* \\ {\boldsymbol{0}}&{ - \dfrac{\lambda }{{{\rho ^2}}}{\boldsymbol{I}}}&* \\ {{{\boldsymbol{A}}_j}{{\boldsymbol{G}}_j}+{{\boldsymbol{B}}_j}{{\boldsymbol{Y}}_j}}&{{{\boldsymbol{E}}_j}}&{ - {\boldsymbol{X}}} \end{array}} \right] \leqslant {\boldsymbol{0}}, $
(23)

$ \left[ {\begin{array}{*{20}{c}} {u_{\max }^2{\boldsymbol{I}}}&* \\ {{\boldsymbol{Y}}_j^T}&{{\boldsymbol{G}}_j^{\text{T}}+{{\boldsymbol{G}}_j} - {\boldsymbol{X}}} \end{array}} \right] \geqslant {\boldsymbol{0}}, $
(24)

$ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{X}} - {{\boldsymbol{G}}_j} - {\boldsymbol{G}}_j^{\text{T}}}&*&*&*&* \\ {\boldsymbol{0}}&{ - \tau \gamma {\boldsymbol{I}}}&*&*&* \\ {{{\boldsymbol{A}}_j}{{\boldsymbol{G}}_j}+{{\boldsymbol{B}}_j}{{\boldsymbol{Y}}_j}}&{\gamma {{\boldsymbol{E}}_j}}&{ - {\boldsymbol{X}}}&*&* \\ {{\boldsymbol{Q}}{{\boldsymbol{G}}_j}}&{\boldsymbol{0}}&{\boldsymbol{0}}&{ - \gamma {\boldsymbol{Q}}}&* \\ {{\boldsymbol{R}}{{\boldsymbol{Y}}_j}}&{\boldsymbol{0}}&{\boldsymbol{0}}&{\boldsymbol{0}}&{ - \gamma {\boldsymbol{R}}} \end{array}} \right] \geqslant {\boldsymbol{0}}. $
(25)

通过求解上述优化问题，得到Yj和Gj. 控制律u(k)由下式计算可得：

$ {\boldsymbol{u}}(k) = \sum\limits_{j = 1}^4 {{\sigma _j}(k)} {{\boldsymbol{Y}}_j}{\boldsymbol{G}}_j^{ - 1}{\boldsymbol{x}}(k). $
(26)

由于该LMI约束中含有松弛项G，增大了优化问题的自由度，增强了所求控制律的最优性. 与Kothare等[6]提出的LMI优化方法相比，本文提出的“min-max RMPC”控制策略具有更小的保守性.

2.2. 鲁棒预测控制器的离线计算方法

对于高阶系统或当系统参数变化较快时，优化问题式（21）的在线求解计算量较大，给控制器带来沉重的计算负担.

在智能汽车的跟踪过程中，需要对外界环境进行快速响应，以保证安全性，控制周期应小于20 ms，因此需要显著地降低控制器的在线计算量，提高实时性[11].

Wan等[20]提出基于渐进稳定椭圆不变集的离线方法，利用该方法能够有效地降低在线计算量. 渐进稳定椭圆不变集的局限是需要系统状态量已知，会带来保守性的风险.

本文对上述方法进行改进，设计了基于等比收缩椭圆集的离线计算方法[21]. 该方法只须系统初始状态量已知，能够在一定程度上降低控制系统的保守性.

定义等比收缩椭圆集如下. 考虑离散后的车辆多胞不确定模型式（11），状态空间的子集Θ={x∈Rn|xTX−1x≤ 1}为等比收缩椭圆集，具有如下特征：若x(k)∈Θ，则x(k+1)∈Θp. 其中Θp={x∈Rn|xTX−1x≤υ 2}，υ∈(0,1.0).

若系统状态处于椭圆集Θp中，则最小收敛速度为υ.

引理2.1　对于车辆多胞不确定模型式（11），若系统有最小收缩率υ，则须满足下式的LMI：

$ \left[ {\begin{array}{*{20}{c}} {{\omega ^2}{\boldsymbol{X}}}&* \\ {{{\boldsymbol{A}}_j}{{\boldsymbol{G}}_j}+{{\boldsymbol{B}}_j}{{\boldsymbol{Y}}_j}}&{\boldsymbol{X}} \end{array}} \right] \geqslant {\boldsymbol{0}};\;j = 1, \cdots ,4. $
(27)

为了减少保守性，设置υ接近于1. 当υ = 1时，该椭圆集变为文献[20]的渐进稳定椭圆不变集. 此处υ可以取0.97.

综上所述，基于“min-max RMPC”的离线计算方法可以描述为算法1.

算法1　基于鲁棒预测控制的路径跟踪控制器离线计算方法

考虑纵向车速的变化范围：Vx,min≤Vx≤Vx,max.

首先设定i = 1.

1）离线地，通过优化问题式（21）计算处于系统状态xi并满足LMI（27）和υ2Xi<Xi+1<Xi的最优参数γi、Xi、Yi、Gi、λi，并保存参数Ki在二维查找表中.

2）如果i<N，则选择系统状态xi+1满足xTi+1Xi−1xi+1 = υ2xiTXi−1xi. 令i = i+1并返回1）.

3）假设系统初始状态x(0)满足：

$ ||{{\boldsymbol{x}}_{j+1}}|{|_{{\boldsymbol{X}}_j^{ - 1}}} \leqslant ||{\boldsymbol{x}}(0)|{|_{{\boldsymbol{X}}_j^{ - 1}}} \leqslant ||{{\boldsymbol{x}}_j}|{|_{{\boldsymbol{X}}_j^{ - 1}}},j \in \{ 1, \cdots ,N\} . $
(28)

式中： $||{{\boldsymbol{x}}}|{|_{{\boldsymbol{X}}^{ - 1}}} $=xTX−1x.

在线地，若k时刻系统状态为x(k)，则施加如下的控制律：

$ {\boldsymbol{u}}(k) = \left\{ \begin{gathered} {{\boldsymbol{K}}_{k+j}}{\boldsymbol{x}}(k),\;k+j \leqslant N; \\ {{\boldsymbol{K}}_N}{\boldsymbol{x}}(k),\;k+j > N. \\ \end{gathered} \right. $
(29)

基于当前时刻的车速和当前时刻系统状态量，在车速-状态二维查找表中寻找满足优化条件的参数γi、Xi、Yi、Gi、λi，对系统施加相应的控制律，以此实现车辆对参考路径的跟踪.

3. 仿真及分析

为了验证所设计的路径跟踪控制器的有效性，分别开展Simulink-Carsim联合仿真和硬件在环试验. 在相同的仿真环境下，对以下3种控制器进行对比. 1）设计基于标称模型的模型预测控制器（MPC）[22]，该控制器采用基于名义侧偏刚度的线性预测模型. 2）设计考虑侧偏刚度不确定性的LMI-MPC控制器[11]，在控制器设计中忽略外部扰动，采用Kothare等[6]提出的一组LMI在线优化方法和基于渐进稳定不变椭圆集的离线方法[20]. 3）本文设计考虑模型不确定性和外部扰动的鲁棒预测控制器（RMPC），采用带松弛变量的LMI在线优化方法和基于等比收缩椭圆集的离线计算方法. 车辆的基本参数如表1所示.

表 1   车辆参数

Tab.1  Vehicle parameters

参数 数值
m/kg 1 230
Iz/(kg·m2) 1 343.1
lf/m 1.22
lr/m 1.36
Cαf/(N·rad−1) −56 864
Cαr/(N·rad−1) −66 864

新窗口打开| 下载CSV


3.1. 不同控制器的跟踪性能对比

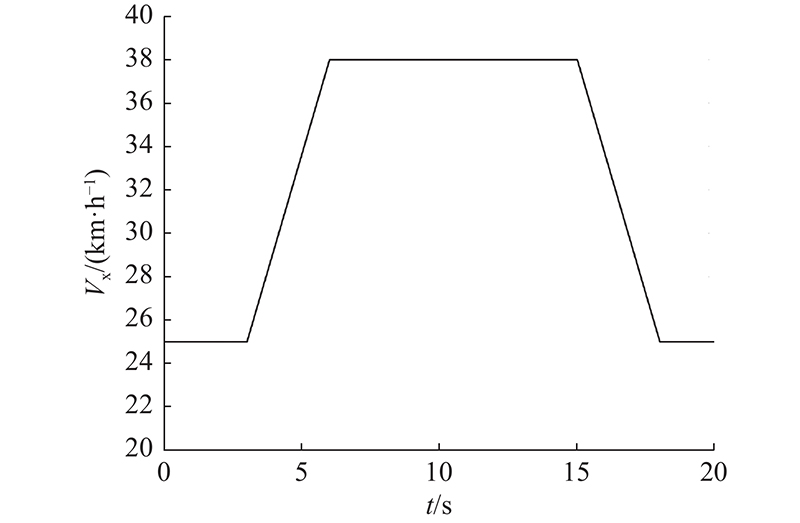
如图4所示，车辆纵向车速随时间变化而变化，最高车速和最低车速分别为38和25 km/h，路面附着系数为0.85.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   参考车速

Fig.4   Reference velocity


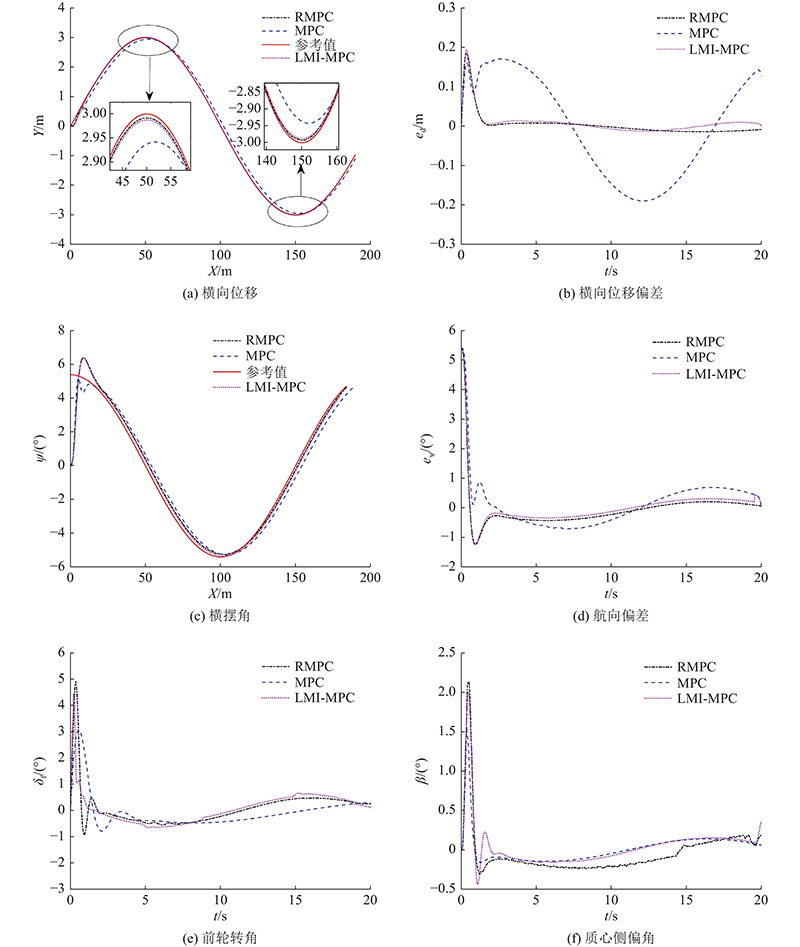
如图5所示为控制器在正弦曲线下的跟踪结果. 从图5（a）、（c）可以看出，3种控制器均能够较好地跟踪参考路径. 表2中，edm为横向位移偏差的最大值，edR为横向跟踪偏差的均方根，eψm为航向偏差的最大值，eψR为航向偏差的均方根. 从表2可知，RMPC控制器具有更好的跟踪精度，edm为0.184 5 m，edR为0.030 7 m. LMI-MPC控制器的edm为0.192 7 m，edR为0.031 6 m. MPC控制器的edm为0.1887 m，edR为0.126 9 m. 3种控制器的航向偏差在刚开始均较大，但RMPC控制器的航向偏差最小，eψR为0.755 5°. 从图5（b）、（d）可知，3种控制器中，RMPC控制器横向位移偏差和航向偏差的收敛速度最快，保守性较小. 图5（e）表明3种控制器的控制量前轮转角均在约束范围（−10°~10°）内. 从图5（f）可知，3种控制器的质心侧偏角均在理想范围（−3°~3°）内，表明3种控制器在保证跟踪精度的同时具有较好的操纵稳定性.

表 2   控制器的跟踪性能对比

Tab.2  Tracking performance comparison of controllers

控制器 edm/m edR/m eψm/(°) eψR/(°)
MPC 0.1887 0.1269 5.3933 0.9250
LMI-MPC 0.1927 0.0316 5.3901 0.7668
RMPC 0.1845 0.0307 5.3894 0.7555

新窗口打开| 下载CSV


图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   不同控制器的路径跟踪仿真结果

Fig.5   Path tracking simulation results for different controllers


综上所述，相较于MPC控制器和LMI-MPC控制器，基于RMPC的路径跟踪控制器在跟踪精度和收敛速度上更优.

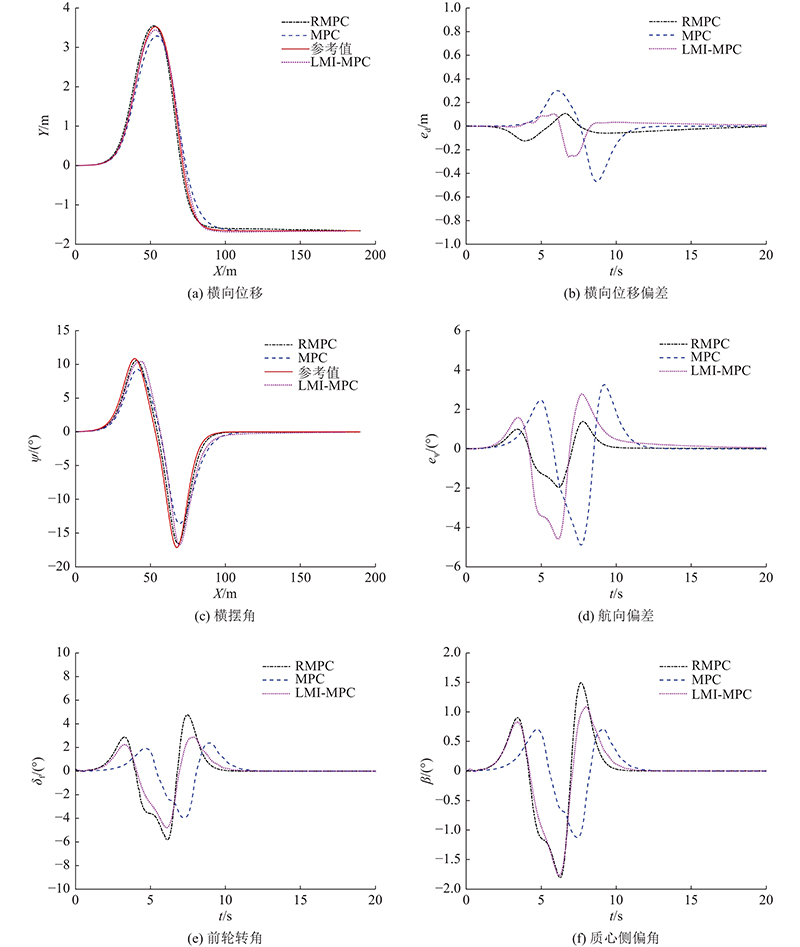
双移线工况常用来模拟车辆超车、换道，能够有效地验证车辆的稳定性. 如图6所示为3种路径跟踪控制器在双移线曲线下的跟踪结果. 图6（a）、（c）表明3种控制器均具有较好的跟踪效果. 从表3可知，RMPC控制器具有更好的跟踪性能，edm为0.123 8 m，edR为0.041 2 m，eψm为1.9488°，eψR为0.625 4°. LMI-MPC控制器的最大横向位移偏差绝对值为0.258 2 m，edR为0.0676 m，eψm为4.533 4°，eψR为1.4212°. MPC控制器的edm为0.465 5 m，edR为0.158 2 m，eψm为4.855 7°，eψR为1.741 4°. 由此可知，考虑模型不确定性的LMI-MPC控制器和RMPC控制器的控制性能均优于基于标称模型的MPC控制器，这是由于2种控制器能够较好地补偿模型不确定性带来的扰动. 如图6（e）所示为3种控制器的控制量前轮转角，控制输出均在约束范围内，RMPC控制器的响应速度更快. 如图6（f）所示为3种控制器的质心侧偏角随时间的变化，均远小于极限值，RMPC控制器的质心侧偏角与MPC控制器和LMI-MPC控制器相比略大，因为鲁棒预测控制器具有较大的控制量输入.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   不同控制器的路径跟踪仿真结果

Fig.6   Path tracking simulation results for different controllers


表 3   控制器的跟踪误差对比

Tab.3  Tracking error comparison of controller

控制器 edm/m edR/m eψm/(°) eψR/(°)
MPC 0.4655 0.1582 4.8557 1.7414
LMI-MPC 0.2582 0.0676 4.5534 1.4212
RMPC 0.1238 0.0412 1.9488 0.6254

新窗口打开| 下载CSV


综上所述，利用设计的控制器，能够快速跟踪期望路径，具备较好的操纵稳定性.

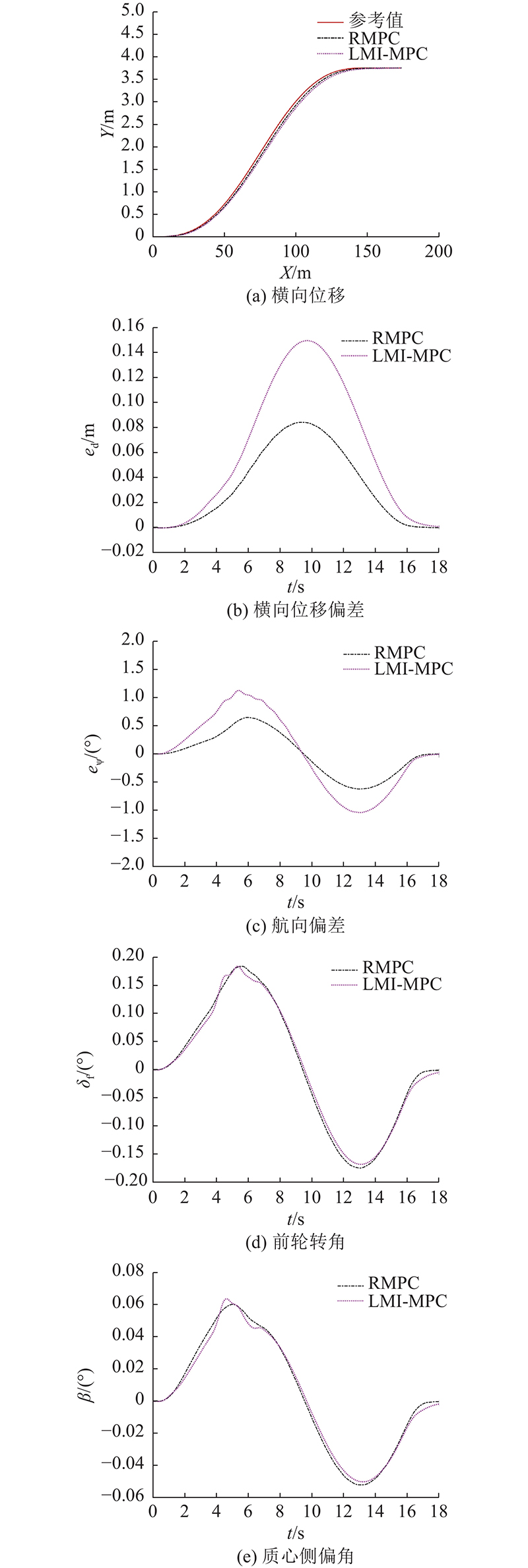
3.2. 硬件在环试验验证

为了验证控制器的有效性和实时性，基于NI实时仿真系统搭建硬件在环试验平台，如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   硬件在环系统

Fig.7   Hardware-in-loop system


在Simulink/Carsim联合仿真平台上编写控制策略，完成模型搭建. 利用Matlab RTW自动生成功能将仿真模型编译成C代码，分别导入到实时仿真机和控制器中，设置相应的数据采集接口和通信接口. 在NI VeriStand软件搭建上位机界面，对数据进行实时监测. HIL系统的部分硬件型号如表4所示.

表 4   部分硬件型号

Tab.4  Some hardware model

硬件名称 型号
实时处理器 NI/PXI-8119
主机箱 NI/PXI-1044
CAN卡 NI/PXI-8512
数字I/O板卡 NI/PXI-6514

新窗口打开| 下载CSV


从图8可知，在换道工况下所设计的RMPC控制器的控制性能优于LMI-MPC控制器. 从图8（b）、（c）可知，横向位移偏差和航向偏差均小于LMI-MPC控制器，表明所设计的RMPC控制器能够较好地抑制不确定性带来的扰动误差并快速跟踪期望路径，具有较小的保守性. 前轮转角和质心侧偏角均变化平缓，表明所设计的控制器具有较好的侧向稳定性. 综上所述，设计的RMPC控制器具有较好的鲁棒性和跟踪精度.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   硬件在环试验结果

Fig.8   Hardware-in-loop test results


4. 结　语

本文基于鲁棒预测控制算法，设计智能汽车路径跟踪控制器. 在控制器设计中，考虑轮胎侧偏刚度的不确定性和纵向车速的时变性及外部扰动等问题，建立车辆多胞不确定模型. 通过一组带松弛变量的线性矩阵不等式，最小化“min-max”情况下的无穷时域二次型目标函数. 为了降低控制器的在线计算负担和保守性，设计在线优化与离线计算的综合优化方法. 为了验证所设计的控制器的有效性，分别进行Simulink-Carsim联合仿真和硬件在环试验. 两者结果均表明所提出的控制器具有较好的跟踪精度和鲁棒性. 在未来的工作中，将研究车辆以较高车速行驶在低附着路面极限工况下的路径跟踪问题，对所提出的控制策略在实车上进行进一步的验证.

参考文献

SUN Yong, WANG Xiang-yu, LI Liang, et al

Modelling and control for economy-oriented car-following problem of hybrid electric vehicle

[J]. IET Intelligent Transport Systems, 2019, 13 (5): 825- 833

DOI:10.1049/iet-its.2018.5421      [本文引用: 1]

陈亮, 秦兆博, 孔伟伟, 等

基于最优前轮侧偏力的智能汽车LQR横向控制

[J]. 清华大学学报: 自然科学版, 2021, 61 (9): 906- 912

[本文引用: 1]

CHEN Liang, QIN Zhao-bo, KONG Wei-wei, et al

Lateral control using LQR for intelligent vehicles based on optimal front-tire lateral force

[J]. Journal of Tsinghua University: Science and Technology, 2021, 61 (9): 906- 912

[本文引用: 1]

任玥, 冀杰, 赵颖, 等

基于最小模型误差估计的智能汽车路径跟踪控制

[J]. 汽车工程, 2021, 43 (4): 580- 587

[本文引用: 1]

REN Yue, JI Jie, ZHAO Ying, et al

Path tracking control of intelligent vehicle based on minimal model error estimation

[J]. Automotive Engineering, 2021, 43 (4): 580- 587

[本文引用: 1]

梁军, 朱方博, 蔡英凤, 等

面向复杂曲率变化的智能车路径跟踪控制

[J]. 汽车工程, 2021, 43 (12): 1771- 1779

[本文引用: 1]

LIANG Jun, ZHU Fang-bo, CAI Ying-feng, et al

Intelligent vehicle path tracking control based on complex curvature variation

[J]. Automotive Engineering, 2021, 43 (12): 1771- 1779

[本文引用: 1]

张维刚, 张朋, 韦昊, 等

一种基于LTVMPC改进的无人驾驶汽车路径跟踪控制算法

[J]. 湖南大学学报: 自然科学版, 2021, 48 (10): 67- 73

[本文引用: 1]

ZHANG Wei-gang, ZHANG Peng, WEI Hao, et al

An improved path tracking control algorithm for autonomous vehicle based on LTVMPC

[J]. Journal of Hunan University: Natural Sciences, 2021, 48 (10): 67- 73

[本文引用: 1]

KOTHARE M V, BALAKRISHNAN V, MORARI M

Robust constrained model predictive control using linear matrix inequalities

[J]. Automatica, 1996, 32 (10): 1361- 1379

DOI:10.1016/0005-1098(96)00063-5      [本文引用: 3]

谢澜涛, 谢磊, 苏宏业

不确定系统的鲁棒与随机模型预测控制算法比较研究

[J]. 自动化学报, 2017, 43 (6): 24

[本文引用: 1]

XIE Lan-tao, XIE Lei, SU Hong-ye

Comparison of robust and stochastic model predictive control algorithms for uncertain systems

[J]. Journal of Automation, 2017, 43 (6): 24

[本文引用: 1]

吴海东, 司振立

基于线性矩阵不等式的智能车轨迹跟踪控制

[J]. 浙江大学学报: 工学版, 2020, 54 (1): 110- 117

[本文引用: 1]

WU Hai-dong, SI Zhen-li

Intelligent vehicle trajectory tracking control based on linear matrix inequality

[J]. Journal of Zhejiang University: Engineering Science, 2020, 54 (1): 110- 117

[本文引用: 1]

CHENG S, LI L, CHEN X, et al

Model-predictive-control-based path tracking controller of autonomous vehicle considering parametric uncertainties and velocity-varying

[J]. IEEE Transactions on Industrial Electronics, 2020, 68 (9): 8698- 8707

[本文引用: 1]

董晴, 季学武, 刘玉龙, 等

基于LPV/H∞鲁棒控制的重型商用车自动循迹

[J]. 清华大学学报: 自然科学版, 2022, 62 (3): 438- 446

[本文引用: 1]

DONG Qing, JI Xue-wu, LIU Yu-long, et al

Robust LPV/H∞ control for automatic path tracking of heavy commercial vehicles

[J]. Journal of Tsinghua University: Science and Technology, 2022, 62 (3): 438- 446

[本文引用: 1]

PENG H, WANG W, AN Q, et al

Path tracking and direct yaw moment coordinated control based on robust MPC with the finite time horizon for autonomous independent-drive vehicles

[J]. IEEE Transactions on Vehicular Technology, 2020, 69 (6): 6053- 6066

DOI:10.1109/TVT.2020.2981619      [本文引用: 3]

RAJAMANI R. Vehicle dynamics and control [M]. Berlin: Springer, 2006.

[本文引用: 1]

GUO J, LUO Y, LI K

Robust gain-scheduling automatic steering control of unmanned ground vehicles under velocity-varying motion

[J]. Vehicle System Dynamics, 2019, 57 (4): 595- 616

DOI:10.1080/00423114.2018.1475677      [本文引用: 1]

谭启凡. 四轮独立转向独立驱动车辆路径跟踪控制策略研究 [D]. 北京: 北京交通大学, 2019.

[本文引用: 3]

TAN Qi-fan. Research on path tracking control strategy of four-wheel independent steering independent driving vehicle [D]. Beijing: Beijing Jiaotong University, 2019.

[本文引用: 3]

余志生. 汽车理论[M]. 第5版. 北京: 机械工业出版社, 2009.

[本文引用: 1]

BASAR T, BERNHARD P. H-infinity optimal control and related minimax design problems: a dynamic game approach [M]. Berlin: Springer, 2008.

[本文引用: 1]

RAIMONDO D M, LIMON D, LAZAR M, et al

Min-max model predictive control of nonlinear systems: a unifying overview on stability

[J]. European Journal of Control, 2009, 15 (1): 5- 21

DOI:10.3166/ejc.15.5-21      [本文引用: 1]

YANG W, FENG G, ZHANG T

Robust model predictive control for discrete-time Takagi–Sugeno fuzzy systems with structured uncertainties and persistent disturbances

[J]. IEEE Transactions on Fuzzy Systems, 2014, 22 (5): 1213- 1228

DOI:10.1109/TFUZZ.2013.2286635      [本文引用: 1]

丁宝苍. 预测控制的理论与方法 [M]. 北京: 机械工业出版社, 2017.

[本文引用: 1]

WAN Z, KOTHARE M V

An efficient off-line formulation of robust model predictive control using linear matrix inequalities

[J]. Automatica, 2003, 39 (5): 837- 846

DOI:10.1016/S0005-1098(02)00174-7      [本文引用: 3]

张隆阁. 基于多胞的鲁棒预测控制研究 [D]. 北京: 华北电力大学, 2015.

[本文引用: 1]

ZHANG Long-ge. Research on robust predictive control based on multicellular [D]. Beijing: North China Electric Power University, 2015.

[本文引用: 1]

FALCONE P, BORRELLI F, ASGARI J, et al

Predictive active steering control for autonomous vehicle systems

[J]. IEEE Transactions on Control Systems Technology, 2007, 15 (3): 566- 580

DOI:10.1109/TCST.2007.894653      [本文引用: 1]

/

〈 〉