在实际中,扰动通常以典型“实现”作用于系统,引入机会约束和场景优化可以降低RMPC保守性[4, 9-15]. 场景优化将时域内扰动的实现视作“场景”,构建RMPC随机最优控制问题[13]. 若控制律对所有场景满足约束,则实际系统以较高的置信度满足预设机会约束. Calafiore等[14]针对线性变参系统,提出在线抽取场景的RMPC策略. Lorenzen等[15]离线抽取场景以保证机会约束满足,给出系统稳定所需的场景数量边界. 通常,场景优化由随机凸优化理论保证机会约束概率,较高概率需要在扰动实现分布中抽取大量场景[16-18],但实际中难以获取扰动实现的完整概率分布,这限制了场景优化的应用范围.
为了建立少量数据下的约束满足,可以使用学习方法离线建模[19-21],再设计RMPC策略[22],如集员[23]与Kinky推断方法[24]. 这些方法能够从数据中学习扰动边界,但无法得到扰动随机分布,实现机会约束. 高斯过程(Gaussian process,GP)[25-26]能够同时提供最优预测值与预测方差,已用于随机MPC设计. Li等[26]基于GP提出解析近似MPC算法,处理加性不确定性问题. Grancharova等[27]使用GP设计随机MPC,用于燃烧控制. Wang等[28]基于GP给出针对饮用水网络的MPC算法. Hewing等[19-20]结合GP和MPC,实现车辆的自动驾驶控制. 现有算法在理论上缺少稳定性与可行性结果[27-28],且假定扰动为独立同分布,限制了该算法的理论拓展与应用范围.
本文考虑约束不确定线性系统,提出基于高斯回归的场景优化鲁棒模型预测控制策略. 基于先验数据集进行高斯回归学习,获得扰动的完整概率模型. 在线抽取大量场景构建松弛机会约束下的随机凸优化问题,通过开环优化、闭环反馈镇定系统. 建立保证闭环系统鲁棒稳定性和满足松弛机会约束的充分条件. 应用DC-DC转换器和车辆巡航仿真,验证了本文策略的有效性.
1. 问题描述
考虑离散时间不确定线性系统:
式中:xk、uk和wk分别为k时刻的系统状态变量、控制变量和未知不确定扰动,xk∈Rn,uk∈Rm,wk∈Rn;A和B为已知矩阵;Ni为所有不小于i的整数集合. 系统状态和控制输入满足如下约束:
假设1 系统(1)的不确定扰动w未知但有界,即wk∈W,
假设2 系统(1)存在包含原点的一个凸邻域Xf及其局部控制律u = Kf x,使Xf为闭环系统的鲁棒正不变集(robust positive invariant set,RPI),即Xf={x∈X| (A+BKf)x+w∈Xf, Kf x∈U,
考虑系统(1),用Kf参数化控制输入[26]:
本文的目标是计算系统(1)的控制律(3),使得闭环系统在任意有界扰动w作用下,状态进入并始终保持在集合Xf内,同时系统状态和控制输入满足预设概率为Pp的机会约束:
采用高斯过程回归和模型预测控制方法计算控制律(3).
2. 高斯回归场景优化预测控制
通过GP学习时间指标k到扰动wk的映射,基于预测时域内扰动实现的联合高斯分布抽取场景,构建RMPC优化问题,设计新的场景优化RMPC算法.
考虑系统(1)及先验数据集D,有
先验数据集D中包含任意时刻k的s个扰动值wk,其中
2.1. 高斯过程回归
GP由均值与协方差函数唯一确定. 令向量kD = [0, 1, 2,···, L]T,使用先验数据集D对GP进行训练学习. 在学习完毕后,对于待预测的输入数据向量k*,有如下的联合高斯分布:
GP是概率模型,均值向量的行数与协方差阵的维度等于输入时间指标的数目.
由高斯分布的性质可知,k*相关输出的条件分布服从高斯分布[5],均值向量与协方差矩阵分别为
式中:协方差矩阵K的每一项由预先指定的核函数表述. 选择核函数为径向基函数:
式中:k1与k2为任意2个时间指标标量;待求解参数σ2 用于控制输出信号方差;l反映输入尺度放缩,可以在离线阶段基于D通过极大似然法或者最大后验估计求得. w(k*)的预测是由式(8)、(9)决定的联合高斯分布,其维数等于向量k*中的元素个数. 在系统运行的任一时刻,可以认为预测时域内扰动分布已知,能够在线抽取大量场景.
2.2. 算法设计
令xt为当前时刻t的系统状态测量,根据GP给出的预测时域内的联合高斯分布,在时刻t抽取M个扰动场景
构建时刻t的有限时域最优控制问题如下:
控制量由摄动序列
在线求解优化问题(12),得到最优解
并作用于系统(1). 在下一时刻,测量系统状态,更新优化问题(12)的初始条件,再重复整个计算过程,实现场景优化RMPC的滚动时域优化控制.
引理1[18] 考虑如下优化问题:
式中:c∈Rn×1为常数向量,
其中d为优化变量s的维度,则优化问题
的解s*以1−β的置信度满足P(hδ(s)≤0) ≥ Pp.
注2 式(15)的等号仅对全支撑(fully-supported)问题成立[18]. 在GP学习中,先验数据可能不严格满足高斯过程,或者由于先验数据的不完备使得GP预测存在偏差,式(15)的保守性质缓解了由先验数据带来的控制器性能下降或闭环系统失控问题.
对于优化问题(12),应用引理1的结果,可得关于场景优化非滚动优化控制量的性质.
引理2 考虑优化问题(12)及最优摄动序列解
a)将系统(1)在N步内驱动到终端域Xf内,即
b)使系统(1)满足输入和状态约束(2),即
为了设计新的场景优化RMPC 算法,定义位于终端域Xf中的以原点为中心、φ>0为半径的闭球Bφ={x| ||x||≤φ}
系统(1)的场景优化RMPC算法描述如下.
算法1 场景优化RMPC算法
离线阶段(初始化):
1)设定GP核函数,基于先验数据集D学习GP参数. 设定Pp与β,计算M和终端域Xf ;设定正常数d,使得
2)测量状态xt,求解优化问题(12)得到最优解
在线阶段:
3)令t=t+1,
4)判定如下条件:
a)若
b)若
c)若
5)由Vt第一元素计算控制量utMPC并作用于系统(1),返回3).
在算法1中,
式中:
2.3. 算法性能分析
下面给出场景优化RMPC的机会约束满足和闭环系统的鲁棒稳定性分析.
定理1 若假设1和2成立,且算法参数{M, Pp, β}满足式(15),则闭环系统(1)在算法1控制下将以1−β置信度和松弛qt满足所有概率为Pp的机会约束,即
证明:由算法1的第4步可知,在任意时刻有qt =
1)若qt =
2)若
定理2 若假设1和2成立,算法参数{M, Pp, β}满足式(15),则闭环系统(1) 在算法1控制下以不低于1−β的置信度,以概率Pp收敛于终端域Xf或在有限时间内到达终端域.
证明: 根据算法1的第4步a)条件是否满足,分类讨论如下.
1)不满足第4步的a)条件,即控制器运行4.b)或4.c). 根据第3步中
1.1)若在第3步
1.2)若在第3步
2)当前时刻满足第4步的a)条件. 此时按下一时刻的情况分类考虑如下.
2.1)若下一时刻满足第4步的a)条件,则实际上使用备选解产生RMPC控制量(在极端情况下,使用初始时刻t = 0时的最优解V0* 产生RMPC控制量,即非滚动优化算法). 根据定理1可知,系统以不低于1−β的置信度和松弛qt,以Pp的概率满足约束且收敛于终端域.
2.2)若下一时刻满足4.b)或4.c),则由上述证明过程1)中的讨论可知,系统收敛于终端域. 证毕.
3. 仿真实例
3.1. DC-DC转换器控制
考虑如下DC-DC转换器的线性时不变模型[26]:
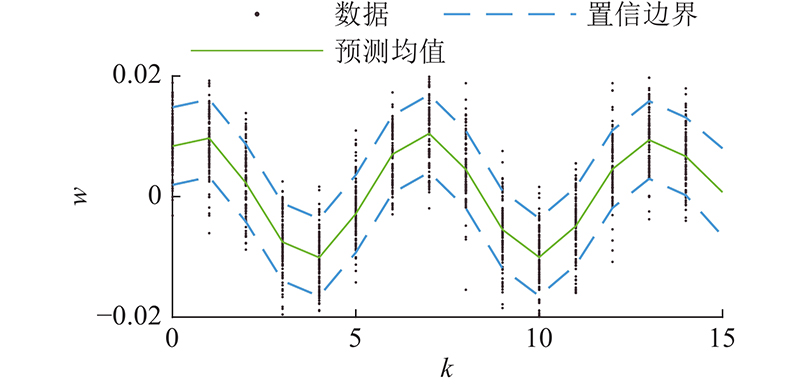
式中:扰动信号wk由持续扰动项0.01sin k和不确定项ek组成,即wk = 0.01sin k + ek,在任一k时刻,e的取值分布为均值为0、方差为0.0052的截断高斯分布. 系统状态、控制输入和扰动约束集合分别为X = {x∈R2| [−2, −3]T≤x≤[2, 3]T}, U = {u∈R|−0.2≤u≤0.2}和W = {w∈R| −0.02≤w≤0.02}.
图 1
图 1 GP拟合结果及双侧0.8置信区间
Fig.1 Fitting results and bilateral 0.8 confidence region of GP
在线控制阶段中,选择预测时域的时间尺度N = 8,置信度β = 10−5,权重矩阵
R = 1,γ = 104,根据式(19)、(20)计算得到φ = 0.345 9,z = 0.119 7. 常数d = 0.05和l = 2,初始点x0 = [3.4, 3.5]T.
为了验证本文算法的机会约束满足和低保守性,使用10 000次蒙特卡洛实验测定机会约束频率pc与优化问题求解时间ts,对比滚动场景优化RMPC(简记为算法1)与非滚动优化设计(简记为算法2). 在算法1中,基于实时松弛量qt 构建松弛约束,并判定其是否违反. 在算法2中,约束判定依赖于t=0时优化问题的松弛约束,在一次模拟中的任何约束违反视作该模拟失败. 2种算法的机会约束统计频率与求解时间如表1所示.
表 1 10 000次蒙特卡洛模拟的统计结果
Tab.1
| Pp(M) | pc | ts/ms | |
| 算法1 | 算法2 | ||
| 0.1(19) | 0.800 1 | 0.636 8 | 10.95 |
| 0.3(30) | 0.862 8 | 0.720 1 | 14.11 |
| 0.5(48) | 0.905 0 | 0.733 6 | 19.90 |
| 0.7(88) | 0.944 3 | 0.808 1 | 29.63 |
| 0.9(285) | 0.982 4 | 0.934 1 | 90.51 |
分析表1可知,当Pp = 0.7或0.9时,M > s,此时满足高概率机会约束需要GP学习. 随着Pp值上升,M增大,统计频率上升说明控制器的鲁棒性更强. 2种算法的实际机会约束概率均高于Pp,即满足机会约束,但存在一定的保守性,这是由于优化问题(12)仅在初始时刻接近全支撑问题. 算法1的保守性更低,这得益于松弛变量的实时更新. 在算法2下,由于初始点离终端域最远,q0值过大导致后续约束违反较难. 算法2由于滚动优化实时刷新qt,降低了保守性. 在时效性上,ts随M的增大而变长,这是由于式(12)的约束数目随着M的增大而增加,但优化问题的严格凸性和可行性保证了该问题的快速求解.
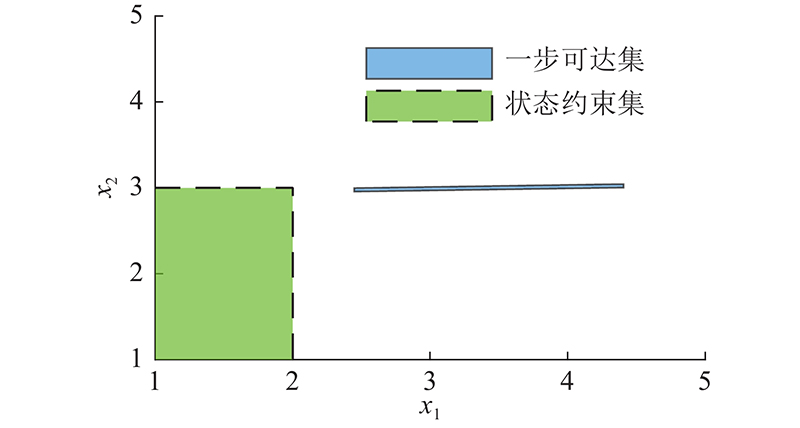
图 2
图 2 初始状态的一步可达集合与状态约束集合
Fig.2 State constraint set and one-step reachable set of initial state
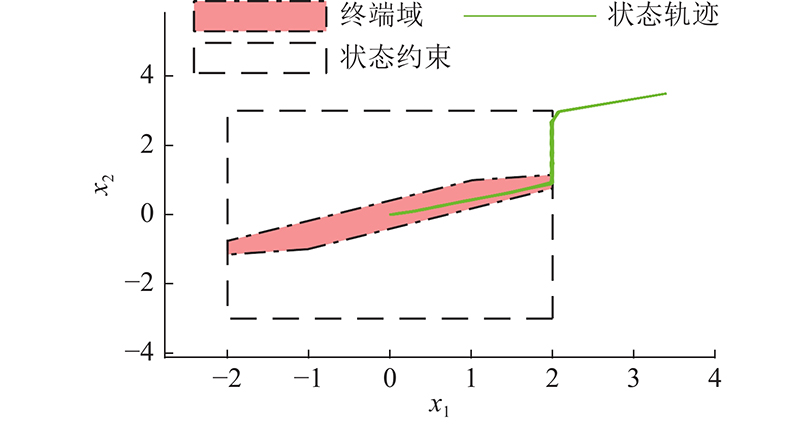
图 3
图 3 算法1在Pp = 0.1时的10 000条蒙特卡洛状态轨迹
Fig.3 10 000 Monte Carlo state trajectories of algorithm 1 at Pp = 0.1
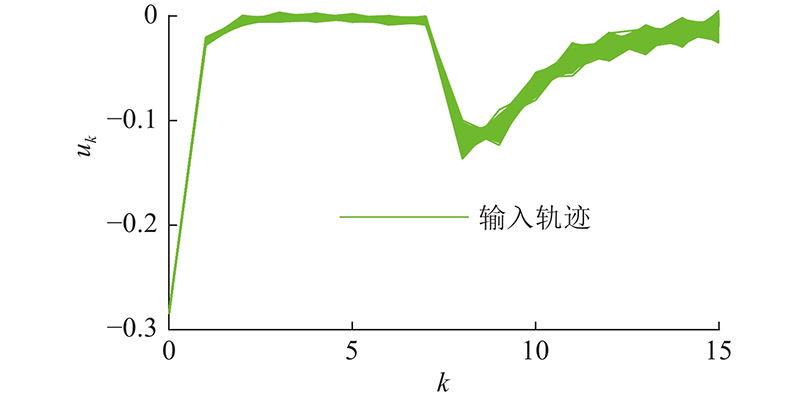
图 4
图 4 算法1在Pp = 0.1时10 000条蒙特卡洛输入轨迹
Fig.4 10 000 Monte Carlo input trajectories of algorithm 1 at Pp = 0.1
3.2. 网联车巡航控制
考虑网联车自主巡航控制系统[34]:
式中:Δd为车间距误差;d为实际车间距,d = xp−xh−l,其中xp和xh分别为前、后车的位移,l为前车车长;ddes为理想车间距,ddes = thvh+d0,其中vh为后车的速度,th为车头时距,d0为最小安全间距;Δv为相对速度,vp为前车的速度;τd为巡航时间常数,ah为后车的加速度,
选择状态变量x = [Δd, Δv, ah]T,输入为ades,扰动为ap(其中ap为前车的加速度),则巡航控制系统(24)的离散时间状态方程为
式中:
其中Tc为采样离散时间,Tc > 0.
仿真中令th = 2.5 s,Tc = 0.4 s,τd= 0.5,γ = 1 500,d = 4,R = 60,Q为三阶单位阵,N = 8,先验轨迹数s = 15,场景数目M = 25. 令v = Gkw,系统扰动范围为W={v| −1≤||v||≤1},且方差为0.122,状态和控制约束为
使用算法1与算法2,在加速和减速2种工况中进行对比实验.
表 2 2种工况下的理想加速度数据
Tab.2
| k | ap /(m·s−2) | |
| 减速 | 加速 | |
| 1 | −0.807 5 | 0.807 5 |
| 2 | −1.684 5 | 1.684 6 |
| 3 | −2.500 0 | 2.500 0 |
| 4 | −2.500 0 | 2.500 0 |
| 5 | −1.684 5 | 1.684 6 |
| 6 | −0.807 5 | 0.807 5 |
| 7 | −0.331 2 | 0.331 2 |
| 8 | −0.127 1 | 0.127 1 |
| ≥9 | 0 | 0 |
图 5
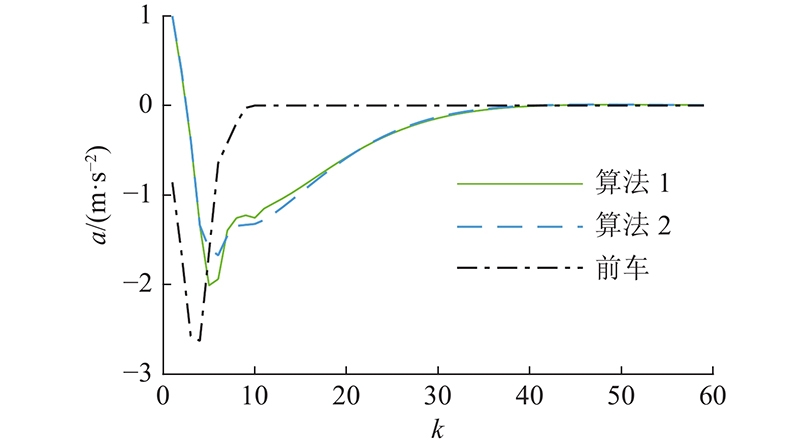
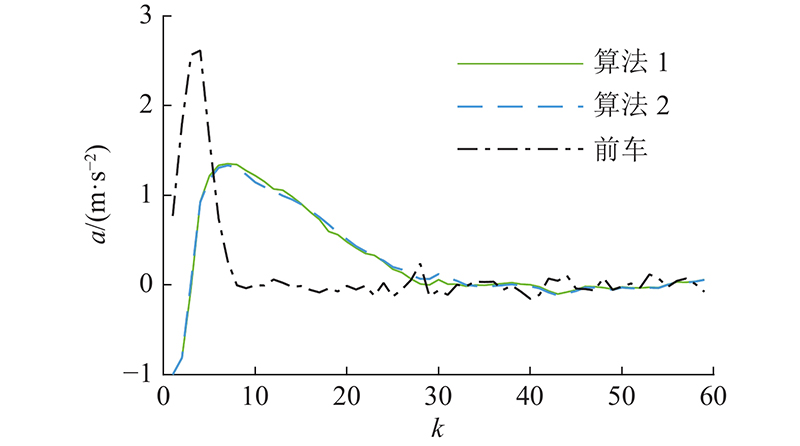
图 5 减速工况下的加速度对比图
Fig.5 Comparison of acceleration under decelerating condition
图 6
图 7
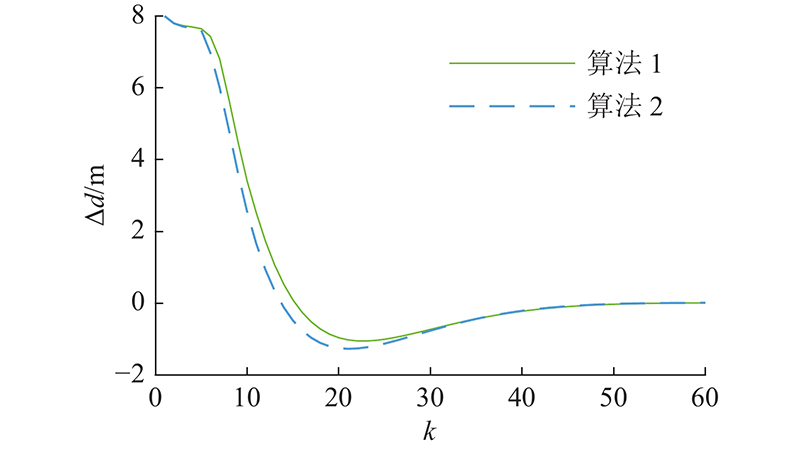
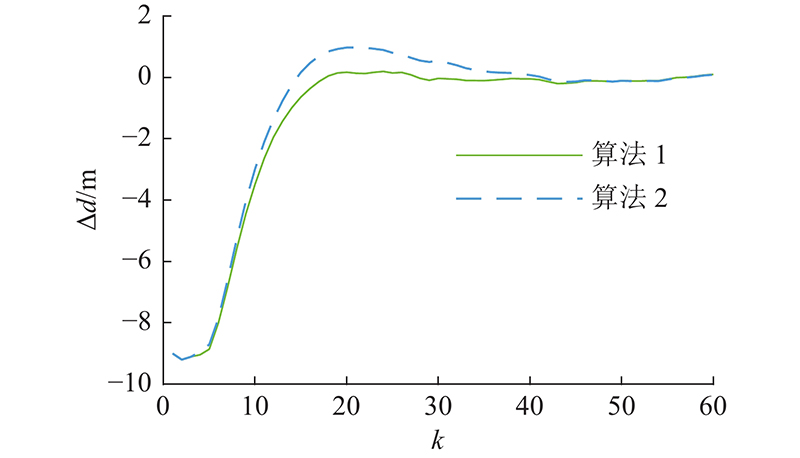
图 7 减速工况下的间距误差对比图
Fig.7 Comparison of spacing error under decelerating condition
图 8
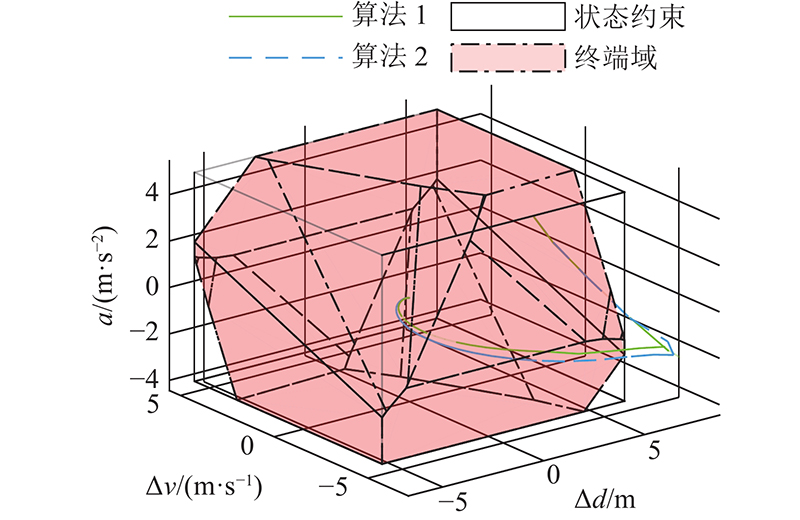
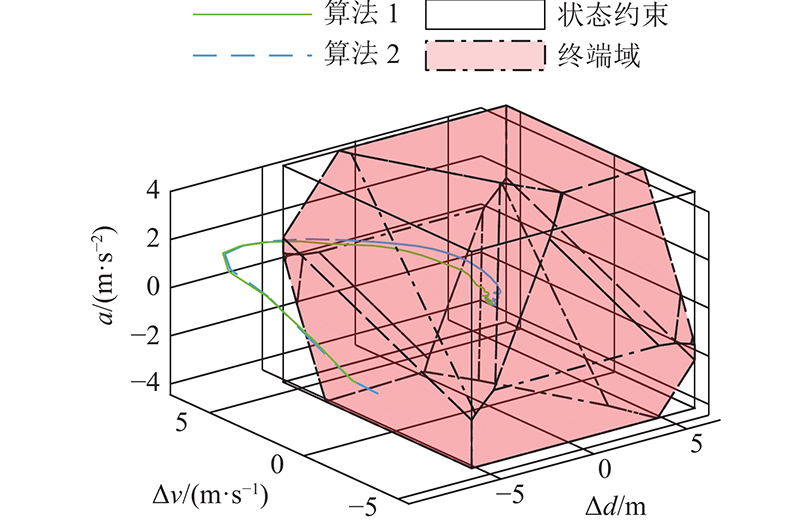
图 8 减速工况下的状态轨迹对比图
Fig.8 Comparison of state trajectory in decelerating condition
图 9
图 9 加速工况下的加速度对比图
Fig.9 Comparison of acceleration under accelerating condition
图 10
图 11
图 11 加速工况下的间距误差对比图
Fig.11 Comparison of spacing error under accelerating condition
图 12
图 12 加速工况下的状态轨迹对比图
Fig.12 Comparison of state trajectory under accelerating case
4. 结 语
本文设计基于GP学习的场景优化RMPC算法. 去除了传统场景优化分布已知或足够场景可获得的假设,通过使用GP学习扰动实现的取值分布,抽取场景构建随机凸优化问题,求解控制摄动序列. 引入松弛变量保证算法可行性,基于随机凸优化引理证明了闭环系统的鲁棒稳定性. DC-DC转换器和网联车巡航控制仿真结果验证了本文算法的有效性和优越性. 后续将进一步研究非准确学习下的RMPC算法及低场景数和高效算法设计.
参考文献
Review on model predictive control: an engineering perspective
[J].
Convergence of stochastic nonlinear systems and implications for stochastic model-predictive control
[J].
Model predictive control: recent developments and future promise
[J].DOI:10.1016/j.automatica.2014.10.128 [本文引用: 3]
Robust and stochastic model predictive control: are we going in the right direction
[J].DOI:10.1016/j.arcontrol.2016.04.006 [本文引用: 2]
Robust tube-based model predictive control of LPV systems subject to adjustable additive disturbance set
[J].DOI:10.1016/j.automatica.2021.109672
Heterogeneously parameterized tube model predictive control for LPV systems
[J].DOI:10.1016/j.automatica.2019.108622
Self-triggered adaptive model predictive control of constrained nonlinear systems: a min–max approach
[J].DOI:10.1016/j.automatica.2022.110424 [本文引用: 1]
Stochastic model predictive control: an overview and perspectives for future research
[J].DOI:10.1109/MCS.2016.2602087 [本文引用: 1]
Stochastic model predictive control with adaptive constraint tightening for non-conservative chance constraints satisfaction
[J].DOI:10.1016/j.automatica.2018.06.026
Model predictive control for drift counteraction of stochastic constrained linear systems
[J].DOI:10.1016/j.automatica.2020.109304
Indirect adaptive MPC for discrete-time LTI systems with parametric uncertainties
[J].
Robust model predictive control via scenario optimization
[J].
Stochastic model predictive control of LPV systems via scenario optimization
[J].DOI:10.1016/j.automatica.2013.02.060 [本文引用: 2]
Stochastic MPC with offline uncertainty sampling
[J].DOI:10.1016/j.automatica.2017.03.031 [本文引用: 2]
Randomized solutions to convex programs with multiple chance constraints
[J].DOI:10.1137/120878719 [本文引用: 1]
Data-driven predictive control for autonomous systems
[J].DOI:10.1146/annurev-control-060117-105215
The exact feasibility of randomized solutions of uncertain convex programs
[J].DOI:10.1137/07069821X [本文引用: 3]
Learning-based model predictive control: toward safe learning in control
[J].DOI:10.1146/annurev-control-090419-075625 [本文引用: 3]
Cautious model predictive control using Gaussian process regression
[J].
Gaussian process-based predictive control for periodic error correction
[J].
Robust multi-rate predictive control using multi-step prediction models learned from data
[J].DOI:10.1016/j.automatica.2021.109852 [本文引用: 1]
A robust adaptive model predictive control framework for nonlinear uncertain systems
[J].DOI:10.1002/rnc.5147 [本文引用: 1]
Componentwise hölder inference for robust learning-based MPC
[J].DOI:10.1109/TAC.2021.3056356 [本文引用: 2]
Adaptive stochastic model predictive control of linear systems using Gaussian process regression
[J].DOI:10.1049/cth2.12070 [本文引用: 6]
Explicit stochastic predictive control of combustion plants based on Gaussian process models
[J].DOI:10.1016/j.automatica.2008.04.002 [本文引用: 2]
Stochastic model predictive control based on Gaussian processes applied to drinking water networks
[J].DOI:10.1049/iet-cta.2015.0657 [本文引用: 2]
Parametric circuit fault diagnosis through oscillation-based testing in analogue circuits: statistical and deep learning approaches
[J].DOI:10.1109/ACCESS.2022.3149324
Internet of vehicles: sensing-aided transportation information collection and diffusion
[J].DOI:10.1109/TVT.2018.2796443 [本文引用: 1]
Data collection in studies on Internet of things (IoT), wireless sensor networks (WSNs), and sensor cloud (SC): similarities and differences
[J].DOI:10.1109/ACCESS.2022.3161929 [本文引用: 1]
Gaussian learning-based fuzzy predictive cruise control for improving safety and economy of connected vehicles
[J].DOI:10.1049/iet-its.2019.0452 [本文引用: 1]