浙江大学学报(工学版)

浙江大学学报(工学版), 2022, 56(8): 1560-1567, 1621 doi: 10.3785/j.issn.1008-973X.2022.08.010

机械与能源工程

基于Bouc-Wen修正模型的柔性关节驱动器迟滞建模

许明,, 张帝, 戎铖, 苏礼荣, 王万强,

杭州电子科技大学 机械工程学院，浙江 杭州 310018

Modified Bouc-Wen based hysteresis modeling of flexible joint actuator

XU Ming,, ZHANG Di, RONG Cheng, SU Li-rong, WANG Wan-qiang,

School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, China

通讯作者: 王万强，男，高级实验师. orcid.org/0000-0002-5751-8551. E-mail： wwq@hdu.edu.cn

收稿日期: 2022-02-12  

基金资助: 国家自然科学基金资助项目(51975171)；浙江省教育厅一般科研项目(专业学位研究生培养模式改革专项)资助项目(Y202146881)

Received: 2022-02-12  

Fund supported: 国家自然科学基金资助项目(51975171)；浙江省教育厅一般科研项目(专业学位研究生培养模式改革专项)资助项目(Y202146881)

作者简介 About authors

许明（1982—），男，教授，博士，从事软体机器人驱动研究.orcid.org/0000-0003-1312-6190.E-mail：jxxuming@hdu.edu.cn , E-mail：jxxuming@hdu.edu.cn

摘要

为了研究柔性关节驱动器输出力的迟滞影响，提高力控制精度，构建了柔性关节驱动力的迟滞实验台,提出柔性关节驱动器输出力的Bouc-Wen修正方法对力迟滞进行精确建模，并通过龙格-库塔-费尔贝格算法对Bouc-Wen修正模型进行参数辨识. 在Bouc-Wen模型的基础上，引入具有方向性的修正项，克服柔性关节驱动器的输出力-转角迟滞的非对称性. 利用关节驱动器在60、80、100、120 kPa充气压力下的力迟滞实验数据，建立Bouc-Wen修正模型. 在70、90、110 kPa充气压力下，将Bouc-Wen修正模型所预测的柔性关节力迟滞曲线与经典Bouc-Wen模型以及实验曲线进行对比. 结果表明所提出的力迟滞Bouc-Wen修正模型，在各充气压力下的最大相对误差仅为7.75%，平均偏差小于0.45 N，模型拟合优度大于0.99. 说明所提出的Bouc-Wen修正模型能够对柔性关节驱动器的力迟滞进行准确建模，为力闭环控制提供基础，也为其他超弹性材料柔性驱动器的迟滞建模提供参考方法.

关键词： 柔性关节驱动器 ; 迟滞建模 ; Bouc-Wen修正模型 ; 软体机器人 ; 参数辨识

Abstract

A hysteresis test bench for flexible joint driving force was constructed, in order to study the force hysteresis characteristic of the flexible joint actuator and improve the force control accuracy. The modified Bouc-Wen method was proposed to accurately model the force hysteresis of the joint actuator, and the parameters of the modified Bouc-Wen model were identified by the Runge-Kutta-Fehlberg method. On the basis of the conventional Bouc-Wen model, a directional correction term was introduced to overcome the asymmetry of the output force-angle hysteresis of the flexible joint actuator. The modified Bouc-Wen model was established, using the experimental data of force hysteresis of joint actuator at 60, 80, 100 and 120 kPa inflation pressure. The hysteresis curve predicted by the proposed Bouc-Wen model was compared with that of the conventional Bouc-Wen and the experimental curve at 70, 90 and 110 kPa inflation pressure. Experimental results show that the maximum relative error of the proposed Bouc-Wen based force hysteresis model for the flexible joint actuator under each inflation pressure was only 7.75%, the average deviation remained within 0.45 N, and the fitting goodness of the model was more than 0.99. Results show that the proposed modified Bouc-Wen model can accurately describe the force hysteresis of the flexible joint actuator, which lays a foundation for the force closed-loop control and also provides a promising method for the hysteresis modeling of other hyperelastic flexible actuators.

Keywords： flexible joint actuator ; hysteresis modeling ; modified Bouc-Wen model ; soft robot ; parameter identification

PDF (2207KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

许明, 张帝, 戎铖, 苏礼荣, 王万强. 基于Bouc-Wen修正模型的柔性关节驱动器迟滞建模. 浙江大学学报(工学版)[J], 2022, 56(8): 1560-1567, 1621 doi:10.3785/j.issn.1008-973X.2022.08.010

XU Ming, ZHANG Di, RONG Cheng, SU Li-rong, WANG Wan-qiang. Modified Bouc-Wen based hysteresis modeling of flexible joint actuator. Journal of Zhejiang University(Engineering Science)[J], 2022, 56(8): 1560-1567, 1621 doi:10.3785/j.issn.1008-973X.2022.08.010

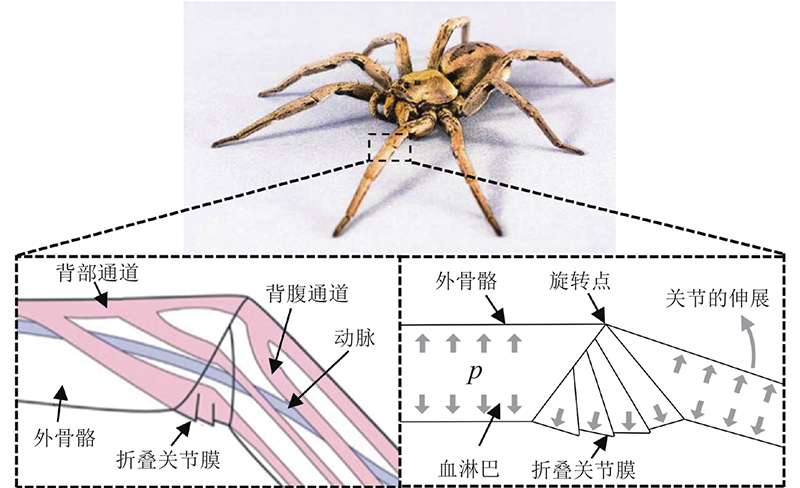
软体机器人作为新一代的机器人，在很多领域有着得天独厚的优势[1]. 软体机器人具有大范围连续变形的能力，对环境有着极强的适应能力，近年来已经成为了机器人研究的热点[2]. 柔性关节驱动器作为软体机器人的核心技术[3-5]，已经被开发用于各种应用，包括软夹具、人工肌肉、可穿戴设备、触觉设备和医疗设备等[6-7]，具有广泛的应用前景. 柔性关节驱动器通常采用柔性材料制造，由于柔性材料内部摩擦力、周期性松弛和强非线性等方面的原因，柔性关节驱动器具有非常复杂的输出特性[8]. 目前国内外对柔性驱动器的迟滞特性研究还处于初步阶段，研究人员将压电陶瓷、形状记忆合金中的迟滞理论引入到柔性驱动器中，将其迟滞看作是一种扰动量进行研究，尚未有针对柔性驱动器迟滞特性的统一建模方法[9].

根据超弹性材料理论和驱动器结构的分析，柔性关节驱动器的迟滞原因主要如下：1）硅橡胶的内摩擦（内黏性）；2）诱导结晶；3）柔性关节驱动器外界摩擦；4）纤维增强或约束情况下，纤维编织网与硅胶基体间的干摩擦[6-7]. 目前的迟滞建模方法主要有唯象模型和物理模型[10]2大类. 唯象模型是仅根据输入和输出之间的关系而建立的抽象模型，常用的唯象模型主要有Preisach模型、KP模型、PI模型等[11]. 物理模型是从不同的迟滞物理机制出发，来具体描述迟滞过程. 物理模型的参数具有物理意义，因此物理模型更加直观精确，但通用性不足，往往只能描述特定的对象，且模型的参数往往需要与实际系统的各个参数相对应，在建模过程中须根据实际情况对模型参数进行改进和修正.

目前常用的物理迟滞模型主要有Jile-Atherton模型、Maxwell模型、Duhem模型、Bouc-Wen模型等[12]. Jile-Atherton模型是最常见的物理迟滞模型之一，通常用于描述磁化过程中的磁滞特性，无法用于动态驱动力的描述[13]. Maxwell模型是针对黏弹性材料提出的微积分模型，由于有记忆项，参数过多且不便被辨识，其复杂程度远高于不具备记忆功能的模型[14]. Duhem模型是由Duhem提出的一种基于微分方程的动态模型，其输出与输入信号频率及方向相关，具有明确的函数表达式，由于其模型参数获取方式复杂，不易表征复杂的迟滞非线性[15]. Bouc-Wen模型是一种微分模型，所描述的迟滞呈双曲线对称，已被广泛应用于迟滞建模. 此外，Bouc-Wen模型具有方向性，能够满足关节驱动器中关节伸展和收缩的物理描述需求[16].

本研究选择Bouc-Wen作为柔性关节驱动器动态输出力的迟滞建模本体模型，其包含A、β、γ、n共4个参数，Bouc-Wen模型参数辨识易收敛，可以通过最小二乘法、遗传算法、粒子群优化等实现. 在迟滞实验的基础上，提出Bouc-Wen修正模型，并通过龙格-库塔-费尔贝格法进行参数辨别，能够将柔性关节驱动器的转角φ与输出力F之间的迟滞拟合精度显著提高. 对柔性关节驱动器的力迟滞进行准确建模，可以为力闭环控制提供基础，也为其他超弹性材料柔性驱动器的迟滞建模提供参考方法.

1. 仿生柔性关节驱动器

1.1. 柔性关节驱动器设计

蜘蛛腿的运动主要是由腿节-膝节关节和胫节-后跗节关节（统称为液压关节）的驱动来实现，这2个关节处只有屈肌而没有伸肌[17]. 液压关节由坚硬的外骨骼和柔软的折叠关节膜组成，外骨骼中的多个通道中充满蜘蛛的血淋巴，血淋巴即蜘蛛的血液. 血淋巴通过蜘蛛前体的肌肉加压，进而驱动柔软的关节膜产生膨胀，从而推动腿部伸展，如图1所示. 腿部屈曲则主要依赖于外骨骼内的屈肌，以及关节膜本身的弹性恢复[19].

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   仿蜘蛛腿的柔性关节驱动器原理[18]

Fig.1   Principle of flexible joint actuator inspired by spider legs[18]


蜘蛛腿关节的驱动特征与现有的流体弹性驱动器相类似[20]. 目前，关节式气动驱动器研究还相对较少，尤其是具有微小型结构的气动驱动器. 且大多数气动柔性驱动器为了简化分析和控制的难度，结构均设计为规则的形状，例如圆柱状、矩体状、尺蠖型、象鼻型等[21]. 不规则形状的驱动器由于理论方面较复杂，研究相对较少. 本研究基于蜘蛛腿液压关节的结构和驱动原理，设计了一种新型的仿生柔性关节驱动器，呈不规则的扇形结构，运动原理与蜘蛛腿关节膜相似，并采用气动驱动方法，满足了质量轻、结构简单、性能优良等要求，其结构及原理如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   柔性关节驱动器设计

Fig.2   Design of flexible joint actuator


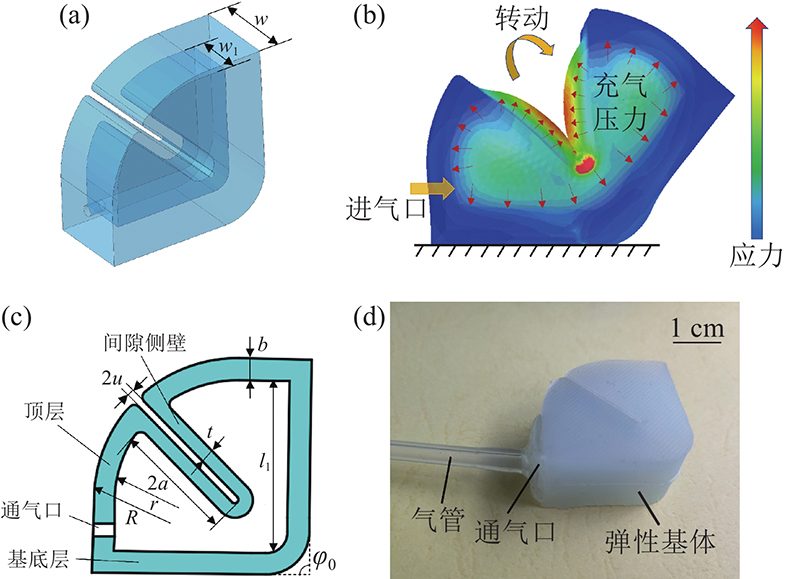
所设计的柔性关节驱动器是一种双连通式气囊弹性驱动器，考虑到气囊弹性驱动器体积较小、基体制备难度大，将驱动器设计为一体式气腔结构，具有不易破损、结构简单、性能稳定、制备相对容易等优势. 柔性关节驱动器气腔内部形状为一个具有2个腔室的扇形，2个腔室紧密连通，2个腔室之间的间隙侧壁厚度比柔性关节驱动器的其他侧壁厚度要小. 这种非对称式几何结构对驱动器产生局部约束、定向膨胀的作用，当驱动器空腔内的压力增加时，2个间隙侧壁膨胀从而相互挤压，实现驱动器转动. 其驱动原理如图2（b）所示.

1.2. 柔性关节驱动器制造

柔性关节驱动器结构的主要参数如表1、图2（c）所示. 表中，b为两侧面扇形层的厚度；w为驱动器宽度；w1为气囊腔室厚度，w1=w−2b；r为驱动器内腔的曲率半径.

表 1   柔性关节驱动器结构参数

Tab.1  Structural parameters of flexible joint actuator

参数 数值/mm 参数 数值/mm
w 15 a 7.5
w1 9 d1 3
R 30 d2 2
r 27 u 0.25
l1 24 b 3

新窗口打开| 下载CSV


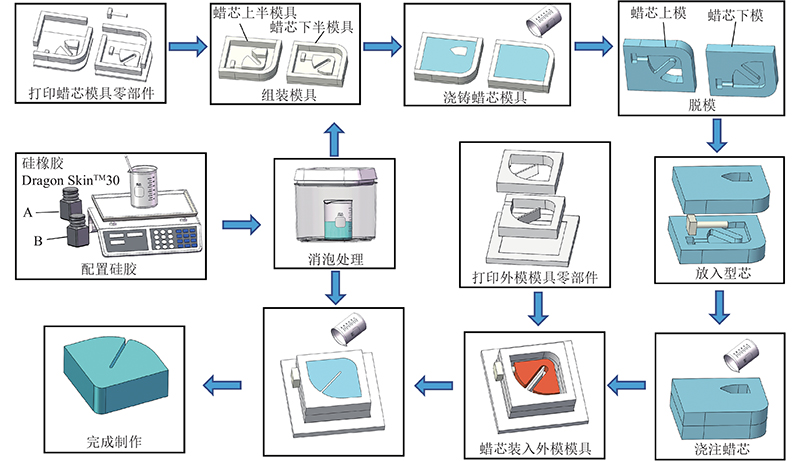
柔性关节驱动器制造材料为Dragon SkinTM30硅橡胶. 为了提高柔性驱动器的驱动性能和抗压强度，采用一体化失蜡铸造方法进行制造，如图3所示，避免了由于局部受力不均匀而导致驱动器的破损，大大提高了驱动器使用寿命. 其主要步骤如下：1）3D打印软关节失蜡铸造模具；2）制作气腔蜡芯模具；3）硅胶模具浇筑出气腔蜡芯；4）将气腔蜡芯装入柔性关节驱动器外模具；5）浇筑柔性关节驱动器半成品；6）取下柔性关节驱动器半成品，放入水浴中加热融化蜡芯，得到柔性关节驱动器.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   柔性关节驱动器的制造方法

Fig.3   Manufacturing method of flexible joint actuator


2. 柔性关节驱动器迟滞实验

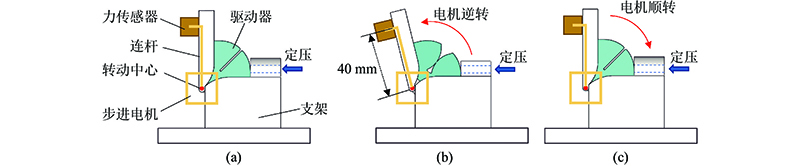
影响柔性关节驱动器迟滞的主要因素有材料特性[6-7,10]、驱动器结构、充气压力等. 制造柔性关节驱动器的均为Dragon Skin30硅橡胶材料，其特性对迟滞的影响在此不进行讨论. 主要讨论的是充气压力对柔性关节驱动器迟滞的影响.

构建如图4所示的迟滞实验平台，柔性关节驱动器的充气由气泵完成，并通过精密调节阀（IR2000-02BG）进行压力调节. 采用3D打印方法制造的刚性支架将柔性关节驱动器底面固定，支架侧面同关节驱动器侧面相约束，随关节转动而转动. 在转动中心处，同轴安装有一个42步进电机，用以控制关节驱动器转动角度. 支架侧面连接有高精度力传感器，测量驱动器在不同转动角度时的输出力大小. 控制器为Arduino，控制步进电机转动，并对力传感器数据进行采集.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   柔性关节驱动器迟滞实验台

Fig.4   Hysteresis test bench of flexible joint actuator


在进行迟滞实验之前，须获得驱动器在不同充气压力下的最大转动角度. 即将关节驱动器底面固定，在侧面无支架约束情况下，对于不同恒定充气压力分别测定驱动器的转动角度. 当驱动器充气压力小于60 kPa时，驱动器转动角度过小，测试误差较大，而当气压大于120 kPa时，由于材料特性及气密性不足，驱动器容易爆裂或漏气，因此将充气压力限定在60~120 kPa.

柔性关节驱动器的迟滞实验原理如图5所示. 首先，向驱动器通入恒定压力压缩空气，并控制步进电机以5˚/s逆时针恒速转动，如图5（b）所示，直至驱动器伸展至该气压下的最大转角处. 由于关节驱动器在步进电机带动下被动匀速伸展，将该过程称为回程. 然后，控制步进电机以5˚/s顺时针恒速转动，如图5（c）所示，压缩驱动器直至其初始状态（底面和侧面呈90˚），该过程称为去程. 为了保证实验结果的准确性，制造了5个柔性驱动器进行测试，取平均测试数据.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   驱动器迟滞实验原理

Fig.5   Principle of actuator hysteresis test


分别通入60、80、100、120 kPa的恒定气压进行测试，测得周期下转角与驱动力的关系，结果如图6（a）~（d）所示. 此外，为了更进一步分析驱动器的力特性，控制步进电机每5˚转动一次，每次停顿5 s，测得驱动器的静态输出力. 并将静态输出力与动态输出力进行比较，如图6（e）、（f）所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

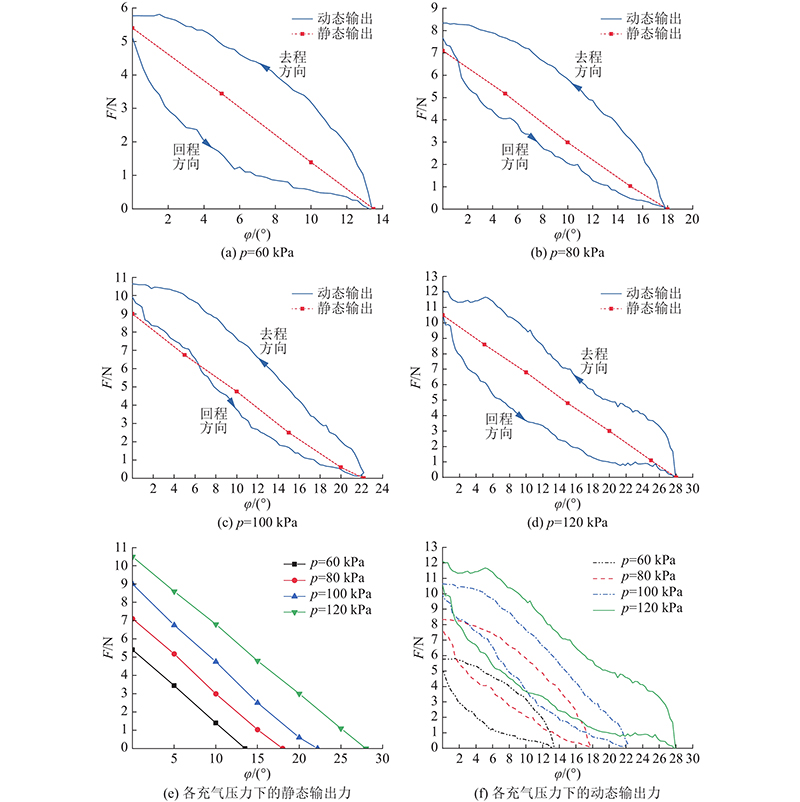
图 6   不同气压下输出力与转角迟滞关系

Fig.6   Driving force and rotation angle hysteresis under variable inflation pressure


如图6（a）~（d）所示，柔性关节驱动器的输出力和转动角度之间存在明显的迟滞现象，具体表现在去程与回程时的力-位特征不同. 当驱动器为去程时，随着转角的减小，输出力随之增大，去程的各转角对应输出力均大于静态输出力；当驱动器为回程时，随着转角的增大，输出力随之减小，回程的各转角对应输出力在大部分情况下要小于静态输出力. 同时，不同气压下的迟滞曲线均不闭合，回程起点的输出力略微小于去程终点的输出力，这是硅橡胶松弛和惯性力的影响所导致的.

由图6（e）可以看出，静态测量的关节驱动器输出力F与转角φ之间大体呈现线性关系. 当驱动器角度φ一定时，关节的输出力F与充气压力p近似成正比关系，充入气体的压力越大，输出力也越大. 输出力与转角关系曲线的斜率可以看作是转动刚度，由图6（e）可知，在静态输出时，柔性关节驱动器的转动刚度与充气压力及转角均无关.

由图6（f）可以发现，在动态输出时，转动刚度随着驱动器转角变化而呈非线性变化. 在回程过程中，转动刚度减小速度会随着转角增大先快后慢，且驱动器整体刚度较静态时偏小；在去程过程中，转动刚度增大的速度会随着转角的减小而先快后慢，且与静态时相比整体刚度偏大.

由图6综合可得，在静态情况下，柔性关节驱动器的输出性能比较稳定，且可以看作是线性变化，而动态下的力输出与转动角度之间，则具有明显的迟滞效应. 驱动器内部气压越大，其输出力的迟滞效应越明显，在60、80、100 、120 kPa这4种充气压力情况下，只有60 kPa时的迟滞曲线才近乎对称.

3. 修正Bouc-Wen迟滞建模

柔性关节驱动器采用的是超弹性非线性硅橡胶材料，在运动过程中具有较强的时变性. 将运动过程中驱动器的输出力F( $\varphi $, p)分解为静态力Fs( $\varphi $, p)和非线性项Fn( $\varphi $, p)[22]，即

$ F\left(\varphi ,p\right)={F}_{\mathrm{s}}\left(\varphi ,p\right)+{F}_{\mathrm{n}}\left(\varphi ,p\right) .$
(1)

式中：Fs( $\varphi $, p)为驱动器静态输出力，Fn( $\varphi $, p)为驱动器运动过程中的迟滞力， $\varphi $为驱动器转角，p为驱动器内部的气体压力.

如图6所示，通过静态实验详细测得驱动器的静态输出力. 为了进一步描述运动过程中的动态输出力，引入Bouc-Wen 模型，将动态输出力z =Fn( $\varphi $, p)表示为非线性微分方程的形式[22]：

$ \dot{z}=A\Delta \dot{\varphi }-\beta \left|\Delta \dot{\varphi }\right|{\left|z\right|}^{n-1}z-\gamma \Delta \dot{\varphi }{\left|z\right|}^{n} . $
(2)

式中：z为柔性关节驱动器的输出力， $ \Delta \dot{\varphi } $为柔性关节驱动器的角速度，A为比例系数，β、γ分别为滞回环宽度调节参数和高度调节参数，n为曲线圆滑系数，

Bouc-Wen 模型是一种光滑双曲线迟滞模型，被广泛应用于非线性结构单元的迟滞建模. 但是通过经典的Bouc-Wen 模型所建立的迟滞曲线属于对称滞回曲线[23]，而柔性关节驱动器的输出力-转角迟滞并不是严格的对称曲线，因此为了建立更精确的迟滞模型，须对经典Bouc-Wen 模型进行修正.

根据柔性驱动器的超弹性材料构成可知，造成驱动器动态输出曲线在去程和回程时非对称的一个很大因素是硅橡胶分子链间的内摩擦，而内摩擦力一般具有明确的方向性. 另外，在柔性关节驱动器伸展/收缩时，转动速度较快，囤积在硅橡胶内的热能无法完全消散，从而导致驱动器能量损失的不确定性，造成应变能储存与释放的非均匀性，引起柔性关节驱动器不同的输出力.

在Bouc-Wen模型的基础上，添加一个具有方向性的修正项 $\phi \left({\rm{sign}}\;(\mathrm{\Delta }\dot{\varphi }\right)+{\rm{sign}}\;\left(z\right))$，能够极大地克服滞回的不确定性因素，且精度较高、计算简单高效，便于参数的拟合. 修正后的Bouc-Wen模型可以表示为

$ \begin{split} \dot{z}=&A\Delta \dot{\varphi }-\beta \left|\Delta \dot{\varphi }\right|{\left|z\right|}^{n-1}z-\gamma \Delta \dot{\varphi }{\left|z\right|}^{n}+ \\&\phi \left(\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\;\left(\mathrm{\Delta }\dot{\varphi }\right)+\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\;\left(z\right)\right). \end{split} $
(3)

式中： $\phi $为迟滞模型的回环系数.

采用龙格-库塔-费尔贝格法(Runge-Kutta-Fehlberg method，RKF45)对修正迟滞模型的参数进行辨识[24]，主要过程是确定合适的步长h，其原理如下：在每一次计算中，比较Runge-Kutta法的4阶近似解和5阶较优解. 如果上述2个解的绝对差符合规定的精度，则采用4阶近似解，并按变步长方法增大步长h，加快计算速度；反之，则减小步长h. 每一次计算都须使用以下6个值[25]：

$ \left. \begin{aligned} &{k}_{1}=hf\left({t}_{k},{y}_{k}\right) , {k}_{2}=hf\left({t}_{k}+\frac{1}{4}h,\;{y}_{k}+\frac{1}{4}{k}_{1}\right),\\ &{k}_{3}=hf\left({t}_{k}+\frac{3}{8}h,{y}_{k}+\frac{3}{32}{k}_{1}+\frac{9}{32}{k}_{2}\right), \\ &{k}_{4}=hf\left({t}_{k}+\frac{12}{13}h,{y}_{k}+\frac{1\;932}{2\;197}{k}_{1}-\frac{7\;200}{2\;197}{k}_{2}+\frac{7\;296}{2\;197}{k}_{3}\right),\\ &{k}_{5}=hf\left({t}_{k}+h,{y}_{k}+\frac{439}{216}{k}_{1}-8{k}_{2}+\frac{3\;680}{513}{k}_{3}-\frac{845}{4\;104}{k}_{4}\right),\\ &{k}_{6}=hf\left({t}_{k}+\frac{1}{2}h,{y}_{k}-\frac{8}{27}{k}_{1}+2{k}_{2}-\right. \\ & \left.\frac{3\;544}{2\;565}{k}_{3}+\frac{1\;859}{4\;104}{k}_{4}-\frac{11}{40}{k}_{5}\right). \end{aligned}\right\}$
(4)

式中：k1~k6为系数，h为步长，tk为柔性关节驱动器转角，yk为柔性关节驱动器输出力.

使用4 阶Runge-Kutta法对非线性微分方程的解进行近似[25]：

$ {y}_{k+1}={y}_{k}+\frac{25}{216}{k}_{1}+\frac{1\;408}{2\;565}{k}_{3}+\frac{2\;197}{4\;104}{k}_{4}-\frac{1}{5}{k}_{5}. $
(5)

使用5阶Runge-Kutta法确定较优解[25]：

$ {z}_{k+1}={y}_{k}+\frac{16}{135}{k}_{1}+\frac{6\;656}{12\;825}{k}_{3}+\frac{28\;561}{56\;430}{k}_{4}-\frac{9}{50}{k}_{5}+\frac{2}{55}{k}_{6}. $
(6)

Runge-Kutta-Fehlberg 方法的误差[25]，即4阶近似解与5阶较优解的绝对差为

$ |{z}_{k+1}-{y}_{k+1}|=\left|\frac{1}{360}{k}_{1}-\frac{128}{4\;275}{k}_{3}-\frac{2\;197}{75\;240}{k}_{4}+\frac{1}{50}{k}_{5}\frac{2}{55}{k}_{6}\right|.$
(7)

下一次计算过程中的步长通过将标量s乘以当前步长h来确定[25]. s的表达式为

$ \mathrm{s}\le {\left(\frac{\varepsilon h}{2\left|{z}_{k+1}-{y}_{k+1}\right|}\right)}^{{1}/{4}}\approx 0.84{\left(\frac{\varepsilon h}{\left|{z}_{k+1}-{y}_{k+1}\right|}\right)}^{{1}/{4}}. $
(8)

式中：ε为指定的误差控制值，yk+1及zk+1分别为使用4阶、5阶Rung-Kutta方法所确定的近似解和较优解.

模型参数的辨识结果如表2所示.

表 2   改进Bouc-Wen模型参数表

Tab.2  Parameters of modified Bouc-Wen model

p/kPa A β n γ φ
60 3.102 −12.030 0.251 −10.110 3.249
80 1.674 −6.137 0.500 −5.615 1.965
100 0.625 0.004 4.440 0.004 1.845
120 0.350 1.265 −2.416 −1.277 0.494

新窗口打开| 下载CSV


进一步，采用多项式数值拟合方法，建立了各参数与气压之间的关系：

$ \left.\begin{aligned} &A=8\;229{p}^{3}-1\;501{p}^{2}+17p+5.71 ,\\& \beta =-106\;833{p}^{3}+25\;950{p}^{2}-1\;757p+23 ,\\& n=-301\;812{p}^{3}+77\;048{p}^{2}-6\;307p+166, \\ &\gamma =-167\;166{p}^{3}+41\;525{p}^{2}-4\;114p+63 ,\\& \varphi =-49\;895{p}^{3}+13\;430{p}^{2}-1\;206p+38. \end{aligned}\right\}$
(9)

由此得到了动态输出力迟滞模型中的各参数.

4. Bouc-Wen修正模型的验证

为了验证Bouc-Wen修正模型的准确性，将驱动器在恒定充气压力为70、90、110 kPa下的实验数据与2种模型仿真数据进行对比，包括经典Bouc-Wen模型以及Bouc-Wen修正模型，结果如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

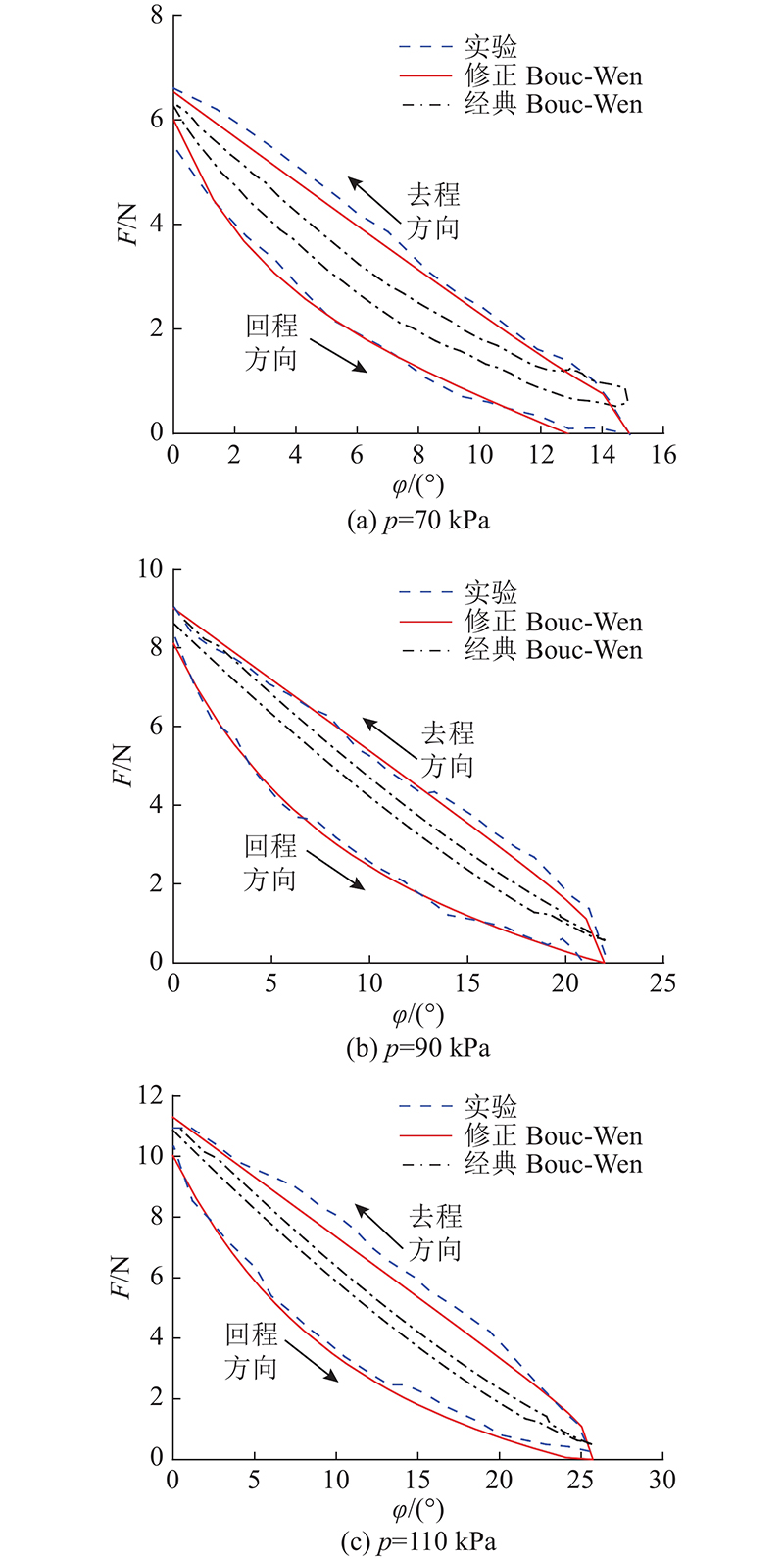
图 7   2种模型仿真结果与实验数据对比

Fig.7   Comparison between two model simulation results and experiments


定义模型的最大相对误差：

$ {\delta }_{\mathrm{M}\mathrm{A}\mathrm{X}}=\frac{\mathrm{\Delta }{F}_{\mathrm{M}\mathrm{A}\mathrm{X}}}{{F}_{\mathrm{M}\mathrm{A}\mathrm{X}}}\times 100{\text{%}} . $
(10)

式中：FMAX为实验测量的输出力最大值， $ \Delta {F_{{\text{MAX}}}} $为模型与实验相比的最大输出力误差.

定义R2统计量来检验修正模型的拟合优度：

$ R ^2 = \frac{{{\rm{SSR}}}}{{{\rm{SST}}}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{{\hat F}_i} - \bar F} \right)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{F_i} - \bar F} \right)}^2}} }} . $
(11)

式中：Fi为实验测得柔性关节驱动器的输出力， $ \bar{F} $为实验测得柔性关节驱动器输出力的平均值， ${{\hat F}_{i}}$为修正模型得到的柔性关节驱动器输出力. R2用来描述仿真模型与实验值的拟合程度，范围为[0, 1.0]，越接近1.0说明拟合优度越好.

如图7所示，相较于经典Bouc-Wen模型，所提出的Bouc-Wen修正模型，能够更为准确地描述柔性关节驱动器的迟滞特性. 由表3的3种充气压力情况下的最大误差∆FMAX、最大相对误差δMAX、平均偏差A.D.、均方差MSE以及拟合优度R2都可以看出，与经典Bouc-Wen模型相比较，Bouc-Wen修正模型对于柔性关节驱动器迟滞实验的拟合结果有了明显提高. 在70、90、110 kPa的3种充气压力情况下，Bouc-Wen修正模型的迟滞拟合结果和实验数据相比，柔性关节驱动器去程输出力的最大偏差为0.847 N，去程输出力最大相对误差为7.75%；回程输出力最大偏差0.637 N，回程输出力最大相对误差为7.57%. 去程平均偏差均小于0.45 N，而回程平均偏差则小于0.30 N. 在均方差方面，Bouc-Wen修正模型对于迟滞曲线的拟合结果均小于0.42 N，较经典Bouc-Wen模型也有明显提升. 在模型的拟合优度方面，经典Bouc-Wen模型的R2均小于0.90，而Bouc-Wen修正模型的R2均大于0.99，显示了精确拟合效果.

表 3   柔性关节驱动器迟滞建模评价

Tab.3  Evaluation of hysteresis modeling performance of flexible joint actuator

模型 p/kPa 状态 ∆FMAX/N δMAX/% A.D. /N MSE/N R2
经典Bouc-Wen模型 70 去程 1.990 30.48 1.284 1.1532 0.7036
回程 1.342 20.56 0.863
90 去程 2.440 27.11 1.381 0.6577 0.8796
回程 1.213 13.48 0.571
110 去程 3.050 26.99 1.396 0.8666 0.8789
回程 1.638 14.50 0.552
Bouc-Wen修正模型 70 去程 0.444 6.72 0.184 0.2144 0.9906
回程 0.507 7.57 0.139
90 去程 0.420 4.65 0.186 0.1967 0.9946
回程 0.341 3.78 0.142
110 去程 0.847 7.75 0.416 0.4146 0.9932
回程 0.637 5.83 0.287

新窗口打开| 下载CSV


此外，随着充气压力的增大，修正模型的迟滞偏差有增大的趋势，但均在较小误差范围内. 误差的来源除了实验误差外，最主要的是模型的参数个数和复杂程度，理论上来说，模型的参数越多，模型越复杂，其精度也越高，但过多的参数会导致模型复杂，计算可能不收敛. Bouc-Wen模型本身具有广泛适用性，其修正模型仅针对柔性关节驱动器迟滞曲线的非对称性而提出，可以为类似结构或材料的柔性驱动器迟滞建模研究提供借鉴.

5. 结　语

设计了一款仿蜘蛛液压关节的柔性关节驱动器，针对其输出力的迟滞影响，基于Bouc-Wen修正方法对力迟滞进行建模. 分析柔性关节驱动器产生迟滞的原因，得到不同充气压力下柔性关节驱动器的迟滞特性. 采用实验建模与理论建模相结合的方法，提出Bouc-Wen修正模型，引入一个具有方向性的修正项 $\phi (\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\;\left(\mathrm{\Delta }\dot{\varphi }\right)+\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\;\left(z\right))$，克服滞回的非对称及不确定性，并采用龙格-库塔-费尔贝格方法进行模型参数辨识. 从最大误差、相对误差、平均偏差、均方差以及拟合优度这5个方面对Bouc-Wen修正模型的准确性进行验证，结果表明相较于经典Bouc-Wen模型，柔性关节驱动器的力迟滞建模精度有了极大提升.

下一步将开展柔性关节驱动器的动态迟滞特性研究，如阶跃气压作用下的输出力动态过程实验与建模分析. 并且建立基于力迟滞建模及力反馈的闭环控制系统，研究柔性关节之类的超弹性材料驱动器的控制特性.

参考文献

LI G R, CHEN X P, ZHOU F H, et al

Self-powered soft robot in the Mariana Trench

[J]. Nature, 2021, 591 (7848): 66- 71

DOI:10.1038/s41586-020-03153-z      [本文引用: 1]

管清华, 孙健, 刘彦菊, 等

气动软体机器人发展现状与趋势

[J]. 中国科学:技术科学, 2020, 50 (7): 897- 934

[本文引用: 1]

GUAN Qing-hua, SUN Jian, LIU Yan-ju, et al

Status of and trends in soft pneumatic robotics

[J]. Scientia Sinica Technologica, 2020, 50 (7): 897- 934

[本文引用: 1]

CHEN Y H, CHUNG O A, CHEN B, et al

A lobster-inspired bending module for compliant robotic applications

[J]. Bioinspiration and Biomimetics, 2020, 15 (5): 056009

DOI:10.1088/1748-3190/ab9c8d      [本文引用: 1]

YE X, ZHU S D, QIAN X, et al. V-shape pneumatictorsional actuator: a building block for soft grasper and manipulator [J/OL]. (2021-6-24). https://www.liebertpub.com/doi/10.1089/soro.2020.0128.

PAEZ L, AGARWAL G, PAIK J

Design and analysis of a soft pneumatic actuator with origami shell reinforcement

[J]. Soft Robotics, 2016, 3 (3): 109- 119

DOI:10.1089/soro.2016.0023      [本文引用: 1]

LI M, PAL A, AGHAKHANI A, et al

Soft actuators for real-world applications

[J]. Nature Reviews Materials, 2022, 7 (3): 235- 249

DOI:10.1038/s41578-021-00389-7      [本文引用: 3]

ZHOU L, REN L L, CHEN Y

Bio-inspired soft grippers based on impactive gripping

[J]. Advanced Science, 2021, 8 (9): 2002017

DOI:10.1002/advs.202002017      [本文引用: 3]

郝天泽, 肖华平, 刘书海, 等

集成化智能软体机器人研究进展

[J]. 浙江大学学报:工学版, 2021, 55 (2): 229- 243

[本文引用: 1]

HAO Tian-ze, XIAO Hua-ping, LIU Shu-hai, et al

Research status of integrated intelligent soft robots

[J]. Journal of Zhejiang University: Engineering Science, 2021, 55 (2): 229- 243

[本文引用: 1]

徐彦, 方琴, 张超, 等

气动软体自折叠机械臂的驱动和负载性能

[J]. 浙江大学学报:工学版, 2020, 54 (2): 398- 406

[本文引用: 1]

XU Yan, FANG Qin, ZHANG Chao, et al

Driving and load performance of pneumatic soft self-folding manipulator

[J]. Journal of Zhejiang University: Engineering Science, 2020, 54 (2): 398- 406

[本文引用: 1]

ZOU J, GU G Y

Modeling the viscoelastic hysteresis of dielectric elastomer actuators with a modified rate-dependent Prandtl-Ishlinskii model

[J]. Polymers, 2018, 10 (5): 525

DOI:10.3390/polym10050525      [本文引用: 2]

KONDA R, ZHANG J

Hysteresis with lonely stroke in artificial muscles: characterization, modeling, and inverse compensation

[J]. Mechanical Systems and Signal Processing, 2022, 164: 108240

DOI:10.1016/j.ymssp.2021.108240      [本文引用: 1]

HASSANI V, TJAHJOWIDODO T, DO T N

A survey on hysteresis modeling, identification and control

[J]. Mechanical Systems and Signal Processing, 2014, 49 (1/2): 209- 233

[本文引用: 1]

CUI R G, LI S H, WANG Z, et al

A modified residual stress dependent Jile-Atherton hysteresis model

[J]. Journal of Magnetism and Magnetic Materials, 2018, 465: 578- 584

DOI:10.1016/j.jmmm.2018.06.021      [本文引用: 1]

SHAO B, CHEN B, CAO Y, et al

Nonlinear tensile behavior of cotton fabric reinforced polypropylene composites

[J]. Journal of Applied Polymer Science, 2020, 138 (5): 49780

[本文引用: 1]

李梦梦, 李原, 王庆林

EAP柔性智能驱动材料的建模、控制及应用研究进展

[J]. 机器人, 2018, 40 (5): 660- 672

DOI:10.13973/j.cnki.robot.180210      [本文引用: 1]

LI Meng-meng, LI Yuan, WANG Qing-lin

Research progress on modeling, control and application of EAP flexible intelligent driving materials

[J]. Robot, 2018, 40 (5): 660- 672

DOI:10.13973/j.cnki.robot.180210      [本文引用: 1]

THAI M T, PHAN P T, HOANG T T, et al

Design, fabrication, and hysteresis modeling of soft microtubule artificial muscle (SMAM) for medical applications

[J]. IEEE Robotics and Automation Letters, 2021, 6 (3): 5089- 5096

DOI:10.1109/LRA.2021.3072599      [本文引用: 1]

HEPP J, BADRI-SPRÖWITZ A. A novel spider-inspired rotary-rolling diaphragm actuator with linear torque characteristic and high mechanical efficiency [J/OL]. (2021-6-21). https://www.liebertpub.com/doi/full/10.1089/soro.2020.0108.

[本文引用: 1]

KELLARIS N, ROTHEMUND P, ZENG Y, et al

Spider-inspired electrohydraulic actuators for fast, soft-actuated joints

[J]. Advanced Science, 2021, 8 (14): 2100916

DOI:10.1002/advs.202100916      [本文引用: 2]

GÖTTLER C, AMADOR G, VAN D K T, et al

Fluid mechanics and rheology of the jumping spider body fluid

[J]. Soft Matter, 2021, 17 (22): 5532- 5539

DOI:10.1039/D1SM00338K      [本文引用: 1]

XU M, RONG C, HE L

Design and modeling of a bio-inspired flexible joint actuator

[J]. Actuators, 2021, 10 (5): 95

DOI:10.3390/act10050095      [本文引用: 1]

CHEN S E, CAO Y T, SARPARAST M, et al

Soft crawling robots: design, actuation, and locomotion

[J]. Advanced Materials Technologies, 2020, 5 (2): 1900837

DOI:10.1002/admt.201900837      [本文引用: 1]

LIN C J, LIN C R, YU S K, et al

Hysteresis modeling and tracking control for a dual pneumatic artificial muscle system using Prandtl-Ishlinskii model

[J]. Mechatronics, 2015, 28: 35- 45

DOI:10.1016/j.mechatronics.2015.03.006      [本文引用: 2]

ZHANG Q, DONG Y, PENG Y, et al

Asymmetric Bouc-Wen hysteresis modeling and inverse compensation for piezoelectric actuator via a genetic algorithm-based particle swarm optimization identification algorithm

[J]. Journal of Intelligent Material Systems and Structures, 2019, 30 (8): 1263- 1275

DOI:10.1177/1045389X19831360      [本文引用: 1]

PAUL S, MONDAL S P, BHATTACHARYA P

Numerical solution of LotkaVolterra prey predator model by using Runge-Kutta-Fehlberg method and Laplace Adomian decomposition method

[J]. Alexandria Engineering Journal, 2016, 55 (1): 613- 617

DOI:10.1016/j.aej.2015.12.026      [本文引用: 1]

PENG G R, LI W H, DU H, et al

Modelling and identifying the parameters of a magneto-rheological damper with a force-lag phenomenon

[J]. Applied Mathematical Modelling, 2014, 38 (15/16): 3763- 3773

[本文引用: 5]

/

〈 〉