随着航天器在轨服务需求越来越迫切，空间机器人代替宇航员执行太空任务已成为趋势，关于空间机器人在轨服务技术的研究也在全世界范围开展 ^{[ 1]} . 相较于单臂空间机器人系统，双臂空间机器人具有负载力更大、工作灵活性更高、可操作性更强等优势，已成为新的研究趋势 ^{[ 2]} . 在太空微重力环境中，基座与机械臂存在着多重动力学耦合，双臂空间机器人的动力学建模与轨迹跟踪控制一直是空间机器人控制的难点之一.

针对双臂空间机器人高精度轨迹跟踪的问题，研究者进行了深入研究 ^{[ 3- 5]} . 朱安等 ^{[ 6]} 设计的基于神经网络的全阶滑模控制器，实现了双臂空间机器人的柔顺避碰操作. Shi等 ^{[ 7]} 提出任务空间内双臂空间机器人基座和机械臂协调运动的滑模变结构控制方法. Yan等 ^{[ 8]} 设计了双臂空间机器人捕获翻滚目标接近过程中可操作性最大化和基座扰动最小化的多目标配置优化方法. 随着太空探索的不断深入，对双臂空间机器人轨迹跟踪的快速性与准确性提出了更高的要求，在上述文献中，系统稳定时间的问题均未解决.

有限时间控制具有良好的动态性能、较高的稳态精度以及有限时间收敛的特性，在机器人控制上得到了广泛的应用 ^{[ 9- 10]} . 但是，有限时间控制依赖系统初始条件，实际系统的初始值可能无法提前获得，从而无法准确计算出系统的收敛时间. 固定时间控制方法的收敛时间上界与初始条件无关，已成为新的研究热点 ^{[ 11]} . Zhang等 ^{[ 12]} 提出基于扩张状态观测器的固定时间输出反馈滑模跟踪控制方法，用以实现系统跟踪误差在固定时间内稳定到原点. Zuo ^{[ 13]} 针对存在匹配扰动的二阶非线性系统提出固定时间终端滑模控制策略. Ni等 ^{[ 14]} 提出固定时间稳定系统，并基于此系统推导出固定时间非奇异快速终端滑模控制器. 由于变指数幂次的存在，该收敛系统比常值幂次项的系统具有更快的收敛速度.

本研究考虑存在扰动情况下的双臂空间机器人轨迹跟踪问题，提出固定时间非奇异快速终端滑模控制策略. 将固定时间滑模面与固定时间趋近律结合，设计固定时间非奇异快速终端滑模控制器，实现基座以及机械臂关节在固定时间内跟踪上期望轨迹.

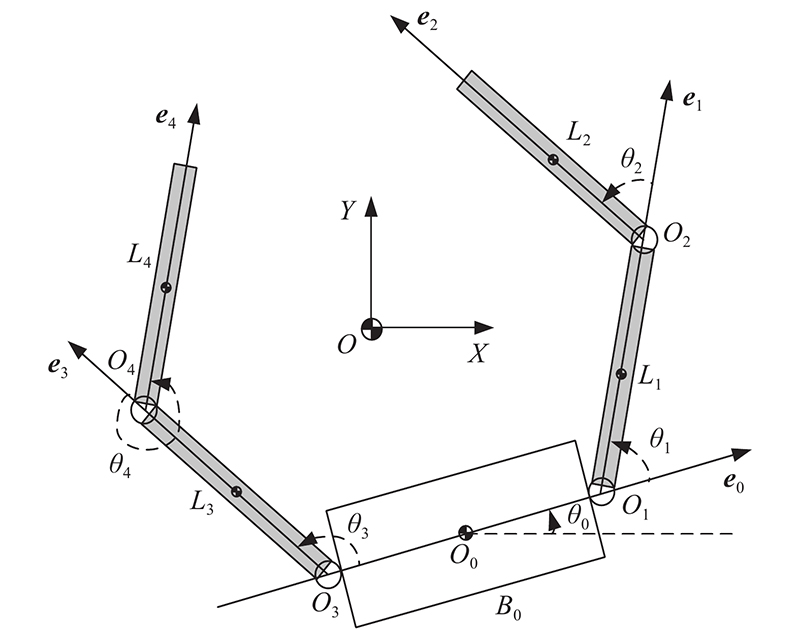
如 图1所示，以平面双臂空间机器人为例，建立其动力学模型.该结构包含中心基座 $ {B_0} $；由刚性连杆 $ {L_3} $、 $ {L_4} $，转动关节 $ {O_{\text{3}}} $、 $ {O_4} $构成的左臂；以及由刚性连杆 $ {L_{\text{1}}} $、 $ {L_2} $，转动关节 $ {O_{\text{1}}} $、 $ {O_2} $构成的右臂. 图中， ${\boldsymbol{e}}_0 $为基座基矢量， ${\boldsymbol{e}}_3 $、 ${\boldsymbol{e}}_4 $为左臂基矢量， ${\boldsymbol{e}}_1 $、 ${\boldsymbol{e}}_2 $为右臂基矢量.

双臂空间机器人系统的动力学方程 ^{[ 15]} ：

(1) $ {\boldsymbol{D}}({\boldsymbol{q}}){\boldsymbol{\ddot q}} + {\boldsymbol{H}}({\boldsymbol{q}},{{\dot {\boldsymbol{q}}}}){\boldsymbol{\dot q}} = {\boldsymbol{\tau }} . $

式中： ${\boldsymbol{D}}({\boldsymbol{q}}) $为正定对称惯量矩阵， ${{\boldsymbol{D}}({\boldsymbol{q}})} \in {{\bf{R}}^{5 \times 5}}$； ${\boldsymbol{H}}({\boldsymbol{q}}， {\boldsymbol{\dot q}}) {\boldsymbol{\dot q}}$为包含科氏力和离心力的向量， ${\boldsymbol{H}}({\boldsymbol{q}}， {\boldsymbol{\dot q}}) {\boldsymbol{\dot q}} \in {{{\bf{R}}}^5}$； ${\boldsymbol{q}} $为广义坐标， ${\boldsymbol{q}} = [{\theta _0}， {\theta _1}， {\theta _2}， {\theta _3}， {\theta _4}]^{\text{T}} \in {{{\bf{R}}}^5}$，其中 $ {\theta _0} $为基座姿态角， ${\theta _i}(i = 1， 2， 3， 4)$为连杆 ${L_i}(i = 1， 2， 3， 4)$的关节角； ${\boldsymbol{\tau }} $为系统控制力矩， ${\boldsymbol{\tau }} \in {{{\bf{R}}}^5}$. 考虑到空间机器人系统还受到多种不确定空间环境干扰力矩的影响，式(1)可以写为

(2) $ {\boldsymbol{D}}({\boldsymbol{q}}){\boldsymbol{\ddot q}} + {\boldsymbol{H}}({\boldsymbol{q}},{\boldsymbol{\dot q}}){\boldsymbol{\dot q}} + {{\boldsymbol{\tau }}_{\text{d}}} = {\boldsymbol{\tau }} . $

式中： $ {{\boldsymbol{\tau }}_{\text{d}}} $为集总外部扰动.

假设1　在动力学方程式(1)、(2)中，惯量矩阵 $ {\boldsymbol{D}}({\boldsymbol{q}}) $有界，即 $\left| {{\boldsymbol{D}}({\boldsymbol{q}})} \right| \leqslant {D_{\max }}$，其中 ${D_{\max }}$为已知常数. 外部扰动 $ {{\boldsymbol{\tau }}_{\text{d}}} $有界且界已知，即 $\left| {{{\boldsymbol{\tau }}_{\text{d}}}} \right| \leqslant {h_{\max }}$，其中 ${h_{\max }}$为已知常数.

针对式(2)，在假设成立的条件下，设计固定时间非奇异快速终端滑模控制律 ${\boldsymbol{\tau }}$，实现扰动情况下双臂空间机器人的快速高精度轨迹跟踪控制，并保证双臂空间机器人控制系统的跟踪误差在固定时间收敛.

引理1　考虑非线性系统 ${\boldsymbol{\dot x}} = f({\boldsymbol{x}}(t)),{\boldsymbol{x}} \in {{{\bf{R}}}^n}, {\boldsymbol{x}}(0) = {{\boldsymbol{x}}_0}$，其中 $f:{{\bf{R}}^n} \to {{\bf{R}}^n}$表示非线性函数，如果存在李雅普诺夫函数 $V({\boldsymbol{x}})$，以及参数 $\alpha \gt 0$、 $\; \beta \gt 0$、 $0 \lt p \lt 1$、 $q \gt 1$，使得 $\dot V({{\boldsymbol{x}}}) \leqslant - (\alpha V{({{\boldsymbol{x}}})^p} + \beta V{({{\boldsymbol{x}}})^q})$，那么系统 ${\dot {\boldsymbol{x}}} = f({{\boldsymbol{x}}}(t))$是固定时间稳定的，收敛时间 $T$满足 ^{[ 16]} ：

(3) $ T \leqslant \frac{1}{{\alpha (1 - p)}} + \frac{1}{{\beta (q - 1)}} . $

引理2　考虑如下的非线性系统

(4) $ \left.\begin{split} &\dot y = - {l_1}{\text{si}}{{{g}}^{{{\psi (}}{{{\varepsilon }}_{\text{1}}}{\text{)}}}}(y) - {l_2}{\text{si}}{{\text{g}}^{\phi {\text{(}}{{{\varepsilon }}_{\text{2}}}{\text{)}}}}(y),\\ &\psi ({\varepsilon _1}) = 1{{ +0.5 }}{{{\varepsilon _1}}}\left( {1{{ + }}{{\rm{sgn}}} \;(\left| y \right| - 1)} \right),\\ &\phi ({\varepsilon _2}) = 1 - 0.5{{{\varepsilon _2}}}( 1 - {{\rm{sgn}}} \;(\left| y \right| - 1) ).\,\,\, \end{split}\right\} $

式中： ${\text{sig}}^{P}(·)={|·|}^{P}\mathrm{sgn}(·)$，其中 $P\geqslant 0 $， $ \mathrm{sgn}(·) $为符号函数；如果系统参数满足 ${l_1} \gt 0$、 ${l_2} \gt 0$、 ${\varepsilon _1} \gt 0$、 $0 \lt {\varepsilon _2} \lt {0.5} $，则该系统状态将在固定时间内收敛到原点,且收敛时间满足

$ T \leqslant \left({{{l_2}{\varepsilon _1}}}\right)^{-1}\ln \;\left(1 + {{{l_2}}}/{{{l_1}}}\right) + \left({{{l_1}{\varepsilon _2}}}\right)^{-1} \ln\; \left(1 + {{{l_1}}}/{{{l_2}}}\right). $

证明　式(4)可被分解为分段函数：

(5) $ \dot{y}=\left\{\begin{array}{ll}-{l}_{1}{\text{sig}}^{1+{\varepsilon }_{1}}y-{l}_{2}y\text{，}& \left|y\right|\geqslant 1\text{；}\\ -{l}_{1}y-{l}_{2}{\text{sig}}^{1-{\varepsilon }_{2}}y\text{，}& \left|y\right| \lt 1.\end{array}\right. $

变换式（5），当 $\left| y \right| \gt 1$时，令 $z = \left| y \right|$,当 $\left| y \right| \lt 1$时，令 $z = {\left| y \right|^{{\varepsilon _2}}}$. 式(5)可以写为

(6) $ \dot{z}=\left\{\begin{array}{ll}-{l}_{1}{z}^{1+{\varepsilon }_{1}}-{l}_{2}z\text{，}& z\geqslant 1\text{；}\\ -{\varepsilon }_{2}{l}_{1}z-{\varepsilon }_{2}{l}_{2}\text{，}& 0 \lt z \lt 1.\end{array}\right. $

求解式(6)得到系统的收敛时间上界为

(7) $ \begin{split} \mathop {\lim }\limits_{{z_0} \to \infty } T({z_0}) = & \mathop {\lim }\limits_{{z_0} \to \infty } \left({\int_0^1 {\frac{1}{{{\varepsilon _2}{l_1}z + {\varepsilon _2}{l_2}}}{\text{d}}z + \int_1^{{z_0}} {\frac{1}{{{l_1}{z^{1 + {\varepsilon _1}}} + {l_2}z}}{\text{d}}z} } } \right) = \\& \frac{1}{{{l_1}{\varepsilon _2}}}\ln \;\left( {\frac{{{l_1} + {l_2}}}{{{l_2}}}} \right) + \frac{1}{{{l_2}{\varepsilon _1}}}\ln\; \left( {\mathop {\lim }\limits_{{z_0} \to \infty } \frac{{({l_1} + {l_2})z_0^{{\varepsilon _1}}}}{{{l_1}z_0^{{\varepsilon _1}} + {l_2}}}} \right) = \\ & \frac{1}{{{l_1}{\varepsilon _2}}}\ln\; \left( {\frac{{{l_1} + {l_2}}}{{{l_2}}}} \right) + \frac{1}{{{l_2}{\varepsilon _1}}}\ln\;\left( {\frac{{{l_1} + {l_2}}}{{{l_1}}}} \right). \\[-10pt] \end{split} $

引理2中系统固定时间收敛特性得证.

注1　相比于文献[ 13]、[ 14]，本研究设计的控制器不但在 $\left| y \right| \lt 1$时提高了系统的收敛速度，而且在系统状态远离平衡点( $\left| y \right| \geqslant 1$)时，将 $ {l_2}{\rm{si}}{{\rm{g}}^{{p}/{q}}}y $变换为 $ {l_2}y $来提高系统的收敛速度. 另外，通过对比收敛时间上界，同样可以得出：本研究设计的固定收敛系统比文献[ 13]、[ 14]的收敛速度更快.

为了方便控制器设计，将式(2)改写为如下的状态方程形式：

(8) $ \left. \begin{gathered} {{{\dot {\boldsymbol{x}}}}_{\text{1}}} = {{{\boldsymbol{x}}}_{\text{2}}}, \hfill \\ {{{\dot {\boldsymbol{x}}}}_2} = {{\boldsymbol{F}}} + {{\boldsymbol{G}}}{\boldsymbol{\tau }} + {{\boldsymbol{D}}}{\text{.}} \hfill \end{gathered} \right\} $

式中： ${{{\boldsymbol{x}}}_{\text{1}}} = {\boldsymbol{q}}$， ${{{\boldsymbol{x}}}_{\text{2}}} = {\boldsymbol{\dot q}}$， ${{\boldsymbol{F}}} = - {{\boldsymbol{D}}^{ - 1}}({\boldsymbol{q}}){\boldsymbol{H}}({\boldsymbol{q}},{\boldsymbol{\dot q}}){\boldsymbol{\dot q}}$， ${{\boldsymbol{G}}} = {{\boldsymbol{D}}^{ - 1}}({\boldsymbol{q}})$， ${{\bar {\boldsymbol{D}}}} = - {{\boldsymbol{D}}^{ - 1}}({\boldsymbol{q}}){{\boldsymbol{\tau }}_{\text{d}}}$. 根据假设1可知， ${{\bar {\boldsymbol{D}}}}$有界，且满足 $ \left| {{{\bar {\boldsymbol{D}}}}} \right| \lt {\bar D_{\max }} $，其中 ${\bar D_{\max }} = {{{h_{\max }}}}/{{{D_{\max }}}}$为扰动上界.

将基座期望姿态角以及各关节给定的期望轨迹记为 ${{\boldsymbol{q}}_{\text{d}}} = {[{\theta _{{\text{0d}}}},{\theta _{{\text{1d}}}},{\theta _{{\text{2d}}}},{\theta _{{\text{3d}}}},{\theta _{{\text{4d}}}}]^{\text{T}}}$，定义状态误差为 $ {{\boldsymbol{e}}} = {{\boldsymbol{q}}} - {{{\boldsymbol{q}}}_{\text{d}}} $，则误差对时间的导数为 $ {\dot {\boldsymbol{e}}} = {\dot {\boldsymbol{q}}} - {{\dot {\boldsymbol{q}}}_{\text{d}}} $. 为了1）避免出现终端滑模控制器控制力矩无法求解的问题，2）提高跟踪误差在远离平衡点和靠近平衡点时的收敛速度,设计固定时间非奇异快速终端滑模面 ${{\boldsymbol{S}} = }{{\text{[}}{{{S}}_1},{{{S}}_2},{{{S}}_3},{{{S}}_4},{{{S}}_5}{\text{]}}^{\text{T}}}$，其中

(9) $ \begin{array}{*{20}{c}} {{S_i} = {{\dot e}_i} + {\beta _1}{\rm{si}}{{\rm{g}}^{{\psi _i}({\varepsilon _1})}}({e_i}) + {R_i}({\boldsymbol{e}}),}&{i = 1,2,3,4,5} . \end{array} $

式中： ${\beta _1} $主要用来调节系统跟踪误差远离平衡点时的收敛速度， ${\beta _1} \gt 0$； $\psi_{i}\left(\varepsilon_{1}\right) = 1 + 0.5 \varepsilon_{1}(1 + \operatorname{sgn}\;(\left|e_{i}\right| - 1));$ ${e_i}$为 ${{\boldsymbol{e}}}$的第 $i$行元素； $ {R_i}({\boldsymbol{e}}) $的表达式为

(10) $ \left.\begin{split} &{R_i}({\boldsymbol{e}}) =\left\{ \begin{array}{l} {\beta _2}{\rm{si}}{{\rm{g}}^{{\phi _i}({{{\varepsilon }}_{\text{2}}})}}({e_i}), \;\,\,\quad\left| {{e_i}} \right| \geqslant \delta ;\hfill \\ {\lambda _1}{e_i} + {\lambda _2}{\rm{si}}{{\rm{g}}^\gamma }({e_i}),\,\;\left| {{e_i}} \right| \lt \delta . \hfill \end{array} \right.\\ &{\lambda _1} = {{{\beta _2}(\phi_i ({\varepsilon _2}) - \gamma )}}{\delta ^{\phi_i ({\varepsilon _2}) - 1}}/\left({{1 - \gamma }}\right),\hfill \\ &\lambda_{2}=\beta_{2}\left(\phi_i\left(\varepsilon_{2}\right)-1\right)\delta ^{\phi_i\left(\varepsilon_{2}\right)-\gamma}/\left( 1-\gamma\right),\hfill \\ &{\phi _i}({\varepsilon _2}) = 1 - 0.5{{{\varepsilon _2}}}\left( {1 - {{\rm{sgn}}} (\left| {{e_i}} \right| - 1)} \right). \end{split} \right\} $

式中： $\gamma $为滑模面待定系数， $\gamma \gt 1$； $ \delta $为很小的正常数； ${\beta _2} $控制跟踪误差靠近平衡点时的收敛速度， ${\beta _2} \gt 0$. 对式(9)求导可得

(11) $ {\dot S_i} = {\ddot e_i} + {\beta _1}{\psi _i}({\varepsilon _1}){\left| {{e_i}} \right|^{{\psi _i}({\varepsilon _1}) - 1}}{\dot e_i} + {\dot R_i}({\boldsymbol{e}}) . $

(12) $ {\dot R_i}({\boldsymbol{e}}) = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} {\beta _2}{\phi _i}({\varepsilon _2}){\left| {{e_i}} \right|^{{\phi _i}({\varepsilon _2}) - 1}}{{\dot e}_i}, \hfill \\ {\lambda _1}{{\dot e}_i} + {\lambda _2}\gamma {\left| {{e_i}} \right|^{\gamma - 1}}{{\dot e}_i}, \hfill \\ \end{gathered} &\begin{gathered} \left| {{e_i}} \right| \geqslant \delta ; \hfill \\ \left| {{e_i}} \right| \lt \delta . \hfill \\ \end{gathered} \end{array}} \right. $

注2　如式(12)所示，当 $\left| {{e_i}} \right| \to 0$时，由于 $\gamma \gt 1$，解决了系统的奇异性问题. 不仅如此，滑模面中的参数 ${\lambda _1}$、 ${\lambda _2}$的巧妙设计，保证了滑模面 ${S}$及其导数 ${\dot S}$的连续性. 另外，相比于文献[ 17]、[ 18]中引入的定常数幂次项，本研究设计的滑模面非奇异项 $ {R_i}({\boldsymbol{e}}) $，在 $\left| {{e_i}} \right| \lt \delta $时具有更快的收敛速度.

令 ${\dot {\boldsymbol{S}}} = {{\bf{0}}}$,可以得到等效控制项：

(13) $ {{\boldsymbol{\tau}} }_{\text{eq}}={\boldsymbol{D}}({\boldsymbol{q}})\left({\ddot{{\boldsymbol{q}}}}_{\text{d}}-{\beta }_{1}{\bf\textit{ψ}} ({\varepsilon }_{1}){\left|\boldsymbol{e}\right|}^{{\bf\textit{ψ}} ({\varepsilon }_{1})-1}\dot{{\boldsymbol{e}}}-\dot{{\boldsymbol{R}}}({{\boldsymbol{e}}})\right)+{\boldsymbol{H}}({{\boldsymbol{q}}},\dot{{\boldsymbol{q}}})\dot{{\boldsymbol{q}} } . $

式中： ${\boldsymbol{\psi }}({\varepsilon _1}) \in {{\bf R}^{5 \times 1}}$、 ${\boldsymbol{\dot R}}({{\boldsymbol{e}}}) \in {{\bf R}^{5 \times 1}}$分别为 ${\psi _i}({\varepsilon _1})$和 ${\dot R_i}({{\boldsymbol{e}}})$依次组成的向量.

为了提高滑模控制趋近阶段的收敛速度，削弱滑模控制固有的抖振问题，设计趋近律：

(14) $ \begin{split} {{\dot S}_i} =& - {K_0}{{\rm{sgn}}}\; ({S_i}) - {K_1}{\rm{s i}}{{\rm{g}}^{1 + 0.5{{{\alpha _1}}}\left( {1 + {{\rm{sgn}}}\; (\left| {{S_i}} \right| - 1)} \right)}}({S_i}) - \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {K_2}{{\rm{s}}} {\rm{i}}{{\rm{g}}^{1 - 0.5{{{\alpha _2}}}\left( {1 - {{\rm{sgn}}}\; (\left| {{S_i}} \right| - 1)} \right)}}({S_i}). \\ \end{split} $

式中： ${K_0}$、 ${K_1}$、 ${K_2}$为正常数.

结合式(8)、(13)、(14)，本研究设计的固定时间非奇异快速终端滑模律为

(15) $ \begin{split}{\boldsymbol{\tau}} =& {{\boldsymbol{\tau}} }_{\text{eq}}-{\boldsymbol{D}}({\boldsymbol{q}})\Big({K}_{0}\mathrm{sgn}\;(\boldsymbol{S})+{K}_{1}{\text{sig}}^{1+{\scriptstyle 0.5{{\alpha }_{1}}}\left(1+\mathrm{sgn}\;(\left|\boldsymbol{S}\right|-1)\right)}(\boldsymbol{S})+\\& {K}_{2}{\text{sig}}^{1-{\scriptstyle 0.5{{\alpha }_{2}}}\left(1-\mathrm{sgn}\;(\left|\boldsymbol{S}\right|-1)\right)}(\boldsymbol{S})\Big).\\[-10pt]\end{split} $

式中： ${\text{si}}{{\text{g}}^{1 + 0.5{{{\alpha _1}}}\left( {1 + {{\rm{sgn}}}\; (\left| {{\boldsymbol{S}}} \right| - 1)} \right)}}({{\boldsymbol{S}}})$为 ${\text{si}}{{\text{g}}^{1 + 0.5{{{\alpha _1}}}\left( {1 + {{\rm{sgn}}} \;(\left| {{S_i}} \right| - 1)} \right)}}({S_i})$依次组成的向量.

定理 　考虑双臂空间机器人系统，采用本研究设计的固定时间非奇异快速终端滑模面. 在固定时间控制律的作用下，滑模面 ${\boldsymbol{S}}$与跟踪误差 ${\boldsymbol{e}}$是固定时间收敛的，并且收敛时间上界 $ {T_{\max }} $仅与设计参数有关.

证明 　构造李雅普诺夫函数：

(16) $ V = \frac{1}{2}{{\boldsymbol{S}}^{\text{T}}}{\boldsymbol{S}} . $

对(16)求导，同时结合式(8)、(11)、(12)可以得到

(17) $ \begin{split} \dot V =& {{{\boldsymbol{S}}}^{\text{T}}}{\dot {\boldsymbol{S}} = } \hfill \\& {{{\boldsymbol{S}}}^{\text{T}}}\left[{\ddot {\boldsymbol{e}}} + {\beta _1}{\bf\textit{ψ}} ({\varepsilon _1}){\left| {{\boldsymbol{e}}} \right|^{{\bf\textit{ψ}} ({\varepsilon _1}) - 1}}{\dot {\boldsymbol{e}}} + \dot {\boldsymbol{R}}({{\boldsymbol{e}}})\right] = \hfill \\& {{{\boldsymbol{S}}}^{\text{T}}}\left[{{\boldsymbol{F}}} + {{\boldsymbol{G}}}{\boldsymbol{\tau }} + {{\boldsymbol{D}}} - {{{\ddot {\boldsymbol{q}}}}_{\text{d}}} + {\beta _1}{\bf\textit{ψ}} ({\varepsilon _1}){\left| {{\boldsymbol{e}}} \right|^{{\bf\textit{ψ}} ({\varepsilon _1}) - 1}}{\dot {\boldsymbol{e}}} + \dot {\boldsymbol{R}}({{\boldsymbol{e}}})\right]. \hfill \end{split} $

将式(13)、(15)代入式(17)，有

(18) $ \begin{split} \dot V{ = }&{{{\boldsymbol{S}}}^{\text{T}}}\Big( - {K_0}{{\rm{sgn}}}\; ({{\boldsymbol{S}}}) - {K_1}{{\rm{s}}} {\rm{i}}{{\rm{g}}^{1 + 0.5{{{\alpha _1}}}\left( {1 + {{\rm{sgn}}} \;(\left| {{\boldsymbol{S}}} \right| - 1)} \right)}}({{\boldsymbol{S}}}) - \Big. \hfill \\& \Big. {K_2}{{\rm{s}}} {\rm{i}}{{\rm{g}}^{1 - 0.5{{{\alpha _2}}}\left( {1 - {{\rm{sgn}}} \;(\left| {{\boldsymbol{S}}} \right| - 1)} \right)}}({{\boldsymbol{S}}}) + {\bar {\boldsymbol{D}}}\Big) \leqslant \hfill \\& {{{\boldsymbol{S}}}^{\text{T}}}\Big( - {K_1}{{\rm{s}}} {\rm{i}}{{\rm{g}}^{1 + 0.5{{{\alpha _1}}}\left( {1 + {{\rm{sgn}}} \;(\left| {{\boldsymbol{S}}} \right| - 1)} \right)}}({{\boldsymbol{S}}})-\Big.\hfill \\& \Big.{K_2}{{\rm{s}}} {\rm{i}}{{\rm{g}}^{1 - 0.5{{{\alpha _2}}}\left( {1 - {{\rm{sgn}}} \;(\left| {{\boldsymbol{S}}} \right| - 1)} \right)}}({{\boldsymbol{S}}})\Big) = \hfill \\& - {K_1}{\sum\limits_{i = 1}^5 {\left| {{S_i}} \right|} ^{2 + 0.5{{{\alpha _1}}}\left( {1 - {{\rm{sgn}}} \;(\left| {{S_i}} \right| - 1)} \right)}} - \hfill \\& {K_2}{\sum\limits_{i = 1}^5 {\left| {{S_i}} \right|} ^{2 - 0.5{{{\alpha _2}}}\left( {1 - {{\rm{sgn}}} \;(\left| {{S_i}} \right| - 1)} \right)}} = \hfill \\& - {K_1}{(2V)^{1 + 0.25{{{\alpha _1}}}\left( {1 + {{\rm{sgn}}} \;(\left| {{\boldsymbol{S}}} \right| - 1)} \right)}} - \hfill \\ &{K_2}{(2V)^{1 - 0.25{{{\alpha _2}}}\left( {1 - {{\rm{sgn}}} \;(\left| {{\boldsymbol{S}}} \right| - 1)} \right)}}. \hfill \end{split} $

当 $\left| {{S_i}} \right| \geqslant 1$时，

(19) $ \dot V \leqslant - {2^{1 + 0.5{{{\alpha _1}}}}}{K_1}{V^{1 + 0.5{{{\alpha _1}}}}} - 2{K_2}V ; $

当 $\left| {{S_i}} \right| \lt 1$时，

(20) $ \dot V \leqslant - 2{K_1}V - {2^{1 - 0.5{{{\alpha _2}}}}}{K_2}{V^{1 - 0.5{{{\alpha _2}}}}} . $

根据李雅普诺夫稳定性定理和引理2可知，系统跟踪误差在固定时间 ${t_1}$内收敛到 ${\boldsymbol{S}} = {{\bf{0}}}$. 满足

(21) $ \begin{split} {t_1} \lt {T_1} = & \frac{1}{{2{K_2}0.5{{{\alpha _1}}}}}\ln\; \left( {1 + \frac{{2{K_2}}}{{{2^{1 + 0.5{{{\alpha _1}}}}}{K_1}}}} \right) + \\ &\frac{1}{{2{K_1}0.5{{{\alpha _2}}}}}\ln\;\left( {1 + \frac{{2{K_1}}}{{{2^{1 - 0.5{{{\alpha _2}}}}}{K_2}}}} \right). \end{split}$

此时，由式(9)可知 $ {\dot e_i} = - {\beta _1}{\rm{si}}{{\rm{g}}^{{\psi _i}({\varepsilon _1})}}({e_i}) - R({e_i}) $.

当 $ \left| {{e_i}} \right| \geqslant \delta $时， ${\dot e_i} = - {\beta _1}{\rm{si}}{{\rm{g}}^{{\psi _i}({\varepsilon _1})}}({e_i}) - {\beta _2}{\rm{si}}{{\rm{g}}^{{\varphi _i}({\varepsilon _2})}}({e_i})$. 根据引理2可知，系统误差在固定时间 ${t_2}$内收敛到 $ \left| {{e_i}} \right| \lt \delta $，并且满足：

(22) $ {t_2} \lt {T_2} = \frac{1}{{{\beta _2}{\varepsilon _1}}}\ln \;\left( {1 + \frac{{{\beta _2}}}{{{\beta _1}}}} \right) + \frac{1}{{{\beta _1}{\varepsilon _2}}}\ln\; \left( {1 + \frac{{{\beta _1}}}{{{\beta _2}}}} \right) . $

此时， $ \left| {{{\dot e}_i}} \right| \leqslant {\beta _1}\left| {{e_i}} \right| + {\beta _2}{\left| {{e_i}} \right|^{1 - {\varepsilon _2}}} \lt {\beta _1}\delta + {\beta _2}{\delta ^{1 - {\varepsilon _2}}} $.

当 $ \left| {{e_i}} \right| \lt \delta $时,由于 $ 0 \lt \delta \lt 1 $,则 $ \left| {{e_i}} \right| \lt \delta \lt 1 $,此时根据式(9)、(10)可以得到

(23) $ \begin{split} {{\dot e}_i}{ = } &- {\beta _1}{\rm{si}}{{\rm{g}}^{{\psi _i}({\varepsilon _1})}}({e_i}) - {\lambda _1}{e_i} - {\lambda _2}{\rm{si}}{{\rm{g}}^\gamma }({e_i}) = \\ & - {\beta _1}{e_i} - {\lambda _1}{e_i} - {\lambda _2}{\rm{si}}{{\rm{g}}^\gamma }({e_i}). \end{split} $

因此

(24) $ \begin{split} \left| {{{\dot e}_i}} \right| \leqslant & {\beta _1}\left| {{e_i}} \right| + {\lambda _1}\left| {{e_i}} \right| + {\lambda _2}{\left| {{e_i}} \right|^\gamma } \leqslant \hfill \\& {\beta _1}\delta + \frac{{{\beta _2}(1 - {\varepsilon _2} - \gamma )}}{{1 - \gamma }}{\delta ^{ - {\varepsilon _2}}}\delta + \frac{{{\beta _2}( - {\varepsilon _2})}}{{1 - \gamma }}{\delta ^{1 - {\varepsilon _2} - \gamma }}{\delta ^\gamma } \leqslant \hfill \\& {\beta _1}\delta + {\beta _2}{\delta ^{1 - {\varepsilon _2}}}. \end{split} $

综上，系统跟踪误差在固定时间内收敛且收敛时间满足 $ T \lt {T_{\max }} = {T_1} + {T_2} $.

为了验证所提控制算法的有效性，以 图1所示的双臂空间机器人为例进行仿真实验. 仿真中使用的双臂空间机器人系统参数标称值参照文献[ 15]，如 表1所示. 表中， m为质量， $l$为长度， $I$为转动惯量.

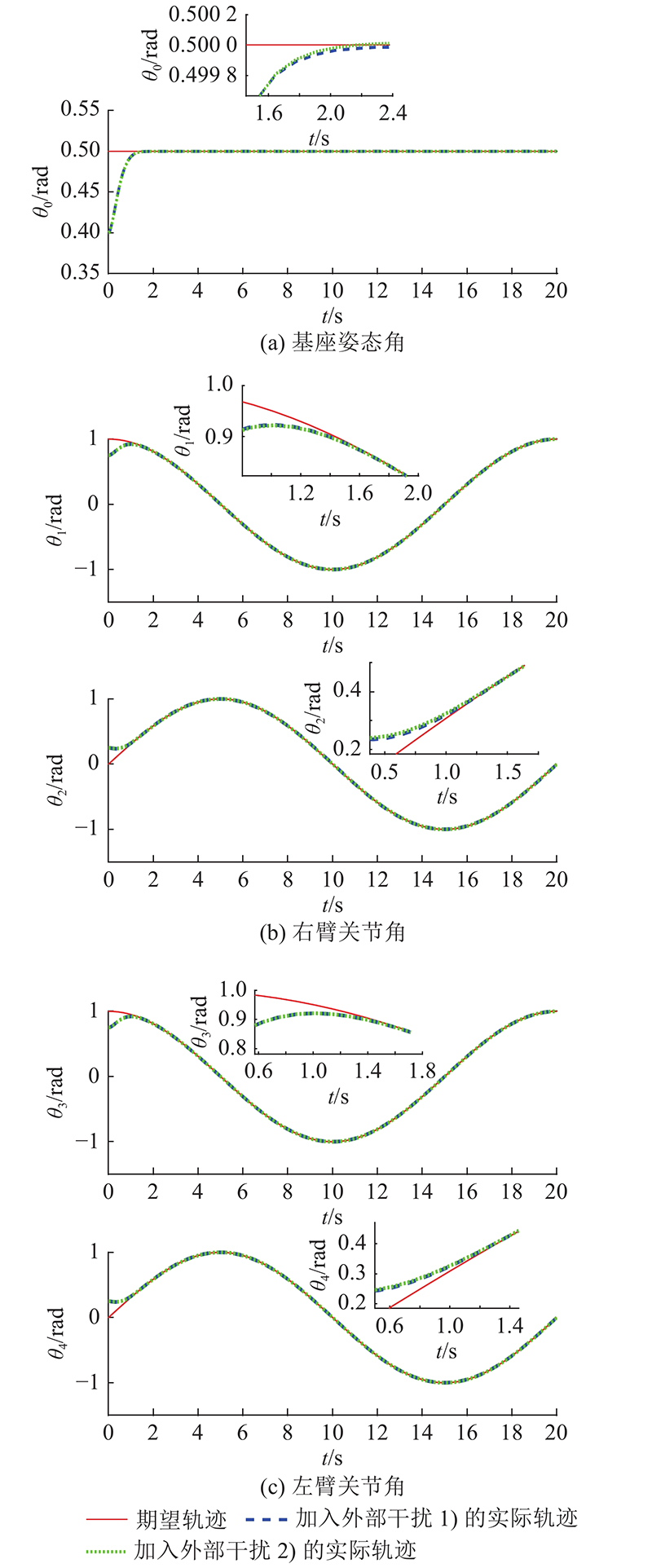
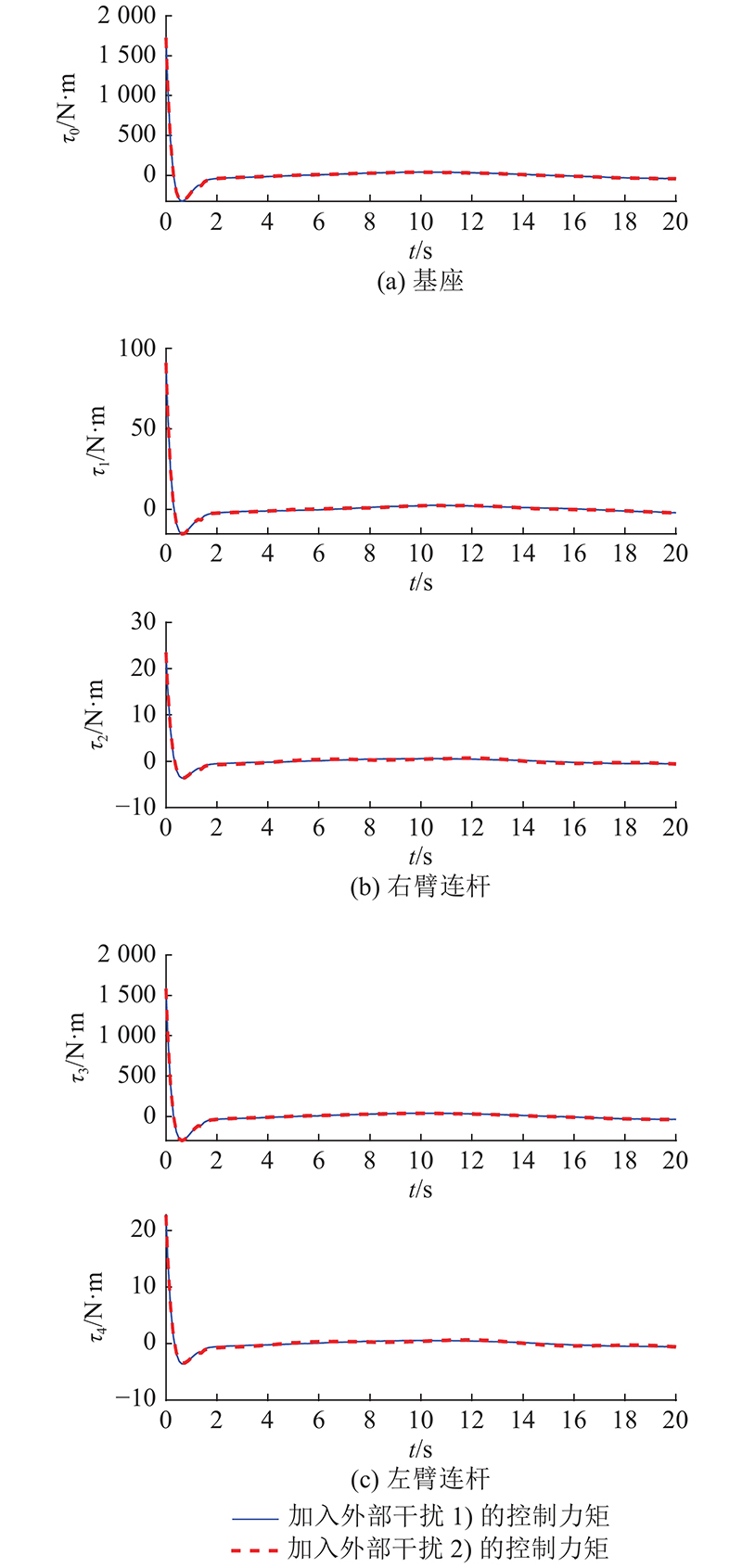
仿真1　基座姿态角以及机械臂关节角的初始状态为 ${{\boldsymbol{q}}_{\text{0}}} = {\left[0.4,0.75,0.25,0.75,0.25\right]^{\text{T}}}\;{\text{rad}}$，期望值为 q _d = $\left[0.5,\cos\; ({\text{0}}{{. 1{\text{π}} }}t),\sin \;({\text{0}}{{. 1{\text{π}} }}t),\cos\; ({\text{0}}{{. 1{\text{π}} }}t), \sin\; ({\text{0}}{{. 1{\text{π}} }}t)\right]^{\text{T}} {\text{rad}}$， 仿真时间为10 s. 为了验证所提控制算法的有效性，分别考虑2组动态扰动，外部干扰1）为 ${{\boldsymbol{\tau}} _{{\text{d1}}}} = $ $ {[0.1\sin \,(t),0.1\sin \,(t),0.1\sin \,(t),0.1\sin \,(t),0.1\sin \,(t)]^{\text{T}}} $N·m，外部干扰2）为 ${{\boldsymbol{\tau}} _{{\text{d2}}}} =[0.2\cos\; (t),0.2\cos\; (t),0.2\cos\; (t), 0.2\cos\; (t), 0.2\cos\; (t)]^{\text{T}}$ $ \text{N}·\text{m} $，所设计的固定时间控制律参数均为 $ \;{\beta _1} = 1 $、 $\; {\beta _2} = 1 $、 ${\varepsilon _1} = 1$、 ${\varepsilon _2} = 0.25$、 $\delta = 0.01$、 $\gamma = 10$、 ${\alpha _1} = 1$、 ${\alpha _2} =0.25$、 ${K_0} = 0.01$、 ${K_1} = 1$、 ${K_2} = 1$. 轨迹跟踪结果如 图2所示，控制力矩如 图3所示. 图中， ${{\tau }_0}$为基座的控制力矩， $ {\tau _i}(i = 1,2,3,4) $为连杆 $ L_{i}(i=1,2,3,4) $的控制力矩.由 图2可以看出，在有不同外部动态干扰存在的情况下，本研究设计的控制器能够保证系统良好的控制性能，基座以及机械臂关节均能够在0~2 s跟踪上期望轨迹，表明所设计的控制器具有较强的鲁棒性. 由 图3可以看出，系统控制力矩连续且没有明显的抖振现象.

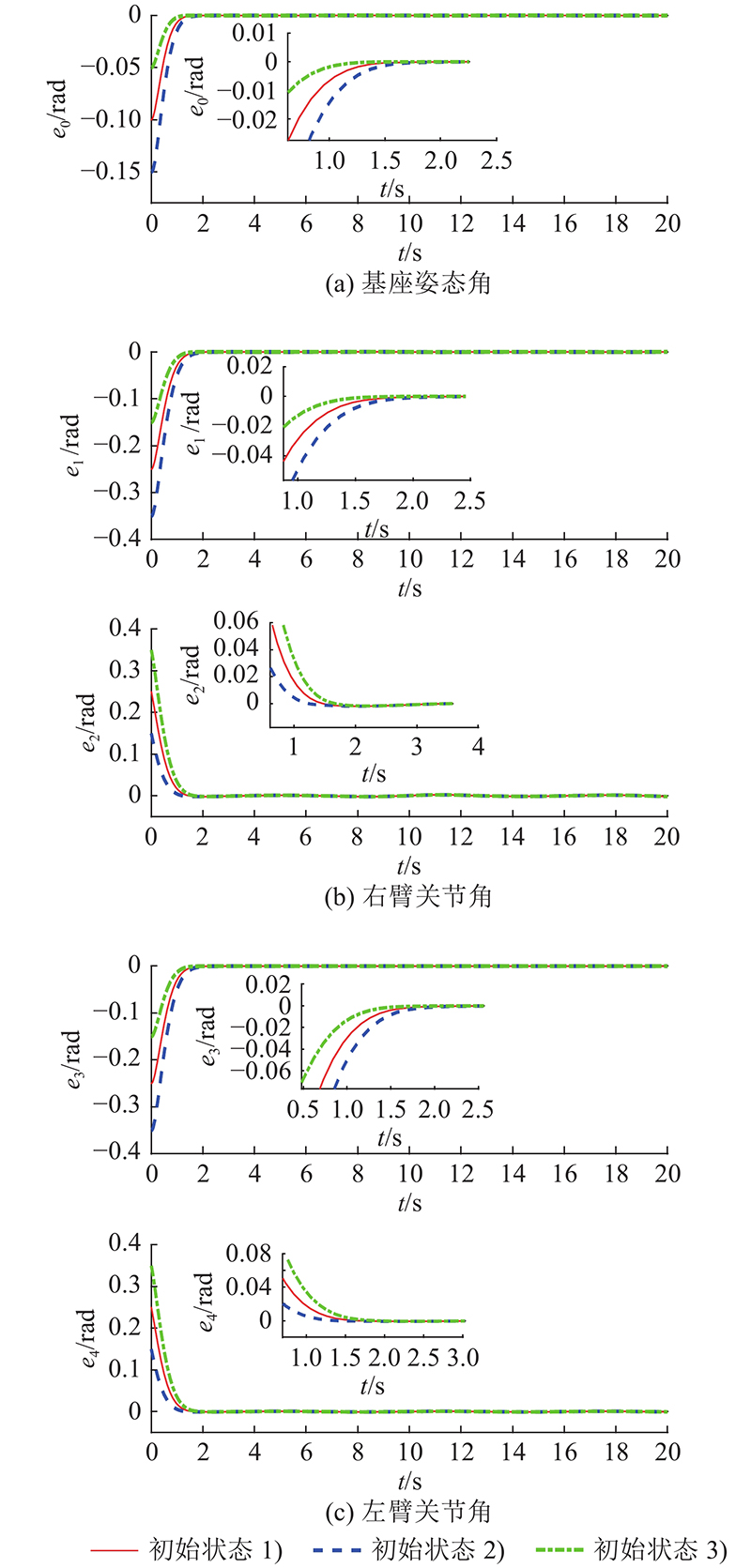
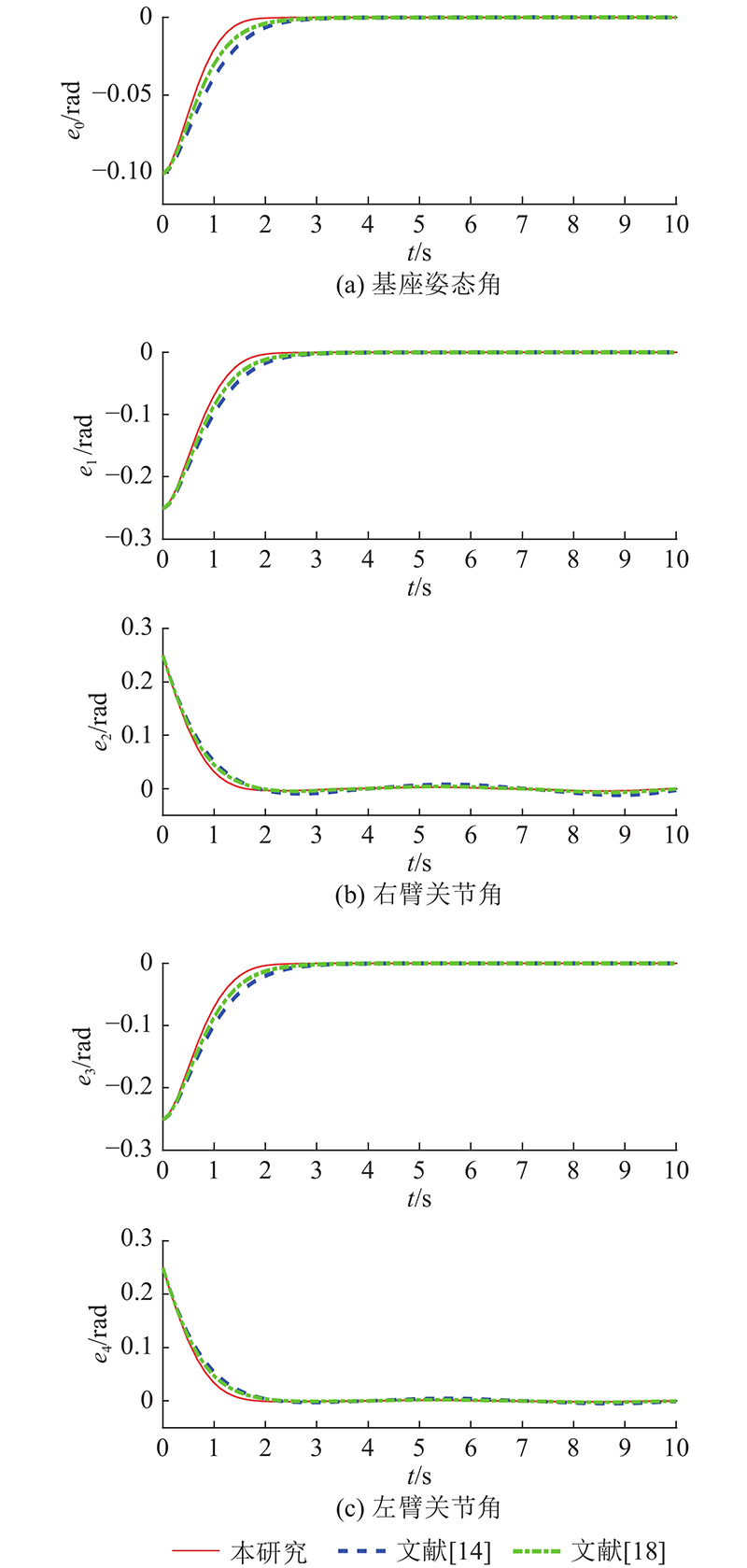
仿真2　为了验证本研究所提固定时间控制算法的跟踪效果不受系统初始状态的影响，定义仿真1中基座姿态角以及机械臂关节角的初始状态为初始状态1）. 再设置初始状态2）为

$ \boldsymbol{q}_{0}=[0.3,0.65,0.15,0.65,0.15]^{\mathrm{T}} \mathrm{rad}; $

初始状态3）为

$ \boldsymbol{q}_{0}=[0.5,0.85, 0.55,0.85,0.55]^{\mathrm{T}} \mathrm{rad}.$

控制律参数保持不变，基座及双臂关节轨迹跟踪结果如 图4所示. 图中， ${{e}_0}$为基座的姿态角跟踪误差， ${e_i}(i = 1,2,3,4)$为连杆 $ L_{i}(i=1,2,3,4) $的关节角轨迹跟踪误差. 可以看出，基座姿态角和机械臂关节角在不同初始状态下均能在所设定的时间上界内跟踪上期望值. 这表明基座和机械臂关节角跟踪误差收敛时间与系统初始状态无关，证明所设计的控制算法具有固定时间收敛特性.

仿真3　为了进一步验证本研究所提固定时间控制算法对双臂空间机器人轨迹跟踪的有效性，在相同初始条件、期望轨迹和外部干扰的情况下，将本研究设计的固定时间非奇异快速终端滑模控制器与文献[ 14]、[ 18]所提固定时间控制器进行仿真对比. 基座和关节角跟踪误差收敛时间如 图5所示. 可以看出，与其他2种固定时间控制方法相比，本研究所提控制方法在响应速度和收敛速度上有了较大提升，可以实现基座姿态角和机械臂关节角跟踪误差在0~2 s收敛到原点附近. 同时，相比于其他控制器，本研究设计的控制器具有更小的稳态误差，表明了该控制器的优越性.

(1)针对扰动情况下双臂空间机器人轨迹跟踪问题，提出固定时间非奇异快速终端滑模控制策略，实现基座姿态角和机械臂关节角在固定时间内跟踪期望轨迹，证明收敛时间与系统初始值无关.

(2)在滑模面设计部分，利用固定时间理论，设计非奇异快速终端滑模面. 该滑模面不但具有固定时间收敛特性，而且比现有固定时间滑模面的收敛速度更快.

(3)提出快速终端滑模形式的趋近律，不但提高了系统趋近阶段收敛速度，而且削弱了控制力矩抖振现象.

(4)本研究局限于空间机器人的关节轨迹跟踪控制，在后续的研究工作中，将关注双臂空间机器人末端轨迹的跟踪控制.