滑模控制方法因简单易行、鲁棒性强的特点,在欠驱动USV的轨迹跟踪控制领域得到广泛的应用[17-21]. Ashrafiuon等[17]将滑模控制方法引入欠驱动船舶的轨迹跟踪问题中,实现直线和曲线轨迹的跟踪,但是该方法未考虑外界干扰的影响,且滑模面抖振严重. 随后,Xu等[18]基于外界干扰力连续可导的假设,结合PD滑模控制和反步法提出新型轨迹跟踪控制器,提高了系统的鲁棒性. 在此基础上,Sun等[19]基于USV速度变化缓慢的假设,结合PI滑模控制和自适应控制提出新型控制器,放宽了对环境干扰力连续可导的限制. 之后,Sun等[20]又提出带有参数估计的自适应滑模控制方法,放宽了横荡运动无源有界的假设.在上述滑膜控制方法中除文献[19]外,其他的方法未能实现全局指数稳定,鲁棒性有待提高[22-23]. 此外,上述滑模控制方法易引起抖振现象. 为了缓解抖振,一些学者从控制理论出发,对切换增益采取自适应调节[24-26].Qu等[24]提出新型的切换增益自适应率(switching-gain adaptation, SGA),不仅能提高收敛速度,还能缓解抖振现象. 因此,该方法被应用于光盘驱动器伺服系统[24]和有杆抽油系统[27],但是其不能实现全局指数稳定.
本研究提出基于改进SGA(improved SGA, ISGA)的欠驱动USV滑模轨迹跟踪控制算法,以提高系统鲁棒性、抑制滑模抖振. 同时,该算法结合反步法和PI滑模控制,以保证欠驱动USV跟踪并保持期望的轨迹.
1. 运动模型
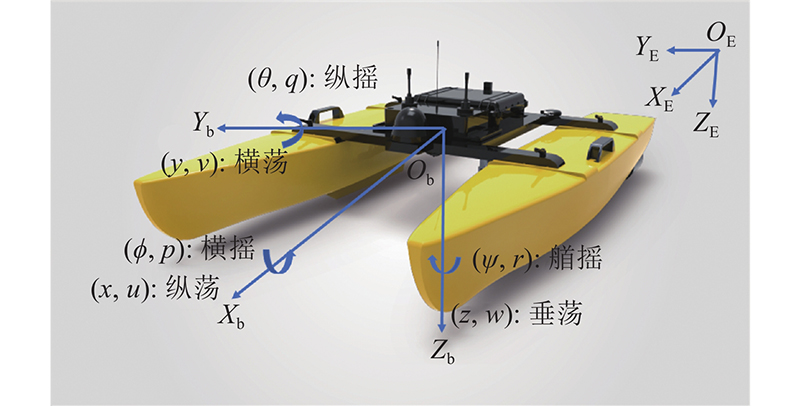
如图1所示,欠驱动USV的运动一般包含纵荡、横荡、垂荡、纵摇、横摇和艏摇,共6个部分.图中,
图 1
式中:
式中:
设定目标轨迹
本研究的目标为设计一款控制器,在存在参数不确定性和外界干扰的情况下,使位姿控制误差
式中:
2. 控制器设计及稳定性分析
2.1. ISGA
SGA可抑制滑模抖振,但仅能实现全局渐近稳定. 本研究提出的基于理想增益的ISGA方法,可实现系统的全局指数稳定. 本研究方法利用新型自适应率更新切换增益值,使其基于理想增益自动调节,在减弱抖动的同时实现全局指数稳定.
针对非线性系统,其表达式为
式中:
式中:
式中:ae为控制误差,
切换增益
设计理想切换增益
式中:
式中:
根据
式(19)可以转化为
1)当
2)当
由1)、2)可得
2.2. 轨迹跟踪控制器设计
2.2.1. 设计 $ {u_{\rm{d}}} $ $ {\bar \alpha _{\rm{d}}} $
构造李雅普诺夫函数:
式中:
传统的轨迹跟踪控制方式大多基于横荡速度无源有界的假设,在推导广义速度无源有界的过程中存在循环证明的问题. 为了避免横荡速度无源有界的假设,设虚拟速度变量:
为了保证
式中:
将式(26)~(30)代入(25),可得
2.2.2. 设计推力 $ F $
通过合理设计
构造李雅普诺夫函数:
定义滑模面
式中:
因此,
构造李雅普诺夫函数:
根据式(35)~(39),可以得到
式中:
式中:
设置
式中:
式中:
2.2.3. 设计 ${r_{\rm{d}}}$
通过合理设计虚拟控制量
构造李雅普诺夫函数:
为了使
式中:
式中:
式中:
式中:
构造李雅普诺夫函数:
2.2.4. 设计转矩 T
通过合理设计T,使误差
构造李雅普诺夫函数:
设计滑模面函数
式中:
式(61)可表示为
构造李雅普诺夫函数:
根据
式中:
式中:
理想增益
式中:
式中:
构建李雅普诺夫函数:
根据式(72)、(74)和(76)可得:
根据式(22)~(23)的ISGA特性,
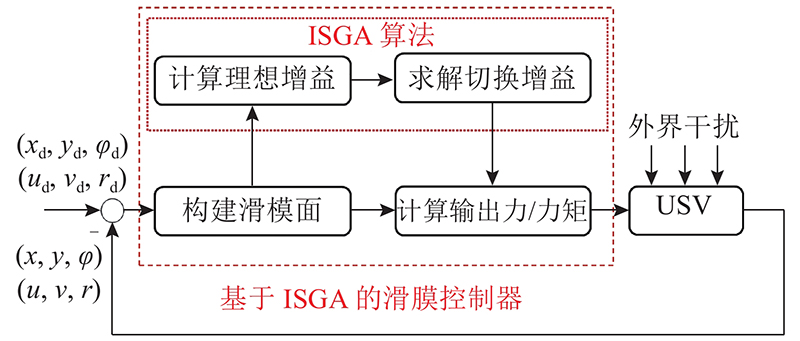
如图2所示为基于ISGA的控制器原理图,具体控制方法见式(24) ~ (78). 该方法先将目标位姿与实际位姿对比,构建滑模面;再采用ISGA算法计算理想增益,求解切换增益数值;最终根据滑模面和切换增益的数值,求取输出力/力矩.
图 2
图 2 基于改进切换增益自适应率的控制器原理
Fig.2 Control principle based on improved switching-gain adaptation
2.3. 稳定性分析
定理1 考虑欠驱动USV的运动学模型和动力学模型式(1)~(6)满足假设1,存在控制器如式(41)、(54)、(70),切换增益如式(44)、(57)、(74),保证轨迹跟踪闭环系统全局指数稳定,跟踪误差
假设1 目标轨迹
证明:给定李雅普诺夫函数
得到
虽然本研究的稳定性证明过程较复杂,但是在实际运用过程中,设计
3. 仿真分析
表 1 欠驱动无人艇的仿真参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| | 200 | | 2 | |
| | 80 | | 100 | |
| | | | | |
| | | | 0 | |
| | 70 | | 250 | |
| | 50 | | 0 | |
| | | — | — |
目标轨迹和初始状态如下:
式中:
表 2 基于改进切换增益自适应率的控制器参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | |||
| | 0.04 | | 0.23 | | 0.01 | | 1.00 | |||
| | 0.08 | | 10.00 | | 3.01 | | 1.00 | |||
| | 0.16 | | 9.48 | | 1.00 | | 2.00 | |||
| | 9.36 | | 0.01 | | 3.00 | | 1.00 | |||
| | 10.00 | | 0.01 | | 1.00 | | 2.03 |
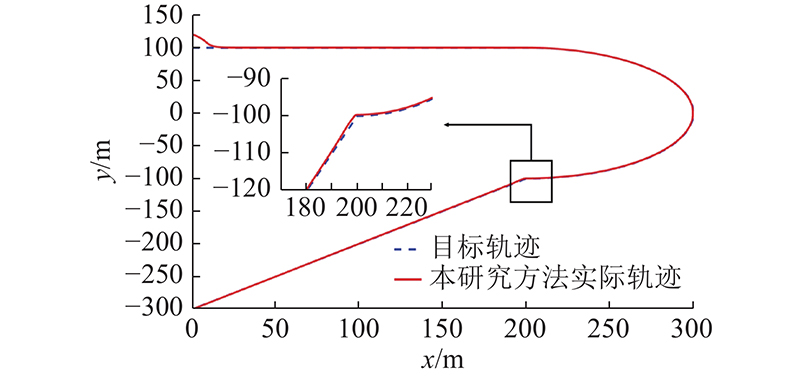
图 3
表 3 不同算法的轨迹跟踪误差
Tab.3
图 4
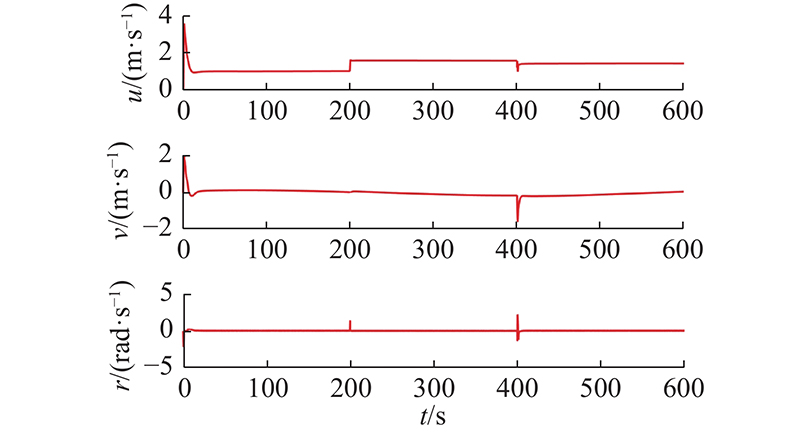
图 5
图 5 改进切换增益自适应率的欠驱动无人艇速度
Fig.5 Velocities of improved switching-gain adaptation based underactuated USV
图 6
4. 结 论
(2)相较SGA,所提算法可实现全局指数稳定.
(3)所提算法同时放宽环境干扰连续可导、USV速度缓慢变化和横荡速度无源有界的条件,更适于工程应用.
(4)后续将针对更为复杂的欠驱动USV模型进行控制器的设计,并进行实验验证. 小型USV多采用电池供电,因此节能优化技术显得尤为重要,针对欠驱动USV开展基于实时海况的节能轨迹规划将是重要的研究方向.
参考文献
Prescribed-time formation control of surface vessels with asymmetric constraints on LOS range and bearing angles
[J].DOI:10.1007/s11071-021-06462-8 [本文引用: 1]
A novel cooperative platform design for coupled USV-UAV systems
[J].
大型中层拖网网具系统的仿真研究
[J].
Simulation study of large mid-water trawl system
[J].
Guidance and control based on adaptive sliding mode strategy for a USV subject to uncertainties
[J].
Developing a navigation, guidance and obstacle avoidance algorithm for an unmanned surface vehicle (USV) by algorithms fusion
[J].DOI:10.1016/j.oceaneng.2018.04.018 [本文引用: 1]
Path following optimization for an underactuated USV using smoothly-convergent deep reinforcement learning
[J].
水下自主机器人接驳碰撞过程分析
[J].
Impact analysis during docking process of autonomous underwater vehicle
[J].
Asymptotic stabilization of USVs with actuator dead-zones and yaw constraints based on fixed-time disturbance observer
[J].
Fixed-time switching control of underactuated surface vessels with dead-zones: global exponential stabilization
[J].DOI:10.1016/j.jfranklin.2019.05.030 [本文引用: 1]
A robust localization method for unmanned surface vehicle (USV) navigation using fuzzy adaptive Kalman filtering
[J].DOI:10.1109/ACCESS.2019.2909151 [本文引用: 1]
Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances
[J].DOI:10.1016/j.oceaneng.2015.10.038 [本文引用: 1]
欠驱动USV神经网络自适应轨迹跟踪控制
[J].DOI:10.11918/201905049 [本文引用: 1]
Adaptive neural network trajectory tracking control for underactuated unmanned surface vehicle
[J].DOI:10.11918/201905049 [本文引用: 1]
A bioinspired neural dynamics-based approach to tracking control of autonomous surface vehicles subject to unknown ocean currents
[J].
Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances
[J].DOI:10.1016/j.neucom.2015.08.033 [本文引用: 1]
Trajectory tracking control of underactuated USV based on modified backstepping approach
[J].DOI:10.1515/ijnaoe-2015-0058 [本文引用: 1]
Adaptive fuzzy backstepping-based formation control of unmanned surface vehicles with unknown model nonlinearity and actuator saturation
[J].DOI:10.1109/TVT.2020.3039220 [本文引用: 2]
Sliding-mode tracking control of surface vessels
[J].DOI:10.1109/TIE.2008.2005933 [本文引用: 3]
Dynamical sliding mode control for the trajectory tracking of underactuated unmanned underwater vehicles
[J].DOI:10.1016/j.oceaneng.2015.06.022 [本文引用: 7]
Robust adaptive trajectory tracking control of underactuated unmanned surface vessel in fields of marine practice
[J].DOI:10.1007/s00773-017-0524-0 [本文引用: 2]
Research on the sliding mode control for underactuated unmanned surface vessels via parameter estimation
[J].DOI:10.1007/s11071-017-3937-8 [本文引用: 7]
A sliding mode approach to H∞ non-fragile observer-based control design for uncertain Markovian neutral-type stochastic systems
[J].DOI:10.1016/j.automatica.2014.10.095 [本文引用: 2]
Design of three exponentially convergent robust controllers for the trajectory tracking of autonomous underwater vehicles
[J].DOI:10.1016/j.oceaneng.2017.02.006 [本文引用: 1]
Sliding-mode disturbance observer with switching-gain adaptation and its application to optical disk drives
[J].DOI:10.1109/TIE.2009.2025719 [本文引用: 1]
Trajectory exponential tracking control of unmanned surface ships with external disturbance and system uncertainties
[J].DOI:10.1016/j.isatra.2017.12.020 [本文引用: 3]
Sliding mode nonlinear disturbance observer-based adaptive back-stepping control of a humanoid robotic dual manipulator
[J].
Sliding mode controller design for supercavitating vehicles
[J].DOI:10.1016/j.oceaneng.2019.04.066 [本文引用: 1]
Finite-time unknown observer-based interactive trajectory tracking control of asymmetric underactuated surface vehicles
[J].
Stereovision-based target tracking system for USV operations
[J].DOI:10.1016/j.oceaneng.2017.01.024 [本文引用: 1]
Hybrid strategy based model parameter estimation of irregular-shaped underwater vehicles for predicting velocity
[J].DOI:10.1016/j.robot.2020.103480 [本文引用: 1]