复合材料因高比强度、高比模量、耐疲劳、耐腐蚀和耐高温等优异性能，被广泛应用于航空航天领域^[1]. 自动铺丝机是复合材料工业化生产的关键设备，根据其结构构型，可以分为龙门式、卧式和机器人式3种^[2]，其中龙门式铺丝机工作空间大，适用于机翼壁板、机身蒙皮、翼梢小翼等大型复材构件的生产铺放. 在工作过程中，根据离线软件生成的铺放文件，龙门式铺丝机可以单独控制数根复合材料预浸料丝束动作，并将其集成为一条宽度可变的预浸带，再热压在模具表面上定型^[3-4]，然而，其精度不足可能会造成搭接、间隙、角度偏差等缺陷，增加人工干涉的风险，不仅降低产品质量，还影响铺放效率.

影响龙门式铺丝机精度的因素主要有几何误差、受力变形误差和热误差^[5]. 由于复材铺放需要恒温恒湿的工作环境，龙门铺丝机的热误差可以忽略不计；龙门铺丝机具有大质量、大尺寸、高重心等特点，其力变形误差主要是重力变形. 因此，研究几何误差和重力变形的综合作用，并采取相应的补偿措施，对提高龙门铺丝机铺放精度具有重要意义.

几何误差在总误差中占有较大的比重，主要源于零件制造、部件装配过程^[6]. 对几何误差的研究方法通常有建模、测量、辨识等^[7-9]. 付国强等^[10]提出基于球杆仪的六圈法几何误差辨识方法，该方法能根据旋转轴各几何误差项性质辨识得到包括垂直度误差和安装误差的全部10项几何误差；Lee等^[11]将位置相关和位置无关的几何误差分别建模为具有C1连续的n阶多项式和常数，然后通过球杆仪获得测量数据，并结合最小二乘法辨识出模型中的相关参数；凡志磊等^[12]提出数控机床几何误差多项式模型的最优阶数选择方法，提高了几何误差模型的精确性和鲁棒性. 上述文献均通过测量获取几何误差数据，但测量数据中一般同时包含几何误差与重力变形，在较小设备中重力变形可以忽略，但是针对大型重载龙门铺丝机，必须考虑重力变形对精度的影响.

研究设备重力变形的主要方法有解析法和有限元法. Xiang等^[13]使用解析法计算大型龙门滑轨磨床横梁的重力变形，并通过激光干涉仪对其准确性进行验证；Wu等^[14]基于弹性梁模型通过解析法求解结合面的重力变形，在此基础上建立了考虑重力变形的龙门铺丝机运动学模型，极大提高了模型精度；Wang等^[15]使用有限元法计算对齐装置在不同位姿的变形，然后利用三次样条插值和包络面拟合方法，得到装置在整个工作空间中的重力变形，以修正测量得到的位姿误差；He等^[16]使用有限元方法计算机床大型零部件的重力变形，然后根据小变形的线性叠加原理，将这些变形叠加以计算机床关键结合面的变形. 采用解析法分析重力变形在计算效率上具有较大的优势，但要求研究人员具备良好的力学和结构学基础. 另外，针对复杂结构，解析法需要大量简化和等效替代，难以保证精度. 有限元法作为数值计算方法，能对任意结构进行仿真，具有较强的灵活性和适用性，是力学分析的常用方法.

误差补偿技术能以较低成本有效提高设备精度，因而被广泛应用^[17-19]. 按照误差补偿的作用时机不同，可以分为误差的实时补偿和离线补偿. 王维等^[20]提出数控机床几何与热误差综合建模方法，并应用综合误差实时补偿系统进行误差在线补偿；Hsu等^[21]在对五轴机床几何误差建模的基础上，提出将平动轴与转动轴分离的解耦补偿法，并在后处理过程中通过修改刀具路径的方式，实现对几何误差的预补偿.

一般情况下，设备的重力变形和几何误差相互耦合，如果在误差建模过程中不对两者进行分离和综合，会影响最终建模精度及补偿效果. 为此，本研究提出重力变形与几何误差的综合建模与补偿方法，该方法首先通过有限元仿真与空间网格化方法建立重力变形模型，其次基于齐次变换矩阵与切比雪夫多项式建立几何误差模型，然后基于综合误差提出G代码修正策略以实现综合补偿，最后通过实验验证所提方法的可行性和有效性.

本研究对象是一台大型六轴龙门自动铺丝机，如图1所示，主要由3个直线轴X、Y、Z轴，3个旋转轴B、A、C轴，以及一个16丝束铺丝头组成. 该龙门铺丝机具有大行程、大跨度、重载荷等特点，其龙门架高度为7.8 m，横梁跨度为13.3 m，铺丝头重量约为850 kg.

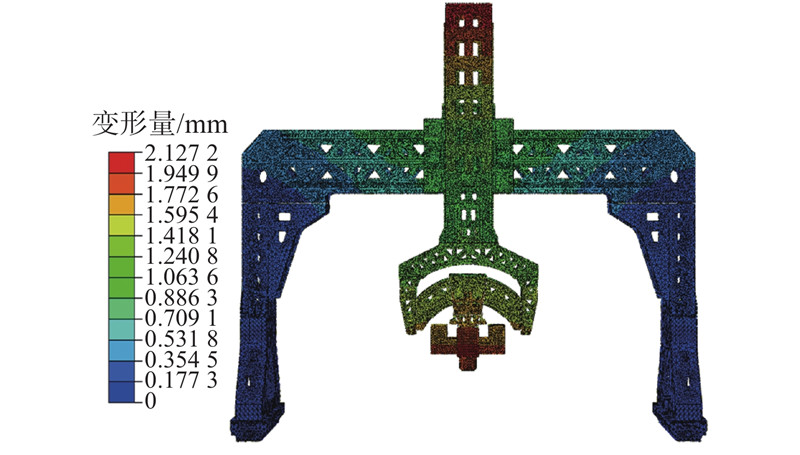
该龙门铺丝机结构复杂，难以用解析法计算其任意姿态下的重力变形，本研究采用有限元法进行分析. 使用有限元软件Abaqus建立龙门铺丝机有限元模型，在建模过程中，考虑到铺丝头结构的复杂性，设计了一个形状相同、质量均匀的部件取代铺丝头，并通过材料密度设置使得该部件质量与实际铺丝头相同. 另外，删除了数模中扶梯、护栏、风琴罩等不必要的零部件，忽略尺寸较小的工艺孔、倒角、凹槽等工艺特征；对于滑座和立柱结合面、立柱和横梁结合面，使用Tie连接；对于导轨滑块可动结合面，定义为接触. 对该有限元模型进行静力仿真，得到龙门铺丝机在重力影响下的变形，如图2所示.

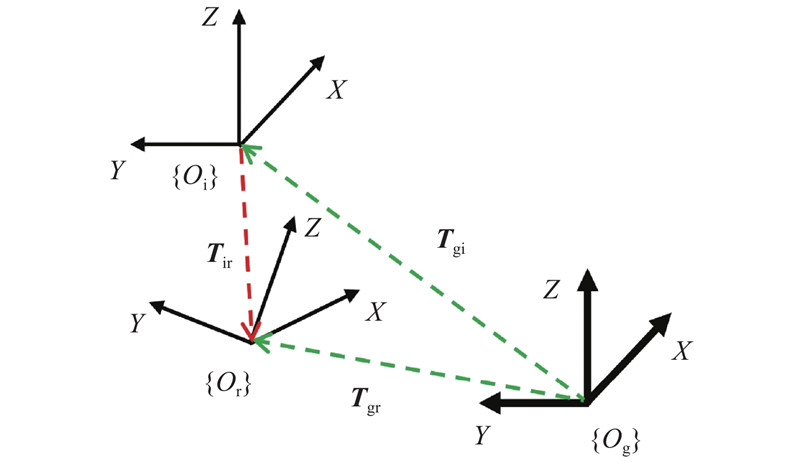
定义龙门铺丝机受重力影响变形前后铺丝头末端坐标系位置和姿态的变化为龙门铺丝机重力变形，如图3所示. 图中，坐标系{O_g}固定在地面上，其位置和姿态不受重力影响，为参考坐标系；{O_i}为铺丝头末端重力变形前理论坐标系；{O_r}为铺丝头末端重力变形后实际坐标系.

根据上述坐标定义，龙门铺丝机重力变形表示为

(1) $ {{\boldsymbol{T}}_{{\rm{ir}}}} = {{\boldsymbol{T}}_{{\rm{gr}}}} - {{\boldsymbol{T}}_{{\rm{gi}}}}. $

式中： ${{\boldsymbol{T}}_{{\rm{ir}}}}$为重力变形量， ${{\boldsymbol{T}}_{{\rm{gi}}}}$为重力变形前铺丝头末端理论位姿， ${{\boldsymbol{T}}_{{\rm{gr}}}}$为重力变形后铺丝头末端实际位姿.

为了得到整个工作空间中任意位置的重力变形，采用工作空间网格化方法建立龙门铺丝机重力变形模型，即利用工作空间中有限个位置的已知重力变形对其他位置的未知重力变形进行插值预测. 分析龙门铺丝机结构可知，X轴和C轴的运动不会引起设备重心的变化，因此只须考虑Y轴、Z轴、B轴、A轴4个轴位置对重力变形的影响.

龙门铺丝机的工作空间与关节空间存在映射关系，为了便于与各轴几何误差统一处理，将龙门铺丝机重力变形由工作空间转化为关节空间表示. 另外，在对关节空间进行网格划分时，为了减小计算量、提高计算效率，将龙门铺丝机的关节空间视为平动轴关节空间{YZ}和旋转轴关节空间{BA}的线性叠加^[22]，进而龙门铺丝机工作空间中的重力变形可以看成2个关节空间下重力变形的线性叠加，即

(2) $ {{\boldsymbol{E}}_{{\rm{gr}}}}\left( {y,z,b,a} \right) = {\boldsymbol{E}}_{{\rm{gr}}}^{\rm{t}}(y,z) + {\boldsymbol{E}}_{{\rm{gr}}}^{\rm{r}}(b,a). $

式中： ${{\boldsymbol{E}}_{{\rm{gr}}}}$为龙门铺丝机工作空间下重力变形， ${\boldsymbol{E}}_{{\rm{gr}}}^{\rm{t}}$为{YZ}空间下的重力变形， ${\boldsymbol{E}}_{{\rm{gr}}}^{\rm{r}}$为{BA}空间下的重力变形.

对2个关节空间分别进行网格化，其中重力误差越大的区域网格节点越密，如图4所示.

借助Abaqus提供的用户子程序接口，将各节点关节作为可变参数编写Python脚本，运行得到2个空间所有节点处的末端重力变形，如图5所示. 图中， ${\sigma _{YZ}}$为{YZ}空间位置误差， ${\gamma _{YZ}}$为{YZ}空间姿态误差， ${\sigma _{BA}}$为{BA}空间位置误差， ${\gamma _{BA}}$为{BA}空间姿态误差.

在得到2个关节空间样本点处的重力变形数据后，空间中任意位置的重力变形均可以通过插值计算得出. 由于{YZ}空间和{BA}空间均为二维空间，选择双三次插值函数作为重力变形的插值函数，表达式如下：

(3) $ {e_{{\rm{gr}}}} = \sum\limits_{i = 0}^3 {\sum\limits_{j = 0}^3 {{w_{ij}}{e_{ij}}} } . $

式中： ${w_{ij}}$为样本点的误差权值， ${e_{ij}}$为周围16个样本点处的误差.

选择拉格朗日基函数作为计算样本点误差权值的基函数，其分段表达式为

(4) $ w = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{{\left| d \right|}^3} - {{\left| d \right|}^2} - \dfrac{1}{2}\left| d \right| + 1},&{0 \leqslant \left| d \right| < 1.0}; \\ { - \dfrac{1}{6}{{\left| d \right|}^3} + {{\left| d \right|}^2} - \dfrac{{11}}{6}\left| d \right| + 1},&{1.0 \leqslant \left| d \right| < 2.0}; \\ 0,&{{\rm{其他}}} .\end{array}} \right. $

式中： $d$为待插值点和样本点之间的归一化距离.

利用基于拉格朗日基函数的双三次插值方法，便可以建立关节轴变量空间中任意点的重力变形与样本点重力变形之间的关系，再将2个关节空间下的重力变形进行叠加，从而得到龙门铺丝机总重力变形.

几何误差元素按其误差是否随各轴的运动而变化，可以分为位置相关的几何误差元素和位置无关的几何误差元素. 位置相关的几何误差元素包括运动轴的定位误差、转角误差，它们的值随轴关节位置的变化而变化；位置无关的几何误差元素，如移动轴之间的垂直度误差、旋转轴之间的平行度误差，它们的值为常量.

在建立几何误差模型前，首先要建立龙门铺丝机运动学模型. 基于多体系统理论，定义龙门铺丝机相关坐标系，其中基坐标系{O_Base}为全局坐标系，是用于描述机床部件运动的理论参考，位置和姿态不随各轴运动而变化；参考坐标系{O_R}为使用激光跟踪仪建立的测量基准，可以看成在测量过程中重建的基坐标系；运动轴坐标系{O_X}、{O_Y}、{O_Z}、{O_B}、{O_A}、{O_C}为局部坐标系，用于描述各轴的运动；铺丝头坐标系{O_T}为工具坐标系，位于铺丝头末端. 各坐标系原点位置如图6所示. 另外，以上坐标系正方向均与X轴、Y轴、Z轴运动正方向相同.

根据各坐标系定义，利用齐次变换矩阵建立龙门铺丝机理论运动学模型：

(5) $ \begin{split} {}_{\rm{\;\;\;\;\;\;T}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}} =\;& {}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}}\;{}_X^{\rm{R}}{{\boldsymbol{T}}^{\rm{i}}}(x){}_Y^X{{\boldsymbol{T}}^{\rm{i}}}(y){}_Z^Y{{\boldsymbol{T}}^{\rm{i}}}(z) \times \hfill \\ \;&{}_B^Z{{\boldsymbol{R}}^{\rm{i}}}(\beta ){}_A^B{{\boldsymbol{R}}^{\rm{i}}}(\alpha ){}_C^A{{\boldsymbol{R}}^{\rm{i}}}(\gamma ){}_{\rm{T}}^C{{\boldsymbol{M}}^{\rm{i}}} . \end{split} $

式中： $x$、 $y$、 $z$、 $\beta $、 $\alpha $、 $\gamma $分别为各轴运动量， ${}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}}$为 $4 \times 4$的单位矩阵，表示理论上基坐标系{O_Base}和参考坐标系{O_R}没有偏差；其他变换矩阵表示各轴运动及工具坐标系位置，表达式分别为

$ {}_X^{\rm{R}}{{\boldsymbol{T}}^{\rm{i}}}(x) = \left[ {\begin{array}{*{20}{l}} 1&0&0&x \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，} {}_Y^X{{\boldsymbol{T}}^{\rm{i}}}(y) = \left[ {\begin{array}{*{20}{l}} 1&0&0&{\text{0}} \\ 0&1&0&y \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，} $

$ \begin{split} {}_Z^Y{{\boldsymbol{T}}^{\rm{i}}}(z) = \;&\left[ {\begin{array}{*{20}{l}} 1&0&0&{\text{0}} \\ 0&1&0&0 \\ 0&0&1&z \\ 0&0&0&1 \end{array}} \right] \text{，}\\ {}_B^Z{{\boldsymbol{R}}^{\rm{i}}}(\beta ) =\;& \left[ {\begin{array}{*{20}{l}} {\cos\; \beta }&0&{\sin\; \beta }&0 \\ 0&1&0&0 \\ { - \sin\; \beta }&0&{\cos\; \beta }&0 \\ 0&0&0&1 \end{array}} \right] \text{，} \end{split} $

$ \begin{split} {}_A^B{{\boldsymbol{R}}^{\rm{i}}}(\alpha ) =\;& \left[ {\begin{array}{*{20}{l}} 1&0&0&{\text{0}} \\ 0&{\cos\; \alpha }&{ - \sin\; \alpha }&0 \\ 0&{\sin\; \alpha }&{\cos\; \alpha }&{ - {z_{A0}}} \\ 0&0&0&1 \end{array}} \right] \text{，}\\ {}_C^A{{\boldsymbol{R}}^{\rm{i}}}(\gamma ) =\;& \left[ {\begin{array}{*{20}{l}} {\cos\; \gamma }&{ - \sin\; \gamma }&0&{\text{0}} \\ {\sin\; \gamma }&{\cos\; \gamma }&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，} \end{split} $

$ {}_{\rm{T}}^C{{\boldsymbol{M}}^{\rm{i}}} = \left[ {\begin{array}{*{20}{l}} 1&0&0&{\text{0}} \\ 0&1&0&{\text{0}} \\ 0&0&1&{ - {z_{{\rm{T}}0}}} \\ 0&0&0&1 \end{array}} \right]. $

其中， $ {z_{A0}} $为坐标系{O_A}与{O_B}之间的偏置， ${z_{{\rm{T}}0}}$为坐标系{O_T}与{O_C}之间的偏置.

每个运动轴在三维空间内都有6个自由度，当各运动轴运动时，受位置相关的几何误差影响，运动轴的实际运动相对其理想运动将在6个自由度方向上产生不同程度的偏移，包括3个方向的位置误差 ${\delta _x}$、 ${\delta _y}$、 ${\delta _z}$和3个方向的姿态误差 ${\varepsilon _x}$、 ${\varepsilon _y}$、 ${\varepsilon _z}$. 根据小角度假设，相应的误差变换矩阵为

(6) $ {{\boldsymbol{E}}^{\rm{r}}}{\text{ = }}\left[ {\begin{array}{*{20}{l}} 1&{ - {\varepsilon _x}}&{{\varepsilon _y}}&{{\delta _x}} \\ {{\varepsilon _x}}&1&{ - {\varepsilon _x}}&{{\delta _y}} \\ { - {\varepsilon _y}}&{{\varepsilon _x}}&1&{{\delta _z}} \\ 0&0&0&1 \end{array}} \right]. $

位置相关的几何误差元素具有位置相关性，可以表示为各轴位置的函数. 第1类切比雪夫多项式具有正交性质，是几何误差元素拟合常用的一种多项式^[23-24]. 为了避免拟合多项式次数过高而产生过拟合且增加辨识难度，采用三次切比雪夫多项式对龙门铺丝机几何误差元素进行拟合：

(7) $ \varepsilon (i) = {a_0}{T_0}(i) + {a_1}{T_1}(i) + {a_2}{T_2}(i) + {a_3}{T_3}(i) . $

式中： $ i $为对应轴关节位置； $ {T_0} $、 $ {T_1} $、 $ {T_2} $、 $ {T_3} $分别为切比雪夫多项式前4项， $ {T_0}(i) = 1 $， $ {T_1}(i) = i $， $ {T_2}(i) = $ $ 2{i^2} - 1 $， $ {T_3}(i) = 4{i^3} - 3i $； $ {a_0} $、 $ {a_1} $、 $ {a_{\text{2}}} $、 $ {a_{\text{3}}} $为多项式系数.

龙门铺丝机有6个运动轴，因此一共需要36个位置相关的几何误差元素完全描述. 每个几何误差元素采用三次切比雪夫正交多项式拟合，共有4个系数，因此36个位置相关的几何误差共引入144个拟合系数.

位置无关的几何误差可以看成是各坐标系之间的初始常量误差，包括参考坐标系{O_R}相对基坐标系{O_Base}的3个位置误差x_R、y_R、z_R和3个姿态误差α_R、β_R、γ_R；3个垂直轴之间的垂直度和平行度误差S_xy、S_xz、S_yz；3个旋转轴的平行度误差η_xB、η_zB、η_yA、η_zA、η_xC、η_yC；A轴坐标系{O_A}相对B轴坐标系{O_B}的原点偏置误差x_A、y_A、z_A；铺丝头坐标系{O_T}相对C轴坐标系{O_C}的原点偏置误差x_T、y_T、z_T，具体如表1所示，一共引入了21项位置无关的几何误差元素.

根据位置无关的几何误差定义，相应的误差变换矩阵分别为

(8) $ \left.{\begin{aligned} {}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{E}}^{{\rm{ir}}}}=\;&\left[ {\begin{array}{*{20}{l}} 1&{ - {\gamma _{\rm{R}}}}&{{\beta _{\rm{R}}}}&{{x_{\rm{R}}}} \\ {{\gamma _{\rm{R}}}}&1&{ - {\alpha _{\rm{R}}}}&{{x_{\rm{R}}}} \\ { - {\beta _{\rm{R}}}}&{{\alpha _{\rm{R}}}}&1&{{x_{\rm{R}}}} \\ 0&0&0&1 \end{array}} \right]\text{，}\\ {}_Y^X{{\boldsymbol{E}}^{{\rm{ir}}}} =\;& \left[ {\begin{array}{*{20}{l}} 1&{ - {S_{xy}}}&0&0 \\ {{S_{xy}}}&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，}\\ {}_Z^Y{{\boldsymbol{E}}^{{\rm{ir}}}} =\;& \left[ {\begin{array}{*{20}{l}} 1&0&{{S_{xz}}}&0 \\ 0&1&{ - {S_{yz}}}&0 \\ { - {S_{xz}}}&{{S_{yz}}}&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，}\\ {}_B^Z{{\boldsymbol{E}}^{{\rm{ir}}}} = \;&\left[ {\begin{array}{*{20}{l}} 1&{ - {\eta _{xB}}}&0&0 \\ {{\eta _{xB}}}&1&{ - {\eta _{zB}}}&0 \\ 0&{{\eta _{zB}}}&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，} \\ {}_A^B{{\boldsymbol{E}}^{{\rm{ir}}}} = \;&\left[ {\begin{array}{*{20}{l}} 1&{ - {\eta _{yA}}}&{{\eta _{zA}}}&{{x_A}} \\ {{\eta _{yA}}}&1&0&{{y_A}} \\ { - {\eta _{zA}}}&0&1&{{z_A}} \\ 0&0&0&1 \end{array}} \right] \text{，}\\ {}_C^A{{\boldsymbol{E}}^{{\rm{ir}}}} = \;&\left[ {\begin{array}{*{20}{l}} 1&0&{{\eta _{xC}}}&0 \\ 0&1&{ - {\eta _{yC}}}&0 \\ { - {\eta _{xC}}}&{{\eta _{yC}}}&1&0 \\ 0&0&0&1 \end{array}} \right] \text{，} \\ {}_{\rm{T}}^C{{\boldsymbol{E}}^{{\rm{ir}}}} =\;& \left[ {\begin{array}{*{20}{l}} 1&0&0&{{x_{\rm{T}}}} \\ 0&1&0&{{y_{\rm{T}}}} \\ 0&0&1&{{z_{\rm{T}}}} \\ 0&0&0&1 \end{array}} \right] . \end{aligned}}\right\}$

描述相邻2个坐标系之间实际运动的齐次变换矩阵可以通过理想齐次变换矩阵左乘位置无关误差的变换矩阵、右乘位置相关误差的变换矩阵得到：

(9) $ {{\boldsymbol{T}}^{{\rm{r}}}} = {{\boldsymbol{E}}^{{\rm{ir}}}} {{\boldsymbol{T}}^{\rm{i}}} {{\boldsymbol{E}}^{\rm{r}}}. $

利用各坐标系之间的理想齐次变换矩阵和误差变换矩阵建立实际齐次变换矩阵：

(10) $ \left. {\begin{array}{*{20}{l}} {{}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{r}}} = {}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{E}}^{\rm{ir}}} {}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}}}, \\ {{}_X^{\rm{R}}{{\boldsymbol{T}}^{\rm{r}}}(x) = {}_X^{\rm{R}}{{\boldsymbol{T}}^{\rm{i}}}(x) {}_X^{\rm{R}}{{\boldsymbol{E}}^{\rm{r}}}(x)}, \\ {{}_Y^X{{\boldsymbol{T}}^{\rm{r}}}(y) = {}_Y^X{{\boldsymbol{E}}^{\rm{ir}}} {}_Y^X{{\boldsymbol{T}}^{\rm{i}}}(y) {}_Y^X{{\boldsymbol{E}}^{\rm{r}}}(y)}, \\ {{}_Z^Y{{\boldsymbol{T}}^{\rm{r}}}(z) = {}_Z^Y{{\boldsymbol{E}}^{\rm{ir}}} {}_Z^Y{{\boldsymbol{T}}^{\rm{i}}}(z) {}_Z^Y{{\boldsymbol{E}}^{\rm{r}}}(z)}, \\ {{}_B^Z{{\boldsymbol{R}}^{\rm{r}}}(\beta ) = {}_B^Z{{\boldsymbol{E}}^{\rm{ir}}} {}_B^Z{{\boldsymbol{R}}^{\rm{i}}}(\beta ) {}_B^Z{{\boldsymbol{E}}^{\rm{r}}}(\beta )}, \\ {{}_A^B{{\boldsymbol{R}}^{\rm{r}}}(\alpha ) = {}_A^B{{\boldsymbol{E}}^{\rm{ir}}} {}_A^B{{\boldsymbol{R}}^{\rm{i}}}(\alpha ) {}_A^B{{\boldsymbol{E}}^{\rm{r}}}(\alpha )}, \\ {{}_C^A{{\boldsymbol{R}}^{\rm{r}}}(\gamma ) = {}_C^A{{\boldsymbol{E}}^{\rm{ir}}} {}_C^A{{\boldsymbol{R}}^{\rm{i}}}(\gamma ) {}_C^A{{\boldsymbol{E}}^{\rm{r}}}(\gamma )}, \\ {{}_{\rm{T}}^C{{\boldsymbol{M}}^{\rm{r}}} = {}_{\rm{T}}^C{{\boldsymbol{E}}^{\rm{ir}}} {}_{\rm{T}}^C{{\boldsymbol{M}}^{\rm{i}}}}. \end{array}} \right\} $

由此得到在基坐标系中描述的龙门铺丝机末端的实际位置和姿态：

(11) $ \begin{split} {}_{\rm{\;\;\;\;\;\;T}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{r}}} =\;& {}_{\rm{\;\;\;\;\;\;R}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{r}}}{}_X^{\rm{R}}{{\boldsymbol{T}}^{\rm{r}}}(x){}_Y^X{{\boldsymbol{T}}^{\rm{r}}}(y){}_Z^Y{{\boldsymbol{T}}^{\rm{r}}}(z)\times \hfill \\ \;&{}_B^Z{{\boldsymbol{R}}^{\rm{r}}}(\beta ){}_A^B{{\boldsymbol{R}}^{\rm{r}}}(\alpha ){}_C^A{{\boldsymbol{R}}^{\rm{r}}}(\gamma ){}_{\rm{T}}^C{{\boldsymbol{M}}^{\rm{r}}} . \end{split} $

以末端的位姿误差来描述几何误差，则几何误差模型可以表示为机床末端的实际位姿和理想位姿之间的偏差，即

(12) $ {{\boldsymbol{E}}_{{\rm{ge}}}}({\boldsymbol{q}}) = {}_{\rm{\;\;\;\;\;\;T}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{r}}}({\boldsymbol{q}}) - {}_{\rm{\;\;\;\;\;\;T}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}}({\boldsymbol{q}}). $

式中： $ {{\boldsymbol{E}}_{{\rm{ge}}}}({\boldsymbol{q}}) $表示龙门铺丝机的轴关节变量 ${\boldsymbol{q}}(x,y,z,\alpha ,\beta ,\gamma )$到龙门铺丝几何误差的映射. 考虑到几何误差的复杂性，计算时将忽略式中二阶及以上的无穷小量.

为了确定式(12)中未知的21项位置无关的几何误差元素以及144个位置相关的几何误差的拟合系数，一种可行且高效的方法是对龙门铺丝机的空间误差进行测量，并从中分离出几何误差分量，然后结合几何误差模型构建目标函数，最后利用优化算法对目标函数中的未知数进行优化求解.

在静态条件下测量到的误差包含几何误差和重力变形两部分，基于几何误差和重力变形线性叠加的假设，使用已经建立的重力变形模型将测量误差中的重力变形分量去除，得到误差测量值中的几何误差分量，即

(13) $ {}^{\rm{m}}{{\boldsymbol{E}}_{{\rm{ge}}}}({\boldsymbol{q}}){\text{ = }}{}^{\rm{m}}{{\boldsymbol{E}}_{\rm{s}}}({\boldsymbol{q}}) - {{\boldsymbol{E}}_{{\rm{gr}}}}({\boldsymbol{q}}). $

式中： ${}^{\rm{m}}{{\boldsymbol{E}}_{\rm{s}}}({\boldsymbol{q}})$为测量总误差， ${}^{\rm{m}}{{\boldsymbol{E}}_{{\rm{ge}}}}({\boldsymbol{q}})$为测量数据中的几何误差分量， ${{\boldsymbol{E}}_{{\rm{gr}}}}({\boldsymbol{q}})$为由重力变形模型计算得到的重力变形分量.

在建立目标函数时，考虑到位置误差和姿态误差的单位不同，两者之间相差几个数量级，因此将位置误差和姿态误差分开，再赋予不同的权重构造一个单目标函数：

(14) $ \left. {\begin{array}{*{20}{l}} {{J_{\rm{P}}} = \displaystyle\sum\limits_{j = 1}^n {{{\left\| {{{({\boldsymbol{E}}_{\rm{P}}^{\rm{i}})}_j} - {{({\boldsymbol{E}}_{\rm{P}}^{\rm{m}})}_j}} \right\|}_2}} }, \\ {{J_{\rm{R}}} = \displaystyle\sum\limits_{j = 1}^n {{{\left\| {{{({\boldsymbol{E}}_{\rm{R}}^{\rm{i}})}_j} - {{({\boldsymbol{E}}_{\rm{R}}^{\rm{m}})}_j}} \right\|}_2}} }, \\ {J = {\kappa _1}{J_{\rm{P}}} + {\kappa _2}{J_{\rm{R}}}}. \end{array}} \right\} $

式中： ${\boldsymbol{E}}_{\rm{P}}^{\rm{i}}$、 ${\boldsymbol{E}}_{\rm{R}}^{\rm{i}}$为由几何误差模型计算得到的位置和姿态误差， ${\boldsymbol{E}}_{\rm{P}}^{\rm{m}}$和 ${\boldsymbol{E}}_{\rm{R}}^{\rm{m}}$为测量得到的几何误差分量中的位置和姿态误差， $ {\left\| {\boldsymbol{M}} \right\|_2} $表示矩阵 $ {\boldsymbol{M}} $二范数， $n$为测量点个数，权重 $ {\kappa _1} $、 $ {\kappa _2} $的确定主要取决于位置误差和姿态误差的数量级.

为了能够对式(14)中的几何误差元素进行优化求解，须采集工作空间中足够样本点位姿误差测量值. 本研究采用激光跟踪仪测量，并搭建用于获取末端位姿的测量工装，如图7所示，该工装上安装有3个跟踪仪靶座，依次测量靶座上3坐标，即可计算出末端位置和姿态.

在龙门铺丝机工作空间中随机选取253个采样点，然后采用激光跟踪仪测量采样点处末端位姿，由此得到末端误差测量值：

(15) $ {}^{\rm{m}}{{\boldsymbol{E}}_{\rm{s}}}({\boldsymbol{q}}) = {{\boldsymbol{M}}_{\rm{m}}} - {}_{\rm{\;\;\;\;\;\;T}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}}. $

式中： ${{\boldsymbol{M}}_{\rm{m}}}$为测量末端位姿， ${}_{\rm{\;\;\;\;\;\;T}}^{{\rm{Base}}}{{\boldsymbol{M}}^{\rm{i}}}$由理论运动学模型计算得到.

在完成所有样本点末端位姿误差测量后，将误差数据去除重力变形分量，然后代入目标函数中利用优化算法进行求解. 针对此类非线性优化问题，存在多种优化算法，如高斯牛顿法（Gauss-Newton，GN）、LM（Levenberg-Marquardt）算法、鲍威尔（Powell）算法等. 其中，GN算法和LM算法均须计算目标函数的雅可比矩阵，在求解参数较多的情况下，雅可比矩阵维度较大，计算效率较低. Powell算法使用一维搜索的方式确定迭代方向，无须对目标函数进行求导，在目标函数形式较复杂、待求参数较多的场合，在计算效率和精度上更有优势. 因此，本研究选择Powell算法作为参数辨识算法，并将21项位置无关的几何误差元素以及144个位置相关的几何误差的拟合系数初值全设为0，同时收敛准则选取点距准则 ${\rm{Tol_X}} = {10^{ - 6}}$和函数下降量准则 ${\rm{Tol_{Fun}}} = {10^{ - 6}}$.

在经过计算后，辨识得到位置无关的几何误差元素以及位置相关的几何误差元素. 为了验证几何误差元素的辨识结果以及几何误差模型的正确性，另外随机选取23个测量点，用于实测值和模型预测值之间的对比. 为了便于比较，将实测值和预测值位置误差定义为

(16) $ \Delta P = \sqrt {P_x^2 + P_y^2 + P_z^2} . $

在计算姿态误差时，先将 $3 \times 3$的姿态矩阵转换成XYZ固定角形式下的欧拉角，再计算姿态误差：

(17) $ \Delta \theta = \sqrt {\theta _x^2 + \theta _y^2 + \theta _z^2} . $

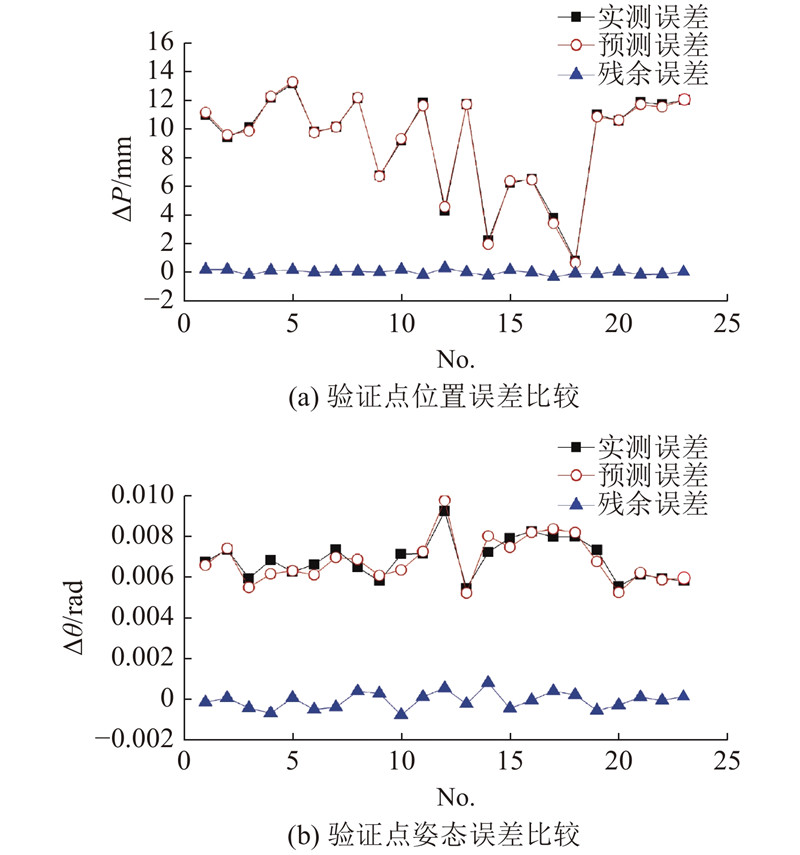
同时还计算两者的残差值，最终结果如图8所示. 图中，No. 为验证组测量点编号. 可以看出，不管是位置误差还是姿态误差，其误差预测值和误差实测值基本保持一致，两者的残差值基本维持在零线附近，证明了几何误差辨识结果的准确性.

根据上文所建立的重力变形模型和几何误差模型，任意轴关节变量处龙门铺丝机的综合误差可以表示为两者的线性叠加：

(18) $ {{\boldsymbol{E}}_{\rm{s}}}({\boldsymbol{q}}){\text{ = }}{{\boldsymbol{E}}_{{\rm{gr}}}}({\boldsymbol{q}}) + {{\boldsymbol{E}}_{{\rm{ge}}}}({\boldsymbol{q}}). $

在综合误差补偿时，本研究采取离线补偿方法，该补偿法中误差值和补偿值的计算、路径点的重新生成都在设备工作前完成，具有实现简单、实用性强、实施代价低等优点，适合不随时间变化的误差的补偿.

离线补偿的基本思想是将位置和姿态误差反向作用到工作路径点上生成新的工作路径. 龙门铺丝机的运动控制指令以轴关节变量形式给出，为了使实际位姿和目标位姿重合，首先通过理论正运动学模型计算得到末端原始指令位姿 ${\boldsymbol{O}}_0^{{\rm{ins}}}$，结合指令位姿处反向作用的综合误差 ${\boldsymbol{E}}_{\rm{s}}^0$，得到新的指令位姿 ${\boldsymbol{O}}_1^{{\rm{ins}}}$：

(19) $ {\boldsymbol{O}}_1^{{\rm{ins}}} = {\boldsymbol{O}}_0^{{\rm{ins}}} - {\boldsymbol{E}}_{\rm{s}}^0. $

然而，当铺丝机运动到新的指令位置 ${\boldsymbol{O}}_1^{{\rm{ins}}}$时，实际上会产生新的误差 ${\boldsymbol{E}}_{\rm{s}}^{\text{1}}$，因此须迭代补偿，直至 $n$次补偿后的残余误差 ${\boldsymbol{E}}_{\rm{s}}^n$小于或等于误差允许值，如图9所示. 最后，通过逆运动学得到补偿后的各关节指令，覆盖原始指令完成G代码修正.

选取ARJ21翼梢小翼的一条铺放路径进行综合误差补偿验证实验，如图7所示. 实验平台主要包括龙门铺丝机、控制台、激光跟踪仪、测量工装等，其中激光跟踪仪放置在稳固的基座上，并且在测量过程中不受干扰.

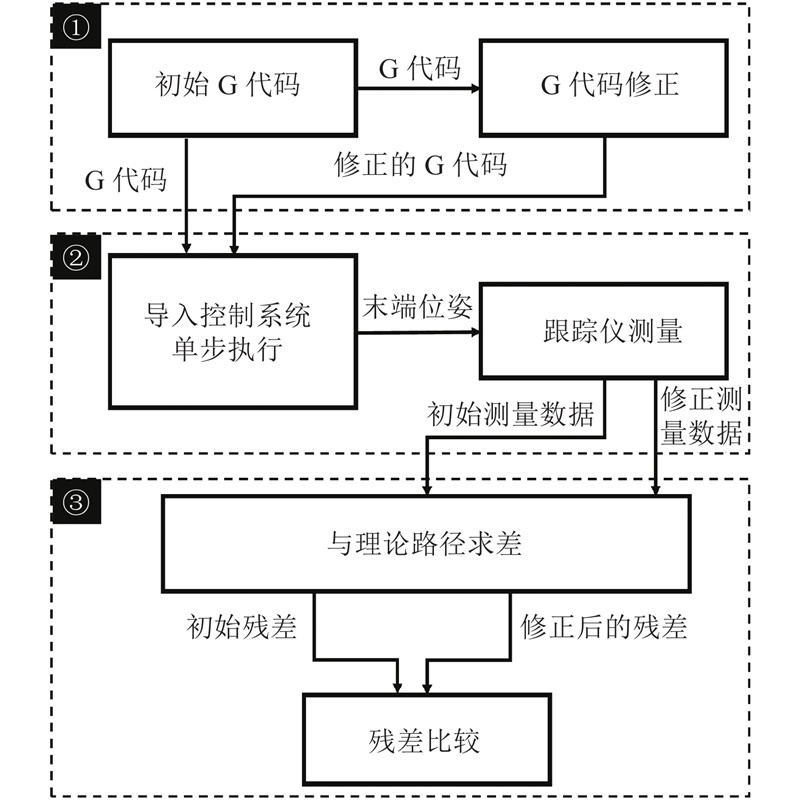
综合误差补偿对比实验原理如图10所示，可以分为3个阶段. 1）实验准备阶段，主要是生成路径补偿前、后的G代码；2）实验操作阶段，分别将补偿前、后的G代码依次导入铺丝机控制系统中单步执行，然后使用激光跟踪仪对龙门铺丝机末端的位置和姿态进行测量；3）数据处理阶段，将补偿前、后的末端测量位姿和理论末端位姿求差进行比较，证明补偿的有效性. 为了提高数据的可信度，对比实验重复执行5次取平均值.

数据处理结果如图11所示. 可以看出，由于选取的是一条连续的铺放路径，龙门铺丝机的运动范围不大，补偿前位置误差和姿态误差变化幅度也不大，位置误差约为8.7 mm，姿态误差约为7.5×10⁻³ rad. 经过补偿后，位置误差和姿态误差相比补偿前都有了大幅度的减小. 补偿前的误差偏大是因为龙门铺丝机本身装配误差较大，而末端位姿误差测量值是以龙门铺丝机的理论运动学模型作为基准计算的，且这个理论运动学模型是未标定的.

为了更直观地看出误差的减小程度，对补偿前后X、Y、Z这3个方向的位置误差∆P_X、∆P_Y、∆P_Z和姿态误差∆θ_X、∆θ_Y、∆θ_Z分别进行数据统计，如表2所示. 相比补偿前，位置误差平均值在3个方向上分别减小98.9%、93.4%、99.0%，而姿态误差平均值分别减小93.1%、84.0%、84.8%，各方向位置和姿态精度均有大幅度提高，证明了综合误差补偿的有效性. 另外须说明的是，虽然Z方向是重力变形的敏感方向，但由于几何误差和结构尺寸偏差的存在，该方向的综合误差不一定最大；Y方向零件尺寸偏差和部件安装偏差的存在则使得该方向的综合误差较大，以至于不进行补偿无法满足精度要求.

一般要求复合材料铺放误差不得大于1.270 mm. 补偿后龙门铺丝机最大误差为0.532 mm，说明应用了本研究所提出的重力变形与几何误差的综合误差建模与补偿方法后，大型重载龙门铺丝机的精度大幅度提高，满足了铺放精度的需求.

重力变形和几何误差是影响龙门铺丝机静态精度的主要因素，本研究针对如何提高大型龙门铺丝机精度，围绕重力变形和几何误差综合建模与补偿开展深入研究.

（1）采用分离和综合的概念，通过有限元和工作空间网格化方法，建立龙门铺丝机重力变形模型；根据重力变形模型分离出测量数据中几何误差部分，结合Powell算法辨识得到基于齐次变换矩阵和切比雪夫多项式建立的几何误差模型；综合重力变形和几何误差，采用G代码修正策略实现综合误差的补偿.

（2）通过数据对比发现，在补偿前由于龙门铺丝机本身存在较大的装配误差，其精度无法满足铺放精度的需求. 经过补偿后，龙门铺丝机末端位置和姿态精度均得到大幅度提高，满足铺放精度要求，证明所提出的误差建模与补偿方法的有效性.

（3）本研究从静态角度研究龙门铺丝机的精度，而铺丝是一个持续动态的过程，特别是在高速铺放的情况下，动态误差可能取代静态误差成为影响龙门铺丝机精度的主要因素，未来须进一步对动态误差进行更深入的研究，全面提高龙门铺丝机铺放精度.