[1]
GHAFOURI A, LASZKA A, DUBEY A, et al. Optimal detection of faulty traffic sensors used in route planning [C]// Proceedings of the 2nd International Workshop on Science of Smart City Operations and Platforms Engineering . New York: ACM, 2017: 1-6.
[本文引用: 2]
[2]
LIEBIG T, PIATKOWSKI N, BOCKERMANN C, et al Dynamic route planning with real-time traffic predictions
[J]. Information Systems , 2017 , 64 : 258 - 265
DOI:10.1016/j.is.2016.01.007
[3]
ÖZAL A, RANGANATHAN A, TATBUL N. Real-time route planning with stream processing systems: a case study for the city of lucerne [C]// Proceedings of the 2nd ACM SIGSPATIAL International Workshop on Geo Streaming . Chicago: ACM, 2011: 21-28.
[4]
SHAO S, GUAN W, RAN B, et al Electric vehicle routing problem with charging time and variable travel time
[J]. Mathematical Problems in Engineering , 2017 , 2 : 1 - 13
[5]
TAHA A E M. Facilitating safe vehicle routing in smart cities [C]// 2017 IEEE International Conference on Communications . Paris: IEEE, 2017: 1-5.
[6]
DANIEL T. Multi-modal route planning in road and transit networks [D]. Freiburg: University of Karlsruhe, 2018.
[7]
TONG Y X, ZENG Y X, ZHOU Z M, et al A unified approach to route planning for shared mobility
[J]. Proceedings of the VLDB Endowment , 2018 , 11 (11 ): 1633 - 1646
DOI:10.14778/3236187.3236211
[8]
DEMIRYUREK U, BANAEI-KASHANI F, SHAHABI C, et al. Online computation of fastest path in time-dependent spatial networks [C]// International Symposium on Spatial and Temporal Databases . Berlin: Springer, 2011: 92-111.
[本文引用: 2]
[9]
WANG H N, LI G L, HU H Q, et al R3: a real-time route recommendation system
[J]. Proceedings of the VLDB Endowment , 2014 , 7 (13 ): 1549 - 1552
DOI:10.14778/2733004.2733027
[本文引用: 1]
[10]
MALVIYA N, MADDEN S, BHATTACHARYA A. A continuous query system for dynamic route planning [C]// 2011 IEEE 27th International Conference on Data Engineering . Hannover: IEEE, 2011: 792-803.
[本文引用: 2]
[11]
XU J J, GUO L M, DING Z M, et al. Traffic aware route planning in dynamic road networks [C]// International Conference on Database Systems for Advanced Applications . Berlin: Springer, 2012: 576-591.
[本文引用: 2]
[12]
ZHANG D X, YANG D Y, WANG Y, et al Distributed shortest path query processing on dynamic road networks
[J]. The VLDB Journal , 2017 , 26 (3 ): 399 - 419
DOI:10.1007/s00778-017-0457-6
[本文引用: 3]
[13]
WANG S Z, CAO J N, YU P. Deep learning for spatio-temporal data mining: a survey [EB/OL]. [2021-07-01]. https://ieeexplore.ieee.org/document/9204396.
[本文引用: 1]
[14]
WANG Y S, YUAN Y, MA Y L, et al Time-dependent graphs: definitions, applications, and algorithms
[J]. Data Science and Engineering , 2019 , 4 : 352 - 366
DOI:10.1007/s41019-019-00105-0
[本文引用: 1]
[15]
HART P E, NILSSON N J, RAPHAEL B A formal basis for the heuristic determination of minimum cost paths
[J]. IEEE Transactions on Systems Science and Cybernetics , 1968 , 4 (2 ): 100 - 107
DOI:10.1109/TSSC.1968.300136
[本文引用: 1]
[17]
刘军, 冯硕, 任建华 移动机器人路径动态规划有向D*算法
[J]. 浙江大学学报:工学版 , 2020 , 54 (2 ): 291 - 300
[本文引用: 1]
LIU Jun, FENG Shuo, REN Jian-hua Directed D* algorithm for dynamic path planning of mobile robots
[J]. Journal of ZheJiang University: Engineering Science , 2020 , 54 (2 ): 291 - 300
[本文引用: 1]
[18]
OUYANG D, YUAN L, QIN L, et al Efficient shortest path index maintenance on dynamic road networks with theoretical guarantees
[J]. Proceedings of the VLDB Endowment , 2020 , 13 (5 ): 602 - 615
DOI:10.14778/3377369.3377371
[本文引用: 1]
[19]
WU S W, LI D M, ZHANG G L, et al. Density-based dynamic revision path planning in urban area via VANET [C]// International Conference on Machine Learning and Intelligent Communications . Shanghai: Springer, 2016: 129-138.
[本文引用: 1]
[20]
DAI T L, ZHENG W C, SUN J, et al Continuous route planning over a dynamic graph in real-time
[J]. Procedia Computer Science , 2020 , 174 : 111 - 114
DOI:10.1016/j.procs.2020.06.065
[本文引用: 2]
[21]
HOLZER M, SCHULZ F, WAGNER D Engineering multilevel overlay graphs for shortest-path queries
[J]. Journal of Experimental Algorithmics , 2009 , 13 : 156 - 170
[本文引用: 1]
[22]
WANG S Z, HAO M, CHEN H, et al. Multi-task adversarial spatial-temporal networks for crowd flow prediction [C]// Proceedings of the 29th ACM International Conference on Information and Knowledge Management . 2020: 1555-1564.
[本文引用: 1]
[23]
WANG S Z, CAO J N, CHEN H, et al SeqST-GAN: Seq2Seq generative adversarial nets for multi-step urban crowd flow prediction
[J]. ACM Transactions on Spatial Algorithms and Systems , 2020 , 6 (4 ): 1 - 24
[本文引用: 1]
[24]
REZAEI M, NOORI H, RAZLIGHI M M, et al ReFOCUS+: multi-layers real-time intelligent route guidance system with congestion detection and avoidance
[J]. IEEE Transactions on Intelligent Transportation Systems , 2019 , 22 (1 ): 1 - 14
[本文引用: 1]
[25]
XIE J Y, SONG Z Y, LI Y P, et al A survey on machine learning-based mobile big data analysis: challenges and applications
[J]. Wireless Communications and Mobile Computing , 2018 , 8738613
[本文引用: 1]
[26]
LI J L, LUO G Y, CHENG N, et al An end-to-end load balancer based on deep learning for vehicular network traffic control
[J]. IEEE Internet of Things Journal , 2018 , 6 (1 ): 953 - 966
[本文引用: 1]
[27]
JEFFREY L A, VICTOR J B A cooperative multi-agenttransportation management and route guidance system
[J]. Transportation Research Part C: Emerging Technologies , 2002 , 10 (5/6 ): 433 - 454
[本文引用: 1]
[28]
WANG M, SHAN H G, LU R X, et al Real-time path planning based on hybrid-vanet-enhanced transportation system
[J]. IEEE Transactions on Vehicular Technology , 2015 , 64 (5 ): 1664 - 1678
DOI:10.1109/TVT.2014.2335201
[本文引用: 1]
[29]
李博涵, 张潮, 李东静, 等 支持室内障碍空间的DSP-Topk查询优化算法研究
[J]. 计算机研究与发展 , 2017 , 54 (3 ): 557
DOI:10.7544/issn1000-1239.2017.20150895
[本文引用: 1]
LI Bo-han, ZHANG Chao, LI Dong-jing, et al A DSP-Topk query optimization algorithm supporting indoor obstacle space
[J]. Journal of Computer Research and Development , 2017 , 54 (3 ): 557
DOI:10.7544/issn1000-1239.2017.20150895
[本文引用: 1]
[30]
YU Z Q, YU X H, KOUDAS N, et al. Distributed processing of k shortest path queries over dynamic road networks [C]// Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data . Portland: ACM, 2020: 665-679.
[本文引用: 3]
[31]
YUAN J, ZHENG Y, XIE X, et al. Driving with knowledge from the physical world [C]// Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . San Diego: ACM, 2011: 316-324.
[本文引用: 1]
[32]
YUAN J, ZHENG Y, ZHANG C Y, et al. T-drive: driving directions based on taxi trajectories [C]// Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems . San Jose: ACM, 2010: 99-108.
[本文引用: 1]
2
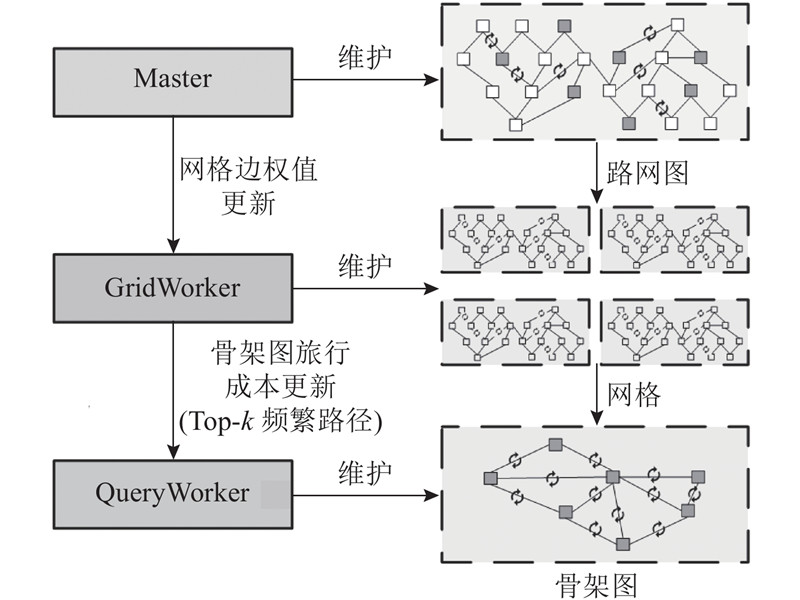
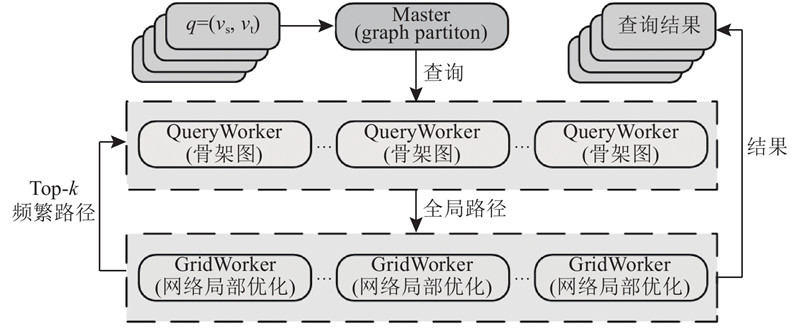
... 近年来,路径规划问题一直受到持续的关注,但是上述挑战并未被完全解决[1 -12 ] . 过去的许多工作都在研究动态路网上的路线问题,根据行驶时间找到最短的路径,为了保证规划的路线始终是最短的,须在动态路网上重复计算最短路径,这对于动态的超大型路网来说,计算代价很大. 此外,大多数现有的工作集中于处理单个路径规划查询,而较少关注大量并发查询的处理. 与反复计算从用户位置到目的地之间最短路径的精确计算相比,在较小的响应时间内自适应调整基于当前路况的近似最优路线更为可行. 基于这一思想,并考虑到大量并发查询的需求,提出路径规划的并行算法(parallel optimization of route planning,PORP),旨在通过Master-Worker模式,实现基于动态路网路径规划的并行优化策略. ...
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
Dynamic route planning with real-time traffic predictions
0
2017
Electric vehicle routing problem with charging time and variable travel time
0
2017
A unified approach to route planning for shared mobility
0
2018
2
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
... [8 ]所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
R3: a real-time route recommendation system
1
2014
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
2
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
... [10 ]提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
2
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
... [11 ]研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
Distributed shortest path query processing on dynamic road networks
3
2017
... 近年来,路径规划问题一直受到持续的关注,但是上述挑战并未被完全解决[1 -12 ] . 过去的许多工作都在研究动态路网上的路线问题,根据行驶时间找到最短的路径,为了保证规划的路线始终是最短的,须在动态路网上重复计算最短路径,这对于动态的超大型路网来说,计算代价很大. 此外,大多数现有的工作集中于处理单个路径规划查询,而较少关注大量并发查询的处理. 与反复计算从用户位置到目的地之间最短路径的精确计算相比,在较小的响应时间内自适应调整基于当前路况的近似最优路线更为可行. 基于这一思想,并考虑到大量并发查询的需求,提出路径规划的并行算法(parallel optimization of route planning,PORP),旨在通过Master-Worker模式,实现基于动态路网路径规划的并行优化策略. ...
... 上述解决方案主要是集中式路径规划模式,这种模式很难支持并行查询. 为了解决这个问题,文献[12 ]提出了CANDS,一种基于动态路网的分布式连续路径规划算法. CANDS将整个图划分为多个子图,并为所有子图形内的每对边界点之间的最短路径构建索引,依靠最短路径索引,CANDS持续为动态图上的用户计算最佳路径. 然而,最短路径索引维护的代价较高,因为随着路网的行驶代价的不断变化,边界点之间的最短路径须频繁更新. 为了解决这个问题,Yu等[30 ] 提出称为DTLP的分布式边界路径索引,该索引有助于Top-k 最短路径的计算,从而避免了权重不断变化的影响,但是这项工作并未考虑如何连续计算从用户位置到目标的最短路径. ...
... 为了验证算法的有效性,采用Naive和CANDS[12 ] 作为基准方法. 1)Naive:朴素方法采用暴力搜索模式,不断优化动态图上的规划路径.具体来说,一旦用户移动到新的位置,它就会重复计算从用户位置到目标的最短路径,一直重复计算直至用户到达目的地. 2)CANDS:CANDS是一项连续最优最短路径查询的算法,基于分布式流处理模式来不断优化动态图上的导航路径. 须遵循其分布式原则,在多个模拟Master-Worker模型的线程上实现CANDS. ...
1
... 基于位置服务LBS的时空查询问题已经引起学者们的广泛关注[13 ] . 在导航路径推荐服务中,基于复杂变化的路况[14 ] ,为正在使用导航的用户及时调整导航路径,能够在很大程度上规避突发拥堵、节约出行成本,其本质是基于动态路网的导航路径持续查询问题. ...
Time-dependent graphs: definitions, applications, and algorithms
1
2019
... 基于位置服务LBS的时空查询问题已经引起学者们的广泛关注[13 ] . 在导航路径推荐服务中,基于复杂变化的路况[14 ] ,为正在使用导航的用户及时调整导航路径,能够在很大程度上规避突发拥堵、节约出行成本,其本质是基于动态路网的导航路径持续查询问题. ...
A formal basis for the heuristic determination of minimum cost paths
1
1968
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
基于改进RRT的路径规划算法
1
2019
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
基于改进RRT的路径规划算法
1
2019
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
移动机器人路径动态规划有向D*算法
1
2020
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
移动机器人路径动态规划有向D*算法
1
2020
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
Efficient shortest path index maintenance on dynamic road networks with theoretical guarantees
1
2020
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
1
... A*算法是静态图中最短路线的经典算法[15 ] ,已经被广泛应用在许多工作中. Demiryurek等[8 ] 提出基于双向A*搜索算法的方法.R3系统[9 ] 基于A*算法计算最佳导航路径,与Demiryurek等[8 ] 所提方法不同的是,R3系统引入了历史数据以提高路径规划效率. 除了对最短路径的计算进行研究以外,一些工作还研究了路径规划中的其他因素. 刘晓倩等[16 ] 提出改进的RRT(rapid-exploration random tree)路径规划算法,该算法引入贪心剪枝思想,对冗余节点进行剪枝,可以提高路径规划效率. 有向D*算法[17 ] 通过引入导向函数缩小路径规划的搜索空间,从而减少规划时间,同时引入路径平滑度函数以保证算法的全局最优性. Ouyang等[18 ] 设计了辅助结构SS-Graph,并基于此结构提出动态道路网络上的最短路径索引,该索引可以通过理论上的保证得到有效更新.Wu等[19 ] 提出以路段密度为主要交通状态测度的动态路径规划方法,通过分析车辆的行驶时间和等待时间来决定是否修正当前的路径. ...
Continuous route planning over a dynamic graph in real-time
2
2020
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
... [20 ]提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
Engineering multilevel overlay graphs for shortest-path queries
1
2009
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
1
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
SeqST-GAN: Seq2Seq generative adversarial nets for multi-step urban crowd flow prediction
1
2020
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
ReFOCUS+: multi-layers real-time intelligent route guidance system with congestion detection and avoidance
1
2019
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
A survey on machine learning-based mobile big data analysis: challenges and applications
1
2018
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
An end-to-end load balancer based on deep learning for vehicular network traffic control
1
2018
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
A cooperative multi-agenttransportation management and route guidance system
1
2002
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
Real-time path planning based on hybrid-vanet-enhanced transportation system
1
2015
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
支持室内障碍空间的DSP-Topk查询优化算法研究
1
2017
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
支持室内障碍空间的DSP-Topk查询优化算法研究
1
2017
... 以上工作均重复计算从用户位置到目的地的最短路径,这使得路径规划的成本较高.为了解决这个问题,一些工作[10 -11 ,20 ] 着重于寻找近似的最佳路线. Malviya等[10 ] 提出2种基于不断变化的交通状况来计算近似最佳路线的方法. Xu等[11 ] 研究基于动态路网的导航路线的优化,在起点和目标之间选择几个固定的中间目标,以减少重新计算的复杂性. Dai等[20 ] 提出一种连续路径规划算法,该算法根据变化的交通状况实时不断调整推荐路线. Holzer等[21 ] 引用多层地图来加速路径规划查询的过程. 还有一些工作专注于路网交通状况的预测,Wang等[22 ] 提出多任务对抗时空网络模型,该模型能够同时预测起点到目标点的人群流量. 此外,该团队最近提出了sequence-to-sequence对抗网模型来预测多步人群流动[23 ] . Ghafouri等[1 ] 提出基于高斯过程的故障交通传感器检测模型,而Rezaei等[24 ] 在搜索最优规划路线时,同时考虑当前和未来的交通状况. 一些研究试图在规划路径时考虑未来的交通状况[25 -26 ] ,且只有当足够多的司机遵照算法调度时,这些研究才有效. 另外,大数据和机器学习在减少交通拥堵、改善道路安全、提高驾驶舒适性方面也发挥着重要的作用[27 -28 ] . 除此以外,李博涵等[29 ] 提出多目标优化算法DSP-Topk,该算法利用基于最大夹角差的可视区域方法,提高计算距离的效率,并通过剪枝策略提高运算效率,但是该算法是基于某种度量的方法,且受限于室内查询. ...
3
... 上述解决方案主要是集中式路径规划模式,这种模式很难支持并行查询. 为了解决这个问题,文献[12 ]提出了CANDS,一种基于动态路网的分布式连续路径规划算法. CANDS将整个图划分为多个子图,并为所有子图形内的每对边界点之间的最短路径构建索引,依靠最短路径索引,CANDS持续为动态图上的用户计算最佳路径. 然而,最短路径索引维护的代价较高,因为随着路网的行驶代价的不断变化,边界点之间的最短路径须频繁更新. 为了解决这个问题,Yu等[30 ] 提出称为DTLP的分布式边界路径索引,该索引有助于Top-k 最短路径的计算,从而避免了权重不断变化的影响,但是这项工作并未考虑如何连续计算从用户位置到目标的最短路径. ...
... 采用文献[30 ]中的路网模型,对道路网络上的边权值进行动态变化,使用 $ \alpha $ $ -\tau ,\; \tau $ 30 ],设定 $\alpha =$ 35 %以及 $ \tau = $ 30 %,路网信息如表1 所示. ...
... ]表示权重变化的范围.根据文献[30 ],设定 $\alpha =$ 35 %以及 $ \tau = $ 30 %,路网信息如表1 所示. ...
1
... 在以下3个真实路网上进行实验:Beijing(BJ)① ② ② [31 -32 ] ,包含10357辆出租车的17662998条GPS轨迹,但是T-drive的轨迹无法覆盖北京图的每条边,因此选择北京的最大连通加权子图作为实验数据集,其中包含188229个顶点和436648条边. ...
1
... 在以下3个真实路网上进行实验:Beijing(BJ)① ② ② [31 -32 ] ,包含10357辆出租车的17662998条GPS轨迹,但是T-drive的轨迹无法覆盖北京图的每条边,因此选择北京的最大连通加权子图作为实验数据集,其中包含188229个顶点和436648条边. ...