(13) $ {{\boldsymbol{K}}_{\text{S}}} = \frac{{{\text{d}}{{\boldsymbol{J}}_{{\text{RO}}}}^{\text{T}}}}{{{\text{d}}{\boldsymbol{X}}}}{{\boldsymbol{T}}_{{\text{RO}}}} = \frac{{{\text{d}}\left( {{{\boldsymbol{e}}_1}, {{\boldsymbol{e}}_2} ,{{\boldsymbol{e}}_3},{{\boldsymbol{e}}_{{\text{e}}1}}, {\boldsymbol{e}}_{{\text{e}}2} ,{\boldsymbol{e}}_{{\text{e}}3}} \right)}}{{{\text{d}}{\boldsymbol{X}}}}{{\boldsymbol{T}}_{{\text{RO}}}} . $
(14) $ \begin{split} & {{\boldsymbol{K}}_{\text{T}}} = {{\boldsymbol{J}}_{{\rm{RO}}}}^{\text{T}}\frac{{{\text{d}}{{\boldsymbol{T}}_{{\text{RO}}}}}}{{{\text{d}}{\boldsymbol{X}}}} = {{\boldsymbol{J}}_{{\text{RO}}}}^{\text{T}}\frac{{{\text{d}}{{\boldsymbol{T}}_{{\text{RO}}}}}}{{{\text{d}}{{\boldsymbol{L}}_i}}}\frac{{{\text{d}}{{\boldsymbol{L}}_i}}}{{{\text{d}}{\boldsymbol{X}}}} = - {{\boldsymbol{J}}_{{\text{RO}}}}^{\text{T}}\frac{{{\text{d}}{{\boldsymbol{T}}_{{\text{RO}}}}}}{{{\text{d}}{{\boldsymbol{L}}_i}}}{{\boldsymbol{J}}_{{\text{RO}}}}^{\text{T}} \hfill {\text{ = }}\\ & - {{\boldsymbol{J}}_{{\text{RO}}}}^{\text{T}}{\rm{diag}}\;[{k_1}, {k_2} ,{k_3},{k_{{\text{e}}1}}, {k_{{\text{e}}3}} ,{k_{{\text{e}}3}}]{{\boldsymbol{J}}_{{\text{RO}}}}^{\text{T}} .\hfill \\ \end{split} $
以以下结构参数的康复机器人为例,在MATLAB软件中通过计算分析康复机器人的使用安全性,评价指标的合理性. 过轮位置B 1 = [x 1 , 0]T ,B 2 = [0, 800]T mm,B 3 = [1680, 800]T mm,绳索最小预紧力T min = [10, 10, 10, 10]T N,绳索最大允许拉力T max = [500, 500, 500]T N. 假设作用在下肢牵引点P 的外力为垂直方向的力,即F T N,下肢康复机器人中驱动绳索采用GB/T 20118—2006中6×7+IWS的直径为1.8 mm的钢丝绳,最小破断拉力为1.69×103 N,弹性模量E i = 1.9402×105 MPa. 构成仿生肌肉绳索的弹性元件的线径为1.4 mm,外径为11 mm,材料为304不锈钢,即弹性元件的阻尼系数 ${c_{{\rm{e}}i}}$ [30 ] 给出的弹性元件的弹性系数和康复机器人的结构参数,确定本研究中并联弹性元件的结构参数,不同工况下仿生肌肉绳索中弹性元件的参数如表1 所示.
[1]
United Nations. 2019 revision of world population prospects [R]. New York: Department of Economic and Social Affairs, United Nations, 2019.
[本文引用: 1]
[2]
WANG Y L, WANG K Y, ZHAO W Y, et al Effects of single crouch walking gaits on fatigue damages of lower extremity main muscles
[J]. Journal of Mechanics in Medicine and Biology , 2019 , 19 (6 ): 1940046
[本文引用: 1]
[3]
DE-LA-TORRE R, OÑA E D, BALAGUER C, et al Robot-aided systems for improving the assessment of upper limb spasticity: a systematic review
[J]. Sensors , 2020 , 20 (18 ): 5251
DOI:10.3390/s20185251
[本文引用: 1]
[4]
BASTERIS A, NIJENHUIS S M, STIENEN A H A Training modalities in robot-mediated upper limb rehabilitation in stroke: a framework for classification based on a systematic review
[J]. Journal of Neuroengineering and Rehabilitation , 2014 , 11 : 111 - 126
DOI:10.1186/1743-0003-11-111
[本文引用: 1]
[5]
WANG Y L, WANG K Y, ZHANG Z X, et al Design, comprehensive evaluation, and experimental study of a cable-driven parallel robot for lower limb rehabilitation
[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering , 2020 , 42 (7 ): 371
DOI:10.1007/s40430-020-02443-x
[本文引用: 1]
[6]
WANG Y L, WANG K Y, WANG W L, et al Appraise and analysis of dynamical stability of cable-driven lower limb rehabilitation training robot
[J]. Journal of Mechanical Science and Technology , 2019 , 33 (11 ): 5461 - 5472
DOI:10.1007/s12206-019-1040-4
[本文引用: 1]
[7]
CUI X, CHEN W H, JIN X, et al Design of a 7-DOF cable-driven arm exoskeleton (CAREX-7) and a controller for dexterous motion training or assistance
[J]. IEEE/ASME Transactions on Mechatronics , 2017 , 22 (1 ): 161 - 172
DOI:10.1109/TMECH.2016.2618888
[本文引用: 1]
[8]
ALIMAN N, RAMLI R, HARIS S M Design and development of lower limb exoskeleton: a survey
[J]. Robotics and Autonomous Systems , 2017 , 95 : 102 - 116
DOI:10.1016/j.robot.2017.05.013
[本文引用: 1]
[9]
AMIRI M S, RAMLI R, TARMIZI M A A, et al Simulation and control of a six degree of freedom lower limb exoskeleton
[J]. Journal Kejuruteraan , 2020 , 32 (2 ): 197 - 204
[本文引用: 1]
[10]
ARMANNSDOTTIR A L, BECKERLE P, MORENO J C, et al Assessing the involvement of users during development of lower limb wearable robotic exoskeletons: a survey study
[J]. Human Factors , 2020 , 62 (3 ): 351 - 364
DOI:10.1177/0018720819883500
[本文引用: 1]
[11]
KINO H, YOSHITAKE T, WADA R, et al 3-DOF planar parallel-wire driven robot with an active balancer and its model-based adaptive control
[J]. Advanced Robotics , 2018 , 32 (14 ): 766 - 777
DOI:10.1080/01691864.2018.1493397
[本文引用: 1]
[12]
QIAN S, ZI B, WANG W, et al A review on cable-driven parallel robots
[J]. Chinese Journal of Mechanical Engineering , 2018 , 31 (1 ): 66 - 77
DOI:10.1186/s10033-018-0267-9
[本文引用: 1]
[13]
ZOU Y P, WANG N, WANG X Q, et al Design and experimental research of movable cable-driven lower limb rehabilitation robot
[J]. IEEE Access , 2019 , 7 : 2315 - 2326
DOI:10.1109/ACCESS.2018.2887233
[本文引用: 1]
[14]
ZOU Y. P, LIU K, WANG N, et al. Design and optimization of movable cable-driven lower-limb rehabilitation robot [C]// 3rd International Conference on Advanced Robotics and Mechatronics. Singapore: IEEE, 2018: 714-719.
[本文引用: 1]
[15]
ZI B, YIN G C, LI Y, et al. Kinematic performance analysis of a hybrid-driven waist rehabilitation robot [C]// 2nd International Conference on Mechatronics and Robotics Engineering. Nice: Springer, 2016.
[本文引用: 1]
[16]
SCALERA L, GALLINA P, SERIANI S, et al Cable-based robotic crane (CBRC): design and implementation of overhead traveling cranes based on variable radius drums
[J]. IEEE Transactions on Robotics , 2018 , 34 (2 ): 474 - 485
DOI:10.1109/TRO.2018.2791593
[本文引用: 1]
[17]
SERIANI S, GALLINA P Variable radius drum mechanisms
[J]. Journal of Mechanisms and Robotics-Transactions of the ASME , 2016 , 8 (2 ): 021016
DOI:10.1115/1.4031951
[本文引用: 1]
[18]
WANG Y L, WANG K Y, ZHANG Z X, et al Analysis of dynamical stability of rigid-flexible hybrid-driven lower limb rehabilitation robot
[J]. Journal of Mechanical Science and Technology , 2020 , 34 (4 ): 1735 - 1748
DOI:10.1007/s12206-020-0335-9
[本文引用: 2]
[19]
WANG K Y, YIN P C, YANG H P, et al. The man-machine motion planning of rigid-flexible hybrid lower limb rehabilitation robot [J]. Advances in Mechanical Engineering , 2018, 10(6): 1687814018775865.
[本文引用: 1]
[20]
WANG Y L, WANG K Y, ZHANG Z X, et al Appraisement and analysis of dynamical stability of under-constrained cable-driven lower limb rehabilitation training robot
[J]. Robotica , 2020 , 39 (6 ): 1023 - 1036
[本文引用: 1]
[21]
王砚麟, 赵志刚, 苏程, 等 欠约束多机协调吊运系统工作空间和运动稳定性分析
[J]. 振动与冲击 , 2017 , 36 (16 ): 44 - 50
URL
[本文引用: 1]
WANG Yan-lin, ZHAO Zhi-gang, SU Cheng, et al Analysis of the workspace and dynamic stability of a multi-robot collaboratively towing system
[J]. Journal of Vibration and Shock , 2017 , 36 (16 ): 44 - 50
URL
[本文引用: 1]
[22]
赵志刚, 王砚麟, 李劲松 多机器人协调吊运系统力位姿混合运动稳定性评价方法
[J]. 哈尔滨工程大学学报 , 2018 , 39 (1 ): 148 - 155
URL
[本文引用: 1]
ZHAO Zhi-gang, WANG Yan-lin, LI Jin-song Appraise of dynamical stability of multi-robots cooperatively lifting system based on hybrid force-position-pose approach
[J]. Journal of Harbin Engineering University , 2018 , 39 (1 ): 148 - 155
URL
[本文引用: 1]
[23]
ZHAO T, ZI B, QIAN S, et al Algebraic method-based point-to-point trajectory planning of an under-constrained cable-suspended parallel robot with variable angle and height cable mast
[J]. Chinese Journal of Mechanical Engineering , 2020 , 33 (1 ): 54
DOI:10.1186/s10033-020-00473-z
[本文引用: 1]
[25]
WANG Y L, WANG K Y, ZHANG Z X, et al Control strategy and experimental research of a cable-driven lower limb rehabilitation robot
[J]. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science , 2020 , 235 (13 ): 2468 - 2481
[本文引用: 1]
[26]
CHEN Q, ZI B, SUN Z, et al Design and development of a new cable-driven parallel robot for waist rehabilitation
[J]. IEEE/ASME Transactions on Mechatronics , 2019 , 24 (4 ): 1497 - 1507
DOI:10.1109/TMECH.2019.2917294
[本文引用: 1]
[27]
PLOOIJ M, KELLER U, STERKE B, et al Design of RYSEN: an intrinsically safe and low-power three-dimensional overground body weight support
[J]. IEEE Robotics and Automation Letters , 2018 , 3 (3 ): 2253 - 2260
DOI:10.1109/LRA.2018.2812913
[本文引用: 1]
[28]
吴博松. 基于仿肌肉柔索驱动的下肢康复机器人研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
[本文引用: 1]
WU Bo-song. Research on lower limb rehabilitation robot based on imitating muscle wire-drive [D]. Harbin: Harbin Engineering University, 2017.
[本文引用: 1]
[29]
DUAN Q J, VASHISTA V, AGRAWAL S K Effect on wrench-feasible workspace of cable-driven parallel robots by adding springs
[J]. Mechanism and Machine Theory , 2015 , 86 : 201 - 210
DOI:10.1016/j.mechmachtheory.2014.12.009
[本文引用: 1]
[30]
WANG Y L, WANG K Y, ZHANG Z, et al Mechanical characteristics analysis of a bionic muscle cable-driven lower limb rehabilitation robot
[J]. Journal of Mechanics in Medicine and Biology , 2020 , 20 (10 ): 2040037
DOI:10.1142/S0219519420400370
[本文引用: 1]
1
... 《2019 Revision of World Population Prospects》报告显示:中国老龄化人口占比为12.0%,到2050年预计为26.1%[1 ] . 老龄人是运动机能退化、脑中卒和偏瘫等疾病的高发人群,还有一些自然和非自然原因导致许多年轻人存在不同程度的运动障碍[2 -3 ] . 研究科学的可实现重复训练的康复机器人对提高患者的训练效率和减轻康复师的工作量具有现实意义[4 ] . ...
Effects of single crouch walking gaits on fatigue damages of lower extremity main muscles
1
2019
... 《2019 Revision of World Population Prospects》报告显示:中国老龄化人口占比为12.0%,到2050年预计为26.1%[1 ] . 老龄人是运动机能退化、脑中卒和偏瘫等疾病的高发人群,还有一些自然和非自然原因导致许多年轻人存在不同程度的运动障碍[2 -3 ] . 研究科学的可实现重复训练的康复机器人对提高患者的训练效率和减轻康复师的工作量具有现实意义[4 ] . ...
Robot-aided systems for improving the assessment of upper limb spasticity: a systematic review
1
2020
... 《2019 Revision of World Population Prospects》报告显示:中国老龄化人口占比为12.0%,到2050年预计为26.1%[1 ] . 老龄人是运动机能退化、脑中卒和偏瘫等疾病的高发人群,还有一些自然和非自然原因导致许多年轻人存在不同程度的运动障碍[2 -3 ] . 研究科学的可实现重复训练的康复机器人对提高患者的训练效率和减轻康复师的工作量具有现实意义[4 ] . ...
Training modalities in robot-mediated upper limb rehabilitation in stroke: a framework for classification based on a systematic review
1
2014
... 《2019 Revision of World Population Prospects》报告显示:中国老龄化人口占比为12.0%,到2050年预计为26.1%[1 ] . 老龄人是运动机能退化、脑中卒和偏瘫等疾病的高发人群,还有一些自然和非自然原因导致许多年轻人存在不同程度的运动障碍[2 -3 ] . 研究科学的可实现重复训练的康复机器人对提高患者的训练效率和减轻康复师的工作量具有现实意义[4 ] . ...
Design, comprehensive evaluation, and experimental study of a cable-driven parallel robot for lower limb rehabilitation
1
2020
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Appraise and analysis of dynamical stability of cable-driven lower limb rehabilitation training robot
1
2019
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Design of a 7-DOF cable-driven arm exoskeleton (CAREX-7) and a controller for dexterous motion training or assistance
1
2017
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Design and development of lower limb exoskeleton: a survey
1
2017
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Simulation and control of a six degree of freedom lower limb exoskeleton
1
2020
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Assessing the involvement of users during development of lower limb wearable robotic exoskeletons: a survey study
1
2020
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
3-DOF planar parallel-wire driven robot with an active balancer and its model-based adaptive control
1
2018
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
A review on cable-driven parallel robots
1
2018
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Design and experimental research of movable cable-driven lower limb rehabilitation robot
1
2019
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
1
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
1
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Cable-based robotic crane (CBRC): design and implementation of overhead traveling cranes based on variable radius drums
1
2018
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Variable radius drum mechanisms
1
2016
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Analysis of dynamical stability of rigid-flexible hybrid-driven lower limb rehabilitation robot
2
2020
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
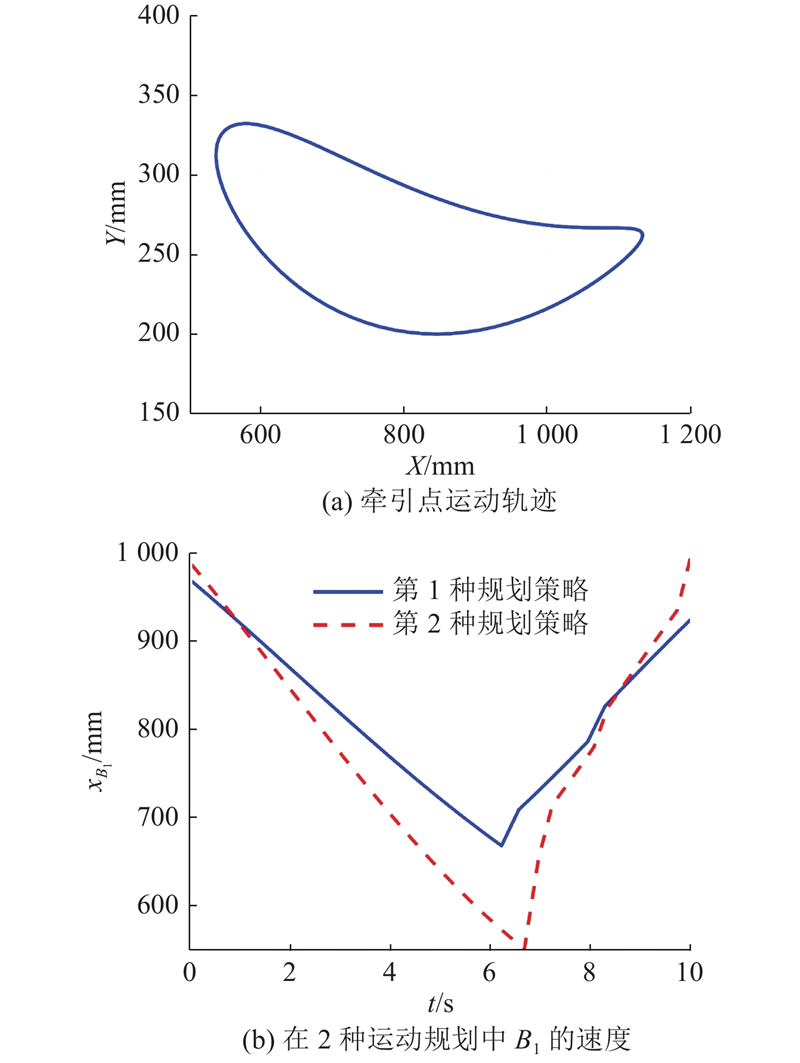
... 选择健康年轻人的正常行走步态运动轨迹为牵引点的运动轨迹[18 ] ,如图2 (a)所示. 在2种运动规划策略中滑块B 1 的运动轨迹如图2 (b)所示. 在第1种规划策略中,滑块的运动轨迹变化比第2种规划策略滑块的运动轨迹变化范围和波动性小. ...
1
... 康复机器人是康复医学、生物力学、机械学和自动控制等多学科领域的综合研究成果. 根据康复机器人的结构特点,主要研究的康复机器人可以分为两大类:外骨骼型和末端牵引型[5 -6 ] . 外骨骼型康复机器人具有很强的训练针对性,对关节的对应关系有严格的要求. 比较典型的应用有CAREX-7[7 ] 、6自由度的LLE [8 -9 ] 、LLWRE[10 ] 等. 外骨骼型康复机器人结构复杂,控制难度大,训练形式单一,存在较大的误差积累,人机相容性较差等. 末端牵引型康复机器人一般采用柔性绳索驱动训练对象实现康复训练,具有结构简单、灵活性和人机相容性好、系统刚度易于调整和训练形式多样化等特点,因此该类机器人已被应用于康复医疗领域[11 -12 ] ,例如可移动式绳索驱动下肢康复机器人[13 -14 ] 、绳索驱动的腰部康复机器人[15 ] 、具变直径牵引轮的绳索机器人[16 -17 ] 和含有刚性运动支链的下肢康复机器人[18 -19 ] ,均被有效应用于康复领域. ...
Appraisement and analysis of dynamical stability of under-constrained cable-driven lower limb rehabilitation training robot
1
2020
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
欠约束多机协调吊运系统工作空间和运动稳定性分析
1
2017
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
欠约束多机协调吊运系统工作空间和运动稳定性分析
1
2017
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
多机器人协调吊运系统力位姿混合运动稳定性评价方法
1
2018
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
多机器人协调吊运系统力位姿混合运动稳定性评价方法
1
2018
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
Algebraic method-based point-to-point trajectory planning of an under-constrained cable-suspended parallel robot with variable angle and height cable mast
1
2020
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
高速绳牵引摄像机器人的运动稳定控制
1
2016
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
高速绳牵引摄像机器人的运动稳定控制
1
2016
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
Control strategy and experimental research of a cable-driven lower limb rehabilitation robot
1
2020
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
Design and development of a new cable-driven parallel robot for waist rehabilitation
1
2019
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
Design of RYSEN: an intrinsically safe and low-power three-dimensional overground body weight support
1
2018
... 虽然绳索驱动的康复机器人具有上述性能优势,但由于绳索只对末端提供拉力,这使得该类机器人的安全性控制成为较大的挑战和研究前沿[20 ] . 为了提高绳索驱动康复机器人的安全性,研究人员开展了以下几个方面的研究工作. 1)系统稳定性是系统安全运动的前提条件,笔者等[21 -22 ] 研究机器人的静态和动态稳定性;2)运动轨迹规划是提高系统运动性能的重要途径,Zhao等[23 -24 ] 分别对绳索机器人的动态运动轨迹、启动和制动过程进行规划. Wang等[25 ] 设计在主被动训练模式下的复合控制器,有效地减小由末端执行器运动产生的多余力. Chen等[26 ] 设计模糊PID复合控制器,有效提高了训练效率和患者的安全性. Plooij等[27 ] 根据系统在竖直面和水平面内运动所需要的功率差异,定义了系统的安全性. ...
1
... 为了实现绳索驱动并联机器人的主被动刚度配置,在绳索机器人中增加了弹簧以改善系统的工作性能. 吴博松[28 ] 将弹簧串联在电机和过轮之间的绳索上,在弹簧之间增加绳芯以控制弹簧长度的阈值. Duan等[29 ] 用弹簧代替机器人中的1、2根绳索进行研究,结果显示,机器人的工作空间和工作性能均受到影响. ...
1
... 为了实现绳索驱动并联机器人的主被动刚度配置,在绳索机器人中增加了弹簧以改善系统的工作性能. 吴博松[28 ] 将弹簧串联在电机和过轮之间的绳索上,在弹簧之间增加绳芯以控制弹簧长度的阈值. Duan等[29 ] 用弹簧代替机器人中的1、2根绳索进行研究,结果显示,机器人的工作空间和工作性能均受到影响. ...
Effect on wrench-feasible workspace of cable-driven parallel robots by adding springs
1
2015
... 为了实现绳索驱动并联机器人的主被动刚度配置,在绳索机器人中增加了弹簧以改善系统的工作性能. 吴博松[28 ] 将弹簧串联在电机和过轮之间的绳索上,在弹簧之间增加绳芯以控制弹簧长度的阈值. Duan等[29 ] 用弹簧代替机器人中的1、2根绳索进行研究,结果显示,机器人的工作空间和工作性能均受到影响. ...
Mechanical characteristics analysis of a bionic muscle cable-driven lower limb rehabilitation robot
1
2020
... 以以下结构参数的康复机器人为例,在MATLAB软件中通过计算分析康复机器人的使用安全性,评价指标的合理性. 过轮位置B 1 = [x 1 , 0]T ,B 2 = [0, 800]T mm,B 3 = [1680, 800]T mm,绳索最小预紧力T min = [10, 10, 10, 10]T N,绳索最大允许拉力T max = [500, 500, 500]T N. 假设作用在下肢牵引点P 的外力为垂直方向的力,即F T N,下肢康复机器人中驱动绳索采用GB/T 20118—2006中6×7+IWS的直径为1.8 mm的钢丝绳,最小破断拉力为1.69×103 N,弹性模量E i = 1.9402×105 MPa. 构成仿生肌肉绳索的弹性元件的线径为1.4 mm,外径为11 mm,材料为304不锈钢,即弹性元件的阻尼系数 ${c_{{\rm{e}}i}}$ [30 ] 给出的弹性元件的弹性系数和康复机器人的结构参数,确定本研究中并联弹性元件的结构参数,不同工况下仿生肌肉绳索中弹性元件的参数如表1 所示. ...