自动化立体仓库是当代物流技术、仓储技术、自动化技术和计算机技术高度集成的产物，集存储、输送、管理等众多功能于一身，具有存储容量大、占地面积小等特点，被众多物流中心和生产企业采用^[1]. 自动化立体仓库不仅包括传统意义上的仓库货架，还包括相应的分拣设备、输送设备、堆垛机设备等^[2]. 堆垛机是自动化仓库的关键部件，主要功能是穿梭于高层货架中，将货架中的货物存放或取出，完成货物流动. 当前我国传统的堆垛机体积普遍较大且笨重，定位精度约为3 mm^[3]；堆垛机高且窄的结构导致其受力复杂，易产生强度与刚度不足的问题.

为了解决上述问题，研究人员对堆垛机展开大量的研究工作. 李杲^[4]对双立柱堆垛机进行结构建模和受力计算，利用有限元分析方法验证静态性能.宁波等^[5]对单立柱堆垛机进行结构优化，将整体刚度提高了7.69%，下横梁质量减少了9.96%. 马维金等^[6]提出可识别冲击载荷的声信号特征信息提取方法，可以用于减小冲击载荷对堆垛机振动的影响. Takahashi等^[7]采用鲁棒自适应控制，提出抑制残余振动的设计方法. Hajdu等^[8]提出基于增益调度的控制器设计方法，增强了堆垛机的稳定性和定位精度. 当前研究人员对堆垛机的研究主要集中在结构优化与控制方案上^[9-11]，对于刚度建模方面的研究仅是简单地求解三级货叉或立柱的挠度^[12]，还没有通过有限元求解结果及实验验证理论建模准确性的研究，对堆垛机整体刚度的影响因素分析及整体刚度建模很少涉及.

对于某些工程运用中如核工业领域内，使用传统的堆垛设备精确搬运重载组件时，由于承受载荷较大（多达800 kg），结构会产生较大的弹性变形，导致定位精度及搬运可靠性变差，因此堆垛设备须具备较强的刚度抵抗这种变形，这需要对堆垛设备进行刚度建模与分析. 针对上述情况，本文以重载智能堆垛装备为研究对象，开展刚度建模与结构优化. 提出重载智能堆垛装备的组成部分与工作原理，建立堆垛装备的刚度理论模型，开展实例计算. 采用有限元软件，求解V型导轨的接触刚度及堆垛装备的综合变形量. 建立基于刚度最大为目标函数的优化模型，对龙门立柱进行拓扑优化，对货叉进行多目标的参数优化.对优化后的堆垛装备进行实机承载试验，检测静态承载下的综合挠度.

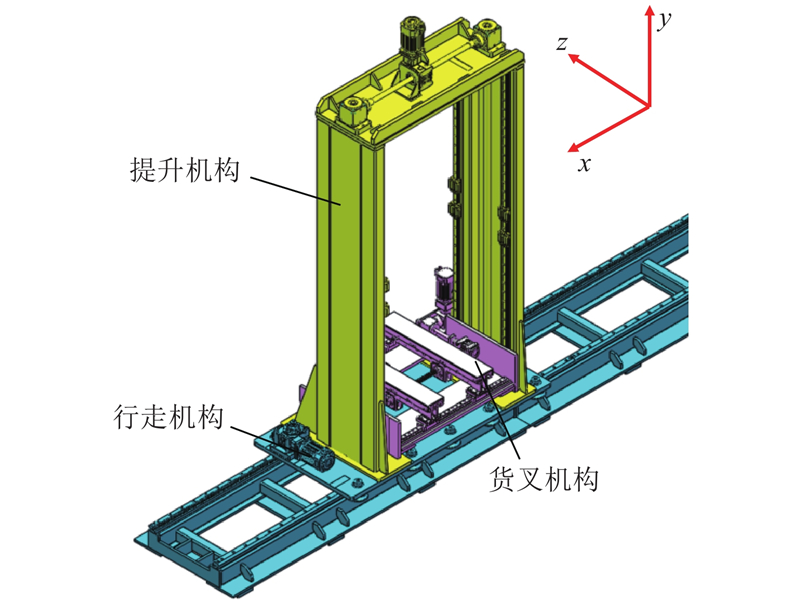
传统的堆垛机无法满足核工业热室内重载货物精确对接、长距离搬运等要求，本文设计的重载智能堆垛装备具备一定的刚度，能够实现重载、定位精度高、长距离搬运等需求. 总体结构如图1所示，主要由行走机构、提升机构、货叉机构、电气控制设备和安全保护装置等组成.

行走机构用于驱动整机在水平方向精确、快速、稳定地移动，因此行走机构需要具备重复定位精度高、响应速度快、运行平稳、可靠性高等特性，主要由多段拼接式框架底座、两组V型滚轮导轨、平移底板、齿轮齿条传动和电机驱动模块等组成.

提升机构用于带动已经承载货物的货叉机构提升与下降，由龙门立柱、两组丝杠传动模块和电机驱动模块等组成，具备重复定位精度高、刚度高、抗屈曲性强等特性.

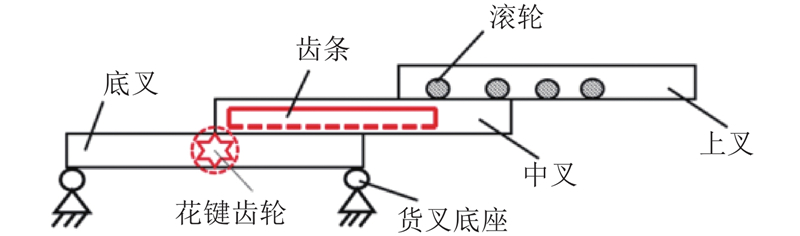
考虑货叉收回及伸展状态的空间受限，将货叉结构设计为三级直线差动式，主要由上叉、中叉、底叉及传动系4部分组成. 三级货叉伸缩原理如图2所示，底叉固定在可移动底座上，驱动电机通过减速器驱动花键轴，从而带动花键齿轮运动，通过齿轮齿条机构驱动中叉相对底叉运动. 上叉和中叉之间装有特殊的滚轮传动装置，使得中叉相对底叉运动的同时上叉也相对中叉运动，从而实现2倍的差动传动.

货叉机构由2组三级货叉组件、货叉横移模块、电动驱动模块、货叉支架等组成. 货叉组件具有两向伸缩功能，货叉底部装有可以横向调整位置的直线导轨，可以兼容不同宽度的货物.

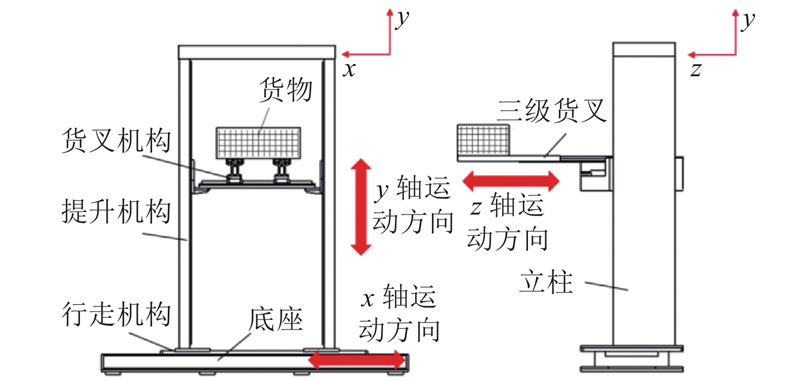
为了满足货物精准搬运至指定位置要求，将堆垛装备分解成x、y、z 3个独立运动轴，由伺服电机驱动数字化控制. 为了便于对堆垛装备运动描述的统一与规范，规定x轴为行走机构、y轴为提升机构、z轴为货叉机构，工作原理如图3所示. 货物搬运的步骤如下：堆垛装备整机沿x轴水平移动，货叉机构沿y轴竖直提升，货叉机构沿z轴伸缩，3个轴协同作用即可完成货物搬运.

传统的堆垛机地面铺设单根钢轨，行走采用2个或4个普通滚轮，竖直提升采用起重链条与链轮组合结构. 相比于传统堆垛机，重载智能堆垛装备具有以下优势.

1）x轴采用V型滚轮与导轨作为引导、齿轮齿条作为传动，2组V型导轨具备一定的抗倾覆能力、自清洁能力，可以适应存在一定不平度的地面.

2）y轴采用直线滚动导轨为引导、滚珠丝杠为传动方式，龙门立柱整体刚性较好，定位精度高.

3）z轴采用2组三级货叉组成，可以减小整体安装空间，对不同宽度的货物进行叉取.

4）堆垛装备底座及货叉采用不锈钢材料，可以适应热室内恶劣的理化环境.

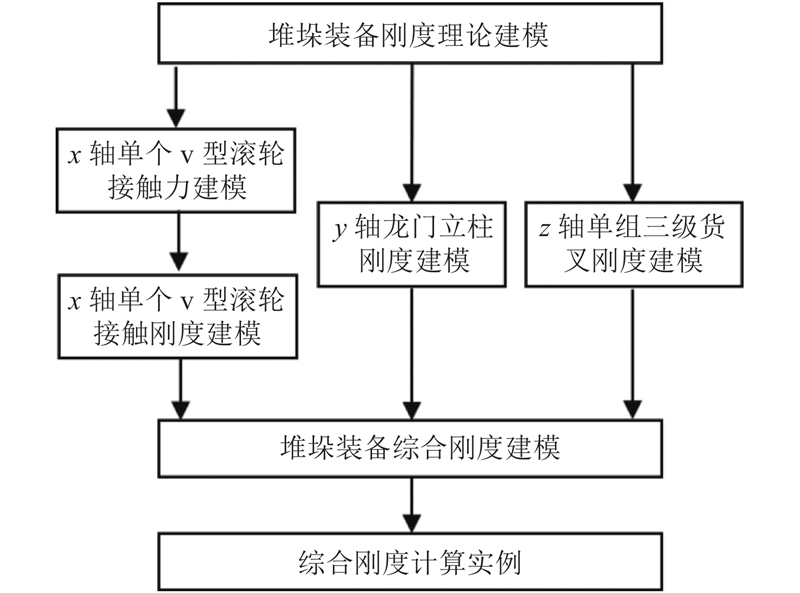
根据堆垛装备的结构与工作原理可知，V型导轨、龙门立柱及三级货叉是堆垛装备的主要承载受力部件，这三者的刚度决定堆垛装备的综合刚度.通过三者的几何关系叠加，得到堆垛装备综合刚度，建模流程如图4所示.

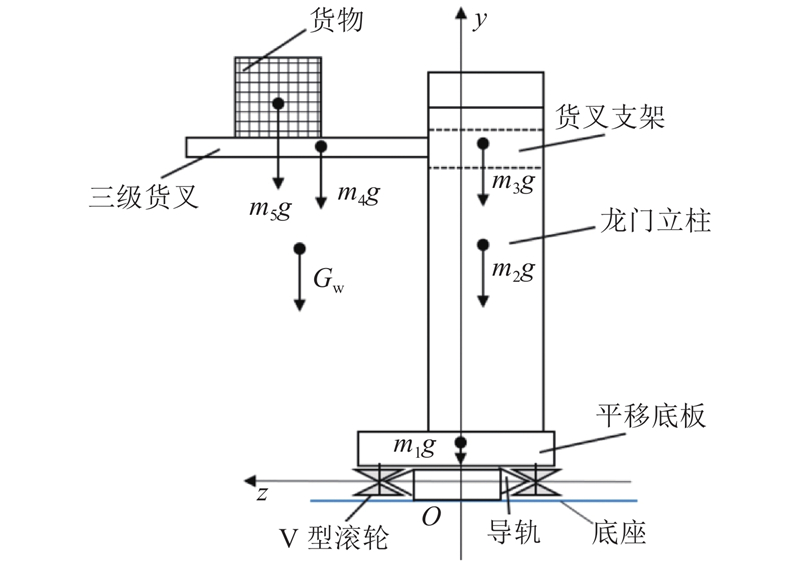
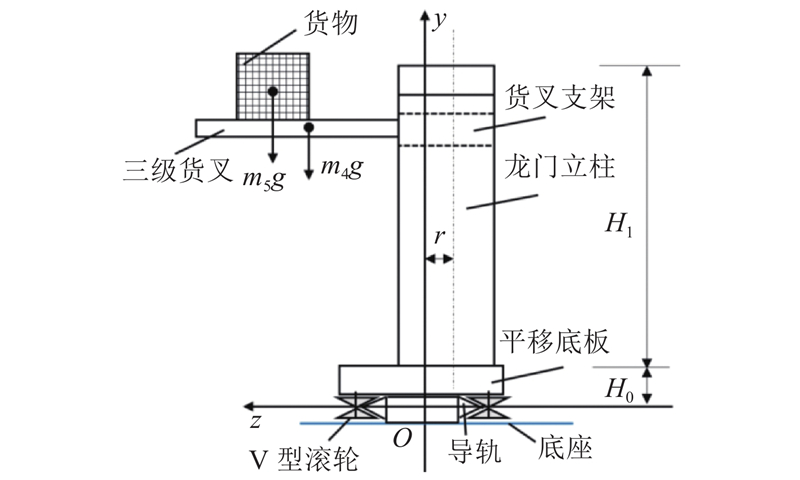
将堆垛装备货叉取货的模型简化如图5所示. 图中，m_i (i=1,2,···,5)分别为平移底板、龙门立柱、货叉支架、三级货叉、货物的质量，V型滚轮与导轨接触，支撑整个堆垛装备及货物的重力.

为了简化运算，对各组件及货物重量求取整体重力G_w及总体质心的横坐标z_w，如下：

(1) $\left. {\begin{array}{*{20}{l}} {{G_{\rm{w}}} = \displaystyle\sum\limits_{i = 1}^5 {{m_i}g} ,}\\ {{z_{\rm{w}}} = \left( {\displaystyle\sum\limits_{i = 1}^5 {{m_i}{z_i}} } \right)\Bigg/\left( {\displaystyle\sum\limits_{i = 1}^5 {{m_i}} } \right).} \end{array}} \right\}$

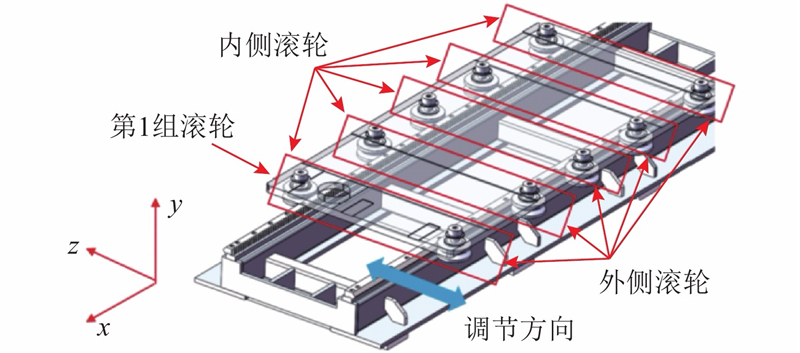
为了便于分析滚轮受力，定义靠近货物一侧的滚轮为内侧滚轮，另一侧为外侧滚轮. 如图6所示为滚轮组安装示意图. 平移底板上5组滚轮均匀分布，滚轮轴线必须成直线，使得与V型导轨能够均匀接触，这可以通过机械加工保证. 每组滚轮安装时，先固定内侧滚轮作为基准，外侧滚轮可沿z方向上进行调整，使得外侧滚轮与另一条V型导轨充分接触. 通过对5组滚轮依次安装调整，使得同一侧的滚轮受力尽可能均匀一致.

根据货叉伸出状况，V型滚轮受力可以分为以下2种不同状态.

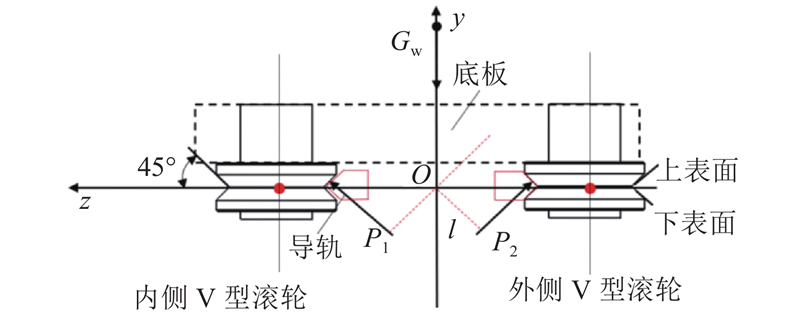
1）稳定状态为货叉缩回，货物固定在货叉支架上，不会对整机产生倾覆力矩，V型滚轮导轨受到装备整体及货物的重力，两侧滚轮均为上表面承力，如图7所示.

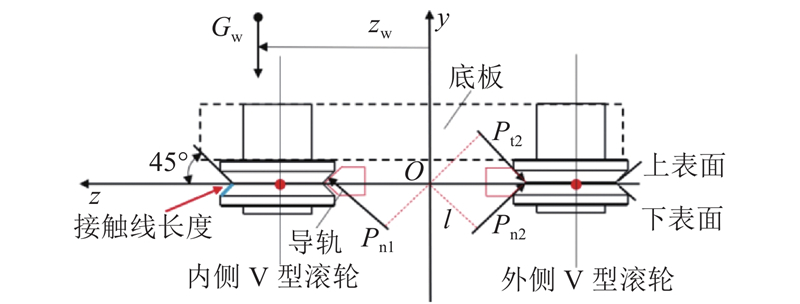
2）倾覆状态为货叉伸出至极限位置，对整机产生一定的倾覆力矩，即受力为垂直载荷以及逆时针力矩的复合载荷，此时外侧V型滚轮上、下表面均受力，如图8所示.

为了简化力学建模过程，将5组滚轮组受力的空间力系简化为单组滚轮组受力的平面力系. 考虑到5组滚轮组接触受力的不均匀性，引入载荷分布不均匀系数k_v(通常取0.70~0.80)，使得计算更加符合真实情况. 在稳定状态（见图7）下，对滚轮受力进行分析，滚轮受到G_w及导轨对滚轮的接触力P₁、P₂. 根据理论力学平面力系原理，建立平衡方程：

(2) $ \left. {\begin{array}{*{20}{l}} {5{k_{\rm{v}}}{P_1}\sin \;{{45}^\circ } - 5{k_{\rm{v}}}{P_2}\sin \;{{45}^\circ } = 0,}\\ {5{k_{\rm{v}}}{P_1}\cos \;{{45}^\circ } + 5{k_{\rm{v}}}{P_2}\cos \;{{45}^\circ } - {G_{\rm{w}}} = 0.} \end{array}} \right\}$

将式（2）化简，可以求得接触力为

(3) $ {P_1}{\text{ = }}{P_2}{\text{ = }}\frac{G_{\rm{w}}}{{5\sqrt 2 {k_{\rm{v}}}}} . $

在倾覆状态下（见图8），对滚轮受力进行分析. 忽略滚轮自身的结构尺寸，可将滚轮视作质点，滚轮受到G_w以及导轨对滚轮的接触力P_n1、P_n2、P_t2，可知平衡方程：

(4) $ \left. {\begin{array}{*{20}{l}} {5{k_{\rm{v}}}{P_{{\rm{n}}1}}{\rm{cos}}\;{\rm{4}}{{\rm{5}}^\circ }{\rm{ = 5}}{k_{\rm{v}}}\cos \;{{45}^\circ }({P_{{\rm{n}}2}} + {P_{{\rm{t}}2}}),}\\ {5{k_{\rm{v}}}{\rm{sin}}\;{\rm{4}}{{\rm{5}}^\circ }({P_{{\rm{n1}}}}{\rm{ + }}{P_{{\rm{n}}2}}) = 5{k_{\rm{v}}}{P_{{\rm{t}}2}}\sin \;{{45}^\circ } + {G_{\rm{w}}}.} \end{array}} \right\}$

根据滚轮位置的几何关系，P_n1、P_n2、P_t2的力臂均为l，对原点O求矩可列平衡方程：

(5) $ G_{\rm{w}}{z_{\rm{w}}} + 5{k_{\rm{v}}}\left( {{P_{{\rm{n}}2}} - {P_{{\rm{t}}2}} - {P_{{\rm{n}}1}}} \right)l{\text{ = }}0 . $

联立式(4)、（5），可以得到内、外侧滚轮的接触力：

(6) $ {P_{{\rm{n}}1}} = \frac{{\sqrt 2 }}{{10{k_{\rm{v}}}}}G_{\rm{w}} + \frac{{G_{\rm{w}}{z_{\rm{w}}}}}{{10l{k_{\rm{v}}}}} . $

(7) $\left. {\begin{array}{*{20}{l}} {{P_{{\rm{n}}2}} = \dfrac{{\sqrt 2 }}{{10{k_{\rm{v}}}}}{G_{\rm{w}}},}\\ {{P_{{\rm{t}}2}} = \dfrac{{G_{\rm{w}}{z_{\rm{w}}}}}{{10l{k_{\rm{v}}}}}.} \end{array}} \right\} $

由于式（6）、（7）引入k_v，可以将该求解结果视作2种状态下5组滚轮中的最大接触力. 根据式(6)、(7)可以求得内、外侧滚轮接触力，为求解V型导轨接触刚度及优化设计提供理论基础.

V型导轨的接触刚度会极大地影响堆垛装备的整体刚度及运行的平稳性^[13]，V型滚轮与导轨为线接触. 在工程运用中，采用Palmgren得出的经验公式^[14]求解接触变形量：

(8) $ \delta {\text{ = }}3.81 \times {\left[\frac{{2(1 - {\mu ^2})}}{{{\text{π}} E}}\right]^{9/10}}\frac{{{P^{9/10}}}}{{{l_{\rm{V}}}^{8/10}}} . $

式中：δ为单个V型滚轮弹性变形量，μ和E分别为V型滚轮与导轨的泊松比与弹性模量，P为滚轮与导轨的法向接触力，l_V为滚轮与V型导轨斜面接触线段长度（见图8）. 滚轮与导轨采用高质量轴承钢制成，E为206 GPa，μ为0.3，将参数代入式（8），可得接触力P与变形量δ的关系：

(9) $ P = {(3.85 \times {10^{ - 5}})^{ - 10/9}}{\delta ^{10/9}}{l_{\rm{V}}}^{8/9} = {k_{\rm{n}}}{\delta ^{10/9}} . $

将k_n定义为类刚度系数，V型导轨选择英国HEPCO公司生产的直线导轨，选择V型滚轮型号为HJR150，参考HEPCO产品样本可以得到l_V为21.64 mm，求得类刚度系数为1.24×10⁶ N·mm^−10/9. 根据刚度的定义，可得V型导轨的接触刚度：

(10) $ {K_{\rm{N}}} = \frac{{{\rm{d}}P}}{{{\rm{d}}\delta }} = \frac{{10}}{9}{k_{\rm{n}}}{\delta ^{1/9}} = \frac{{10}}{9}k_{\rm{n}}^{9/10}{P^{1/10}} . $

由此可知，可以通过求得δ、P来获得V型导轨的接触刚度.

在稳定状态下，令滚轮与平移底板整体竖直下滑量为δ₁，V型滚轮法向接触位移δ_N为

(11) $ {\delta _{\rm{N}}}{\text{ = }}\frac{{{\delta _1}}}{{\cos \;45^\circ }} = \sqrt 2 {\delta _1} . $

由式(3)、(9)可知G_w与δ₁的关系，由此可得该载荷下V型导轨的接触刚度K_N1：

(12) $ {G_{\rm{w}}} = 5\sqrt 2 {k_{\rm{n}}}{\delta _{\rm{N}}}^{10/9} = 1.29 \times {10^7}{\delta _1}^{10/9}{\rm{N}} \cdot {\rm{m}}{{\rm{m}}^{ - 10/9}},$

(13) $ {K_{{\rm{N}}1}}{\rm{ = }}1.13 \times {10^6}{G_{\rm{w}}}^{1/10}{{\rm{N}}^{9/10}} \cdot {\rm{m}}{{\rm{m}}^{ - 1}}. $

在倾覆状态下，内侧滚轮接触力最大，为P_n1，同理可得内侧V型导轨接触刚度K_N2为

(14) $ {P_{{\rm{n}}1}}{\text{ = 1}}{\text{.82}} \times {10^6}{\delta _{{\rm{n}}1}}^{10/9}{\rm{N\cdot m}}{{\text{m}}^{ - 10/9}} , $

(15) $ {K_{{\rm{N}}2}} = \frac{{10}}{9}k_{\rm{n}}^{9/10}{P_{{\rm{n}}1}}^{1/10}{\text{ = }}3.39 \times {10^5}{P_{{\rm{n}}1}}^{1/10}{{\rm{N}}^{9/10}}\cdot{\text{m}}{{\text{m}}^{ - 1}} . $

式中：δ_n1为倾覆状态下内侧滚轮的竖直下滑量，同理可求外侧滚轮的竖直下滑量δ_n2、δ_t2，可以近似看成整个堆垛装备向内侧滚轮倾斜，

(16) $ \alpha {\text{ = }}\frac{{{\delta _{\rm{q}}}}}{d}{\text{ = }}\frac{{{\delta _{{\rm{n}}1}} - {\delta _{{\rm{n}}2}} + {\delta _{{\rm{t}}2}}}}{d} . $

式中：d为平移底板宽度，δ_q为内侧滚轮相对于外侧滚轮的竖直下滑量.

堆垛装备取货时(货叉伸展至最远端)，货叉组件受货叉与货物重力共同作用，立柱发生弯曲变形，受力分析如图9所示，立柱中心与y轴的距离为r.

根据材料力学理论可知，当货叉组件在y方向提升至纵坐标为y时，立柱顶端的转角β与挠度u如下：

(17) $ \left. {\begin{array}{*{20}{l}} {\beta = \dfrac{{M(y - {H_0})}}{{EI}},}\\ {u = \dfrac{{M{{(y - {H_0})}^2}}}{{2EI}} + \beta ({H_1} + {H_0} - y),}\\ {M = \displaystyle\sum\limits_{i = 4}^5 {{m_i}g({z_i} + r)} .} \end{array}} \right\}$

式中：M为货物与货叉重力对立柱产生的弯矩，I为立柱截面惯性矩，H₁为立柱高度，H₀为立柱底部与滚轮中心的高度差. 当货叉组件提升至最大纵坐标y_max时，立柱最大转角及挠度为

(18) $ {\beta _{\max }} = \frac{{{y_{\max }} - {H_0}}}{{EI}}\sum\limits_{i = 4}^5 {{m_i}g({z_i} + r)} , $

(19) $ {u_{\max }} = \frac{{(2{H_1} + {H_0} - {y_{\max }})({y_{\max }} - {H_0})}}{{2EI}}\sum\limits_{i = 4}^5 {{m_i}g\left( {{z_i} + r} \right)} . $

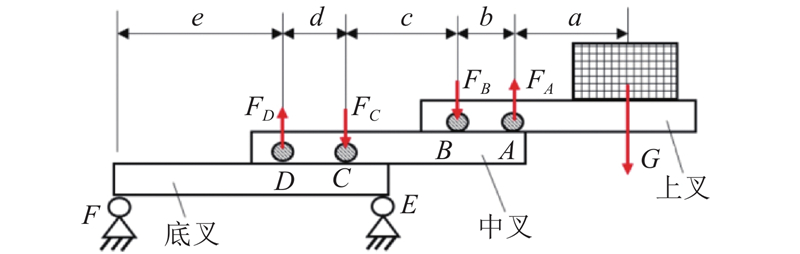
货叉作为堆垛装备的核心部件，取货时货叉受到货物重力G会产生弯曲变形. 计算时，将载荷均分给2组货叉组件，将三级货叉的受力点简化为4个支点，受力分析如图10所示.

分别对上叉、中叉及底叉进行受力分析. 根据平面力系的平衡方程，可得各支点的受力：

(20) $\left. {\begin{array}{*{20}{l}} {{F_A} = - 0.5G(a + b)/b,} \\ {{F_B} = 0.5Ga/b,} \\ {{F_C} = 0.5G(a + b + c + d)/d,} \\ {{F_D} = - 0.5G(a + b + c)/d.} \end{array}} \right\}$

式中：F_A、F_B、F_C、F_D分别为各支点的支反力，a、b、c、d、e为各支点的间距. 运用材料力学理论对各级货叉单独进行挠度计算，得到各级货叉的最大转角与最大挠度.

(21) $\left. {\begin{array}{*{20}{l}} {{\theta _{\max 1}} = \dfrac{{G{a^2}}}{{4E{I_1}}},} \\ {{\theta _{\max 2}} = - \dfrac{{{F_A}{{(b + c)}^2}}}{{2E{I_2}}} - \dfrac{{{F_B}{c^2}}}{{2E{I_2}}},} \\ {{\theta _{\max 3}} = - \dfrac{{{F_D}ed(d + 2e)}}{{6E{I_3}(e + d)}}.} \end{array}} \right\} $

(22) $ \left. {\begin{array}{*{20}{l}} {{w_{\max 1}} = \dfrac{{G{a^3}}}{{6E{I_1}}},} \\ {{w_{\max 2}} = - \dfrac{{{F_A}{{(b + c)}^3}}}{{3E{I_2}}} - \dfrac{{{F_B}{a^2}(3b + 2c)}}{{6E{I_2}}},} \\ {{w_{\max 3}} = \dfrac{{{F_D}d{{\left[ {{{(e + d)}^2} - {d^2}} \right]}^{3/2}}}}{{9\sqrt 3 E{I_3}(e + d)}}.} \end{array}} \right\}$

式中：θ_maxi 、w_maxi、I_i(i = 1, 2, 3)为上、中、底叉的最大转角、最大挠度、截面惯性矩. 将货叉3部分挠度叠加，可得货叉总转角θ及总挠度w：

(23) $ \begin{split} \theta =& \displaystyle\sum\limits_{i = 1}^3 {{\theta _{\max i}}} =\\ &\dfrac{{G{a^2}}}{{4E{I_1}}} - \dfrac{{{F_A}{{(b + c)}^2} + {F_B}{c^2}}}{{2E{I_2}}} - \dfrac{{{F_D}ed(d + 2e)}}{{6E{I_3}(e + d)}} , \end{split}$

(24) $ \begin{array}{l}w={\displaystyle \sum _{i=1}^{2}{w}_{\text{max}i}}+{\displaystyle \sum _{i=1}^{2}{L}_{{i}}{\theta }_{\mathrm{max}（i+1）}}=\dfrac{G{a}^{3}}{6E{I}_{1}}-\dfrac{{F}_{A}{(b+c)}^{3}}{3E{I}_{2}}-\\ \dfrac{{{F_B}{a^2}(3b + 2c)}}{{6E{I_2}}} - {L_1}\left[ {\dfrac{{{F_A}{{(b + c)}^2}}}{{2E{I_2}}} + \dfrac{{{F_B}{c^2}}}{{2E{I_2}}}} \right] -\\ {L_2}\dfrac{{{F_D}ed(d + 2e)}}{{6E{I_3}(e + d)}} . \\[-18pt]\end{array}$

式中：L₁为上叉相对中叉的伸长量，L₂为货叉伸长量.

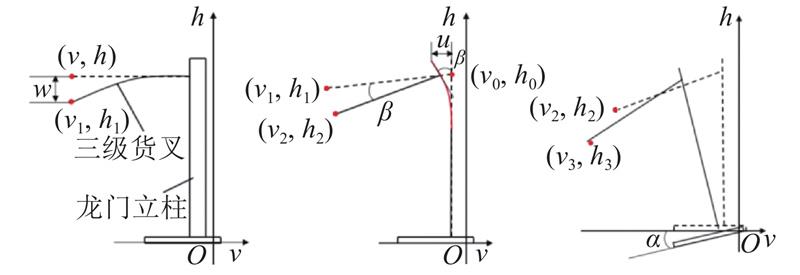
为了便于计算，以外侧滚轮为原点建立直角坐标系，如图11所示. 通过求解货叉末端承载后的坐标值变化，可以得到堆垛装备的综合刚度.

考虑Z轴三级货叉弯曲变形，三级货叉的弯曲量为w，弯曲角度为θ，三级货叉末端的初始坐标值为(v, h)，受力弯曲变后为(v₁, h₁)，可得

(25) $ \left[ \begin{array}{l} {{{v}}_1} \\ {h_1} \\ 1 \\ \end{array} \right] = \left[ \begin{array}{l} v \\ h \\ 1 \\ \end{array} \right] + \left[ \begin{array}{l} 0 \\ - w \\ 0 \\ \end{array} \right] . $

考虑y轴龙门立柱的弯曲变形，整个龙门立柱的弯曲量为u，弯曲角度为β. 为了简便计算，将三级货叉保持直线状态，则三级货叉整体绕点(v₀, h₀)逆时针旋转β，考虑龙门立柱变形后的坐标为(v₂, h₂)，可得

(26) $ \left[ \begin{array}{l} {v_2} \\ {h_2} \\ 1 \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{{c} _2}}&{ - {s_2}}&{\left( {1 - {{c} _2}} \right){v_0} + {h_0}{s_2}} \\ {{s_2}}&{{{c} _2}}&{(1 - {{c} _2}){h_0} - {v_0}{s_2}} \\ 0&0&1 \end{array}} \right]\left[ \begin{array}{l} {v_1} - u \\ {h_1} \\ 1 \\ \end{array} \right] . $

式中：s₂、c₂分别表示sin β、cos β.考虑x轴导轨的接触变形，仅考虑整个堆垛装备绕O逆时针转动的角度为α，考虑整体变形后的坐标为(v₃, h₃), 则有

(27) $ \left[ \begin{array}{l} {v_3} \\ {h_3} \\ 1 \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }&0 \\ {\sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right]\left[ \begin{array}{l} {v_2} \\ {h_2} \\ 1 \\ \end{array} \right] . $

由此可知，综合挠度由货叉末端在y、z方向上的位移决定，因此定义装备的综合挠度为

(28) $ {\boldsymbol{\varDelta}} {\text{ = }}\left[ \begin{array}{l} {{{\varDelta}} _z} \\ {{{\varDelta}} _y} \\ \end{array} \right] = \left[ \begin{array}{l} v \\ h \\ \end{array} \right] - \left[ \begin{array}{l} {v_3} \\ {h_3} \\ \end{array} \right] . $

式中：Δ_z、Δ_y定义为堆垛装备的水平综合挠度、垂直综合挠度. 将式(25)~（27）代入式(28)，进行简化得到

(29) $ {\boldsymbol{\varDelta}} = \left[ \begin{array}{l} v - {c_1}\left[ {(v - u){c_2} - (h - w){s_2} + (1 - {c_2}){v_0} + {h_0}{s_2}} \right] + {{s} _1}\left[ {(v - u){s_2} + (h - w){c_2} + (1 - {c_2}){h_0} - {v_0}{s_2}} \right] \\ \\ h - {{s} _1}\left[ {(v - u){c_2} - (h - w){s_2} + (1 - {c_2}){v_0} + {h_0}{s_2}} \right] - {c_1}\left[ {(v - u){s_2} + (h - w){c_2} + (1 - {c_2}){h_0} - {v_0}{s_2}} \right] \\ \end{array} \right] . $

式中：s₁、c₁分别表示sin α、cos α，(h,v)初始值及(h₀,v₀)的坐标值由堆垛装备的结构而定，变形量u、w及转角α、β、θ由堆垛装备的结构、材料及货物的重力决定.

根据重载智能堆垛装备的设计结构和尺寸，求解整体综合挠度装备各部件的材料参数，如表1所示. 表中，ρ为材料的密度，E为材料的弹性模量，ν为材料的泊松比.

在三维软件中可以直接查找各部件质量及各部件质心的横坐标参数，如表2所示.

V型滚轮受力的力臂l为587 mm，平移底板宽度d为1 000 mm，k_v取0.8. 根据式（3）、（6）、（7）可得，稳定状态下单个V型滚轮的接触力的最大值为5196 N；倾覆状态下单个内侧滚轮的接触力最大值P_n1以及外侧滚轮接触力P_n2、P_t2分别为7925、5196、2729 N.

y轴组件各参数为：H₁ = 2800 mm，H₀ = 300 mm，y_max = 2700 mm，I =6.94×10⁸ mm⁴, r = 100 mm. 货叉伸长1200 mm时，各级货叉的截面惯性矩以及各位置点的距离如表3所示.

根据上述参数，可以求得V型导轨、龙门立柱及三级货叉的挠度与转角，如表4所示.

堆垛装备的初始值(v, h)为(−2 000, 2 400), (v₀, h₀)为(−200, 2 400)，将参数代入式（29），可得堆垛装备的综合挠度为： $ {\boldsymbol{\varDelta}} $=[0.426，13.297]^T mm.

根据堆垛装备的刚度建模方法可知综合刚度的影响因素，给定刚度要求后，可以求解结构设计参数，为装备的结构优化提供参考依据.

计算式（6）、（7）可知，内侧滚轮受力最大，仅对内侧滚轮接触力进行求解. 将堆垛装备模型进行简化并导入ANSYS workbench中，材料参数的设置如表1所示. V型滚轮与导轨间添加不分离接触，采用自动网格划分方法进行网格划分，货叉组件的网格控制为5 mm，提升机构的网格控制为20 mm. 设置重力加速度g以及在货叉末端施加竖直向下7840 N的集中力，对底座进行固定，有限元计算模型如图12所示，将内侧滚轮编号为1~5.

求解内侧滚轮与导轨的接触力，如表5所示. 表中，F_x、F_y、F_z分别为x、y、z方向上的受力，F为合力. 从表5可知，2、3号滚轮受力较小，5号滚轮受力最大，其值为7 827 N. 滚轮的校核计算应当考虑受力最大值进行对比，可知有限元计算的受力最大值与滚轮最大受力的理论值7 925 N较接近，验证了理论计算方法的准确性.

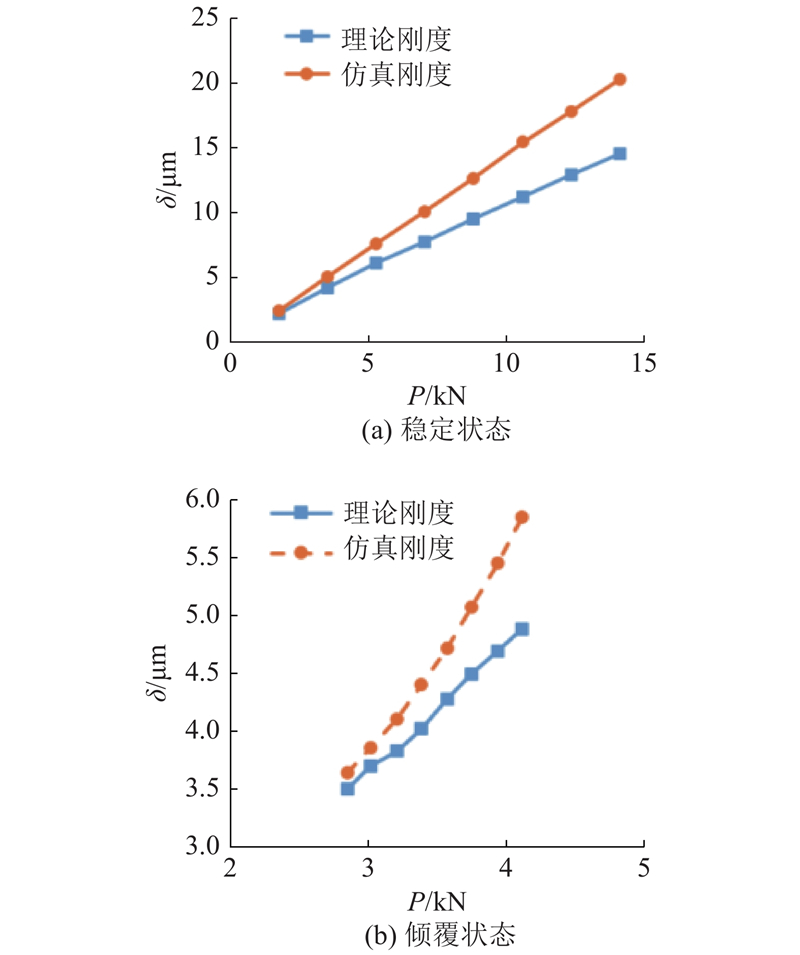
为了计算稳定状态下V型导轨的接触刚度，施加的总载荷为10~80 kN. 根据式(3)可以求得单个滚轮接触力为1.76~14.1 kN，通过式(12)可以求得各载荷对应的理论变形量.

在倾覆状态下，货物的重力对底板产生倾覆力. 当货物质量为100~800 kg时，伸展距离为1.7 m，可以通过式（6）求得内侧滚轮接触力为2.83~4.10 kN，利用式(14)可以求得对应的理论变形量.

绘制2种状态下导轨接触力P与变形量δ的散点图，采用线性拟合对理论与仿真刚度进行求解，如图13所示. 刚度的定义是接触力与变形量的比值，即图13中斜率的倒数. 根据拟合曲线可知，堆垛装备稳定状态导轨的理论刚度与仿真接触刚度分别为8.16×10⁵、7.37×10⁵ N/mm；堆垛装备倾覆状态导轨的理论刚度与仿真刚度分别为7.65×10⁵、5.87×10⁵ N/mm.

有限元处理步骤与3.1节一致，对总变形、y方向变形、z方向变形进行求解，结果如图14所示.

从图14可知，堆垛装备综合变形量d_a的最大值为14.407 mm，发生在货叉最远端，将y、z方向的变形量与理论计算结果进行对比，如表6所示. 表中，d_T为理论计算值，d_F为有限元计算值，E_d为理论值与有限元的误差.

从表6可知，理论计算与有限元计算结果较接近，验证了刚度建模理论的准确性.

根据理论计算与有限元分析结果可知，龙门立柱与三级货叉的刚度是影响堆垛装备刚度的关键因素. 为了进一步改善堆垛装备的整体结构刚度，对龙门立柱与三级货叉进行结构优化.

由于V型滚轮与导轨的承载能力有限，利用接触力理论计算方法，可以求得堆垛装备所能承受的最大载荷，将其作为载荷量对龙门立柱与货叉进行结构优化. 根据式（1）、（6），可以反求最大货物重力G_max，作为结构优化的加载力：

(30) $ {G_{\max }}{\text{ = }}\frac{{10l{k_{\rm{v}}}{P_{\max }} - \sqrt 2 l\displaystyle\sum\limits_{i = 1}^4 {{m_i}g} - \displaystyle\sum\limits_{i = 1}^4 {{m_i}g} {z_i}}}{{\sqrt 2 l + {z_5}}} . $

式中：P_max为单个滚轮所能承受的最大载荷.

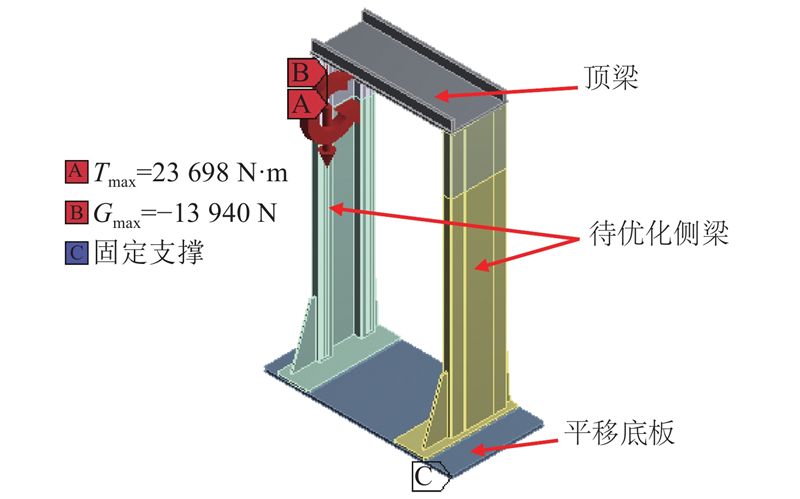
单个滚轮可承载的最大载荷为17 000 N. 取安全系数为1.5，从而保证滚轮受力的安全裕度，则单个滚轮接触力最大值为11 333 N. 为了确保滚轮正常运行，根据式（30）及堆垛装备参数，可以求得本次优化的加载力为13 940 N.

根据有限元分析可知，龙门立柱整体结构刚性较好，结构较笨重. 为了减小能源消耗及节约制造成本，对龙门立柱结构进行轻量化设计^[15-16]. 根据堆垛装备的结构特点，采用变密度法对龙门立柱进行结构拓扑优化.

将龙门立柱的变形量最小，即刚度最大作为优化目标函数，保存80%的质量作为约束，立柱两侧梁区域的单元为设计变量. 拓扑优化模型如下：

(31) $ \left. \begin{array}{l} {\boldsymbol{\rho}} = \left[ {{\rho _1},{\rho _2}, \cdots ,{\rho _N}} \right] ;\\ \min\;{\boldsymbol{C}}\left( {\boldsymbol{\rho}} \right)={{\boldsymbol{U}}^{\rm{T}}}\left( {\boldsymbol{\rho}} \right){\boldsymbol{K}}\left( {\boldsymbol{\rho}} \right){\boldsymbol{U}}\left({\boldsymbol{ \rho}} \right); \\ {\rm{st}}.\;{\boldsymbol{V}}^ *{({\boldsymbol{\rho}} ) } < f{\boldsymbol{V}}({\boldsymbol{\rho}} ), \\ {\boldsymbol{F}}\left({\boldsymbol{ \rho}} \right)={\boldsymbol{ K}}\left( {\boldsymbol{\rho }} \right){\boldsymbol{U}}\left( {\boldsymbol{\rho}} \right), \\ 0 < {\rho _{\min }} \leqslant {\rho _i} \leqslant 1\left( {i = 1,2, \cdots ,n} \right). \end{array} \right\} $

式中：ρ_i为设计变量，表示该材料离散单元的相对密度；C(ρ)为整体结构柔度；K(ρ)为整体结构的刚度；F(ρ)为施加的载荷矩阵，U(ρ)为整体变形量，V(ρ)与V*(ρ)为优化前、后的体积，f为体积保留系数.

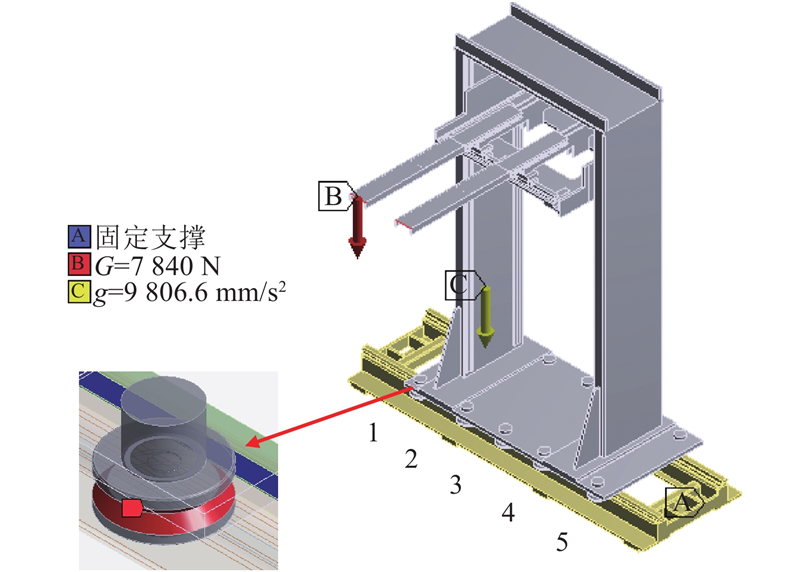
龙门立柱的初步结构示意图如图15所示，整体结构由两块侧梁以及顶梁组成. 图中，T_max为受到的最大转矩. 对该模型进行静力学分析，对立柱施加13 940 N的力以及23 698 N·m的力矩，将平移底板固定，求取最大变形量.

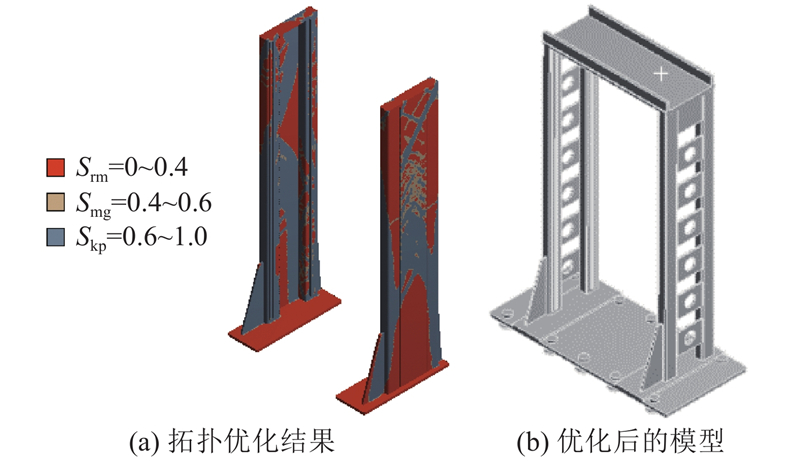
根据优化模型对龙门立柱模型添加设计变量、目标函数、响应约束，生成拓扑优化的计算结果. 如图16(a)所示，S_rm为移除系数，即图中深色部分，该部分可去除；S_kp为保留系数，即图中浅色部分，该部分须保留；S_mg为边缘系数.

拓扑优化结果中存在较多的不规则形状，在实际应用中深色区域不能完全去除. 为了便于零件加工，优化后的龙门立柱采用方管及钢板焊接而成，如图16(b)所示，在减小材料的同时，可以保证一定的刚度.

求解立柱优化后的模型，如表7所示. 表中，d_co为立柱的变形量，σ_co为立柱的最大应力，m_co为立柱的总质量. 可知，立柱的最大变形量及最大应力有所增加，但增加的幅度很小，立柱总质量减小了12.5%，减重效果较明显.

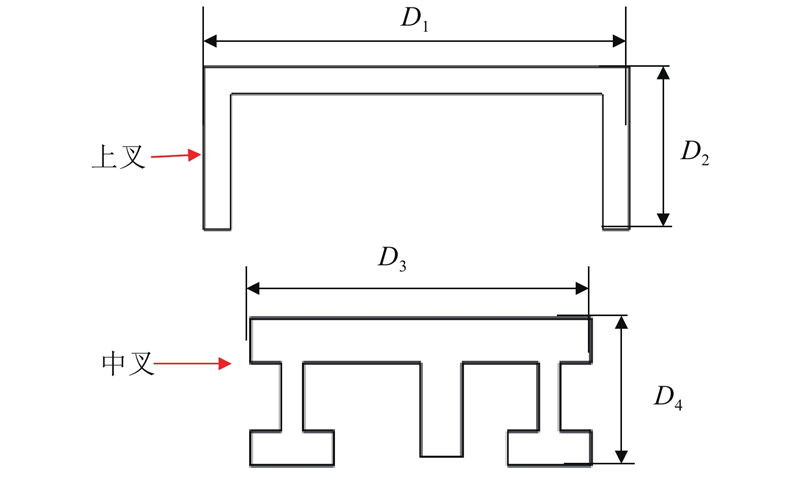
货叉刚度决定叉取货物的准确性与稳定性，为了增强货叉刚度，对三级货叉的截面进行参数优化，选取最优参数. 采用workbench中的响应面优化模块，对三级货叉中的上叉与中叉进行多目标参数优化设计，优化参数如图17所示.

综合考虑有限元求解的精度与速度，采用Screening筛选算法对三级货叉参数进行优化. 设置优化的目标为使整体的最大变形量最小(刚度最大)以及整体的最大应力和整体质量最小. 优化模型如下：

(32) $\left. \begin{array}{l} \min \;F({\boldsymbol{d}}_{\text{v}}) = \min \;\{ m({\boldsymbol{d}}_{\rm{v}}),d({\boldsymbol{d}}_{\rm{v}}),\sigma ({\boldsymbol{d}}_{\rm{v}})\}, \\ {\sigma _{\max }} < {\sigma _{\rm{s}}}, \\ d_{{{\rm{v}}i\min }} \leqslant d_{{\rm{v}}i} \leqslant d_{{{\rm{v}}i\max }}. \\ \end{array} \right\} $

式中：d_v=[D₁,D₂,D₃,D₄]^T为设计参数，m(d_v)为总质量，σ(d_v)为应力，d(d_v)为变形量，σ_max为最大应力，σ_s为材料的许用应力，d_vimax、d_vimin为该参数的取值上限与下限.

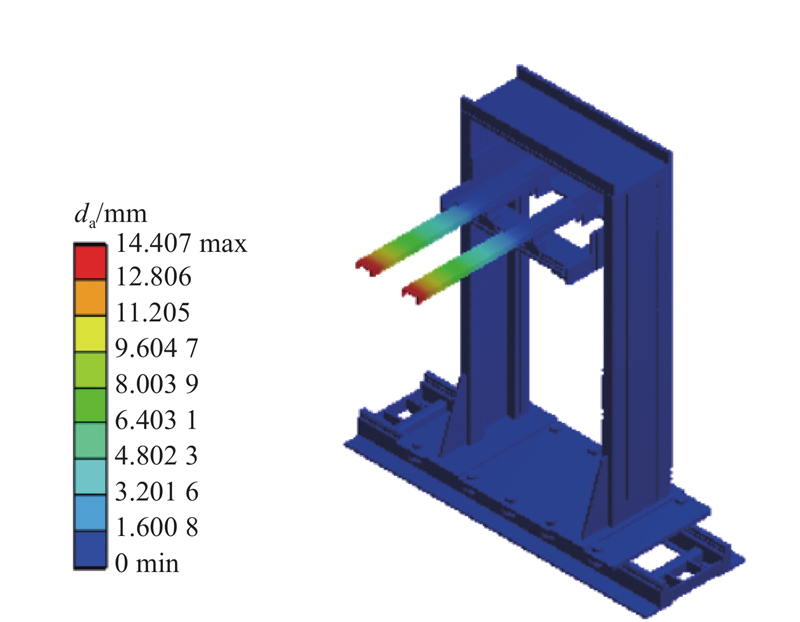
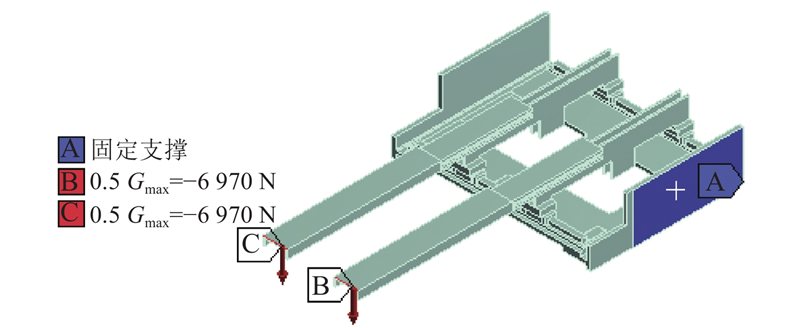
对底叉进行固定，在上叉末端各施加6 970 N竖直向下的集中力，如图18所示. 对变形及应力进行求解，将上叉与中叉的质量、变形量的最大值以及最大应力定义为设计参数.

设置如表8所示的优化参数，分别设置中心合成的实验类型、面心设计类型及增强模板类型，点击平台预览可以生成多个设计点，更新产生设计点的计算结果.

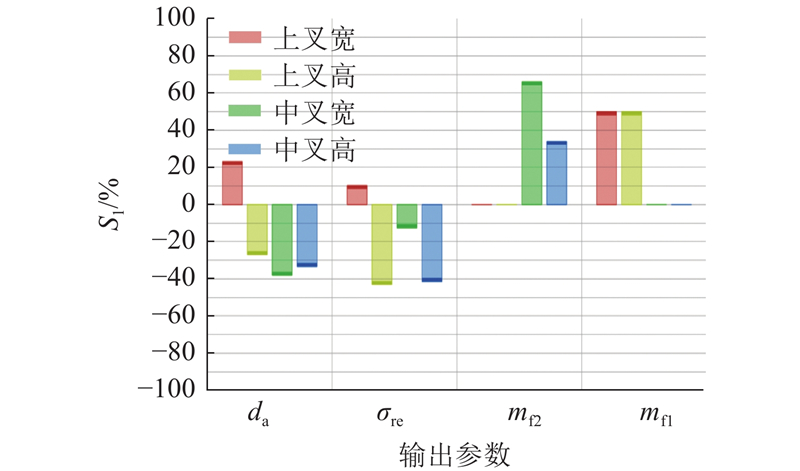
绘制局部灵敏度S₁的示意图，如图19所示. 图中，σ_re为最大应力，m_f1为上叉质量，m_f2为中叉质量. 可知，上叉宽度对货叉总变形量的灵敏度为正，可以适当减小上叉的宽度，从而增大货叉刚度. 中叉宽度对变形量的敏感度最大且为负，为了增大货叉的刚度，可以优先考虑增大该尺寸.

根据优化模型设置多目标函数，更新计算模型可以得到3组参考点的计算结果，如表9所示. 表中，方案1为优化前的初始方案，方案2~4为仿真计算得到的3组优化方案，方案5为取整后的优化方案. 选取参考点2为最优参数点，取整再进行静力学求解.

将优化后的龙门立柱与三级货叉重新装配，形成优化后的堆垛装备. 采用有限元方法可以求解优化后的装备综合变形量，对货叉施加竖直向下、大小为13 940 N的集中力，步骤与3.1节一致. 将求解结果与优化前的计算结果进行对比，如表10所示. 表中，d_y为y方向上的变形量，d_z为z方向上的变形量. 可知，优化后的堆垛装备整体刚度提升了23.9%，优化效果明显.

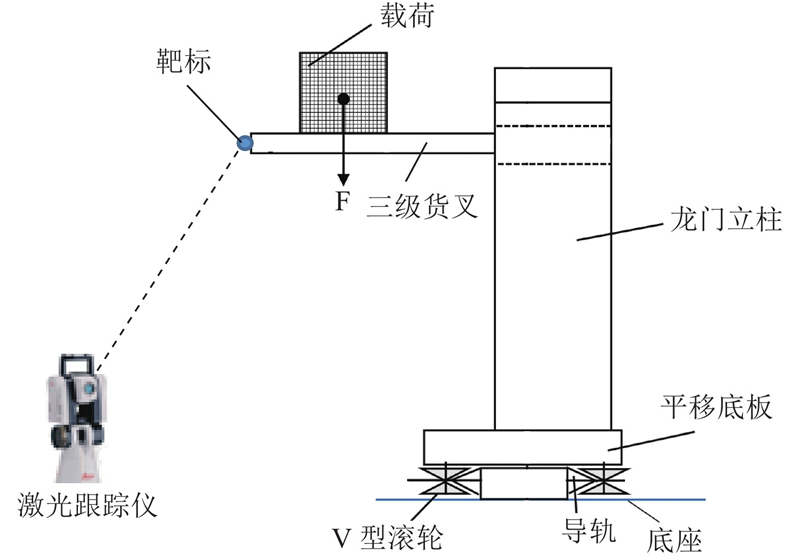
为了分析优化后堆垛装备在实际承载下的刚度及整机运行情况，开展实机承载运行以及静态载荷下的综合挠度检测试验. 在装配完成后，将800 kg配重块固定在三级货叉的末端，如图20所示为测试原理图.

堆垛装备运行平稳，可以实现货物搬运的要求. 运行一段时间后，导轨表面保持光滑，且划痕较少，验证了优化后的堆垛装备可以满足工程应用的需求.

本次检测采用Leica LTD640型号的激光跟踪仪作为检测工具，如图21所示，测量半径可达40 m，分辨率为0.001 mm，在全行程范围内测量精度可达(15 $ \pm $5)×10⁻⁶. 激光跟踪仪具备高精度、高效率、实时跟踪测量、安装便捷等特点，广泛运用于高精度检测领域，如汽车制造、飞机装配、多轴精密机床等^[17].

将激光跟踪仪放置在货叉正下方的地面上，对货叉末端中间位置安装测量靶标，测量货叉末端由空载到某载荷作用过程中该靶标点的坐标位置，通过计算位置变化值，可得货叉末端的垂向挠度.

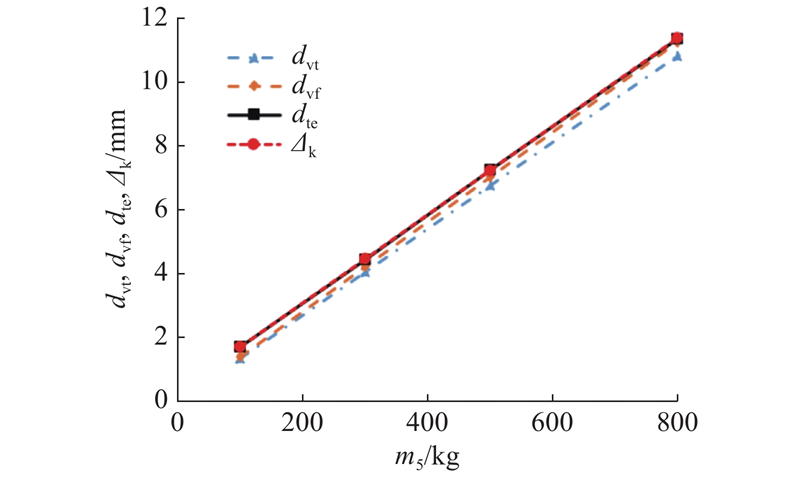
当载荷为100、300、500、800 kg时，检测货叉末端的垂向挠度. 根据理论与有限元方法，可以求得优化后的堆垛装备Y方向综合挠度的理论值与有限元计算值，将三者进行比较，如表11所示. 表中，d_vt为垂向理论挠度，d_vf为垂向挠度有限元计算值，d_te为垂向挠度检测值.

采用线性回归方程对检测值进行模拟，得到d_te(单位为mm)与载荷m₅(单位为kg)的关系：

(33) ${d_{{\text{te}}}} = 0.013\;8{m_5} + 0.330. $

由于理论计算与有限元求解中忽略了堆垛装备运动过程产生的间隙，导致实际检测值普遍偏大.考虑修正函数为一次函数，对货叉垂向挠度的理论计算进行修正：

(34) $ {\varDelta _{\rm{k}}}{\text{ = }}{k_1}{\varDelta _{\rm{y}}} + {k_0} . $

其中：Δ_k为修正后的挠度；Δ_y为修正前的挠度；k₁、k₀为修正系数，其值为1.022、0.321. 根据式(29)、(34)可得理论修正值，将其与理论计算值、有限元计算值、试验检测值进行对比，如图22所示.

从图22可知，货叉的挠度与承载货物的质量呈现较好的线性关系. 修正后的理论值曲线与实验值曲线较拟合，验证了修正公式的正确性.

（1）提出重载智能堆垛装备的结构方案. 根据堆垛装备的工作原理，给出V型滚轮与导轨的接触力理论计算方法. 基于该方法建立堆垛装备综合刚度的计算理论模型，给出计算实例.

（2）采用有限元分析方法，求解V型导轨在2种状态下的接触刚度及堆垛装备的综合变形量，验证了理论计算方法的准确性.

（3）建立基于刚度最大为优化目标的优化模型，采用变密度法对龙门立柱进行拓扑优化，使得整体质量减轻了12.5%. 采用多目标优化方法，选取三级货叉的最优截面参数. 开展有限元求解，可知优化后堆垛装备的整体刚度提升了23.9%.

（4）对堆垛装备进行综合挠度的现场检测，试验结果表明，优化后的堆垛装备能够满足工程运用的需求. 本文针对堆垛装备刚度建模及结构优化的方法可以为我国建造新型智能货仓以及特殊环境下重载货物的精准搬运提供新方法和新思路.