随着人工智能技术的应用与发展,移动机器人更多应用在无人参与的复杂环境中,如深海探测、自动导引小车等,对动态规划的要求更高. Khatib[9]提出人工势场法以处理机器人路径动态规划问题,其优点在于只须进行简单数学分析,无须进行大量计算即可规划出光滑路径并具有较好的实时性,但利用该方法难以获得全局最优解. Yang等[10-12]均对人工势场法进行改进,但仍存在规划时间随障碍物复杂度的增加而增大、路径拐点较多等问题. Koenig等[13]引入环境增量信息提出LPA*(lifelong planning A*)算法,但该算法规划效率较低. Patle等[14]利用萤火虫算法进行不确定环境下的路径规划,但存在无效转弯、机器人移动时间成本增加的问题. Panda等[15]提出基于遗传算法的动态网格进化搜索算法,在一定程度上提高了搜索效率,但后期收敛速度较慢.
D*算法[16]是由Stentz提出的动态规划算法,机器人在向目标点移动过程中只检查最短路径临近节点的变化情况,因此具有较高的动态搜索效率,且可以处理任何成本参数发生变化的路径成本优化问题[17]. 由于其通过等势线逐级扩展的方式进行搜索,搜索空间较大,尤其在初始路径规划、环境复杂程度较高时,搜索空间大的问题更加突出;在单次扩展搜索时仅考虑欧几里得距离,易出现在小范围区域内多次转弯的问题,增加移动时间成本[18]. 为此,Stentz[19]提出Focussed D*(focussed dynamic A*)算法,通过增加偏置函数来降低搜索空间,在一定程度上降低了路径规划时间,但机器人在小范围区域内多次转弯的问题没有得到有效解决;Koenig等[20]提出D* Lite(dynamic A* Lite)算法,该算法在一定程度上提高了算法效率,但存在节点重复计算问题;Ganapathy等[21]提出Enhanced D* Lite(enhanced dynamic A* Lite)算法,避免了移动机器人穿越尖角等一系列不安全路径,但机器人在小范围区域内多次转弯的问题依然没有得到有效解决.
传统移动机器人动态路径规划算法在确定子节点时遍历所有节点因而搜索效率低、存在多次转弯而增加移动时间成本. 针对上述问题提出有向D*算法,算法通过引入关键节点概念,逐级扩展确定可行路径,并结合障碍物位置信息引入导向函数缩小路径规划的搜索空间,提高搜索效率;在欧几里得距离评价标准的基础上引入平滑度函数,对规划路径与理想路径的偏移程度进行惩罚,减少路径拐点数量,提高路径平滑度,并对平滑度函数中转弯因子的确定方法、特点进行说明. 在此基础上,对有向D*算法的收敛性进行证明并给出算法流程. 在3种大小不同、障碍物复杂情况不同的环境空间内对算法进行测试,仿真实验表明所提方法能较好的兼顾局部搜索与系统最优性,尤其适用于障碍物较多的复杂环境.
1. 问题描述
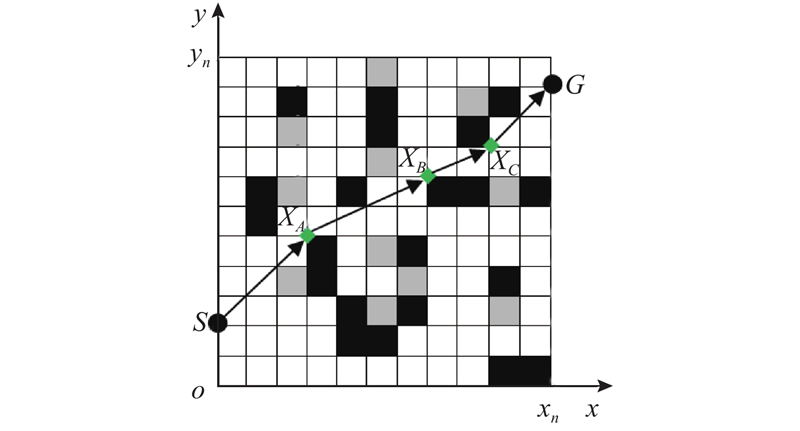
移动机器人路径规划的环境建模方法主要有栅格法、几何特征法、自由空间法等. 由于栅格法数据结构简单、能有效表达空间的可变性,本研究采用如图1所示的栅格法对移动机器人的工作环境进行建模. 图中,笛卡尔坐标系中横坐标
图 1
相邻栅格的交点为路径规划的节点. 假设节点
令
须注意的是:不考虑设备硬件情况,仅从路径规划算法角度出发,离线规划时间由规划算法的迭代次数、障碍物的数量和环境大小等决定;在线移动时间由路径距离、路径平滑度决定;N则受未知环境中障碍物大小、数量和障碍物的复杂程度等影响. 移动机器人路径动态规划的主要难点之一在于如何协调局部搜索与全局规划,以最少的节点扩展使路径搜索离线规划时间与机器人移动时间成本均达到最小. 随着环境或障碍物复杂程度的增加,上述问题的难度及规划需要愈发突出,因此本研究提出有向D*算法来解决该问题.
2. 有向D*机器人路径动态规划算法
2.1. 基本思想
传统机器人路径动态规划D*算法较其他诸多算法有较好的全局收敛性,但其存在以下问题. 1)传统D*算法在离线路径规划时采用类似等势线逐级扩展的方式,从目标点开始对地图节点进行遍历,导致搜索范围较大. 尤其当搜索地图区域较大时,问题更为突出. 本研究考虑障碍物及目标点位置信息,引入关键节点概念对节点进行区分(关键节点为障碍物所确定的相关节点),从初始点开始只对关键节点进行访问,缩小搜索空间;再结合目标点位置信息,引入导向函数以确定单次扩展时所需比较的路径节点,确定可行路径,提高路径规划速度. 2)一般D*算法在确定最优路径时使用欧几里得距离指标进行评价,忽略障碍物尤其是未知障碍物可能导致最终规划路径存在小范围区域内多次无效转弯的问题. 针对该问题,本研究引入平滑度函数对规划路线偏离理想路径的程度进行惩罚,用以控制最终规划路径的拐点数量,避免机器人在小范围区域内无效转弯.
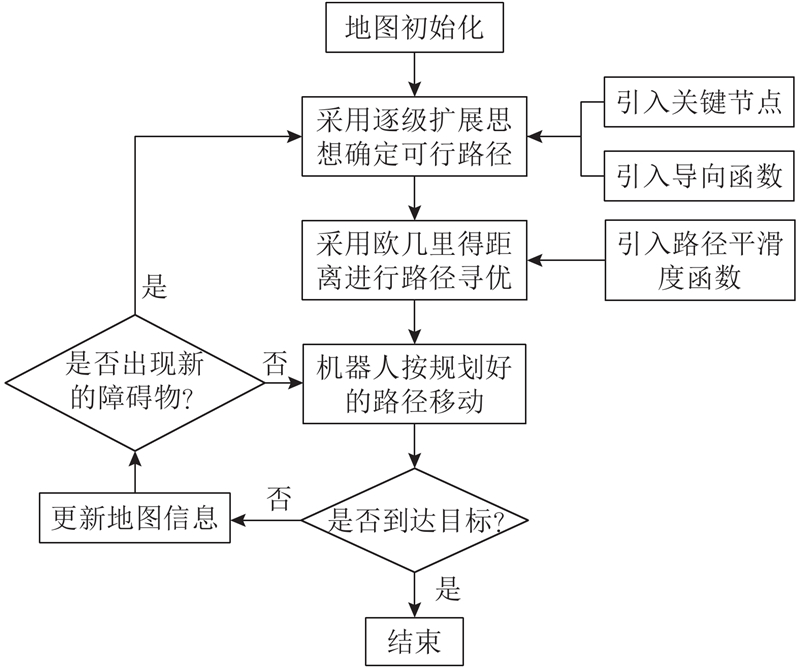
综上所述,本研究在D*算法的基础上提出有向D*动态规划算法,该算法首先结合目标点位置及已知障碍物信息确定关键节点,并结合导向函数,通过逐级扩展搜索的方式确定可行路径;在欧几里得评价指标的基础之上,通过引入平滑度函数对可行路径进行寻优,主要系统结构如图2所示.
图 2
2.2. 可行路径确定
D* 算法在初始路径规划时使用类似等势线逐级扩展的方式,会遍历较多不必要节点,导致D*算法搜索空间较大. 为了缩小搜索空间,提出以下技术改进措施.
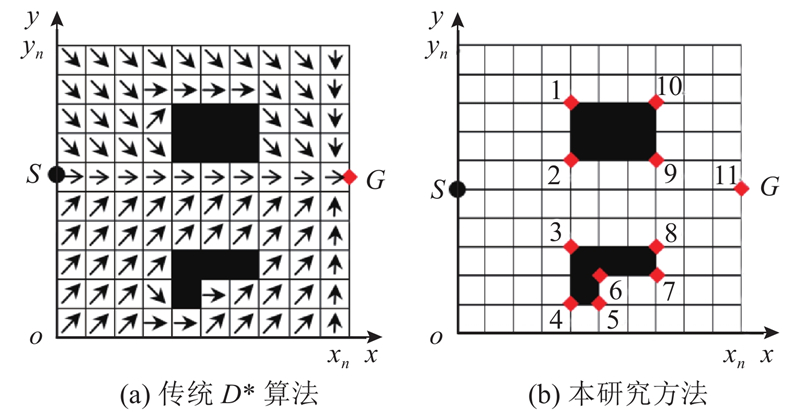
1)改进搜索方式. 对节点进行区分,将障碍物近似为四边形,以其4个顶点作为关键节点,主要针对关键节点进行搜索、筛选,并从初始点开始由前往后通过由父节点逐级确定子节点的方式确定可行路径. 采用逐级扩展的方式既能将每一个关键节点访问到,同时可以避免对不必要的关键节点进行路径成本计算,以提高规划效率.
图 3
图 3 传统D*算法与本研究算法的搜索方法对比
Fig.3 Searching method comparison between traditional D* algorithm and proposed algorithm
2)关键节点筛选. 传统D*算法由目标点开始反向采用类似等势线逐级扩展的方式确定可行路径;本研究从出发点开始,对于关键节点采用由父节点逐级确定子节点的方式,通过引入导向函数
式中:
上述2种处理方式优点如下. 1)可以较好地缩小搜索空间、减小计算机数据的运算量,提高搜索效率;2)在工程实践中,障碍物位置区域一般仅为地图的小部分区域,从总体上看搜索空间相对有限,所提出的四边形的障碍物建模方式简化了搜索过程且降低了关键节点的搜索数量;3)可以通过平滑度函数控制寻优方向,能较好地兼顾局部搜索与规划路径的系统整体最优性,避免一般D*及传统路径动态规划算法易产生冗余路径的问题.
2.3. 路径寻优
传统D*算法在对可行路径进行寻优时,未考虑移动机器人在运动中躲避障碍物时可能出现多次无效转弯的问题,导致规划路径非全局最优,增加移动时间成本. 针对该问题,本研究在欧几里得距离评价基础上引入平滑度函数对规划路径偏离理想路径(理想路径即初始点与目标点的连线)的程度进行惩罚,筛选出每一次扩展时偏移程度相对较小的路径,从而最大限度避免移动机器人的无效转弯. 建立成本函数如下:
式中:
定义路径平滑度惩罚函数如下:
式中:
2.3.1. 平滑度函数 $f\left( {{\theta _i}} \right)$
考虑到环境的复杂程度会随着地图的增大而变化,对不同大小的环境应采取分段处理方式,结合实践建议分段方式如下:对于小尺寸地图(小于
路径夹角θ取值范围为(0, 2π),根据第
另外,考虑到不同路径因具有相同距离成本而无法判定最优关键节点的情况,须对
1)相似关键节点的位置. 考虑障碍物四边形的建模方式,可以认为障碍物的顶点均在网格交点(即路径节点)处,则路径位置为正方形对角线、栅格边、长方形对角线3种情况. 当路径位置为正方形对角线时,由于
2)不同路径之间的区分度. 不同的
表 1 z=15、25、50时不同分段情况下事件A发生k次的概率
Tab.1
| k | z=15 | z=25 | z=50 | |||||||||||
| b=4 | b=6 | b=8 | b=10 | b=4 | b=6 | b=8 | b=10 | b=4 | b=6 | b=8 | b=10 | |||
| 3 | 1.8×10−1 | 9.3×10−2 | 5.1×10−2 | 3.1×10−2 | 2.4×10−1 | 2.0×10−1 | 1.4×10−1 | 9.3×10−2 | 7.2×10−2 | 1.9×10−1 | 2.3×10−1 | 2.2×10−1 | ||
| 6 | 5.7×10−3 | 7.7×10−4 | 1.7×10−4 | 4.9×10−5 | 5.4×10−2 | 1.1×10−2 | 3.1×10−3 | 1.0×10−3 | 1.7×10−1 | 1.2×10−1 | 5.5×10−2 | 2.6×10−2 | ||
| 9 | 1.7×10−5 | 5.8×10−7 | 4.9×10−8 | 7.2×10−9 | 1.8×10−3 | 9.8×10−5 | 1.1×10−5 | 1.8×10−6 | 7.8×10−2 | 1.4×10−2 | 2.6×10−3 | 6.0×10−4 | ||
| 12 | 4.4×10−9 | 3.9×10−11 | 1.3×10−12 | 9.5×10−14 | 1.3×10−5 | 1.9×10−7 | 8.0×10−9 | 6.5×10−10 | 1.1×10−2 | 5.0×10−4 | 3.7×10−5 | 4.2×10−6 | ||
综上所述,对于小尺寸地图、中等尺寸地图,
2.3.2. 平滑度函数 $f\left( {{\theta _i}} \right)$
平滑度函数
表 2 关键节点平均距离与环境维数的关系
Tab.2
| ES | NE | NO | NK | DK |
| 502 | 2.5×103 | 1.5×103 | 3.0×102 | 8 |
| 1002 | 1.0×104 | 6.0×103 | 1.2×103 | 8 |
| 5002 | 2.5×105 | 1.5×105 | 3.0×104 | 8 |
| 1 0002 | 1.0×106 | 6.0×105 | 1.2×105 | 8 |
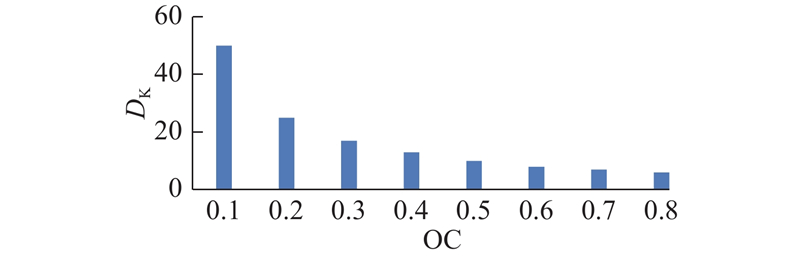
2)当环境大小一定,障碍物覆盖面积不同时,对2个关键节点距离进行多次测试、计算,结果如图4所示. 当障碍物覆盖率为10%时,两关键节点间平均距离最大;当障碍物覆盖率为80%时,两关键节点间平均距离最小. 可以看出,两关键节点间平均距离随碍物覆盖率的增加而减小.
图 4
图 4 平均距离与障碍物覆盖率的关系
Fig.4 Relationship between average distance and obstacle coverage rate
综上所述,
2.4. 移动机器人路径规划实现
机器人路径规划的具体实现过程如下. 将地图初始化筛选出关键节点,定义OPEN列表存放关键节点;CLOSED列表存放父节点;DELETE列表存放每次迭代中除子节点以外的关键节点. 在初始路径规划时通过导向函数
在算法过程中,通过导向函数
移动机器人按初始路径的关键节点序列
Function: INITIAL PATH
1 sort by the value of h(Xi,Yi) in OPEN
2 while ~is empty(OPEN) && t(X)~= G
3 if correct point
4 calculation h(Xi,Yi)
5 find hmin (Xi,Yi)
6 if t (X )~=hmin (Xi,Yi) && xYi≤xXi && yYi≤yXi
7 t(X)=DELETE
8 else if t (X)=hmin (Xi,Yi)
9 t (X)=CLOSED
10 starting from t(X)
11 else
12 t (X)=OPEN
13 end
14 else
15 t (X)=OPEN
16 end
17 end
2.5. 有向D*算法收敛性证明
若要证明算法收敛,只须证明每次扩展后得到的新的父节点横/纵坐标与目标点横/纵坐标的差值均趋于减小. 令
证明:
令
在第
在第
根据算法的搜索策略,只要存在离目标更近的关键节点,则一定有
因此,当单次迭代的搜索空间剩余状态数趋近于零时,有
综上所述,算法具有收敛性.
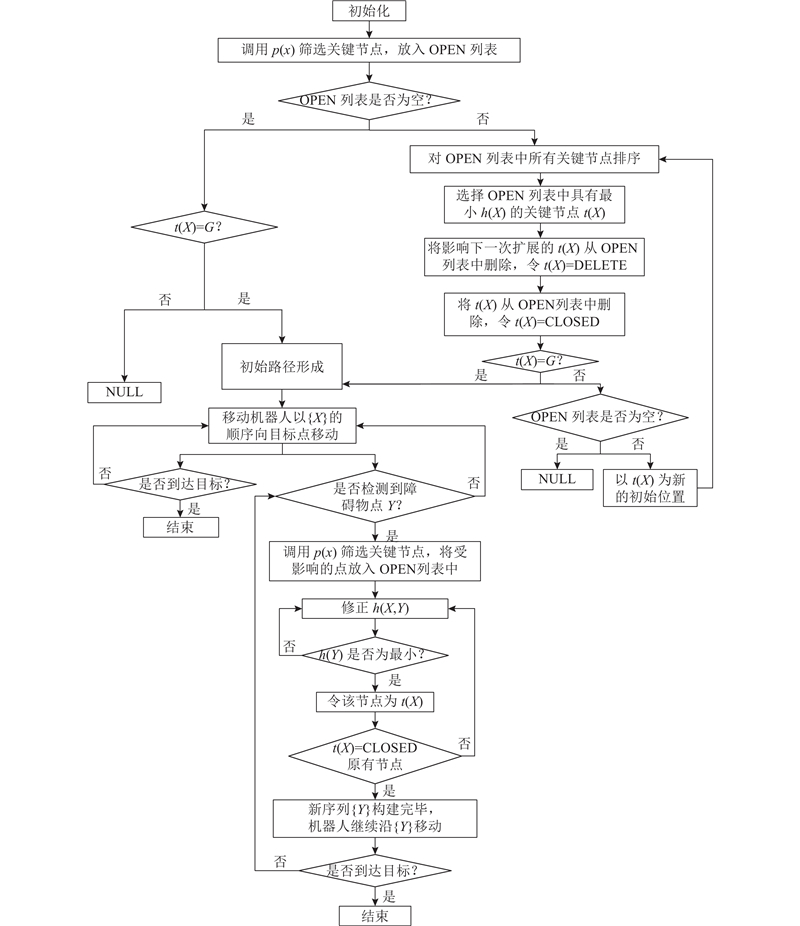
2.6. 算法流程
1)初始化栅格地图,设置起点、终点以及障碍物. 2)依据地图中的障碍物位置信息选取关键节点. 3)所有关键节点分为3组:CLOSED列表、OPEN列表、DELETE列表. 4)通过导向函数
图 5
3. 实验结果与分析
3.1. 仿真环境和测试对象
仿真环境如下:Intel(R)Core(TM)i3-3240 CPU &3.40 GHz双核处理器、Win7旗舰版32位系统以及MATLAB 2010a软件.
表 3 不同复杂程度的环境参数
Tab.3
| 环境 | 起始节点 | 目标节点 |
| 502 | (1, 1) | (50, 50) |
| 1002 | (1, 1) | (100, 100) |
| 5002 | (1, 1) | (500, 500) |
图 6
图 6 不同复杂程度的环境示意图
Fig.6 Environment diagrams with varying degrees of complexity
3.2. 实验结果与分析
如表4所示,从路径距离方面对实验结果进行分析. 可以看出,在
表 4 不同环境下路径长度对比
Tab.4
| ES | 有向D* | D* Lite | Focussed D* |
| 502 | 72.06 | 77.09 | 75.24 |
| 1002 | 155.28 | 161.49 | 158.78 |
| 5002 | 828.62 | 860.72 | 1 134.80 |
如表5所示,从路径规划时间角度对实验结果进行分析. 可以看出,在
表 5 不同环境下路径规划时间对比
Tab.5
| 算法 | ES=502 | ES=1002 | ES=5002 | |||
| O(T) | F(T) | O(T) | F(T) | O(T) | F(T) | |
| 有向D* | 14.56 | 0.65 | 55.70 | 1.12 | 113.50 | 18.90 |
| D* Lite | 14.02 | 2.14 | 50.70 | 10.46 | 114.34 | 764.20 |
| Focussed D* | 17.29 | 2.67 | 65.01 | 14.41 | 150.88 | 860.41 |
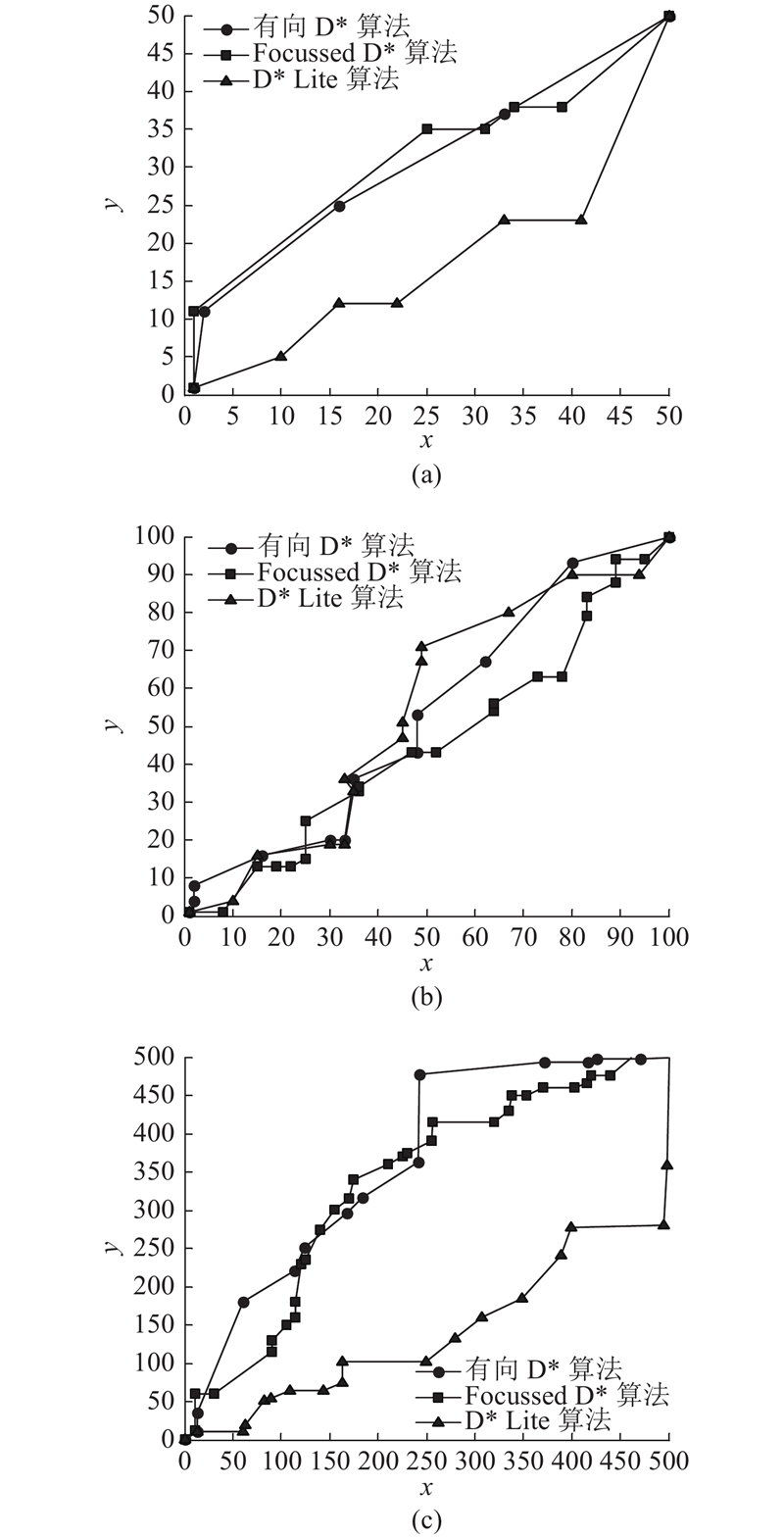
如图7(a)~(c)所示为不同环境下相关算法所规划的路径,其拐点数量如表6所示. 如图7(a)所示,当地图面积较小、障碍物数量较少时,由于Focussed D*算法在规划路径时仅使用欧几里得评价指标,规划的路径平滑度不高;D* Lite算法主要在缩小搜索范围方面进行了改进,因此路径平滑度与Focussed D*算法基本持平;本研究所提出的有向D*算法的平滑度明显优于前2种算法. 如图7(b)所示,当地图面积与障碍物等环境复杂程度相较于图7(a)而言都有一定程度的增加时,有向D*算法的路径拐点个数比D* Lite、Focussed D*算法分别减少23%、50%,可以有效减少机器人的在线移动时间. 如图7(c)所示,当环境面积、环境复杂程度相较于图7(b)均更高时,利用有向D*算法规划的路径在拐点数量上比D* Lite、Focussed D*算法分别减少29%、52%,在平滑度方面的优势更加突出. 原因在于所提算法在选取子节点时引入路径平滑度函数
图 7
表 6 不同环境下拐点数目对比
Tab.6
| 算法 | 拐点数目 | ||
| ES=502 | ES=1002 | ES=5002 | |
| 有向D* | 3 | 10 | 12 |
| D* Lite | 5 | 13 | 17 |
| Focussed D* | 5 | 20 | 25 |
综上可知,随着环境地图的增大及障碍物的增加,有向D*算法相较于其他2种传统经典算法所规划的路径拐点数量更少、路径更短;离线规划时间及在线移动时间更少,并且可以在较小的迭代次数内获得最优解.
4. 结 语
本研究在D* 算法的基础上提出有向D*算法. 该算法通过引入导向函数使路径规划具有一定的方向性,缩小搜索空间从而减少离线规划时间;引入路径平滑度函数,在考虑路径长度的同时考虑路径的平滑度,最大限度减少机器人在线移动时间,提高移动效率,保证算法的全局最优性. 仿真实验结果证明本研究算法的可行性与有效性,环境越复杂,本研究算法的规划效率、路径长度较其他传统算法的优势越明显. 该算法仍存在有待改进之处,例如,如何进一步提高路径的动态更新效率;在特殊环境下由父节点确定子节点时,仅比较第N、N−1代父节点与第N代子节点之间的路径长度,可能存在路径无效转弯导致达不到全局最优的问题,这也是下一阶段的研究工作.
参考文献
Multi-robot multi-target dynamic path planning using artificial bee colony and evolutionary programming in unknown environment
[J].DOI:10.1007/s11370-017-0244-7 [本文引用: 1]
Robot path planning based on Dijkstra’s algorithm and genetic algorithm
[J].
移动机器人路径规划算法综述
[J].
Overview of path planning algorithms for mobile robots
[J].
A formal basis for the heuristic determination of minimum cost paths
[J].DOI:10.1109/TSSC.1968.300136 [本文引用: 1]
Methodology for path planning and optimization of mobile robots: a review
[J].DOI:10.1016/j.procs.2018.07.018 [本文引用: 1]
移动机器人路径规划技术综述
[J].
Overview of path planning techniques for mobile robots
[J].
Real-time obstacle avoidance for manipulators and mobile robot
[J].DOI:10.1177/027836498600500106 [本文引用: 1]
Lifelong planning A*
[J].
Path planning in uncertain environment by using firefly algorithm
[J].DOI:10.1016/j.dt.2018.06.004 [本文引用: 1]
基于分层改进D~*算法的室内路径规划
[J].DOI:10.3969/j.issn.1001-3695.2015.12.018 [本文引用: 1]
Indoor path planning based on hierarchical improved D~* algorithm
[J].DOI:10.3969/j.issn.1001-3695.2015.12.018 [本文引用: 1]
Fast replanning for navigation in unknown terrain
[J].DOI:10.1109/TRO.2004.838026 [本文引用: 1]
Enhanced D* Lite algorithm for autonomous mobile robot
[J].