(12) ${{{x}}_{\rm{S}}} = {\left[ {{{\hat f}_{\rm{C}}}\,,\,{{\hat f}_{\rm{S}}}\,,\,\hat v_{\rm{s}},\,{{\hat f}_{\rm{V}}}\,,\,{{\hat f}_{\rm{P}}}} \right]^{\,{\rm{T}}}}.$
在利用模拟退火混合遗传算法进行参数辨识时,取种群规模 $W = 100$ $T = 500$ ${\rm{Pc}}{_1} = 0.9,\;{\rm{Pc}}{_2} = 0.6$ ${\rm{Pm}}{_1} = $ 0.1 , ${\rm{Pm}}{_2} = $ $ 0.001$ $k = 0.99$ ${f_{\rm{C}}} \in $ $ \left[ {5\;,\;20} \right]$ ${f_{\rm{S}}} \in \left[ {15\;,\;50} \right]$ ${f_{\rm{V}}} \in \left[ {10\;,\;40} \right]$ $v_{\rm{s}} \in \left[ {0.001\;,\;0.100} \right]$ ${f_{\rm{P}}} \!\in\! \left[ { - 1\;,\;1} \right]$ ${\dot q_{\rm{0}}}\! \in\! \left[ {0\;,\;0.1} \right]$ .
[1]
LEE S D, AHN K H, SONG J B. Torque control based sensorless hand guiding for direct robot teaching [C]// 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) . Daejeon: IEEE, 2016: 745-750.
[本文引用: 1]
[2]
LEE S D, KIM M C, SONG J B. Sensorless collision detection for safe human-robot collaboration [C]// 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) . Hamburg: IEEE, 2015: 2392-2397.
[本文引用: 1]
[3]
GROTJAHN M, DAEMI M, HEIMANN B Friction and rigid body identification of robot dynamics
[J]. International Journal of Solids and Structures , 2001 , 38 (10−13 ): 1889 - 1902
DOI:10.1016/S0020-7683(00)00141-4
[本文引用: 1]
[4]
HAMON P, GAUTIER M, GARREC P. Dynamic identification of robots with a dry friction model depending on load and velocity [C]// 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems . Taipei: IEEE, 2010: 6187-6193.
[本文引用: 1]
[5]
吴文祥, 朱世强, 王宣银, 等 基于摩擦模糊建模与补偿的机器人低速控制
[J]. 电机与控制学报 , 2013 , 17 (8 ): 70 - 77
URL
[本文引用: 1]
WU Wen-xiang, ZHU Shi-qiang, WANG Xuan-yin Slow motion control of serial robots with friction compensation based on fuzzy logic system
[J]. Electric Machines and Control , 2013 , 17 (8 ): 70 - 77
URL
[本文引用: 1]
[6]
IWASAWA S, OHISHI K, YOKOKURA Y, et al. Fine sensorless force control using Stribeck model for injection molding machine [C]// 10th France-Japan/8th Europe-Asia Congress on Mecatronics (MECATRONICS2014-Tokyo) . Tokyo: IEEE, 2014: 201-206.
[本文引用: 1]
[7]
KERMANI M R, PATEL R V, MOALLEM M Friction identification and compensation in robotic manipulators
[J]. IEEE Transactions on Instrumentation and Measurement , 2007 , 56 (6 ): 2346 - 2353
DOI:10.1109/TIM.2007.907957
[本文引用: 1]
[8]
HENSEN R, MOLENGRAFT M, STEINBUCH M Friction induced hunting limit cycles: a comparison between the LuGre and switch friction model
[J]. Automatica , 2003 , 39 (12 ): 2131 - 2137
DOI:10.1016/S0005-1098(03)00234-6
[本文引用: 1]
[9]
ARMSTRONG-HELOUVRY B. Control of machines with friction [M]. Berlin: Springer Science and Business Media, 2012.
[本文引用: 1]
[10]
MARTON L, LANTOS B Modeling, identification, and compensation of stick-slip friction
[J]. IEEE Transactions on Industrial Electronics , 2007 , 54 (1 ): 511 - 521
DOI:10.1109/TIE.2006.888804
[本文引用: 2]
[12]
KENNEDY C, DESAI J P Modeling and control of the Mitsubishi PA-10 robot arm harmonic drive system
[J]. IEEE-ASME Transactions on Mechatronics , 2005 , 10 (3 ): 263 - 274
DOI:10.1109/TMECH.2005.848290
[本文引用: 1]
[13]
孙洪鑫, 王修勇, 陈政清. 辩识LuGre摩擦模型参数的2种智能算法 [C]// 第五届全国电磁流变液及其应用学术会议. 大连: 大连理工大学电子音像出版社, 2008: 1-6.
[本文引用: 1]
SUN Hong-xin, WANG Xiu-yong, CHEN Zheng-qing. Two intelligent algorithms of LuGrefriction model for parameter identification [C]// The 5th National Conference on Electro-rheological Fluids and Magnetorheological Suspensions . Dalian: Electronic and Audiovisual Press of Dalian University of Technology, 2008: 1-6.
[本文引用: 1]
[14]
CRAI G, JOHN J. Introduction to Robotics: Mechanics and Control [M]. New York: Pearson Education, Inc, 1986.
[本文引用: 3]
[15]
KHALIL W, DOMBRE E. Modeling, identification and control of robots [M]. Oxford: Butterworth-Heinemann, 2004.
[本文引用: 1]
[16]
吴文祥, 朱世强, 靳兴来 基于改进傅里叶级数的机器人动力学参数辨识
[J]. 浙江大学学报: 工学版 , 2013 , 47 (2 ): 231 - 237
URL
[本文引用: 1]
WU Wen-xiang, ZHU Shi-qiang, JIN Xing-lai Dynamic identification for robot manipulators based on modified Fourier series
[J]. Journal of Zhejiang University: Engineering Science , 2013 , 47 (2 ): 231 - 237
URL
[本文引用: 1]
[17]
KHALIL W, GAUTIER M, LEMOINE P. Identification of the payload inertial parameters of industrial manipulators [C]// Proceedings 2007 IEEE International Conference on Robotics and Automation . Rome: IEEE, 2007: 4943-4948.
[本文引用: 1]
[18]
SOUSA C D, CORTESAO R Physical feasibility of robot base inertial parameter identification: a linear matrix inequality approach
[J]. The International Journal of Robotics Research , 2014 , 33 (6 ): 931 - 944
DOI:10.1177/0278364913514870
[本文引用: 1]
[19]
ARMSTRONG-HELOUVRY B. Stick-slip arising from Stribeck friction [C]// Proceedings, IEEE International Conference on Robotics and Automation . Cincinnati: IEEE, 1990: 1377-1382.
[本文引用: 1]
[20]
HONG H Research on the parameter identification of friction model for servo systems based on genetic algorithms
[J]. Systems Engineering and Electronics , 2003 , 2 (1 ): 1116 - 1120
[本文引用: 1]
[21]
SRINIVAS M, PATNAIK L M Adaptive probabilities of crossover and mutation in genetic algorithms
[J]. IEEE Transactions on Systems, Man, and Cybernetics , 1994 , 24 (4 ): 656 - 667
DOI:10.1109/21.286385
[本文引用: 1]
[22]
任子武, 伞冶 实数遗传算法的改进及性能研究
[J]. 电子学报 , 2007 , 35 (2 ): 269 - 274
URL
[本文引用: 1]
REN Zi-wu, SAN Ye Improvement of real-valued genetic and performance study
[J]. Acta Electronica Sinica , 2007 , 35 (2 ): 269 - 274
URL
[本文引用: 1]
[23]
METROPOLIS N, ROSENBLUTH A W, ROSENBLUTH M N, et al Equation of state calculations by fast computing machines
[J]. The Journal of Chemical Physics , 1953 , 21 (6 ): 1087 - 1092
DOI:10.1063/1.1699114
[本文引用: 1]
[24]
PEI D, QUIREIN J A, CORNISH B E, et al Velocity calibration for microseismic monitoring: a very fast simulated annealing (VFSA) approach for joint-objective optimization
[J]. Geophysics , 2009 , 74 (6 ): WCB47 - WCB55
DOI:10.1190/1.3238365
[本文引用: 1]
1
... 随着人们对机器人需求的不断上升,机器人的应用范围不断扩大,已广泛应用于打磨、抛光、装配等领域. 在手动示教、人机共存之类的操作中,人与机器人的工作空间重叠,对机器人的防碰撞具有更高的要求,在这些应用场景中,往往需要机器人的力感知能力. 通常有2种途径实现机器人的力感知,即增加力/力矩传感器或者直接通过检测机器人电机电流来感知机器人的外部力信息. 由于力/力矩传感器价格昂贵,研究人员通过检测电机电流而获得关节力矩,并利用机器人动力学方程得到机器人末端的受力情况. 机器人关节的运动是通过RV减速器或谐波减速器将伺服电机的运动传递到手臂的,由于减速器各个运动部件间存在摩擦,在机器人动力学方程的建立中须考虑关节传动的摩擦力. 因此,结合机器人关节摩擦模型,可以建立更加精确的机器人动力学模型,以提高机器人末端力感知的精度[1 -2 ] . ...
1
... 随着人们对机器人需求的不断上升,机器人的应用范围不断扩大,已广泛应用于打磨、抛光、装配等领域. 在手动示教、人机共存之类的操作中,人与机器人的工作空间重叠,对机器人的防碰撞具有更高的要求,在这些应用场景中,往往需要机器人的力感知能力. 通常有2种途径实现机器人的力感知,即增加力/力矩传感器或者直接通过检测机器人电机电流来感知机器人的外部力信息. 由于力/力矩传感器价格昂贵,研究人员通过检测电机电流而获得关节力矩,并利用机器人动力学方程得到机器人末端的受力情况. 机器人关节的运动是通过RV减速器或谐波减速器将伺服电机的运动传递到手臂的,由于减速器各个运动部件间存在摩擦,在机器人动力学方程的建立中须考虑关节传动的摩擦力. 因此,结合机器人关节摩擦模型,可以建立更加精确的机器人动力学模型,以提高机器人末端力感知的精度[1 -2 ] . ...
Friction and rigid body identification of robot dynamics
1
2001
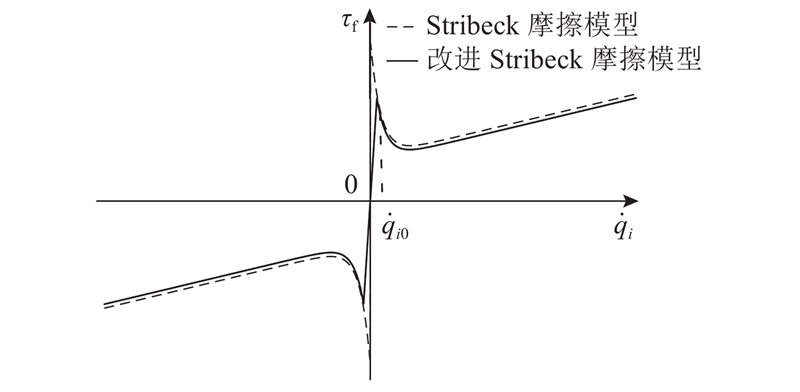
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
1
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
基于摩擦模糊建模与补偿的机器人低速控制
1
2013
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
基于摩擦模糊建模与补偿的机器人低速控制
1
2013
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
1
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
Friction identification and compensation in robotic manipulators
1
2007
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
Friction induced hunting limit cycles: a comparison between the LuGre and switch friction model
1
2003
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
1
... 由于机器人运动学方程存在非线性,关节的运动速度变化较大,如何将满足不同运动速度的较高精度的摩擦模型综合到动力学方程中是机器人推广应用的关键问题之一. 机器人关节减速器传动的摩擦模型有库伦+黏性摩擦、Stribeck摩擦和LuGre摩擦模型等. Grotjahn等[3 ] 在库伦+黏性摩擦模型的基础上,通过在关节低速的情况下引入反正切函数,克服机器人关节在转速为0时摩擦力矩不连续的缺点. Hamon等[4 -5 ] 通过对机器人进行摩擦测量实验时发现,外力作用会导致机器人关节内部零件接触面间作用力发生改变,进而影响摩擦力,故提出考虑负载力矩影响的扩展摩擦模型以描述关节摩擦特性. Iwasawa等[6 ] 考虑到在系统速度较低时摩擦力所产生的Stribeck效应,提出与Stribeck摩擦模型相结合的分段式摩擦模型,在某一速度阈值内采用特定函数实现摩擦力的连续性. Kermani等[7 ] 引入能够全面描述低速阶段摩擦力特性的LuGre摩擦模型,并基于两步法理论辨识出摩擦参数,以多自由度机器人为实验平台进行摩擦补偿实验,进一步改善了系统的轨迹跟踪性能. 虽然动态摩擦模型能够更全面、更精确地反映真实的摩擦力特性,具有更好的连续性,但静态摩擦模型在工程实践应用中的地位同样重要. 如Hensen等[8 ] 将加入零速区间的Stribeck摩擦模型和Lugre摩擦模型的实验结果进行对比分析,发现2种摩擦模型在系统中所引起的极限环振荡效果基本一致,而且有实验表明,好的静态摩擦模型能够以90%的精确程度近似拟合低速区域的真实摩擦力[9 ] . 同样,动态摩擦模型也会使模型结构变得复杂,包含参数变多,辨识难度也随之增加. 例如,Lugre摩擦模型引入了表示接触表面平均变形量的状态z ,而变量z 难以测量导致模型中的动态参数辨识变得困难. Stribeck摩擦模型作为静态摩擦模型的典型代表,能够较好地描述低速段摩擦力的变化趋势,且具有结构简单、适用性广的特点. 因此,本研究以Stribeck摩擦模型作为研究对象. ...
Modeling, identification, and compensation of stick-slip friction
2
2007
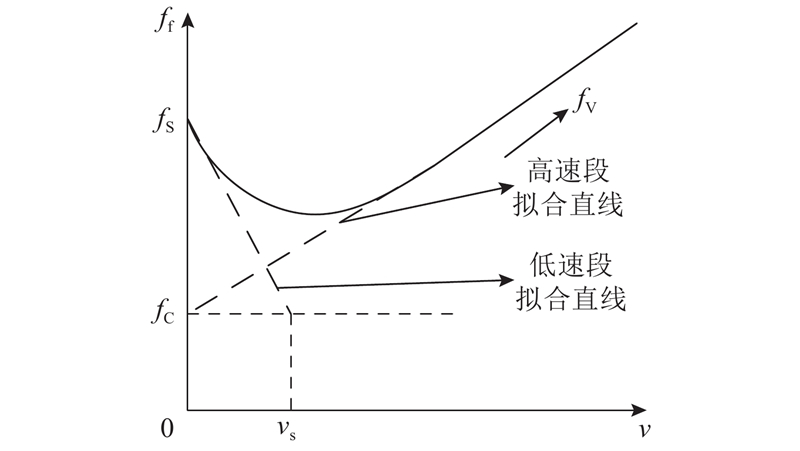
... 结合摩擦过程分析和数学模型,学者们针对Stribeck摩擦模型相继提出了多种辨识方法. 例如,Marton等[10 ] 将Stribeck摩擦模型进行泰勒展开,线性化处理为低速区和高速区2个分段,并根据摩擦力与稳态速度之间的关系对模型参数进行辨识. 然而,近似化处理在简化Stribeck效应的同时也降低了原始模型的准确性. Vakil等[11 ] 在给定的输入信号下,基于能量法则得到包含Stribeck模型参数的非线性优化目标函数,并采用最小二乘求根法辨识出摩擦参数. Kennedy等[12 ] 让机器人在速度控制模式下,采集关节在不同速度稳态所对应的摩擦力矩信息,得到速度-摩擦力矩之间的映射关系,再利用曲线拟合的方法计算出摩擦模型参数值. 然而,关节在有限的运动范围内保证稳态高速运动是困难的. 孙洪鑫等[13 ] 在建立理论的静力Stribeck曲线后,分别采用改进遗传算法和粒子群算法来辨识摩擦模型参数,并通过仿真实验验证了2种算法的可行性. ...
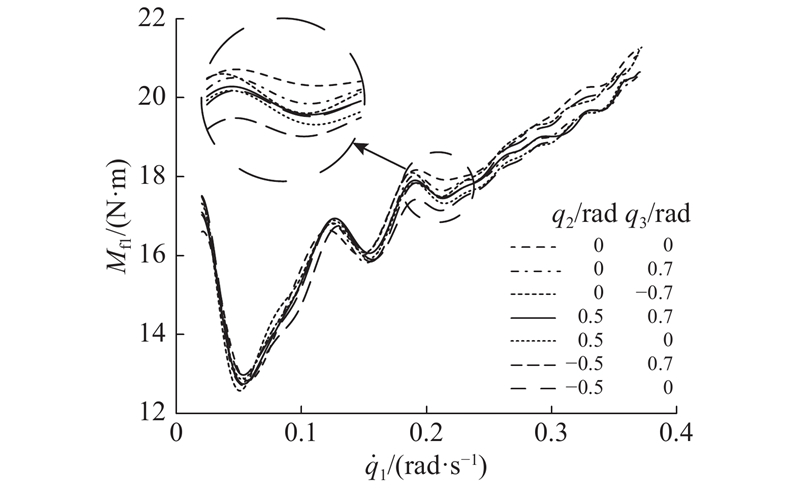
... 采用描图法[10 ] 对Stribeck曲线进行拟合的基本方法如图2 所示,高速段的拟合直线在纵轴上的截距为库伦摩擦系数 ${f_{\rm{C}}}$ ${f_{\rm{V}}}$ ${f_{\rm{S}}}$ ${f_{\rm{C}}}$ $v_{\rm{s}}$ ${f_{\rm{S}}}$ $v_{\rm{s}}$ ${f_{\rm{C}}}$ ${f_{\rm{V}}}$ . 为了更全面准确地辨识出摩擦参数,不能采用单一的余弦规律运动轨迹方案,故本研究采取高速余弦轨迹和低速余弦轨迹相结合的运动方案,利用混合遗传算法辨识改进的Stribeck关节摩擦模型参数. ...
Energy-based approach for friction identification of robotic joints
2
2011
... 结合摩擦过程分析和数学模型,学者们针对Stribeck摩擦模型相继提出了多种辨识方法. 例如,Marton等[10 ] 将Stribeck摩擦模型进行泰勒展开,线性化处理为低速区和高速区2个分段,并根据摩擦力与稳态速度之间的关系对模型参数进行辨识. 然而,近似化处理在简化Stribeck效应的同时也降低了原始模型的准确性. Vakil等[11 ] 在给定的输入信号下,基于能量法则得到包含Stribeck模型参数的非线性优化目标函数,并采用最小二乘求根法辨识出摩擦参数. Kennedy等[12 ] 让机器人在速度控制模式下,采集关节在不同速度稳态所对应的摩擦力矩信息,得到速度-摩擦力矩之间的映射关系,再利用曲线拟合的方法计算出摩擦模型参数值. 然而,关节在有限的运动范围内保证稳态高速运动是困难的. 孙洪鑫等[13 ] 在建立理论的静力Stribeck曲线后,分别采用改进遗传算法和粒子群算法来辨识摩擦模型参数,并通过仿真实验验证了2种算法的可行性. ...
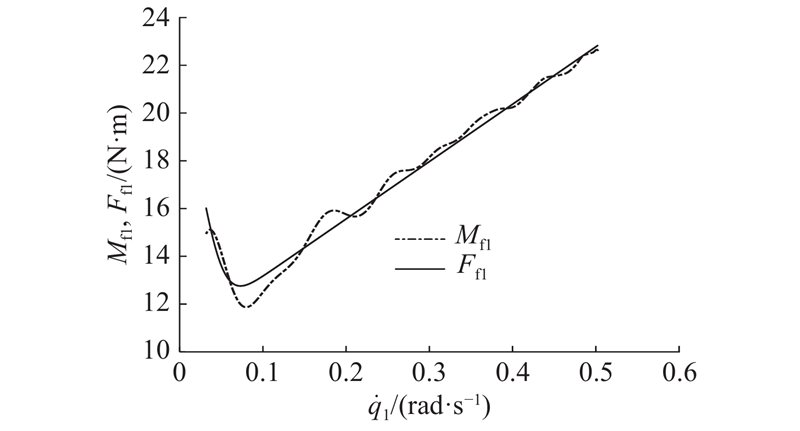
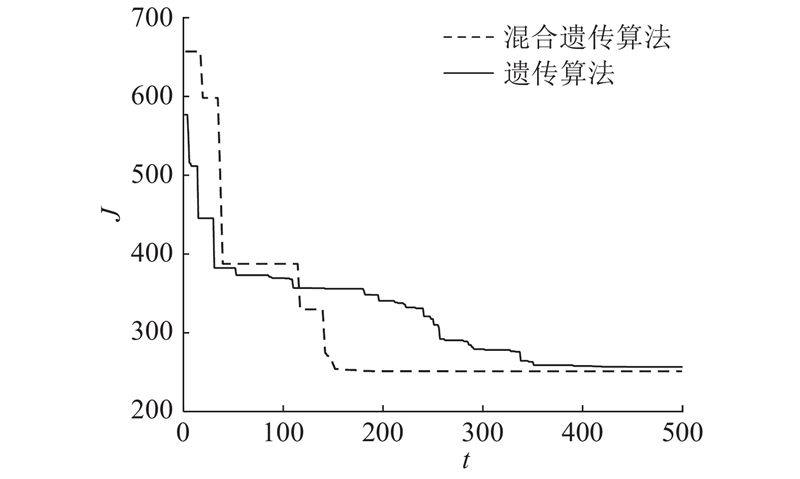
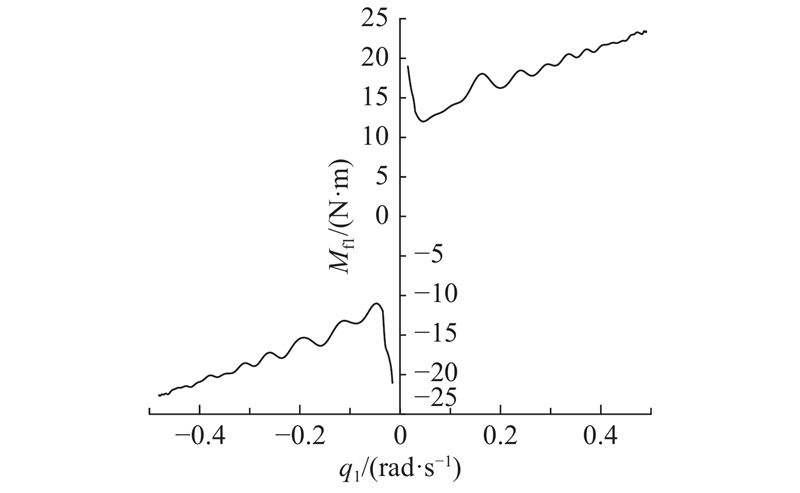
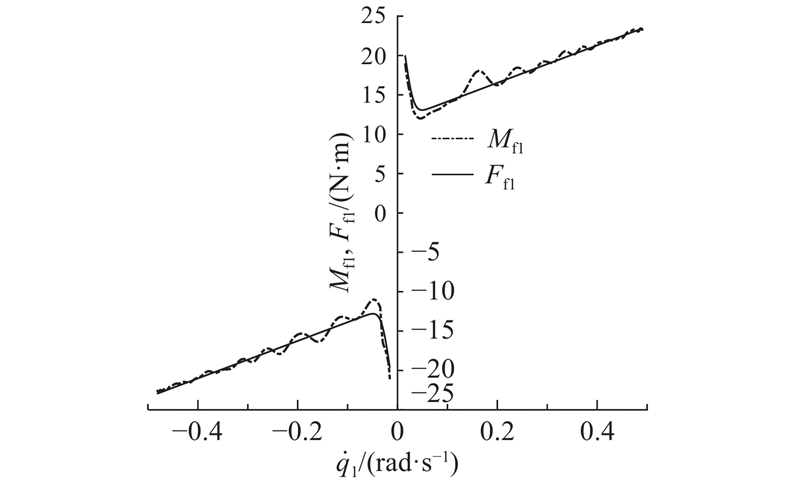
... 参照Vakil等[11 ] 提出的最小二乘求根法,依次求出所有的摩擦参数,再利用图描法得到各参数的预估值作为遗传算法和混合遗传算法的参数初值,并为辨识参数设定一个搜索范围,上述3种算法所得到的摩擦参数辨识结果如表1 所示. 可以看出,3种算法的辨识结果基本一致. 由此绘制的Stribeck拟合曲线如图7 所示. 图中,F f1 为关节1摩擦力矩的计算值. 可以看出,曲线拟合的结果与原始数据基本重合,说明上述算法对摩擦力矩的精确求解使得拟合的偏差较小,3种算法均能准确地对摩擦参数进行辨识. 如图8 所示为目标函数 $J$ 表2 所示,可以看出,选择混合遗传算法进行摩擦参数辨识为最佳方案. ...
Modeling and control of the Mitsubishi PA-10 robot arm harmonic drive system
1
2005
... 结合摩擦过程分析和数学模型,学者们针对Stribeck摩擦模型相继提出了多种辨识方法. 例如,Marton等[10 ] 将Stribeck摩擦模型进行泰勒展开,线性化处理为低速区和高速区2个分段,并根据摩擦力与稳态速度之间的关系对模型参数进行辨识. 然而,近似化处理在简化Stribeck效应的同时也降低了原始模型的准确性. Vakil等[11 ] 在给定的输入信号下,基于能量法则得到包含Stribeck模型参数的非线性优化目标函数,并采用最小二乘求根法辨识出摩擦参数. Kennedy等[12 ] 让机器人在速度控制模式下,采集关节在不同速度稳态所对应的摩擦力矩信息,得到速度-摩擦力矩之间的映射关系,再利用曲线拟合的方法计算出摩擦模型参数值. 然而,关节在有限的运动范围内保证稳态高速运动是困难的. 孙洪鑫等[13 ] 在建立理论的静力Stribeck曲线后,分别采用改进遗传算法和粒子群算法来辨识摩擦模型参数,并通过仿真实验验证了2种算法的可行性. ...
1
... 结合摩擦过程分析和数学模型,学者们针对Stribeck摩擦模型相继提出了多种辨识方法. 例如,Marton等[10 ] 将Stribeck摩擦模型进行泰勒展开,线性化处理为低速区和高速区2个分段,并根据摩擦力与稳态速度之间的关系对模型参数进行辨识. 然而,近似化处理在简化Stribeck效应的同时也降低了原始模型的准确性. Vakil等[11 ] 在给定的输入信号下,基于能量法则得到包含Stribeck模型参数的非线性优化目标函数,并采用最小二乘求根法辨识出摩擦参数. Kennedy等[12 ] 让机器人在速度控制模式下,采集关节在不同速度稳态所对应的摩擦力矩信息,得到速度-摩擦力矩之间的映射关系,再利用曲线拟合的方法计算出摩擦模型参数值. 然而,关节在有限的运动范围内保证稳态高速运动是困难的. 孙洪鑫等[13 ] 在建立理论的静力Stribeck曲线后,分别采用改进遗传算法和粒子群算法来辨识摩擦模型参数,并通过仿真实验验证了2种算法的可行性. ...
1
... 结合摩擦过程分析和数学模型,学者们针对Stribeck摩擦模型相继提出了多种辨识方法. 例如,Marton等[10 ] 将Stribeck摩擦模型进行泰勒展开,线性化处理为低速区和高速区2个分段,并根据摩擦力与稳态速度之间的关系对模型参数进行辨识. 然而,近似化处理在简化Stribeck效应的同时也降低了原始模型的准确性. Vakil等[11 ] 在给定的输入信号下,基于能量法则得到包含Stribeck模型参数的非线性优化目标函数,并采用最小二乘求根法辨识出摩擦参数. Kennedy等[12 ] 让机器人在速度控制模式下,采集关节在不同速度稳态所对应的摩擦力矩信息,得到速度-摩擦力矩之间的映射关系,再利用曲线拟合的方法计算出摩擦模型参数值. 然而,关节在有限的运动范围内保证稳态高速运动是困难的. 孙洪鑫等[13 ] 在建立理论的静力Stribeck曲线后,分别采用改进遗传算法和粒子群算法来辨识摩擦模型参数,并通过仿真实验验证了2种算法的可行性. ...
3
... 对于关节型机器人,其机器人动力学方程是关于机器人关节力矩、关节位置、关节角速度和关节角加速度之间的表达式[14 ] ,即 ...
... 考虑到机器人关节运动过程中摩擦力的影响,令关节摩擦力矩为 ${{{\tau }}_{\rm{f}}}$ [14 ] 表示为 ...
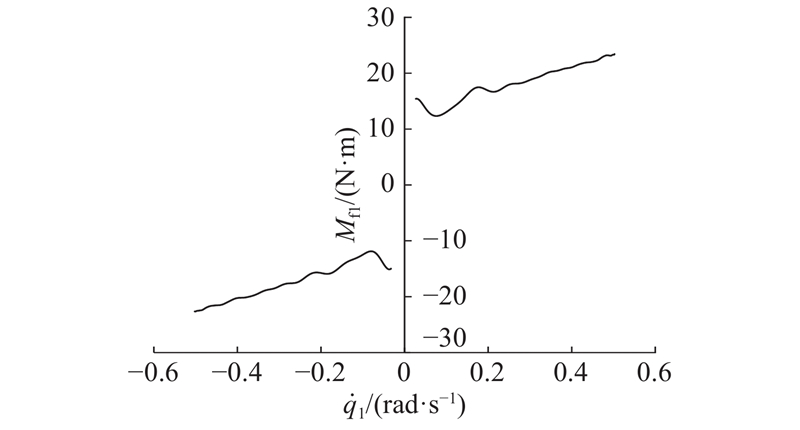
... 基于第1章所述方法计算得到机器人的动力学方程[14 ] 后,设计机器人第1关节的运动轨迹为 ${q_1} = 0.8\cos \;(0.2{\text{π}} t)$ $\left\{ {{{\dot q}_1}} \right\}_{j = 1}^N$ $\left\{ {{M_{{\rm{f1}}}}} \right\}_{j = 1}^N$ 图6 所示. ...
1
... 根据Khalil等[15 ] 的相关研究,可以将式(1)中机器人的未知参数定义为一组模型参数向量 ${{\beta }}$ ${{{H}}_{\rm{b}}}$ . 此时,可以将机器人动力学方程线性化表示为 ...
基于改进傅里叶级数的机器人动力学参数辨识
1
2013
... 采用优化后的周期性傅里叶级数作为激励轨迹[16 ] ,采集机器人在该轨迹下运动所得到的关节力矩信息,并对采样数据进行平均化及滤波处理. 通过加权最小二乘法[17 ] 和基于半正定规划(semidefinite programming, SDP)的物理可行性分析法[18 ] 相结合的辨识算法,可以得到机器人动力学方程的未知参数 ${{\beta }}$ . ...
基于改进傅里叶级数的机器人动力学参数辨识
1
2013
... 采用优化后的周期性傅里叶级数作为激励轨迹[16 ] ,采集机器人在该轨迹下运动所得到的关节力矩信息,并对采样数据进行平均化及滤波处理. 通过加权最小二乘法[17 ] 和基于半正定规划(semidefinite programming, SDP)的物理可行性分析法[18 ] 相结合的辨识算法,可以得到机器人动力学方程的未知参数 ${{\beta }}$ . ...
1
... 采用优化后的周期性傅里叶级数作为激励轨迹[16 ] ,采集机器人在该轨迹下运动所得到的关节力矩信息,并对采样数据进行平均化及滤波处理. 通过加权最小二乘法[17 ] 和基于半正定规划(semidefinite programming, SDP)的物理可行性分析法[18 ] 相结合的辨识算法,可以得到机器人动力学方程的未知参数 ${{\beta }}$ . ...
Physical feasibility of robot base inertial parameter identification: a linear matrix inequality approach
1
2014
... 采用优化后的周期性傅里叶级数作为激励轨迹[16 ] ,采集机器人在该轨迹下运动所得到的关节力矩信息,并对采样数据进行平均化及滤波处理. 通过加权最小二乘法[17 ] 和基于半正定规划(semidefinite programming, SDP)的物理可行性分析法[18 ] 相结合的辨识算法,可以得到机器人动力学方程的未知参数 ${{\beta }}$ . ...
1
... 式中:F 为摩擦力; $i$ $i=1,2,{\cdots},6$ ${\dot q_{{i}}}$ $i$ ${f_{\rm{C}}}$ ${f_{\rm{S}}}$ $v_{\rm{s}}$ $\gamma $ [19 ] , $\gamma = 2.0$ ${f_{\rm{V}}}$
Research on the parameter identification of friction model for servo systems based on genetic algorithms
1
2003
... 实验发现,机器人所测得的关节摩擦力矩相对于正、负速度并不是完全对称的,为了解决这个问题,Hong[20 ] 在伺服系统转动方向不同时采用2组不同的静态摩擦模型参数进行摩擦特性描述. 本研究考虑到模型的简便性和实用性,在Gauss指数模型中添加偏置参数 ${f_{\rm{P}}}$
Adaptive probabilities of crossover and mutation in genetic algorithms
1
1994
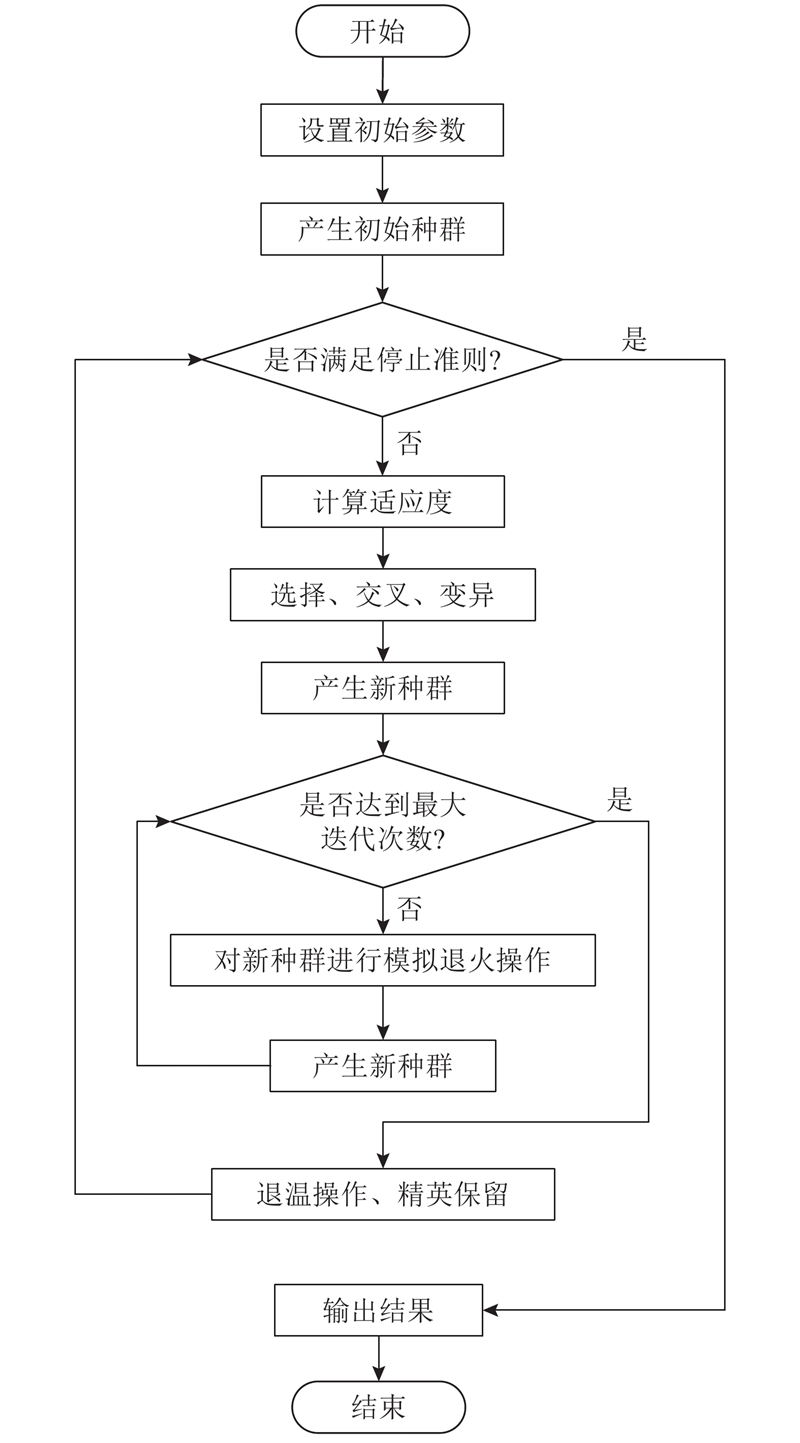
... 3)选择、交叉、变异操作. 选择操作采用轮盘赌算法,为了保证前期群体的多样性,交叉算子采用随代数增加而逐步减小的策略,而变异算子随着代数的增加呈上升趋势是为了避免进化后期群体太过单一的问题,故交叉、变异参数选择自适应参数[21 ] : ...
实数遗传算法的改进及性能研究
1
2007
... 变异方式采用单点变异,假设在个体 ${{{x}}_k}$ [22 ] 为 ...
实数遗传算法的改进及性能研究
1
2007
... 变异方式采用单点变异,假设在个体 ${{{x}}_k}$ [22 ] 为 ...
Equation of state calculations by fast computing machines
1
1953
... 4)模拟退火操作. 给予经遗传算法得到的较优解一定的扰动后得到新种群,而该新种群中的个体相对于扰动前群体中的个体在品质上有所差异,若新个体优于旧个体,则接受该新个体;若新个体劣于旧个体,则以特定的概率 ${{p}}$ [23 ] : ...
Velocity calibration for microseismic monitoring: a very fast simulated annealing (VFSA) approach for joint-objective optimization
1
2009
... 扰动方式采用Pei等[24 ] 提出的快速模拟退火(very fast simulated annealing,VFSA)算法: ...