动态融合蚁群算法与遗传算法的路径规划方法研究

doi:10.3785/j.issn.1006-754X.2025.05.143

动态融合蚁群算法与遗传算法的路径规划方法研究

车健波^,^,¹, 唐东林^,^,¹, 何媛媛¹^,², 胡远遥¹, 卢炳盛¹, 张俊辉¹

1.西南石油大学机电工程学院，四川成都 610500

2.四川省特种设备检验研究院，四川成都 610000

Research on path planning method based on dynamic fusion of ant colony optimization and genetic algorithm

CHE Jianbo^,^,¹, TANG Donglin^,^,¹, HE Yuanyuan¹^,², HU Yuanyao¹, LU Bingsheng¹, ZHANG Junhui¹

1.School of Mechanical and Electrical Engineering, Southwest Petroleum University, Chengdu 610500, China

2.Sichuan Special Equipment Inspection Institute, Chengdu 610000, China

通讯作者: 唐东林（1970—），男，教授，博士，从事无损检测、机器人技术和光机电一体化技术等研究，E-mail: tdl840451816@163.com，https://orcid.org/0000-0002-3922-1711

收稿日期: 2025-06-09 修回日期: 2025-07-08

基金资助:

四川省自然科学基金资助项目.  2024NSFSC2003
四川省市场监督管理总局科技项目.  SCSJS2024006
南充市-西南石油大学市校科技战略合作项目.  23XNSYSX0048
南充市-西南石油大学市校科技战略合作项目.  23XNSYSX0061

Received: 2025-06-09 Revised: 2025-07-08

作者简介 About authors

车健波（1996—），男，硕士生，从事机器人路径规划研究，E-mail:13540786343@163.com，https://orcid.org/0009-0003-8155-520X , E-mail：13540786343@163.com

摘要

结合蚁群算法（ant colony optimization, ACO）与遗传算法（genetic algorithm, GA）的传统路径规划方法普遍存在路径不平滑、收敛速度慢及能耗较高等问题。为解决上述问题，提出了一种动态融合ACO与GA（dynamic fusion of ACO and GA, DACO-GA）的路径规划方法，以提升路径规划的效率与精度。该方法初期采用ACO生成初始种群，并引入GA进行优化调整；在后续阶段，通过动态切换2种算法的主导角色，实现全局与局部搜索的协调互补。算法设计中融合了自适应信息素分布、动态挥发因子及自适应交叉/变异概率调节机制，有效提升了搜索能力并缓解了局部最优问题。最后，围绕DACO-GA中的关键控制参数开展优化实验，以验证各改进机制的有效性。在多个典型场景下将DACO-GA与传统算法进行对比，以进一步评估其在复杂环境下的适应性。结果表明，所提出的算法可生成更平滑且长度更短的路径，展现出良好的全局优化能力以及较快的收敛速度。DACO-GA不仅为复杂路径规划问题提供了有效的解决方案，还可为多智能体协作、机器人导航等领域的优化提供技术参考。

关键词： 路径规划 ; 动态融合 ; 蚁群算法 ; 遗传算法

Abstract

The traditional path planning algorithms that combine ant colony optimization (ACO) and genetic algorithm (GA) commonly suffer from unsmooth paths, slow convergence speed and high energy consumption. To address these issues, a path planning method based on dynamic fusion of ACO and GA (DACO-GA) is proposed to improve the efficiency and accuracy of path planning. In the initial stage, ACO was used to generate the initial population, and GA was introduced for optimization and adjustment. In later stages, the leading role of the two algorithms was dynamically switched, enabling coordinated complementarity between global and local search. The algorithm integrated adaptive pheromone distribution, dynamic evaporation factors and adaptive crossover/mutation probability adjustment mechanisms, which effectively enhanced search capability and mitigate the tendency to fall into local optima. Finally, optimization experiments were conducted on the key control parameters of the DACO-GA to validate the effectiveness of each improvement mechanism. The DACO-GA was compared with traditional algorithms across multiple typical scenarios to further evaluate its adaptability in complex environments. The results showed that the proposed algorithm could generate smoother and shorter paths, demonstrating strong global optimization ability and faster convergence speed. The DACO-GA not only provides an effective solution for complex path planning problems, but also offers technical references for the optimization in areas such as multi-agent cooperation and robot navigation.

Keywords： path planning ; dynamic fusion ; ant colony optimization ; genetic algorithm

PDF (4727KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

车健波, 唐东林, 何媛媛, 胡远遥, 卢炳盛, 张俊辉. 动态融合蚁群算法与遗传算法的路径规划方法研究[J]. 工程设计学报, 2025, 32(6): 789-802 doi:10.3785/j.issn.1006-754X.2025.05.143

CHE Jianbo, TANG Donglin, HE Yuanyuan, HU Yuanyao, LU Bingsheng, ZHANG Junhui. Research on path planning method based on dynamic fusion of ant colony optimization and genetic algorithm[J]. Chinese Journal of Engineering Design, 2025, 32(6): 789-802 doi:10.3785/j.issn.1006-754X.2025.05.143

路径规划算法可分为全局路径规划与局部路径规划两类^[1-2]。常见的全局路径规划算法包括Dijkstra算法^[3]、A*算法^[4]和快速扩展随机树（rapidly-exploring random tree, RRT）^[5]；常见的局部路径规划算法包括人工势场法（artificial potential field, APF）^[6]、动态窗口法（dynamic window approach, DWA）^[7]等。尽管这些算法在不同的应用场景中表现出独特的优势，但它们也存在一定的局限性^[8]。例如：全局路径规划算法能够解决复杂的路径规划问题并避免局部最优解，但通常需要较大的计算开销且收敛速度较慢^[9]；局部路径规划算法适用于已知初始解或问题规模较小的情况，其具有较高的计算效率和较快的收敛速度，但容易陷入局部最优^[10-11]。与此同时，许多受生物学原理启发的优化算法被广泛应用于路径规划。常见的启发式优化算法包括模拟退火（simulated annealing, SA）算法^[12]、粒子群优化（particle swarm optimization, PSO）算法^[13]、遗传算法（genetic algorithm, GA）^[14]和蚁群算法（ant colony optimization, ACO）^[15]等。

GA模仿自然选择和遗传过程，通过适应度评估和遗传操作（如交叉、变异）来不断优化路径^[16]。Ab-Wahab等人^[17]提出了一种改进的GA，用于解决低效的种群初始化以及低质量解问题；Chong等人^[18]提出了一种改进的自适应GA（improved adaptive GA, IAGA），提升了自主式水下航行器的导航精度。尽管GA能够有效解决复杂的全局优化问题，但仍存在实时性差和易陷入局部最优解的问题。相较于GA，ACO在动态环境中具有更强的适应性和鲁棒性，能够更好地处理路径规划等需要实时调整的任务^[19]。ACO是一种模拟蚂蚁觅食行为的优化算法，通过模拟蚂蚁寻找食物的路径选择和信息素传播机制，在解空间中寻找全局最优解^[20]。Huo等人^[21]使用B样条曲线对ACO所规划路径的平滑度进行了改进，使得路径既符合最大曲率限制，又减少了转弯次数，从而降低了能源消耗。虽然ACO具有较强的适应能力，但其仍存在收敛速度较慢、受参数的影响较大等缺陷。

为此，许多学者在处理复杂的路径规划问题时，尝试将不同的算法融合，以克服单一算法的局限性。Châari等人^[22]结合改进的ACO和GA，解决了移动机器人在静态环境中的全局路径规划问题；Niu等人^[23]针对AGV（automated guided vehicle，自动导引车）的路径规划问题，通过改进GA的种群初始化方法、交叉与变异操作以及引入路径平滑度约束，并与ACO相融合，有效地提高了算法的收敛速度和路径平滑度；Heng等人^[24]在探索自动驾驶车辆路径规划方法时，提出将ACO与GA相结合，有效地改善了最短路径的质量，但该混合算法在复杂场景下存在易陷入局部最优的问题。

为解决上述问题，本文提出了一种动态融合ACO与GA（dynamic fusion of ACO and GA, DACO-GA）的优化算法，通过对ACO、GA各自的核心机制及其融合方式进行协同改进，以提高算法的收敛速度和灵活性。同时，在静态环境与动态障碍物环境下对DACO-GA进行仿真实验，以验证其在移动机器人路径规划中的可行性与环境适应性。

1 环境模型与传统算法

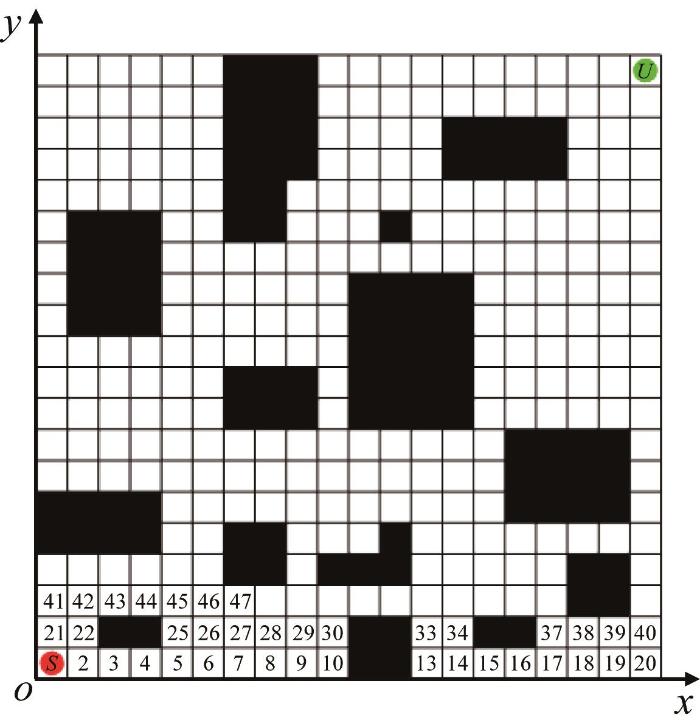
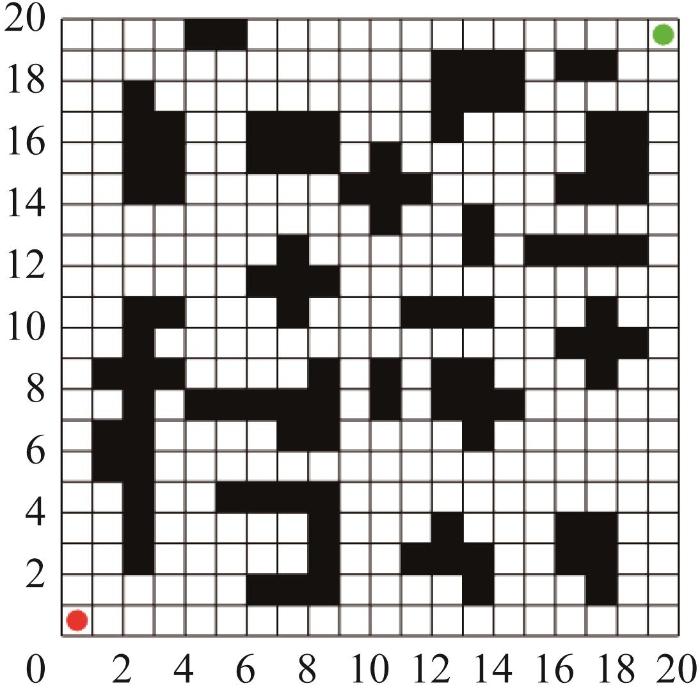
在构建环境模型时通常采用栅格地图。栅格地图由可移动网格和障碍网格组成。可移动网格通常用白色表示，在算法中对应的值为0；障碍网格用黑色表示，在算法中对应的值为1。同时，为每个网格分配一个唯一的序列号。如图1所示，在20×20的栅格地图中，起始点用S表示，目标点用U表示。序列号从起点开始，依次编号直至终点。具体地，第n个网格的坐标可表示为：

\{\begin{array}{l} x_{n} = m o d (n, R_{x}) - 0.5 \\ y_{n} = R_{y} + 0.5 - c e i l (n / R_{y}) \end{array}

式中： $(x_{n}, y_{n})$ 表示第n个网格的坐标； $m o d (n, R_{x})$ 表示余数函数，用于确定当前网格在x轴方向上的位置，并确保它在每个周期内重复； $R_{x}$ 和 $R_{y}$ 分别表示栅格地图的行数和列数； $c e i l (n / R_{y})$ 表示舍入函数，用于确定当前网格在y轴方向上的位置。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 栅格地图

Fig.1 Raster map

上述坐标映射方法能够确保网格在栅格地图中的排列顺序正确，从而实现从编号到二维坐标的有效映射。

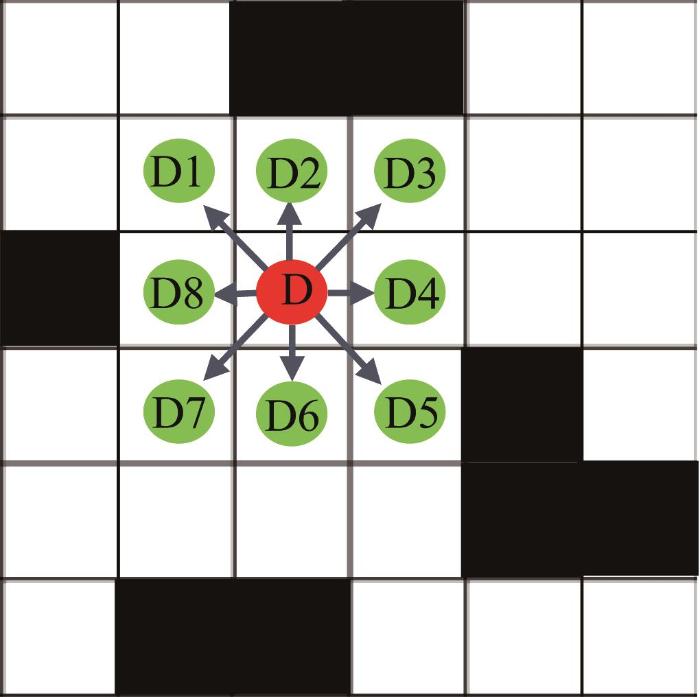
在栅格地图中，每一个网格有8个可移动的方向，移动方向用D1至D8表示，如图2所示。若网格周围有X个障碍或不可移动网格时，则可移动方向的数量为8-X。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 栅格可移动方向示意

Fig.2 Schematic of movable direction of raster

2 DACO-GA算法

2.1　改进初始信息素浓度

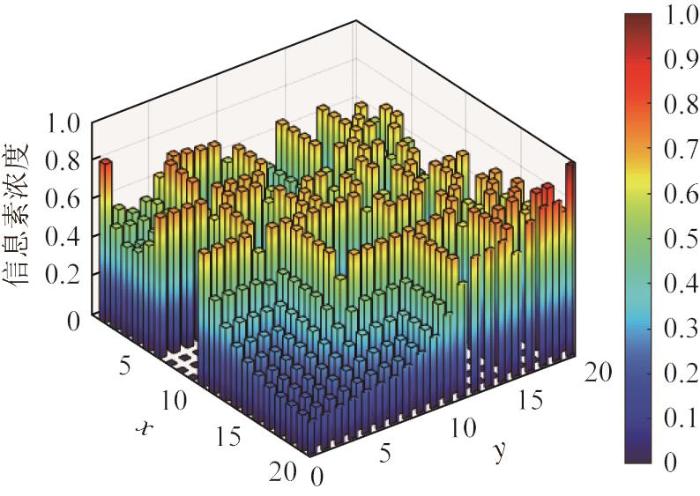
为了提高ACO的收敛速度和收敛效率，本文提出了一种动态的初始信息素分布策略，即将信息素浓度集中在距离起始点和目标点较近的节点上，以加快路径搜索的收敛速度。自适应初始信息素的分布效果如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 自适应初始信息素分布

Fig.3 Adaptive initial pheromone distribution

改进后初始信息素浓度的计算式如下：

τ_{i, j} (0) = \{\begin{array}{l} 0, & j 是障 碍物 \\ (γ \cdot \frac{1}{d_{S_{i}, j} + d_{j, U}}) \cdot τ_{0}, & 其他 \end{array}

(2)

式中： $τ_{i, j} (0)$ 表示节点 $j$ 在第 $i$ 行的初始信息素浓度；γ表示调节参数，用于控制距离对信息素浓度的影响程度，一般情况下γ的取值范围为[0, 1]； $τ_{0}$ 表示传统ACO中的初始信息素浓度，为恒定值； $d_{j, U}$ 表示节点 $j$ 到目标点U的欧式距离； $d_{S_{i}, j}$ 表示节点 $j$ 到当前行的起始点 $S_{i}$ 的欧式距离。

同时，为了避免算法陷入局部最优解，本文提出了逐行更新起始点的策略。在第2行及后续的每一行中，选择信息素浓度最高的节点作为新的起始点，并以此为基础，继续进行下一行的路径搜索。具体更新公式如下：

S_{i + 1} = a r g \underset{_{j \in {j_{1}, j_{2}, \dots, j_{k}}}}{m a x} τ_{i, j} (0)

(3)

式中： $S_{i + 1}$ 表示第 $i + 1$ 行的起始点，{ $j_{1}, j_{2}, \dots, j_{k}$ }表示第 $i$ 行所有非障碍物节点的集合。

通过选择信息素浓度最高的节点作为新的起始点，蚂蚁能够更有效地引导搜索过程，减少无效路径的探索，加速搜索过程并提高收敛速度。具体步骤如下：

1）在第2行及之后的每一行中，先计算该行所有非障碍物节点的初始信息素浓度 $τ_{i, j} (0)$ ，并根据新的初始信息素分配机制对所有节点的信息素浓度进行分配。

2）选择信息素浓度最高的节点作为新的起始点 $S_{i + 1}$ ，然后继续进行路径搜索。

3）重复上述操作，直到所有行的路径均搜索完毕。

2.2　引入动态挥发因子

在传统的ACO中，挥发因子通常设定为固定值。然而，固定的挥发因子无法适应搜索过程中不同阶段的需求：在初期需要较少的路径方向，以加快收敛速度；在后期需要增强全局搜索能力，以避免陷入局部最优。因此，本文提出了一种动态的挥发因子调整策略，并推导了随迭代次数动态变化的挥发因子计算公式，以更好地平衡局部搜索与全局搜索。在挥发因子的设定上，参考文献[25]中的方法。文献[25]指出：较小的挥发因子能够提高收敛速度，并使蚂蚁在早期搜索阶段具有较强的方向性，从而避免随机性的影响；较大的挥发因子能够增强全局搜索能力，防止陷入局部最优解。动态挥发因子的计算式如下：

ρ (t_{A} + 1) = ρ_{m i n} + (ρ_{m a x} - ρ_{m i n}) \cdot s i n^{2} (\frac{π}{2} \cdot \frac{t_{A}}{T_{A}})

(4)

式中： $ρ (t_{A} + 1)$ 表示第t_A+1次迭代后的挥发因子，t_A表示ACO的当前迭代次数，T_A表示ACO的最大迭代次数， $ρ_{m i n}$ 表示挥发因子的最小值， $ρ_{m a x}$ 表示挥发因子的最大值。

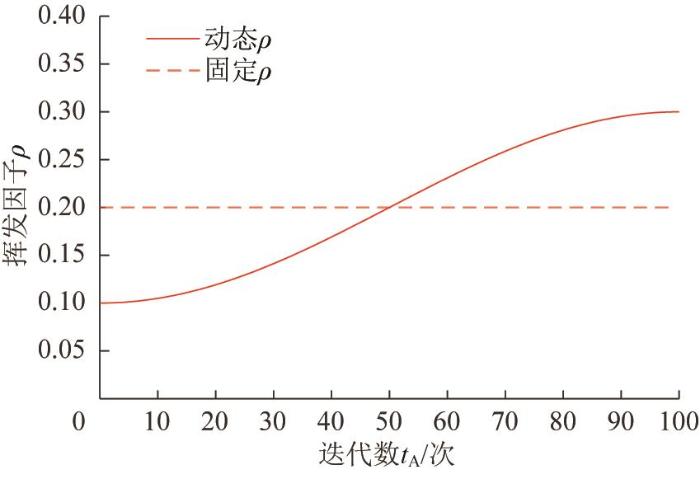
与传统的固定挥发因子相比，动态挥发因子能够根据算法迭代的不同阶段进行自适应调整，其随迭代次数的变化曲线如图4所示。其中，在动态挥发机制中，设定 $ρ_{m i n}$ =0.1，以有效防止迭代早期挥发率过低而导致信息素过度积累，从而引发路径过早收敛及收敛次数增加等问题；同时设定 $ρ_{m a x}$ =0.3，以避免迭代后期信息素挥发速度过快而造成陷入局部最优等问题。此外，在迭代过程中，动态挥发因子的变动较为平缓，可以避免突变性挥发所造成的路径信息丢失。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 动态挥发因子的变化曲线

Fig.4 Variation curve of dynamic volatilization factor

为避免陷入局部最优，ACO在每轮迭代中保留当前最优路径并用于下一轮迭代，从而确保关键路径信息的持续保留。此外，在后续的算法融合阶段，通过路径多样性判定机制动态切换主导算法，也能进一步修正前期路径选择所造成的易陷入局部最优的问题。

2.3　引入自适应交叉概率和变异概率

在GA中，固定的交叉概率P_c和变异概率P_m难以兼顾搜索效率与稳定性，易导致算法陷入局部最优，限制其全局优化能力。因此，本文采用自适应的交叉概率和变异概率，以提升GA的全局搜索能力。自适应的交叉概率和变异概率可分别表示为：

P_{c} (t_{G}) = P_{c, m a x} \cdot e^{- \frac{t_{G}}{T_{G}^{K c}}}

(5)

P_{m} (t_{G}) = P_{m, m a x} \cdot e^{- |\frac{t_{G} - T_{G} / 2}{T_{G} / (4 K_{m})}|}

(6)

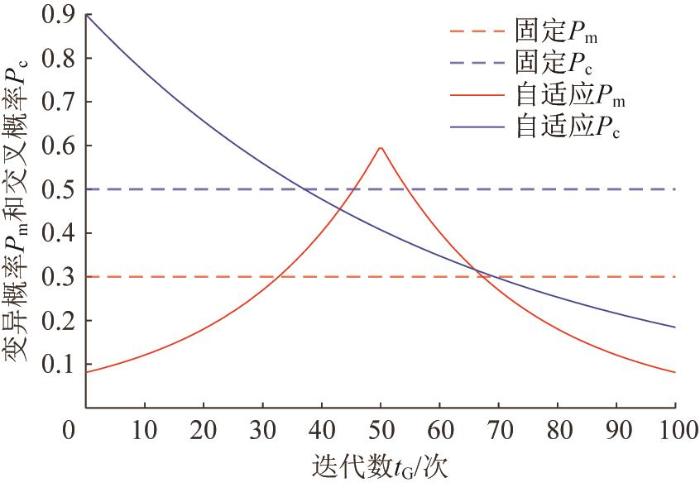
式中： $P_{c} (t_{G})$ 表示第t_G代的交叉概率， $P_{m} (t_{G})$ 表示第t_G代的变异概率， $P_{c, m a x}$ 表示交叉概率的最大值， $P_{m, m a x} 表示$ 变异概率的最大值，t_G表示GA的当前迭代次数，T_G表示GA的最大迭代次数， $K_{c}$ 表示交叉概率的调节系数， $K_{m}$ 表示变异概率的调节系数。针对 $K_{c}$ 以及 $K_{m}$ 的设定，本文取 $K_{c}$ =0.8， $K_{m}$ =0.9。

自适应交叉概率和变异概率的变化曲线如图5所示。由图5可知，在迭代早期，交叉概率P_c设为较大值，变异概率P_m设为较小值，这样可有效增强算法的全局搜索能力，避免其过早地陷入局部最优，从而降低优良个体被破坏的概率；在迭代中期，P_c逐渐减小到中等水平，以保持算法在中期也具有全局探索能力，P_m逐渐增大并达到最大值，以增加中期的种群多样性，从而跳出局部最优；在迭代后期，P_c和P_m进一步降低，减少了随机干扰，提高了收敛精度。但是，P_c与P_m的值不宜过大，故本文设置了取值上限。通过P_c与P_m的自适应调整，可以有效地解决GA易陷入局部最优的问题。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 自适应交叉概率和变异概率的变化曲线

Fig.5 Variation curves of adaptive crossover probability and mutation probability

2.4　增加删除算法

为了减少迭代过程中生成的冗余节点和无效路径对路径规划复杂度的影响，设计了一种删除算法，用于识别并剔除无效路径，提高融合算法的整体收敛效率和路径规划质量。

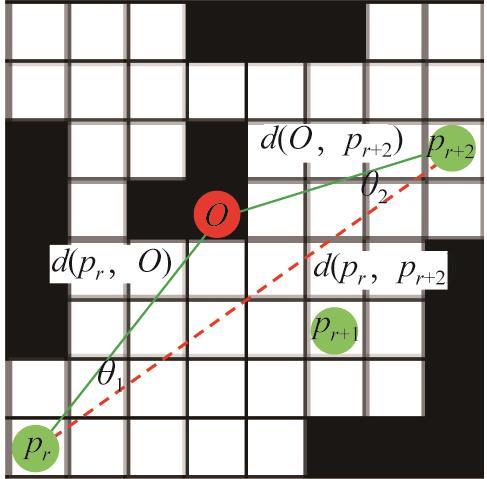
删除算法的原理如图6所示。在路径规划过程中，路径节点集合 $P = \{p_{1}, p_{2}, \dots, p_{N}\}$ 由N个连续节点构成，每2个相邻节点 $p_{r}$ 和 $p_{r + 1}$ 共同定义一段路径。为了判断路径段是否与障碍物发生碰撞，引入了一个判定公式，基于路径段与障碍物的最短距离 $d_{l i n e}$ 来识别冗余节点：若 $d_{l i n e}$ 大于设定阈值 $ϵ$ （通常为一个栅格斜对角线长度的一半），则认为该路径段与障碍物未发生碰撞，需删除对应的路径节点，更新路径节点集合为 $P^{'} 。$

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 删除算法原理

Fig.6 Principle of deletion algorithm

为了精确计算路径段（以节点 $p_{r}$ 与 $p_{r + 2}$ 组成的路径为例）与障碍物之间的最短距离 $d_{l i n e}$ ，首先要计算路径节点 $p_{r}$ 与 $p_{r + 2}$ 之间的欧式距离，并结合各路径节点与障碍物 $O$ 之间的欧式距离来计算。路径节点 $p_{r}$ 与 $p_{r + 2}$ 之间的欧式距离计算式如下：

d (p_{r}, p_{r + 2}) = \sqrt[]{(x_{r} - x_{r + 2})^{2} + (y_{r} - y_{r + 2})^{2}}

(7)

式中：(x_r, y_r )和(x_r₊₂, y_r₊₂)分别表示路径节点 $p_{r}$ 和 $p_{r + 2}$ 的坐标。

接着，基于余弦定理计算角度 $θ_{1}$ 和 $θ_{2}$ 。其中： $θ_{1}$ 表示障碍物 $O$ 、路径节点 $p_{r}$ 和路径节点 $p_{r + 2}$ 形成的角度； $θ_{2}$ 表示障碍物 $O$ 、路径节点 $p_{r + 2} 和路径节点 p_{r}$ 形成的角度。选择角度 $θ_{1}$ 和 $θ_{2}$ 中的较大角度 $θ$ 来判断路径段是否与障碍物碰撞。根据角度 $θ$ 的大小，最短距离d_line分为2种情况：

1）当 $θ < 90 °$ 时，使用三角形面积 $A$ 来计算路径段与障碍物的最短距离d_line：

d_{l i n e} = \frac{2 A}{d (p_{r}, p_{r + 2})}

(8)

式中： $A$ 表示由海伦公式计算得到的三角形面积，即路径节点 $p_{r}$ 、障碍物 $O$ 和路径节点 $p_{r + 2}$ 所构成的三角形的面积。

2）当 $θ \geq 90 °$ 时，根据各路径节点到障碍物的欧式距离来确定最短距离d_line：

d_{l i n e} = m i n (d (p_{r}, O), d (O, p_{r + 2}))

(9)

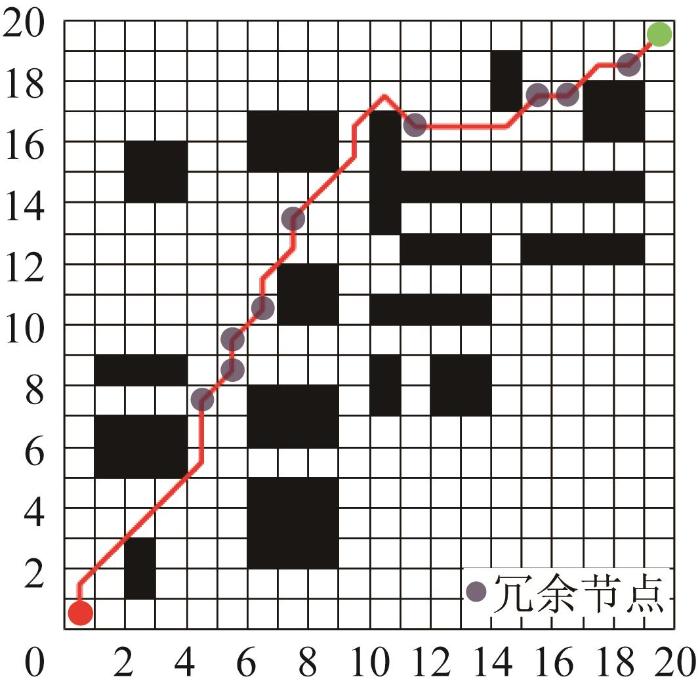
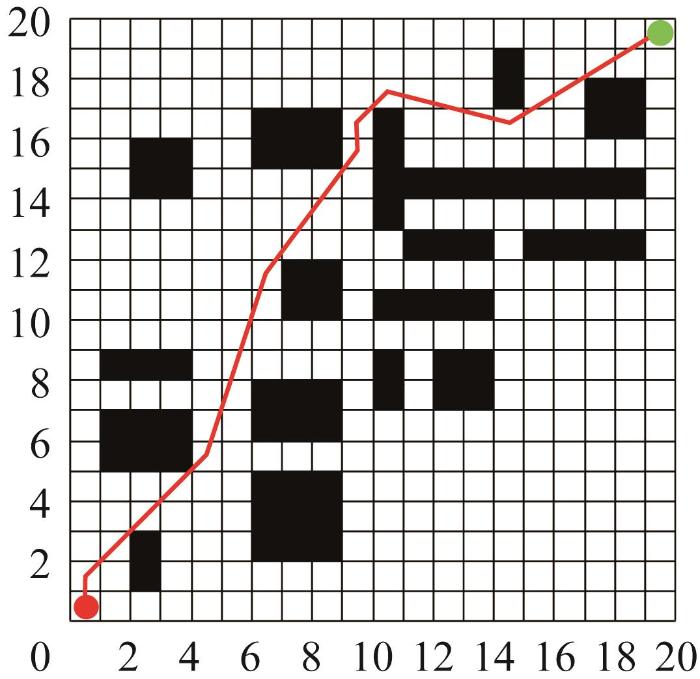
如图7所示，在应用删除算法之前，路径中包含较多冗余节点；在经删除算法处理后，冗余节点显著减少，如图8所示。由此可知，所提出的删除算法能够有效减少无效路径的数量，降低计算复杂度，并优化路径规划过程中的资源分配和时间成本。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 使用删除算法前的路径规划结果

Fig.7 Path planning result before using deletion algorithm

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 使用删除算法后的路径规划结果

Fig.8 Path planning result after using deletion algorithm

2.5　算法融合

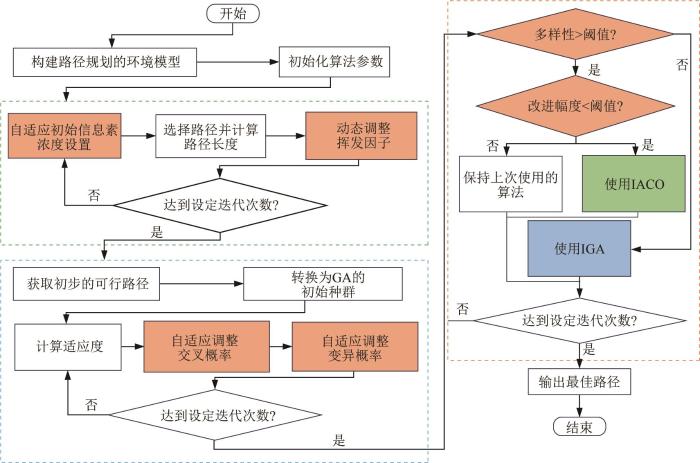
传统的单一优化算法受限于局部最优解，而简单的融合方式无法充分发挥不同优化算法的互补优势，导致融合算法的灵活性和动态调整能力较差。传统的融合算法常常通过固定的阶段划分，将不同算法分开执行，在优化过程中易出现效率低下的问题。例如：GA的初期种群质量不高，可能会影响ACO后续的搜索质量。为此，本文提出了DACO-GA算法。该算法通过动态调整ACO与GA的主导角色，可根据实际优化过程动态选用ACO或GA，从而发挥2种算法的优势并弥补各自的不足。

DACO-GA的具体流程如下：首先，在迭代初期，使用改进后的ACO（improved ACO, IACO）快速生成一批初步可行的路径。然后，为进一步提升路径的质量，使用改进后的GA（improved GA, IGA）来增强路径的多样性并提高算法的全局搜索能力。最后，进入融合阶段，设定一个多样性阈值作为判断标准，通过比较输出路径的多样性与设定阈值，决定主导算法。路径多样性计算式如下：

D_{i} = \frac{Q_{p}}{m T_{A}}

(10)

式中：D_i表示路径多样性；Q_p表示路径的去重数，即唯一路径的数量； $m$ 表示蚁群规模。

若多样性不超过多样性阈值，则说明路径的多样性较差，可能会导致次优解出现，故以GA为主导算法，通过交叉和变异操作扩大搜索范围，以提高路径的多样性。若多样性超过多样性阈值，则计算当前路径的改进幅度，并与改进幅度阈值进行比较：若改进幅度小于改进幅度阈值，则以ACO为主导算法，利用信息素更新路径选择的概率，以增强局部搜索能力；反之，则说明路径正在快速收敛，继续使用上一次的优化算法。同时，为了避免最优路径在ACO的操作中被破坏，在每次通过动态机制判断后，用当前迭代的最优路径替换下一次迭代的最差路径。此外，在动态融合阶段的每一次迭代中，均实时计算路径的多样性，并根据结果动态调整主导算法，以实现对路径的针对性优化。

还需要注意的是，由于是将ACO阶段生成的路径作为GA的初始输入，GA的自适应交叉函数在优化初期设有较高的交叉概率，这有助于提升种群的全局搜索能力和解的多样性，从而跳出ACO初始搜索可能导致的局部最优解。与此同时，当路径长度在优化过程中出现快速收敛趋势时，DACO-GA可通过动态判断机制自动切换主导优化方式，以增强整体搜索过程的灵活性与适应性，从而进一步提升算法的全局寻优能力。综上，DACO-GA算法的流程如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 DACO-GA算法流程

Fig.9 DACO-GA algorithm flow

2.6　DACO-GA参数优化

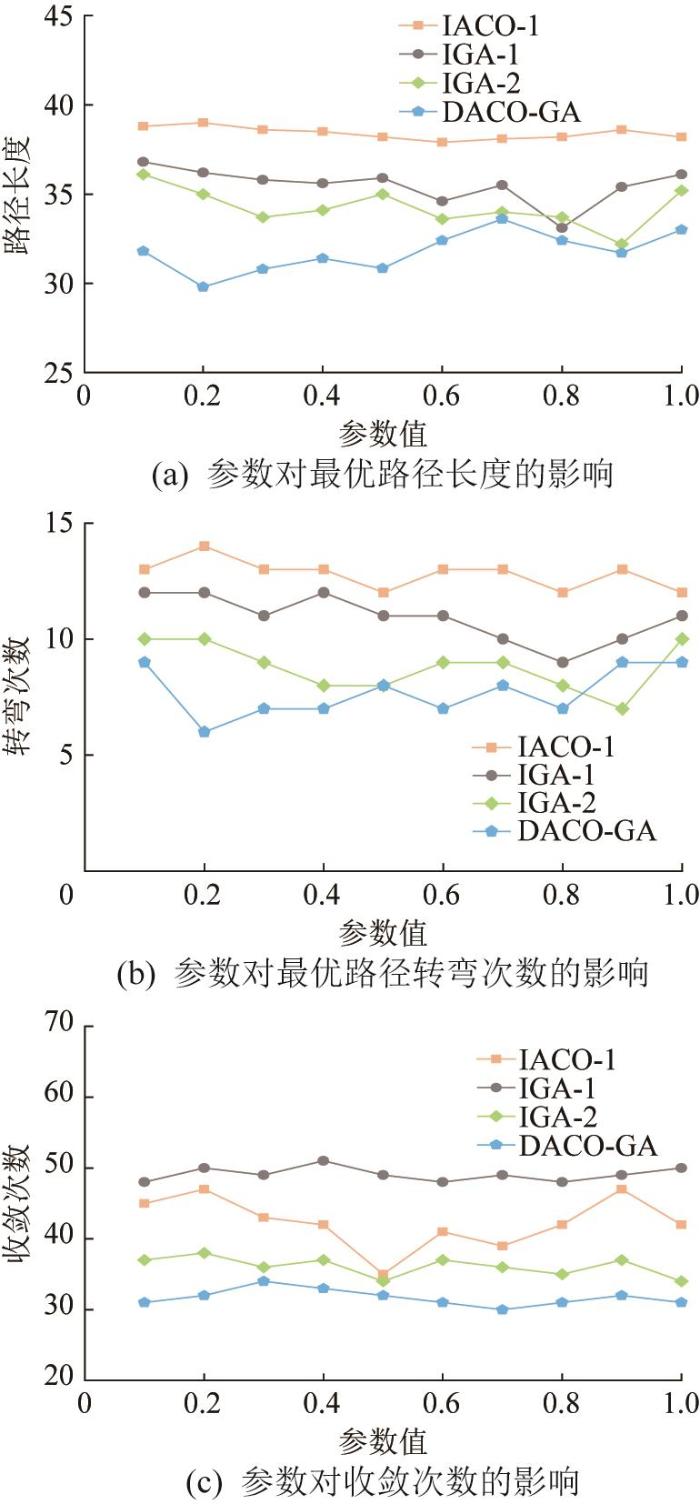
优化算法的参数对其性能有显著影响，但现阶段仍缺乏完善的理论分析方法来确定算法参数的最优值。为了得到DACO-GA的最优参数，对初始信息素浓度的调节参数γ、自适应交叉概率的调节系数 $K_{c}$ 、自适应变异概率的调节系数 $K_{m}$ 以及改进幅度阈值进行了一系列的优化实验。为方便后续对比，将改进初始信息素浓度的ACO称为IACO-1，将改进初始信息素浓度和挥发因子的ACO称为IACO-2；将改进交叉概率的GA称为IGA-1，将改进交叉概率和变异概率的GA称为IGA-2。为避免参数之间相互影响，在每次实验时只改变其中一个参数，其他参数设为常量。同时，为了保证公平性，每改变一个参数时均进行10次实验，并选择优化效果最好的实验结果进行后续比较。参数优化实验用栅格地图如图10所示，其他实验参数如表1所示。其中：α为ACO中的信息素重要度，β为信息重要度因子，T_CH为算法后期融合阶段的最大迭代次数；各变量的间隔设置为0.1。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 参数优化用栅格地图

Fig.10 Raster map for parameter optimization

表1 DACO-GA的参数取值

Table 1 Parameter values of DACO-GA

算法	ACO阶段								GA阶段					融合阶段
算法	$T_{A}$	$m$	α	β	γ	$τ_{0}$	$ρ_{m i n}$	$ρ_{m a x}$	$T_{G}$	$P_{c, m a x}$	$P_{m, m a x}$	$K_{c}$	$K_{m}$	$T_{C H}$	多样性阈值	改进幅度阈值
IACO-1	10	50	6	2	0~1	1	0.1	0.3
IGA-1									10	0.8	0.2	0~1	0.8
IGA-2									10	0.8	0.2	0.9	0~1
DACO-GA	10	50	6	2	0.5	1	0.1	0.3	10	0.8	0.2	0.9	0.8	80	0~1	0.01

新窗口打开| 下载CSV

各参数对算法路径规划性能的影响如图11所示。由图11(a)与图11(b)可知，当交叉概率调节系数 $K_{c}$ 与变异概率调节系数 $K_{m}$ 较大时，最优路径的长度和转弯次数均得到有效改善，但当其数值过大时，反而会导致路径质量降低。当 $K_{c}$ =0.8， $K_{m}$ =0.9时，基于IGA-1生成的最优路径长度为33.1，基于IGA-2生成的最优路径长度为32.2，同时可以得到交叉概率与变异概率同时改进相较于仅改进交叉概率具有更强的全局优化效果；由图11(c)可知， $K_{c}$ 与 $K_{m}$ 对收敛次数的影响较小，而初始信息素浓度调节系数γ对收敛次数的影响显著，尤其是当γ=0.5时，改进初始信息素分布时算法的性能提升最大。综上，DACO-GA综合了上述所有改进策略，可实现路径规划整体性能的最优提升。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 DACO-GA参数对路径规划性能的影响

Fig.11 Influence of DACO-GA parameters on path planning performance

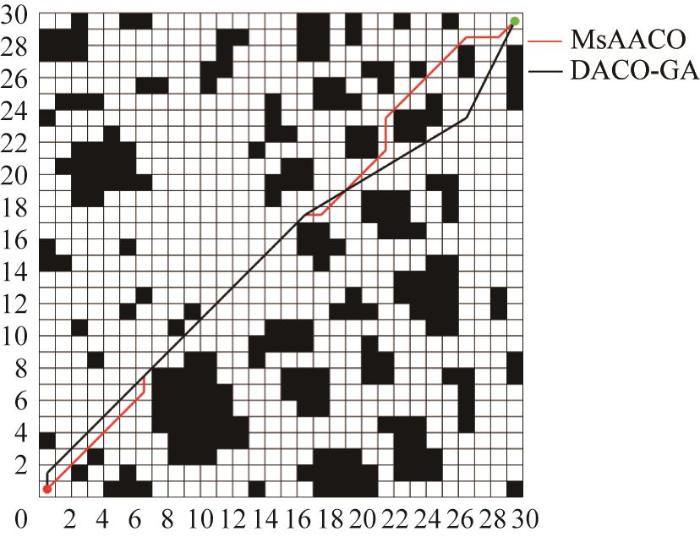
为进一步验证各参数设置的普适性，构建了一个结构更为复杂的栅格地图（30×30），地图设计参考文献[25]。在该场景下，对本文所提出的DACO-GA与文献[25]提出的MsAACO（multi-strategy adaptable ant colony optimization，多策略可适应蚁群算法）的性能进行对比。为了考察最优路径的平滑性，引入平滑度s：

s = \frac{1}{1 + \sum_{h = 1}^{H} (θ_{h} π / 180 °)}

(11)

式中： $θ_{h}$ 表示路径中第 $h$ 次转弯的角度， $H$ 表示路径中的转弯次数。

通过平滑度可以对路径的转弯次数及转弯角度进行综合评判。平滑度的最大值为1，此时的路径为一条直线，没有转弯。

在30×30的栅格地图中，基于DACO-GA与MsAACO生成的最优路径如图12所示。由图12可知，MsAACO在该栅格地图中生成的最优路径长度为42.769，转弯次数为9次，路径平滑度为0.137 3；而DACO-GA生成的最优路径长度为41.997，转弯次数减少至3次，路径平滑度提升至0.385 1，整体路径质量明显优于对比算法。结果表明，通过优化实验确定的参数值在复杂环境下具有普适性，且在不同复杂环境下均能保持良好的稳定性，未出现显著的性能波动，说明所选参数值具备较强的通用性。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 基于DACO-GA与MsAACO的最优路径对比

Fig.12 Comparison of optimal paths based on DACO-GA and MsAACO

3 路径规划仿真实验与结果分析

为了验证DACO-GA在移动机器人路径规划中的有效性，本文开展了多组仿真实验，涵盖不同方面的性能评估。第1组实验主要关注5种改进机制的效果，通过比较这些改进机制在路径规划中的表现，验证各改进机制对算法整体性能的影响。第2组实验重点评估DACO-GA在4种不同静态环境下的适应性，以测试该算法在不同条件下的通用性和可扩展性，从而确保其在多种环境下均能有效运行。在第2组实验中，将DACO-GA与经典的路径规划算法（Dijkstra算法、A*算法和PSO算法）进行对比，以全面评估DACO-GA在路径规划中的实用性和高效性。第3组实验测试了DACO-GA在动态障碍物环境中的路径规划性能，以进一步验证该算法对复杂环境的适应能力和鲁棒性。

由于各优化算法在路径规划中存在不确定性，即同一算法在多次运行时可能会产生不同的解，为确保实验结果的稳定性，每组实验中各算法均重复运行15次，并选取对应的最优路径进行对比分析。

所有实验均使用MATLAB R2020a软件进行仿真，在配置为英特尔酷睿i5-13400、CPU@4.6 GHz、8 GB RAM的Windows 11计算机上运行。

3.1　改进机制的性能实验

为系统评估各项改进机制对路径规划算法性能的影响，并探究对应参数之间可能存在的相互作用，采用逐步引入改进机制的方法进行分组实验。具体而言，在基准算法的基础上，每次引入一个新的改进机制，并与前一版本的算法进行对比，以评估新增改进机制对算法路径规划性能的优化效果。同时，将DACO-GA与文献[24]中的MACOGA（modified ACO and GA）进行对比，以综合验证各改进机制的有效性及其结合效果。本实验中的仿真地图与文献[24]一致，如图13所示。其中：起始点S用红点表示，坐标为（0.5, 0.5），位于地图的左下角；目标点U用绿点表示，坐标为（29.5, 29.5），位于地图的右上角。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 用于改进机制对比的栅格地图

Fig.13 Raster map for improving mechanism comparison

3.1.1　ACO及其变体实验

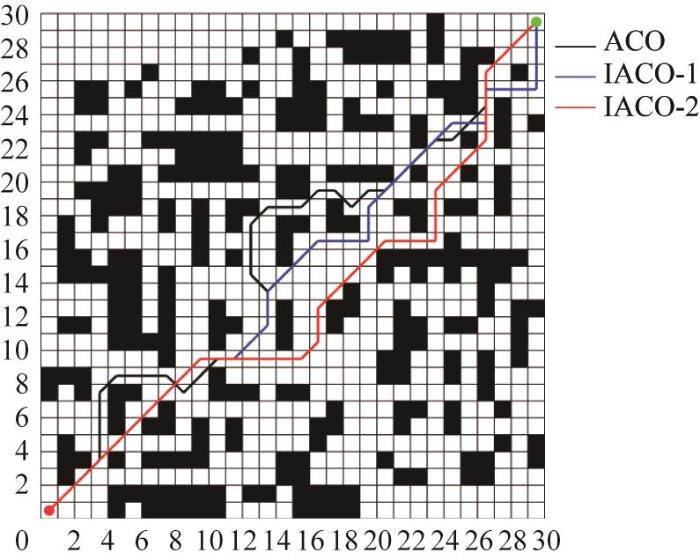
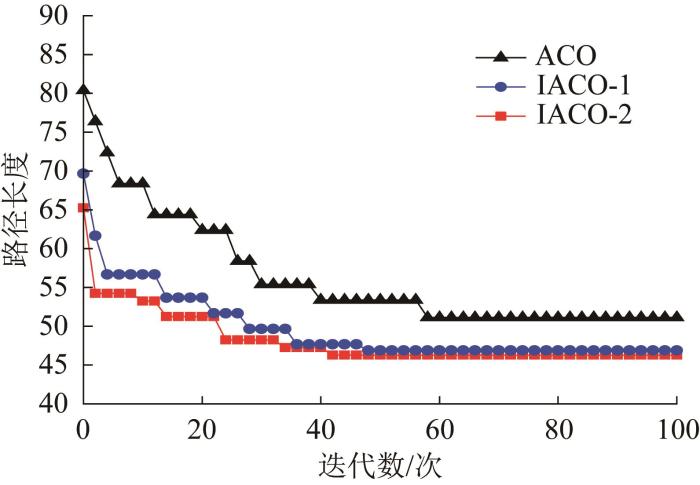
将传统ACO与改进后的ACO（IACO-1和IACO-2）进行对比，以验证其改进的有效性和优越性。基于ACO、IACO-1和IACO-2的最优路径对比如图14所示，各算法的迭代曲线如图15所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 基于ACO、IACO-1和IACO-2的最优路径对比

Fig.14 Comparison of optimal paths based on ACO, IACO-1 and IACO-2

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 ACO、IACO-1和IACO-2的迭代曲线对比

Fig.15 Comparison of iterative curves of ACO, IACO-1 and IACO-2

根据图14和图15，得到ACO、IACO-1和IACO-2的路径规划性能指标，如表2所示。结果表明，基于传统ACO的最优路径长度为51.113，转弯次数为22，平均路径长度为55.275。相比之下，改善了初始信息素浓度的IACO-1所生成的最优路径的长度缩短至46.870，转弯次数减少至11，平均路径长度缩短至50.154。结合图15所示的迭代曲线可知，改进初始信息素浓度显著提高了ACO的收敛速度，且有效提升了算法全局搜索最优路径的能力。通过进一步比较IACO-2与IACO-1，发现IACO-2在所有性能指标上均优于IACO-1，这表明改进初始信息素浓度和引入动态挥发因子有效地提高了ACO的性能，并验证了这2种改进机制的协同效应。

表2 ACO、IACO-1和IACO-2的路径规划性能对比

Table 2 Comparison of path planning performance of ACO, IACO-1 and IACO-2

性能指标	ACO	IACO-1	IACO-2
最优路径长度	51.113	46.870	46.284
平均路径长度	55.275	50.154	49.384
最优路径转弯次数	22	11	9
收敛次数	58	48	42

新窗口打开| 下载CSV

3.1.2　GA及其变体实验

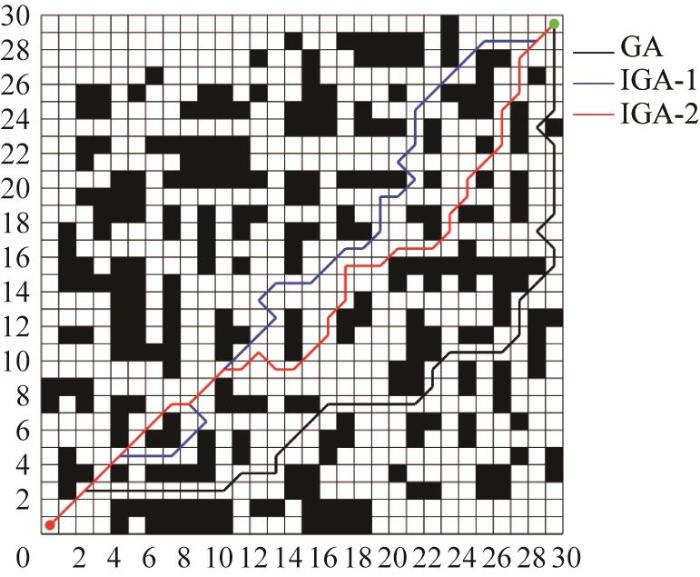
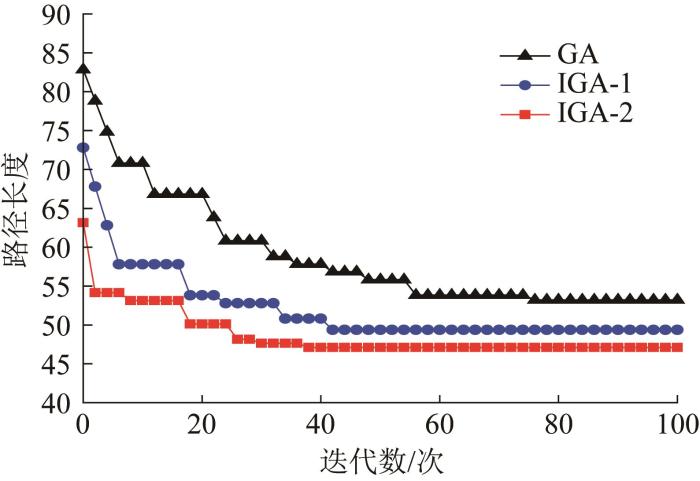
将传统GA与改进后的GA（IGA-1和IGA-2）进行对比，以验证其改进的有效性及优越性。基于GA、IGA-1和IGA-2的最优路径对比如图16所示，各算法的迭代曲线如图17所示。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 基于GA、IGA-1和IGA-2的最优路径对比

Fig.16 Comparison of optimal paths based on GA，IGA-1 and IGA-2

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 GA、IGA-1和IGA-2的迭代曲线对比

Fig.17 Comparison of iterative curves of GA, IGA-1 and IGA-2

根据图16和图17，得到GA、IGA-1和IGA-2的路径规划性能指标，如表3所示。结果显示，基于传统GA的最优路径长度为53.213，转弯次数为20。通过采用交叉概率改进后的IGA-1，最优路径长度缩短到49.355，转弯次数减少至19。对比结果表明，IGA-1通过自适应调整交叉概率显著提升了GA的收敛速度，并有效避免了局部最优解，增强了全局搜索能力。进一步对比IGA-2与IGA-1的性能，发现IGA-2所生成的最优路径的转弯次数虽有所增加，但最优路径长度缩短为47.113。综上，除转弯次数外，IGA-2对应的其余路径规划性能指标均优于IGA-1，表明其改进机制有效提升了GA的整体性能，并验证了自适应交叉概率与自适应变异概率的有效性。由此可知，相比于传统GA和IGA-1，IGA-2能够在更短的时间内获得最优解，且在收敛速度和路径质量上表现出显著优势。

表3 GA、IGA-1和IGA-2的路径规划性能对比

Table 3 Comparison of path planning performance of GA, IGA-1 and IGA-2

性能指标	GA	IGA-1	IGA-2
最优路径长度	53.213	49.355	47.113
平均路径长度	56.432	52.483	50.801
最优路径转弯次数	20	19	22
收敛次数	74	42	38

新窗口打开| 下载CSV

3.1.3　融合算法及其变体实验

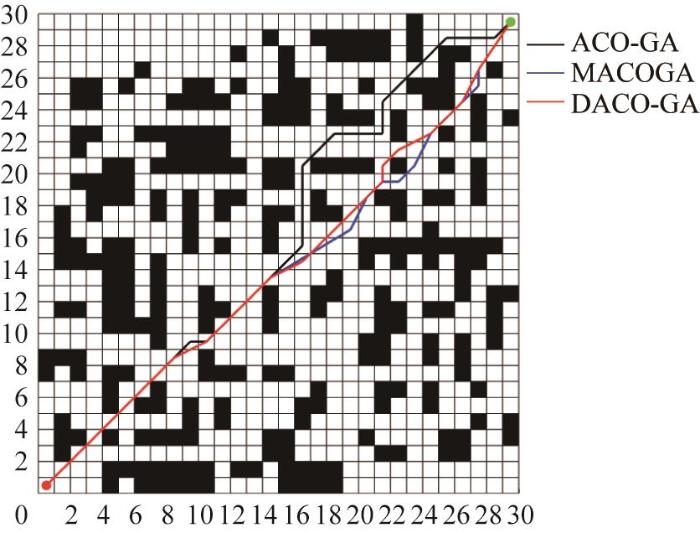
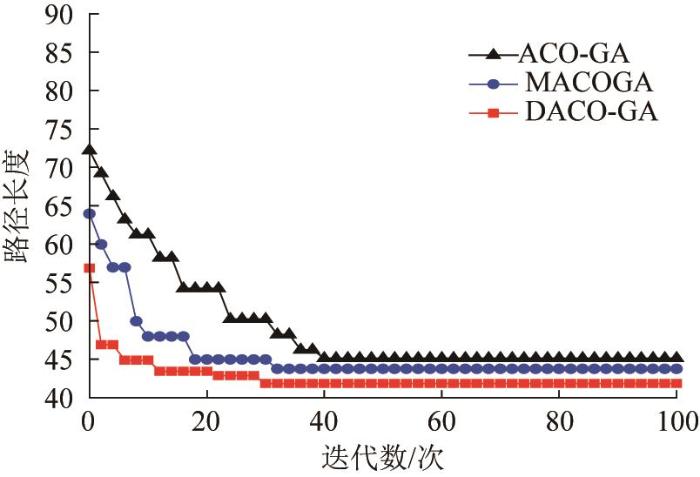
将传统ACO-GA与改进后的融合算法（MACOGA和DACO-GA）进行对比，以验证其改进的有效性及优越性。基于ACO-GA、MACOGA和DACO-GA的最优路径对比如图18所示，各算法的迭代曲线如图19所示。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 基于ACO-GA、MACOGA和DACO-GA的最优路径对比

Fig.18 Comparison of optimal paths based on ACO-GA, MACOGA and DACO-GA

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 ACO-GA、MACOGA和DACO-GA的迭代曲线对比

Fig.19 Comparison of iterative curves of ACO-GA, MACOGA and DACO-GA

根据图18和图19，得到ACO-GA、MACOGA和DACO-GA的路径规划性能指标，如表4所示。结果显示，与传统的ACO-GA相比，MACOGA在收敛速度和最优路径长度上均有所提升。与MACOGA相比，DACO-GA所生成路径的平均长度有所增加（47.895>45.094），但最优路径长度反而缩短（41.834<43.724）。这是因为DACO-GA中引入了动态调整机制，使得迭代后期路径的多样性有所增加，从而使最优路径长度得到改善。结合图19可知，DACO-GA在收敛速度上显著提升，初始阶段有10次ACO迭代，中间阶段有10次GA迭代，融合阶段迭代次数为10，说明DACO-GA能够快速收敛得到最优路径。

表4 ACO-GA、MACOGA和DACO-GA的路径规划性能对比

Table 4 Comparison of path planning performance of ACO-GA, MACOGA and DACO-GA

性能指标	ACO-GA	MACOGA	DACO-GA
最优路径长度	45.113	43.724	41.834
平均路径长度	49.941	45.094	47.895
最优路径转弯次数	9	11	10
收敛次数	40	32	30

新窗口打开| 下载CSV

综上所述，通过逐步引入并对比不同改进机制的性能，充分验证了引入自适应初始信息素浓度、动态挥发因子、自适应交叉概率和自适应变异概率、冗余节点删除机制以及动态融合策略等多项改进机制在提升算法性能方面的有效性。在路径长度、转弯次数、收敛速度等关键性能指标上，各项改进机制均表现出明显的提升优势。同时，在实验过程中并未发现各改进机制之间存在明显冲突，说明这些改进机制具有良好的独立性与协调性，能够协同提升DACO-GA的稳定性与全局优化能力。

3.2　不同静态环境下DACO-GA的性能对比

为了进一步评估DACO-GA在不同环境中的适应性，设计了4种不同静态环境的仿真地图，其特征如表5所示。在本实验中，起始点使用红点表示，坐标为（0.5, 0.5），位于地图的左下角；目标点使用绿点表示，坐标为（19.5, 19.5），位于地图的右上角。将DACO-GA与Dijkstra算法、A*算法和PSO算法进行仿真对比。由于Dijkstra算法、A*算法为确定性搜索，但DACO-GA所得解存在不确定性，因此本实验考察不同环境下最优路径的长度、转弯次数、总转弯角度以及平滑度。

表5 不同栅格地图的特征

Table 5 Characteristics of different raster maps

地图编号	特征	设计目标
1	矩形障碍物布置	评估算法在规则障碍物布局下的全局搜索能力、路径规划和转弯控制能力
2	固定通道障碍物布置	测试算法在狭窄通道和复杂障碍物布局下的局部搜索能力和避障性能
3	U形障碍物布置	考察算法在U形障碍物环境中的路径规划和转弯控制能力
4	阶梯形障碍物布置	评估算法在阶梯形障碍物环境中的适应性和路径规划能力

新窗口打开| 下载CSV

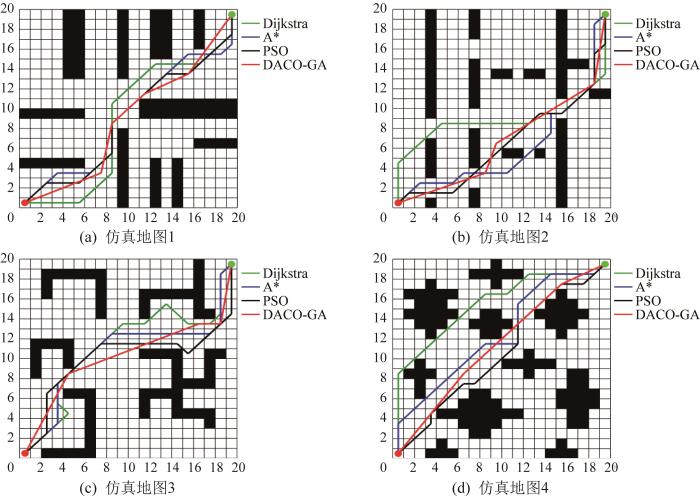
在4个不同的栅格地图中，基于DACO-GA、Dijkstra算法、A*算法和PSO算法的最优路径规划结果如图20所示，各算法的路径规划性能对比如表6所示。结果显示：DACO-GA在路径规划中表现出显著优势。在路径长度方面，DACO-GA所生成的最优路径在所有环境中均优于Dijkstra算法、A*算法和PSO算法。例如：在栅格地图1中，DACO-GA所生成的最优路径的长度为28.641，明显比其他算法所生成的最优路径短（28.641<29.799<30.385<32.142）。在其他环境中，DACO-GA也保持了较短的路径长度，表现出较强的适应性和路径规划能力。此外，DACO-GA在转弯次数方面也表现优异。例如：在栅格地图1中，DACO-GA所生成的最优路径的转弯次数为4，明显低于其他算法；在栅格地图4中，DACO-GA所生成的最优路径的转弯次数仅为2，表现出优越的转弯控制能力。另外，DACO-GA所生成的最优路径的总转弯角度显著低于其他算法。例如：在栅格地图1中，DACO-GA所生成的最优路径的转弯角度为137.361°，明显低于Dijkstra算法、A*算法和PSO算法所生成的路径（依次为270°、315°、315°）。此外，DACO-GA在路径平滑度方面的表现也尤为突出，特别是在布置有阶梯形障碍物的环境中，其所生成的最优路径的平滑度为0.683，远高于其他算法（Dijkstra算法、A*算法和PSO算法所生成路径的平滑度分别为0.203、0.154和0.137）。由此可知，DACO-GA能够有效减少路径的转弯次数并减小转弯角度，且保持较高的路径平滑性。综上，DACO-GA能够适应各种复杂环境，在不同障碍物类型下均能有效找到最优路径，并通过改进机制显著提高路径平滑度，具有较高的适应性。

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 不同环境下基于各算法的最优路径对比

Fig.20 Comparison of optimal paths based on various algorithms in different environments

表6 不同环境下各算法的路径规划性能对比

Table 6 Comparison of path planning performance of various algorithms in different environments

性能指标	算法	仿真地图
性能指标	算法	1	2	3	4
路径长度	Dijkstra	32.142	32.723	34.042	31.556
	A*	30.385	31.556	32.142	30.971
	PSO	29.799	30.385	31.971	28.627
	DACO-GA	28.641	29.594	30.027	27.800
转弯次数	Dijkstra	6	6	10	5
	A*	7	9	6	6
	PSO	7	7	6	8
	DACO-GA	4	3	3	2
总转弯角度/(°)	Dijkstra	270.000	270.000	540.000	225.000
	A*	315.000	450.000	270.000	315.000
	PSO	315.000	315.000	315.000	360.000
	DACO-GA	137.361	137.064	143.973	26.565
平滑度	Dijkstra	0.175	0.175	0.096	0.203
	A*	0.153	0.113	0.175	0.154
	PSO	0.153	0.154	0.154	0.137
	DACO-GA	0.294	0.295	0.285	0.683

注：各性能指标均对应最优路径。

新窗口打开| 下载CSV

3.3　动态环境下DACO-GA的性能验证

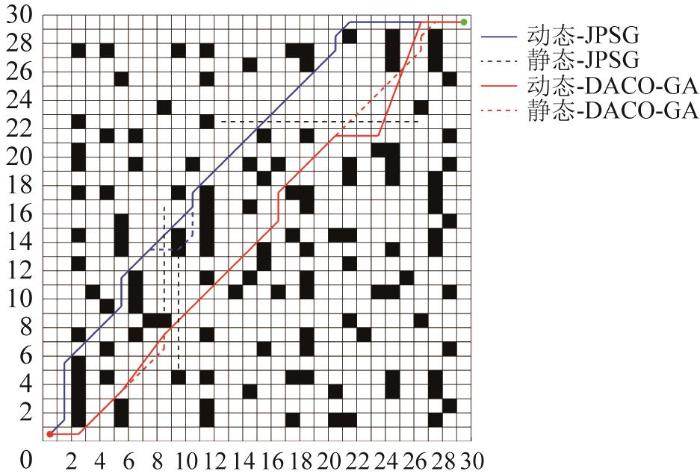
上述仿真实验均在静态环境下进行，实验结果验证了各项改进机制对算法性能的提升效果。然而在实际应用中，移动机器人往往处于动态复杂的工作环境中，需面对如移动障碍物、实时环境变化等挑战。为进一步评估DACO-GA在动态环境中的适应性与鲁棒性，设计了基于动态障碍物的路径规划仿真实验。环境模型同样采用二维栅格地图，并设置多个动态障碍物以固定速度沿固定方向运动，以模拟动态干扰因素。机器人以1格/s的速度匀速移动，感知半径设为3格；动态障碍物的移动速度为2格/s。根据两者的速度与位置关系，计算机器人与障碍物可能发生碰撞的时刻，从而评估算法的实时性以及其所规划路径的可行性。本节实验将DACO-GA与文献[16]中的JPSG（jump point search-genetic，跳点搜索-遗传）算法进行对比。在相同的地图场景下，分别测试动态障碍物与静态障碍物环境下2种算法的路径规划效果。通过横向对比路径的长度、转弯情况及可行性，来验证DACO-GA在动态环境中的稳定性与适应能力。基于DACO-GA和JPSG算法的最优路径对比如图21所示，2种算法的路径规划性能指标如表7所示。

图21

新窗口打开| 下载原图ZIP| 生成PPT

图21 基于DACO-GA和JPSG算法的最优路径对比

Fig.21 Comparison of optimal paths based on DACO-GA and JPSG algorithms

表7 DACO-GA和JPSG算法的路径规划性能对比

Table 7 Comparison of path planning performance of DACO-GA and JPSG algorithms

障碍物类型	算法	最优路径长度	平均路径长度	最优路径转弯次数	最优路径转弯角度/(°)	最优路径平滑度	收敛次数
动态障碍物	JPSG	45.699	47.756	9	405	0.124	48
动态障碍物	DACO-GA	44.757	47.214	8	335	0.146	41
静态障碍物	JPSG	46.870	47.981	11	495	0.104	45
静态障碍物	DACO-GA	43.355	45.208	8	360	0.138	37

新窗口打开| 下载CSV

图21与表7结果表明，在静态障碍物环境下，DACO-GA在路径规划质量和收敛速度方面显著优于JPSG算法：基于DACO-GA的最优路径长度为43.355，较JPSG算法缩短了3.515；转弯次数降至8，总转弯角度为360°，明显优于JPSG算法对应的11次和495°。此外，DACO-GA所规划路径的平滑度达到0.138，高于JPSG算法的0.104，即本文算法所生成的路径更加连贯、平稳。在动态障碍物环境中，DACO-GA同样展现出优异的鲁棒性与适应性，其在面对持续移动的障碍物干扰时，仍能稳定生成高质量路径，最优路径长度为44.757，优于JPSG算法的45.699；仅用41次迭代即能实现收敛，收敛速度更快。在转弯角度控制方面，DACO-GA所生成路径的总转弯角度为335°，平滑度提升至0.146，表明其所规划的路径更为平滑，有助于提升移动机器人动态避障的可靠性。由此可知，所提出的DACO-GA在动、静态环境下均能实现高效、稳定的路径规划，且鲁棒性和适应性较高。

4 结论

针对传统ACO-GA算法在路径规划中存在路径不平滑、收敛速度慢以及易陷入局部最优等问题，本文提出了一种DACO-GA算法。该算法通过在ACO中引入目标引导的初始信息素分布策略和动态挥发因子，有效地提高了算法早期阶段的收敛速度；在GA中引入了自适应的交叉概率和变异概率，增强了解的多样性和全局搜索能力；在算法融合阶段，构建了以路径多样性和改进幅度为判断标准的动态主导控制机制，实现了ACO与GA的灵活切换与协同优化。此外，还引入了基于几何分析的冗余节点删除算法，显著提升了路径平滑性。通过静态与动态环境下的多组对比实验，验证了DACO-GA在路径长度、转弯次数、转弯角度和平滑度等多个关键性能指标上均优于Dijkstra、A*、PSO和JPSG等经典算法，展现出良好的收敛速度和环境适应性。尤其是在动态障碍物环境中，DACO-GA能保持较高的鲁棒性，验证了其在复杂场景中的稳定性和实用价值。然而，DACO-GA仍存在计算复杂度偏高的问题，在面对大规模动态环境或多约束场景时，其资源占用率和实时性仍有优化空间。未来，将重点提升DACO-GA的运行效率，并探索其与深度强化学习等智能方法的融合策略，以提升其在复杂任务中的实用性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

崔衡，马宗方，宋琳，等.

基于连续顶点分区的混凝土3D打印路径规划算法

［J］. 工程设计学报， 2024， 31（3）： 271-279.